Numerical Investigation of Fractional Step-Down ELS Option
Abstract
1. Introduction
2. Fractional Step-Down ELS Model
2.1. Fractional Brownian Motion
- , for any .
- , for any .
- Fractional Brownian motion has self-similarity. For any and , and have the same finite-dimensional distribution.
- When , it is the standard Brownian motion. When H > 0.5, has a long-term dependence. When , has anti persistence.
2.2. Fractional Step-Down ELS Model of One Asset
2.3. Fractional Step-Down ELS Model of Two Assets
2.4. Fractional Step-Down ELS Model of Three Assets
3. Numerical Method
3.1. One Underlying Asset
3.2. Two Underlying Assets
3.3. Three Underlying Assets
4. Numerical Experiments
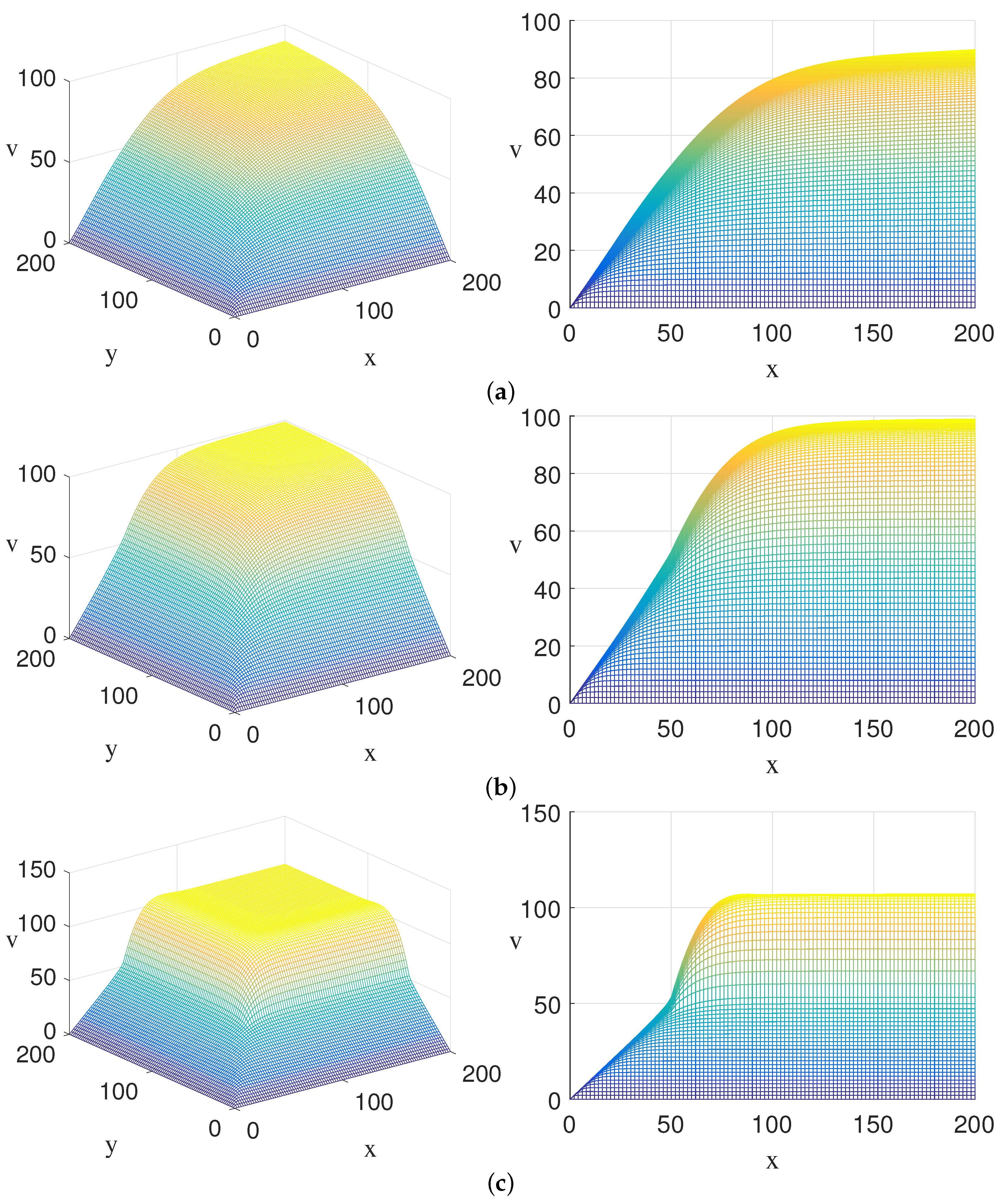
4.1. One Underlying Asset
4.2. Two Underlying Assets
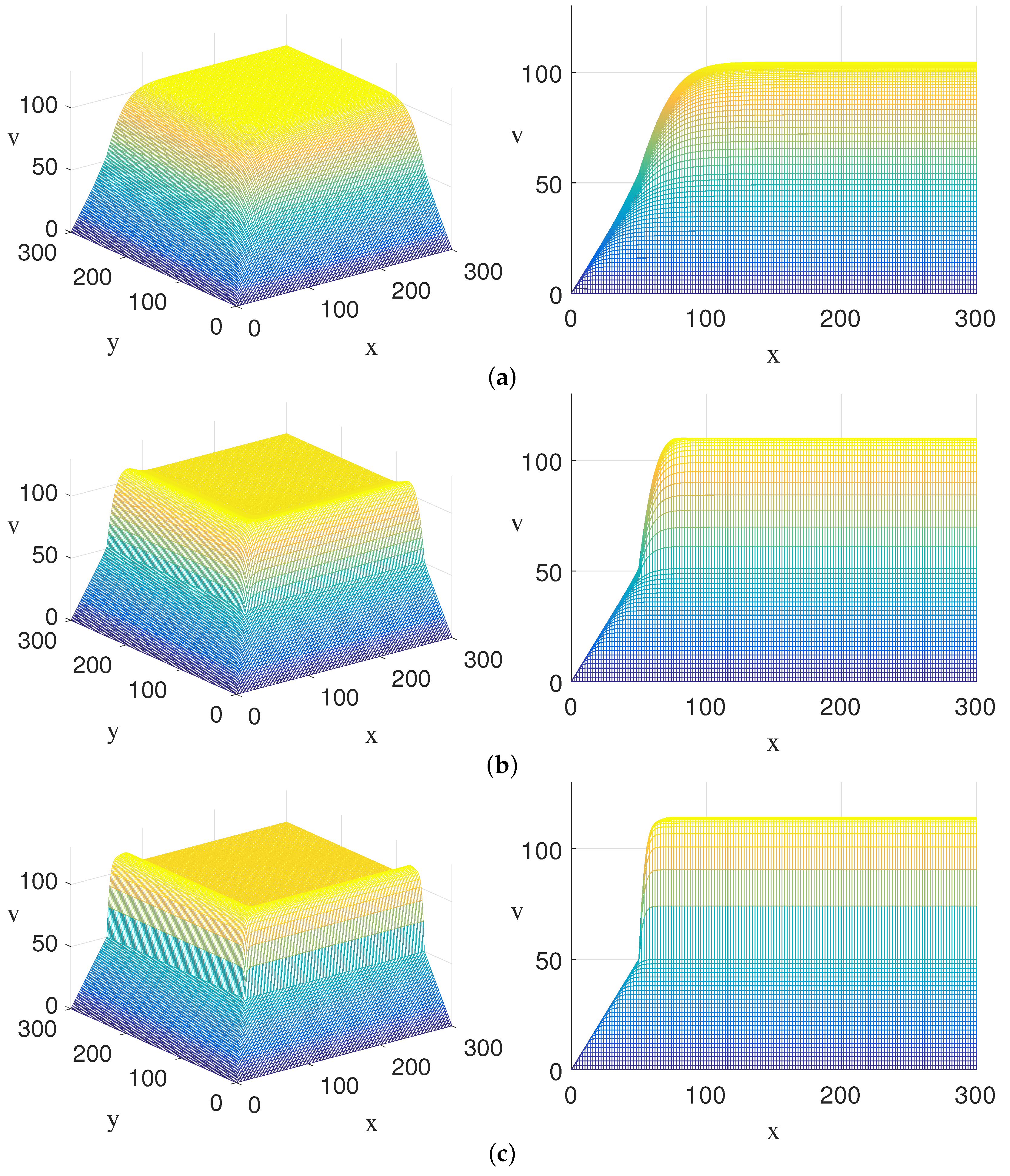
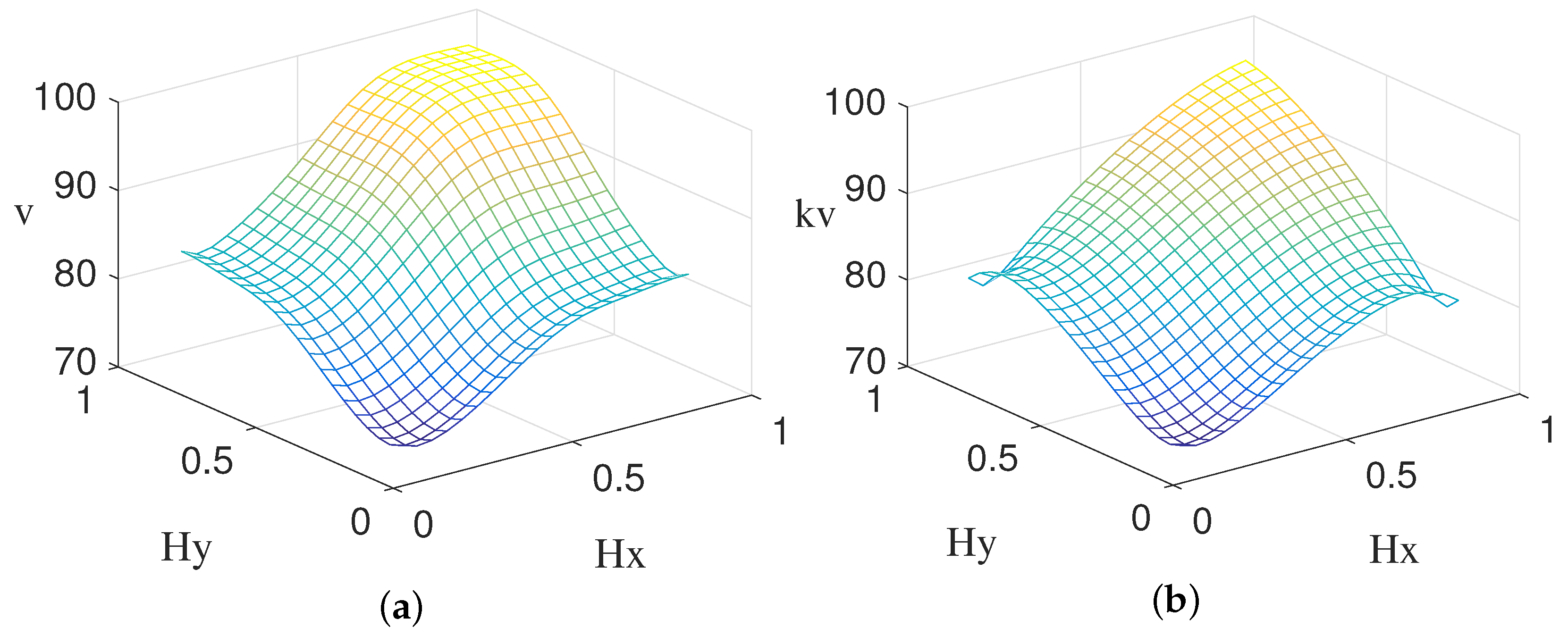
4.3. Three Underlying Assets
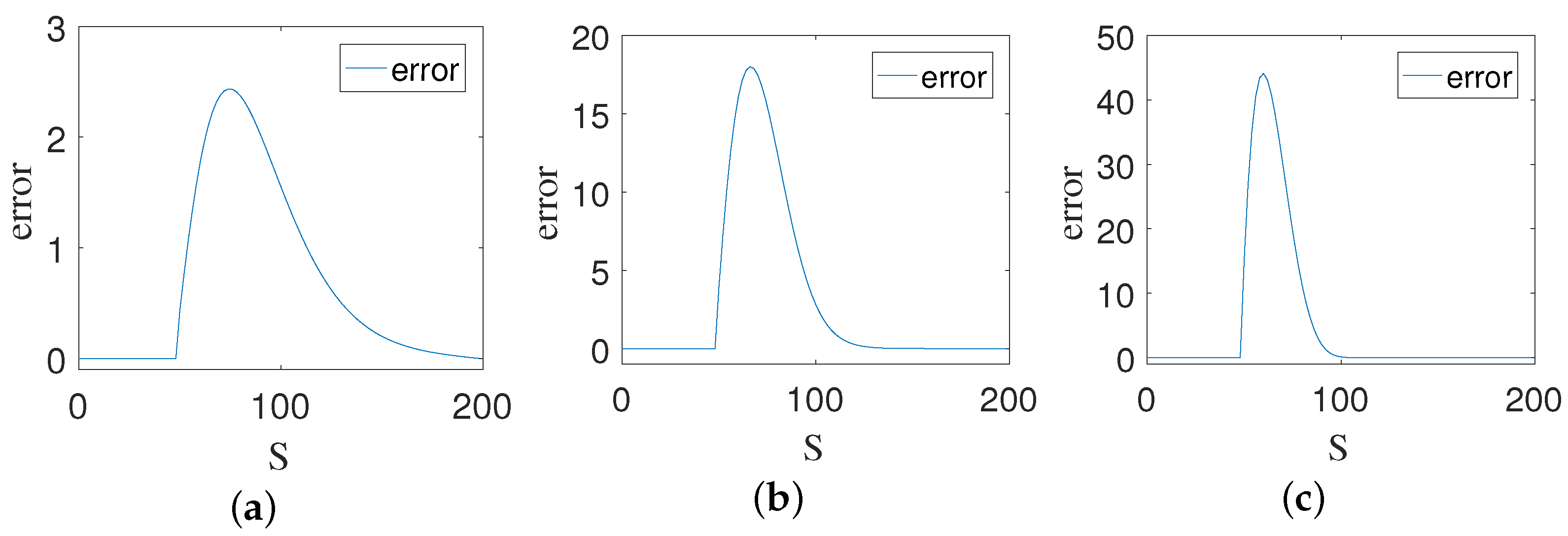
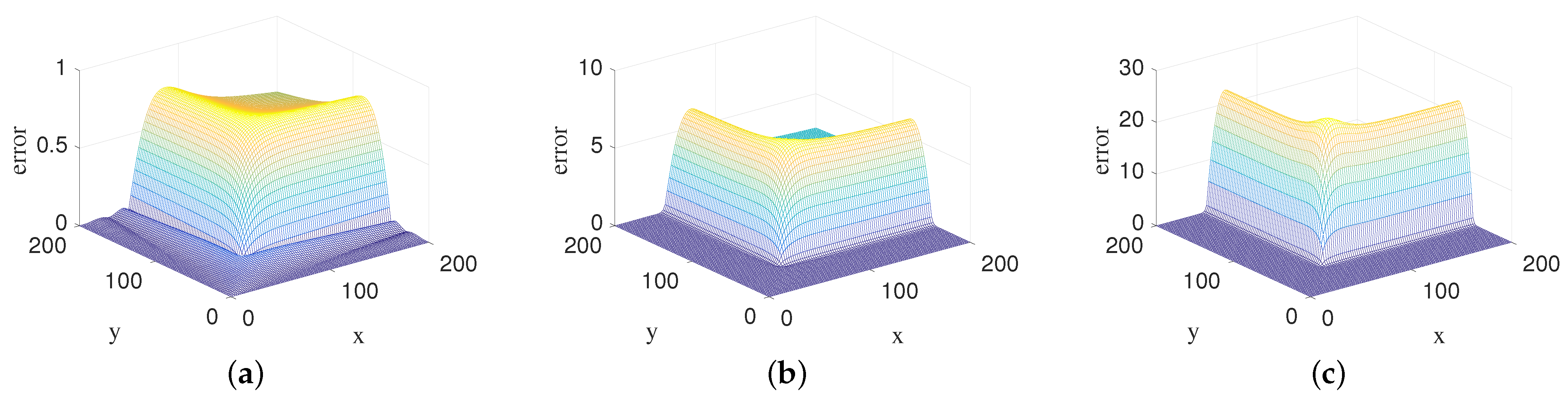
4.4. Empirical Evidence for Well-Posed of the Model and Validation of the Solution
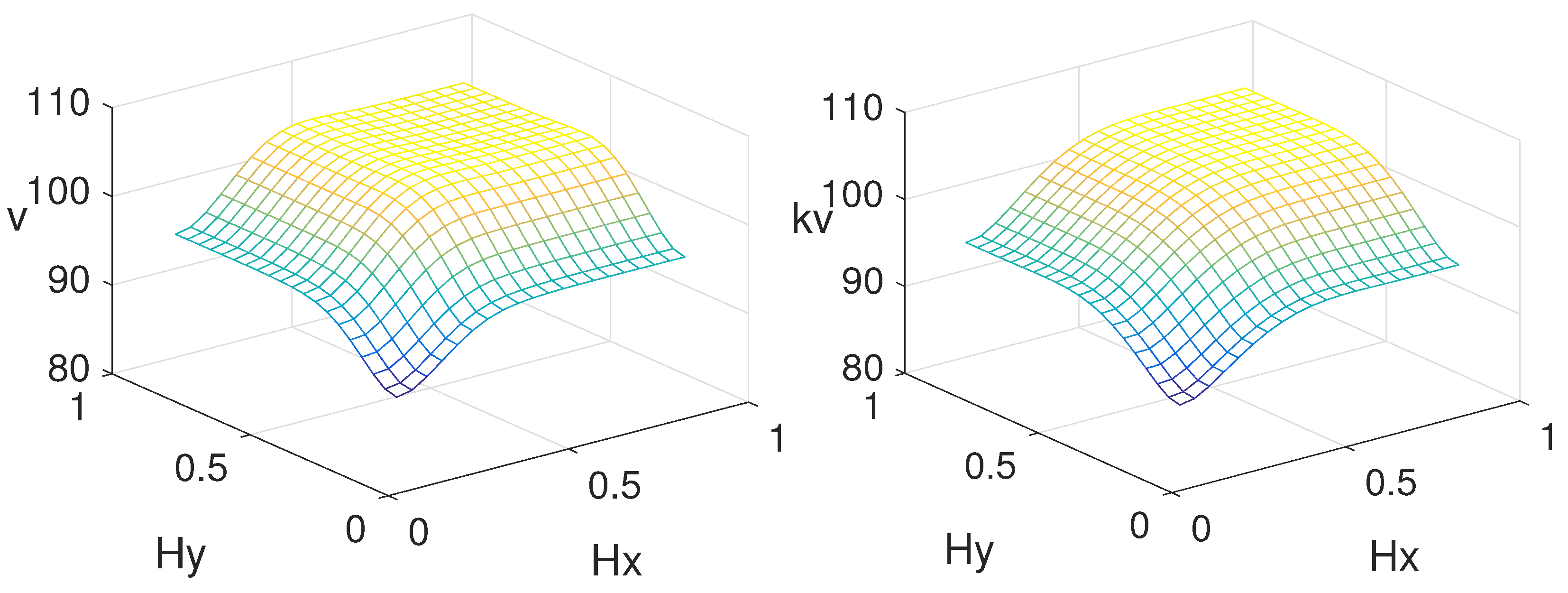
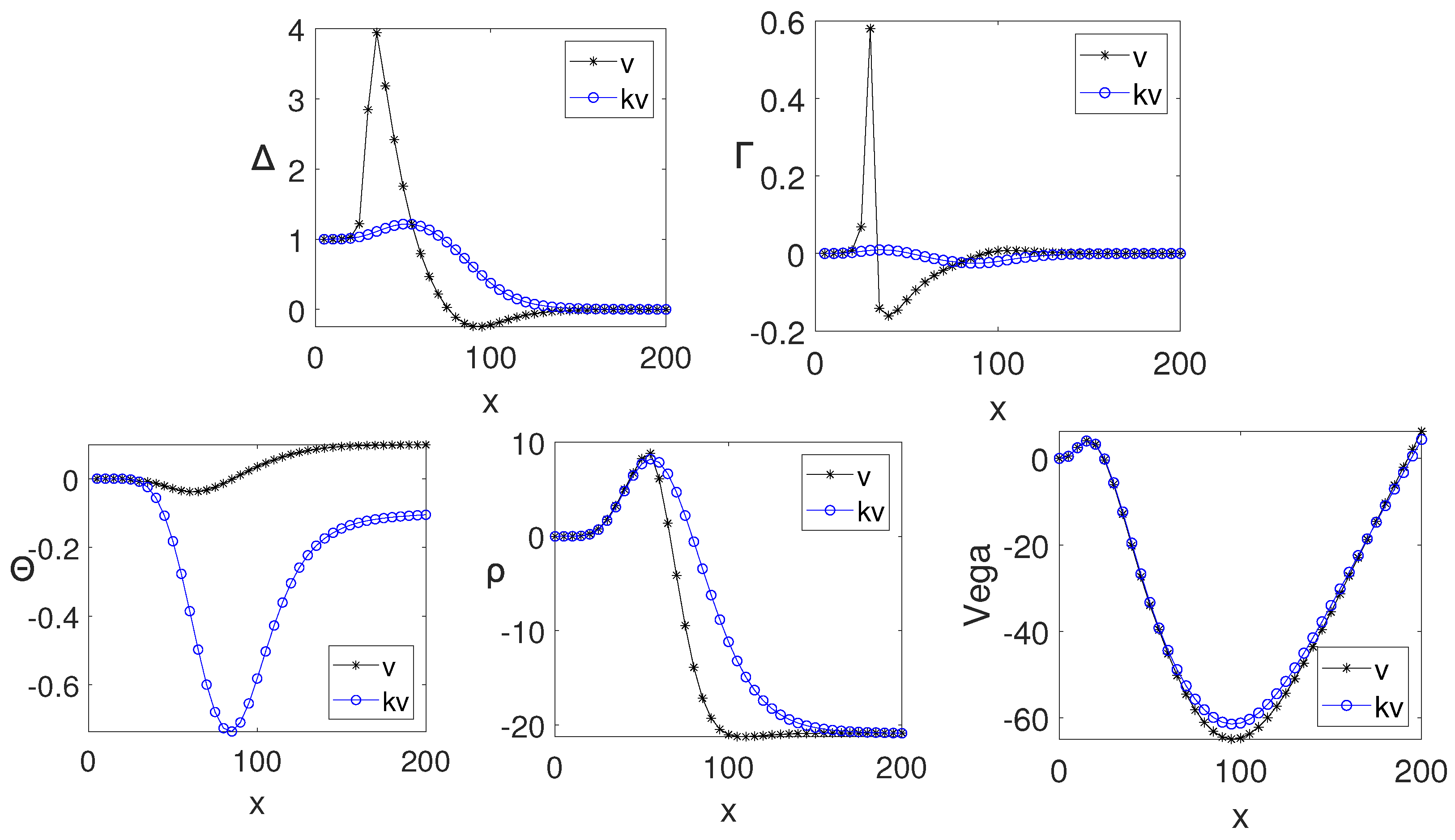
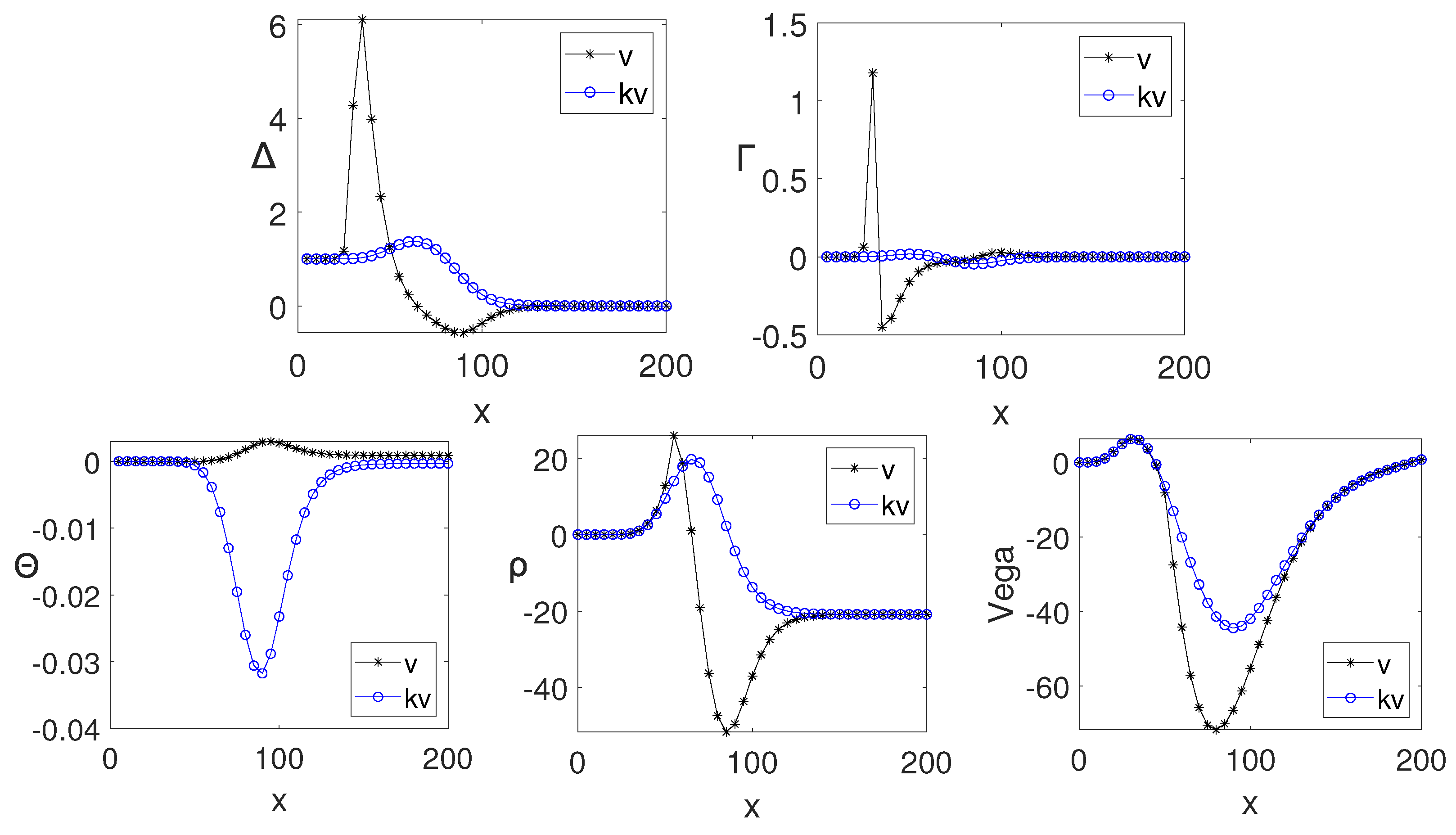
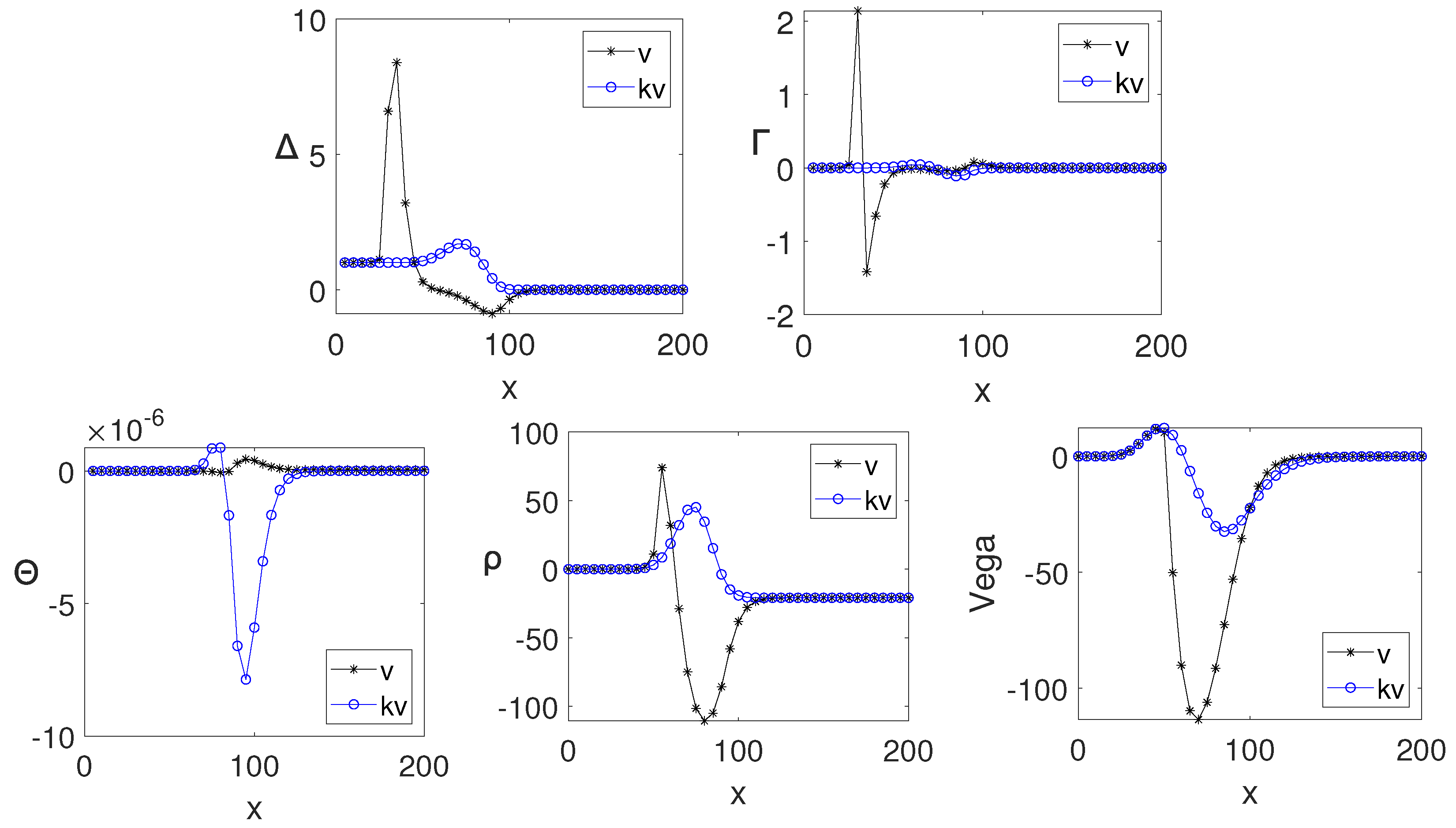
4.5. Greeks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, A.H.; Kensinger, J.W. An analysis of market-index certificates of deposit. J. Financ. Serv. Res. 1990, 4, 93–110. [Google Scholar] [CrossRef]
- Baubonis, C.; Gastineau, G.L.; Purcell, D. The Banker’s Guide to Equity-Linked Certificates of Deposit. J. Deriv. 1993, 1, 87–95. [Google Scholar] [CrossRef]
- Kim, J.; Kim, T.; Jo, J.; Choi, Y.; Lee, S.; Hwang, H.; Yoo, M.; Jeong, D. A practical finite difference method for the three-dimensional Black-Scholes equation. Eur. J. Oper. Res. 2016, 252, 183–190. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, J. A comparison study of ADI and operator splitting methods on option pricing models. J. Comput. Appl. Math. 2013, 247, 162–171. [Google Scholar] [CrossRef]
- Bachelier, L. Theoryofspeculation. In The Random Characterof Stock Market; Ksotner, P., Ed.; MIT Press: Cambridge, NA, USA, 1900. [Google Scholar]
- Sumuelson, P.A. Rational theory of warrant pricing. Ind. Manag. Rev. 1965, 6, 13–31. [Google Scholar]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motion, fractional noises and applications. SIAM Rev. 1968, 10, 422–436. [Google Scholar] [CrossRef]
- Hazhir, A.; Mahsan, T.K.; Hamid, K. Option pricing under finite moment log stable process in a regulated market: A generalized fractional path integral formulation and Monte Carlo based simulation. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105345. [Google Scholar]
- Lin, S.; He, J.X. A regime switching fractional Black–Scholes model and European option pricing. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105222. [Google Scholar] [CrossRef]
- Grzegorz, K.; Marcin, M. A computational weighted finite difference method for American and barrier options in subdiffusive Black–Scholes model. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105676. [Google Scholar]
- Peter, E.E. Fractal Structure in the Captial Market. Financ. Anal. J. 1989, 45, 32–37. [Google Scholar] [CrossRef]
- Karatzas, I.; Shreve, S.E. Brownian motion and stochastic calculus. Acta Appl. Math. 1991, 24, 197–200. [Google Scholar]
- Radu, V. Analysis of the Romanian Capital Market Using the Fractal Dimension. Fractal Fract. 2022, 6, 564. [Google Scholar] [CrossRef]
- Li, Y. Multifractal Characteristics of China’s Stock Market and Slump’s Fractal Prediction. Fractal Fract. 2022, 6, 499. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Zhang, S. A New Homotopy Transformation Method for Solving the Fuzzy Fractional Black–Scholes European Option Pricing Equations under the Concept of Granular Differentiability. Fractal Fract. 2020, 6, 286. [Google Scholar] [CrossRef]
- Sarraj, M.; Ben Mabrouk, A. The Systematic Risk at the Crisis—A Multifractal Non-Uniform Wavelet Systematic Risk Estimation. Fractal Fract. 2021, 5, 135. [Google Scholar] [CrossRef]
- Necula, C. Option Pricing in a Fractional Brownina Motion Environment. Math. Rep. 2002, 2, 259–273. [Google Scholar]
- Liu, S.Y.; Yang, X.Q. Pricing of european option on dividend-paying stock in a fractional Brownian motion environment. Math. Econ. 2002, 19, 35–39. [Google Scholar]
- Murwaningtyas, C.E.; Kartiko, S.H.; Gunardi Suryawan, P.H. European option pricing by using a mixed fractional brownian motion. J. Phys. Conf. Ser. 2019, 1180, 012081. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Y.; Chen, W.B.; Shao, W.; Tang, W.W. Equitylinked securities option pricing by fractional brownian motion. Chaos Solitons Fractals 2021, 144, 110716. [Google Scholar] [CrossRef]
- Ali, A.; Abbas, M.; Akram, T. New group iterative schemes for solving the two-dimensional anomalous fractional sub-diffusion equation. J. Math. Comp. Sci. 2021, 22, 119–127. [Google Scholar] [CrossRef]
- Oderinu, R.A.; Owolabi, J.A.; Taiwo, M. Approximate solutions of linear time-fractional differential equations. J. Math. Comput. Sci. 2023, 29, 60–72. [Google Scholar] [CrossRef]
- Nikan, O.; Golbabai, A.; Machado, J.A.; Nikazad, T. Numerical solution of the fractional Rayleigh–Stokes model arising in a heated generalized second-grade fluid. Eng. Comput. 2021, 37, 1751–1764. [Google Scholar] [CrossRef]
- Golbabai, A.; Ahmadian, D.; Milev, M. Radial basis functions with application to finance: American put option under jump diffusion. Math. Comput. Model. 2012, 55, 1354–1362. [Google Scholar] [CrossRef]
- Golbabai, A.; Nikan, O.; Nikazad, T. Numerical investigation of the time fractional mobile-immobile advection-dispersion model arising from solute transport in porous media. Int. J. Appl. Comput. Math. 2019, 5, 1–22. [Google Scholar] [CrossRef]
- Golbabai, A.; Nikan, O. A computational method based on the moving least-squares approach for pricing double barrier options in a time-fractional Black–Scholes model. Comput. Econ. 2020, 55, 119–141. [Google Scholar] [CrossRef]
- Golbabai, A.; Nikan, O.; Nikazad, T. Numerical analysis of time fractional Black–Scholes European option pricing model arising in financial market. Comput. Appl. Math. 2019, 38, 1–24. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Tenreiro Machado, J.A. Localized kernel-based meshless method for pricing financial options underlying fractal transmission system. Mathematical Methods in the Applied Sciences. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Hu, Y.; Oksendal, B. Fractional white noise calculus and applications to finance. In Infinite Dimensional Analysis Quantum Probability and Related Topics; World Scientific: Singapore, 2003; Volume 6(01), pp. 1–32. [Google Scholar]
- Duffy, D.J. Finite Difference Methods in Financial Engineering: A Partial Differential Equation Approach, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2006. [Google Scholar]
- Jeong, D.; Wee, I.S.; Kim, J. An operator splitting method for pricing the ELS option. J. Korean Soc. Ind. Appl. Math. 2010, 14, 175–187. [Google Scholar]
- Barunik, J.; Kristoufek, L. On Hurst exponent estimation under heavy-tailed distributions. Phys. A 2010, 389, 3844–3855. [Google Scholar] [CrossRef]
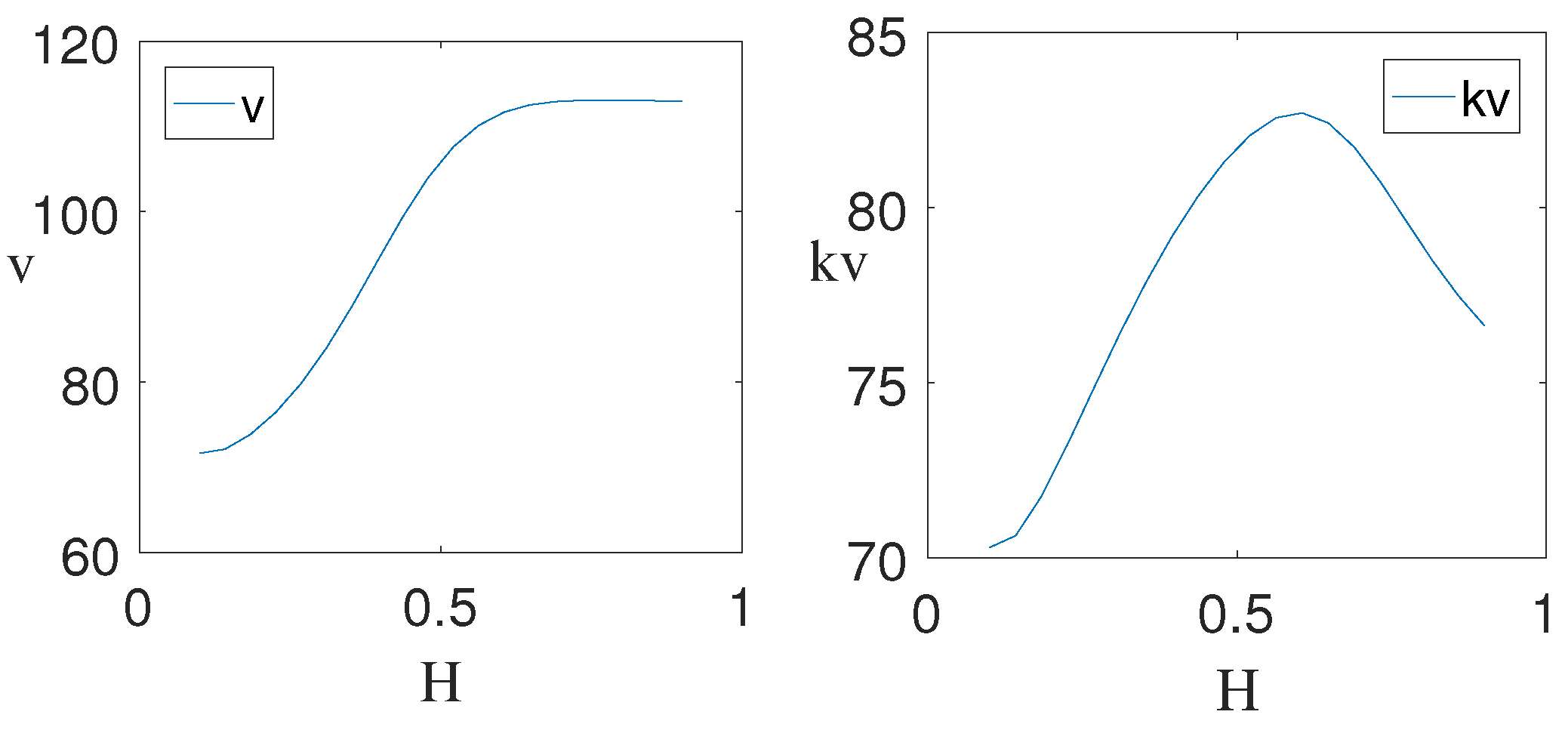





| Hurst Exponent | Strike Price | Underlying Asset Price |
|---|---|---|
| H | K | S |
| Maturity | Knock-in-barrier | Dummy |
| T | D | d |
| Numer of observation dates | Face value | Strike date |
| n | F | |
| Volatility | Risk-free rate | Coupon rate |
| r |
| KOSPI200 | EUROSTOXX50 | S&P500 |
|---|---|---|
| 0.4946 | 0.4941 | 0.4870 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Wen, S.; Shao, W.; Wang, J. Numerical Investigation of Fractional Step-Down ELS Option. Fractal Fract. 2023, 7, 126. https://doi.org/10.3390/fractalfract7020126
Wu X, Wen S, Shao W, Wang J. Numerical Investigation of Fractional Step-Down ELS Option. Fractal and Fractional. 2023; 7(2):126. https://doi.org/10.3390/fractalfract7020126
Chicago/Turabian StyleWu, Xinpei, Shuai Wen, Wei Shao, and Jian Wang. 2023. "Numerical Investigation of Fractional Step-Down ELS Option" Fractal and Fractional 7, no. 2: 126. https://doi.org/10.3390/fractalfract7020126
APA StyleWu, X., Wen, S., Shao, W., & Wang, J. (2023). Numerical Investigation of Fractional Step-Down ELS Option. Fractal and Fractional, 7(2), 126. https://doi.org/10.3390/fractalfract7020126






