Lie Symmetries and Third- and Fifth-Order Time-Fractional Polynomial Evolution Equations
Abstract
1. Introduction
2. Fractional Calculus and Symmetries
3. Symmetry Analysis
4. Reductions and Power Series Solutions
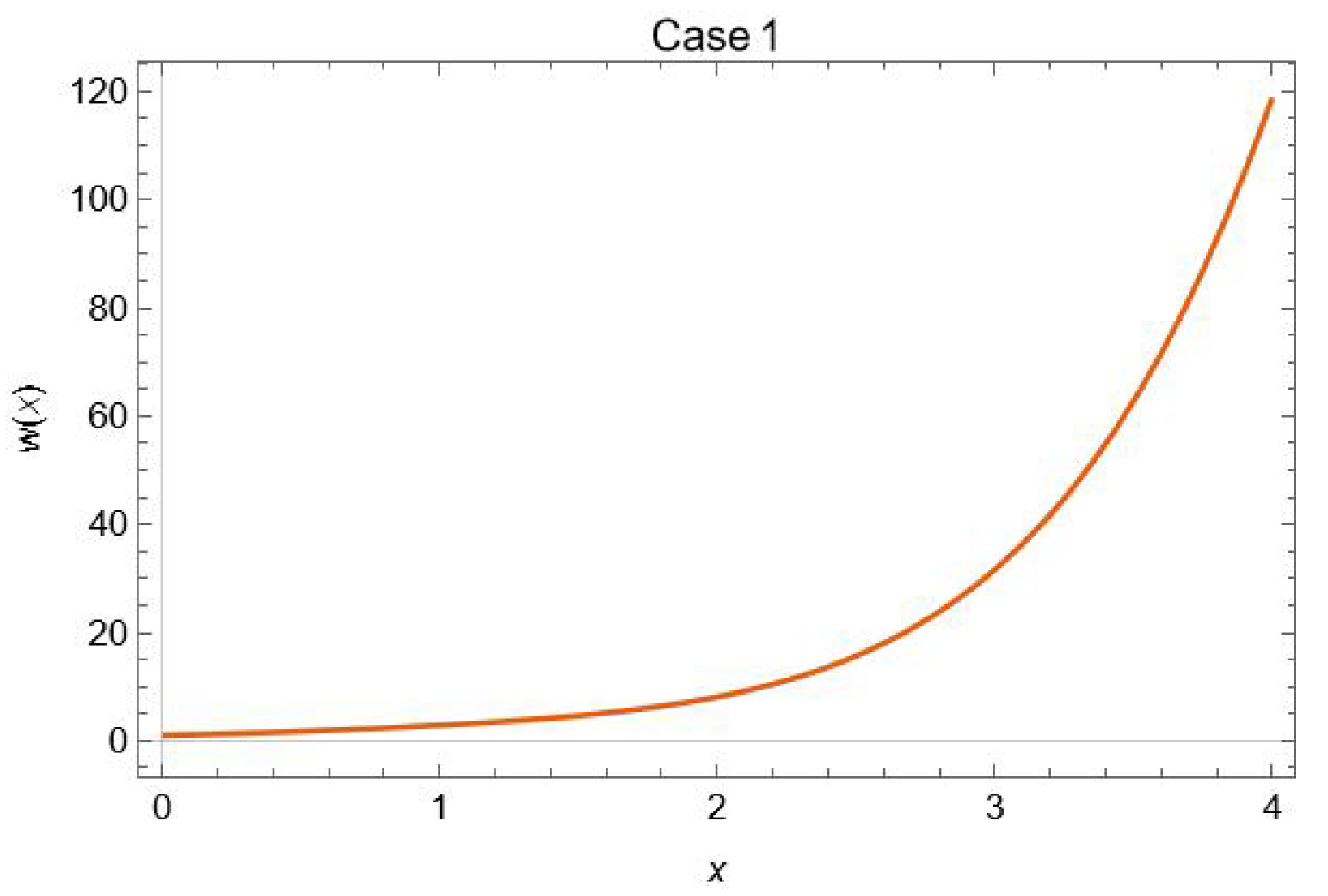
4.1. Case 1
Testing for Convergence
4.2. Case 2
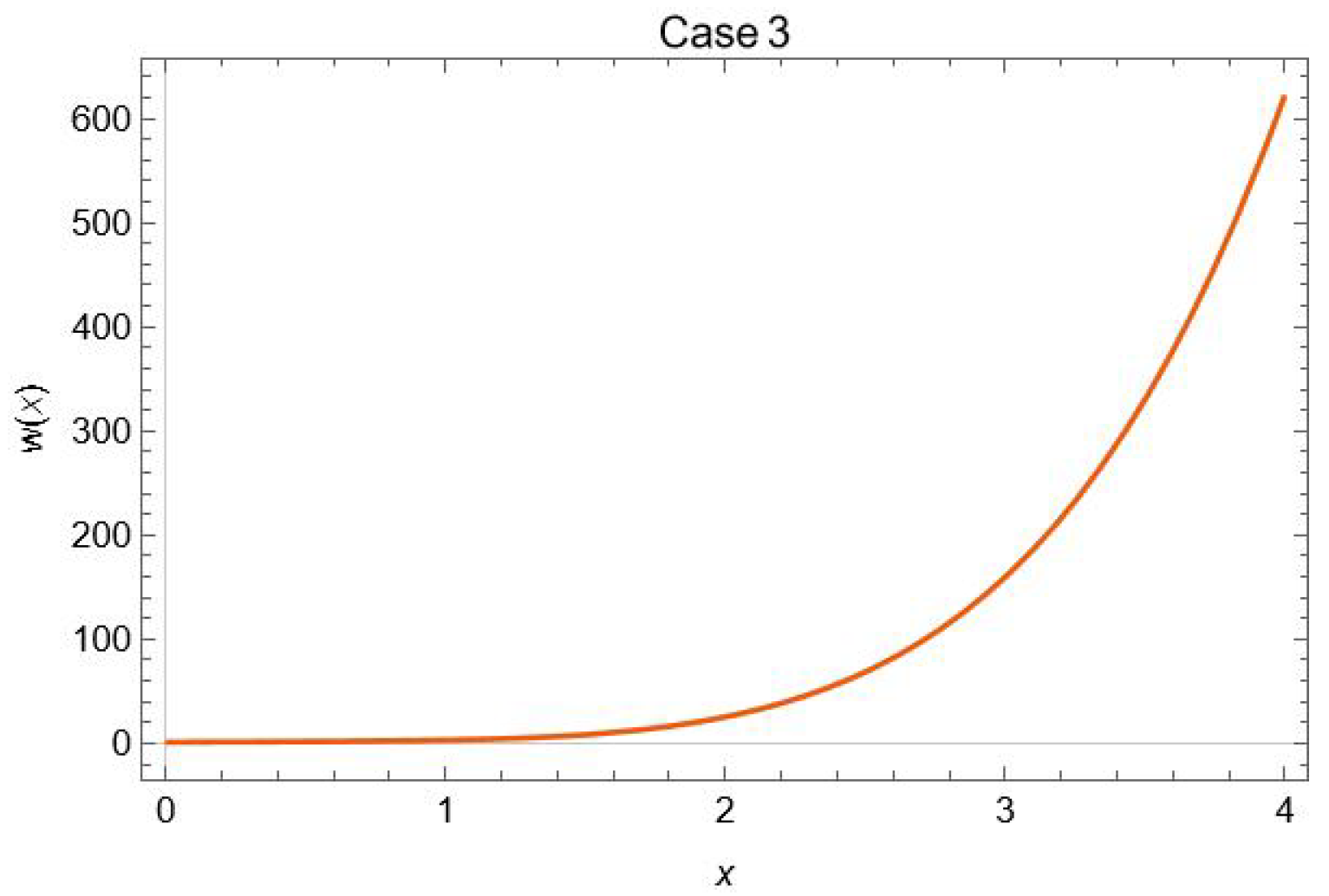
4.3. Case 3
4.4. Case 4
4.5. Case 5
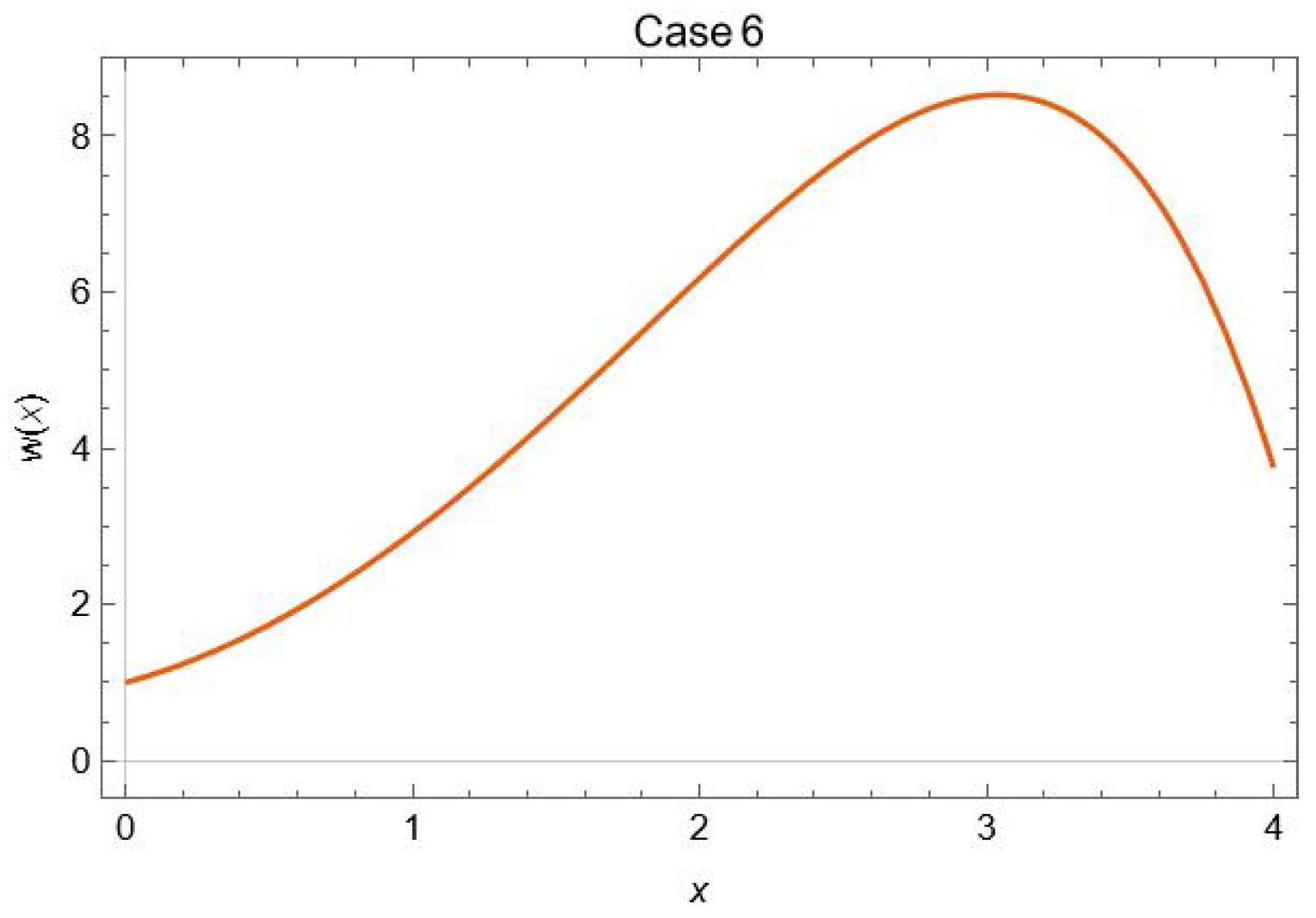
4.6. Case 6
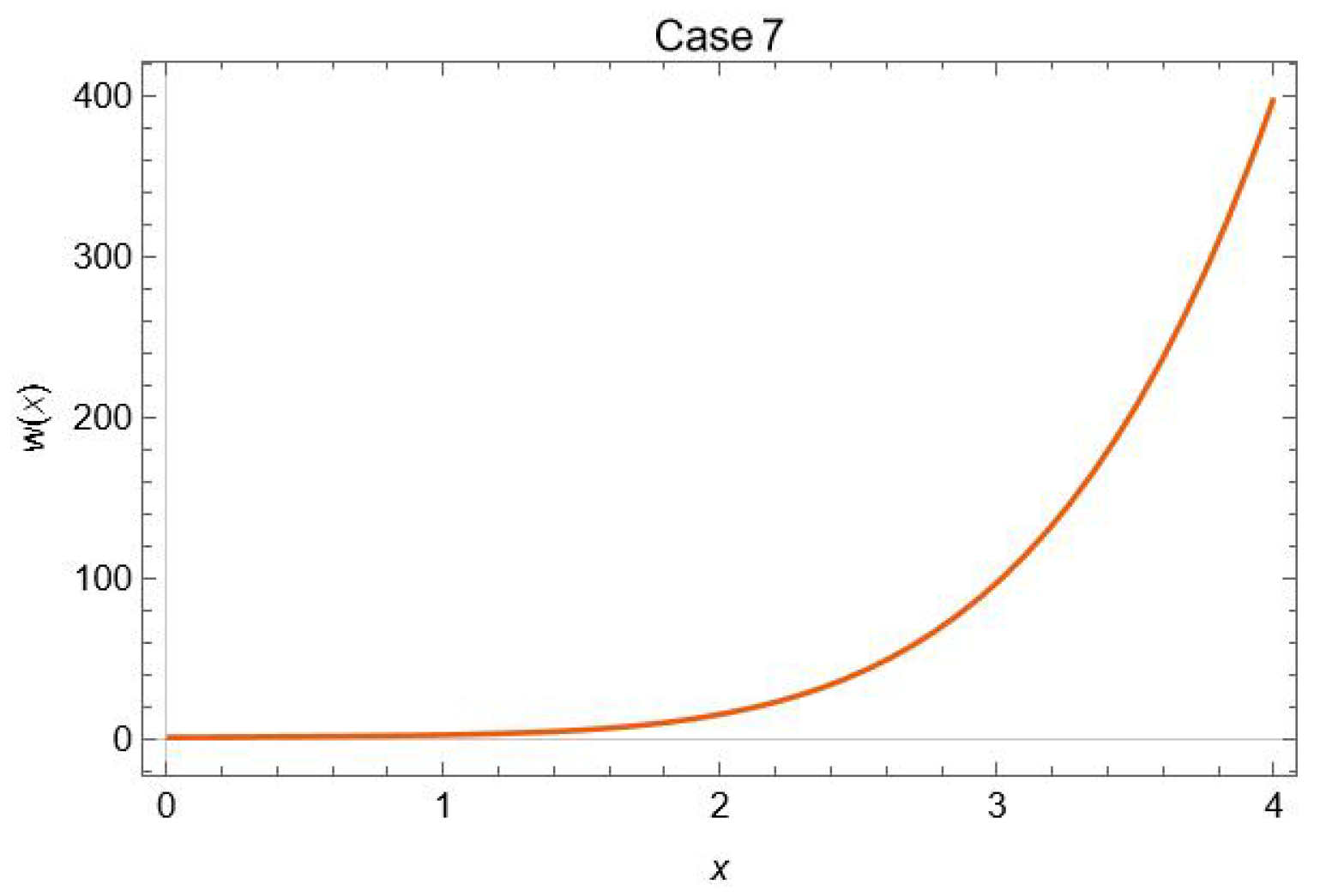
4.7. Case 7
4.8. Case 8
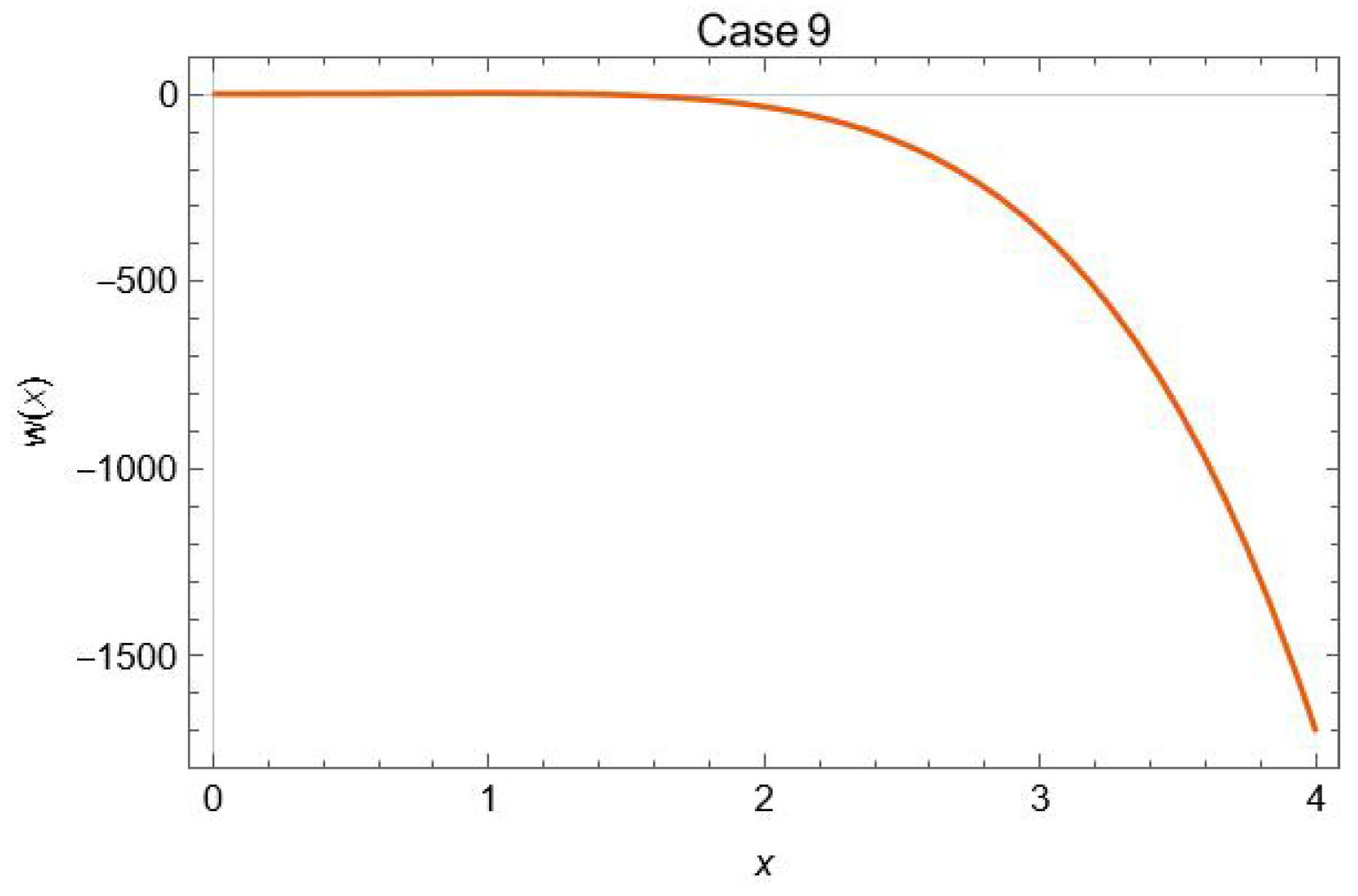
4.9. Case 9
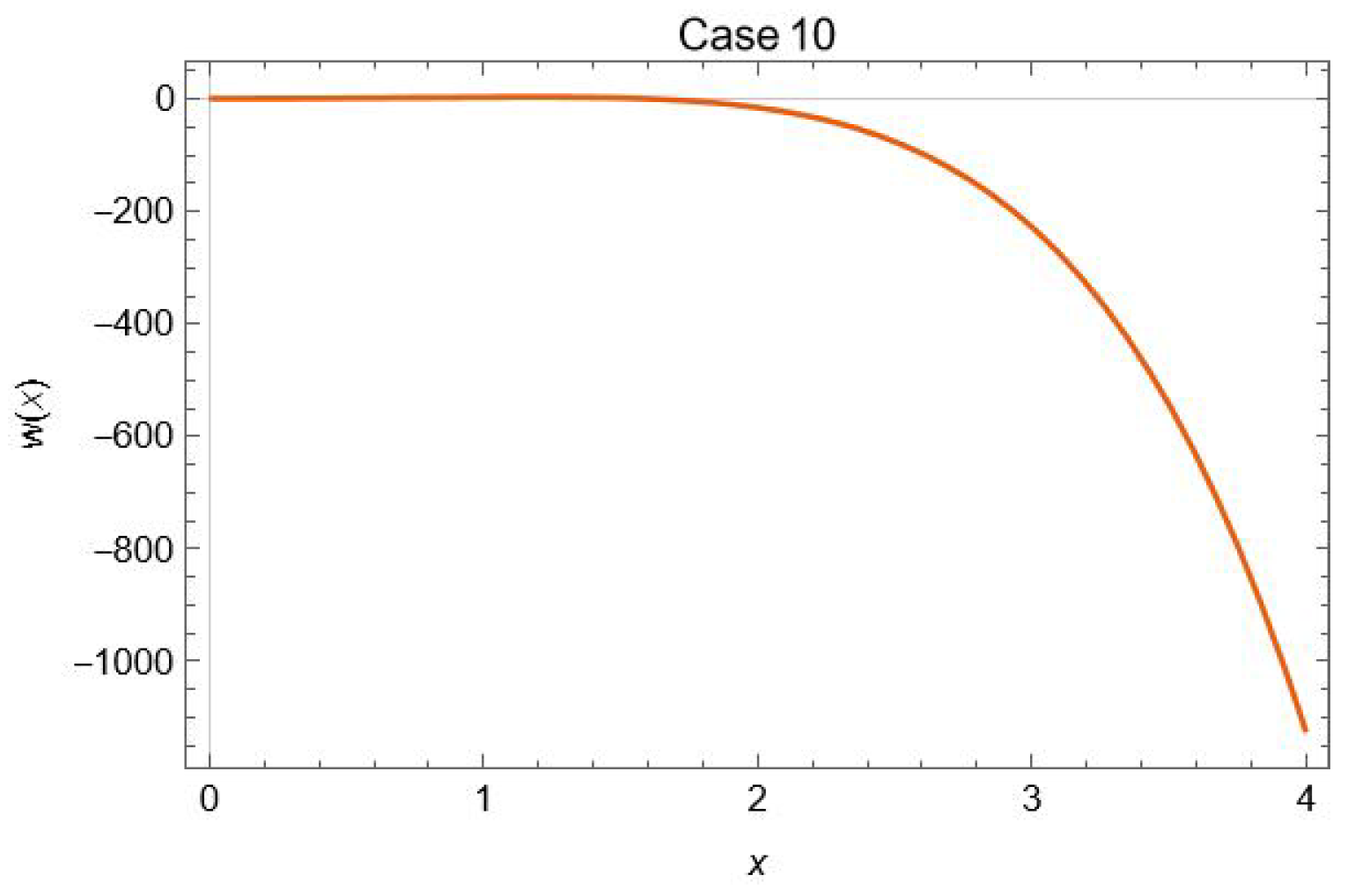
4.10. Case 10
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fujimoto, A.; Watanabe, Y. Polynomial evolution equations of not normal type admitting nontrivial symmetries. Phys. Lett. A 1989, 136, 294–299. [Google Scholar] [CrossRef]
- Olver, P.J. Evolution equations possessing infinitely many symmetries. J. Math. Phys. 1977, 18, 1212. [Google Scholar] [CrossRef]
- Fuchssteiner, B. Application of Hereditary Symmetries to Nonlinear Evolution Equations. Nonlin. Anal. Theory Meth. Appl. 1979, 3, 849–862. [Google Scholar] [CrossRef]
- Sakovich, S.Y. Fujimoto-Watanabe equations and differential substitutions. J. Phys. A Math. Gen. 1991, 24, L519. [Google Scholar] [CrossRef]
- Dong, H.; Fang, Y.; Guo, B.; Liu, Y. Lie point symmetry, conservation laws and exact power series solutions to the Fujimoto-Watanabe equation. Quaest. Math. 2019, 43, 1349–1365. [Google Scholar] [CrossRef]
- Muatjetjeja, B. On the symmetry analysis and conservation laws of the (1 + 1)-dimensional Hénon-Lane-Emden system. Math. Methods Appl. Sci. 2017, 40, 1531–1537. [Google Scholar] [CrossRef]
- Muatjetjeja, B. Coupled Lane-Emden-Klein-Gordon-Fock system with central symmetry: Symmetries and conservation laws. J. Differ. Equ. 2017, 263, 8322–8328. [Google Scholar] [CrossRef]
- Gwaxa, B.; Jamal, S.; Johnpillai, A.G. On the conservation laws, Lie symmetry analysis and power series solutions of a class of third-order polynomial evolution equations, to appear in. Arab. J. Math. 2023. [Google Scholar]
- Dubey, S.; Chakraverty, S. Application of modified extended tanh method in solving fractional order coupled wave equations. Math. Comput. Simul. 2022, 198, 509–520. [Google Scholar] [CrossRef]
- Wang, G.; Shen, B.; He, M.; Guan, F.; Zhang, L. Symmetry Analysis and PT-Symmetric Extension of the Fifth-Order Korteweg-de Vries-Like Equation. Fractal Fract. 2022, 6, 468. [Google Scholar] [CrossRef]
- Mnguni, N.; Jamal, S. Invariant solutions of fractional-order spatio-temporal partial differential equations. Int. J. Nonlinear Sci. Numer. 2021, 22, 1011–1022. [Google Scholar] [CrossRef]
- El-Ajou, A.; Abu Arqub, O.; Al Zhour, Z.; Momani, S. New results on fractional power series: Theories and applications. Entropy 2013, 15, 5305–5323. [Google Scholar] [CrossRef]
- Jamal, S.; Mnguni, N. Moving front solutions of a time-fractional power-law fluid under gravity. Quaest. Math. 2021, 44, 1295–1304. [Google Scholar] [CrossRef]
- Buckwar, E.; Luchko, Y. Invariance of a partial differential equation of fractional order under the Lie group of scaling transformations. J. Math. Anal. Appl. 1998, 227, 81–97. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Kasatkin, A.A.; Lukashchuk, S.Y. Symmetry properties of fractional diffusion equations. Phys. Scr. 2009, T136, 014016. [Google Scholar] [CrossRef]
- Bakkyaraj, T. Lie symmetry analysis of system of nonlinear fractional partial differential equations with Caputo fractional derivative. Eur. Phys. J. Plus 2020, 135, 126. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Baleanu, D. Lie Symmetry Analysis of Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent-II. Geophys. J. R. Astr. Soc. 1967, 13, 529. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Kiryakova, V. Generalised Fractional Calculus and Applications; Pitman Res. Notes in Math; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Leibniz, G.W. Letter from Hanover; Germany; to G.F.A L’Hospital, 30 September 1695. In Leibniz Mathematische Schriften; Olms: Hildesheim, Germany, 1962; pp. 301–302. [Google Scholar]
- Leibniz, G.W. Letter from Hanover; Germany; to Johann Bernoulli, 28 December 1695. In Leibniz Mathematische Schriften; Olms: Hildesheim, Germany, 1962; p. 226. [Google Scholar]
- Leibniz, G.W. Letter from Hanover; Germany; to John Wallis, 30 May 1697. In Leibniz Mathematische Schriften; Olms: Hildesheim, Germany, 1962; p. 25. [Google Scholar]
- Atangana, A.; Secer, A. A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef]
- Asmar, N.H. Partial Differential Equations with Fourier Series and Boundary Value Problems, 2nd ed.; China Machine Press: Beijing, China, 2005. [Google Scholar]
- Rudin, W. Principles of Mathematical Analysis, 3rd ed.; China Machine Press: Beijing, China, 2004. [Google Scholar]
- Guo, B.; Dong, H.; Fang, Y. Symmetry Groups, Similarity Reductions, and Conservation Laws of the Time-Fractional Fujimoto-Watanabe Equation Using Lie Symmetry Analysis Method. Complexity 2020, 2020, 4830684. [Google Scholar] [CrossRef]

| Case | Symmetries | Dimension |
|---|---|---|
| 1 | The Lie algebra spanned by point symmetries | |
| is 3 dimensional. | ||
| 2 | The Lie algebra spanned by point symmetries | |
| is 3 dimensional. | ||
| 3 | The Lie algebra spanned by point symmetries | |
| is 3 dimensional. | ||
| 4 | The Lie algebra spanned by point symmetries | |
| is 2 dimensional. | ||
| 5,8 | The Lie algebra spanned by point symmetries | |
| is 2 dimensional. | ||
| 6 | The Lie algebra spanned by point symmetries | |
| is 4 dimensional. | ||
| 7 | The Lie algebra spanned by point symmetries | |
| is 3 dimensional. | ||
| 9, 10 | The Lie algebra spanned by point symmetries | |
| is 4 dimensional. |
| [,] | |||
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 0 | ||
| 0 | 0 |
| [,] | |||
|---|---|---|---|
| 0 | 0 | ||
| 0 | |||
| 0 | 0 |
| [,] | |||
|---|---|---|---|
| 0 | 0 | ||
| 0 | 0 | 0 | |
| 0 | 0 |
| [,] | ||
|---|---|---|
| 0 | ||
| − | 0 |
| [,] | ||||
|---|---|---|---|---|
| 0 | 0 | |||
| 0 | 0 | 0 | 0 | |
| 0 | 0 | |||
| 0 | 0 |
| [,] | |||
|---|---|---|---|
| 0 | 0 | ||
| 0 | 0 | 0 | |
| 0 | 0 |
| [,] | ||||
|---|---|---|---|---|
| 0 | 0 | 2 | ||
| 0 | 0 | 0 | 0 | |
| 0 | 0 | |||
| −2 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubayi, J.T.; Jamal, S. Lie Symmetries and Third- and Fifth-Order Time-Fractional Polynomial Evolution Equations. Fractal Fract. 2023, 7, 125. https://doi.org/10.3390/fractalfract7020125
Kubayi JT, Jamal S. Lie Symmetries and Third- and Fifth-Order Time-Fractional Polynomial Evolution Equations. Fractal and Fractional. 2023; 7(2):125. https://doi.org/10.3390/fractalfract7020125
Chicago/Turabian StyleKubayi, Jollet Truth, and Sameerah Jamal. 2023. "Lie Symmetries and Third- and Fifth-Order Time-Fractional Polynomial Evolution Equations" Fractal and Fractional 7, no. 2: 125. https://doi.org/10.3390/fractalfract7020125
APA StyleKubayi, J. T., & Jamal, S. (2023). Lie Symmetries and Third- and Fifth-Order Time-Fractional Polynomial Evolution Equations. Fractal and Fractional, 7(2), 125. https://doi.org/10.3390/fractalfract7020125






