Fractional Study of the Non-Linear Burgers’ Equations via a Semi-Analytical Technique
Abstract
1. Introduction
2. Preliminaries
3. General Implementation of Elzaki Residual Power Series Method
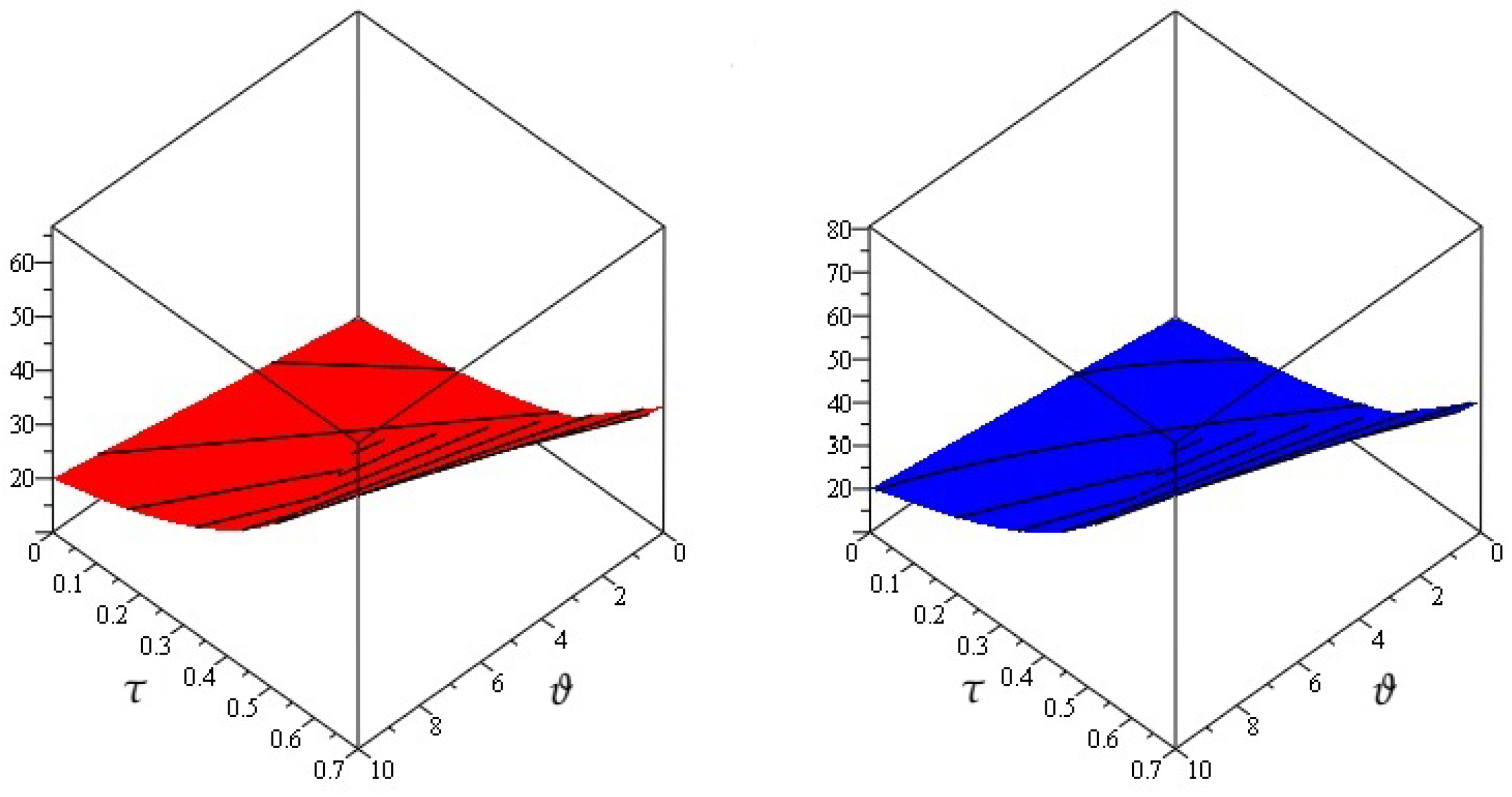
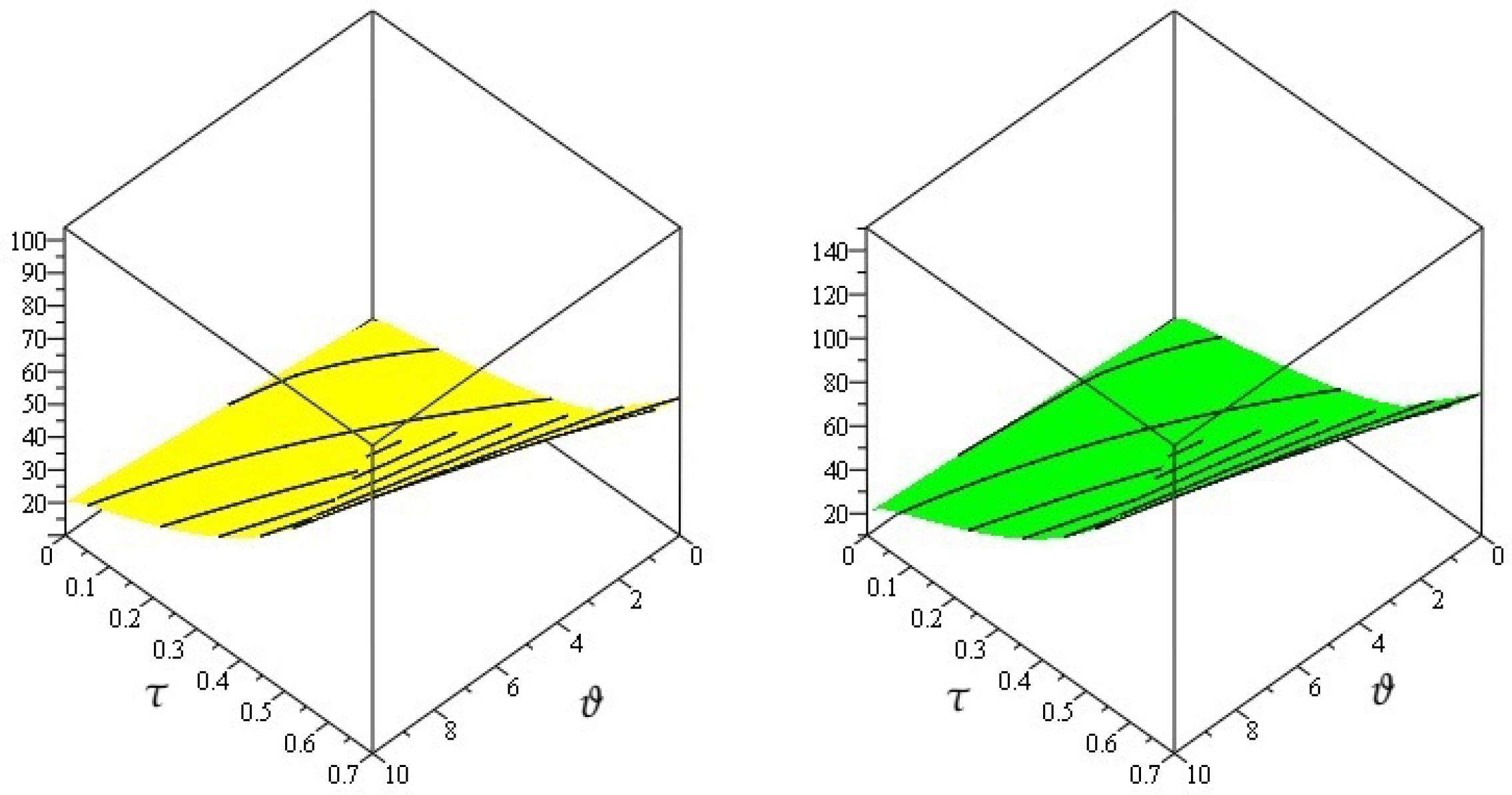
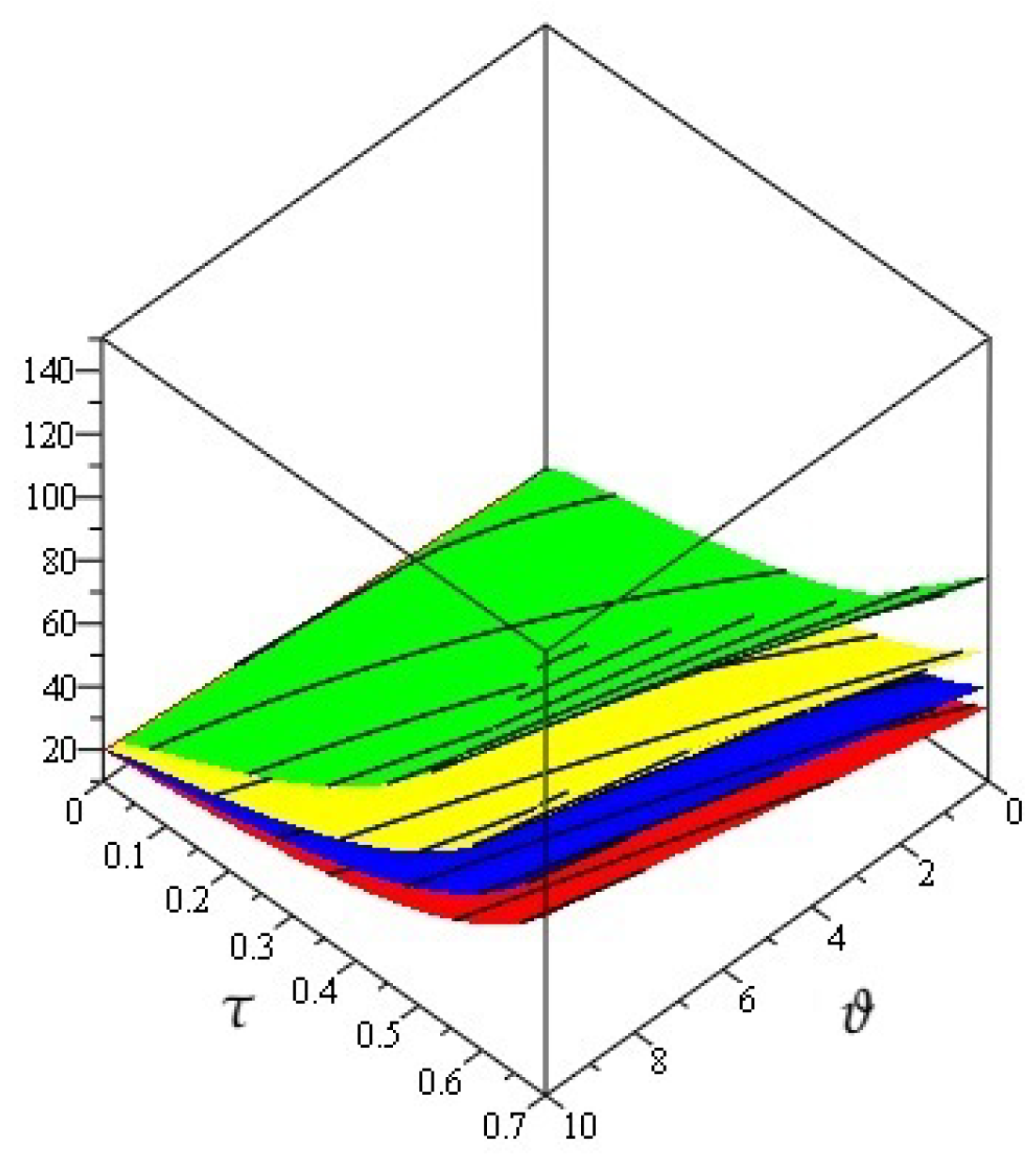
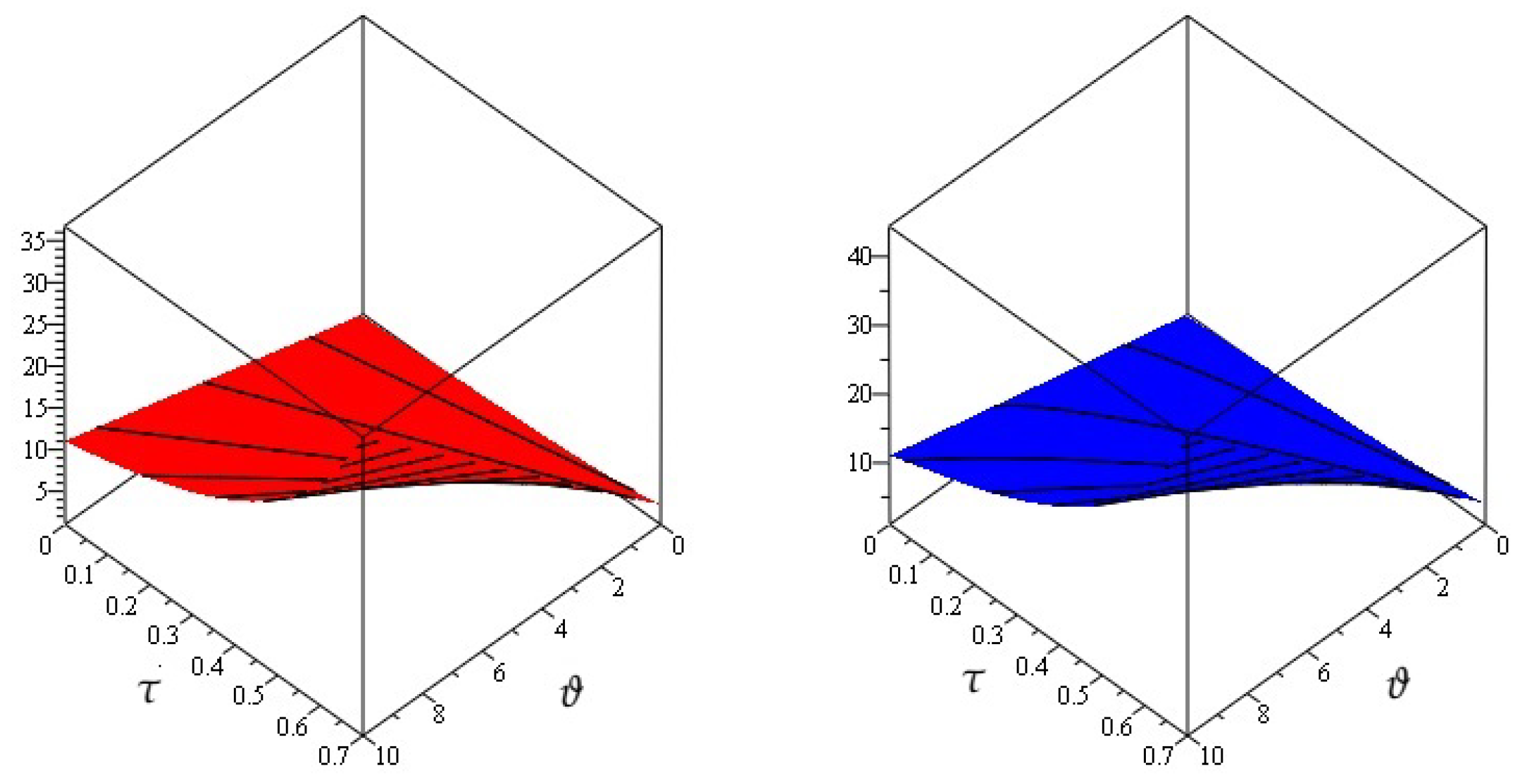
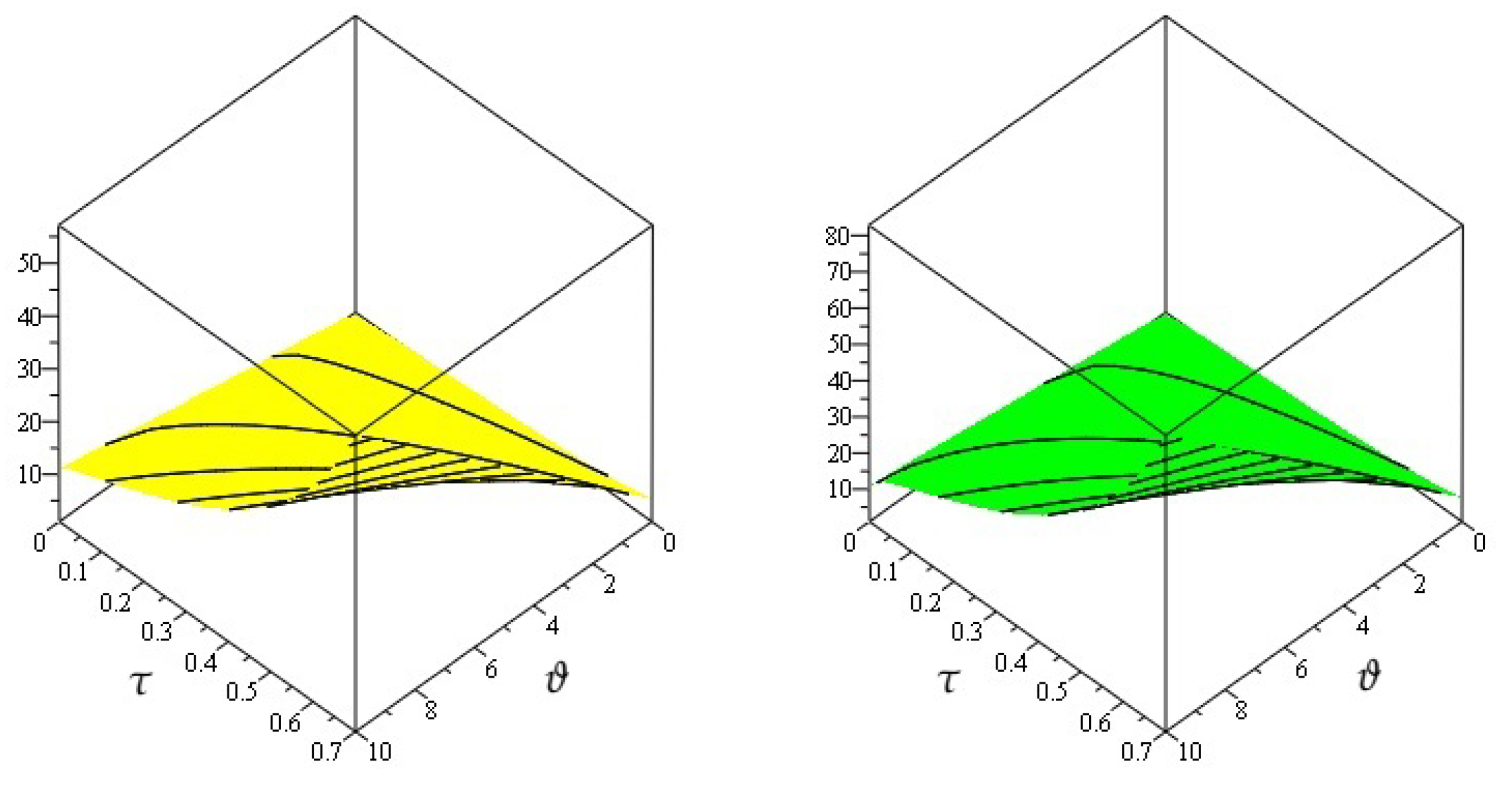
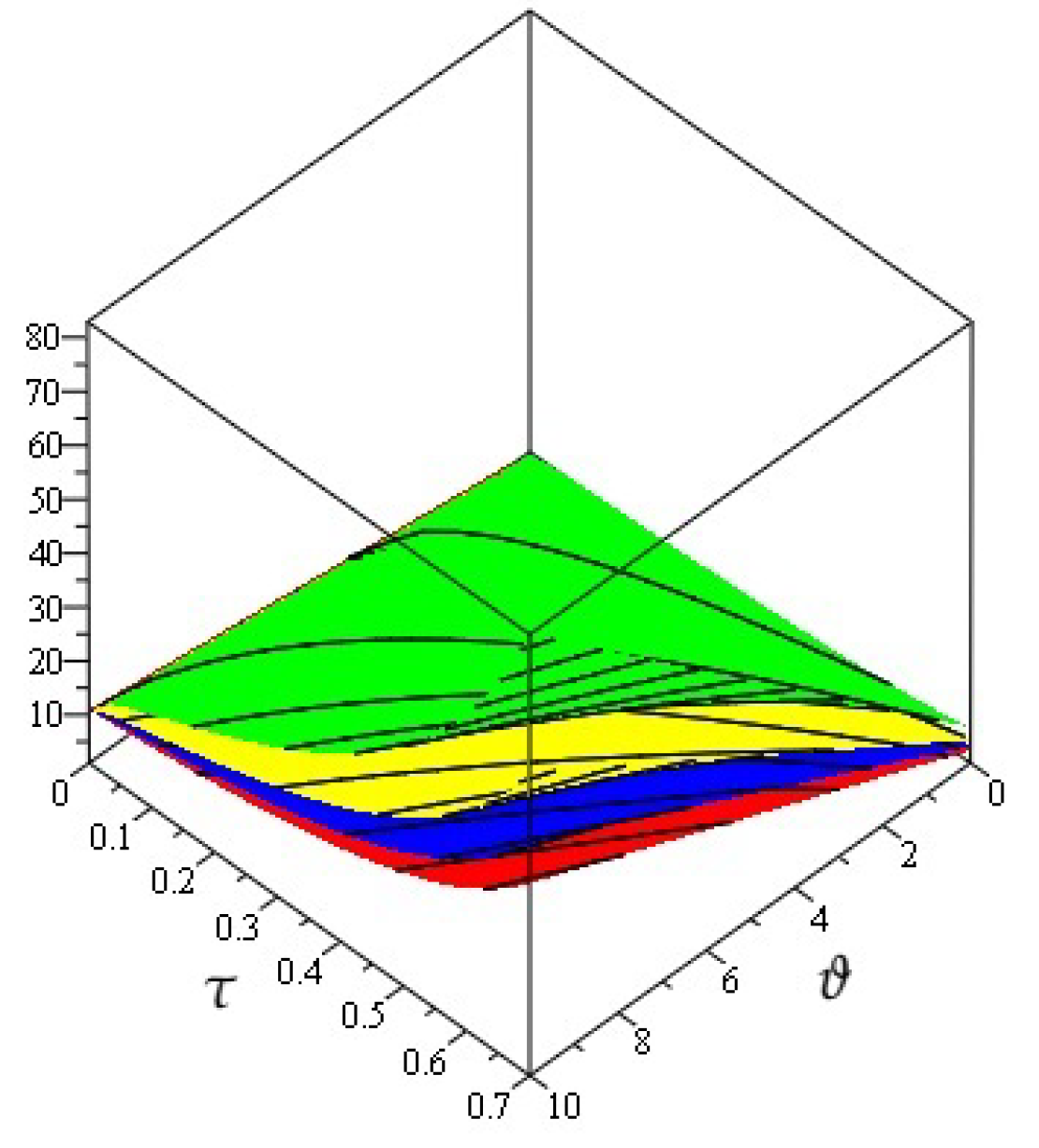
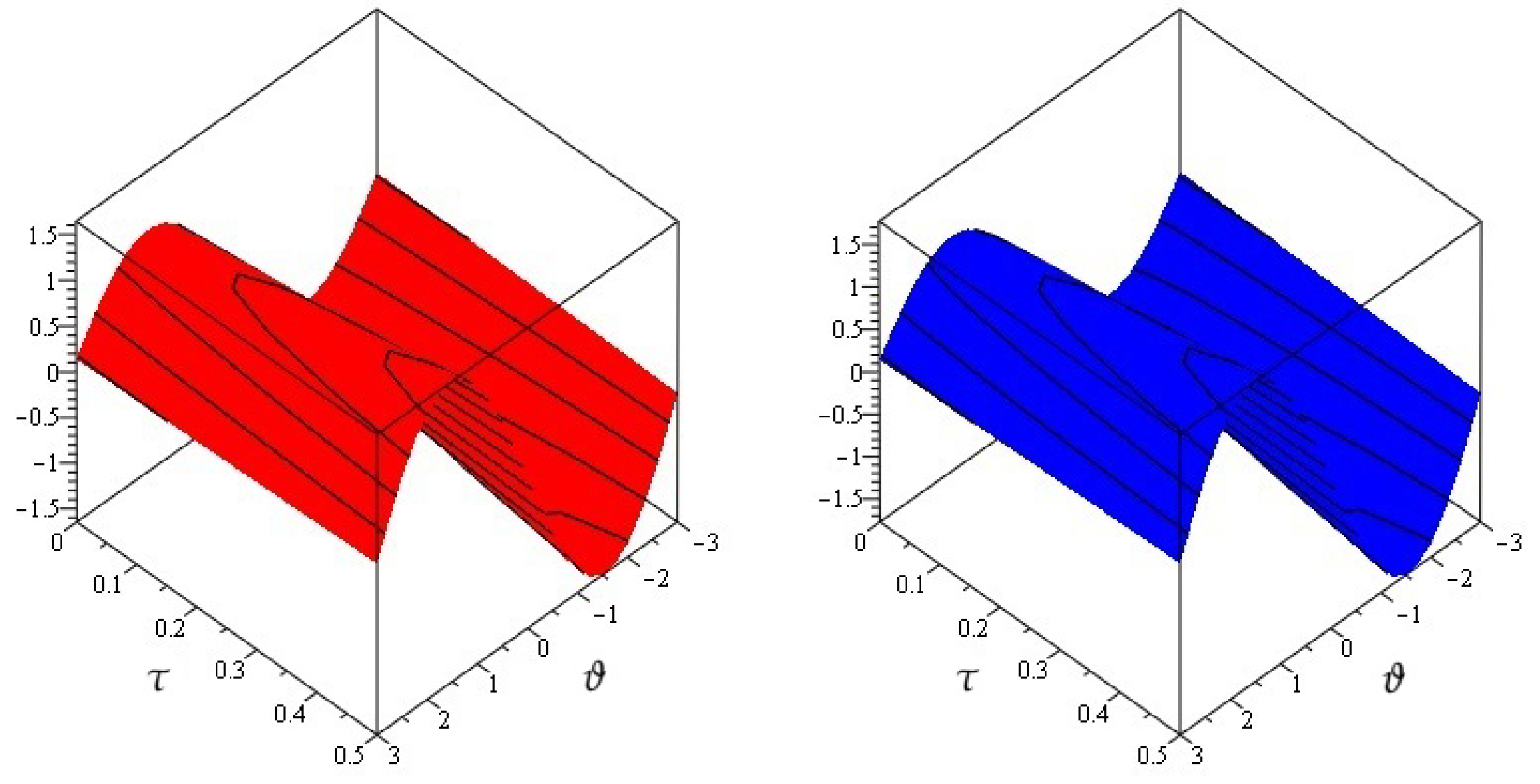
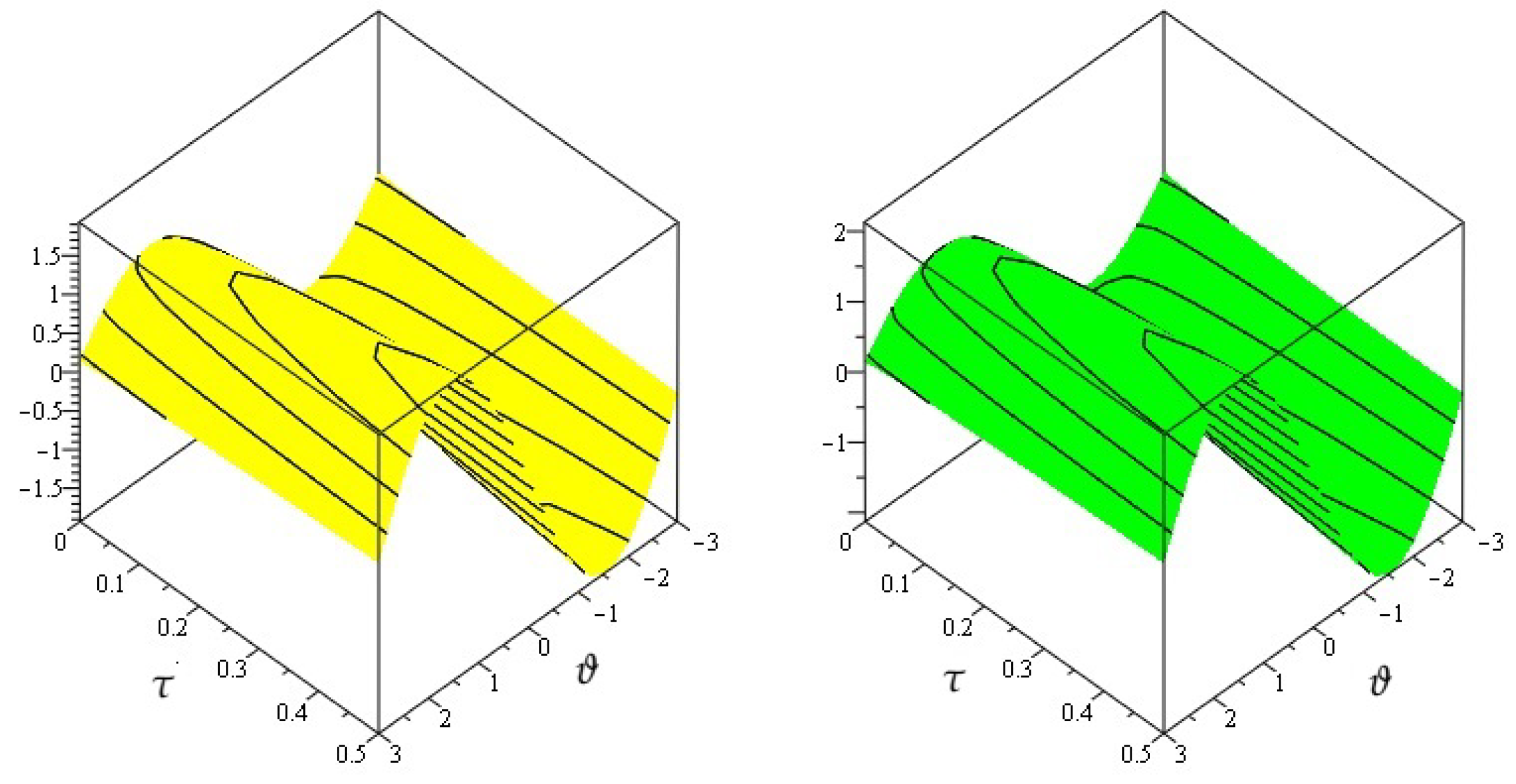
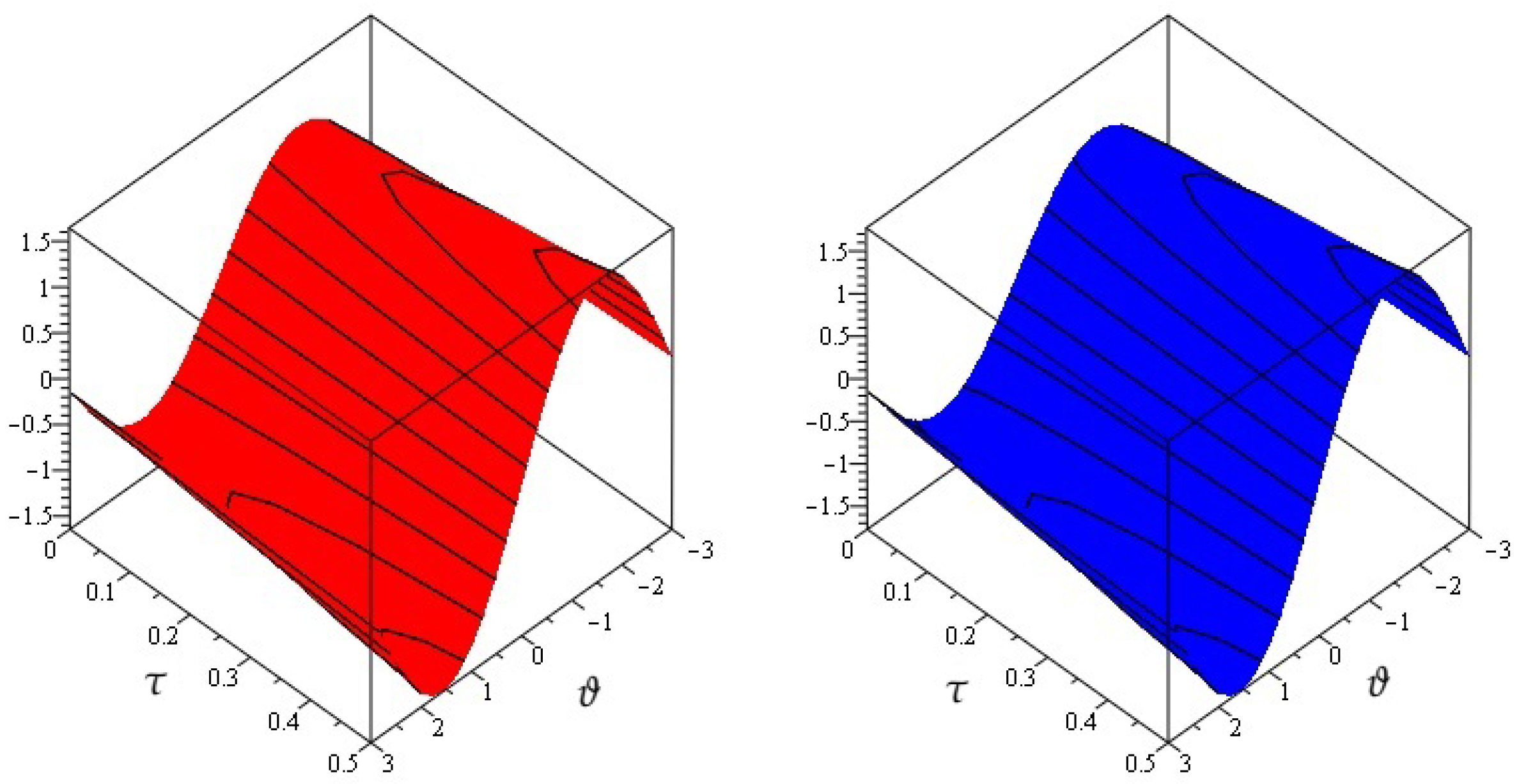
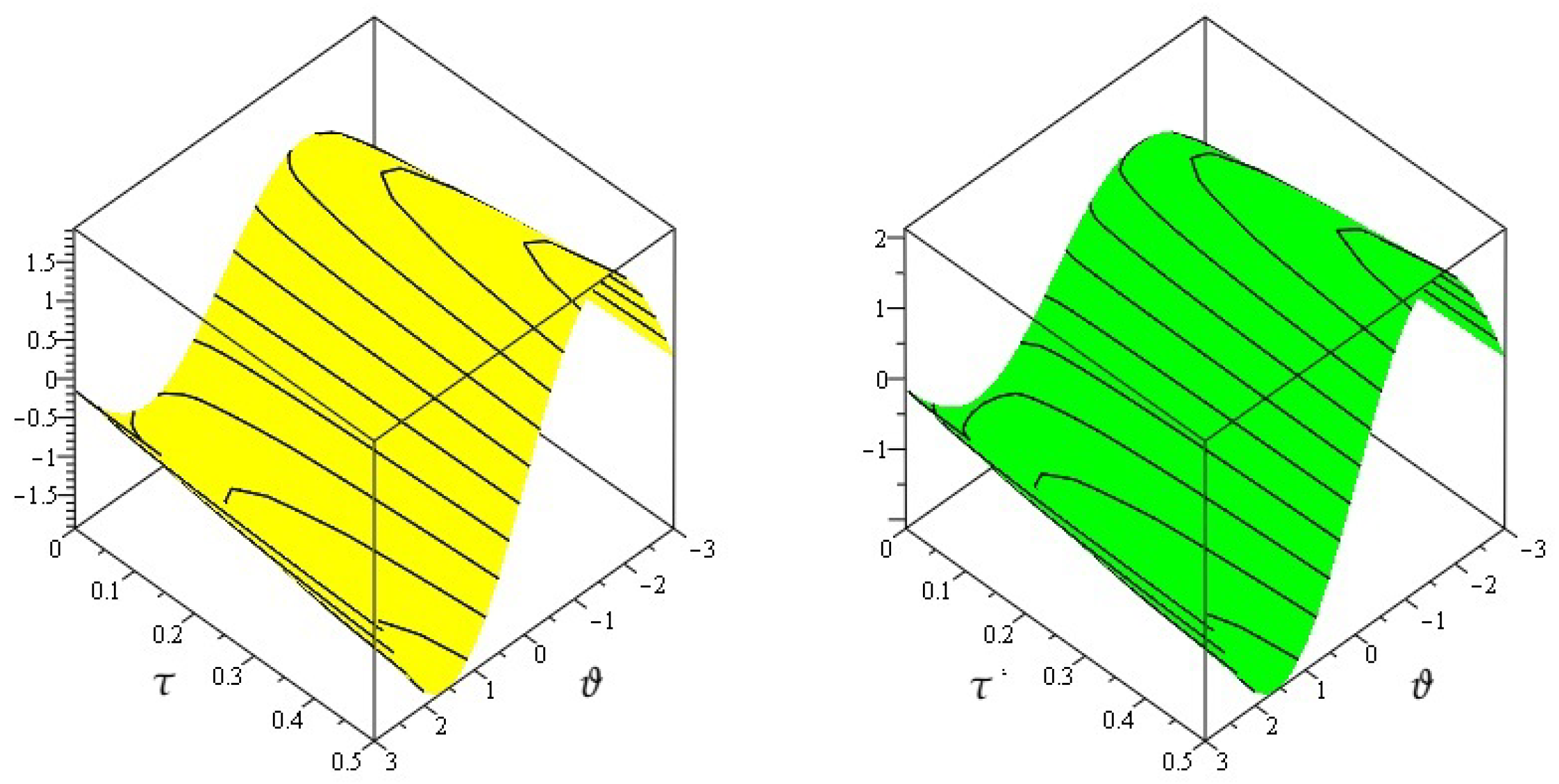
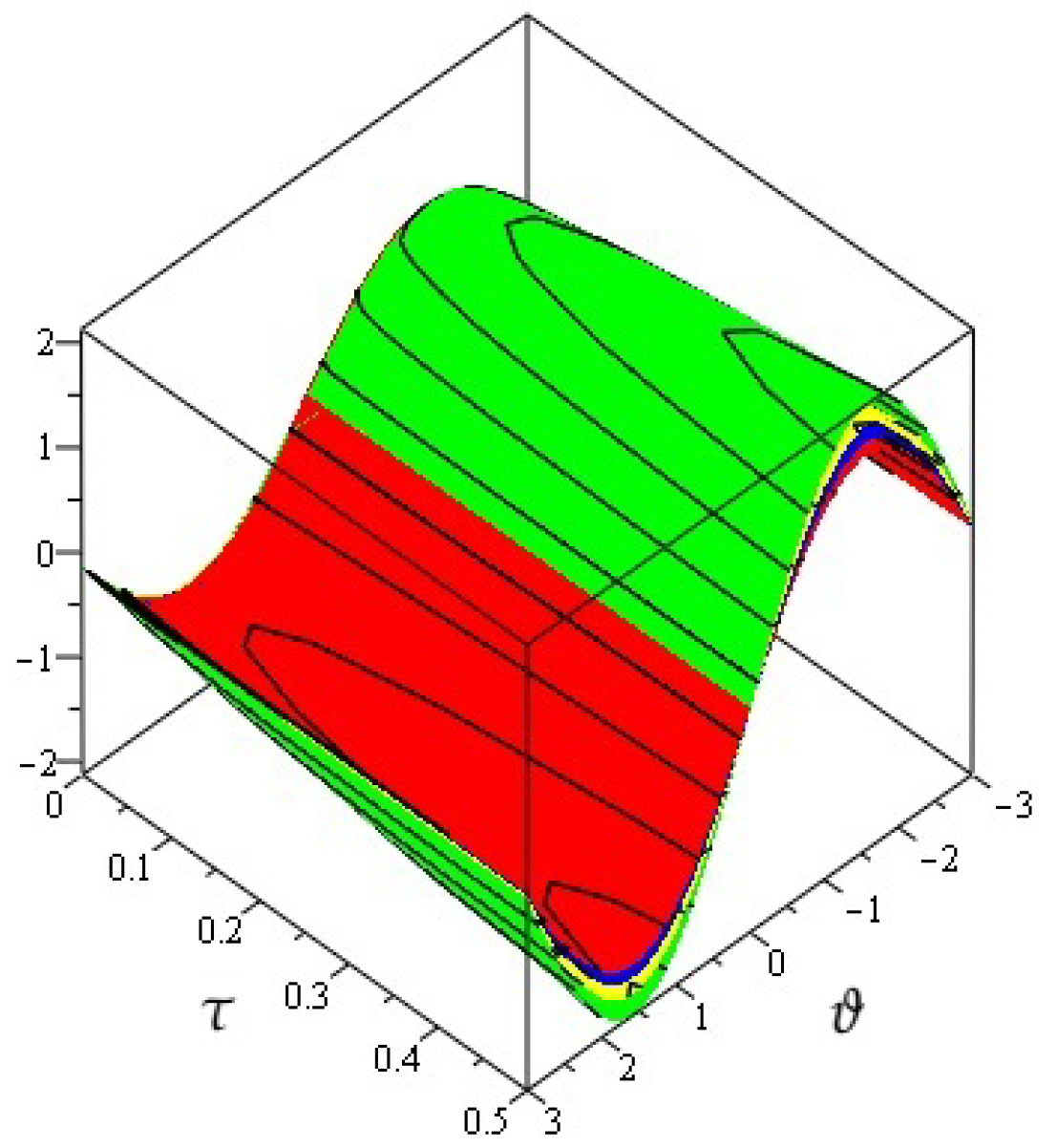
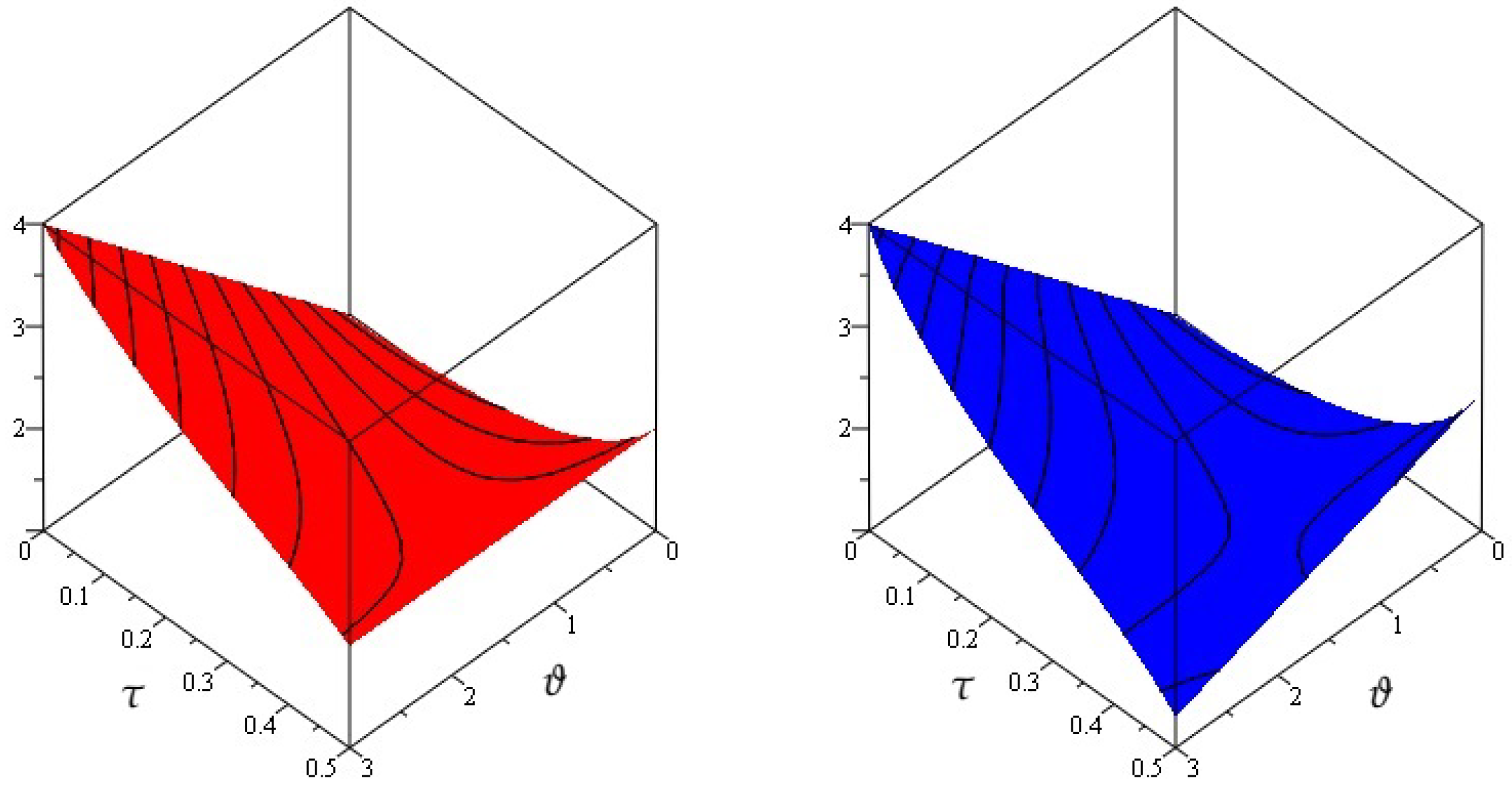
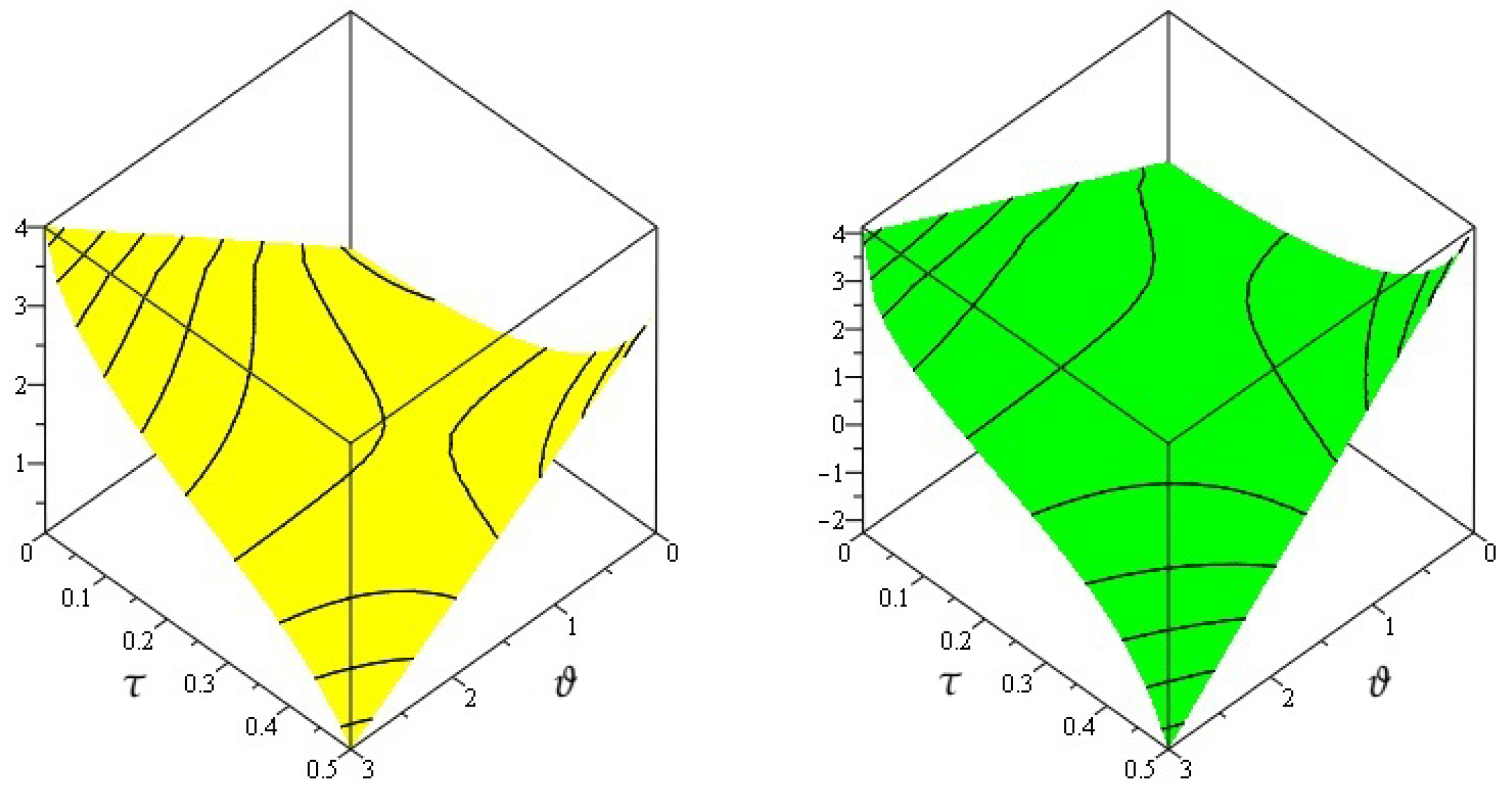
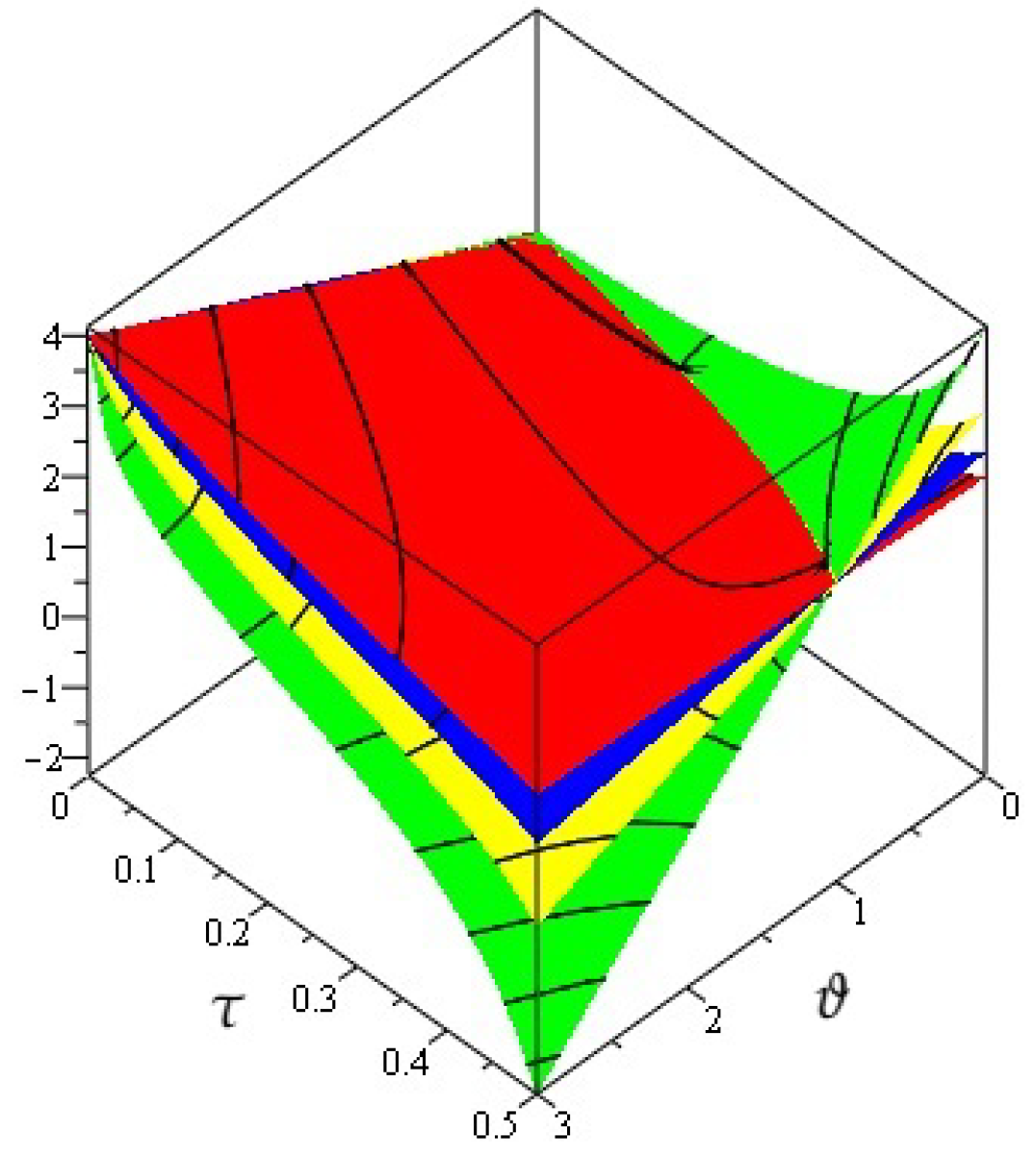
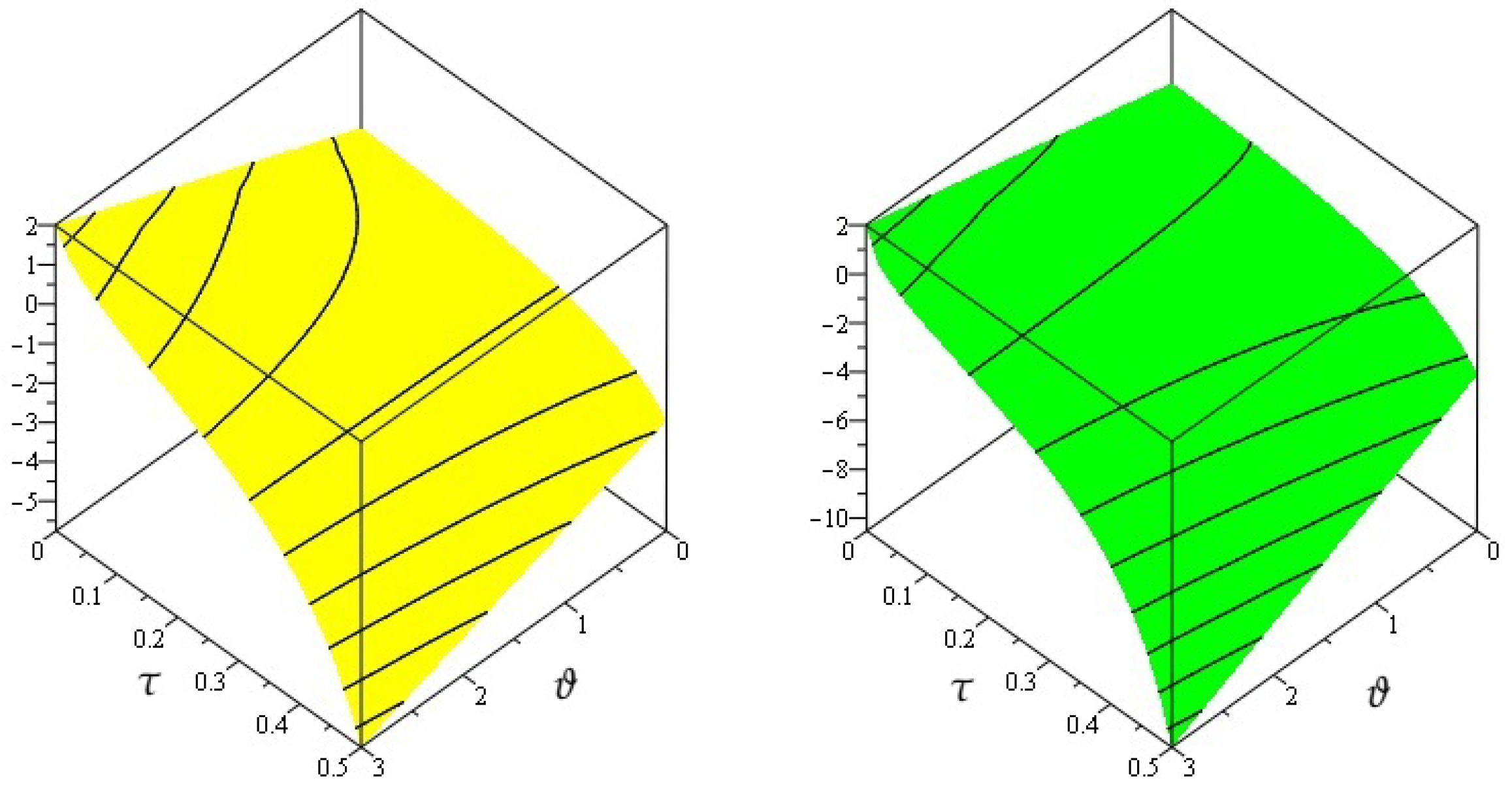
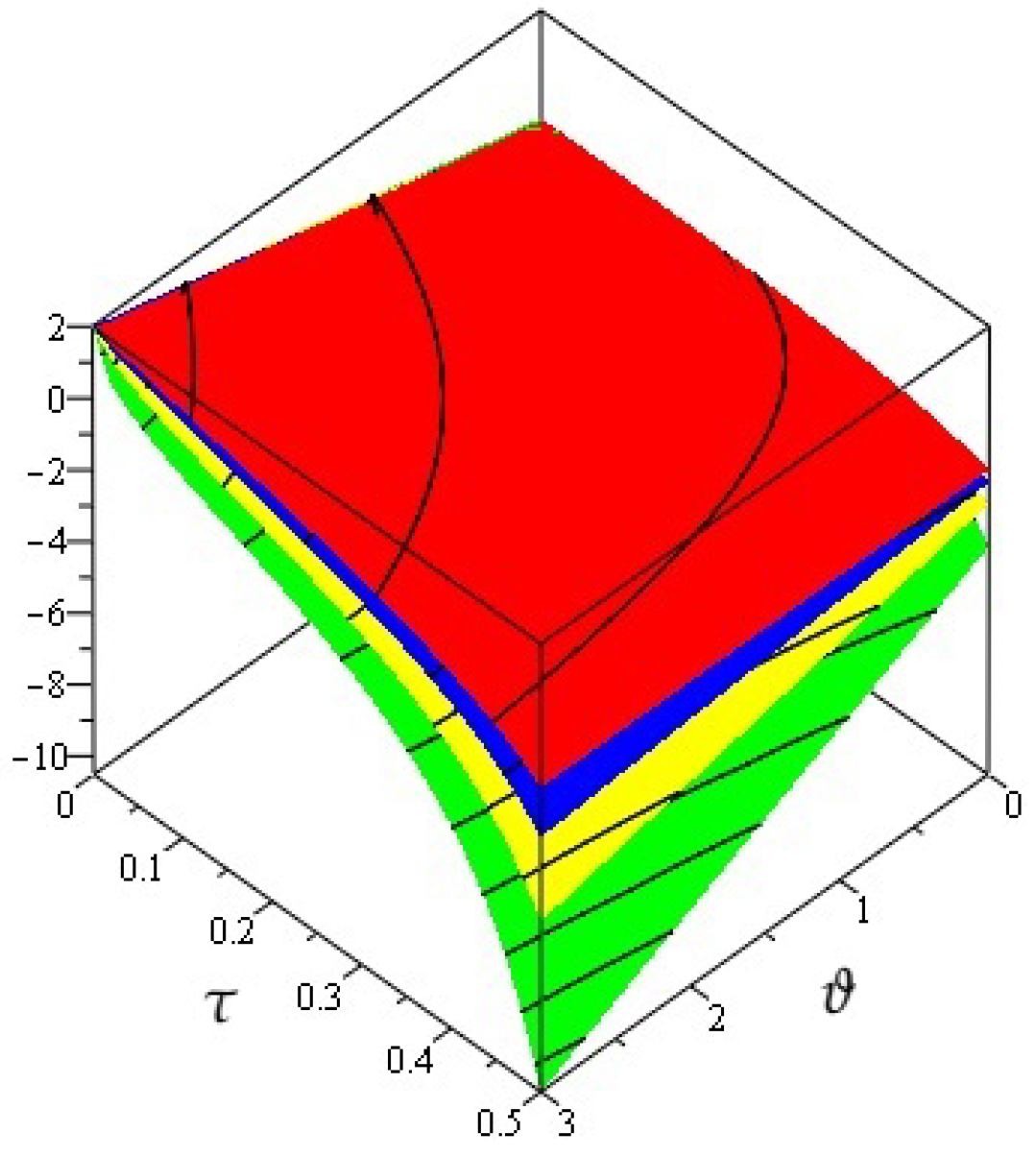
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Sawalha, M.M.; Agarwal, R.P.; Shah, R.; Ababneh, O.Y.; Weera, W. A reliable way to deal with fractional-order equations that describe the unsteady flow of a polytropic gas. Mathematics 2022, 10, 2293. [Google Scholar] [CrossRef]
- Said, L.A.; Madian, A.H.; Radwan, A.G.; Soliman, A.M. Fractional order oscillator with independent control of phase and frequency. In Proceedings of the 2014 2nd International Conference on Electronic Design (ICED), Penang, Malaysia, 19–21 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 224–229. [Google Scholar]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Sabatier, J.A.T.M.J.; Agrawal, O.P.; Machado, J.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007; Volume 4. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Debnath, L. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 2003, 3413–3442. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Alshehry, A.S.; Nonlaopon, K.; Shah, R.; Ababneh, O.Y. Fractional view analysis of delay differential equations via numerical method. AIMS Math. 2022, 7, 20510–20523. [Google Scholar] [CrossRef]
- Mukhtar, S.; Shah, R.; Noor, S. The Numerical Investigation of a Fractional-Order Multi-Dimensional Model of Navier-Stokes Equation via Novel Techniques. Symmetry 2022, 14, 1102. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Alshehry, A.S.; Nonlaopon, K.; Shah, R.; Ababneh, O.Y. Approximate analytical solution of time-fractional vibration equation via reliable numerical algorithm. AIMS Math. 2022, 7, 19739–19757. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Kai, Y.; Chen, S.; Zhang, K.; Yin, Z. Exact solutions and dynamic properties of a non-linear fourth-order time-fractional partial differential equation. Waves Random Complex Media 2022, 1–12. [Google Scholar] [CrossRef]
- Cao, Y.; Nikan, O.; Avazzadeh, Z. A localized meshless technique for solving 2D nonlinear integro-differential equation with multi-term kernels. Appl. Numer. Math. 2023, 183, 140–156. [Google Scholar] [CrossRef]
- Jassim, H.K.; Shareef, M.A. On approximate solutions for fractional system of differential equations with Caputo-Fabrizio fractional operator. J. Math. Comput. Sci. 2021, 23, 58–66. [Google Scholar] [CrossRef]
- Oderinu, R.A.; Owolabi, J.A.; Taiwo, M. Approximate solutions of linear time-fractional differential equations. J. Math. Comput. Sci. 2022, 2023, 60–72. [Google Scholar] [CrossRef]
- Bateman, H. Some recent researches on the motion of fluids. Mon. Weather Rev. 1915, 43, 163–170. [Google Scholar] [CrossRef]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Cole, J.D. On a quasilinear parabolic equations occurring in aerodynamics. Quart. Appl. Math. 1951, 9, 225–236. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Partial Differential Equations: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2002; p. 474. [Google Scholar]
- Naghipour, A.; Manafian, J. Application of the laplace adomian decomposition and implicit methods for solving Burgers’ equation. TWMS J. Pure Appl. Math. 2015, 6, 68–77. [Google Scholar]
- Rashidi, M.M.; Erfani, E. New analytical method for solving Burgers and nonlinear heat transfer equations and comparison with HAM. Comput. Phys. Comm. 2009, 180, 1539–1544. [Google Scholar] [CrossRef]
- Moslem, W.M.; Sabry, R. Zakharov-Kuznetsov-Burgers’ equation for dust ion acoustic waves. Chaos Solitons Fractals 2008, 36, 628–634. [Google Scholar] [CrossRef]
- Basto, M.; Semiao, V.; Calheiros, F. Dynamics and synchronization of numerical solutions of the Burgers’ equation. J. Comput. Appl. Math. 2009, 231, 793–806. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems in Physics: The Decomposition Method; Kluwer Academic: Boston, MA, USA, 1994. [Google Scholar]
- He, J.H. Variational iteration method-a kind of nonlinear analytical technique: Some examples. Int. J. Non Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Engrg. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Zhou, J.K. Differential Transform and Its Application for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986. (In Chinese) [Google Scholar]
- Saadeh, R.; Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, U.K.S. Application of fractional residual power series algorithm to solve Newell–Whitehead–Segel equation of fractional order. Symmetry 2019, 11, 1431. [Google Scholar] [CrossRef]
- Freihet, A.; Hasan, S.; Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, U.K.S. Toward computational algorithm for timefractional Fokker–Planck models. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Arqub, O.A.; Hadid, S. Approximate solutions of nonlinear fractional Kundu–Eckhaus and coupled fractional massive Thirring equations emerging in quantum field theory using conformable residual power series method. Phys. Scripta 2020, 95, 105205. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Arqub, O.A.; Momani, S. Numerical computations of coupled fractional resonant Schrödinger equations arising in quantum mechanics under conformable fractional derivative sense. Phys. Scripta 2020, 95, 075218. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Arqub, O.A.; Hadid, S. An attractive analytical technique for coupled system of fractional partial differential equations in shallow water waves with conformable derivative. Commun. Theor. Phys. 2020, 72, 085001. [Google Scholar] [CrossRef]
- Komashynska, I.; Al-Smadi, M.; Arqub, O.A.; Momani, S. An efficient analytical method for solving singular initial value problems of nonlinear systems. Appl. Math. Inform. Sci. 2016, 10, 647–656. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-smadi, M.; Ahmad, R.R.; Din, U.K.S. Numerical computation of fractional Fredholm integrodifferential equation of order 2b arising in natural sciences. J. Phys. Conf. Ser. 2019, 1212, 012022. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, U.K.S. An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations. Symmetry 2019, 11, 205. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, U.K.S. Computational optimization of residual power series algorithm for certain classes of fuzzy fractional differential equations. Int. J. Diff. Equ. 2018, 2018, 8686502. [Google Scholar] [CrossRef]
- Eriqat, T.; El-Ajou, A.; Oqielat, M.N.; Al-Zhour, Z.; Momani, S. A New Attractive Analytic Approach for Solutions of Linear and Nonlinear Neutral Fractional Pantograph Equations. Chaos Solitons Fract. 2020, 138, 109957. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Li, L.; Zhou, C. Elzaki Transform Residual Power Series Method for the Fractional Population Diffusion Equations. Eng. Lett. 2021, 29, 1561–1572. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, N.; Chughtai, M.T.; Ullah, R. Fractional Study of the Non-Linear Burgers’ Equations via a Semi-Analytical Technique. Fractal Fract. 2023, 7, 103. https://doi.org/10.3390/fractalfract7020103
Iqbal N, Chughtai MT, Ullah R. Fractional Study of the Non-Linear Burgers’ Equations via a Semi-Analytical Technique. Fractal and Fractional. 2023; 7(2):103. https://doi.org/10.3390/fractalfract7020103
Chicago/Turabian StyleIqbal, Naveed, Muhammad Tajammal Chughtai, and Roman Ullah. 2023. "Fractional Study of the Non-Linear Burgers’ Equations via a Semi-Analytical Technique" Fractal and Fractional 7, no. 2: 103. https://doi.org/10.3390/fractalfract7020103
APA StyleIqbal, N., Chughtai, M. T., & Ullah, R. (2023). Fractional Study of the Non-Linear Burgers’ Equations via a Semi-Analytical Technique. Fractal and Fractional, 7(2), 103. https://doi.org/10.3390/fractalfract7020103







