Solitary Waves Propagation Analysis in Nonlinear Dynamical System of Fractional Coupled Boussinesq-Whitham-Broer-Kaup Equation
Abstract
:1. Introduction
2. Methodology and Materials
2.1. Conformable Fractional Derivative
2.2. The Working Procedure of mEDAM
3. Execution of mEDAM
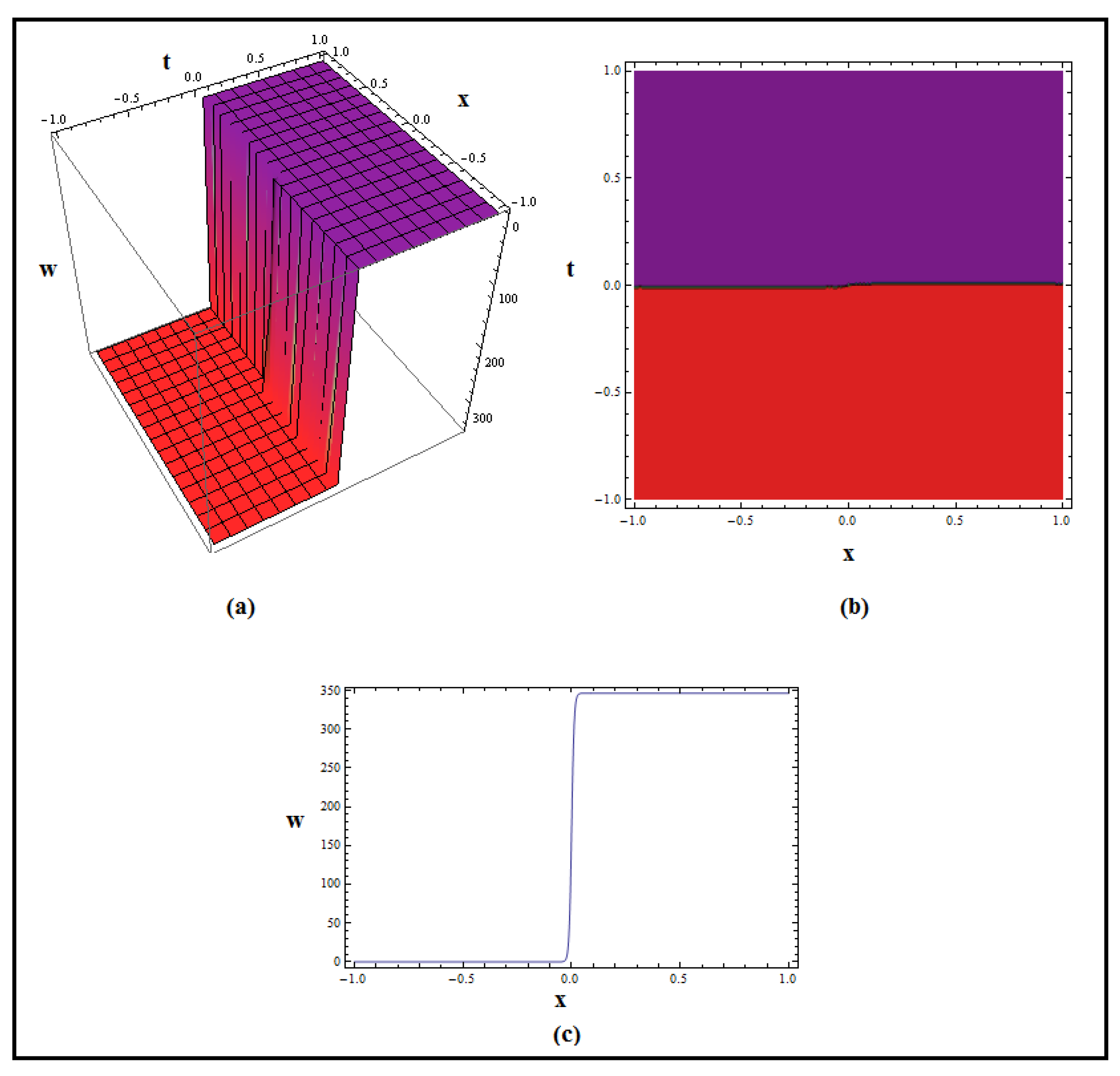
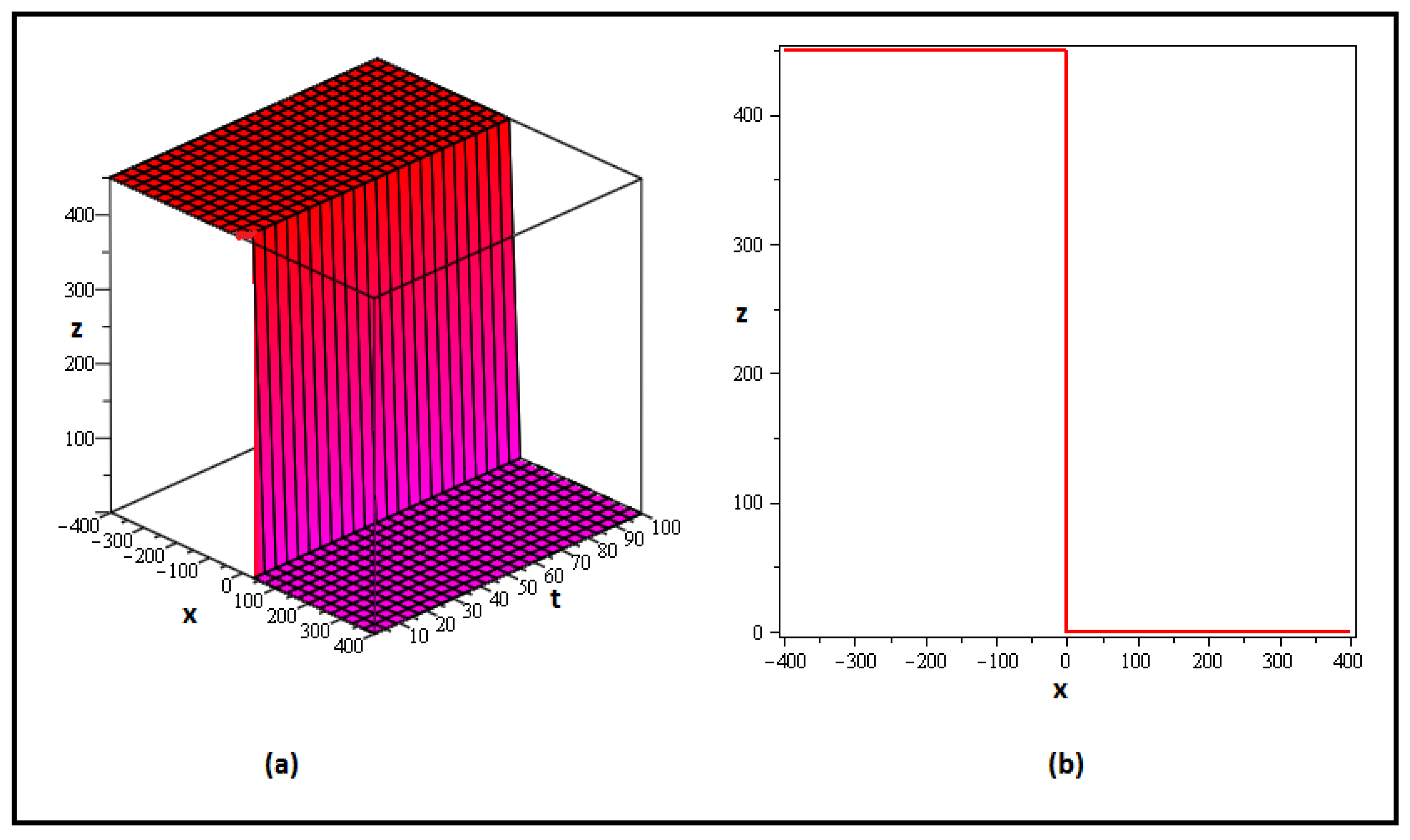
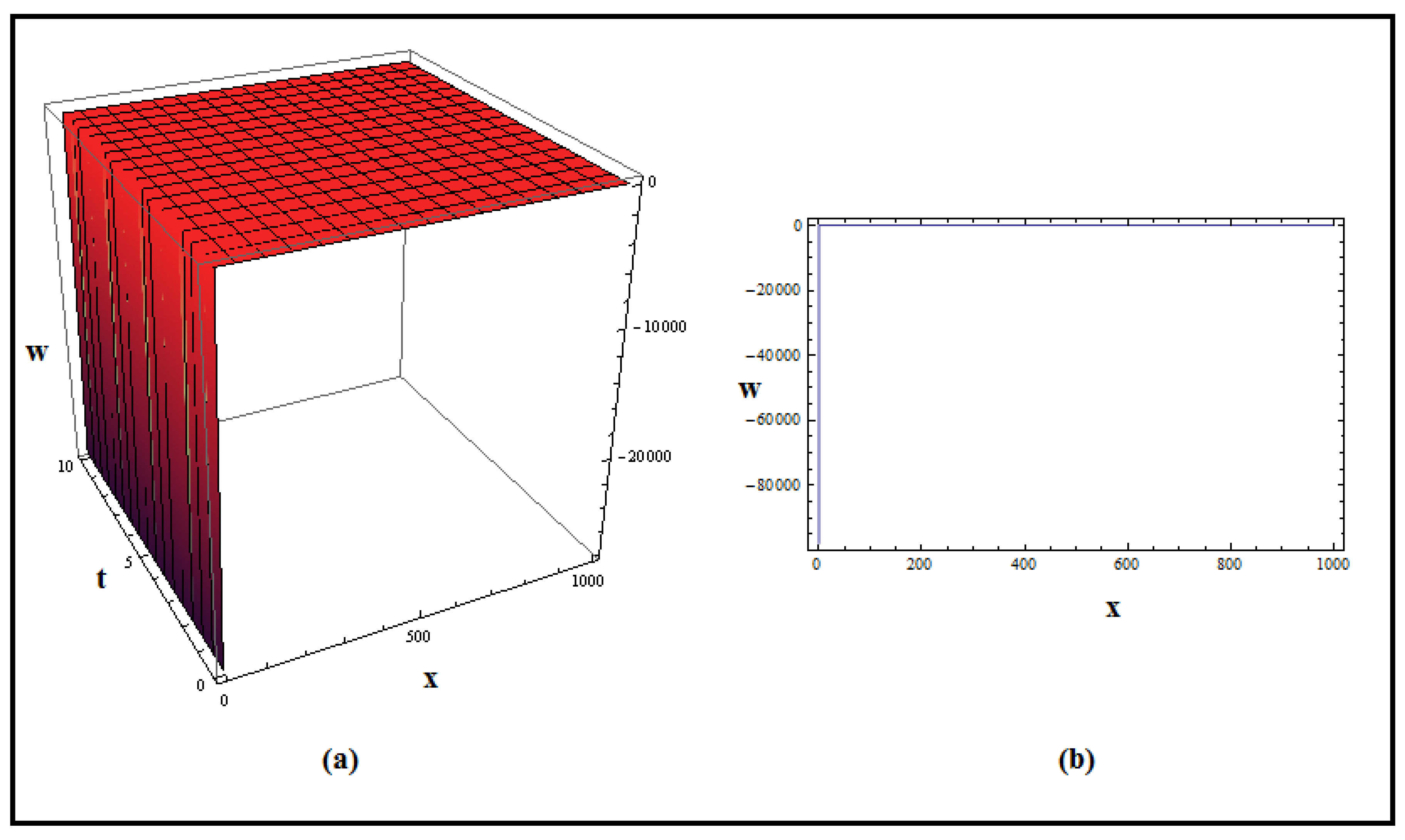
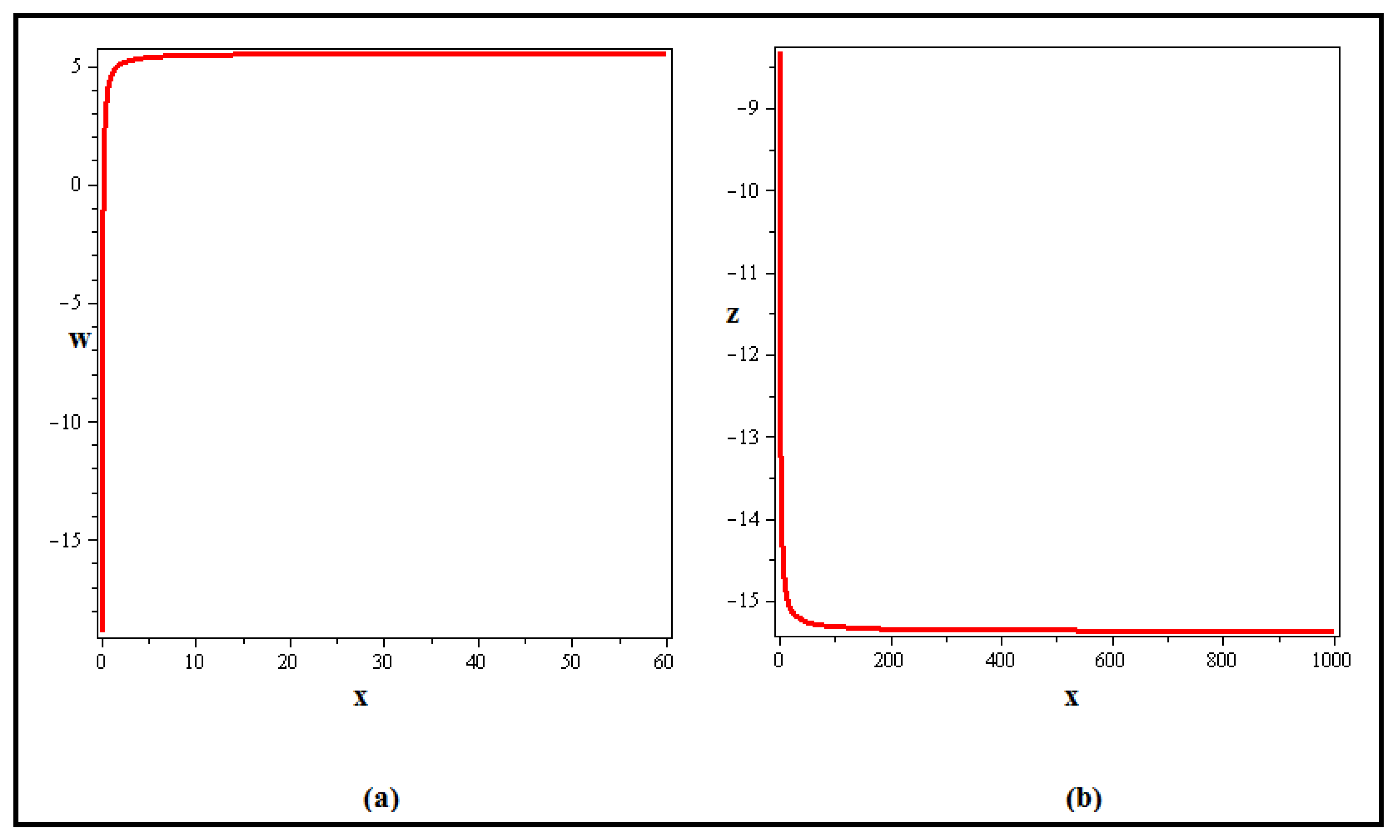
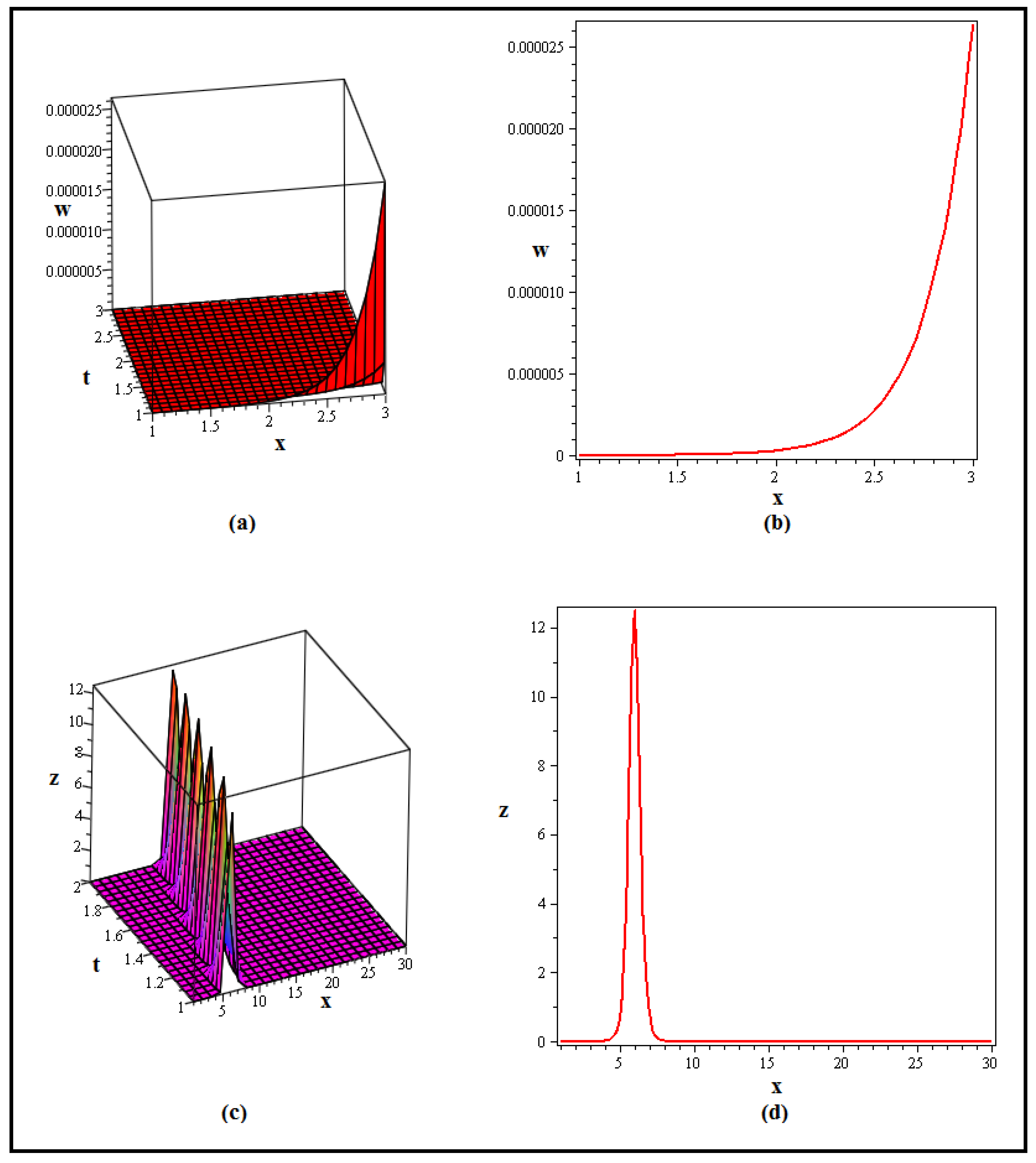
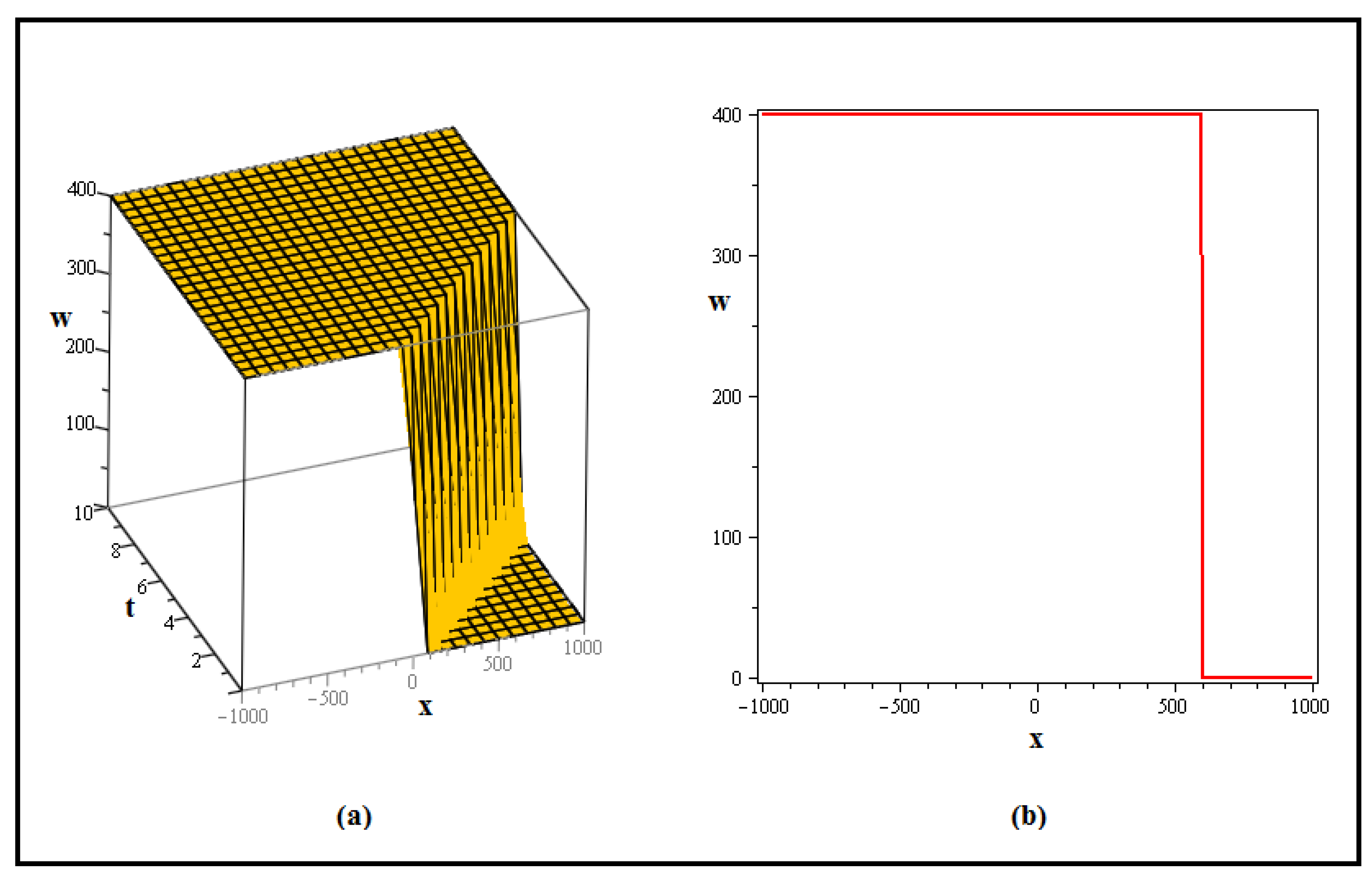
4. Discussion and Graphs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, J.; Kumar, D.; Kılıçman, A. Numerical solutions of nonlinear fractional partial differential equations arising in spatial diffusion of biological populations. Abstr. Appl. Anal. 2014, 2014, 535793. [Google Scholar] [CrossRef]
- Kumar, S. A new fractional modeling arising in engineering sciences and its analytical approximate solution. Alex. Eng. J. 2013, 52, 813–819. [Google Scholar] [CrossRef]
- Dubey, V.P.; Kumar, R.; Kumar, D.; Khan, I.; Singh, J. An efficient computational scheme for nonlinear time fractional systems of partial differential equations arising in physical sciences. Adv. Differ. Equ. 2020, 2020, 46. [Google Scholar] [CrossRef]
- Fareed, A.F.; Elsisy, M.A.; Semary, M.S.; Elbarawy, M.T. Controlled Picard’s Transform Technique for Solving a Type of Time Fractional Navier–Stokes Equation Resulting from Incompressible Fluid Flow. Int. J. Appl. Comput. Math. 2022, 8, 184. [Google Scholar] [CrossRef]
- Murphy, M.L.; Frodl, T. Meta-analysis of diffusion tensor imaging studies shows altered fractional anisotropy occurring in distinct brain areas in association with depression. Biol. Mood Anxiety Disord. 2011, 1, 3. [Google Scholar] [CrossRef]
- Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Phys. A Stat. Mech. Its Appl. 2000, 284, 376–384. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, J.; Yu, S.; Tan, L. Noise detection and image denoising based on fractional calculus. Chaos Solitons Fractals 2020, 131, 109463. [Google Scholar] [CrossRef]
- Burrage, K.; Hale, N.; Kay, D. An efficient implicit FEM scheme for fractional-in-space reaction-diffusion equations. SIAM J. Sci. Comput. 2012, 34, A2145–A2172. [Google Scholar] [CrossRef]
- Javidi, M.; Ahmad, B. Numerical solution of fractional partial differential equations by numerical Laplace inversion technique. Adv. Differ. Equ. 2013, 2013, 375. [Google Scholar] [CrossRef]
- Fu, H.; Ng, M.K.; Wang, H. A divide-and-conquer fast finite difference method for space–time fractional partial differential equation. Comput. Math. Appl. 2017, 73, 1233–1242. [Google Scholar] [CrossRef]
- Baeumer, B.; Kovács, M.; Meerschaert, M.M. Numerical solutions for fractional reaction–diffusion equations. Comput. Math. Appl. 2008, 55, 2212–2226. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Y.; Liu, L. Numerical solution of fractional partial differential equations with variable coefficients using generalized fractional-order Legendre functions. Appl. Math. Comput. 2014, 244, 847–858. [Google Scholar] [CrossRef]
- Marom, O.; Momoniat, E. A comparison of numerical solutions of fractional diffusion models in finance. Nonlinear Anal. Real World Appl. 2009, 10, 3435–3442. [Google Scholar] [CrossRef]
- Mahor, T.C.; Mishra, R.; Jain, R. Analytical solutions of linear fractional partial differential equations using fractional Fourier transform. J. Comput. Appl. Math. 2021, 385, 113202. [Google Scholar] [CrossRef]
- Ganji, Z.Z.; Ganji, D.D.; Ganji, A.D.; Rostamian, M. Analytical solution of time-fractional Navier–Stokes equation in polar coordinate by homotopy perturbation method. Numer. Methods Partial. Differ. Equ. Int. J. 2010, 26, 117–124. [Google Scholar] [CrossRef]
- Shah, K.; Khalil, H.; Khan, R.A. Analytical solutions of fractional order diffusion equations by natural transform method. Iran. J. Sci. Technol. Trans. A Sci. 2018, 42, 1479–1490. [Google Scholar] [CrossRef]
- Manafian, J.; Foroutan, M. Application of tan(ϕ(ξ)/2)tan(ϕ(ξ)/2)-expansion method for the time-fractional Kuramoto–Sivashinsky equation. Opt. Quantum Electron. 2017, 49, 272. [Google Scholar] [CrossRef]
- Alsharidi, A.K.; Bekir, A. Discovery of New Exact Wave Solutions to the M-Fractional Complex Three Coupled Maccari’s System by Sardar Sub-Equation Scheme. Symmetry 2023, 15, 1567. [Google Scholar] [CrossRef]
- Zheng, B.; Wen, C. Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013, 2013, 199. [Google Scholar] [CrossRef]
- Gaber, A.; Ahmad, H. Solitary wave solutions for space-time fractional coupled integrable dispersionless system via generalized kudryashov method. Facta Univ. Ser. Math. Inform. 2021, 35, 1439–1449. [Google Scholar] [CrossRef]
- Bibi, S.; Mohyud-Din, S.T.; Khan, U.; Ahmed, N. Khater method for nonlinear Sharma Tasso-Olever (STO) equation of fractional order. Results Phys. 2017, 7, 4440–4450. [Google Scholar] [CrossRef]
- Zheng, B. Exp-function method for solving fractional partial differential equations. Sci. World J. 2013, 2013, 465723. [Google Scholar] [CrossRef] [PubMed]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Investigating Families of Soliton Solutions for the Complex Structured Coupled Fractional Biswas–Arshed Model in Birefringent Fibers Using a Novel Analytical Technique. Fractal Fract. 2023, 7, 491. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Probing Families of Optical Soliton Solutions in Fractional Perturbed Radhakrishnan–Kundu–Lakshmanan Model with Improved Versions of Extended Direct Algebraic Method. Fractal Fract. 2023, 7, 512. [Google Scholar] [CrossRef]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Investigating Symmetric Soliton Solutions for the Fractional Coupled Konno–Onno System Using Improved Versions of a Novel Analytical Technique. Mathematics 2023, 11, 2686. [Google Scholar] [CrossRef]
- Mirhosseini-Alizamini, S.M.; Rezazadeh, H.; Eslami, M.; Mirzazadeh, M.; Korkmaz, A. New extended direct algebraic method for the Tzitzica type evolution equations arising in nonlinear optics. Comput. Methods Differ. Equ. 2020, 8, 28–53. [Google Scholar]
- Boussinesq, J. Théorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. J. Math. Pures Appl. 1872, 17, 55–108. [Google Scholar]
- Whitham, G.Á. A general approach to linear and non-linear dispersive waves using a Lagrangian. J. Fluid Mech. 1965, 22, 273–283. [Google Scholar] [CrossRef]
- Whitham, G.B. Variational methods and applications to water waves. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1967, 299, 6–25. [Google Scholar]
- Atilgan, E.; Senol, M.; Kurt, A.; Tasbozan, O. New wave solutions of time-fractional coupled Boussinesq–Whitham–Broer–Kaup equation as a model of water waves. China Ocean. Eng. 2019, 33, 477–483. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, H. Coupled Fractional Traveling Wave Solutions of the Extended Boussinesq–Whitham–Broer–Kaup-Type Equations with Variable Coefficients and Fractional Order. Symmetry 2021, 13, 1396. [Google Scholar] [CrossRef]
- Yu, J. Lie symmetry analysis, power series solutions and conservation laws of time fractional coupled Boussinesq-Whitham-Broer-Kaup equations. Authorea Prepr. 2022. [Google Scholar] [CrossRef]
- Tarasov, V.E. On chain rule for fractional derivatives. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 1–4. [Google Scholar] [CrossRef]
- He, J.H.; Elagan, S.K.; Li, Z.B. Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 2012, 376, 257–259. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Budak, H.; Usta, H. On generalized the conformable fractional calculus. TWMS J. Appl. Eng. Math. 2019, 9, 792–799. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sawalha, M.M.; Mukhtar, S.; Shah, R.; Ganie, A.H.; Moaddy, K. Solitary Waves Propagation Analysis in Nonlinear Dynamical System of Fractional Coupled Boussinesq-Whitham-Broer-Kaup Equation. Fractal Fract. 2023, 7, 889. https://doi.org/10.3390/fractalfract7120889
Al-Sawalha MM, Mukhtar S, Shah R, Ganie AH, Moaddy K. Solitary Waves Propagation Analysis in Nonlinear Dynamical System of Fractional Coupled Boussinesq-Whitham-Broer-Kaup Equation. Fractal and Fractional. 2023; 7(12):889. https://doi.org/10.3390/fractalfract7120889
Chicago/Turabian StyleAl-Sawalha, M. Mossa, Safyan Mukhtar, Rasool Shah, Abdul Hamid Ganie, and Khaled Moaddy. 2023. "Solitary Waves Propagation Analysis in Nonlinear Dynamical System of Fractional Coupled Boussinesq-Whitham-Broer-Kaup Equation" Fractal and Fractional 7, no. 12: 889. https://doi.org/10.3390/fractalfract7120889
APA StyleAl-Sawalha, M. M., Mukhtar, S., Shah, R., Ganie, A. H., & Moaddy, K. (2023). Solitary Waves Propagation Analysis in Nonlinear Dynamical System of Fractional Coupled Boussinesq-Whitham-Broer-Kaup Equation. Fractal and Fractional, 7(12), 889. https://doi.org/10.3390/fractalfract7120889





