Exploring Integral ϝ-Contractions with Applications to Integral Equations and Fractional BVPs
Abstract
:1. Introduction
- (B. ⇔ for all ,
- (B. for all ,
- (B. for all and
- (F. Ϝ is strictly increasing,
- (F. If in , then ,
- (F. There exist some such that .
- Let be a metric space and mapping is called Ϝ-contraction if there exists . Where and implies
- (A is complete,
- (A is a continuous, and is compatible.
- Then, and have a unique point of coincidence.
2. Extended Integral Ϝ-Contraction
3. Ω-Ϝ)-Contraction
- . ,
- . ,
- . ℑ is continuous in the second variable.
- . is complete,
- . is complete, is a continuous, and is a compatible pair,
- then and have a unique point of coincidence.
4. Applications of Extended Integral Ϝ-Contraction and Ω-Ϝ)-Contraction
4.1. Application in Nonlinear BVP
4.1.1. Using the Extended Integral Ϝ-Contraction
4.1.2. Using --Contraction
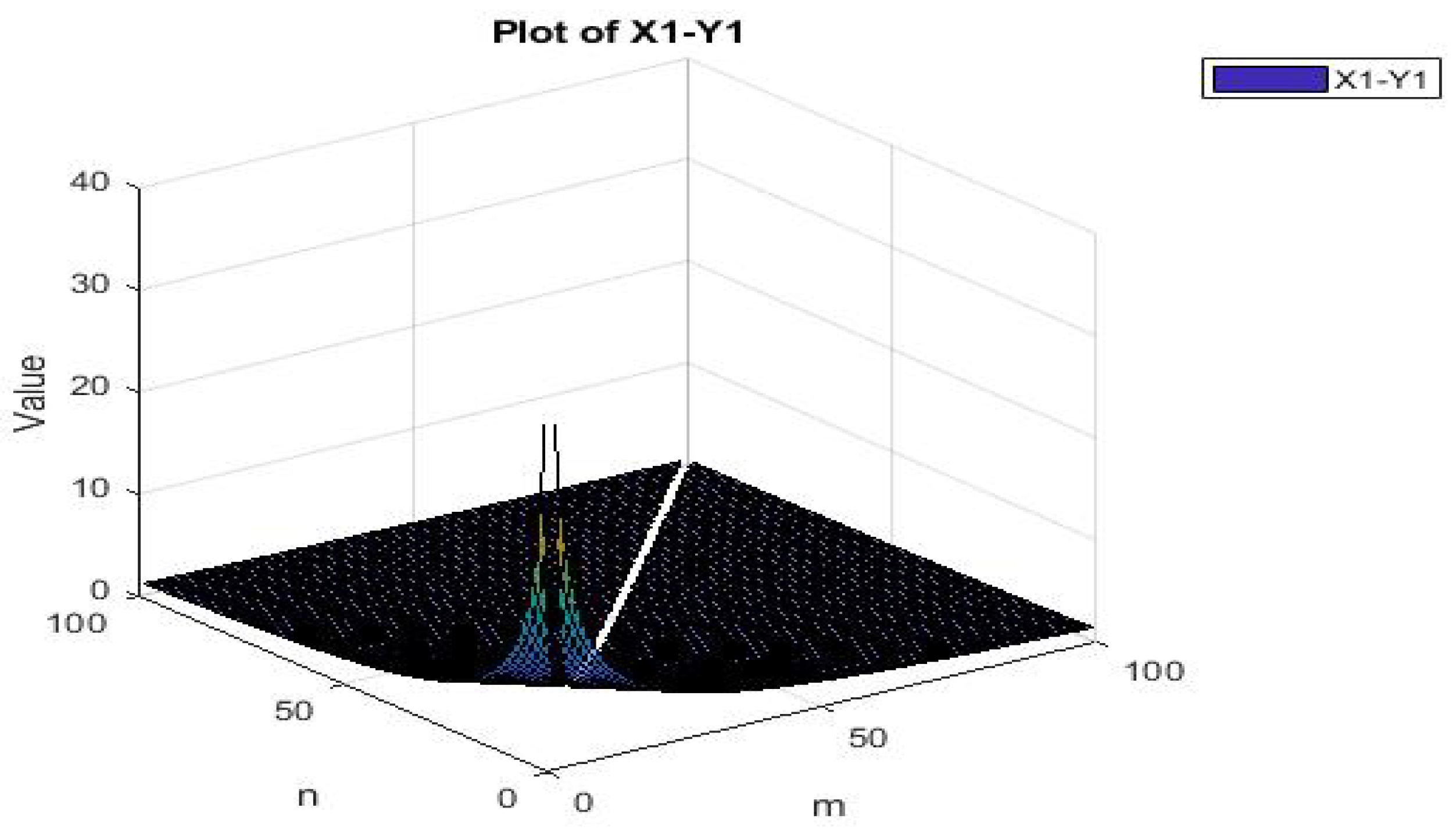
4.2. Solution of Integral Equation Using --Contraction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Branciari, A. A fixed-point theorem for mappings satisfying a general contractive condition of integral type. Int. J. Math. Math. Sci. 2002, 29, 531–536. [Google Scholar] [CrossRef]
- Ozturk, V.; Turkoglu, D. Integral type contractions in partial metric spaces. AIP Conf. Proc. 2019, 2086, 030031. [Google Scholar]
- Czerwik, S. Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostrav. 1993, 1, 5–11. [Google Scholar]
- Czerwik, S. Nonlinear set-valued contraction mappings in b-metric spaces. Atti Semin. Mat. Fis. Univ. Modena 1998, 46, 263–276. [Google Scholar]
- Suzuki, T. Basic inequality on a b-metric space and its applications. J. Inequal. Appl. 2017, 2017, 256. [Google Scholar] [CrossRef] [PubMed]
- Sharma, N. Fixed point theorem in cone b-metric spaces using contractive mappings. Global J. Pure Appl. Math. 2017, 13, 2997–3004. [Google Scholar]
- Kanwal, S.; Hanif, U.; Noorwali, M.E.; Alam, M.A. On fixed-point results of generalized contractions. J. Funct. Spaces 2022, 2022, 9167716. [Google Scholar] [CrossRef]
- Azam, A.; Khan, M.N.; Mehmood, N.; Radenović, S.; Došenović, T. Coincidence point of L-fuzzy sets endowed with graph. Rev. Real Acad. Cienc. Exactas Fis. Nat. Mat. 2018, 112, 915–931. [Google Scholar] [CrossRef]
- Azam, A.; Mehmood, N.; Ahmad, J.; Radenović, S. Multivalued fixed-point theorems in cone b-metric spaces. J. Inequal. Appl. 2013, 582, 1–9. [Google Scholar] [CrossRef]
- Azam, A.; Rashid, M.; Mehmood, N. Coincidence of crisp and fuzzy functions. J. Nonlinear Sci. Appl. 2016, 9, 5909–5930. [Google Scholar]
- Khan, A.N.M.; Azam, A.; Kočinac, R.D.L. Coincidence of multivalued mappings on metric spaces with a graph. Filomat 2017, 31, 4543–4554. [Google Scholar] [CrossRef]
- Mocanu, M.; Valeriu, P. Some fixed-point theorems for mappings satisfying implicit relations in symmetric spaces. Lib. Math. 2008, 28, 1–14. [Google Scholar]
- Paluszynski, M.; Stempak, K. On quasi-metric and metric spaces. Proc. AMS 2009, 137, 4307–4312. [Google Scholar] [CrossRef]
- Rawashdeh, A.A.; Mehmood, N.; Rashid, M. Coincidence and common fixed-points of integral contractions for L-fuzzy maps with applications in fuzzy functional inclusions. J. Intell. Fuzzy Syst. 2018, 35, 2173–2187. [Google Scholar] [CrossRef]
- Zada, B.M.; Sarwar, M.; Mehmood, N. Common fixed-point results for six mappings via integral contractions with applications. Int. J. Anal. 2016, 2016, 7480469. [Google Scholar]
- Wardowski, D. Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 2012, 94. [Google Scholar] [CrossRef]
- Parvaneh, V.; Hussain, N.; Kadelburg, Z. Generalized Wardowski type fixed-point theorems via α-admissible FG-contractions in b-metric spaces. Acta Math. Sci. 2016, 36, 1445–1456. [Google Scholar] [CrossRef]
- Sarwar, M.; Zada, M.B.; Erhan, I.M. Common fixed-point theorems of integral type contraction on metric spaces and its applications to system of functional equations. Fixed Point Theory Appl. 2015, 2015, 217. [Google Scholar] [CrossRef]
- Vujaković, J.Z.; Radenović, S.N. On some F-contraction of Piri-Kumam-Dung-type mappings in metric spaces. Vojnoteh. Glas. 2020, 68, 697–714. [Google Scholar] [CrossRef]
- Wardowski, D. Solving existence problems via Ϝ-contractions. Proc. Am. Math. Soc. 2018, 146, 1585–1598. [Google Scholar] [CrossRef]
- Cosentino, M.; Vetro, P. Fixed point results for F-contractive mappings of Hardy-Rogers-type. Filomat 2014, 28, 715–722. [Google Scholar] [CrossRef]
- Poniecki, A. The Banach Contraction Principle; The University of Chicago: Chicago, IL, USA, 2008; Available online: https://www.math.uchicago.edu/~may/VIGRE/VIGRE2009/REUPapers/Poniecki.pdf (accessed on 13 October 2023).
- Radenovic, S.; Vetro, F.; Vujaković, J. An alternative and easy approach to fixed-point results via simulation functions. Demonstr. 2017, 50, 223–230. [Google Scholar] [CrossRef]
- Carić, E.; Ðekić, D.D.; Mitrović, D.Z.; Pucić, D.; Aydi, H. On some recent results concerning F-Suzuki-contractions in b-metric spaces. Mathematics 2020, 8, 940. [Google Scholar]
- Hammad, A.H.; Sen, L.D.M. Fixed-point results for a generalized almost (s,q)-Jaggi F-contraction-type on b-Metric-Like Spaces. Mathematics 2020, 8, 63. [Google Scholar] [CrossRef]
- Carić, B.; Došenović, T.; George, R.; Mitrović, Z.D.; Radenović, S. On Jungck–Branciari–Wardowski Type Fixed Point Results. Mathematics 2021, 9, 161. [Google Scholar] [CrossRef]
- Huang, H.; Zoto, K.; Mitrović, D.Z.; Radenovií, S. Fixed Point Results for Generalized F-Contractions in b-Metric-like Spaces. Fractal Fract. 2022, 6, 272. [Google Scholar] [CrossRef]
- Mehmood, N.; Khan, I.A.; Nawaz, M.A.; Ahmad, N. Existence results for ABC-fractional BVP via new fixed point results of F-Lipschitzian mappings. Demonstr. Math. 2022, 55, 452–469. [Google Scholar] [CrossRef]
- Berardi, M.; Girardi, G. Modeling plant water deficit by a non-local root water uptake term in the unsaturated flow equation. Commun. Nonlinear Sci. Numer. Simul. 2024, 128, 107583. [Google Scholar] [CrossRef]
- Difonzo, F.V.; Di Lena, F. Numerical modeling of peridynamic Richards’ equation with piecewise smooth initial conditions using spectral methods. Symmetry 2023, 15, 960. [Google Scholar] [CrossRef]
- Kavvas, L.M.; Ercan, A.; Polsinelli, J. Governing equations of transient soil water flow and soil water flux in multi-dimensional fractional anisotropic media and fractional time. Hydrol. Earth Syst. Sci. 2017, 21, 1547–1557. [Google Scholar] [CrossRef]
- Sun, G.H.; Meerschaert, M.M.; Zhang, Y.; Zhu, J.; Chen, W. A fractal Richards’ equation to capture the non-Boltzmann scaling of water transport in unsaturated media. Adv. Water Resour. 2013, 52, 292–295. [Google Scholar] [CrossRef] [PubMed]
- Shah, K.; Zeb, S.; Khan, A.R. Existence of triple positive solutions for boundary value problem of nonlinear fractional differential equations. Comput. Methods Differ. Equ. 2017, 5, 158–169. [Google Scholar]
- Azam, A. Coincidence points of mappings and relations with applications. Fixed Point Theory Appl. 2012, 2012, 50. [Google Scholar] [CrossRef]
- Corduneanu, C. Integral Equations and Applications; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Rahman, M. Integral Equations and Their Applications; WIT Press: Boston, MA, USA, 2007. [Google Scholar]
- Wazwaz, M.A. Linear and Nonlinear Integral Equations, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nisar, Z.; Mehmood, N.; Azam, A.; Ali, F.; Al-Kadhi, M.A. Exploring Integral ϝ-Contractions with Applications to Integral Equations and Fractional BVPs. Fractal Fract. 2023, 7, 833. https://doi.org/10.3390/fractalfract7120833
Nisar Z, Mehmood N, Azam A, Ali F, Al-Kadhi MA. Exploring Integral ϝ-Contractions with Applications to Integral Equations and Fractional BVPs. Fractal and Fractional. 2023; 7(12):833. https://doi.org/10.3390/fractalfract7120833
Chicago/Turabian StyleNisar, Zubair, Nayyar Mehmood, Akbar Azam, Faryad Ali, and Mohammed A. Al-Kadhi. 2023. "Exploring Integral ϝ-Contractions with Applications to Integral Equations and Fractional BVPs" Fractal and Fractional 7, no. 12: 833. https://doi.org/10.3390/fractalfract7120833
APA StyleNisar, Z., Mehmood, N., Azam, A., Ali, F., & Al-Kadhi, M. A. (2023). Exploring Integral ϝ-Contractions with Applications to Integral Equations and Fractional BVPs. Fractal and Fractional, 7(12), 833. https://doi.org/10.3390/fractalfract7120833





