Global Dynamics and Bifurcations of an Oscillator with Symmetric Irrational Nonlinearities
Abstract
:1. Introduction
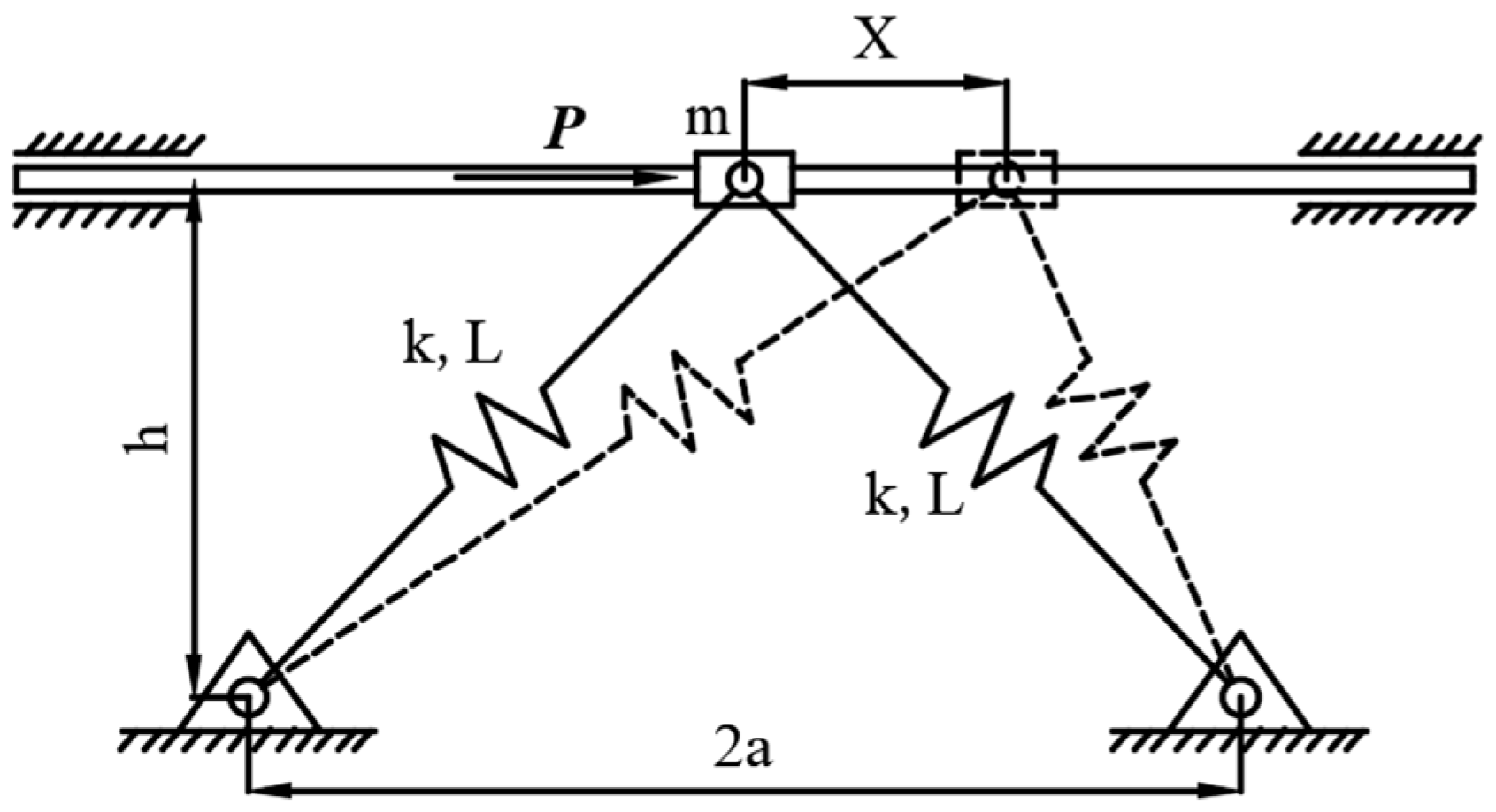
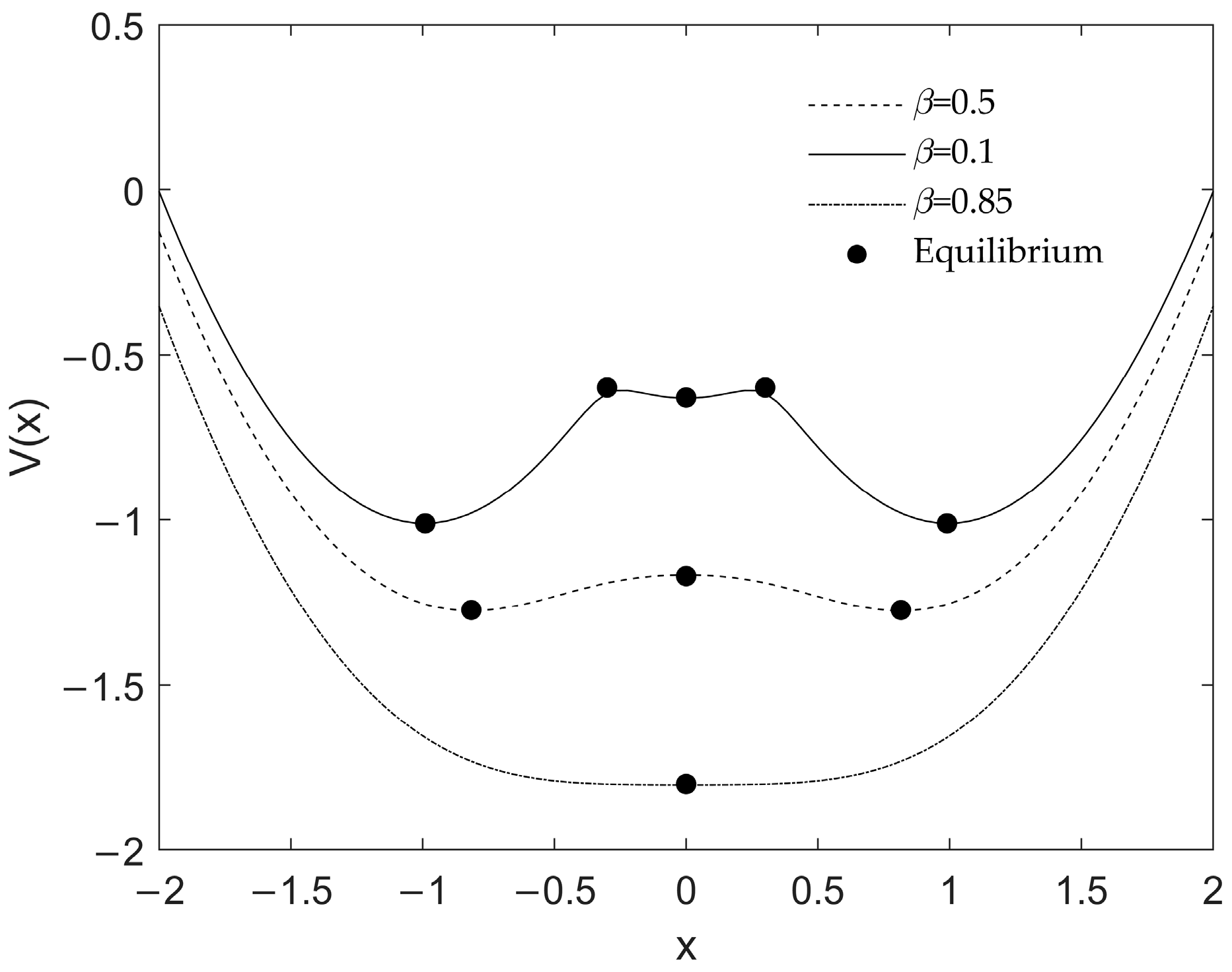
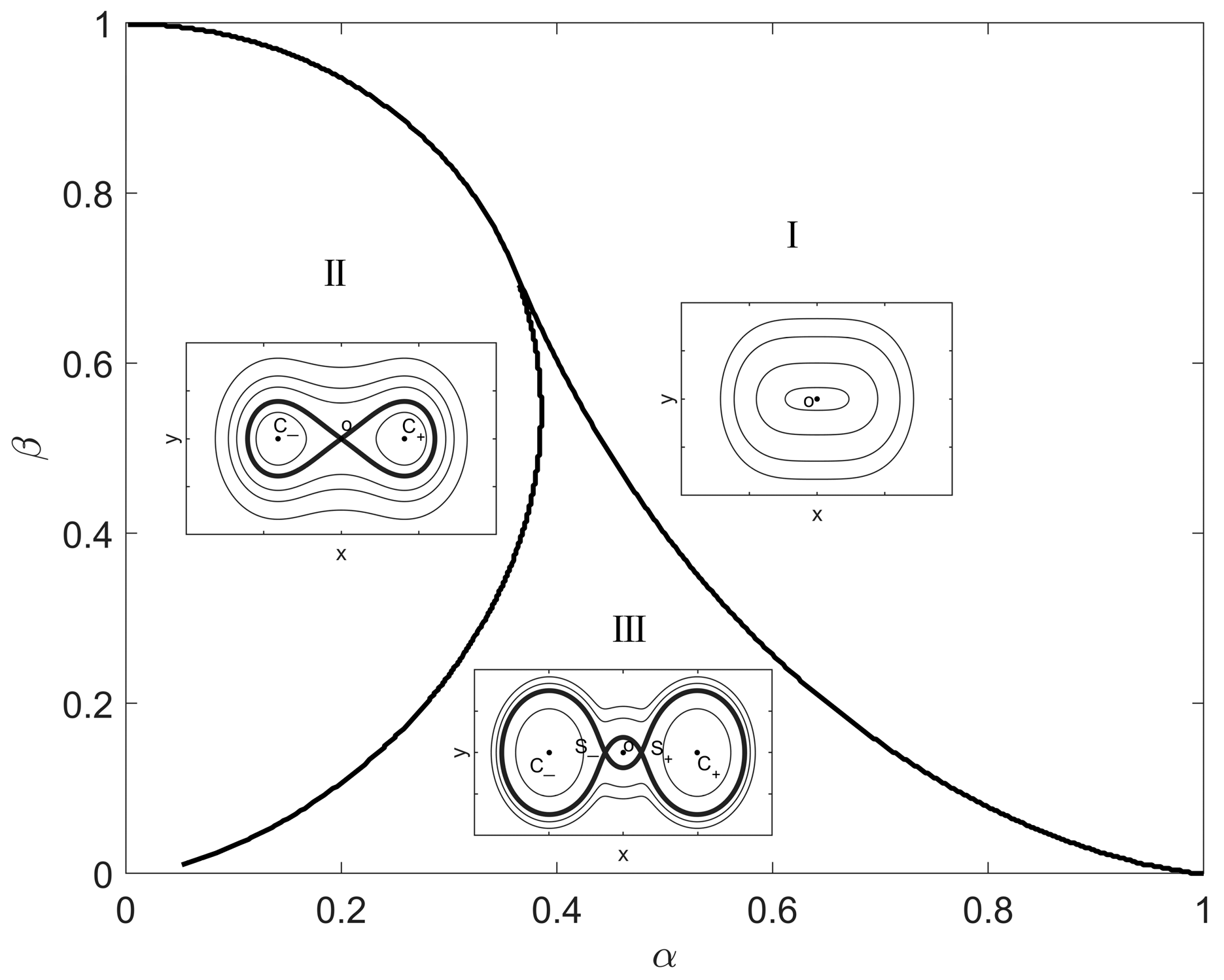
2. Static Analysis of the Irrationally Nonlinear Oscillator
3. Analysis of Resonant Responses
3.1. Resonant Responses in the Case of the Mono-Potential Well
3.2. Periodic Responses in the Case of Double Potential Wells
3.2.1. Periodic Responses near Each Nontrivial Equilibrium Point
3.2.2. Inter-Well Periodic Solutions
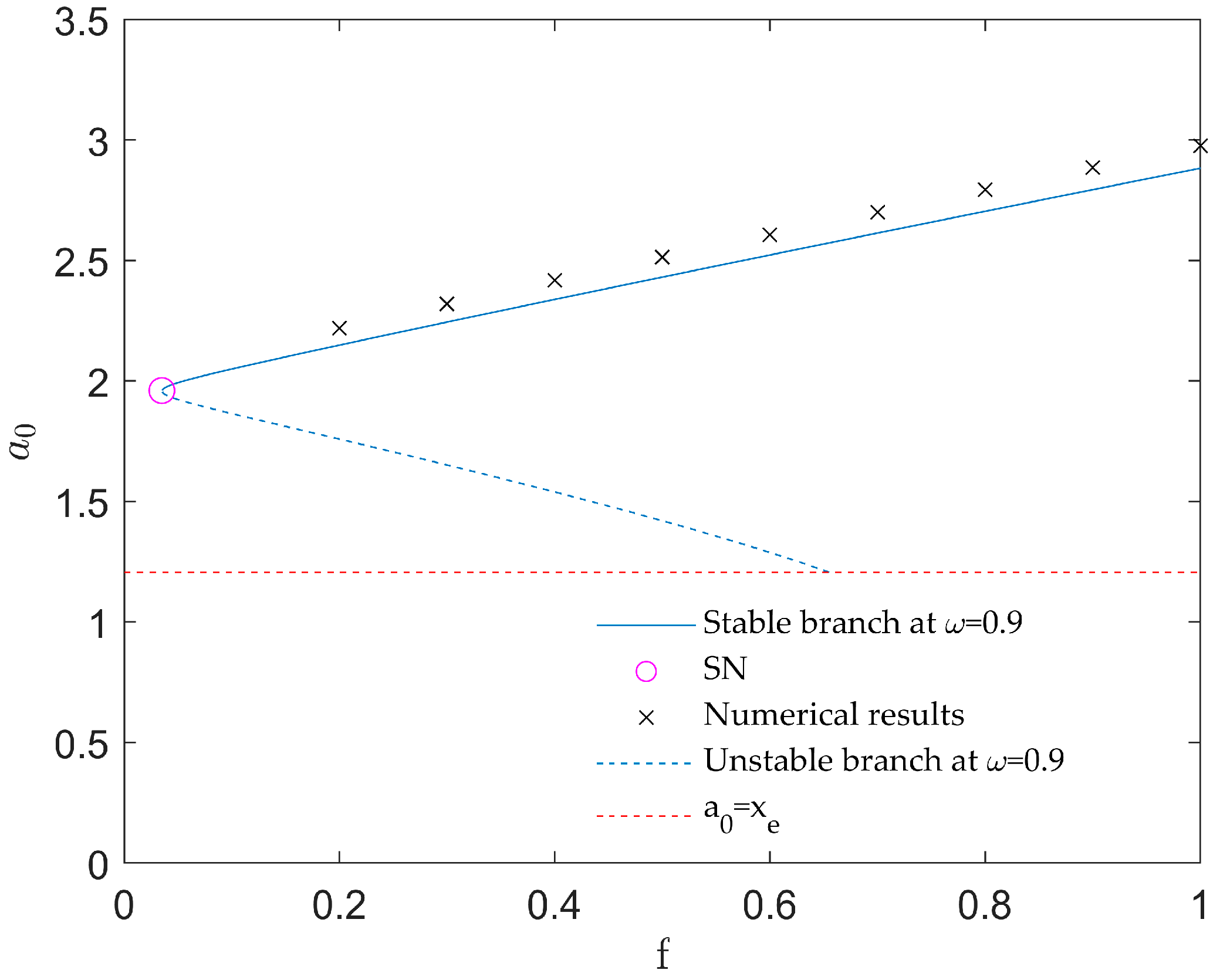
4. Numerical Results
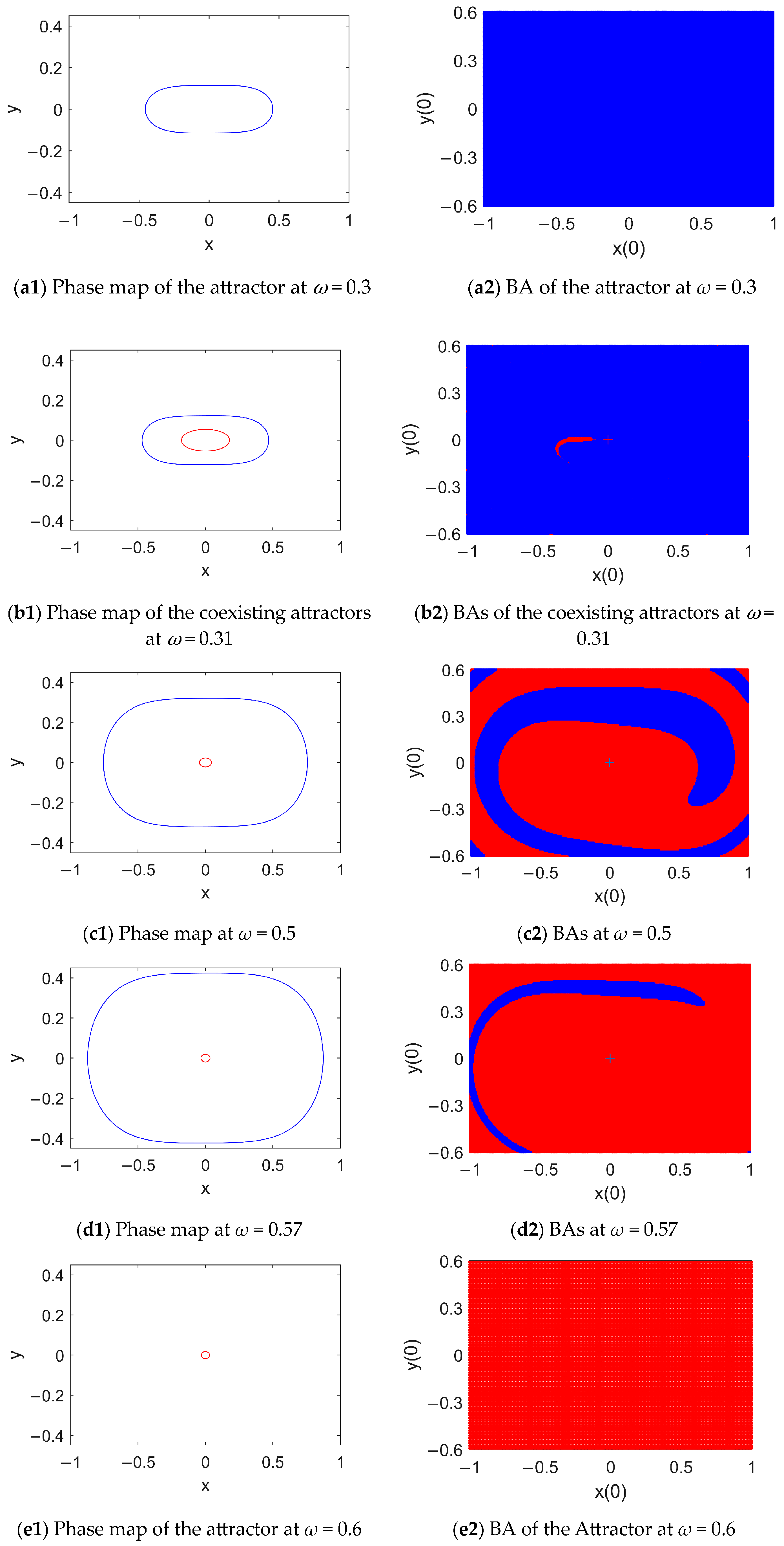
4.1. Attractors and Their BAs in the Case of Mono Potential Well
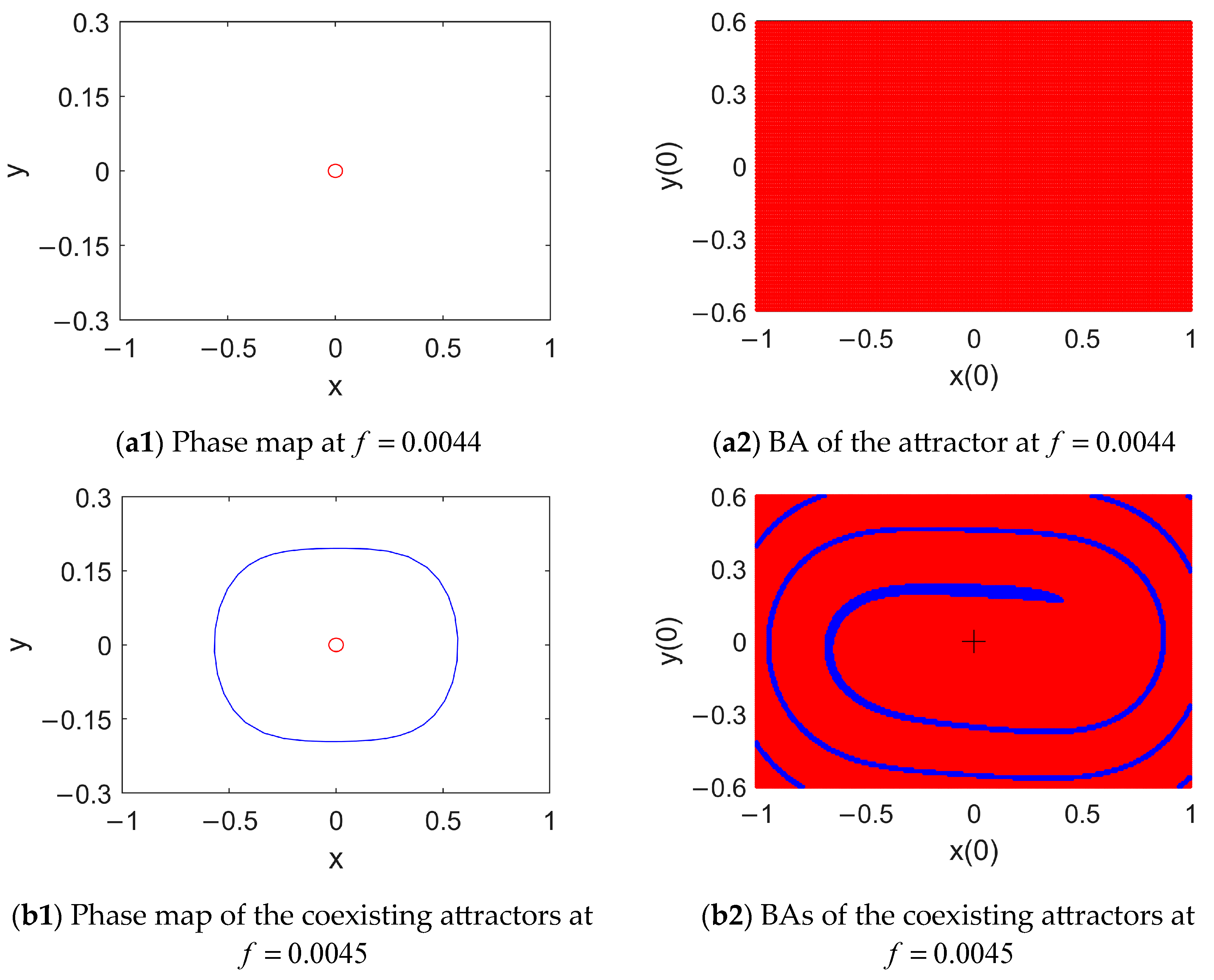
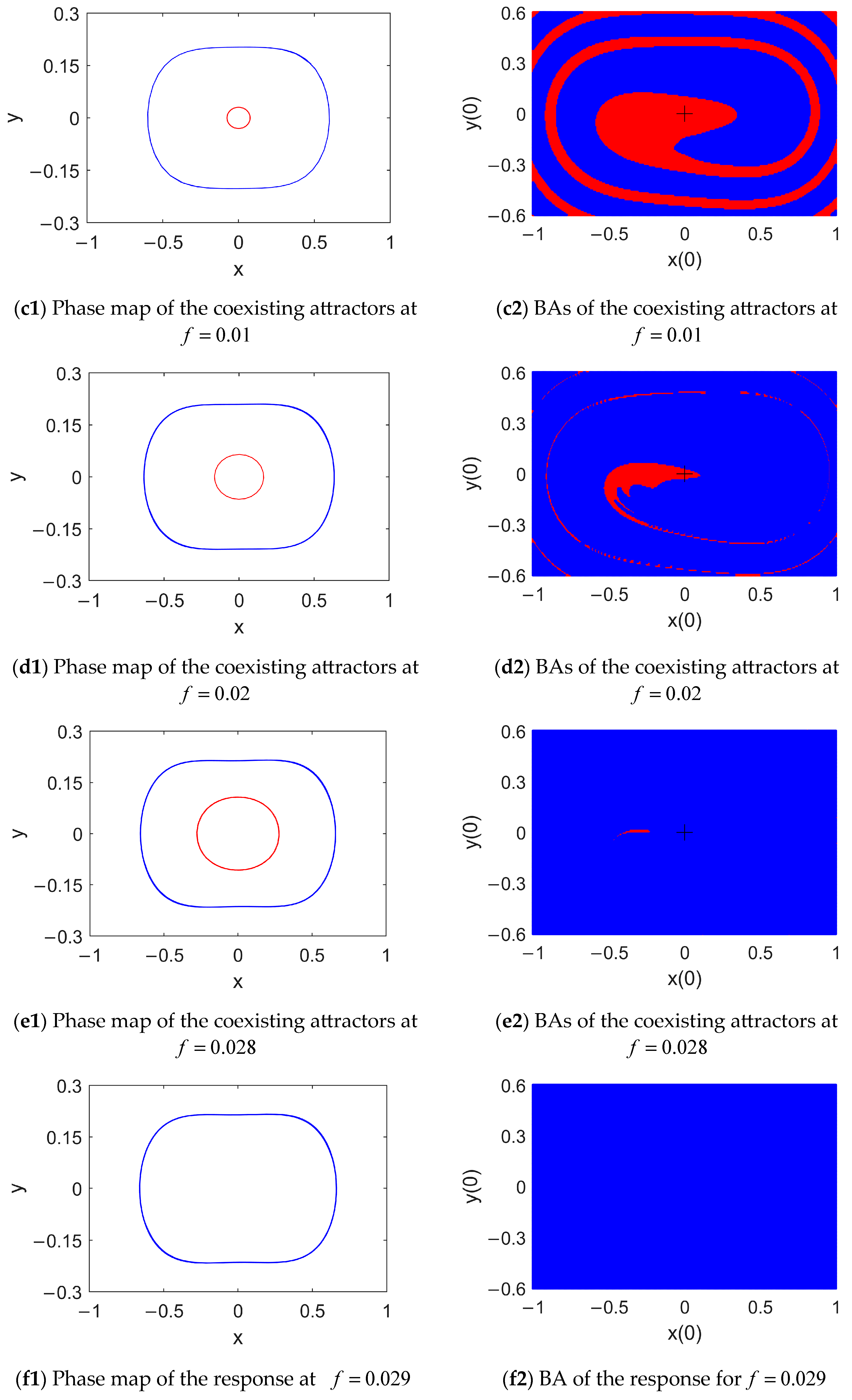
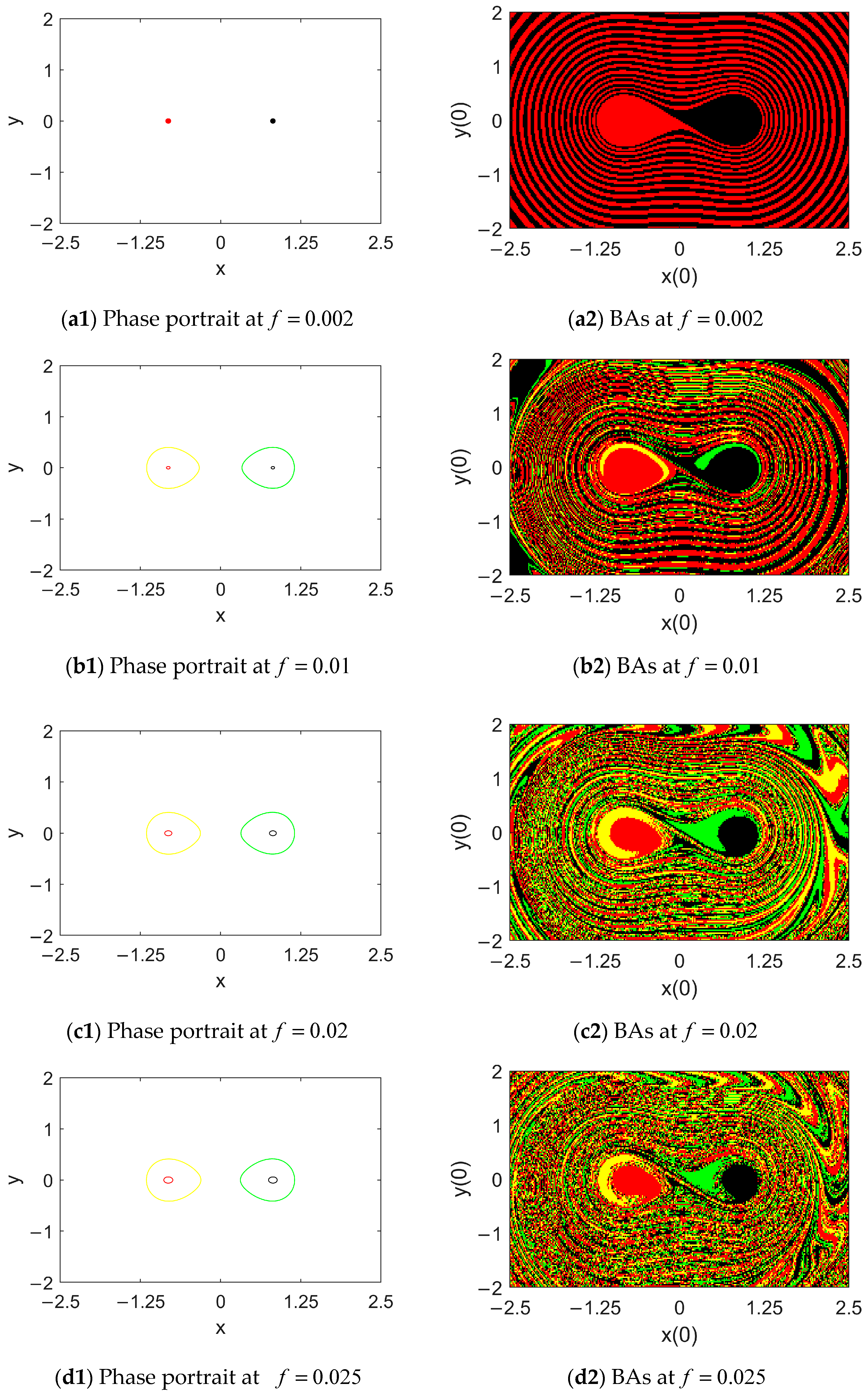
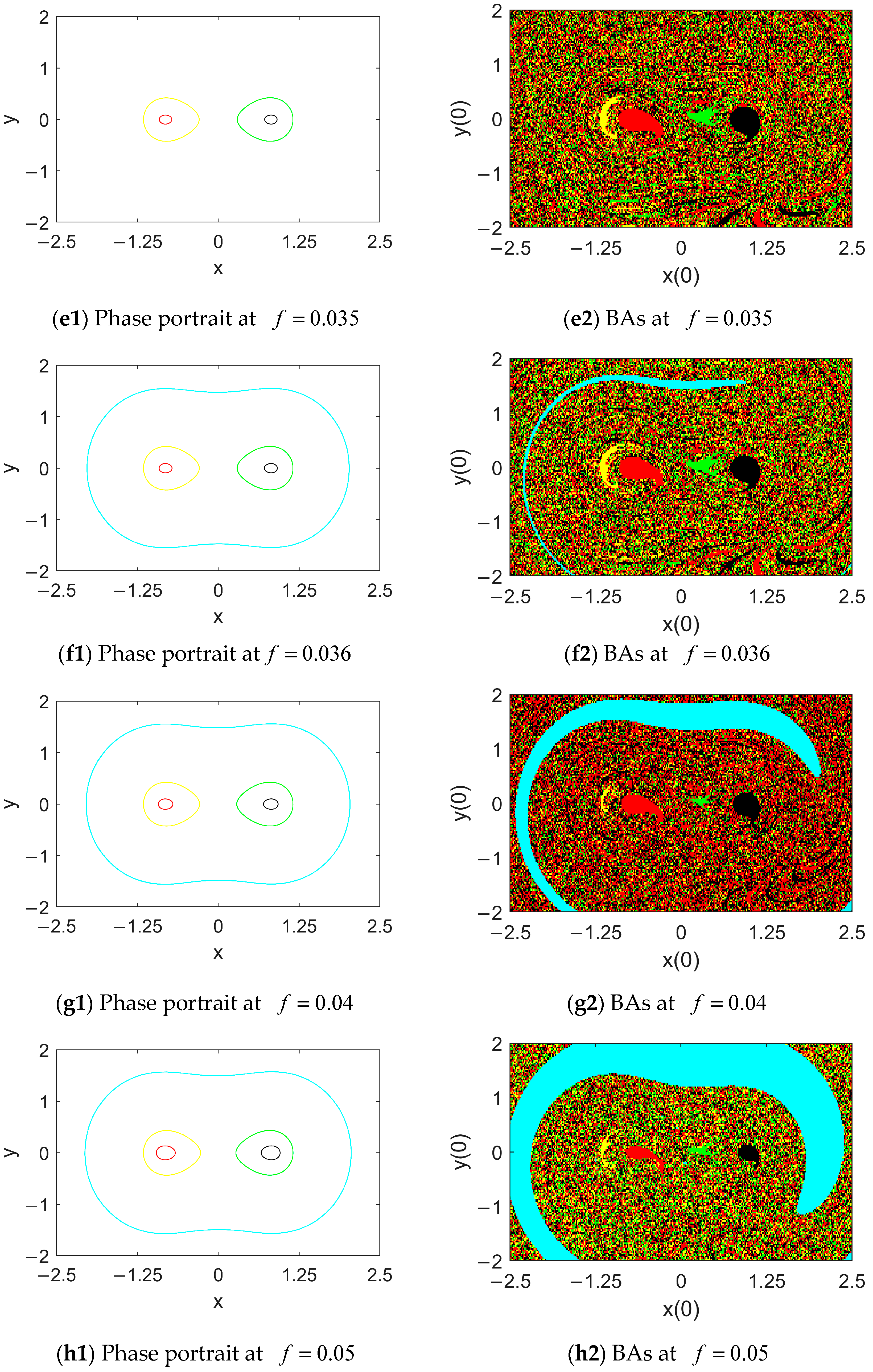
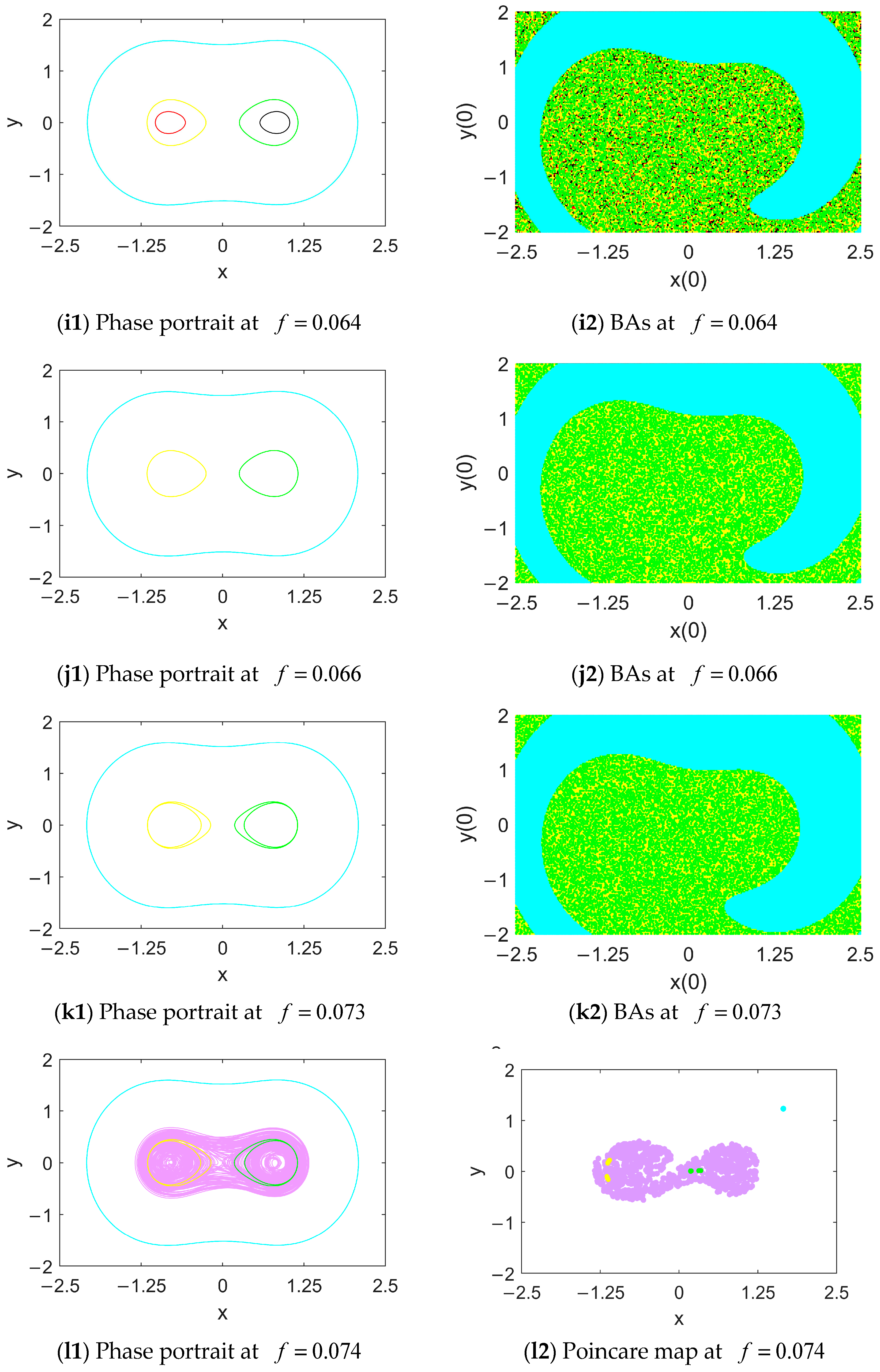
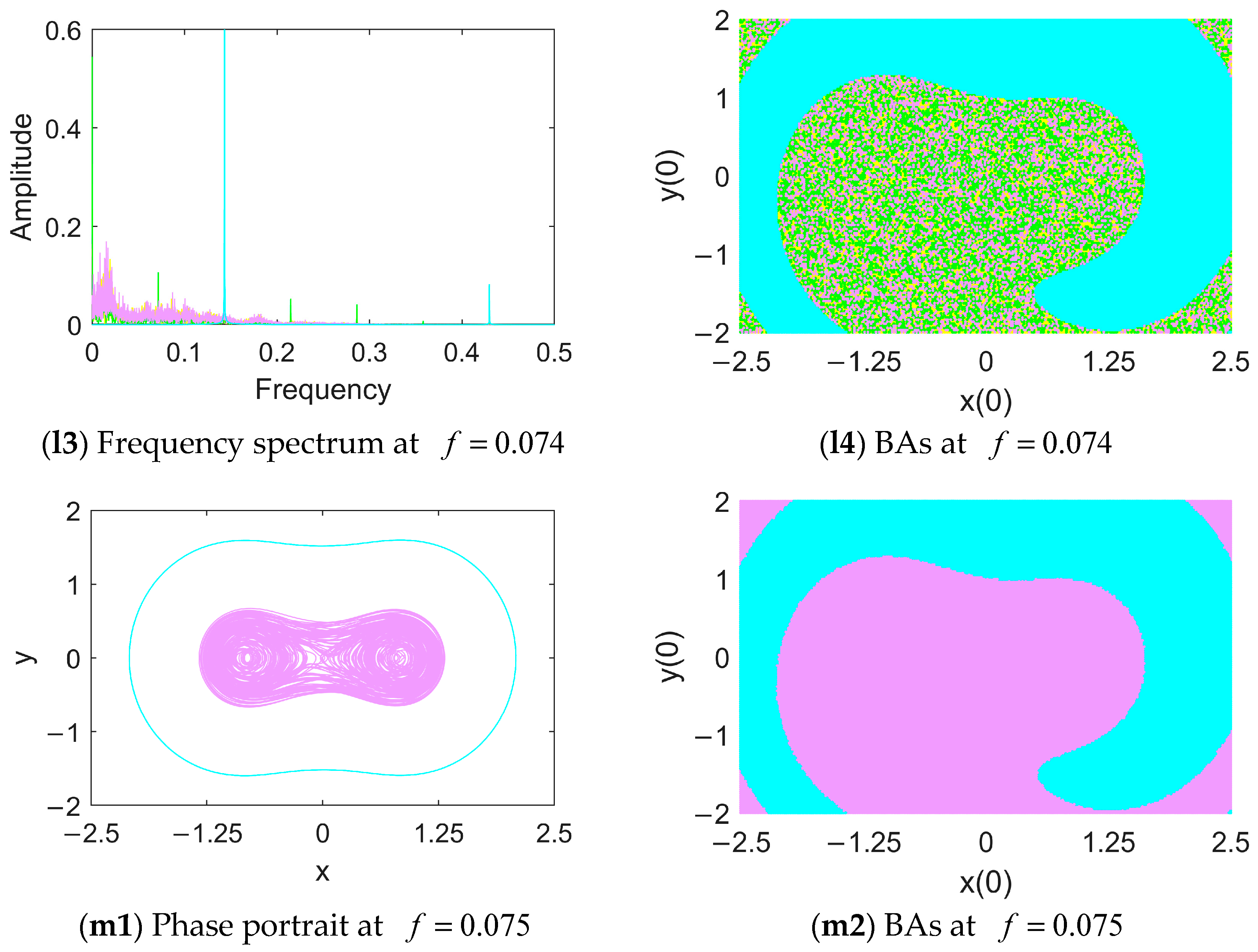
4.2. Attractors and Their BAs in the Case of Double Potential Wells
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Cao, Q. The recent advances for an archetypal smooth and discontinuous oscillator. Int. J. Mech. Sci. 2022, 214, 106904. [Google Scholar] [CrossRef]
- Cao, Q.; Wiercigroch, M.; Pavlovskaia, E.E.; Grebogi, C.; Thompson, J.M.T. Archetypal oscillator for smooth and discontinuous dynamics. Phys. Rev. E 2006, 74, 046218. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, L. Snap-through piezoelectric energy harvesting. J. Sound Vib. 2014, 333, 4314–4325. [Google Scholar] [CrossRef]
- Yang, T.; Cao, Q. Dynamics and high-efficiency of a novel multi-stable energy harvesting system. Chaos Solitons Fractals 2020, 131, 109516. [Google Scholar] [CrossRef]
- Ramlan, R.; Brennan, M.J.; Mace, B.R.; Kovacic, I. Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dyn. 2009, 59, 545–558. [Google Scholar] [CrossRef]
- Han, N.; Cao, Q. A parametrically excited pendulum with irrational nonlinearity. Int. J. Non-Linear Mech. 2017, 88, 122–134. [Google Scholar] [CrossRef]
- Wu, B.; Liu, W.; Zhong, H.; Lim, C.W. A Modified Newton–Harmonic Balance Approach to Strongly Odd Nonlinear Oscillators. J. Vib. Eng. Technol. 2019, 8, 721–736. [Google Scholar] [CrossRef]
- Han, Y.; Cao, Q.; Ji, J. Nonlinear Dynamics of a Smooth and Discontinuous Oscillator with Multiple Stability. Int. J. Bifurc. Chaos 2016, 25, 1530038. [Google Scholar] [CrossRef]
- Adile, A.D.; Kenmogne, F.; Tewa, A.K.S.; Simo, H.; Tahir, A.M.; Kumar, S. Dynamics of a mechanical network consisting of discontinuous coupled system oscillators with strong irrational nonlinearities: Resonant states and bursting waves. Int. J. Non-Linear Mech. 2021, 137, 103812. [Google Scholar] [CrossRef]
- Kenmogne, F.; Noah, P.M.A.; Tafo, J.B.G.; Adoum, D.A.; Sali, M.; Abakar, M.T.; Eno, R.; Bell, E.Y. Stability of modulated signals in the damped mechanical network of discontinuous coupled system oscillators with irrational nonlinearities. Arch. Appl. Mech. 2022, 92, 3077–3091. [Google Scholar] [CrossRef]
- Han, N.; Cao, Q. Global bifurcations of a rotating pendulum with irrational nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 431–445. [Google Scholar] [CrossRef]
- Han, N.; Cao, Q. Rotating pendulum with smooth and discontinuous dynamics. Int. J. Mech. Sci. 2017, 127, 91–102. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Jiang, W.; Ding, H.; Chen, L.; Bi, Q. Bursting oscillation of a pendulum with irrational nonlinearity. Int. J. Non-Linear Mech. 2023, 148, 104299. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, J.; Luo, X. Research on New Types of Suspension Vibration Reduction Systems (SVRSs) with Geometric Nonlinear Damping. Math. Probl. Eng. 2021, 2021, 6627693. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Q.; Wiercigroch, M.; Leger, A. Analysis of the periodic solutions of a smooth and discontinuous oscillator. Acta Mech. Sin. 2013, 29, 575–582. [Google Scholar] [CrossRef]
- Chen, E.; Chu, B.; Wang, Y. Modelling and experimental investigations on the geometrical nonlinear dynamics of the SD oscillator. Int. J. Model. Identif. Control. 2016, 25, 190–198. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Huang, L. Global dynamics and bifurcation for a discontinuous oscillator with irrational nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 2023, 119, 107073. [Google Scholar] [CrossRef]
- Han, Q.; Xu, W.; Sun, J. Stochastic response and bifurcation of periodically driven nonlinear oscillators by the generalized cell mapping method. Phys. A Stat. Mech. Its Appl. 2016, 458, 115–125. [Google Scholar] [CrossRef]
- Han, Y.; Cao, Q.; Chen, Y.; Marian, W. A novel smooth and discontinuous oscillator with strong irrational nonlinearities. Science China Physics. Mech. Astron. 2012, 55, 1832–1843. [Google Scholar] [CrossRef]
- Lai, S.K.; Wu, B.S.; Lee, Y.Y. Free vibration analysis of a structural system with a pair of irrational nonlinearities. Appl. Math. Model. 2017, 45, 997–1007. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J. Power capture performance of an oscillating-body WEC with nonlinear snap through PTO systems in irregular waves. Appl. Ocean. Res. 2015, 52, 261–273. [Google Scholar] [CrossRef]
- Qin, B.; Shang, H. Initial-Sensitive Dynamical Behaviors of a Class of Geometrically Nonlinear Oscillators. Shock Vib. 2022, 2022, 6472678. [Google Scholar] [CrossRef]
- Han, N.; Liu, M. Dynamic Behavior Analysis of a Rotating Smooth and Discontinuous Oscillator with Irrational Nonlinearity. Mod. Appl. Sci. 2018, 12. [Google Scholar] [CrossRef]
- Fakhreddine, H.; Adri, A.; Chajdi, M.; Rifal, S.; Benamar, R. A multimode approach to geometrically non-linear forced vibration of beams carrying point masses. Diagnostyka 2020, 21, 23–33. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Q.; Han, J.; Wang, W.; Wang, T.; Cao, X.; Hao, S. Design and investigation of a quad-stable piezoelectric vibration energy harvester by using geometric nonlinearity of springs. J. Sound Vib. 2023, 547, 117484. [Google Scholar] [CrossRef]
- Ahmadi, A.; Parthasarathy, S.; Natiq, H.; Jafari, S.; Franovic, I.; Rajagopal, K. A non-autonomous mega-extreme multistable chaotic system. Chaos Solitons Fractals 2023, 174, 113765. [Google Scholar] [CrossRef]
- Li, C.; Chen, G.; Kurths, J.; Lei, T.; Liu, Z. Dynamic transport: From bifurcation to multistability. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105600. [Google Scholar] [CrossRef]
- Castro, D.C.H.L.; Orlando, D.; Gonçalves, P.B. Static and dynamic nonlinear behavior of a multistable structural system consisting of two coupled von Mises trusses. Int. J. Non-Linear Mech. 2023, 156, 104510. [Google Scholar] [CrossRef]
- Wang, Z.; Shang, H. Multistability and Jump in the Harmonically Excited SD Oscillator. Fractal Fract. 2023, 7, 7040314. [Google Scholar] [CrossRef]
- Duc, H.D.; Ashraf, M.Z.; Do, V.T. Finite element modeling of free vibration of cracked nanoplates with flexoelectric effects. Eur. Phys. J. Plus 2022, 137, 447. [Google Scholar]
- Pham, T.D.; Do, V.T.; Doan, T.L. Free vibration of Functionally graded sandwice plates with stiffeners based on the thied-order shear deformation theory. Vietnam J. Mech. 2016, 2, 103122. [Google Scholar]
- Nguyen, C.T.; Nguyen, T.T.; Do, V.T. New Numerical Results from Simulations of Beams and Space Frame Systems with a Tuned Mass Damper. Materials 2019, 12, 1329. [Google Scholar]
- Dao, M.T.; Do, V.T.; Phung, V.M.; Nguyen, C.T.; Tran, N.D.; Dao, N.M. The application of the nonlocal theory and various shear strain theories for bending and free vibration analysis of organic nanoplates. Mech. Based Des. Struct. Mach. 2023, 2023, 2186893. [Google Scholar]
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Yang, K.; Harne, R.L.; Wang, K.W.; Huang, H. Investigation of a bistable dual-stage vibration isolator under harmonic excitation. Smart Mater. Struct. 2014, 23, 045033. [Google Scholar] [CrossRef]
- Ilyas, S.; Younis, M.I. Resonator-based M/NEMS logic devices: Review of recent advances. Sens. Actuators A 2020, 302, 111821. [Google Scholar] [CrossRef]
- Vagner, D.S.; Fernando, S.B.; Kelly, C.L.; Lbere, L.C.; Szezech, J.D.; Ricardo, L.V.; Murilo, S.B.; Antonio, M.B. Basin of attraction for chimera states in a network of Rossler oscillators. Chaos 2020, 30, 083115. [Google Scholar]
- Bayani, A.; Rajagopal, K.; Khalaf, A.J.M.; Jafari, S.; Leutcho, G.D.; Kengne, J. Dynamical analysis of a new multistable chaotic system with hidden attractor: Antimonotonicity, coexisting multiple attractors, and offset boosting. Phys. Lett. A 2019, 383, 1450–1456. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Shang, H. Global Dynamics and Bifurcations of an Oscillator with Symmetric Irrational Nonlinearities. Fractal Fract. 2023, 7, 888. https://doi.org/10.3390/fractalfract7120888
Liu R, Shang H. Global Dynamics and Bifurcations of an Oscillator with Symmetric Irrational Nonlinearities. Fractal and Fractional. 2023; 7(12):888. https://doi.org/10.3390/fractalfract7120888
Chicago/Turabian StyleLiu, Rong, and Huilin Shang. 2023. "Global Dynamics and Bifurcations of an Oscillator with Symmetric Irrational Nonlinearities" Fractal and Fractional 7, no. 12: 888. https://doi.org/10.3390/fractalfract7120888
APA StyleLiu, R., & Shang, H. (2023). Global Dynamics and Bifurcations of an Oscillator with Symmetric Irrational Nonlinearities. Fractal and Fractional, 7(12), 888. https://doi.org/10.3390/fractalfract7120888





