Author Contributions
Conceptualization, W.F., Q.W., H.L. and S.Z.; methodology, W.F., Y.R. and K.Q.; software, W.F., Q.W., H.L. and K.Q.; validation, W.F., J.Z. and K.Q.; formal analysis, Y.R. and S.Z.; resources, Y.R., J.Z. and S.Z.; writing—original draft preparation, W.F., Q.W., H.L. and K.Q.; writing—review and editing, W.F., K.Q. and H.W.; supervision, W.F.; project administration, J.Z. and K.Q.; funding acquisition, W.F., K.Q. and H.W. All authors have read and agreed to the published version of the manuscript.
Figure 1.
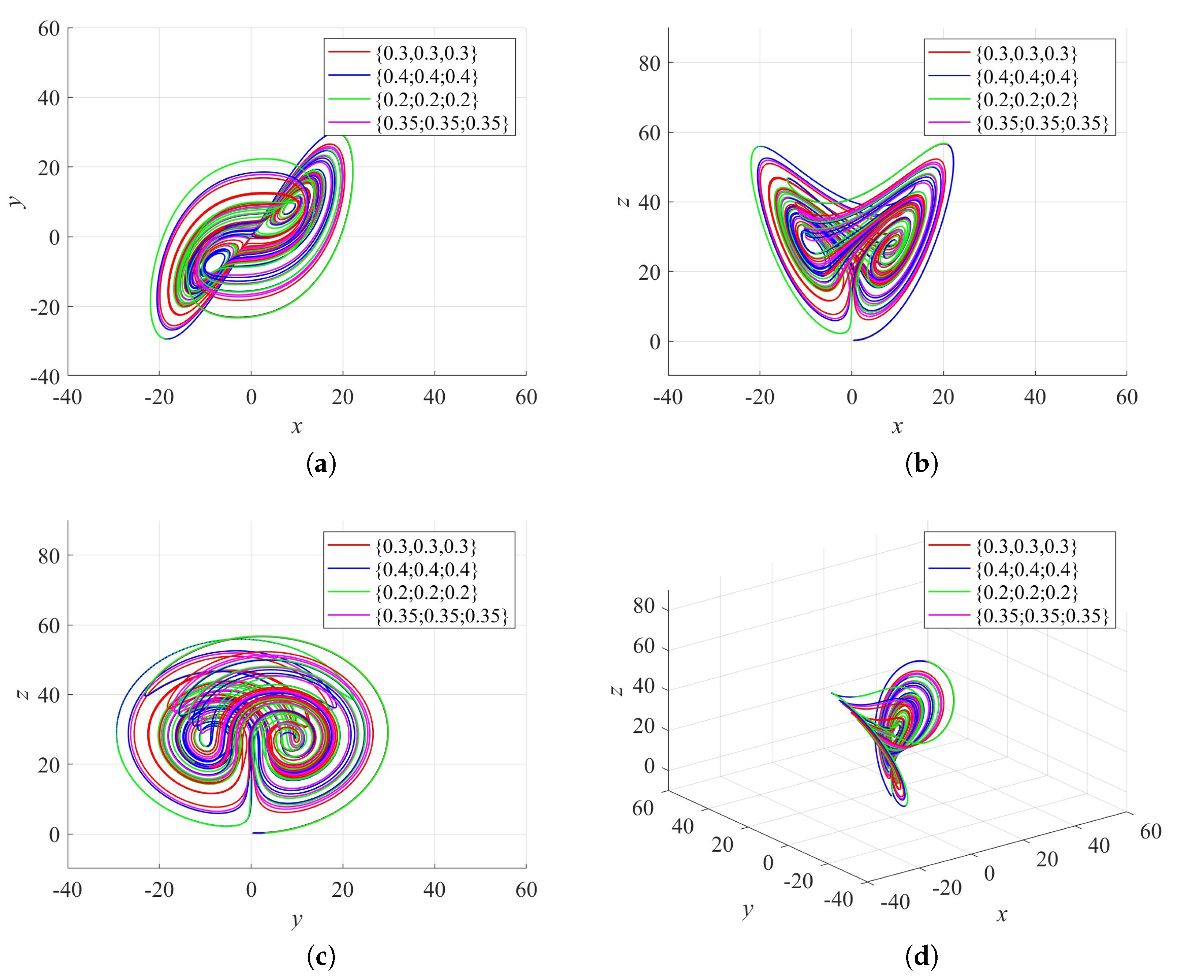
Phase trajectories of the fractional-order 3D Lorenz system with different initial states while the parameters : (a) x-y plane; (b) x-z plane; (c) y-z plane; (d) 3D plot.
Figure 1.
Phase trajectories of the fractional-order 3D Lorenz system with different initial states while the parameters : (a) x-y plane; (b) x-z plane; (c) y-z plane; (d) 3D plot.
Figure 2.
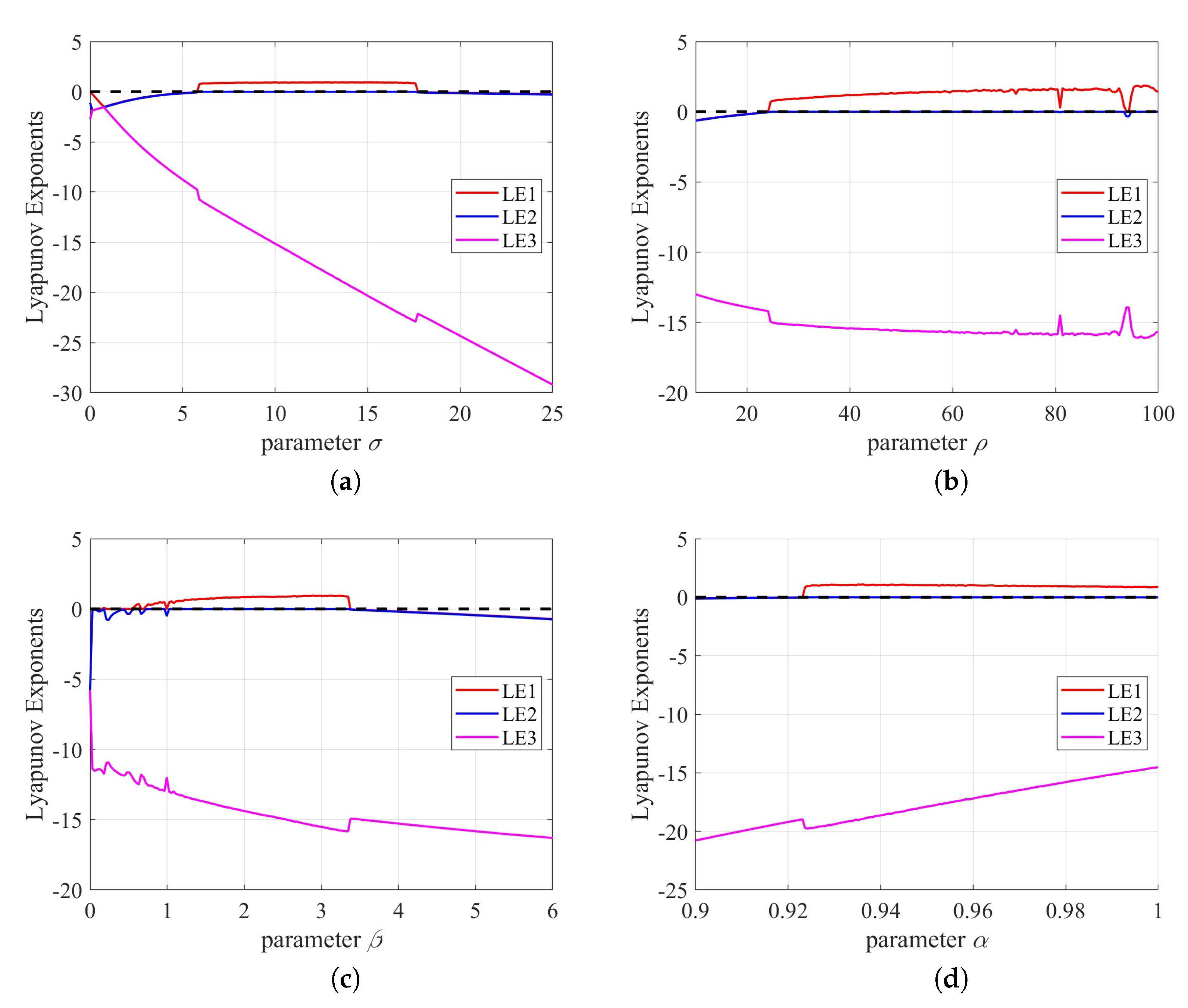
Lyapunov exponent spectrums of the fractional-order 3D Lorenz system: (a) Sweep parameter while ; (b) sweep parameter while ; (c) sweep parameter while ; (d) sweep parameter while .
Figure 2.
Lyapunov exponent spectrums of the fractional-order 3D Lorenz system: (a) Sweep parameter while ; (b) sweep parameter while ; (c) sweep parameter while ; (d) sweep parameter while .
Figure 3.
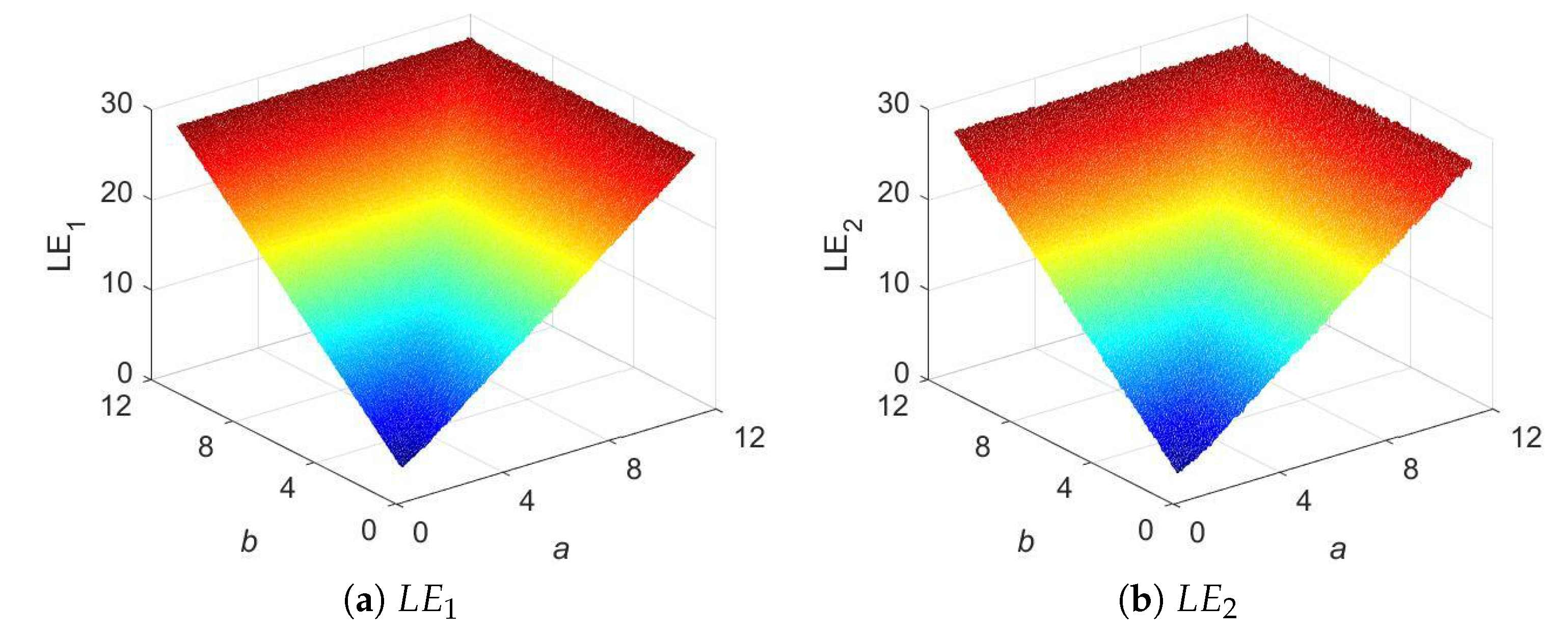
3D LE presentations for 2D-SCPM.
Figure 3.
3D LE presentations for 2D-SCPM.
Figure 4.
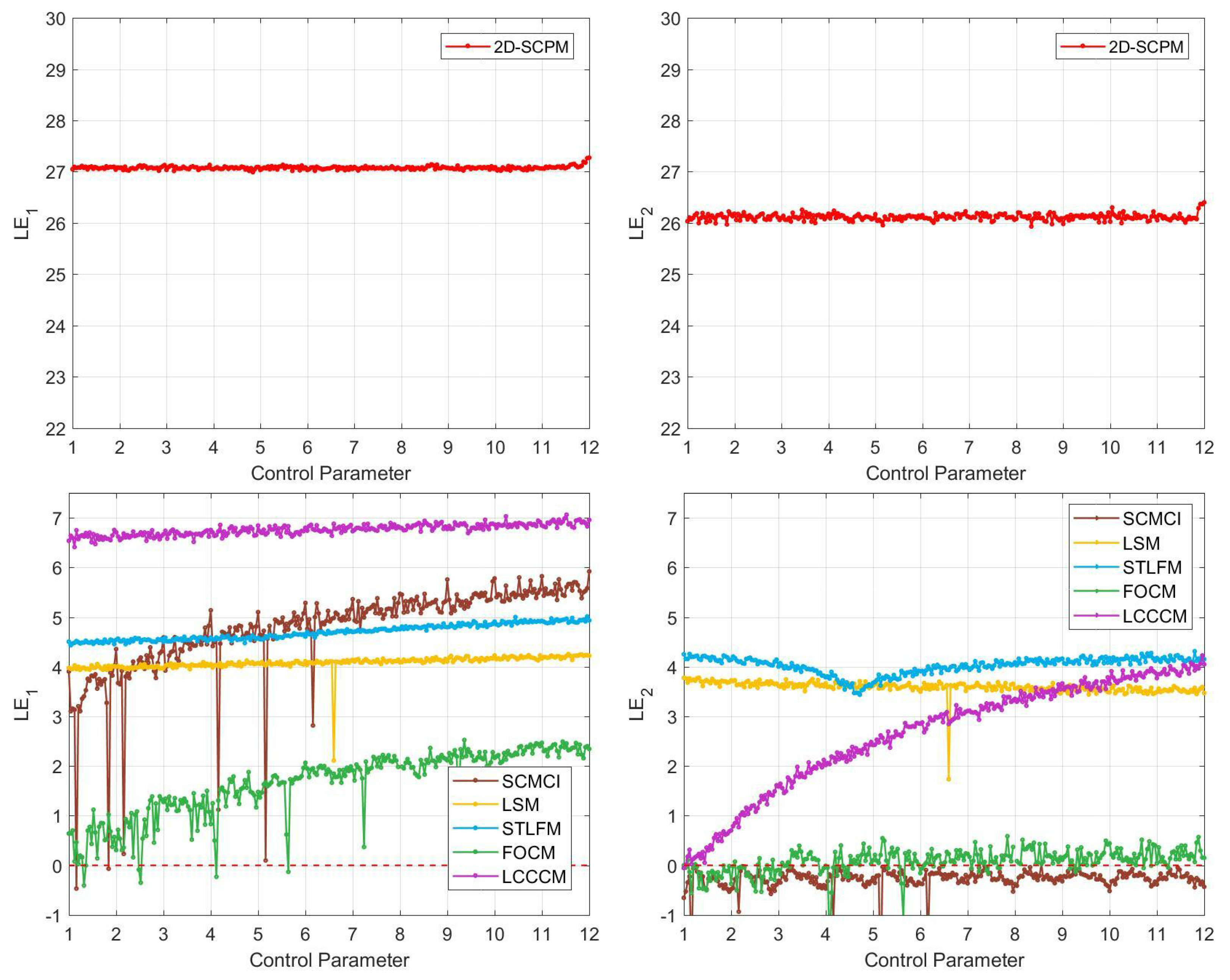
LE experiment results for 2D-SCPM and other five maps: the first column is the LE values of six maps; the second column is the LE values.
Figure 4.
LE experiment results for 2D-SCPM and other five maps: the first column is the LE values of six maps; the second column is the LE values.
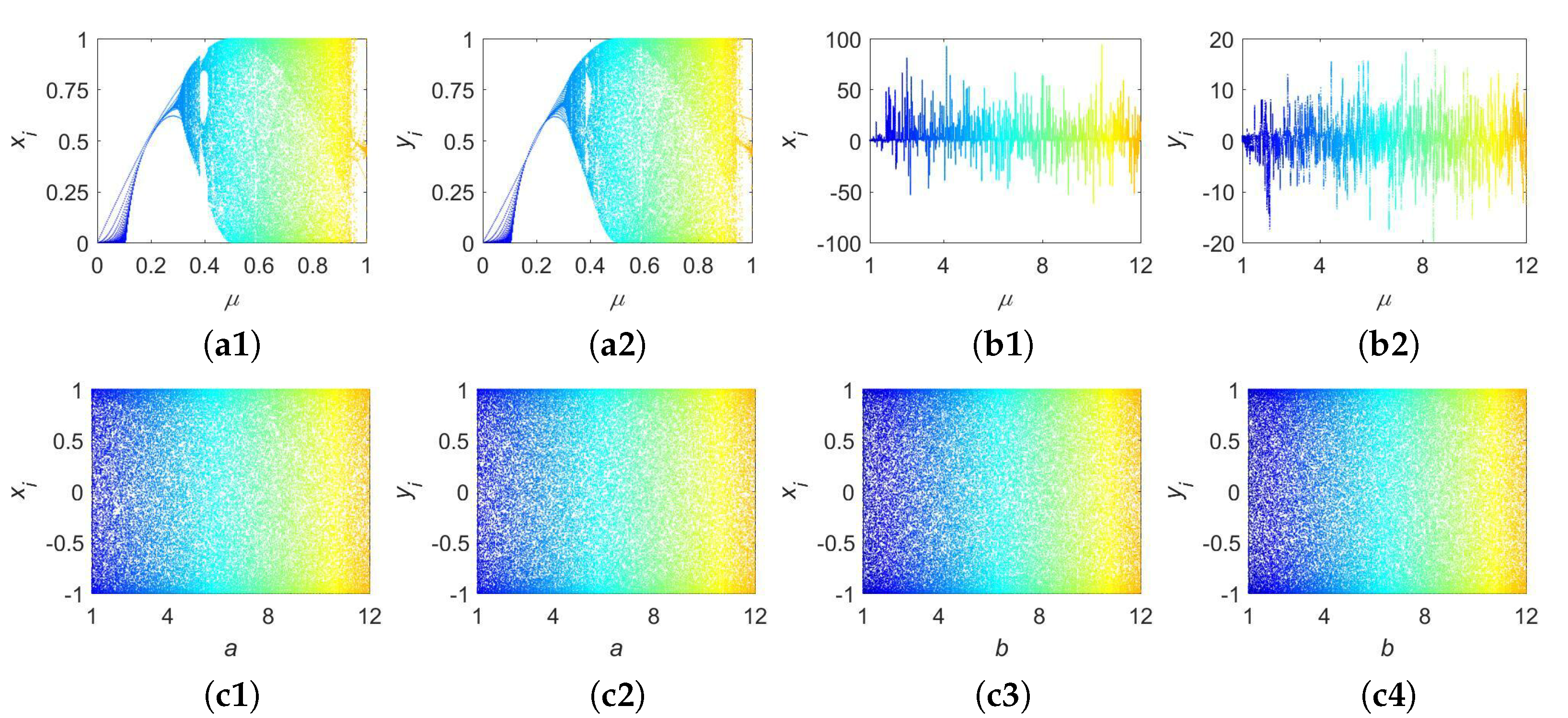
Figure 5.
Bifurcation diagrams for three different maps: (a1,a2) are bifurcation diagrams for LASM; (b1,b2) are two diagrams for FOCM (); (c1–c4) are four diagrams for 2D-SCPM.
Figure 5.
Bifurcation diagrams for three different maps: (a1,a2) are bifurcation diagrams for LASM; (b1,b2) are two diagrams for FOCM (); (c1–c4) are four diagrams for 2D-SCPM.
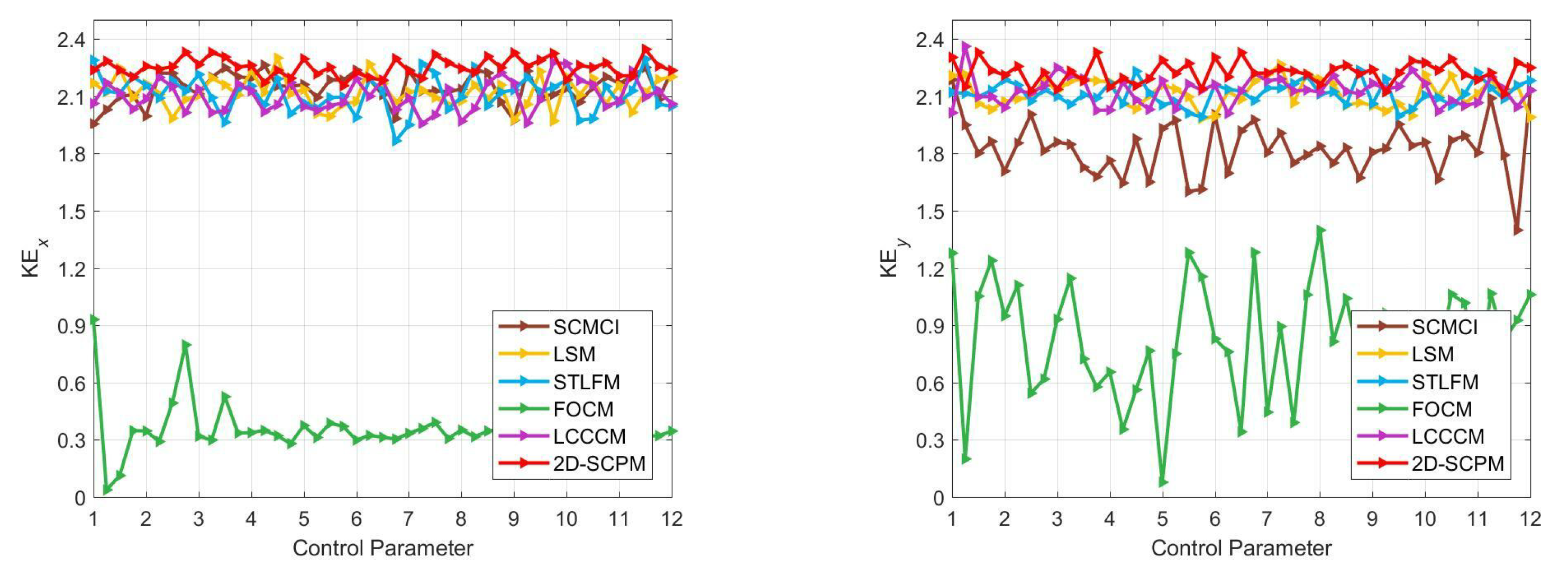
Figure 6.
KE experiment results for 2D-SCPM and other five maps: the first column is the KE values of six maps; the second column is the KE values.
Figure 6.
KE experiment results for 2D-SCPM and other five maps: the first column is the KE values of six maps; the second column is the KE values.
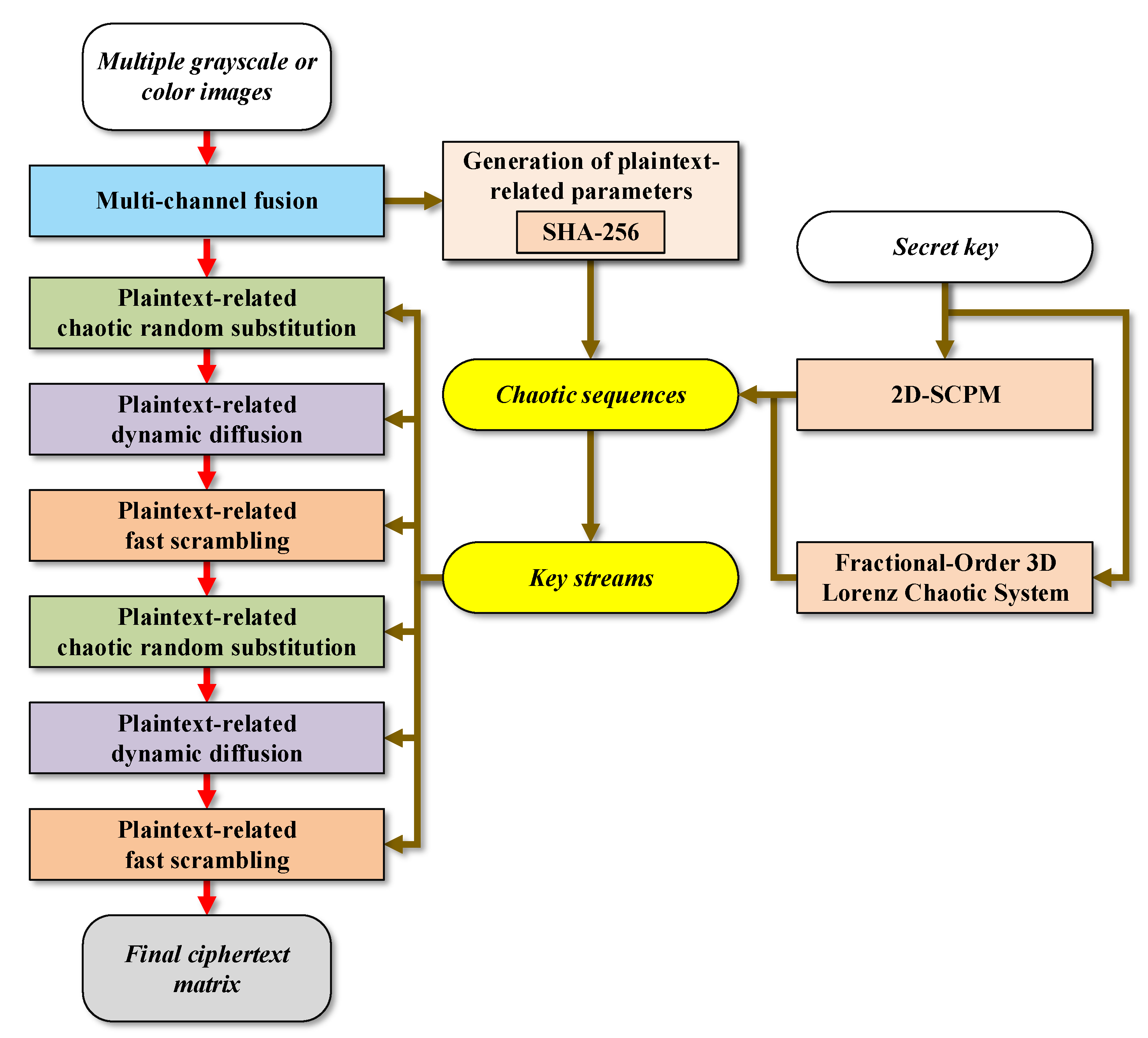
Figure 7.
Encryption process of MIEA-FCSM.
Figure 7.
Encryption process of MIEA-FCSM.
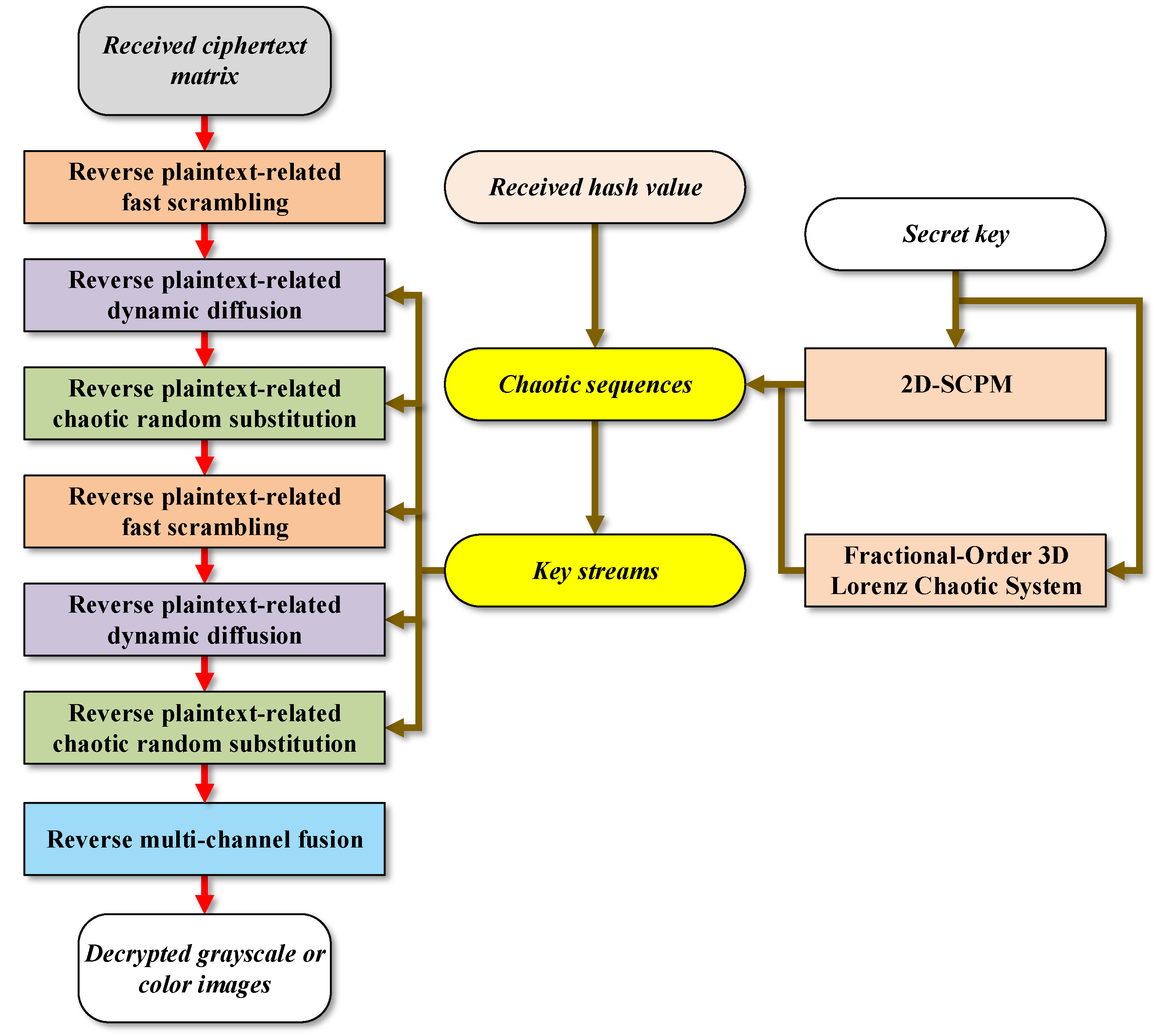
Figure 8.
Decryption process of MIEA-FCSM.
Figure 8.
Decryption process of MIEA-FCSM.
Figure 9.
Visual effect experiment results for MIEA-FCSM: (a,d), six grayscale images and two color images; (b,e), corresponding encrypted images; (c,f), corresponding decrypted images.
Figure 9.
Visual effect experiment results for MIEA-FCSM: (a,d), six grayscale images and two color images; (b,e), corresponding encrypted images; (c,f), corresponding decrypted images.
Figure 10.
Visual presentation of key sensitivity for MIEA-FCSM: (a1) 4.1.07; (a2) ciphertext of 4.1.07; (b1) cihpertext obtained after ; (b2) ; (b3) ; (b4) ; (b5) ; (b6) ; (b7) ; (b8) ; (b9) ; (b10) ; (b11) ; (c1) difference between (b1) and (a2); (c2) between (b2) and (a2); (c3) between (b3) and (a2); (c4) between (b4) and (a2); (c5) between (b5) and (a2); (c6) between (b6) and (a2); (c7) between (b7) and (a2); (c8) between (b8) and (a2); (c9) between (b9) and (a2); (c10) between (b10) and (a2); (c11) between (b11) and (a2).
Figure 10.
Visual presentation of key sensitivity for MIEA-FCSM: (a1) 4.1.07; (a2) ciphertext of 4.1.07; (b1) cihpertext obtained after ; (b2) ; (b3) ; (b4) ; (b5) ; (b6) ; (b7) ; (b8) ; (b9) ; (b10) ; (b11) ; (c1) difference between (b1) and (a2); (c2) between (b2) and (a2); (c3) between (b3) and (a2); (c4) between (b4) and (a2); (c5) between (b5) and (a2); (c6) between (b6) and (a2); (c7) between (b7) and (a2); (c8) between (b8) and (a2); (c9) between (b9) and (a2); (c10) between (b10) and (a2); (c11) between (b11) and (a2).
Figure 11.
Visual presentation of plaintext sensitivity for MIEA-FCSM: (a1) 2.1.06; (a2) the lowest bit of the first pixel on the red channel is negated; (a3) the lowest bit of the last pixel on the blue channel is negated; (b1) difference between (a1) and (a2); (b2) difference between (a1) and (a3); (c1) ciphertext of (a1); (c2) ciphertext of (a2); (c3) ciphertext of (a3); (d1) difference between (c1) and (c2); (d2) difference between (c1) and (c3).
Figure 11.
Visual presentation of plaintext sensitivity for MIEA-FCSM: (a1) 2.1.06; (a2) the lowest bit of the first pixel on the red channel is negated; (a3) the lowest bit of the last pixel on the blue channel is negated; (b1) difference between (a1) and (a2); (b2) difference between (a1) and (a3); (c1) ciphertext of (a1); (c2) ciphertext of (a2); (c3) ciphertext of (a3); (d1) difference between (c1) and (c2); (d2) difference between (c1) and (c3).
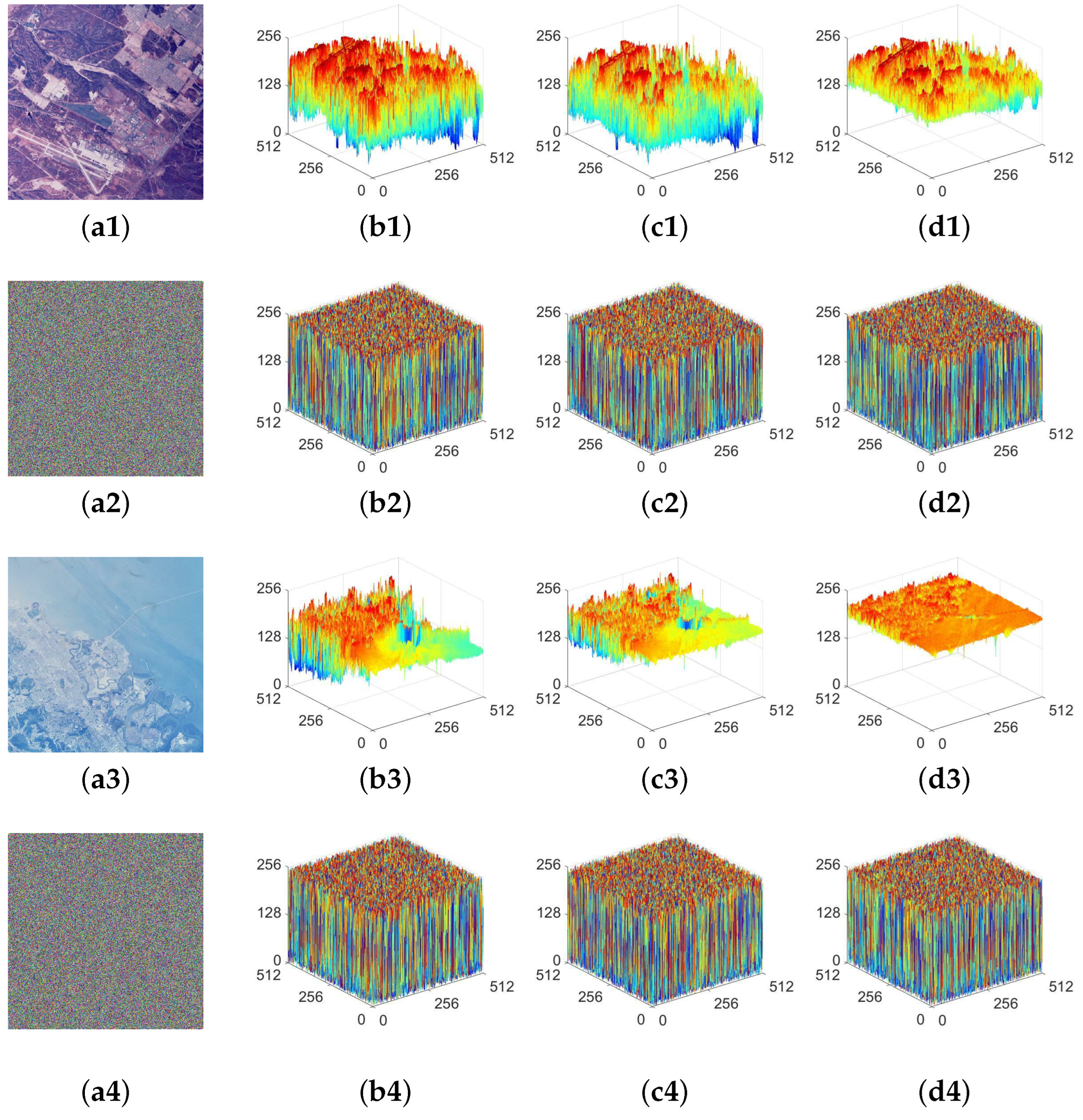
Figure 12.
Pixel distribution representations for MIEA-FCSM: (a1) 2.1.01; (b1,c1,d1) are pixel distribution diagrams for the red, green, and blue channels of (a1); (a2) ciphertext of (a1); (b2,c2,d2) are three pixel distribution diagrams for (a2); (a3) 2.1.07; (b3,c3,d3) are three pixel distribution diagrams for (a3); (a4) ciphertext of (a3); (b4,c4,d4) are three pixel distribution diagrams for (a4).
Figure 12.
Pixel distribution representations for MIEA-FCSM: (a1) 2.1.01; (b1,c1,d1) are pixel distribution diagrams for the red, green, and blue channels of (a1); (a2) ciphertext of (a1); (b2,c2,d2) are three pixel distribution diagrams for (a2); (a3) 2.1.07; (b3,c3,d3) are three pixel distribution diagrams for (a3); (a4) ciphertext of (a3); (b4,c4,d4) are three pixel distribution diagrams for (a4).
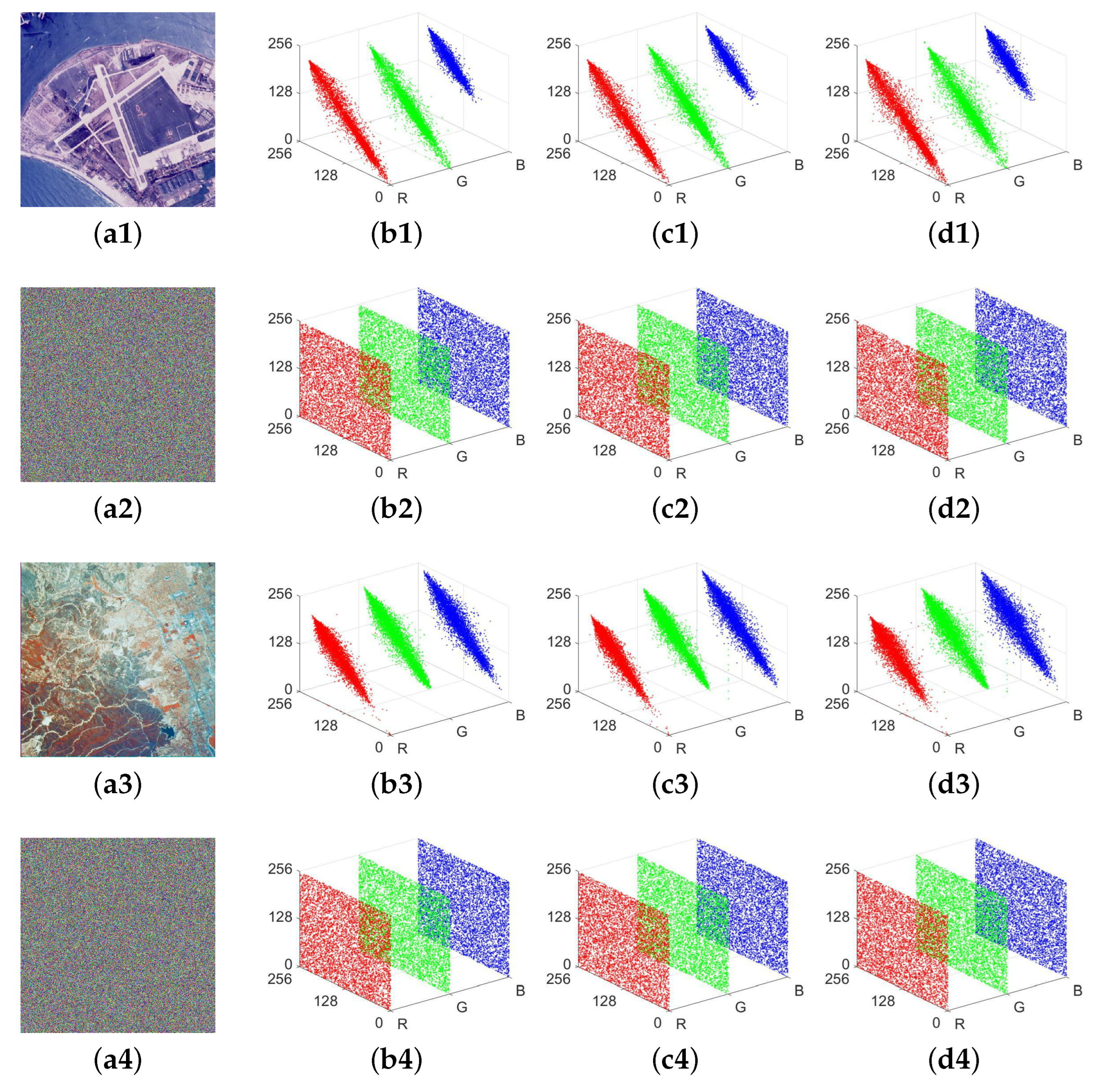
Figure 13.
Adjacent pixel correlation representations: (a1) 2.1.05; (b1) correlation analysis diagram for (a1) in the horizontal direction; (c1) diagram for (a1) in the vertical direction; (d1) diagram for (a1) in the diagonal direction; (a2) ciphertext of 2.1.05; (b2,c2,d2) are correlation analysis diagrams for (a2); (a3) 2.1.06; (b3,c3,d3) are correlation analysis diagrams for (a3); (a4) ciphertext of 2.1.06; (b4,c4,d4) are correlation analysis diagrams for (a2).
Figure 13.
Adjacent pixel correlation representations: (a1) 2.1.05; (b1) correlation analysis diagram for (a1) in the horizontal direction; (c1) diagram for (a1) in the vertical direction; (d1) diagram for (a1) in the diagonal direction; (a2) ciphertext of 2.1.05; (b2,c2,d2) are correlation analysis diagrams for (a2); (a3) 2.1.06; (b3,c3,d3) are correlation analysis diagrams for (a3); (a4) ciphertext of 2.1.06; (b4,c4,d4) are correlation analysis diagrams for (a2).
Figure 14.
Robustness analysis for MIEA-FCSM: (a1–a4) are encrypted images contaminated by varying intensities of noise; (b1–b4) are decrypted images of (a1–a4); (c1–c4) are encrypted images with 25% missing pixels at different positions; (d1–d4) are decrypted images of (c1–c4).
Figure 14.
Robustness analysis for MIEA-FCSM: (a1–a4) are encrypted images contaminated by varying intensities of noise; (b1–b4) are decrypted images of (a1–a4); (c1–c4) are encrypted images with 25% missing pixels at different positions; (d1–d4) are decrypted images of (c1–c4).
Table 1.
Definitions of five recent chaotic maps.
Table 1.
Definitions of five recent chaotic maps.
| Ref. | Name | Definition |
|---|
| [27] | SCMCI (2021) | |
| [28] | LSM (2021) | |
| [29] | STLFM (2022) | |
| [11] | FOCM (2022) | |
| [19] | LCCCM (2022) | |
Table 2.
Configurations and results of LE comparative experiments for 2D-SCPM.
Table 2.
Configurations and results of LE comparative experiments for 2D-SCPM.
| Name | Configuration | LE | LE |
|---|
| Invariable | Variable | Average | Std. Dev. | Average | Std. Dev. |
| SCMCI [27] | | a | 4.7720 | 0.7903 | −0.2738 | 0.0520 |
| LSM [28] | | a | 4.0835 | 0.0202 | 3.5923 | 0.0180 |
| STLFM [29] | | | 4.6961 | 0.0230 | 4.0224 | 0.0301 |
| FOCM [11] | | | 1.6410 | 0.4487 | 0.0794 | 0.0625 |
| LCCCM [19] | | | 6.7625 | 0.0119 | 2.6554 | 1.2474 |
| 2D-SCPM | | a | 27.0762 | 0.0010 | 26.1167 | 0.0040 |
Table 3.
Configurations and results of KE comparative experiments for 2D-SCPM.
Table 3.
Configurations and results of KE comparative experiments for 2D-SCPM.
| Name | Configuration | KE | KE |
|---|
| Invariable | Variable | Average | Std. Dev. | Average | Std. Dev. |
| SCMCI [27] | | a | 2.1476 | 0.0785 | 1.8273 | 0.1467 |
| LSM [28] | | a | 2.1210 | 0.0772 | 2.1169 | 0.0733 |
| STLFM [29] | | | 2.1125 | 0.0929 | 2.1156 | 0.0591 |
| FOCM [11] | | | 0.3539 | 0.1332 | 0.8251 | 0.3020 |
| LCCCM [19] | | | 2.1015 | 0.0810 | 2.1294 | 0.0737 |
| 2D-SCPM | | a | 2.2523 | 0.0466 | 2.2246 | 0.0572 |
Table 4.
NIST test outcomes for 2D-SCPM.
Table 4.
NIST test outcomes for 2D-SCPM.
| Item Name | p Value | Result |
|---|
| x Sequence | y Sequence |
| Frequency (Monobit) | 0.133171 | 0.536575 | Random |
| Frequency (Block) | 0.124135 | 0.517819 | Random |
| Runs | 0.452929 | 0.096436 | Random |
| Longest Runs | 0.638713 | 0.353124 | Random |
| Matrix Rank | 0.067070 | 0.872194 | Random |
| Discrete Fourier Transform | 0.393422 | 0.485537 | Random |
| Non-Overlapping Template | 0.441853 | 0.431362 | Random |
| Overlapping Template | 0.137611 | 0.062761 | Random |
| Universal | 0.777250 | 0.120874 | Random |
| Linear Complexity | 0.633858 | 0.953684 | Random |
| Serial 1 | 0.695361 | 0.291362 | Random |
| Serial 2 | 0.768519 | 0.382965 | Random |
| Approximate Entropy | 0.781378 | 0.229411 | Random |
| Cumulative Sums (Forward) | 0.164709 | 0.548417 | Random |
| Cummulative Sums (Reverse) | 0.145096 | 0.872657 | Random |
| Random Excursions () | 0.311634 | 0.380218 | Random |
| Random Excursions () | 0.162339 | 0.423355 | Random |
| Random Excursions Variant () | 0.118109 | 0.562370 | Random |
| Random Excursions Variant () | 0.177507 | 0.825329 | Random |
Table 5.
NPCR scores of six algorithms.
Table 5.
NPCR scores of six algorithms.
| Size | Name | Channel | MIEA-FCSM | [28] | [32] | [33] | [34] | [35] |
|---|
| 2.1.01 | Red | 99.6089 | 99.6204 | 99.6166 | 99.6215 | 99.6092 | 99.6211 |
| | 2.1.01 | Green | 99.6154 | 99.5853 | 99.6109 | 99.6015 | 99.6184 | 99.6197 |
| | 2.1.01 | Blue | 99.5986 | 99.6052 | 99.6208 | 99.5973 | 99.6239 | 99.6212 |
| | 2.1.02 | Red | 99.5887 | 99.6201 | 99.6246 | 99.6100 | 99.6052 | 99.6148 |
| | 2.1.02 | Green | 99.6116 | 99.6506 | 99.5899 | 99.6054 | 99.5850 | 99.6115 |
| | 2.1.02 | Blue | 99.6139 | 99.6414 | 99.5987 | 99.6057 | 99.5918 | 99.6141 |
| | 2.1.05 | Red | 99.6143 | 99.6002 | 99.6067 | 99.5960 | 99.6387 | 99.6231 |
| | 2.1.05 | Green | 99.6070 | 99.6109 | 99.5853 | 99.6037 | 99.6098 | 99.6165 |
| | 2.1.05 | Blue | 99.6093 | 99.6216 | 99.5998 | 99.6154 | 99.5995 | 99.6232 |
| 2.2.01 | Red | 99.6112 | 99.6277 | 99.6099 | 99.6166 | 99.6095 | 99.6122 |
| | 2.2.01 | Green | 99.6144 | 99.5575 | 99.6076 | 99.6164 | 99.6026 | 99.6131 |
| | 2.2.01 | Blue | 99.6146 | 99.6490 | 99.6110 | 99.6141 | 99.6006 | 99.5956 |
| | 2.2.08 | Red | 99.6172 | 99.6155 | 99.6086 | 99.6169 | 99.6115 | 99.6021 |
| | 2.2.08 | Green | 99.6109 | 99.5834 | 99.6081 | 99.6190 | 99.6103 | 99.5975 |
| | 2.2.08 | Blue | 99.6150 | 99.6246 | 99.6113 | 99.6133 | 99.6055 | 99.5956 |
| | 2.2.11 | Red | 99.6044 | 99.5834 | 99.6119 | 99.6209 | 99.6166 | 99.6002 |
| | 2.2.11 | Green | 99.6092 | 99.6292 | 99.6135 | 99.6057 | 99.6044 | 99.6135 |
| | 2.2.11 | Blue | 99.6125 | 99.6277 | 99.6158 | 99.6015 | 99.6137 | 99.5972 |
| | Average | – | 99.6098 | 99.6141 | 99.6084 | 99.6101 | 99.6087 | 99.6107 |
| | Std. Dev. | – | 0.0069 | 0.0247 | 0.0098 | 0.0081 | 0.0119 | 0.0100 |
Table 6.
UACI scores of six algorithms.
Table 6.
UACI scores of six algorithms.
| Size | Name | Channel | MIEA-FCSM | [28] | [32] | [33] | [34] | [35] |
|---|
| 2.1.01 | Red | 33.4941 | 33.4893 | 33.4753 | 33.5109 | 33.5007 | 33.4930 |
| | 2.1.01 | Green | 33.4700 | 33.3720 | 33.4831 | 33.4686 | 33.4449 | 33.4849 |
| | 2.1.01 | Blue | 33.4736 | 33.4910 | 33.5122 | 33.4622 | 33.4479 | 33.4929 |
| | 2.1.02 | Red | 33.4623 | 33.4873 | 33.5137 | 33.4399 | 33.4839 | 33.4774 |
| | 2.1.02 | Green | 33.4349 | 33.5392 | 33.4412 | 33.4847 | 33.4263 | 33.4671 |
| | 2.1.02 | Blue | 33.4619 | 33.4500 | 33.3946 | 33.4360 | 33.4408 | 33.4752 |
| | 2.1.05 | Red | 33.4699 | 33.5945 | 33.4818 | 33.3924 | 33.4269 | 33.4778 |
| | 2.1.05 | Green | 33.4513 | 33.5220 | 33.4781 | 33.4470 | 33.4241 | 33.4634 |
| | 2.1.05 | Blue | 33.4537 | 33.3360 | 33.5460 | 33.4353 | 33.5226 | 33.4777 |
| 2.2.01 | Red | 33.4739 | 33.4782 | 33.4600 | 33.4887 | 33.4675 | 33.4286 |
| | 2.2.01 | Green | 33.4236 | 33.4194 | 33.4957 | 33.4808 | 33.4682 | 33.4255 |
| | 2.2.01 | Blue | 33.4628 | 33.6140 | 33.4181 | 33.5233 | 33.4399 | 33.4399 |
| | 2.2.08 | Red | 33.4825 | 33.5349 | 33.4666 | 33.4685 | 33.4486 | 33.4211 |
| | 2.2.08 | Green | 33.4789 | 33.4775 | 33.4720 | 33.4728 | 33.4585 | 33.4411 |
| | 2.2.08 | Blue | 33.4588 | 33.6040 | 33.4713 | 33.4726 | 33.4943 | 33.4607 |
| | 2.2.11 | Red | 33.5338 | 33.5236 | 33.4699 | 33.4547 | 33.4316 | 33.4004 |
| | 2.2.11 | Green | 33.4674 | 33.5185 | 33.4829 | 33.4779 | 33.4459 | 33.5004 |
| | 2.2.11 | Blue | 33.4330 | 33.5079 | 33.4347 | 33.5006 | 33.4450 | 33.4658 |
| | Average | – | 33.4659 | 33.4977 | 33.4721 | 33.4676 | 33.4565 | 33.4607 |
| | Std. Dev. | – | 0.0246 | 0.0729 | 0.0353 | 0.0309 | 0.0279 | 0.0284 |
Table 7.
Chi-square test results of MIEA-FCSM.
Table 7.
Chi-square test results of MIEA-FCSM.
| Size | Channel | Ciphertext | Chi-Square Value | Result |
|---|
|
| 2.1.01 | Red | 249.7539 | Pass |
| | 2.1.01 | Green | 266.6308 | Pass |
| | 2.1.01 | Blue | 247.2011 | Pass |
| | 2.1.02 | Red | 259.5214 | Pass |
| | 2.1.02 | Green | 246.7753 | Pass |
| | 2.1.02 | Blue | 254.2734 | Pass |
| | 2.1.05 | Red | 258.1542 | Pass |
| | 2.1.05 | Green | 258.9863 | Pass |
| | 2.1.05 | Blue | 265.4589 | Pass |
| 2.2.01 | Red | 264.2778 | Pass |
| | 2.2.01 | Green | 261.9687 | Pass |
| | 2.2.01 | Blue | 257.9526 | Pass |
| | 2.2.08 | Red | 245.9931 | Pass |
| | 2.2.08 | Green | 256.5932 | Pass |
| | 2.2.08 | Blue | 260.8476 | Pass |
| | 2.2.11 | Red | 243.3730 | Pass |
| | 2.2.11 | Green | 268.8398 | Pass |
| | 2.2.11 | Blue | 257.0625 | Pass |
Table 8.
CC scores of MIEA-FCSM.
Table 8.
CC scores of MIEA-FCSM.
| Size | Name | Channel | Plaintext | Ciphertext |
|---|
| Horizontal | Vertical | Diagonal | Horizontal | Vertical | Diagonal |
| 2.1.01 | Red | 0.8632 | 0.8758 | 0.8516 | −0.0025 | 0.0013 | 0.0009 |
| | 2.1.01 | Green | 0.8685 | 0.8837 | 0.8536 | −0.0022 | 0.0025 | 0.0029 |
| | 2.1.01 | Blue | 0.8760 | 0.8812 | 0.8609 | 0.0018 | −0.0011 | −0.0025 |
| | 2.1.02 | Red | 0.8314 | 0.8498 | 0.7652 | −0.0026 | 0.0012 | 0.0018 |
| | 2.1.02 | Green | 0.7552 | 0.7872 | 0.6740 | −0.0013 | −0.0024 | 0.0019 |
| | 2.1.02 | Blue | 0.7325 | 0.7413 | 0.6312 | 0.0029 | 0.0003 | −0.0010 |
| | 2.1.05 | Red | 0.9570 | 0.9584 | 0.9390 | 0.0005 | −0.0023 | 0.0024 |
| | 2.1.05 | Green | 0.9375 | 0.9356 | 0.9100 | −0.0015 | −0.0020 | −0.0007 |
| | 2.1.05 | Blue | 0.9266 | 0.9193 | 0.8965 | −0.0035 | −0.0035 | 0.0033 |
| 2.2.01 | Red | 0.9256 | 0.9290 | 0.9049 | 0.0001 | 0.0037 | 0.0006 |
| | 2.2.01 | Green | 0.9142 | 0.9173 | 0.8994 | −0.0008 | 0.0023 | 0.0015 |
| | 2.2.01 | Blue | 0.9031 | 0.9107 | 0.8868 | 0.0010 | −0.0036 | −0.0016 |
| | 2.2.08 | Red | 0.9181 | 0.9286 | 0.9015 | 0.0039 | −0.0012 | −0.0026 |
| | 2.2.08 | Green | 0.9141 | 0.9177 | 0.8922 | 0.0009 | 0.0011 | 0.0002 |
| | 2.2.08 | Blue | 0.9011 | 0.8950 | 0.8710 | −0.0012 | −0.0026 | −0.0024 |
| | 2.2.11 | Red | 0.8111 | 0.8095 | 0.7710 | 0.0004 | −0.0034 | 0.0021 |
| | 2.2.11 | Green | 0.7858 | 0.7826 | 0.7186 | 0.0026 | −0.0007 | 0.0037 |
| | 2.2.11 | Blue | 0.7580 | 0.7733 | 0.7061 | −0.0022 | −0.0036 | −0.0027 |
Table 9.
Information entropy scores of MIEA-FCSM.
Table 9.
Information entropy scores of MIEA-FCSM.
| Size | Name | Channel | Plaintext | Ciphertext |
|---|
| 2.1.01 | Red | 7.5091 | 7.9994 |
| | 2.1.01 | Green | 7.3542 | 7.9994 |
| | 2.1.01 | Blue | 6.5966 | 7.9993 |
| | 2.1.02 | Red | 7.4061 | 7.9993 |
| | 2.1.02 | Green | 7.4188 | 7.9994 |
| | 2.1.02 | Blue | 6.5931 | 7.9994 |
| | 2.1.05 | Red | 7.5580 | 7.9993 |
| | 2.1.05 | Green | 7.4597 | 7.9994 |
| | 2.1.05 | Blue | 6.6665 | 7.9994 |
| 2.2.01 | Red | 7.7575 | 7.9998 |
| | 2.2.01 | Green | 7.3387 | 7.9998 |
| | 2.2.01 | Blue | 6.9561 | 7.9998 |
| | 2.2.08 | Red | 7.7229 | 7.9998 |
| | 2.2.08 | Green | 7.5289 | 7.9999 |
| | 2.2.08 | Blue | 6.8318 | 7.9998 |
| | 2.2.11 | Red | 6.6944 | 7.9999 |
| | 2.2.11 | Green | 6.3414 | 7.9998 |
| | 2.2.11 | Blue | 5.1766 | 7.9998 |
Table 10.
Information entropy scores of nine algorithms.
Table 10.
Information entropy scores of nine algorithms.
| Algorithm | Entropy Score |
|---|
| [20] | 7.9984 |
| [37] | 7.9993 |
| [38] | 7.9976 |
| [39] | 7.9993 |
| [35] | 7.9993 |
| [40] | 7.9993 |
| [28] | 7.9992 |
| [34] | 7.9992 |
| MIEA-FCSM | 7.9994 |
Table 11.
LSE test results of MIEA-FCSM.
Table 11.
LSE test results of MIEA-FCSM.
| Size | Ciphertext | Channel | LSE Value | Result |
|---|
| 2.1.01 | Red | 7.902608 | Pass |
| | 2.1.01 | Green | 7.901998 | Pass |
| | 2.1.01 | Blue | 7.902302 | Pass |
| | 2.1.02 | Red | 7.902425 | Pass |
| | 2.1.02 | Green | 7.902242 | Pass |
| | 2.1.02 | Blue | 7.902601 | Pass |
| | 2.1.05 | Red | 7.902229 | Pass |
| | 2.1.05 | Green | 7.901915 | Pass |
| | 2.1.05 | Blue | 7.902005 | Pass |
| 2.2.01 | Red | 7.901944 | Pass |
| | 2.2.01 | Green | 7.902186 | Pass |
| | 2.2.01 | Blue | 7.902156 | Pass |
| | 2.2.08 | Red | 7.902944 | Pass |
| | 2.2.08 | Green | 7.902651 | Pass |
| | 2.2.08 | Blue | 7.902183 | Pass |
| | 2.2.11 | Red | 7.902465 | Pass |
| | 2.2.11 | Green | 7.902302 | Pass |
| | 2.2.11 | Blue | 7.902973 | Pass |
Table 12.
PSNR and SSIM values under different noise intensities.
Table 12.
PSNR and SSIM values under different noise intensities.
| Noise Intensity | Red Channel | Green Channel | Blue Channel |
|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM |
| 0.02 | 19.7562 | 0.7419 | 20.0190 | 0.7539 | 20.1633 | 0.6462 |
| 0.04 | 16.8391 | 0.6155 | 17.0988 | 0.6210 | 17.3881 | 0.4880 |
| 0.06 | 15.1894 | 0.5370 | 15.5601 | 0.5403 | 15.6278 | 0.4015 |
| 0.08 | 14.0505 | 0.4732 | 14.4138 | 0.4722 | 14.5452 | 0.3376 |
| 0.10 | 13.2139 | 0.4246 | 13.5473 | 0.4224 | 13.7136 | 0.2933 |
| 0.12 | 12.5858 | 0.3815 | 12.9287 | 0.3707 | 13.0371 | 0.2555 |
| 0.14 | 12.0616 | 0.3432 | 12.4292 | 0.3366 | 12.5424 | 0.2206 |
| 0.16 | 11.6114 | 0.3095 | 11.9224 | 0.3056 | 12.0879 | 0.2018 |
Table 13.
PSNR and SSIM values under different data losses.
Table 13.
PSNR and SSIM values under different data losses.
| Data Loss | Red Channel | Green Channel | Blue Channel |
|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM |
| pixels | 37.8487 | 0.9922 | 38.9434 | 0.9937 | 39.6916 | 0.9917 |
| pixels | 35.3148 | 0.9876 | 35.9973 | 0.9889 | 36.5064 | 0.9840 |
| pixels | 32.4402 | 0.9763 | 33.1772 | 0.9798 | 33.4375 | 0.9700 |
| pixels | 29.6289 | 0.9618 | 30.2890 | 0.9664 | 30.4249 | 0.9508 |
| pixels | 27.0253 | 0.9358 | 27.6840 | 0.9418 | 28.0802 | 0.9215 |
| pixels | 24.0892 | 0.8974 | 24.6410 | 0.9054 | 24.9010 | 0.8691 |
| pixels | 21.4835 | 0.8434 | 21.8936 | 0.8489 | 22.2412 | 0.8024 |
| pixels | 18.7302 | 0.7676 | 19.1784 | 0.7745 | 19.5178 | 0.7187 |
| pixels | 16.3065 | 0.6941 | 16.7271 | 0.6901 | 16.9790 | 0.6479 |
Table 14.
NIST test outcomes for MIEA-FCSM.
Table 14.
NIST test outcomes for MIEA-FCSM.
| Item Name | p Value (Ciphertext) | Result |
|---|
| 2.1.01 | 2.1.02 | 2.1.05 | 2.1.06 | 2.2.01 | 2.2.08 |
| Frequency (Monobit) | 0.938984 | 0.455468 | 0.636900 | 0.271176 | 0.125786 | 0.959300 | Random |
| Frequency (Block) | 0.377102 | 0.695136 | 0.486114 | 0.919744 | 0.626776 | 0.986615 | Random |
| Runs | 0.848245 | 0.123654 | 0.657268 | 0.983728 | 0.224505 | 0.301428 | Random |
| Longest Runs | 0.554931 | 0.637710 | 0.364070 | 0.558170 | 0.326202 | 0.318947 | Random |
| Matrix Rank | 0.389840 | 0.116814 | 0.209644 | 0.247903 | 0.934658 | 0.998876 | Random |
| Discrete Fourier Transform | 0.200888 | 0.119452 | 0.853707 | 0.523441 | 0.763061 | 0.515849 | Random |
| Non-Overlapping Template | 0.674401 | 0.265663 | 0.126927 | 0.299549 | 0.222029 | 0.709035 | Random |
| Overlapping Template | 0.549943 | 0.995207 | 0.218516 | 0.353877 | 0.598382 | 0.301744 | Random |
| Universal | 0.905732 | 0.975949 | 0.486118 | 0.855998 | 0.293810 | 0.458157 | Random |
| Linear Complexity | 0.167901 | 0.223193 | 0.168184 | 0.564220 | 0.979454 | 0.534705 | Random |
| Serial 1 | 0.887276 | 0.492728 | 0.496104 | 0.177181 | 0.925572 | 0.629930 | Random |
| Serial 2 | 0.664458 | 0.394830 | 0.220287 | 0.827247 | 0.859346 | 0.503489 | Random |
| Approximate Entropy | 0.126032 | 0.443620 | 0.903944 | 0.459428 | 0.581134 | 0.873983 | Random |
| Cumulative Sums (Forward) | 0.649861 | 0.533670 | 0.476382 | 0.213114 | 0.149726 | 0.956529 | Random |
| Cummulative Sums (Reverse) | 0.721430 | 0.406060 | 0.892509 | 0.457783 | 0.876487 | 0.977343 | Random |
| Random Excursions () | 0.070625 | 0.272277 | 0.210229 | 0.121351 | 0.550582 | 0.176783 | Random |
| Random Excursions () | 0.407268 | 0.371559 | 0.122416 | 0.299785 | 0.438516 | 0.302316 | Random |
| Random Excursions Variant () | 0.943201 | 0.331413 | 0.829856 | 0.105968 | 0.134844 | 0.083536 | Random |
| Random Excursions Variant () | 0.412591 | 0.197920 | 0.067770 | 0.355611 | 0.252079 | 0.554221 | Random |
Table 15.
Average times (sec.) required and throughputs (Mbps) achieved by six algorithms.
Table 15.
Average times (sec.) required and throughputs (Mbps) achieved by six algorithms.
| Algorithm | Unit | Time (sec.) and Throughput (Mbps) | Average |
|---|
| | | |
| [33] | sec. | 1.1642 | 2.3685 | 5.3076 | 11.5125 | – |
| Mbps | 5.1538 | 5.0665 | 4.5218 | 4.1694 | 4.7279 |
| [37] | sec. | 0.9373 | 1.9829 | 4.1355 | 8.3301 | – |
| Mbps | 6.4014 | 6.0517 | 5.8034 | 5.7622 | 6.0047 |
| [38] | sec. | 1.8495 | 3.7407 | 7.4928 | 15.3363 | – |
| Mbps | 3.2441 | 3.2080 | 3.2031 | 3.1298 | 3.1962 |
| [39] | sec. | 0.2691 | 0.5594 | 1.1221 | 2.3076 | – |
| Mbps | 22.2965 | 21.4516 | 21.3885 | 20.8008 | 21.4843 |
| [44] | sec. | 1.6118 | 4.0054 | 10.3403 | 23.2284 | – |
| Mbps | 3.7225 | 2.9960 | 2.3210 | 2.0664 | 2.7765 |
| MIEA-FCSM | sec. | 0.0308 | 0.0676 | 0.1504 | 0.3372 | – |
| Mbps | 194.8052 | 177.5148 | 159.5745 | 142.3488 | 168.5608 |