High-Accuracy Simulation of Rayleigh Waves Using Fractional Viscoelastic Wave Equation
Abstract
:1. Introduction
2. Modeling Method
2.1. DFL Viscoelastic Wave Equation
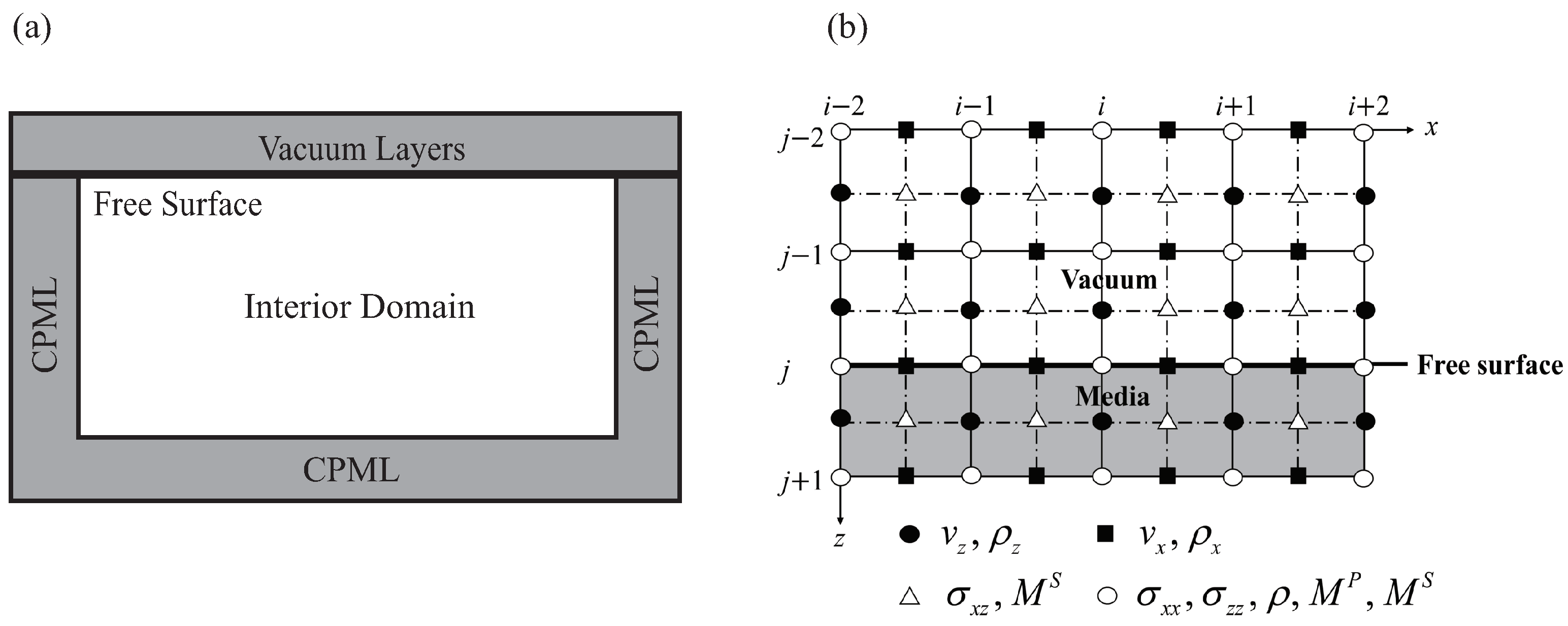
2.2. Boundary Treatment
2.2.1. Free Surface Boundary
2.2.2. Absorbing Boundary
2.3. Numerical Implementation
- 1.
- Calculate the spatial derivatives
- 2.
- Calculate the fractional Laplacians term as follows:
- 3.
- Update the particle velocity and stress as follows:
- 4.
- Update the particle velocity and stress of the absorbing boundary:
3. Numerical Examples
3.1. Homogeneous Half-Space Model
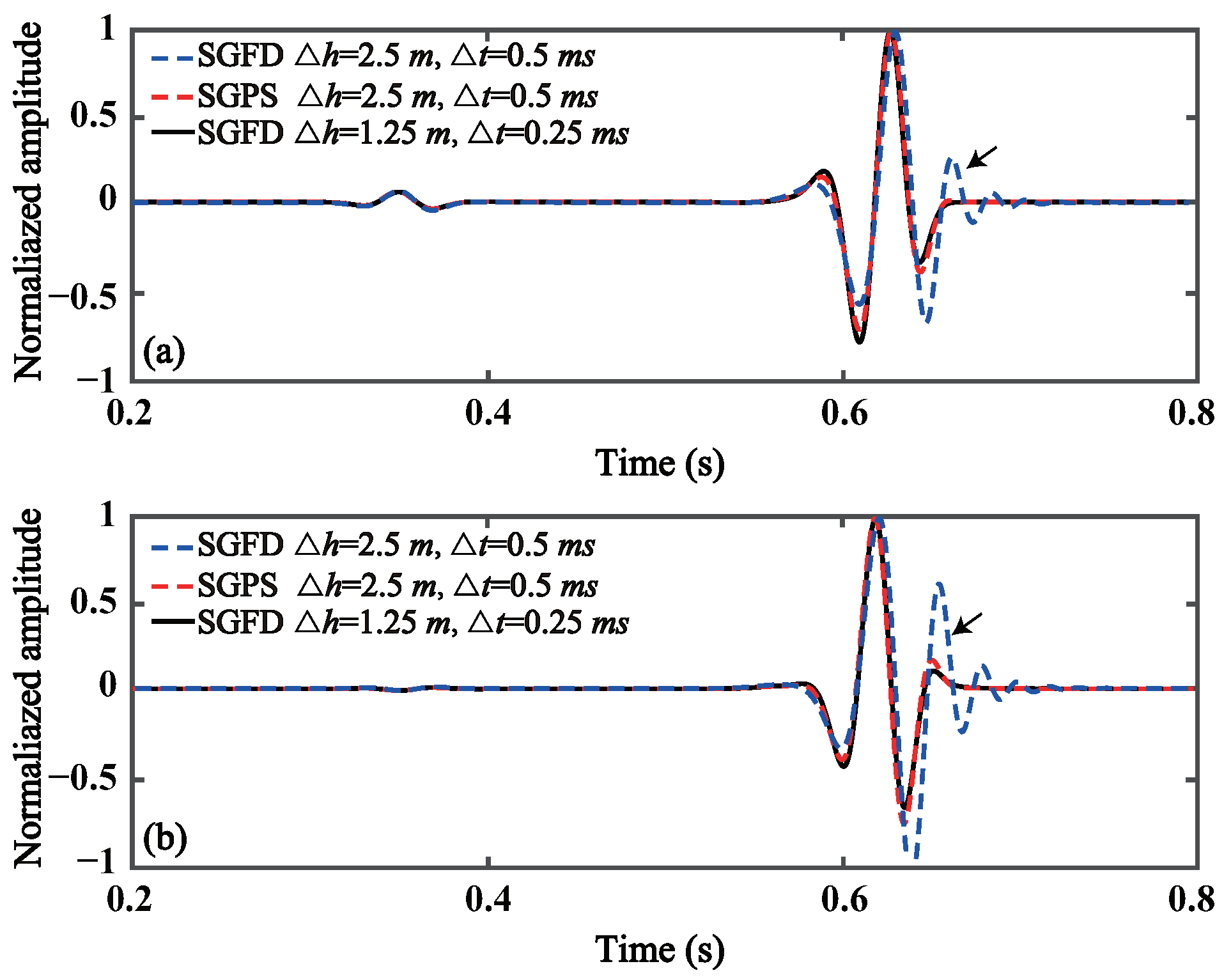
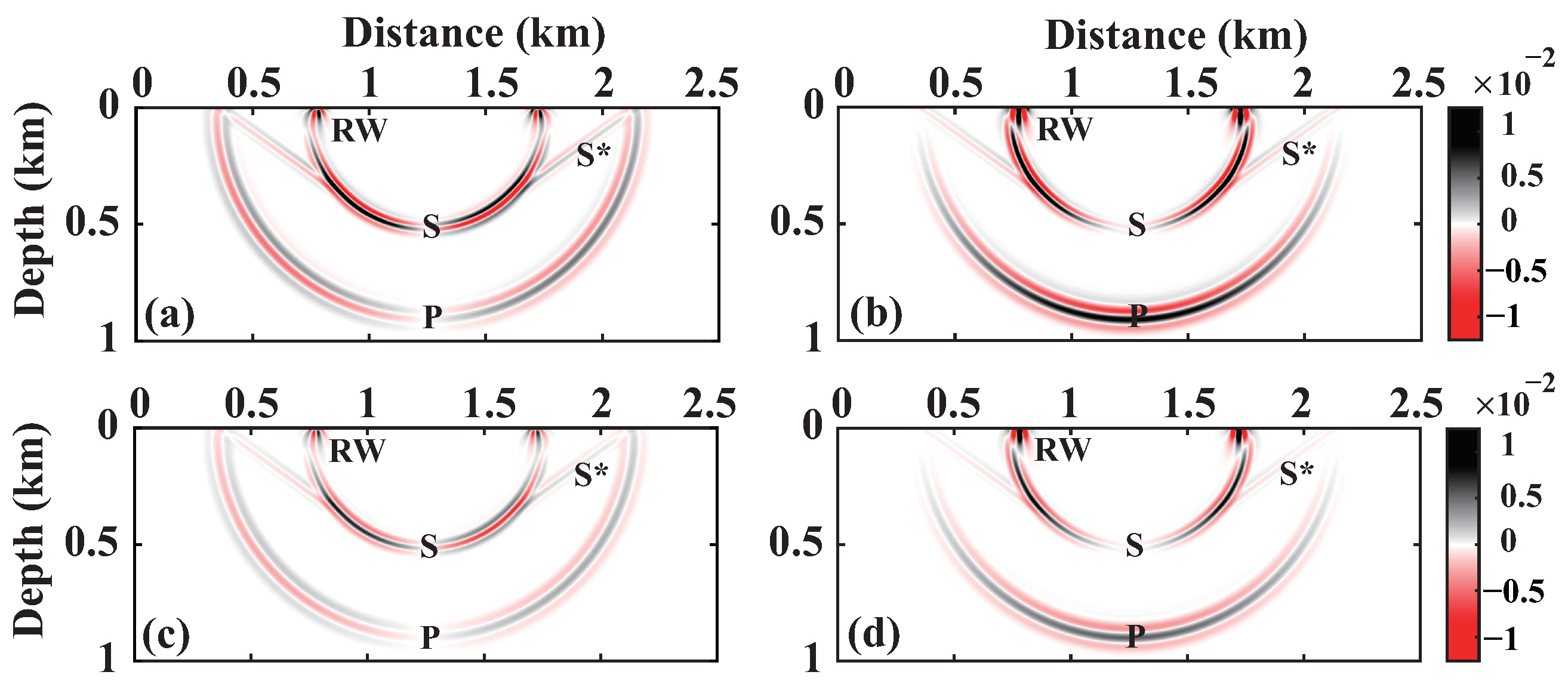
3.1.1. Elastic Medium
3.1.2. Viscoelastic Medium
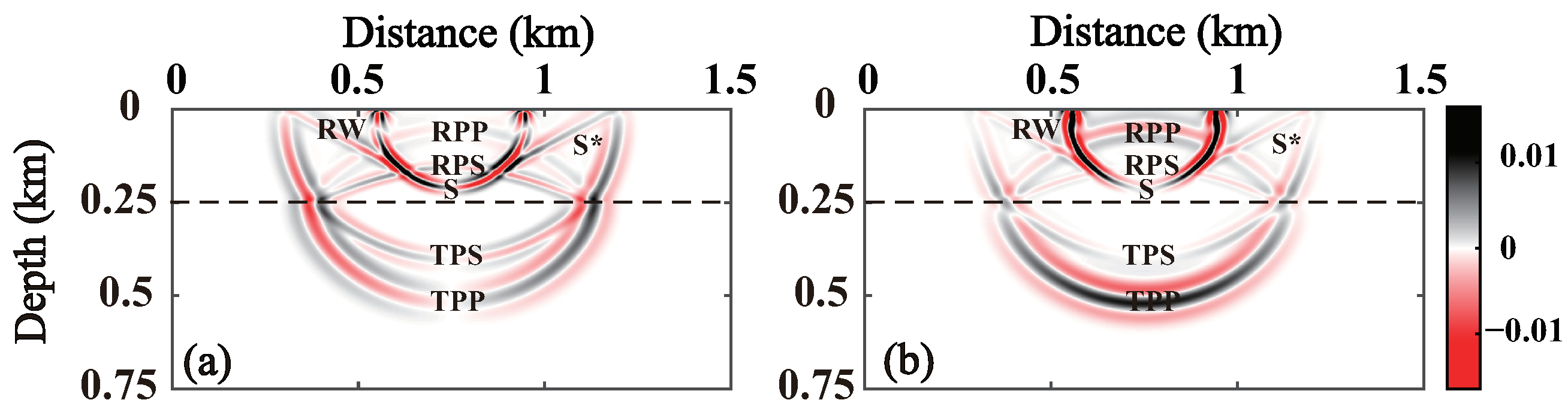
3.2. Two-Layer Model
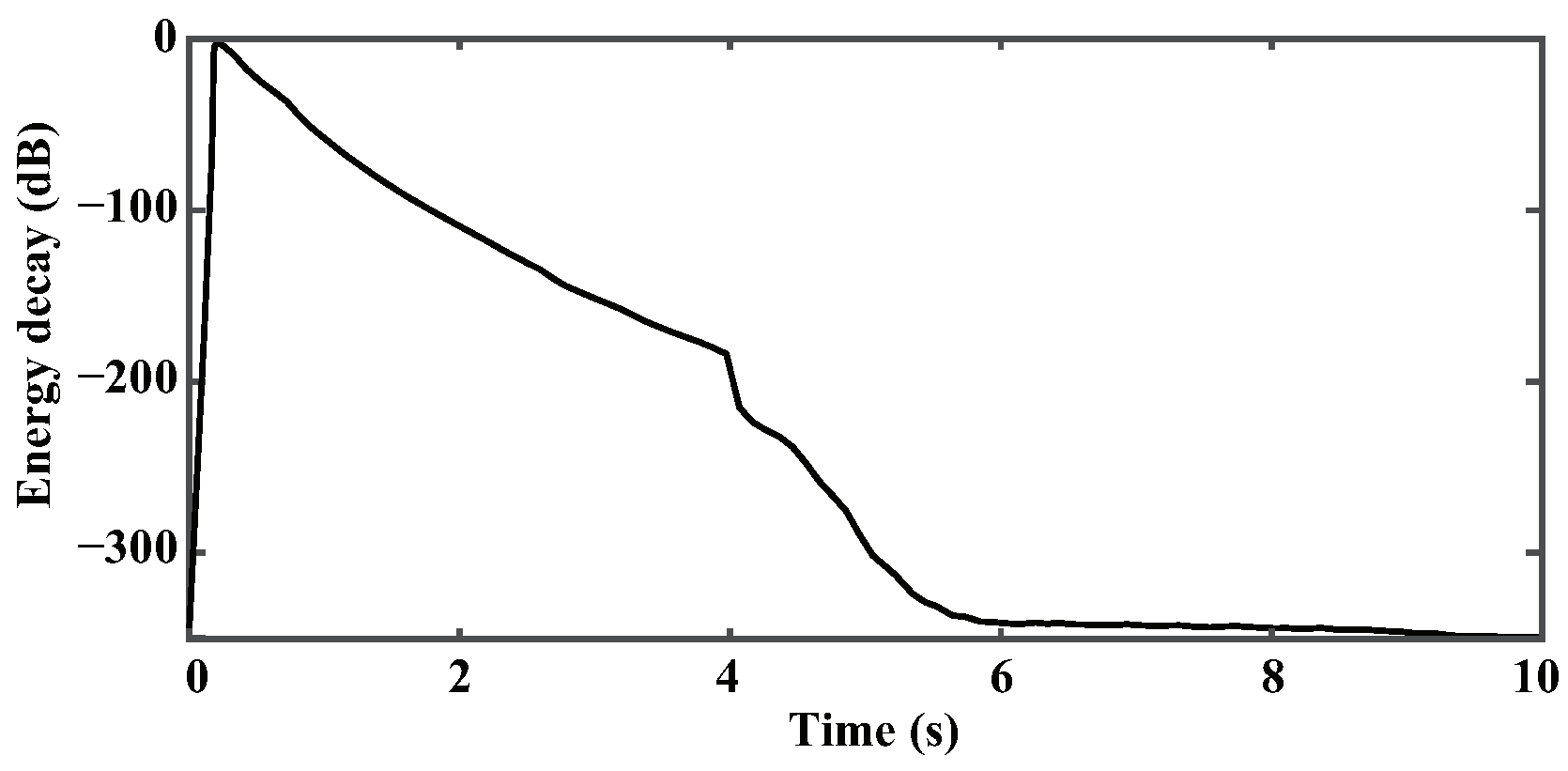
3.3. Marmousi Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Elastic Equation and Numerical Implementation
Appendix B. The GSLS-Model-Based Wave Equation
References
- Rayleigh, L. On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. 1885, 1, 4–11. [Google Scholar] [CrossRef]
- Namazi, E.; Mohamad, H.; Jorat, M.E.; Hajihassani, M. Investigation on the effects of twin tunnel excavations beneath a road underpass. Electron. J. Geotech. Eng. 2011, 16, 441–450. [Google Scholar]
- Jusoh, S.N.; Mohamad, H.; Marto, A.; Yunus, N.M.; Kasim, F. Segment’s joint in precast tunnel lining design. J. Teknol. 2015, 77, 91–98. [Google Scholar] [CrossRef]
- Al-Bared, M.A.; Harahap, I.S.; Marto, A.; Mohamad, H.; Abad, S.V.A.N.K.; Mustaffa, Z. Cyclic behavior of RT-cement treated marine clay subjected to low and high loading frequencies. Geomech. Eng. 2020, 21, 433–445. [Google Scholar] [CrossRef]
- Chaiyasarn, K.; Buatik, A.; Mohamad, H.; Zhou, M.; Kongsilp, S.; Poovarodom, N. Integrated pixel-level CNN-FCN crack detection via photogrammetric 3D texture mapping of concrete structures. Autom. Constr. 2022, 140, 104388. [Google Scholar] [CrossRef]
- Xia, J.; Miller, R.D.; Park, C.B.; Tian, G. Determining Q of near-surface materials from Rayleigh waves. J. Appl. Geophys. 2002, 51, 121–129. [Google Scholar] [CrossRef]
- Xia, J.; Xu, Y.; Miller, R.D.; Chen, C. Estimation of elastic moduli in a compressible Gibson half-space by inverting Rayleigh-wave phase velocity. Surv. Geophys. 2006, 27, 1–17. [Google Scholar] [CrossRef]
- Pan, Y.; Schaneng, S.; Steinweg, T.; Bohlen, T. Estimating S-wave velocities from 3D 9-component shallow seismic data using local Rayleigh-wave dispersion curves—A field study. J. Appl. Geophys. 2018, 159, 532–539. [Google Scholar] [CrossRef]
- Mi, B.; Xia, J.; Tian, G.; Shi, Z.; Xing, H.; Chang, X.; Zhang, H. Near-surface imaging from traffic-induced surface waves with dense linear arrays: An application in the urban area of Hangzhou, China. Geophysics 2022, 87, B145–B158. [Google Scholar] [CrossRef]
- Yuan, D.; Nazarian, S. Automated surface wave method: Inversion technique. J. Geotech. Eng. 1993, 119, 1112–1126. [Google Scholar] [CrossRef]
- Wang, H.; Xu, R.; Feng, B.; Wu, J. Understanding of seismic exploration and viewpoint of seismic data imaging processing in a complex surface exploration area. Geophys. Prospect. Pet. 2023, 62, 789–805. [Google Scholar]
- Xia, J.; Miller, R.D.; Park, C.B. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves. Geophysics 1999, 64, 691–700. [Google Scholar] [CrossRef]
- Bleibinhaus, F.; Rondenay, S. Effects of surface scattering in full-waveform inversion. Geophysics 2009, 74, WCC69–WCC77. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, H.; Zhang, Q.; Chen, H.; Wang, N.; Sun, P.; Wang, S. Effect of surface-related Rayleigh and multiple waves on velocity reconstruction with time-domain elastic FWI. J. Appl. Geophys. 2018, 148, 33–43. [Google Scholar] [CrossRef]
- Beaty, K.S.; Schmitt, D.R.; Sacchi, M. Simulated annealing inversion of multimode Rayleigh wave dispersion curves for geological structure. Geophys. J. Int. 2002, 151, 622–631. [Google Scholar] [CrossRef]
- Luo, Y.; Xia, J.; Liu, J.; Liu, Q.; Xu, S. Joint inversion of high-frequency surface waves with fundamental and higher modes. J. Appl. Geophys. 2007, 62, 375–384. [Google Scholar] [CrossRef]
- Song, X.; Gu, H.; Liu, J.; Zhang, X. Estimation of shallow subsurface shear-wave velocity by inverting fundamental and higher-mode Rayleigh waves. Soil Dyn. Earthq. Eng. 2007, 27, 599–607. [Google Scholar] [CrossRef]
- Lan, H.; Zhang, Z. Comparative study of the free-surface boundary condition in two-dimensional finite-difference elastic wave field simulation. J. Geophys. Eng. 2011, 8, 275–286. [Google Scholar] [CrossRef]
- Zahradník, J.; Hron, F. Robust finite-difference scheme for elastic waves on coarse grids. Stud. Geophys. Geod. 1992, 36, 1–19. [Google Scholar] [CrossRef]
- Frankel, A.; Leith, W. Evaluation of topographic effects on P and S-waves of explosions at the northern Novaya Zemlya test site using 3-D numerical simulations. Geophys. Res. Lett. 1992, 19, 1887–1890. [Google Scholar] [CrossRef]
- Schultz, C.A. A density-tapering approach for modeling the seismic response of free-surface topography. Geophys. Res. Lett. 1997, 24, 2809–2812. [Google Scholar] [CrossRef]
- Bayliss, A.; Jordan, K.E.; LeMesurier, B.J.; Turkel, E. A fourth-order accurate finite-difference scheme for the computation of elastic waves. Bull. Seismol. Soc. Am. 1986, 76, 1115–1132. [Google Scholar] [CrossRef]
- Kosloff, D.; Kessler, D.; Filho, A.Q.; Tessmer, E.; Behle, A.; Strahilevitz, R. Solution of the equations of dynamic elasticity by a Chebychev spectral method. Geophysics 1990, 55, 734–748. [Google Scholar] [CrossRef]
- Levander, A.R. Fourth-order finite-difference P-SV seismograms. Geophysics 1988, 53, 1425–1436. [Google Scholar] [CrossRef]
- Graves, R.W. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bull. Seismol. Soc. Am. 1996, 86, 1091–1106. [Google Scholar] [CrossRef]
- Robertsson, J.O. A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography. Geophysics 1996, 61, 1921–1934. [Google Scholar] [CrossRef]
- Mittet, R. Free-surface boundary conditions for elastic staggered-grid modeling schemes. Geophysics 2002, 67, 1616–1623. [Google Scholar] [CrossRef]
- Xu, Y.; Xia, J.; Miller, R.D. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach. Geophysics 2007, 72, SM147–SM153. [Google Scholar] [CrossRef]
- Zahradník, J.; Priolo, E. Heterogeneous formulations of elastodynamic equations and finite-difference schemes. Geophys. J. Int. 1995, 120, 663–676. [Google Scholar] [CrossRef]
- Bohlen, T.; Saenger, E.H. Accuracy of heterogeneous staggered-grid finite-difference modeling of Rayleigh waves. Geophysics 2006, 71, T109–T115. [Google Scholar] [CrossRef]
- Gottschammer, E.; Olsen, K.B. Accuracy of the explicit planar free-surface boundary condition implemented in a fourth-order staggered-grid velocity-stress finite-difference scheme. Bull. Seismol. Soc. Am. 2001, 91, 617–623. [Google Scholar] [CrossRef]
- Kristek, J.; Moczo, P.; Archuleta, R.J. Efficient methods to simulate planar free surface in the 3D 4th-order staggered-grid finite-difference schemes. Stud. Geophys. Geod. 2002, 46, 355–381. [Google Scholar] [CrossRef]
- Xu, H.; Day, S.M.; Minster, J.B.H. Two-dimensional linear and nonlinear wave propagation in a half-space. Bull. Seismol. Soc. Am. 1999, 89, 903–917. [Google Scholar] [CrossRef]
- Fang, X.; Yao, G.; Niu, F.; Wu, D. Estimating optimal parameters of finite-difference scheme for wavefield modeling. Chin. J. Geophys.-Chin. Ed. 2023, 66, 2520–2533. [Google Scholar]
- Yao, G.; Wu, D.; Debens, H.A. Adaptive finite difference for seismic wavefield modelling in acoustic media. Sci. Rep. 2016, 6, 30302. [Google Scholar] [CrossRef] [PubMed]
- Dutta, G.; Schuster, G.T. Attenuation compensation for least-squares reverse time migration using the viscoacoustic-wave equation. Geophysics 2014, 79, S251–S262. [Google Scholar] [CrossRef]
- Carcione, J.M. Rayleigh waves in isotropic viscoelastic media. Geophys. J. Int. 1992, 108, 453–464. [Google Scholar] [CrossRef]
- Borcherdt, R.D. Rayleigh-type surface wave on a linear viscoelastic half-space. J. Acoust. Soc. Am. 1973, 54, 1651–1653. [Google Scholar] [CrossRef]
- Currie, P.K.; Hayes, M.A.; O’Leary, P.M. Viscoelastic Rayleigh waves. Q. Appl. Math. 1977, 35, 35–53. [Google Scholar] [CrossRef]
- Carcione, J.M. Modeling anelastic singular surface waves in the earth. Geophysics 1992, 57, 781–792. [Google Scholar] [CrossRef]
- Zhang, K.; Luo, Y.; Xia, J.; Chen, C. Pseudospectral modeling and dispersion analysis of Rayleigh waves in viscoelastic media. Soil Dyn. Earthq. Eng. 2011, 31, 1332–1337. [Google Scholar] [CrossRef]
- Yuan, S.; Song, X.; Cai, W.; Hu, Y. Analysis of attenuation and dispersion of Rayleigh waves in viscoelastic media by finite-difference modeling. J. Appl. Geophys. 2018, 148, 115–126. [Google Scholar] [CrossRef]
- Carcione, J.M.; Kosloff, D.; Kosloff, R. Wave propagation simulation in a linear viscoelastic medium. Geophys. J. Int. 1988, 95, 597–611. [Google Scholar] [CrossRef]
- Xu, T.; McMechan, G.A. Composite memory variables for viscoelastic synthetic seismograms. Geophys. J. Int. 1995, 121, 634–639. [Google Scholar] [CrossRef]
- Carcione, J.M. Wave Fields in Real Media: Theory and Numerical Simulation of Wave Propagation in Anisotropic, Viscoelastic, Porous and Electromagnetic Media, 3rd ed.; Elsevier: Oxford, UK, 2014; pp. 385–424. [Google Scholar]
- Savage, B.; Komatitsch, D.; Tromp, J. Effects of 3D attenuation on seismic wave amplitude and phase measurements. Bull. Seismol. Soc. Am. 2010, 100, 1241–1251. [Google Scholar] [CrossRef]
- Zhu, T.; Carcione, J.M.; Harris, J.M. Approximating constant-Q seismic propagation in the time domain. Geophys. Prospect. 2013, 61, 931–940. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, H. A time-domain complex-valued wave equation for modelling visco-acoustic wave propagation. Geophys. J. Int. 2018, 215, 1064–1079. [Google Scholar] [CrossRef]
- Wang, N.; Zhu, T.; Zhou, H.; Chen, H.; Zhao, X.; Tian, Y. Fractional Laplacians viscoacoustic wavefield modeling with k-space-based time-stepping error compensating scheme. Geophysics 2020, 85, T1–T13. [Google Scholar] [CrossRef]
- Wang, N.; Xing, G.; Zhu, T.; Zhou, H.; Shi, Y. Propagating seismic waves in VTI attenuating media using fractional viscoelastic wave equation. J. Geophys. Res.-Solid Earth 2022, 127, e2021JB023280. [Google Scholar] [CrossRef]
- Carcione, J.M.; Cavallini, F.; Mainardi, F.; Hanyga, A. Time-domain modeling of constant-Q seismic waves using fractional derivatives. Pure Appl. Geophys. 2002, 159, 1719–1736. [Google Scholar] [CrossRef]
- Carcione, J.M. Theory and modeling of constant-Q P-and S-waves using fractional time derivatives. Geophysics 2009, 74, T1–T11. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, H. Viscoacoustic reverse time migration using a time-domain complex-valued wave equation. Geophysics 2018, 83, S505–S519. [Google Scholar] [CrossRef]
- Xing, G.; Zhu, T. Modeling frequency-independent Q viscoacoustic wave propagation in heterogeneous media. J. Geophys. Res.-Solid Earth 2019, 124, 11568–11584. [Google Scholar] [CrossRef]
- Wang, N.; Shi, Y.; Zhou, H. Accurately stable Q-compensated reverse-time migration scheme for heterogeneous viscoelastic media. Remote Sens. 2022, 14, 4782. [Google Scholar] [CrossRef]
- Yang, J.; Huang, J.; Zhu, H.; Li, Z.; Dai, N. Viscoacoustic reverse time migration with a robust space-wavenumber domain attenuation compensation operator. Geophysics 2021, 86, S339–S353. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, H.; Rao, Y. Source wavefield reconstruction in fractional Laplacian viscoacoustic wave equation-based full waveform inversion. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6496–6509. [Google Scholar] [CrossRef]
- Hu, B.; Huang, C.; Dong, L.; Zhang, J. A constant fractional Laplacian operator based viscoacoustic full waveform inversion for velocity and attenuation estimation. Chin. J. Geophys.-Chin. Ed. 2023, 66, 2123–2137. [Google Scholar] [CrossRef]
- Li, S.; Shi, Y.; Wang, W.; Wang, N.; Song, L.; Wang, Y. An explicit stable Q-compensated reverse time migration scheme for complex heterogeneous attenuation media. Front. Earth Sci. 2023, 11, 1121648. [Google Scholar] [CrossRef]
- Virieux, J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics 1986, 51, 889–901. [Google Scholar] [CrossRef]
- Berenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Komatitsch, D.; Martin, R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics 2007, 72, SM155–SM167. [Google Scholar] [CrossRef]
- Meza-Fajardo, K.C.; Papageorgiou, A.S. A nonconvolutional, split-field, perfectly matched layer for wave propagation in isotropic and anisotropic elastic media: Stability analysis. Bull. Seismol. Soc. Am. 2008, 98, 1811–1836. [Google Scholar] [CrossRef]
- Zeng, C.; Xia, J.; Miller, R.D.; Tsoflias, G.P. Application of the multiaxial perfectly matched layer (M-PML) to near-surface seismic modeling with Rayleigh waves. Geophysics 2011, 76, T43–T52. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, H.; Li, Q.; Wang, Y. Two efficient modeling schemes for fractional Laplacian viscoacoustic wave equation. Geophysics 2016, 81, T233–T249. [Google Scholar] [CrossRef]
- Wang, N.; Zhou, H.; Chen, H.; Xia, M.; Wang, S.; Fang, J.; Sun, P. A constant fractional-order viscoelastic wave equation and its numerical simulation scheme. Geophysics 2018, 83, T39–T48. [Google Scholar] [CrossRef]
- Xing, G.; Zhu, T. A viscoelastic model for seismic attenuation using fractal mechanical networks. Geophys. J. Int. 2021, 224, 1658–1669. [Google Scholar] [CrossRef]
- Moczo, P.; Kristek, J.; Vavrycuk, V.; Archuleta, R.J.; Halada, L. 3D heterogeneous staggered-grid finite-difference modeling of seismic motion with volume harmonic and arithmetic averaging of elastic moduli and densities. Bull. Seismol. Soc. Am. 2002, 92, 3042–3066. [Google Scholar] [CrossRef]
- Berg, P.; If, F.; Nilsen, P.; Skovgaard, O. Analytical reference solutions: Advanced seismic Modeling. In Modeling the Earth for Oil Exploration; Helbig, K., Ed.; Pergamon Press: Oxford, UK, 1994; pp. 421–427. [Google Scholar]
- Hron, F.; Mikhailenko, B.G. Numerical modeling of nongeometrical effects by the Alekseev-Mikhailenko method. Bull. Seismol. Soc. Am. 1981, 71, 1011–1029. [Google Scholar] [CrossRef]
- Park, C.B.; Miller, R.D.; Xia, J. Multichannel analysis of surface waves. Geophysics 1999, 64, 800–808. [Google Scholar] [CrossRef]
- Xia, J.; Xu, Y.; Miller, R.D. Generating an image of dispersive energy by frequency decomposition and slant stacking. Pure Appl. Geophys. 2007, 164, 941–956. [Google Scholar] [CrossRef]
- Schwab, F.A.; Knopoff, L. Fast Surface Wave and Free Mode Computations. In Methods in Computational Physics; Bolt, B.A., Ed.; Academic Press: New York, NY, USA, 1972; pp. 87–180. [Google Scholar]
- Babuska, V.; Cara, M. Seismic Anisotropy in the Earth; Kluwer Academic Publishing: Dordrecht, The Netherlands, 1991; pp. 30–36. [Google Scholar]











| Method | Advantage | Disadvantage | Formulation |
|---|---|---|---|
| vacuum formalism | simple and easy to implement | low-accuracy and poor numerical stability | |
| characteristic variable method | high accuracy | high computational load | |
| SIM | high computational efficiency and high-accuracy | only for plane waves and semi-infinite media | |
| MS | high computational efficiency | complicated calculation | |
| AEA | high computational efficiency | complicated calculation |
| Depth (m) | (g/cm) | (m/s) | (m/s) | |||
|---|---|---|---|---|---|---|
| Layer 1 | 250 | 1.5 | 700 | 1500 | 30 | 50 |
| Layer 2 | 500 | 2.0 | 1150 | 2000 | 90 | 150 |
| Depth (m) | (g/cm) | (m/s) | (m/s) | |||
|---|---|---|---|---|---|---|
| Layer 1 | 15 | 1.5 | 600 | 2400 | 30 | 50 |
| Layer 2 | 985 | 2.0 | 800 | 3000 | 90 | 150 |
| Points/Minimum Wavelength | Mesh | Spatial Step (m) | Time Step (ms) |
|---|---|---|---|
| 10 | 200 × 160 | 5 | 1 |
| 12.5 | 250 × 200 | 4 | 0.8 |
| 25 | 500 × 400 | 2 | 0.4 |
| 50 | 1000 × 800 | 1 | 0.2 |
| Equation | Spatial Step (m) | Computation Time (s) | misfit (%) |
|---|---|---|---|
| GSLS | 5 | 32 | 207 |
| 4 | 54 | 165 | |
| 2 | 208 | 27.49 | |
| 1 | 1075 | 1.52 | |
| DFL | 5 | 62 | 42.67 |
| 4 | 180 | 29.02 | |
| 2 | 643 | 4.85 | |
| 1 | 3992 | 0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Lu, J.; Shi, Y.; Wang, N.; Han, L. High-Accuracy Simulation of Rayleigh Waves Using Fractional Viscoelastic Wave Equation. Fractal Fract. 2023, 7, 880. https://doi.org/10.3390/fractalfract7120880
Wang Y, Lu J, Shi Y, Wang N, Han L. High-Accuracy Simulation of Rayleigh Waves Using Fractional Viscoelastic Wave Equation. Fractal and Fractional. 2023; 7(12):880. https://doi.org/10.3390/fractalfract7120880
Chicago/Turabian StyleWang, Yinfeng, Jilong Lu, Ying Shi, Ning Wang, and Liguo Han. 2023. "High-Accuracy Simulation of Rayleigh Waves Using Fractional Viscoelastic Wave Equation" Fractal and Fractional 7, no. 12: 880. https://doi.org/10.3390/fractalfract7120880
APA StyleWang, Y., Lu, J., Shi, Y., Wang, N., & Han, L. (2023). High-Accuracy Simulation of Rayleigh Waves Using Fractional Viscoelastic Wave Equation. Fractal and Fractional, 7(12), 880. https://doi.org/10.3390/fractalfract7120880








