Abstract
This paper presents an innovative Mittag–Leffler two-dimensional filter and its application in image processing. The proposed filter leverages the utilization of a Mittag–Leffler function within the probability density function. It introduces three adjustable filter parameters that enable the manipulation of the curve shape and the filter’s forgetting factor. Moreover, a two-dimensional Mittag–Leffler distribution was defined and used for the first time in an image filter. By conducting a comparative analysis against conventional filtering techniques, the paper showcases the distinct advantages of the proposed filter through illustrative examples. Additionally, the paper provides detailed implementation explanations and presents the Matlab function corresponding to the proposed two-dimensional filter.
1. Introduction
Circuits, systems, signal processing techniques, and filters form the cornerstone of modern electronic communication and information processing technologies. They are the fundamental building blocks for designing and implementing various electronic devices, ranging from simple amplifiers to complex microprocessors. Signal processing involves manipulating, analyzing, and modifying signals to extract meaningful information or enhance quality. Filters, integral components of signal processing systems, play a vital role in modifying the frequency content of signals. They enable the separation of desired signals from noise and unwanted components, improving clarity and fidelity. By employing specific filtering techniques, such as low-pass, high-pass, band-pass, or notch filters, engineers can adjust a circuit’s frequency response to specific application requirements. Integrating circuits, systems, and signal processing with filters offers many possibilities for advancements in diverse fields, including telecommunications, audio processing, and image and video processing.
A typical representative of a two-dimensional signal is an image. Image processing is a widely recognized discipline encompassing the manipulation of digital images through mathematical algorithms. Its principal objective revolves around enhancing the visual quality of an image, applying effects such as blurring and extracting valuable information from the image. Image processing is fundamental to various technological domains, including computer vision, robotics, and artificial intelligence. A notable area of focus within image processing entails image filtering and denoising techniques. Image filtering techniques are employed to enhance and modify digital images. These techniques predominantly attenuate high frequencies, known as smoothing techniques, and low frequencies, which involve edge detection or image enhancement. Thus, image filtering can be categorized into two distinct groups based on their effects [1]:
- •
- Low-pass filters, commonly called smoothing filters, effectively eliminate high spatial frequency noise from a digital image. Using a moving window operator, these filters systematically process individual pixels within the image by modifying their values according to a predefined function that incorporates the neighboring region of pixels.
- •
- High-pass filters impart a sharper visual perception to an image (edge detection and sharpening). In direct contrast to low-pass filters, high-pass filters accentuate intricate details within the image. Like low-pass filtering, high-pass filtering operates using a convolution kernel, distinct from low-pass filters.
In the area of image processing, various filters are available, each exhibiting unique strengths and weaknesses. Noteworthy image filter types include, for instance [2,3,4,5,6,7,8]:
- •
- Gaussian filter—this variant of a low-pass filter effectively smooths images, reduces noise, and performs image blurring while simultaneously preserving significant image attributes, such as edges and corners.
- •
- Laplacian filter—a high-pass filter predominantly utilized for enhancing edges and detecting notable features such as edges and corners.
- •
- Median filter—as a non-linear filter, it specifically targets the removal of salt-and-pepper noise while striving to preserve image edges.
- •
- Bilateral filter—an edge-preserving filter that facilitates image smoothing while preserving edges and details.
- •
- Anisotropic filter—an edge-preserving filter capable of smoothing images while preserving edges oriented in a specific direction.
- •
- Homomorphic filter—a frequency-domain filter used to rectify non-uniform illumination and augment image contrast.
- •
- Sobel filter—this filter is commonly employed for detecting edges within an image.
- •
- Wavelet filter—a multi-scale filter that finds utility in image compression, feature extraction, and image denoising.
- •
- Wiener filter—an adaptive filter designed for removing noise from images.
In the following parts of the article, we will focus mainly on the Gaussian filter and its modification to a more general two-dimensional Mittag–Leffler filter with three tunable parameters. As another filter for comparing the properties of both mentioned filters, we will also use the Wiener filter.
The contributions of this paper are summarized as follows:
- Definition of new two-dimensional Mittag–Leffler distribution.
- The novel two-dimensional Mittag–Leffler filter with three adjustable parameters and its practical implementation in Matlab are defined.
- We provide evidence using performance indicators (peak signal-to-noise ratio) that the proposed filter is more flexible and gives better results than a classical filter with similar structure and properties.
The structure of this article is as follows. Section 1 briefly describes the introduction to the problem. Section 2 presents the essential mathematical tools. The novel filter methods are presented in Section 3. The results are shown in Section 4 to demonstrate the main benefits of the new filter. In Section 5, the obtained results are discussed. Finally, some concluding remarks are given in Section 6.
2. Preliminaries
2.1. Gaussian Distribution
The well-known Gaussian function can be expressed in one dimension x in the essential form
where is the standard deviation of the distribution. The distribution is assumed to have zero mean. In two dimensions (2D), it is the product of two such Gaussian functions (one in each direction x and y), and it is given by [9]:
where x is the distance from the origin on the horizontal axis, and y is the distance from the origin in the vertical axis. The variance of two dimensional Gaussian distribution (2) is then .
2.2. Gaussian Filter
The Gaussian filter is named after the Gaussian function that shapes it. This filter blurs or filters an image by convolving it with a two-dimensional bell-shaped function known as the Gaussian kernel. It can be expressed as:
where is the original image and is the filtered image. The kernel has two parameters: the standard deviation , which controls the bell curve’s width, and the kernel size, which determines the extent of smoothing. The Gaussian filter is a linear filter that calculates the weighted average of pixel values. Each pixel’s weight depends on its distance from the kernel center and the Gaussian function’s value at that distance. The farther a pixel is from the center, the lower its weight and the less effect it has on the convolved pixel’s final value. The Gaussian filter finds widespread use in image processing, including edge detection, image enhancement, medical imaging, computer vision, and image smoothing. It is particularly effective in removing noise while preserving essential image features such as edges and corners. The amount of blur is controlled by the Gaussian kernel’s size and the standard deviation. A larger kernel and higher standard deviation result in more blur, while a smaller kernel and lower standard deviation lead to less blur. It acts as a low-pass filter, attenuating high-frequency signals. Thus, Gaussian blur is a powerful tool in image processing that can help enhance image quality and extract valuable information from noisy or low-quality images.
2.3. Mittag–Leffler Distribution
Furthermore, while the exponential law serves as a conventional method for investigating system dynamics, it fails to capture the behavior of numerous systems that exhibit either faster or slower dynamics than those dictated by exponential law. In such scenarios, the Mittag–Leffler function emerges as the most suitable candidate for accurately describing these anomalous changes in dynamics.
The Mittag–Leffler function is a special function dependent on two parameters: and . It can be represented by the following series [10]:
Here, is the gamma function, and setting results in a one-parameter Mittag–Leffler function . The Mittag–Leffler function is known as the queen of the functions in fractional calculus because of its relationships with other functions, for example [10]:
The Mittag–Leffler function is crucial in solving fractional differential equations, playing a significant role in fractional calculus theory [10]. The ordinary and generalized Mittag–Leffler functions demonstrate the ability to interpolate between purely exponential and power-law behaviors, making them highly valuable for implementing filters with variable exponential-type forgetting. In addition to its use in filter design, signal, and image processing, there are methods where fractional-order derivatives and integrals can be directly utilized for these filtering purposes [11,12,13,14].
Figure 1 plots the Mittag–Leffler function behavior for various values of and within interval .
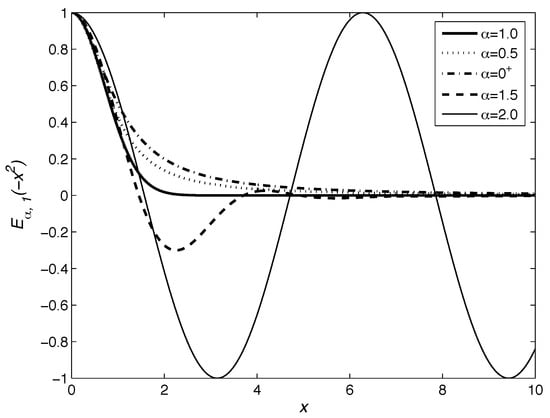
Figure 1.
Behavior of the Mittag–Leffler function for various parameter within interval and fixed .
In [15], the Mittag–Leffler distribution was generalized to include a parameter in the probability density function, which can be expressed as:
where , , and . This distribution has been proven to be attracted to the stable distribution with exponent only, as demonstrated by Pillai in [16] in 1990. The behavior of the Mittag–Leffler function in Figure 1 is related to this result, and the function represents the cumulative distribution function of a probability measure on non-negative real numbers.
Additionally, a Mittag–Leffler distribution with parameters and is defined by its probability density function [15]:
where in (7). If we set , then we obtain the distribution described by (6). Further details on the properties and relations to stochastic processes can be found in [15,16,17,18].
Upon careful examination of Figure 1, it becomes evident that when the parameter exceeds unity (), the Mittag–Leffler function displays oscillatory behavior, thereby yielding a distribution that exhibits associations with signed probability [19].
Building upon this concept, the new Mittag–Leffler distribution function for a signal processing was proposed in [20]. Such probability density function can be described as follows:
where , , and are positive real parameters, and denotes the mean value of the independent variable x.
We have adopted the Mittag–Leffler distribution function concept also in this paper. Following Equation (1), for a 2D case we can use the Mittag–Leffler distribution (8) for , involving both directions x and y:
In Figure 2, is depicted the Mittag–Leffler distribution (9) for parameters , , and with means (0, 0).
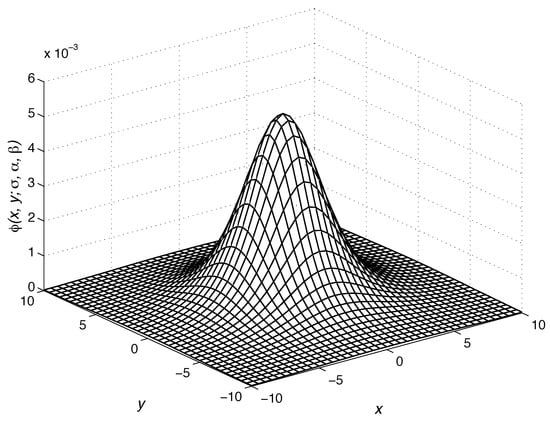
Figure 2.
Mittag–Leffler two-dimensional distribution function (9) for parameters , , and .
3. Methods
3.1. Novel Filter Definition
In [20], the Gaussian filter was generalized to the Mittag–Leffler filter, which was initially used for signal processing but can also be used for image processing (2D signal). The Mittag–Leffler filter is based on the Mittag–Leffler function, which is a generalization of the exponential function. It can be used for image smoothing and noise reduction, especially for images with long-tailed distributions commonly found, for instance, in medical imaging and other applications. The Mittag–Leffler filter convolves an image with a kernel based on the Mittag–Leffler function, which has two parameters: the shape parameter controlling the shape of the function and the scale parameter determining the extent of the smoothing.
Following the idea of a generalization of the exponential function to the Mittag–Leffler function of two parameters, a novel generalized filter, let us name it the Mittag–Leffler 2D filter, can be defined by 2D convolution as follows [20]:
In this manner, we may obtain a filter with adjustable forgetting factors with tuning parameters , , and . In other words, we can shape the curve of the probability density function. On the other hand, the different distribution shapes mean that we use different distribution functions, for instance, normal distribution, Cauchy distribution, and many others from this large family of functions.
Taking into account the Mittag–Leffler distribution (9) and general filter definition (10), we can introduce the new Mittag–Leffler 2D filter as follows:
Obviously, we obtain the classical Gaussian filter (3) for parameters and because of relation . Such a three-parameter image filter is more flexible than the classical one. Except parameter the filter (11) has more degrees of freedom due to the additional two tuning parameters and with which we can shape the distribution curve as needed.
3.2. Implementation Notes
To facilitate the practical application of the Mittag–Leffler filter within the discrete-time domain, established methods outlined in references such as [21,22] can be used. This non-causal nature renders the Mittag–Leffler filter physically unfeasible, as the Mittag–Leffler filter function (11) theoretically necessitates an infinite window length for and . In practical implementation, truncating and utilizing the filter window specifically for narrow windows is reasonable. However, such truncation may introduce considerable errors in some instances. In real-time systems, a delay is incurred since the incoming samples must fill the filter window before the filter can be applied to the processed signal or image. The Mittag–Leffler filter kernel used in convolution remains continuous. The most commonly employed approach to solving this problem is substituting the continuous kernel with its discrete counterpart, which involves sampling points from the continuous kernel. Instead of integration operations during convolution, the discrete equivalent utilizes the summation operations over all sampled points.
In order to ensure applicability in digital devices with limited computational capabilities and the ability to handle multiple stochastic values in measured data, the filter algorithm must possess both mathematical and programming simplicity. Aside from convolution and window length concerns, real-time applications of the Mittag–Leffler function are further complicated by the infinite upper sum limit defined in Equation (4). To mitigate this issue, the integral form of the Mittag–Leffler function, as described by Podlubny [10], can be utilized; however, this approach may encounter difficulties associated with numerical integration methods. To overcome these limitations, Podlubny and Kacenak proposed a practical implementation algorithm for the Mittag–Leffler function in the form of a Matlab function [23]: mlf(alpha,beta,Z,P). Moreover, using the mentioned algorithm, the proposed filter (11) can be easily implemented as a Matlab function. The Matlab function of the suggested Mittag–Leffler filter (11) was also created, and it is freely available together with demo on the MathWorks, Inc. website. It has the following header [24]: [img_filt]=ML_filter_2D(img,sigma,alpha,beta).
3.3. Performance Indicator
We will quantify the quality (performance) of output images using the well-known indicator, which is the related quantity of the peak signal-to-noise ratio (PSNR), objectively measuring the intensity of the error signal in decibels, calculated as [9]:
where d is the maximum possible intensity (pixel value) of the image, and MSE is the mean square error, computed by averaging the squared intensity differences of distorted and reference image pixels. The PSNR is often used because it is simple to calculate (e.g., function psnr() in Matlab) and has precise physical meanings [25]. Higher PSNR values correspond to better quality of reconstructed or filtered image. This indicator can also be used as a cost function for optimal tuning of the filter parameters.
4. Results
Let us use the well-known experimental gray-scale image Lena of size pixels. We applied the Mittag–Leffler filter (11) for various parameters , , and , for the image blur. Further, the denoising of Gaussian and salt-and-pepper noise and the performance indicator computation were performed.
Figure 3 presents the results of the application to the Lena image of the Mittag–Leffler two-dimensional filter (11) for various sets of the parameters , , and . We may observe different degrees of blurring on the smoothed images.


Figure 3.
Results of image blur after applying the Mittag–Leffler filter (11): (a) Original image without using a filter. (b) Filter parameters , , and , i.e., the Gaussian filter (3). (c) Filter with parameters , , and . (d) Filter with parameters , and .
Figure 4 and Figure 5 depict image denoising results and PSNR by applying various filters to two noisy images, respectively.

Figure 4.
Result of image denoising with added Gaussian noise of zero mean and variance equal 0.05: (a) Noised image without filtering. (b) Mittag–Leffler filter (11) with parameters , , and PSNR = 24.20 dB. (c) Wiener filter with neighborhoods of size , and PSNR = 20.93 dB. (d) Gaussian filter (3) with parameter , and PSNR = 22.10 dB.

Figure 5.
Result of image denoising with added salt-and-pepper noise with the density 0.02: (a) Noised image without filtering. (b) Mittag–Leffler filter (11) with parameters , , and PSNR = 29.23 dB. (c) Wiener filter with neighborhoods of size , and PSNR = 23.83 dB. (d) Gaussian filter (3) with parameter , and PSNR = 27.16 dB.
5. Discussion
The filter proposed in this work should not be considered as “just another filter”. As it is well-known, the dynamics of real-world systems can be more effectively captured using fractional calculus concepts than classical calculus-based models because of an additional degree of freedom (extra “tuning knobs”). The proposed filter directly connects to the fractional calculus due to the Mittag–Leffler function. This function is fundamental for solving the fractional differential equation. As we may observe in (5), another well-known function could be expressed by the Mittag–Leffler function with its various parameters. Because of these additional parameters, we can move between the known functions.
In this paper, the proposed Mittag–Leffler filter has a structure similar to the Gaussian filter, with two extra tuning knobs. It allows us to obtain many results that classical filters cannot achieve. Comparison has also been made with the Wiener filter to demonstrate the functionality of the proposed filter and that results are comparable with known filters.
These results were evaluated with the PSNR performance indicator, which indicates the image quality. It should be noted that due to only experimental tuning of the filter parameters, the PSNR indicator is better, with only a few decibels. This is due to the more significant number of adjustable parameters. However, it is evidence that the Mittag–Leffler filter works but as it was mentioned, these parameters were found experimentally, and better values for the PSNR indicator could be obtained with different values for , and . This advantage of several degrees of freedom can also complicate optimally tuning the filter parameters and its subsequent practical implementation. From these first results, we see that some optimization methods with limitations for the interval from which the parameters can be searched using the PSNR indicator as a cost function optimization are suitable for correctly tuning the filter parameters. Based on this suggestion, the well-tuned filter can bring much better results. Moreover, as was already mentioned, the Mittag–Leffler filter is more computationally demanding and requires careful tuning of its parameters for optimal performance. It is still an open problem and will be the idea of further research.
6. Conclusions
This article describes a new generalized low-pass filter based on the Mittag–Leffler two-dimensional distribution function applicable for image processing. An example in order to demonstrate the novel filter benefits is presented. The proposed filter has three adjustable parameters and is more flexible than a classical Gaussian filter. The Gaussian filter is a particular case of the new Mittag–Leffler filter for a specific set of parameters. Compared to other image filters, the Mittag–Leffler filter has several advantages. It is more effective in reducing noise in images with long-tailed distributions and better preserves sharp edges and fine details than other filters due to the filter kernel. However, the Mittag–Leffler filter is more computationally expensive and requires careful tuning of its parameters for optimal performance. A Matlab function of the novel Mittag–Leffler image filter and the demo for its implementation was created [24].
Funding
This research was funded in part by the Slovak Grant Agency for Science under grant VEGA 1/0674/23, by the Slovak Research and Development Agency under contracts No. APVV-18-0526 and No. APVV-22-0508, and by Army Research Office under grant No. W911NF-22-1-0264.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Burger, W.; Burge, M.J. Digital Image Processing: An Algorithmic Introduction; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Matei, R. A Class of directional zero-phase 2D filters designed using analytical approach. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 1629–1640. [Google Scholar] [CrossRef]
- Mafi, M.; Martin, H.; Cabrerizo, M.; Andrian, J.; Barreto, A.; Adjouadi, M. A comprehensive survey on impulse and Gaussian denoising filters for digital images. Signal Process. 2019, 157, 236–260. [Google Scholar] [CrossRef]
- Sumiya, Y.; Otsuka, T.; Maeda, Y.; Fukushima, N. Gaussian Fourier pyramid for local Laplacian filter. IEEE Signal Process. Lett. 2022, 29, 11–15. [Google Scholar] [CrossRef]
- Li, K.; Príncipe, J.C. Functional Bayesian filter. IEEE Trans. Signal Process. 2022, 70, 57–71. [Google Scholar] [CrossRef]
- Deng, G.; Cahill, L.W. An adaptive Gaussian filter for noise reduction and edge detection. In Proceedings of the 1993 IEEE Conference Record Nuclear Science Symposium and Medical Imaging Conference, San Francisco, CA, USA, 31 October–6 November 1993; Volume 3, pp. 1615–1619. [Google Scholar] [CrossRef]
- Chang, S.Y.; Wu, H.C. Tensor Wiener Filter. IEEE Trans. Signal Process. 2022, 70, 410–422. [Google Scholar] [CrossRef]
- Koranga, P.; Singh, G.; Verma, D.; Chaube, S.; Kumar, A.; Pant, S. Image denoising based on wavelet transform using visu thresholding technique. Int. J. Math. Eng. Manag. Sci. 2018, 3, 444–449. [Google Scholar] [CrossRef]
- Seddik, H. A new family of Gaussian filters with adaptive lobe location and smoothing strength for efficient image restoration. EURASIP J. Adv. Signal Process. 2014, 2014, 25. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Chen, D.; Chen, Y.Q.; Xue, D. Digital fractional order Savitzky-Golay differentiator. IEEE Trans. Circuits Syst. II Express Briefs 2011, 58, 758–762. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.Q.; Qiu, T.S. Fractional Processes and Fractional-Order Signal Processing; Springer: London, UK, 2012. [Google Scholar]
- Yang, Q.; Chen, D.; Zhao, T.; Chen, Y.Q. Fractional calculus in image processing: A review. Fract. Calc. Appl. Anal. 2016, 19, 1222–1249. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, S. Design of Mittag–Leffler kernel-based fractional-order digital filter using fractional delay interpolation. Circuits Syst. Signal Process. 2022, 41, 3415–3445. [Google Scholar] [CrossRef]
- Agahi, H.; Alipour, M. Mittag–Leffler–Gaussian distribution: Theory and application to real data. Math. Comput. Simul. 2019, 156, 227–235. [Google Scholar] [CrossRef]
- Pillai, R.N. On Mittag–Leffler functions and related distributions. Ann. Inst. Stat. Math. 1990, 42, 157–161. [Google Scholar] [CrossRef]
- Huillet, T.E. On Mittag–Leffler distributions and related stochastic processes. J. Comput. Appl. Math. 2016, 296, 181–211. [Google Scholar] [CrossRef]
- Albrecher, H.; Bladt, M.; Bladt, M. Matrix Mittag–Leffler distributions and modeling heavy-tailed risks. Extremes 2020, 23, 425–450. [Google Scholar] [CrossRef]
- Leonenko, N.; Podlubny, I. Monte Carlo method for fractional-order differentiation extended to higher orders. Fract. Calc. Appl. Anal. 2022, 25, 841–857. [Google Scholar] [CrossRef]
- Petráš, I. Novel generalized low-pass filter with adjustable parameters of exponential-type forgetting and its application to ECG signal. Sensors 2022, 22, 8740. [Google Scholar] [CrossRef] [PubMed]
- Rau, R.; McClellan, J.H. Efficient approximation of Gaussian filters. IEEE Trans. Signal Process. 1997, 45, 468–471. [Google Scholar] [CrossRef]
- Wells, W.M. Efficient synthesis of Gaussian filters by cascaded uniform filters. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 234–239. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I.; Kacenak, M. Mittag–Leffler Function, MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/8738 (accessed on 31 July 2022).
- Petráš, I. Mittag–Leffler 2D Filter for Image Processing, MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/131039 (accessed on 13 June 2023).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).