Finite Difference Scheme and Finite Volume Scheme for Fractional Laplacian Operator and Some Applications

Abstract

The fractional Laplacian operator is a very important fractional operator that is often used to describe several anomalous diffusion phenomena. In this paper, we develop some numerical schemes, including a finite difference scheme and finite volume scheme for the fractional Laplacian operator, and apply the resulting numerical schemes to solve some fractional diffusion equations. First, the fractional Laplacian operator can be characterized as the weak singular integral by an integral operator with zero boundary condition. Second, because the solutions of fractional diffusion equations are usually singular near the boundary, we use a fractional interpolation function in the region near the boundary and use a classical interpolation function in other intervals. Then, we apply a finite difference scheme to the discrete fractional Laplacian operator and fractional diffusion equation with the above fractional interpolation function and classical interpolation function. Moreover, it is found that the differential matrix of the above scheme is a symmetric matrix and strictly row-wise diagonally dominant in special fractional interpolation functions. Third, we show a finite volume scheme for a discrete fractional diffusion equation by fractional interpolation function and classical interpolation function and analyze the properties of the differential matrix. Finally, the numerical experiments are given, and we verify the correctness of the theoretical results and the efficiency of the schemes.

1. Introduction

The fractional Laplacian operator is a very important fractional operator that is often used to describe several phenomena, such as the thin obstacle problem, optimization, finance, phase transitions, stratified materials, anomalous diffusion, etc., and it can be defined by the following form [1,2,3]:

$$\begin{array}{c}\hfill -{(-\Delta )}^{\frac{\alpha }{2}}u(x)=-{\mathcal{F}}^{-1}{(|\xi |}^{\alpha }\mathcal{F}(u(\xi ))),\end{array}$$

(1)

where $\mathcal{F}$ is the Fourier transform. It can also be represented as the hypersingular integral form

$$\begin{array}{c}\hfill -{(-\Delta )}^{\alpha /2}u(x)=C_{n,\alpha }P.V.{\int }_{R^n}\frac{u(x)-u(y)}{{|x-y|}^{n+\alpha }}dy,\end{array}$$

(2)

where ${\displaystyle C_{n,\alpha }=\frac{\alpha 2^{\alpha 2^{\alpha -1}\mathsf{\Gamma }(\frac{\alpha +n}{2})}}{{\pi }^{n/2}\mathsf{\Gamma }(\frac{2-\alpha }{2})}}$. In particular, one-dimensional fractional Laplacian operator can be expressed as the Riesz fractional derivative [4,5,6,7,8]

$$-{(-\Delta )}^{\alpha /2}u(x)=\frac{{\partial }^{\alpha }}{{\partial \left|x\right|}^{\alpha }}u(x)=-\frac{1}{2cos\frac{\alpha \pi }{2}}{[}_{-\infty }{D}_x^{\alpha }u(x){+}_x{D}_{+\infty }^{\alpha }u(x)],$$

the where ${}_{-\infty }{D}_x^{\alpha }u(x),{}_x{D}_{+\infty }^{\alpha }u(x)$ are left and right Riemann–Liouville fractional derivatives of order $\alpha$, respectively. When $\alpha =2$, the fractional Laplacian operator reduces to the classical Laplacian operator. When $\alpha \ne 2$, the fractional Laplacian operator is a nonlocal generalization of the classical Laplacian operator. By investigating the literature about fractional Laplacian operators, we find that most of the numerical methods [9,10,11,12,13,14,15,16,17,18,19,20,21] for fractional Laplace operators are based on Fourier definition (1). However, the Fourier definition (1) is suitable only for the problems defined either on the whole space or periodic boundary conditions. The fractional Laplacian operator on a bounded domain is of great interest, not only from a mathematical point of view but also in practical applications. Recently, some studies have been carried out on the fractional Laplacian operator with zero boundary conditions. First, based on the Riesz fractional derivative, some finite difference methods, such as the fractional centered difference method, weighted and shifted Grünwald difference method, fourth-order compact method, and the matrix transform method, have been developed for the discrete fractional Laplacian operator. Second, based on the fractional Laplacian operator (2), some numerical methods have been also proposed in [22,23,24,25,26] to discretize the fractional Laplacian operator, and they show corresponding theoretical analyses.

A fractional diffusion equation is an important class of fractional differential equations, and it has been successfully used to simulate some physical phenomena, such as the thin obstacle problem, stratified materials, anomalous diffusion, etc. It is usually difficult to obtain the analytical solution of the fractional diffusion equation with the fractional Laplacian operator. Therefore, numerical methods have been playing more and more important roles in fractional diffusion equations [4,5,6]. In fact, some attention has been paid to theories and numerical methods for some fractional diffusion equations with the fractional Laplacian operator. The main difficulties in dealing with the fraction diffusion equation are (i) the fractional Laplacian operator is a nonlocal operator; (ii) the solution of the fractional diffusion equation is usually singular near the boundary; (iii) and the fractional Laplacian operator is a hypersingular integral operator. Recently, some attention has been paid to theories and numerical methods to overcome these difficulties. First, in order to deal with the hypersingular integral representation of the fractional Laplacian operator, the main approach is to change the hypersingular integral into a weak singular integral. Second, in order to resolve the singularity of the nonsmooth solution of the fractional diffusion equation, several numerical approaches [27,28] have been developed. In [27], some nonuniform refined grids have been employed to solve fractional diffusion equations with nonsmooth solutions at the end-points. In [28], an improved algorithm based on a finite difference scheme has been employed to solve the fractional diffusion equation with a nonsmooth solution. In addition, in order to deal with the nonsmooth solution of the fractional diffusion equation, other numerical methods, such as nonuniform refined grids, correction convolution quadrature, and some nonpolynomial basis functions, have also been developed, and they display corresponding theoretical analyses. However, in these works, only classical interpolation functions are considered. As far as we know, there exist few studies on fractional interpolation functions [29] for the fractional diffusion equation with the fractional Laplacian operator. The main goal of this paper is to construct some numerical schemes for the fractional Laplacian operator based on a fractional interpolation function with zero boundary conditions and apply the resulting numerical schemes to solve some fractional diffusion equations.

In this paper, we mainly use the finite difference method and finite volume method to discretize the fractional Laplacian operator and fractional diffusion equation with zero boundary conditions. First, we deal with the hypersingular integral representation of the fractional Laplacian operator as a weak singular integral by an integral operator ${\mathcal{J}}^{\alpha }(x)$. Second, because the solution of the fractional diffusion equation is usually singular near the boundary, we use a fractional interpolation function in the region near the boundary based on some lemmas and use a classical interpolation function in other intervals. Moreover, applying the resulting numerical scheme of the fractional Laplacian operator to the fractional diffusion equation, we show some corresponding theoretical analyses. Third, we also show a finite volume scheme to solve the fractional Laplacian operator and fractional diffusion equation by fractional interpolation function and classical interpolation function. For simplicity’s sake, we only consider numerical schemes for uniform dissection, but it is easy to generalize to nonuniform dissection by a similar approach.

The outline of this paper is as follows. In Section 2, we present the finite difference scheme to deal with the fractional Laplacian operator by fractional interpolation function and classical interpolation function and apply the resulting numerical scheme to solve some fractional diffusion equations. In Section 3, we present the finite volume scheme to deal with the fractional Laplacian operator and fractional diffuse equation and show the corresponding theoretical analysis. 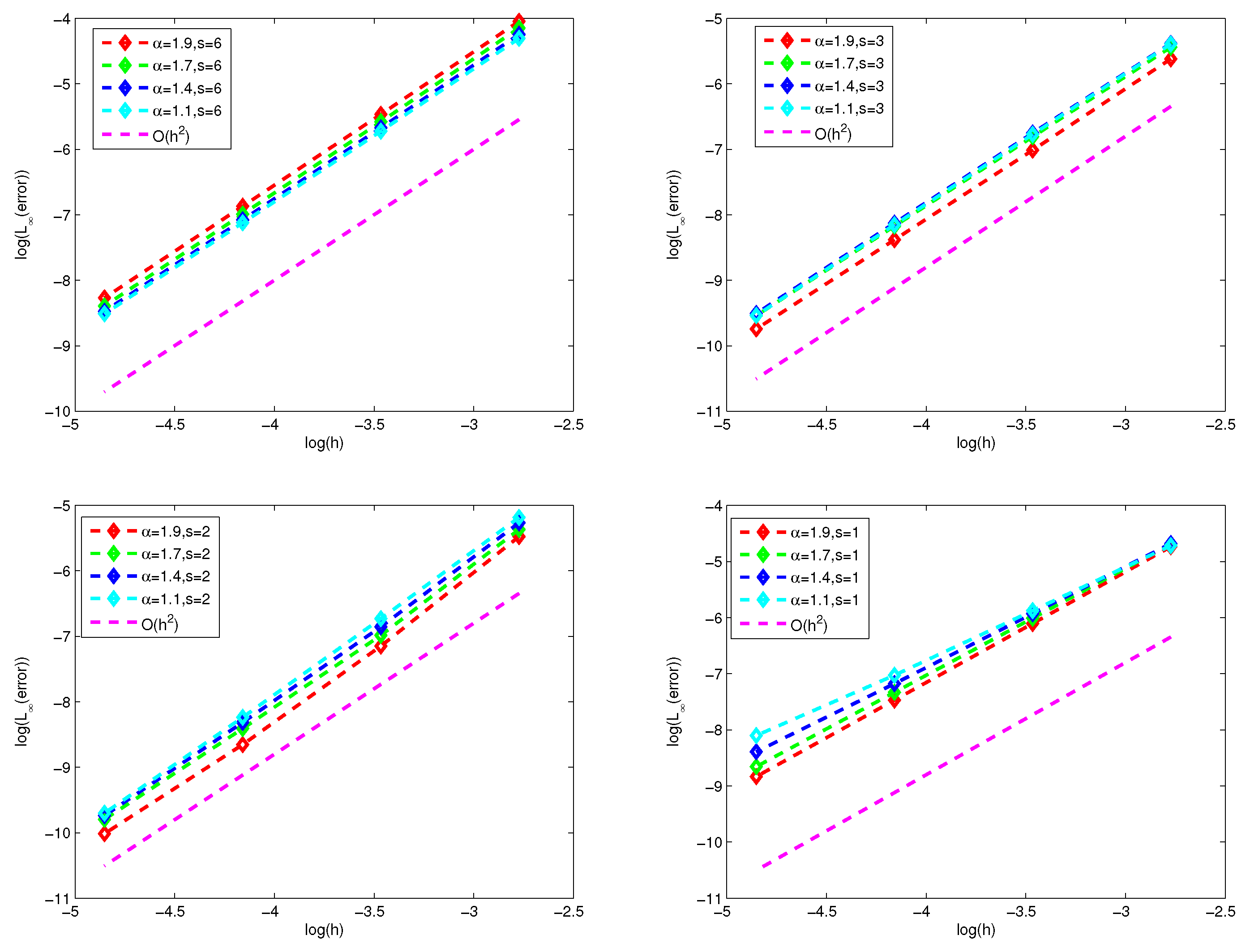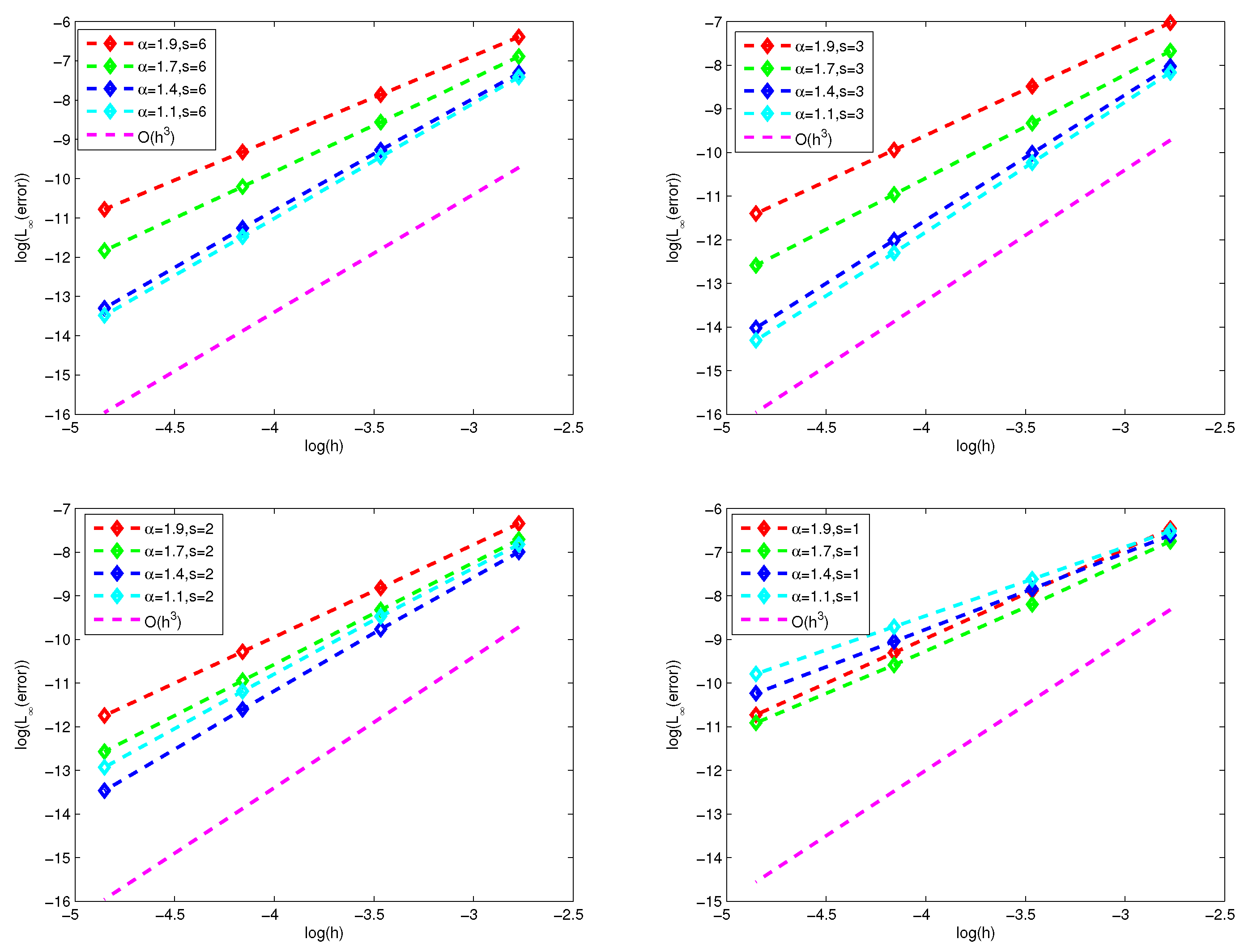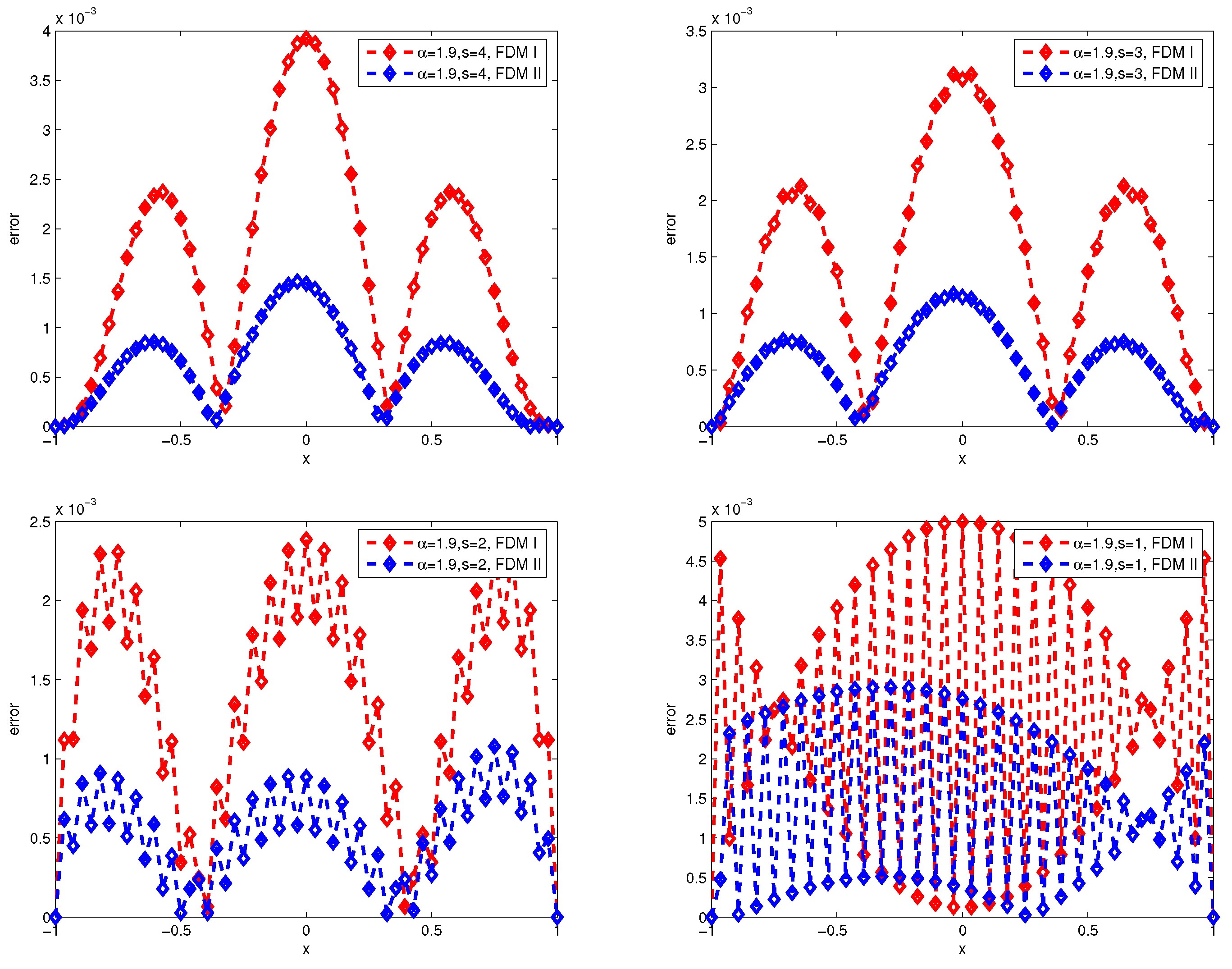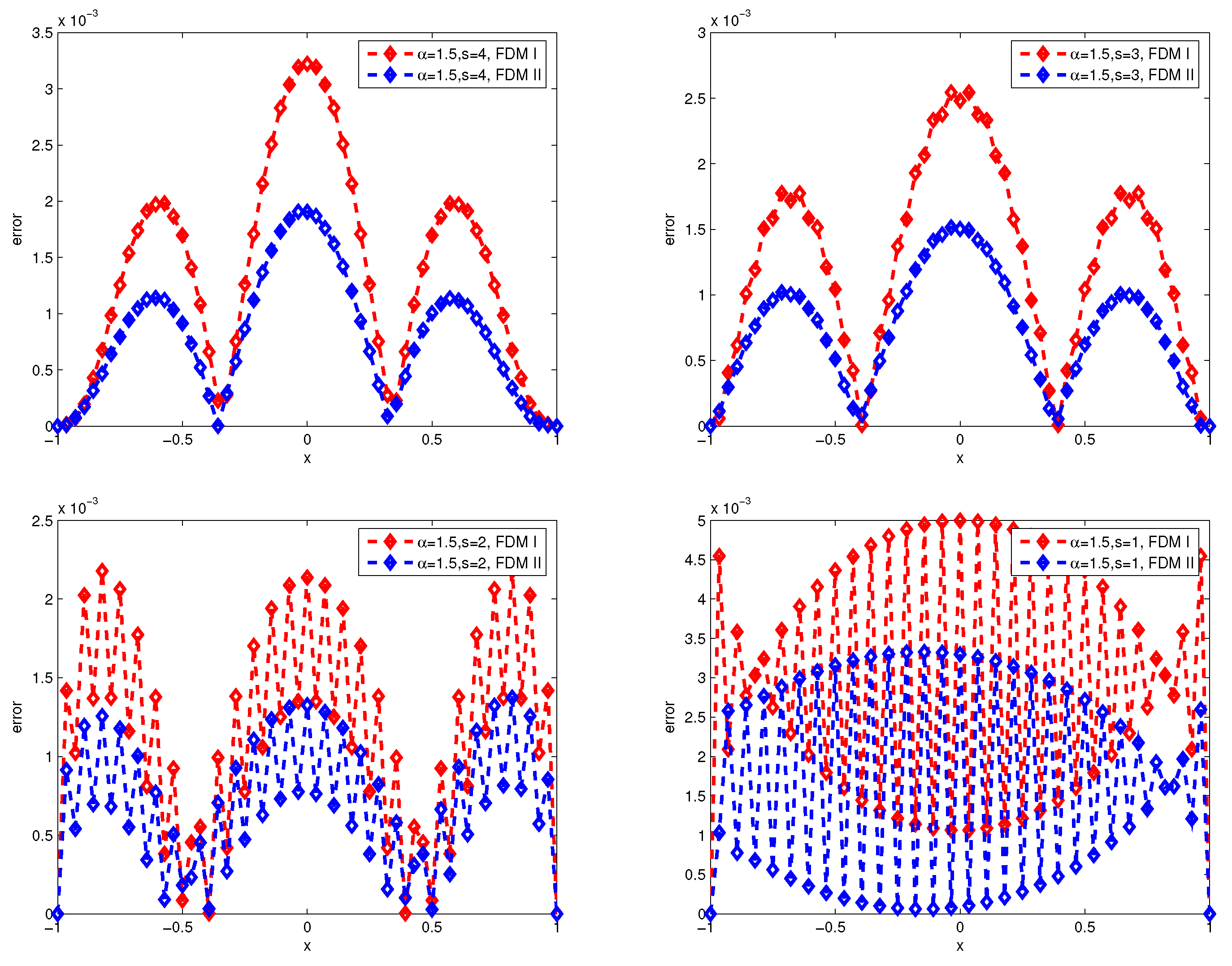In Section 4, the numerical experiments are conducted, and the results verify the efficiency of the schemes. Finally, some conclusions and a discussion are given in Section 5.

2. Finite Difference Method for Fractional Laplacian Operator and Fractional Diffusion Equation

Some finite difference schemes have been designed for the discrete fractional Laplacian operator based on the Riesz fractional derivative, including the shifted Grünwald formula, second-order weighted, shifted Grünwald–Letnikov difference formula, fractional central difference scheme, etc. However, little attention has been paid to approximating the hypersingular integral definition by fractional interpolation function. In this section, we show a finite difference scheme for the fractional Laplacian operator and fractional diffusion equation with zero boundary condition by fractional interpolation function and classical interpolation function.

2.1. Finite Difference Scheme for Fractional Laplacian Operator

From a physical point of view, the fractional Laplacian operator plays a crucial role in describing several phenomena, such as the thin obstacle problem, optimization, phase transitions, anomalous diffusion, etc. In order to deal with the hypersingular integral representation of the fractional Laplacian operator, one key idea is to deal with the hypersingular integral representation of the fractional Laplacian operator as a weak singular integral.

Under the zero boundary condition $u(x)=0,x\in R/\mathsf{\Omega },\mathsf{\Omega }=[a,b]$, it follows from [12] that the fractional Laplacian operator can be expressed as

$$\begin{array}{cc}\hfill {(-\Delta )}^{\alpha /2}u(x)& =C_{1,\alpha }\frac{d}{dx}{\mathcal{J}}^{\alpha }(x),\hfill \end{array}$$

(3)

where

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em} {\mathcal{J}}^{\alpha }(x)& ={\int }_{\mathsf{\Omega }}{|x-y|}^{1-\alpha }{u}^{\prime }(y)dy,0<\alpha <2,\alpha \ne 1,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & ={\int }_{\mathsf{\Omega }}ln|x-y|u^{\prime }(y)dy,\alpha =1.\hfill \end{array}$$

(5)

In this paper, we only consider a numerical scheme for uniform dissection on interval $\mathsf{\Omega }=[-1,1]$. However, it is easy to obtain the numerical scheme for nonuniform dissection on interval $\mathsf{\Omega }=[a,b]$ by a similar approach. For a positive integer N, we set $a=x_0<x_1<x_2<\cdots <x_N=b$, $h_i=x_i-x_{i-1},i=1,2,\cdots ,N,I_j=(x_{j-1},x_j),j=1,2,\cdots ,N$. Define the linear interpolation function of $u(x),x\in [x_{k-1},x_k]$ as ${\pi }_{1,k}u(x)$, i.e.,

$$\begin{array}{c}\hfill {\pi }_{1,k}u(x)=\frac{x_k-x}{x_k-x_{k-1}}{u}_{k-1}+\frac{x-x_{k-1}}{x_k-x_{k-1}}{u}_k,{({\pi }_{1,k}u(x))}^{\prime }={\delta }_x{u}_{k-\frac{1}{2}}=\frac{u_k-u_{k-1}}{x_k-x_{k-1}}.\end{array}$$

(6)

It follows from the central difference scheme that the fractional Laplacian operator (3) can be expressed as the following form

$$\begin{array}{cc}\hfill {(-\Delta )}_h^{\alpha /2}{u}_i& =C_{1,\alpha }\frac{{\mathcal{J}}^{\alpha }(x_{i+1})-{\mathcal{J}}^{\alpha }(x_{i-1})}{2h}+C_{1,\alpha }\frac{{({\mathcal{J}}^{\alpha })}^{‴}(\xi )}{3}{h}^2.\hfill \end{array}$$

(7)

Now, we consider a numerical scheme for the weak singular integral (4). Let $x=x_n$, $0<\alpha <2,\alpha \ne 1$. Then, the integral operator ${\mathcal{J}}^{\alpha }(x_n)$ can be expressed by

$$\begin{array}{cc}\hfill & {\mathcal{J}}^{\alpha }(x_n)={\int }_a^{x_n}{(x_n-y)}^{1-\alpha }{u}^{\prime }(y)dy+{\int }_{x_n}^b{(y-x_n)}^{1-\alpha }{u}^{\prime }(y)dy.\hfill \end{array}$$

(8)

We use ${\pi }_{1,k}u(x)$ to approximate $u(x)$ on every interval $[x_{k-1},x_k]$, and substituting (6) into (8) can yield

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_n)\approx {\mathcal{J}}_h^{\alpha }(x_n)=& \sum _{k=1}^n{\int }_{x_{k-1}}^{x_k}{(x_n-y)}^{1-\alpha }{({\pi }_{1,k}u(y))}^{\prime }dy+\sum _{k=n+1}^N{\int }_{x_{k-1}}^{x_k}{(y-x_n)}^{1-\alpha }{({\pi }_{1,k}u(y))}^{\prime }dy\hfill \\ \hfill =& \sum _{k=1}^n{\delta }_x{u}_{k-\frac{1}{2}}{\int }_{x_{k-1}}^{x_k}{(x_n-y)}^{1-\alpha }dy+\sum _{k=n+1}^N{\delta }_x{u}_{k-\frac{1}{2}}{\int }_{x_{k-1}}^{x_k}{(y-x_n)}^{1-\alpha }dy\hfill \\ \hfill =& \sum _{k=1}^{N-1}\frac{b_{n-k}^{2-\alpha }-b_{n-k-1}^{2-\alpha }}{h^{\alpha -1}}{u}_k,\hfill \end{array}$$

(9)

where

$$\begin{array}{c}\hfill {\displaystyle b_l^{2-\alpha }=\left\{\begin{array}{c}{\displaystyle \frac{{(l+1)}^{2-\alpha }-{(l)}^{2-\alpha }}{2-\alpha },l\ge 0,}\hfill \\ {\displaystyle \frac{{(-l)}^{2-\alpha }-{(-l-1)}^{2-\alpha }}{2-\alpha },l<0.}\hfill \end{array}\right.}\end{array}$$

When $\alpha =1$, the integral operator ${\mathcal{J}}^{\alpha }(x_n)$ can be expressed as

$$\begin{array}{cc}\hfill & {\mathcal{J}}^{\alpha }(x_n)={\int }_a^{x_n}ln(x_n-y)u^{\prime }(y)dy+{\int }_{x_n}^{b}ln(y-x_n)u^{\prime }(y)dy.\hfill \end{array}$$

(10)

Substituting (6) into (10) can yield

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_n)\approx {\mathcal{J}}_h^{\alpha }(x_n)=& \sum _{k=1}^n{\int }_{x_{k-1}}^{x_k}ln(x_n-y){({\pi }_{1,k}u(y))}^{\prime }dy+\sum _{k=n+1}^N{\int }_{x_{k-1}}^{x_k}ln(y-x_n){({\pi }_{1,k}u(y))}^{\prime }dy\hfill \\ \hfill =& \sum _{k=1}^n{\delta }_x{u}_{k-\frac{1}{2}}{\int }_{x_{k-1}}^{x_k}ln(x_n-y)dy+\sum _{k=n+1}^N{\delta }_x{u}_{k-\frac{1}{2}}{\int }_{x_{k-1}}^{x_k}ln(y-x_n)dy\hfill \\ \hfill =& \sum _{k=1}^{N-1}\frac{b_{n-k}-b_{n-k-1}}{h}{u}_k,\hfill \end{array}$$

(11)

where

$$\begin{array}{c}\hfill {\displaystyle b_l=\left\{\begin{array}{c}{\displaystyle (l+1)hln(l+1)h-lhlnlh-h,l\ge 1,}\hfill \\ {\displaystyle (l+1)hln(l+1)h-h,l=0,}\hfill \\ {\displaystyle (-lh)ln(-lh)-h,l=-1,}\hfill \\ {\displaystyle (-lh)ln(-lh)-(-l-1)hln(-l-1)h-h,l<-1.}\hfill \end{array}\right.}\end{array}$$

It follows from numerical schemes (7), (9), and (11) that the fractional Laplacian operator can be approximated by

$$\begin{array}{cc}{(-\Delta )}_h^{\alpha /2}u(x_i)\hfill & \approx C_{1,\alpha }\frac{{\mathcal{J}}_h^{\alpha }(x_{i+1})-{\mathcal{J}}_h^{\alpha }(x_{i-1})}{2h},\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =C_{1,\alpha }\sum _{k=1}^{N-1}\frac{b_{i-k+1}^{2-\alpha }-b_{i-k}^{2-\alpha }-b_{i-k-1}^{2-\alpha }+b_{i-k-2}^{2-\alpha }}{2h^{\alpha -2}}{u}_k,0<\alpha <2,\alpha \ne 1,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & =\frac{1}{\pi }\sum _{k=1}^{N-1}\frac{b_{i-k+1}-b_{i-k}-b_{i-k-1}+b_{i-k-2}}{2h^2}{u}_k,\alpha =1.\hfill \end{array}$$

(13)

The solution of a fractional diffusion equation is usually singular near the boundary. In order to resolve the singularity of the nonsmooth solution of the fractional diffusion equation, some numerical methods have been designed for the discrete fractional Laplacian operator based on nonuniform refined grids. However, little attention has been paid to the fractional interpolation function to deal with fractional problems. In this section, we use the fractional interpolation function for the discrete fractional Laplacian operator.

Lemma 1

([29]). Let $0<{\alpha }_1<{\alpha }_2<\cdots {\alpha }_n$. Then, we have ${(x-x_0)}^{{\alpha }_i},i=1,2,\cdots ,n$ is linearly independent.

Lemma 2

([29]). Given $n+1$ different interpolation points $x_0,x_1,\cdots ,x_n$ and $0<{\alpha }_1<{\alpha }_2<\cdots {\alpha }_n$. Let

$$\begin{array}{c}\hfill D_i(x)=\left|\begin{array}{cccccc}{(x-x_0)}^{{\alpha }_1}& {(x-x_0)}^{{\alpha }_2}& \cdots & {(x-x_0)}^{{\alpha }_i}& \cdots & {(x-x_0)}^{{\alpha }_n}\\ {(x_1-x_0)}^{{\alpha }_1}& {(x_1-x_0)}^{{\alpha }_2}& \cdots & {(x_1-x_0)}^{{\alpha }_i}& \cdots & {(x_1-x_0)}^{{\alpha }_n}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ {(x_{i-1}-x_0)}^{{\alpha }_1}& {(x_{i-1}-x_0)}^{{\alpha }_2}& \cdots & {(x_{i-1}-x_0)}^{{\alpha }_i}& \cdots & {(x_{i-1}-x_0)}^{{\alpha }_n}\\ {(x_{i+1}-x_0)}^{{\alpha }_1}& {(x_{i+1}-x_0)}^{{\alpha }_2}& \cdots & {(x_{i+1}-x_0)}^{{\alpha }_i}& \cdots & {(x_{i+1}-x_0)}^{{\alpha }_n}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ {(x_n-x_0)}^{{\alpha }_1}& {(x_n-x_0)}^{{\alpha }_2}& \cdots & {(x_n-x_0)}^{{\alpha }_i}& \cdots & {(x_n-x_0)}^{{\alpha }_n}\end{array}\right|,\end{array}$$

and

$$\begin{array}{c}\hfill D=\left|\begin{array}{cccc}{(x_1-x_0)}^{{\alpha }_1}& {(x_1-x_0)}^{{\alpha }_2}& \cdots & {(x_1-x_0)}^{{\alpha }_n}\\ {(x_2-x_0)}^{{\alpha }_1}& {(x_2-x_0)}^{{\alpha }_2}& \cdots & {(x_2-x_0)}^{{\alpha }_n}\\ ⋮& ⋮& \ddots & ⋮\\ {(x_n-x_0)}^{{\alpha }_1}& {(x_n-x_0)}^{{\alpha }_2}& \cdots & {(x_n-x_0)}^{{\alpha }_n}\end{array}\right|.\end{array}$$

Then, the fractional interpolation function $p_n(x)$ can be expressed as the following form:

$$\begin{array}{c}\hfill p_n(x)=\sum _{i=0}^n{l}_i(x_i)f(x_i),\end{array}$$

where the fractional interpolation basis function is expressed as

$$\begin{array}{c}\hfill {\displaystyle l_i(x)=\left\{\begin{array}{c}{\displaystyle {(-1)}^{i-1}\frac{D_i(x)}{D},i\ne 0,}\hfill \\ {\displaystyle 1-\sum _{i=1}^n{l}_i(x),i=0.}\hfill \end{array}\right.}\end{array}$$

Because the solution of a fractional diffusion equation is usually singular near the boundary, we use the fractional interpolation function $p_n(x)$ to approximate $u(x)$ on $x\in [x_0,x_1]\cup [x_{N-1},x_N]$ and use the classical interpolation function $I_m(x)$ to approximate $u(x)$ on every interval $x\in [x_{i-1},x_i],i=2,3,\cdots ,N-1$. Moreover, $I_m(x),p_n(x)$ can be represented by the following form:

$$\begin{array}{cc}\hfill I_m(x)& =\sum _{j=0}^m{\widehat{l}}_j(x)f(x_{ij}),x\in [x_{i-1},x_i],2\le i\le N-1,\hfill \\ \hfill p_n(x)& =\left\{\begin{array}{c}{\displaystyle \sum _{j=0}^n{l}_j(x)f(x_{1j}),x\in [x_0,x_1],}\hfill \\ {\displaystyle \sum _{j=0}^n{l}_j(x)f(x_{Nj}),x\in [x_{N-1},x_N],}\hfill \end{array}\right.\hfill \end{array}$$

where ${\widehat{l}}_j(x)$ is the classical interpolation basis function, and

$$\begin{array}{cc}\hfill & x_0=x_{10}<x_{11}<\cdots <x_{1n}=x_1,\hfill \\ \hfill & x_{i-1}=x_{i0}<x_{i1}<\cdots <x_{im}=x_i,2\le i\le N-1,\hfill \\ \hfill & x_{N-1}=x_{N0}<x_{N1}<\cdots <x_{Nn}=x_N.\hfill \end{array}$$

When $0<\alpha <2,\alpha \ne 1$, substituting the above interpolation function into the weak singular integral operator (8) can yield

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_n)\approx {\mathcal{J}}_h^{\alpha }(x_n)=& {\int }_{x_0}^{x_1}{(x_n-y)}^{1-\alpha }{(\sum _{j=0}^n{l}_j(x)u(x_{1j}))}^{\prime }dy+\sum _{k=2}^n{\int }_{x_{k-1}}^{x_k}{(x_n-y)}^{1-\alpha }{(\sum _{j=0}^m{\widehat{l}}_j(x)u(x_{kj}))}^{\prime }dy\hfill \\ \hfill & +\sum _{k=n+1}^{N-1}{\int }_{x_{k-1}}^{x_k}{(y-x_n)}^{1-\alpha }{(\sum _{j=0}^m{\widehat{l}}_j(x)u(x_{kj}))}^{\prime }dy+{\int }_{x_{N-1}}^{x_N}{(y-x_n)}^{1-\alpha }{(\sum _{j=0}^n{l}_j(x)u(x_{Nj}))}^{\prime }dy.\hfill \end{array}$$

When $\alpha =1$, the weak singular integral (10) can be approximated by

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_n)\approx {\mathcal{J}}_h^{\alpha }(x_n)=& {\int }_{x_0}^{x_1}ln(x_n-y){(\sum _{j=0}^n{l}_j(x)u(x_{1j}))}^{\prime }dy+\sum _{k=2}^n{\int }_{x_{k-1}}^{x_k}ln(x_n-y){(\sum _{j=0}^m{\widehat{l}}_j(x)u(x_{kj}))}^{\prime }dy\hfill \\ \hfill & +\sum _{k=n+1}^{N-1}{\int }_{x_{k-1}}^{x_k}ln(y-x_n){(\sum _{j=0}^m{\widehat{l}}_j(x)u(x_{kj}))}^{\prime }dy+{\int }_{x_{N-1}}^{x_N}ln(y-x_n){(\sum _{j=0}^n{l}_j(x)u(x_{Nj}))}^{\prime }dy.\hfill \end{array}$$

In this paper, we only consider the following fractional interpolation function and classical interpolation function to approach $u(x)$, i.e.,

$$\begin{array}{cc}\hfill {\pi }_{{\alpha }_1,1}u(x)=& \frac{{(x-x_0)}^{{\alpha }_1}}{h^{{\alpha }_1}}{u}_1+(1-\frac{{(x-x_0)}^{{\alpha }_1}}{h^{{\alpha }_1}})u_0,x\in [x_0,x_1],\hfill \end{array}$$

(14)

$${\pi }_{{\alpha }_1,N}u(x)=\frac{{(x_N-x)}^{{\alpha }_1}}{h^{{\alpha }_1}}{u}_{N-1}+(1-\frac{{(x_N-x)}^{{\alpha }_1}}{h^{{\alpha }_1}})u_N,x\in [x_{N-1},x_N],$$

(15)

$${\pi }_{2,k}u(x)=\frac{(x-x_k)(x-x_{k-1})}{(x_{k-2}-x_k)(x_{k-2}-x_{k-1})}{u}_{k-2}+\frac{(x-x_k)(x-x_{k-2})}{(x_{k-1}-x_k)(x_{k-1}-x_{k-2})}{u}_{k-1}$$

$$+\frac{(x-x_{k-1})(x-x_{k-2})}{(x_k-x_{k-1})(x_k-x_{k-2})}{u}_k,x\in [x_{k-1},x_k],2\le k\le N-1.$$

(16)

It is easy to obtain

$$\begin{array}{cc}\hfill {({\pi }_{{\alpha }_1,1}u(x))}^{\prime }& ={\alpha }_1\frac{{(x-x_0)}^{{\alpha }_1-1}}{h^{a_1-1}}{\delta }_x{u}_{N-\frac{1}{2}},x\in [x_0,x_1],\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {({\pi }_{{\alpha }_1,N}u(x))}^{\prime }& ={\alpha }_1\frac{{(x_N-x)}^{{\alpha }_1-1}}{h^{a_1-1}}{\delta }_x{u}_{N-\frac{1}{2}},x\in [x_{N-1},x_N],\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {({\pi }_{2,k}u(x))}^{\prime }& ={\delta }_x{u}_{j-\frac{1}{2}}+{\delta }_x^2{u}_{k-1}(x-x_{k-\frac{1}{2}}),x\in [x_{k-1},x_k],2\le k\le N-1,\hfill \end{array}$$

(19)

where ${\displaystyle {\delta }_x^2{u}_k=\frac{1}{x_k-x_{k-1}}({\delta }_x{u}_{k+\frac{1}{2}}-{\delta }_x{u}_{k-\frac{1}{2}})}$. It is easy to obtain the numerical scheme for other complicated interpolation functions by a similar approach.

Suppose $u(x)\in C^{{\alpha }_1}[x_0,x_1]\cup [x_{N-1},x_N]$, we use ${\pi }_{{\alpha }_1,1}u(x),{\pi }_{{\alpha }_1,N}u(x)$ to approximate $u(x)$ on the two small intervals $[x_0,x_1]\cup [x_{N-1},x_N]$ and ${\pi }_{2,k}u(x),2\le k\le N-1$ to approximate $u(x)$ on the interval $[x_{k-1},x_k]$. When $\alpha \ne 1$, substituting (14)–(16) into (8) can yield

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_n)\approx {\mathcal{J}}_h^{\alpha }(x_n)=& {\int }_{x_0}^{x_1}{(x_n-y)}^{1-\alpha }{({\pi }_{{\alpha }_1,1}u(y))}^{\prime }dy+\sum _{k=2}^n{\int }_{x_{k-1}}^{x_k}{(x_n-y)}^{1-\alpha }{({\pi }_{2,k}u(y))}^{\prime }dy\hfill \\ \hfill & +\sum _{k=n+1}^{N-1}{\int }_{x_{k-1}}^{x_k}{(y-x_n)}^{1-\alpha }{({\pi }_{2,k}u(y))}^{\prime }dy+{\int }_{x_{N-1}}^{x_N}{(y-x_n)}^{1-\alpha }{({\pi }_{{\alpha }_1,N}u(y))}^{\prime }dy\hfill \\ \hfill =& \frac{{\alpha }_1}{h^{a_1-1}}{\delta }_x{u}_{\frac{1}{2}}{\int }_{x_0}^{x_1}{(x_n-y)}^{1-\alpha }{(y-x_0)}^{{\alpha }_1-1}dy+\frac{{\alpha }_1}{h^{a_1-1}}{\delta }_x{u}_{N-\frac{1}{2}}{\int }_{x_{N-1}}^{x_N}{(y-x_n)}^{1-\alpha }{(y-x_N)}^{{\alpha }_1-1}dy\hfill \\ \hfill & +\sum _{k=2}^{N-1}{\delta }_x{u}_{k-\frac{1}{2}}{\int }_{x_{k-1}}^{x_k}{(x_n-y)}^{1-\alpha }dy+\sum _{k=n+1}^N{\delta }_x{u}_{k-\frac{1}{2}}{\int }_{x_{k-1}}^{x_k}{(y-x_n)}^{1-\alpha }dy\hfill \\ \hfill & +\sum _{k=2}^n{\delta }_x^2{u}_{k-1}{\int }_{x_{k-1}}^{x_k}{(x_n-y)}^{1-\alpha }(y-x_{k-\frac{1}{2}})dy+\sum _{k=n+1}^{N-1}{\delta }_x^2{u}_{k-1}{\int }_{x_{k-1}}^{x_k}{(y-x_n)}^{1-\alpha }(y-x_{k-\frac{1}{2}})dy\hfill \\ \hfill =& \sum _{k=1}^N{\widehat{b}}_{n-k}^{2-\alpha }\frac{u_k-u_{k-1}}{h^{\alpha -1}}+\sum _{k=1}^N{a}_{n-k}^{2-\alpha }\frac{u_k-2u_{k-1}+u_{k-2}}{h^{\alpha -1}}\hfill \\ \hfill =& \sum _{k=1}^{N-1}\frac{{\widehat{b}}_{n-k}^{2-\alpha }-{\widehat{b}}_{n-k-1}^{2-\alpha }}{h^{\alpha -1}}{u}_k+\sum _{k=1}^N\frac{a_{n-k}^{2-\alpha }-2a_{n-k-1}^{2-\alpha }-a_{n-k-2}^{2-\alpha }}{h^{\alpha -1}}{u}_k,\hfill \end{array}$$

(20)

where

$$\begin{array}{c}\hfill {\displaystyle {\widehat{b}}_{n-k}^{2-\alpha }=\left\{\begin{array}{c}{\displaystyle \frac{{\alpha }_1}{h^{a_1-1}}{\int }_{x_0}^{x_1}{(x_n-y)}^{1-\alpha }{(y-x_0)}^{{\alpha }_1-1}dy,k=1,}\hfill \\ {\displaystyle \frac{{\alpha }_1}{h^{a_1-1}}{\int }_{x_{N-1}}^{x_N}{(y-x_n)}^{1-\alpha }{(y-x_N)}^{{\alpha }_1-1}dy,k=N,}\hfill \\ {\displaystyle b_{n-k}^{2-\alpha },1<k<N,}\hfill \end{array}\right.}\end{array}$$

and

$$\begin{array}{c}\hfill {\displaystyle a_l^{2-\alpha }=\left\{\begin{array}{c}{\displaystyle \frac{l^{3-\alpha }-{(l+1)}^{3-\alpha }}{3-\alpha }-\frac{(l+\frac{1}{2})(l^{2-\alpha }-{(l+1)}^{2-\alpha })}{2-\alpha },l\ge 0,}\hfill \\ {\displaystyle \frac{{(-l)}^{3-\alpha }-{(-l-1)}^{3-\alpha }}{3-\alpha }-\frac{(-l-\frac{1}{2})({(-l)}^{2-\alpha }-{(-l-1)}^{2-\alpha })}{2-\alpha },l<0.}\hfill \end{array}\right.}\end{array}$$

When $\alpha =1$, weak singular integrals (10) can be approximated by

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_n)\approx {\mathcal{J}}_h^{\alpha }(x_n)=& {\int }_{x_0}^{x_1}ln(x_n-y){({\pi }_{{\alpha }_1,1}u(y))}^{\prime }dy+\sum _{k=2}^n{\int }_{x_{k-1}}^{x_k}ln(x_n-y){({\pi }_{2,k}u(y))}^{\prime }dy\hfill \\ \hfill & +\sum _{k=n+1}^{N-1}{\int }_{x_{k-1}}^{x_k}ln(y-x_n){({\pi }_{2,k}u(y))}^{\prime }dy+{\int }_{x_{N-1}}^{x_N}ln(y-x_n){({\pi }_{{\alpha }_1,N}u(y))}^{\prime }dy\hfill \\ \hfill =& \frac{{\alpha }_1}{h^{a_1-1}}{\delta }_x{u}_{\frac{1}{2}}{\int }_{x_0}^{x_1}ln(x_n-y){(y-x_0)}^{{\alpha }_1-1}dy+\frac{{\alpha }_1}{h^{a_1-1}}{\delta }_x{u}_{N-\frac{1}{2}}{\int }_{x_{N-1}}^{x_N}ln(y-x_n){(y-x_N)}^{{\alpha }_1-1}dy\hfill \\ \hfill & +\sum _{k=2}^{N-1}{\delta }_x{u}_{k-\frac{1}{2}}{\int }_{x_{k-1}}^{x_k}ln(x_n-y)dy+\sum _{k=n+1}^N{\delta }_x{u}_{k-\frac{1}{2}}{\int }_{x_{k-1}}^{x_k}ln(y-x_n)dy\hfill \\ \hfill & +\sum _{k=2}^n{\delta }_x^2{u}_{k-1}{\int }_{x_{k-1}}^{x_k}ln(x_n-y)(y-x_{k-\frac{1}{2}})dy+\sum _{k=n+1}^{N-1}{\delta }_x^2{u}_{k-1}{\int }_{x_{k-1}}^{x_k}ln(y-x_n)(y-x_{k-\frac{1}{2}})dy\hfill \\ \hfill =& \sum _{k=1}^N{\widehat{b}}_{n-k}\frac{u_k-u_{k-1}}{h}+\sum _{k=1}^N{a}_{n-k}\frac{u_k-2u_{k-1}+u_{k-2}}{h^2}\hfill \\ \hfill =& \sum _{k=1}^{N-1}\frac{{\widehat{b}}_{n-k}-{\widehat{b}}_{n-k-1}}{h}{u}_k+\sum _{k=1}^N\frac{a_{n-k}-2a_{n-k-1}-a_{n-k-2}}{h^2}{u}_k,\hfill \end{array}$$

(21)

where

$$\begin{array}{c}\hfill {\displaystyle {\widehat{b}}_{n-k}=\left\{\begin{array}{c}{\displaystyle \frac{{\alpha }_1}{h^{a_1-1}}{\int }_{x_0}^{x_1}ln(x_n-y){(y-x_0)}^{{\alpha }_1-1}dy,k=1,}\hfill \\ {\displaystyle \frac{{\alpha }_1}{h^{a_1-1}}{\int }_{x_{N-1}}^{x_N}ln(y-x_n){(y-x_N)}^{{\alpha }_1-1}dy,k=N,}\hfill \\ {\displaystyle b_{n-k},1<k<N,}\hfill \end{array}\right.}\end{array}$$

and

$$\begin{array}{c}\hfill {\displaystyle a_l=\left\{\begin{array}{c}{\displaystyle (l+\frac{1}{2})[(l+1)hln(l+1)h-lhlnlh-h]+\frac{1}{2}lnlh{(lh)}^2-\frac{1}{2}ln(l+1)h{((l+1)h)}^2+\frac{1}{4}({((l+1)h)}^2-{(lh)}^2),l\ge 1,}\hfill \\ {\displaystyle (l+\frac{1}{2})[(l+1)hln(l+1)h-h]-\frac{1}{2}ln(l+1)h{((l+1)h)}^2+\frac{1}{4}{((l+1)h)}^2,l=0,}\hfill \\ {\displaystyle (l+\frac{1}{2})[(-lh)ln(-lh)-h]+\frac{1}{2}ln(-lh){(-lh)}^2-\frac{1}{4}{(-lh)}^2,l=-1,}\hfill \\ {\displaystyle (l+\frac{1}{2})[(-lh)ln(-lh)-(-l-1)hln(-l-1)h-h]}\hfill \\ {\displaystyle +\frac{1}{2}ln(-lh){(-lh)}^2-\frac{1}{2}ln(-l-1)h{((-l-1)h)}^2+\frac{1}{4}({((-l-1)h)}^2-{(-lh)}^2),l<-1.}\hfill \end{array}\right.}\end{array}$$

It follows from schemes (7), (20), and (21) that the fractional Laplacian operator can be approximated by

$$\begin{array}{cc}\hfill {(-\Delta )}_h^{\alpha /2}{u}_i& =C_{1,\alpha }\frac{{\mathcal{J}}_h^{\alpha }(x_{i+1})-{\mathcal{J}}_h^{\alpha }(x_{i-1})}{2h}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =C_{1,\alpha }\sum _{k=1}^{N-1}\frac{{\widehat{b}}_{i-k+1}^{2-\alpha }-{\widehat{b}}_{i-k}^{2-\alpha }-{\widehat{b}}_{i-k-1}^{2-\alpha }+{\widehat{b}}_{i-k-2}^{2-\alpha }}{2h^{\alpha -2}}{u}_k+C_{1,\alpha }\sum _{k=1}^{N-1}\frac{a_{i-k+1}^{2-\alpha }-2a_{i-k}^{2-\alpha }+2a_{i-k-2}^{2-\alpha }-a_{i-k-3}^{2-\alpha }}{2h^{\alpha -2}}{u}_k,0<\alpha <2,\alpha \ne 1,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & =\frac{1}{\pi }\sum _{k=1}^{N-1}\frac{{\widehat{b}}_{i-k+1}-{\widehat{b}}_{i-k}-{\widehat{b}}_{i-k-1}+{\widehat{b}}_{i-k-2}}{2h^2}{u}_k+\frac{1}{\pi }\sum _{k=1}^{N-1}\frac{a_{i-k+1}-2a_{i-k}+2a_{i-k-2}-a_{i-k-3}}{2h^3}{u}_k,\alpha =1.\hfill \end{array}$$

(23)

2.2. Finite Difference Scheme for Fractional Diffusion Equation

In the last subsection, we showed two numerical schemes of the fractional Laplacian operator based on interpolation functions (6) and (14)–(16). In this subsection, we apply the numerical schemes to solve the following fractional diffusion equation:

$$\begin{array}{cc}& \mu u(x)+{(-\Delta )}^{\frac{\alpha }{2}}u(x)=f(x),x\in \mathsf{\Omega },0<\alpha <2,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & u(x)=0,x\in {\mathsf{\Omega }}^c.\hfill \end{array}$$

(25)

First, applying numerical scheme (12)–(13) of the fractional Laplacian operator to fractional diffusion Equation (24), we can obtain the following discrete numerical schemes:

$$\begin{array}{cc}\hfill & \mu IU+\frac{C_{1,\alpha }}{2h^{\alpha -2}}{\tilde{A}}^{\alpha }U=F,0<\alpha <2,\alpha \ne 1,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & \mu IU+\frac{1}{2\pi h^2}{\tilde{A}}^{\alpha }U=F,\alpha =1,\hfill \end{array}$$

(27)

where $U=[u_1,u_2,\cdots ,u_{N-1}],F=[f(x_1),f(x_2),\cdots ,f(x_{N-1})]$, and I is the unit matrix. When $0<\alpha <2,\alpha \ne 1$, then

$$\begin{array}{c}\hfill {\displaystyle {\tilde{A}}_{ij}^{\alpha }=\left\{\begin{array}{c}{\displaystyle 2b_1^{2-\alpha }-2b_0^{2-\alpha },i=j,}\hfill \\ {\displaystyle b_2^{2-\alpha }-b_1^{2-\alpha },i-j=1,}\hfill \\ {\displaystyle b_{-3}^{2-\alpha }-b_{-2}^{2-\alpha },i-j=-1,}\hfill \\ {\displaystyle b_{k+1}^{2-\alpha }-b_k^{2-\alpha }-b_{k-1}^{2-\alpha }+b_{k-2}^{2-\alpha },i-j=k>1,}\hfill \\ {\displaystyle b_{-k+1}^{2-\alpha }-b_{-k}^{2-\alpha }-b_{-k-1}^{2-\alpha }+b_{-k-2}^{2-\alpha },i-j=-k<-1,}\hfill \end{array}\right.}\end{array}$$

when $\alpha =1$, then

$$\begin{array}{c}\hfill {\displaystyle {\tilde{A}}_{ij}^{\alpha }=\left\{\begin{array}{c}{\displaystyle 2b_1-2b_0,i=j,}\hfill \\ {\displaystyle b_2-b_1,i-j=1,}\hfill \\ {\displaystyle b_{-3}-b_{-2},i-j=-1,}\hfill \\ {\displaystyle b_{k+1}-b_k-b_{k-1}+b_{k-2},i-j=k>1,}\hfill \\ {\displaystyle b_{-k+1}-b_{-k}-b_{-k-1}+b_{-k-2},i-j=-k<-1.}\hfill \end{array}\right.}\end{array}$$

Second, applying numerical scheme (22)–(23) of the fractional Laplacian operator to fractional diffusion Equation (24), we can obtain the following discrete numerical schemes:

$$\begin{array}{cc}\hfill & \mu IU+\frac{C_{1,\alpha }}{2h^{2-\alpha }}{A}^{\alpha }U=F,0<\alpha <2,\alpha \ne 1,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & \mu IU+\frac{1}{\pi }{A}^{\alpha }U=F,\alpha =1,\hfill \end{array}$$

(29)

when $0<\alpha <2,\alpha \ne 1$, then

$$\begin{array}{c}\hfill {\displaystyle A_{ij}^{\alpha }=\left\{\begin{array}{c}{\displaystyle 2{\widehat{b}}_1^{2-\alpha }-2{\widehat{b}}_0^{2-\alpha }+2a_1^{2-\alpha }-4a_0^{2-\alpha },i=j,}\hfill \\ {\displaystyle {\widehat{b}}_2^{2-\alpha }-{\widehat{b}}_1^{2-\alpha }+a_2^{2-\alpha }-2a_1^{2-\alpha }+3a_0^{2-\alpha },i-j=1,}\hfill \\ {\displaystyle {\widehat{b}}_{-3}^{2-\alpha }-{\widehat{b}}_{-2}^{2-\alpha }-3a_{-1}^{2-\alpha }+2a_{-2}^{2-\alpha }-a_{-3}^{2-\alpha },i-j=-1,}\hfill \\ {\displaystyle {\widehat{b}}_{k+1}^{2-\alpha }-{\widehat{b}}_k^{2-\alpha }-{\widehat{b}}_{k-1}^{2-\alpha }+{\widehat{b}}_{k-2}^{2-\alpha }+a_{k+1}^{2-\alpha }-2a_k^{2-\alpha }+2a_{k-1}^{2-\alpha }-a_{k-2}^{2-\alpha },i-j=k>1,}\hfill \\ {\displaystyle {\widehat{b}}_{-k+1}^{2-\alpha }-{\widehat{b}}_{-k}^{2-\alpha }-{\widehat{b}}_{-k-1}^{2-\alpha }+{\widehat{b}}_{-k-2}^{2-\alpha }+a_{-k+1}^{2-\alpha }-2a_{-k}^{2-\alpha }+2a_{-k-1}^{2-\alpha }-a_{-k-2}^{2-\alpha },i-j=-k<-1,}\hfill \end{array}\right.}\end{array}$$

when $\alpha =1$, then

$$\begin{array}{c}\hfill {\displaystyle A_{ij}^{\alpha }=\left\{\begin{array}{c}{\displaystyle \frac{1}{2h^2}(2{\widehat{b}}_1-2{\widehat{b}}_0)+\frac{1}{2h^3}(2a_1-4a_0),i=j,}\hfill \\ {\displaystyle \frac{1}{2h^2}({\widehat{b}}_2-{\widehat{b}}_1)+\frac{1}{2h^3}(a_2-2a_1+3a_0),i-j=1,}\hfill \\ {\displaystyle \frac{1}{2h^2}({\widehat{b}}_{-3}-{\widehat{b}}_{-2})+\frac{1}{2h^3}(-3a_{-1}+2a_{-2}-a_{-3}),i-j=-1,}\hfill \\ {\displaystyle \frac{1}{2h^2}({\widehat{b}}_{k+1}-{\widehat{b}}_k-{\widehat{b}}_{k-1}+{\widehat{b}}_{k-2})+\frac{1}{2h^3}(a_{k+1}-2a_k+2a_{k-1}-a_{k-2}),i-j=k>1,}\hfill \\ {\displaystyle \frac{1}{2h^2}({\widehat{b}}_{-k+1}-{\widehat{b}}_{-k}-{\widehat{b}}_{-k-1}+{\widehat{b}}_{-k-2})+\frac{1}{2h^3}(a_{-k+1}-2a_{-k}+2a_{-k-1}-a_{-k-2}),i-j=-k<-1.}\hfill \end{array}\right.}\end{array}$$

Theorem 1.

When ${\alpha }_1=1$,$0<\alpha <2,\alpha \ne 1$, the matrix $A^{\alpha }$ is a symmetric matrix and strictly row-wise diagonally dominant.

Proof. 

When $l>0$, $a_l^{2-\alpha }$ satisfy $b_l^{2-\alpha }=b_{-l-1}^{2-\alpha },a_l^{2-\alpha }=-a_{-l-1}^{2-\alpha }$. Then, we have

$$\begin{array}{cc}\hfill & b_2^{\alpha }-b_1^{2-\alpha }=b_{-3}^{\alpha }-b_{-2}^{2-\alpha },a_2^{2-\alpha }-2a_1^{2-\alpha }+3a_0^{2-\alpha }=-3a_{-1}^{2-\alpha }+2a_{-2}^{2-\alpha }-a_{-3}^{2-\alpha },\hfill \\ \hfill & b_{k+1}^{\alpha }-b_k^{2-\alpha }-b_{k-1}^{2-\alpha }+b_{k-2}^{2-\alpha }=b_{-k+1}^{\alpha }-b_{-k}^{2-\alpha }-b_{-k-1}^{2-\alpha }+b_{-k-2}^{2-\alpha },\hfill \\ \hfill & a_{k+1}^{2-\alpha }-2a_k^{2-\alpha }+2a_{k-1}^{2-\alpha }-a_{k-2}^{2-\alpha }=a_{-k+1}^{2-\alpha }-2a_{-k}^{2-\alpha }+2a_{-k-1}^{2-\alpha }-a_{-k-2}^{2-\alpha }.\hfill \end{array}$$

Thus, $A^{\alpha }$ is a symmetric matrix.

Now, we prove the matrix $A^{\alpha }$ is strictly row-wise diagonally dominant. Let

$$\begin{array}{cc}\hfill {\tilde{c}}_k& =a_{k+1}^{2-\alpha }-2a_k^{2-\alpha }+2a_{k-1}^{2-\alpha }-a_{k-2}^{2-\alpha }={(k+2)}^{2-\alpha }-2{(k+1)}^{2-\alpha }+2{(k-1)}^{2-\alpha }-{(k-2)}^{2-\alpha },\hfill \\ \hfill {\widehat{c}}_k& =b_{k+1}^{2-\alpha }-b_k^{2-\alpha }-b_{k-1}^{2-\alpha }+b_{k-2}^{2-\alpha }={(k+2)}^{2-\alpha }-{(k+1)}^{2-\alpha }-{(k-1)}^{2-\alpha }+{(k-2)}^{2-\alpha }.\hfill \end{array}$$

Then, ${\tilde{c}}_k={\tilde{c}}_{-k},{\widehat{c}}_k={\widehat{c}}_{-k}$. Let

$$\begin{array}{cc}\hfill f_1(x)& ={(x+2)}^{2-\alpha }-2{(x+1)}^{2-\alpha }+2{(x-1)}^{2-\alpha }-{(x-2)}^{2-\alpha },\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill f_2(x)& ={(x+2)}^{2-\alpha }-{(x+1)}^{2-\alpha }-{(x-1)}^{2-\alpha }+{(x-2)}^{2-\alpha }.\hfill \end{array}$$

(31)

Then,

$$\begin{array}{cc}\hfill f_1^{\prime }(x)& =(2-\alpha )[{(x+2)}^{1-\alpha }-2{(x+1)}^{1-\alpha }+2{(x-1)}^{1-\alpha }-{(x-2)}^{1-\alpha }]\hfill \\ \hfill & =(2-\alpha )[({(x+2)}^{1-\alpha }-2{(x+1)}^{1-\alpha }+x^{1-\alpha })-(x^{1-\alpha }-2{(x-1)}^{1-\alpha }+{(x-2)}^{1-\alpha })],\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill f_2^{\prime }(x)& =(2-\alpha )[{(x+2)}^{1-\alpha }-{(x+1)}^{1-\alpha }-{(x-1)}^{1-\alpha }+{(x-2)}^{1-\alpha }]\hfill \\ \hfill & =(2-\alpha )[({(x+2)}^{1-\alpha }-{(x+1)}^{1-\alpha })-({(x-1)}^{1-\alpha }-{(x-2)}^{1-\alpha })].\hfill \end{array}$$

(33)

Let $g_1(x)=x^{1-\alpha }-2{(x-1)}^{1-\alpha }+{(x-2)}^{1-\alpha },g_2(x)={(x-1)}^{1-\alpha }+{(x-2)}^{1-\alpha }$. Then,

$$f_1^{\prime }(x)=(2-\alpha )[g_1(x+2)-g_1(x)],f_2^{\prime }(x)=(2-\alpha )[g_2(x+3)-g_2(x)].$$

It follows from [5] that $g_1(x+1)>g_1(x)$. Thus, $g_1(x+2)>g_1(x)$. It follows from (32) that

$$\begin{array}{c}\hfill f_1^{\prime }(x)>0.\end{array}$$

(34)

With the same method, we can obtain $f_2^{\prime }(x)>0$.

It follows from (30)–(31) that ${\tilde{c}}_k=f_1(k),{\widehat{c}}_k=f_2(k)$. According to (30)–(31) and (34), we obtain ${\tilde{c}}_k>0,{\tilde{c}}_k<{\tilde{c}}_{k+1}$ and ${\widehat{c}}_k>0,{\widehat{c}}_k<{\widehat{c}}_{k+1}$. It follows from Taylor’s formula that

$$\begin{array}{cc}\hfill & \underset{x\to \infty }{lim}(x^{2-\alpha }-2{(x+1)}^{2-\alpha }+2{(x+3)}^{2-\alpha }-{(x+4)}^{2-\alpha })\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{2-\alpha }(1-2{(1+\frac{1}{x})}^{2-\alpha }+2{(1+\frac{3}{x})}^{2-\alpha }-{(1+\frac{4}{x})}^{2-\alpha })\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{2-\alpha }(1-2(1+\frac{2-\alpha }{x}+O(\frac{1}{x^2}))+2(1+\frac{3(2-\alpha )}{x}+O(\frac{1}{x^2}))-(1+\frac{4(2-\alpha )}{x}+O(\frac{1}{x^2})))\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{2-\alpha }O(\frac{1}{x^2})=0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \underset{x\to \infty }{lim}(x^{2-\alpha }-{(x+1)}^{2-\alpha }-{(x+3)}^{2-\alpha }+{(x+4)}^{2-\alpha })\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{2-\alpha }(1-{(1+\frac{1}{x})}^{2-\alpha }-{(1+\frac{3}{x})}^{2-\alpha }+{(1+\frac{4}{x})}^{2-\alpha })\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{2-\alpha }(1-(1+\frac{2-\alpha }{x}+O(\frac{1}{x^2}))-(1+\frac{3(2-\alpha )}{x}+O(\frac{1}{x^2}))+(1+\frac{4(2-\alpha )}{x}+O(\frac{1}{x^2})))\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{2-\alpha }O(\frac{1}{x^2})=0.\hfill \end{array}$$

According to (34), we obtain ${\displaystyle \underset{k\to \infty }{lim}{\tilde{c}}_k=0,\underset{k\to \infty }{lim}{\widehat{c}}_k=0}$.

Let $A_{ii}=2b_1-2b_0+2a_1-4a_0$. Then,

$$\begin{array}{cc}\hfill \sum _{k=1,k\ne i}^{N-1}{A}_{ij}=& \sum _{k=-1}^{-N+2}{b}_{-k+1}-b_{-k}-b_{-k-1}+b_{-k-2}+a_{-k+1}-2a_{-k}+2a_{-k-1}-a_{-k-2}\hfill \\ \hfill & +\sum _{k=1}^{N-2}{b}_{k+1}-b_k-b_{k-1}+b_{k-2}+a_{k+1}-2a_k+2a_{k-1}-a_{k-2}\hfill \\ \hfill \le & \sum _{k=-1}^{-\infty }{b}_{-k+1}-b_{-k}-b_{-k-1}+b_{-k-2}+a_{-k+1}-2a_{-k}+2a_{-k-1}-a_{-k-2}\hfill \\ \hfill & +\sum _{k=1}^{+\infty }{b}_{k+1}-b_k-b_{k-1}+b_{k-2}+a_{k+1}-2a_k+2a_{k-1}-a_{k-2}\hfill \\ \hfill \le & 2b_1-2b_0+2a_1-4a_0=A_{ii}.\hfill \end{array}$$

□

In a similar method, the matrix ${\tilde{A}}^{\alpha }$ is also a symmetric matrix and strictly row-wise diagonally dominant.

3. Finite Volume Method for Fractional Diffusion Equation

In this section, we show the finite volume method for the fractional diffusion equation with zero boundary conditions. Here, one key idea is to deal with the hypersingular integral representation of the fractional Laplacian operator as a weak singular integral.

3.1. Finite Volume Method Based on a Linear Interpolation Function

We take the integration of fractional diffusion Equation (24) over a control volume $[x_{i-1/2},x_{i+1/2}]$, which leads to

$$\begin{array}{cc}\hfill & \mu {\int }_{x_{i-1/2}}^{x_{i+1/2}}u(x)dx+C_{1,\alpha }({\mathcal{J}}^{\alpha }(x_{i+1/2})-{\mathcal{J}}^{\alpha }(x_{i-1/2}))={\int }_{x_{i-1/2}}^{x_{i+1/2}}f(x)dx,0<\alpha <2,\alpha \ne 1,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & \mu {\int }_{x_{i-1/2}}^{x_{i+1/2}}u(x)dx+\frac{1}{\pi }({\mathcal{J}}^{\alpha }(x_{i+1/2})-{\mathcal{J}}^{\alpha }(x_{i-1/2}))={\int }_{x_{i-1/2}}^{x_{i+1/2}}f(x)dx,\alpha =1.\hfill \end{array}$$

(36)

We use ${\pi }_{1,k}u(x)$ to approximate $u(x)$ on the interval $[x_{k-1},x_k]$. When $0<\alpha <2,\alpha \ne 1$, the integral operator ${\mathcal{J}}^{\alpha }(x_{n+1/2})$ can be expressed by

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_{n+1/2})\approx {\mathcal{J}}_h^{\alpha }(x_{n+1/2})=& \sum _{k=1}^n{\int }_{x_{k-1}}^{x_k}{(x_{n+1/2}-y)}^{1-\alpha }{({\pi }_{1,k}u(y))}^{\prime }dy+\sum _{k=n+2}^N{\int }_{x_{k-1}}^{x_k}{(y-x_{n+1/2})}^{1-\alpha }{({\pi }_{1,k}u(y))}^{\prime }dy\hfill \\ \hfill & +{\int }_{x_n}^{x_{n+1/2}}{(y-x_{n+1/2})}^{1-\alpha }{({\pi }_{1,k}u(y))}^{\prime }dy+{\int }_{x_{n+1/2}}^{x_{n+1}}{(y-x_{n+1/2})}^{1-\alpha }{({\pi }_{1,k}u(y))}^{\prime }dy\hfill \\ \hfill =& \sum _{k=1}^N{b}_{n-k}^{2-\alpha }\frac{u_k-u_{k-1}}{h^{\alpha -1}}\hfill \\ \hfill =& \sum _{k=1}^{N-1}\frac{b_{n-k}^{2-\alpha }-b_{n-k-1}^{2-\alpha }}{h^{\alpha -1}}{u}_k,\hfill \end{array}$$

(37)

where

$$\begin{array}{c}\hfill {\displaystyle b_l^{2-\alpha }=\left\{\begin{array}{c}{\displaystyle \frac{{(l+1+\frac{1}{2})}^{2-\alpha }-{(l+\frac{1}{2})}^{2-\alpha }}{2-\alpha },l\ge 0,}\hfill \\ {\displaystyle \frac{2}{2^{2-\alpha }(2-\alpha )},l=-1,}\hfill \\ {\displaystyle \frac{{(-l-\frac{1}{2})}^{2-\alpha }-{(-l-1-\frac{1}{2})}^{2-\alpha }}{2-\alpha },l\le -2.}\hfill \end{array}\right.}\end{array}$$

When $\alpha =1$, the integral operator ${\mathcal{J}}^{\alpha }(x_{n+1/2})$ can be expressed by

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_{n+1/2})\approx {\mathcal{J}}_h^{\alpha }(x_{n+1/2})=& \sum _{k=1}^n{\int }_{x_{k-1}}^{x_k}ln(x_{n+1/2}-y){({\pi }_{1,k}u(y))}^{\prime }dy++\sum _{k=n+2}^N{\int }_{x_{k-1}}^{x_k}ln(y-x_{n+1/2}){({\pi }_{1,k}u(y))}^{\prime }dy\hfill \\ \hfill & +{\int }_{x_n}^{x_{n+1/2}}ln(y-x_{n+1/2}){({\pi }_{1,k}u(y))}^{\prime }dy+{\int }_{x_{n+1/2}}^{x_{n+1}}ln(y-x_{n+1/2}){({\pi }_{1,k}u(y))}^{\prime }dy\hfill \\ \hfill =& \sum _{k=1}^N{b}_{n-k}\frac{u_k-u_{k-1}}{h}\hfill \\ \hfill =& \sum _{k=1}^{N-1}\frac{b_{n-k}-b_{n-k-1}}{h}{u}_k,\hfill \end{array}$$

(38)

where

$$\begin{array}{c}\hfill {\displaystyle b_l=\left\{\begin{array}{c}{\displaystyle (l+1+\frac{1}{2})hln(l+1+\frac{1}{2})h-(l+\frac{1}{2})hln(l+\frac{1}{2})h-h,l\ge 1,}\hfill \\ {\displaystyle (l+1+\frac{1}{2})hln(l+1+\frac{1}{2})h-h,l=0,}\hfill \\ {\displaystyle ((-l-\frac{1}{2})h)ln((-l-\frac{1}{2})h)-h,l=-1,}\hfill \\ {\displaystyle ((-l-\frac{1}{2})h)ln(-lh)-(-l-1)hln(-l-1-\frac{1}{2})h-h,l<-1.}\hfill \end{array}\right.}\end{array}$$

Then, applying numerical schemes (37)–(38) of the integral operator ${\mathcal{J}}^{\alpha }(x_{n+1/2})$ to fractional diffusion Equation (24), we can obtain the following discrete numerical schemes:

$$\begin{array}{cc}\hfill & \mu \tilde{B}U+\frac{C_{1,\alpha }}{h^{\alpha -1}}{\tilde{A}}^{\alpha }U=F,0<\alpha <2,\alpha \ne 1,\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & \mu \tilde{B}U+\frac{1}{\pi h}{\tilde{A}}^{\alpha }U=F,\alpha =1,\hfill \end{array}$$

(40)

where $U=[u_1,u_2,\cdots ,u_{N-1}],F=[{\int }_{x_{1/2}}^{x_{1+1/2}}f(x)dx,{\int }_{x_{1+1/2}}^{x_{2+1/2}}f(x)dx,\cdots ,{\int }_{x_{N-3/2}}^{x_{N-1/2}}f(x)dx]$,

$$\begin{array}{c}\hfill \tilde{B}=\left[\begin{array}{ccccccc}6h/8& h/8& 0& \cdots & 0& 0& 0\\ h/8& 6h/8& h/8& \cdots & 0& 0& 0\\ 0& h/8& 6h/8& \cdots & 0& 0& 0\\ \cdots & \cdots & \cdots & \ddots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & 6h/8& h/8& 0\\ 0& 0& 0& \cdots & h/8& 6h/8& h/8\\ 0& 0& 0& \cdots & 0& 6h/8& h/8\end{array}\right].\end{array}$$

When $0<\alpha <2,\alpha \ne 1$, then

$$\begin{array}{c}\hfill {\displaystyle {\tilde{A}}_{ij}^{\alpha }=\left\{\begin{array}{c}{\displaystyle 2b_0^{2-\alpha }-2b_{-1}^{2-\alpha },i=j,}\hfill \\ {\displaystyle b_1^{2-\alpha }-2b_0^{2-\alpha }+b_{-1}^{2-\alpha },i-j=1,}\hfill \\ {\displaystyle b_{-1}^{2-\alpha }-2b_{-2}^{2-\alpha }+b_{-3}^{2-\alpha },i-j=-1,}\hfill \\ {\displaystyle b_k^{2-\alpha }-2b_{k-1}^{2-\alpha }+b_{k+1}^{2-\alpha },i-j=k>1,}\hfill \\ {\displaystyle b_{-k}^{2-\alpha }-2b_{-k-1}^{2-\alpha }+b_{-k-2}^{2-\alpha },i-j=-k<-1.}\hfill \end{array}\right.}\end{array}$$

(41)

When $\alpha =1$, then

$$\begin{array}{c}\hfill {\displaystyle {\tilde{A}}_{ij}=\left\{\begin{array}{c}{\displaystyle 2b_0-2b_{-1},i=j,}\hfill \\ {\displaystyle b_1-2b_0+b_{-1},i-j=1,}\hfill \\ {\displaystyle b_{-1}-2b_{-2}+b_{-3},i-j=-1,}\hfill \\ {\displaystyle b_k-2b_{k-1}+b_{k+1},i-j=k>1,}\hfill \\ {\displaystyle b_{-k}-2b_{-k-1}+b_{-k-2},i-j=-k<-1.}\hfill \end{array}\right.}\end{array}$$

(42)

Theorem 2.

For $0<\alpha <2,\alpha \ne 1$, the matrix ${\tilde{A}}^{\alpha }$ is strictly row-wise diagonally dominant.

Proof. 

When $l>0$, $b_l^{2-\alpha }$ satisfy $b_l^{2-\alpha }=b_{-l-2}^{2-\alpha }$. Then, we have

$$\begin{array}{cc}\hfill & b_1^{\alpha }-2b_0^{2-\alpha }+b_{-1}^{2-\alpha }=b_{-1}^{\alpha }-2b_{-2}^{2-\alpha }+b_{-3}^{2-\alpha },\hfill \\ \hfill & b_{k+3/2}^{\alpha }-b_{k+1/2}^{2-\alpha }-b_{k-1/2}^{2-\alpha }-b_{k-3/2}^{2-\alpha }=b_{-k+3/2}^{\alpha }-b_{-k+1/2}^{2-\alpha }-b_{-k-1/2}^{2-\alpha }-b_{-k-3/2}^{2-\alpha }.\hfill \end{array}$$

Thus, ${\tilde{A}}^{\alpha }$ is a symmetric matrix.

Now, we prove the matrix ${\tilde{A}}^{\alpha }$ is strictly row-wise diagonally dominant. Let

$$\begin{array}{c}\hfill c_k=b_{k+3/2}^{\alpha }-b_{k+1/2}^{2-\alpha }-b_{k-1/2}^{2-\alpha }-b_{k-3/2}^{2-\alpha }={(k+3/2)}^{2-\alpha }-3{(k+1/2)}^{2-\alpha }+3{(k-1/2)}^{2-\alpha }-{(k-3/2)}^{2-\alpha }.\end{array}$$

Then, $c_k=c_{-k}$. Let

$$\begin{array}{c}\hfill f(x)={(x+2)}^{2-\alpha }-3{(x+1)}^{2-\alpha }+3{(x)}^{2-\alpha }-{(x-1)}^{2-\alpha }.\end{array}$$

(43)

Then,

$$\begin{array}{cc}\hfill f^{\prime }(x)& =(2-\alpha )[{(x+2)}^{1-\alpha }-3{(x+1)}^{1-\alpha }+3x^{1-\alpha }-{(x-1)}^{1-\alpha }]\hfill \\ \hfill & =(2-\alpha )[({(x+2)}^{1-\alpha }-2{(x+1)}^{1-\alpha }+x^{1-\alpha })-({(x+1)}^{1-\alpha }-2x^{1-\alpha }+{(x-1)}^{1-\alpha })].\hfill \end{array}$$

(44)

Let $g(x)=x^{1-\alpha }-2{(x-1)}^{1-\alpha }+{(x-2)}^{1-\alpha }$. Then, $f^{\prime }(x)=(2-\alpha )[g(x+1)-g(x)].$ It follows from [5] that $g(x+1)>g(x)$. Thus, $g(x+2)>g(x)$. It follows from (44) that

$$\begin{array}{c}\hfill f^{\prime }(x)>0.\end{array}$$

(45)

It follows from (43) that $c_k=f(k)$. According to (43) and (45), we obtain $c_k<0,c_k<c_{k+1}$. It follows from Taylor’s formula that

$$\begin{array}{cc}\hfill & \underset{x\to \infty }{lim}(x^{\lambda }-3{(x-1)}^{\lambda }+3{(x-2)}^{\lambda }-{(x-3)}^{\lambda })\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{\lambda }(1-3{(1-\frac{1}{x})}^{\lambda }+3{(1-\frac{2}{x})}^{\lambda }-{(1-\frac{3}{x})}^{\lambda })\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{\lambda }(1-3(1+\frac{\lambda }{x}+O(\frac{1}{x^2}))+3(1+\frac{2\lambda }{x}+O(\frac{1}{x^2}))-(1+\frac{3\lambda }{x}+O(\frac{1}{x^2})))\hfill \\ \hfill =& \underset{x\to \infty }{lim}{x}^{\lambda }O(\frac{1}{x^2})=0.\hfill \end{array}$$

(46)

According to (46), we obtain ${\displaystyle \underset{k\to \infty }{lim}{c}_k=0}$.

When $l>0$, $c_l$ satisfies $c_l=c_{-l}$. Thus, ${\tilde{A}}^{\alpha }$ is a symmetric matrix. Let ${\tilde{A}}_{ii}=2{(3/2)}^{2-\alpha }-2{(1/2)}^{2-\alpha }$. Then,

$$\begin{array}{cc}\hfill \sum _{k=1,k\ne i}^{N-1}{\tilde{A}}_{ij}& =\sum _{j=-1}^{-N+2}{c}_k+\sum _{j=1}^{N-2}{c}_k\hfill \\ \hfill & \le \sum _{j=-1}^{-\infty }{c}_k+\sum _{j=1}^{+\infty }{c}_k\hfill \\ \hfill & \le 2{(3/2)}^{2-\alpha }-2{(1/2)}^{2-\alpha }={\tilde{A}}_{ii}.\hfill \end{array}$$

□

3.2. Finite Volume Method Based on Fractional Interpolation Function

In this subsection, in order to resolve the singularity of the nonsmooth solution of the fractional diffusion equation, we use the fractional interpolation function for the discrete fractional diffusion equation.

Suppose $u(x)\in C^{{\alpha }_1}[x_0,x_1]\cup [x_{N-1},x_N]$, we use ${\pi }_{{\alpha }_1,1}u(x),{\pi }_{{\alpha }_1,N}u(x)$ to approximate $u(x)$ on the two small intervals $[x_0,x_1]\cup [x_{N-1},x_N]$ and ${\pi }_{2,k}u(x),2\le k\le N-1$ to approximate $u(x)$ on the interval $[x_{k-1},x_k]$. Let $x=x_{n+1/2}$, $0<\alpha <2,\alpha \ne 1$, the integral operator ${\mathcal{J}}^{\alpha }(x_{n+1/2})$ can be expressed by

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_{n+1/2})\approx {\mathcal{J}}_h^{\alpha }(x_{n+1/2})=& {\int }_{x_0}^{x_1}{(x_{n+1/2}-y)}^{1-\alpha }{({\pi }_{{\alpha }_1,1}u(y))}^{\prime }dy+\sum _{k=2}^n{\int }_{x_{k-1}}^{x_k}{(x_{n+1/2}-y)}^{1-\alpha }{({\pi }_{2,k}u(y))}^{\prime }dy\hfill \\ \hfill & +{\int }_{x_n}^{x_{n+1/2}}{(y-x_{n+1/2})}^{1-\alpha }{({\pi }_{2,k}u(y))}^{\prime }dy+{\int }_{x_{n+1/2}}^{x_{n+1}}{(y-x_{n+1/2})}^{1-\alpha }{({\pi }_{2,k}u(y))}^{\prime }dy\hfill \\ \hfill & +\sum _{k=n+2}^{N-1}{\int }_{x_{k-1}}^{x_k}{(y-x_{n+1/2})}^{1-\alpha }{({\pi }_{2,k}u(y))}^{\prime }dy+{\int }_{x_{N-1}}^{x_N}{(y-x_{n+1/2})}^{1-\alpha }{({\pi }_{{\alpha }_1,N}u(y))}^{\prime }dy\hfill \\ \hfill =& \sum _{k=1}^N{\widehat{b}}_{n-k}^{2-\alpha }\frac{u_k-u_{k-1}}{h^{\alpha -1}}+\sum _{k=1}^N{a}_{n-k}^{2-\alpha }\frac{u_k-2u_{k-1}+u_{k-2}}{h^{\alpha -1}}\hfill \\ \hfill =& \sum _{k=1}^{N-1}\frac{{\widehat{b}}_{n-k}^{2-\alpha }-{\widehat{b}}_{n-k-1}^{2-\alpha }}{h^{\alpha -1}}{u}_k+\sum _{k=1}^N\frac{a_{n-k}^{2-\alpha }-2a_{n-k-1}^{2-\alpha }+a_{n-k-2}^{2-\alpha }}{h^{\alpha -1}}{u}_k,\hfill \end{array}$$

(47)

where

$$\begin{array}{c}\hfill {\displaystyle {\widehat{b}}_{n-k}^{2-\alpha }=\left\{\begin{array}{c}{\displaystyle \frac{{\alpha }_1}{h^{a_1-1}}{\int }_{x_0}^{x_1}{|x_{n+1/2}-y|}^{1-\alpha }{(y-x_0)}^{{\alpha }_1-1}dy,k=1,}\hfill \\ {\displaystyle \frac{{\alpha }_1}{h^{a_1-1}}{\int }_{x_{N-1}}^{x_N}{|y-x_{n+1/2}|}^{1-\alpha }{(y-x_N)}^{{\alpha }_1-1}dy,k=N,}\hfill \\ {\displaystyle b_{n-k}^{2-\alpha },1<k<N,}\hfill \end{array}\right.}\end{array}$$

and

$$\begin{array}{c}\hfill {\displaystyle a_l^{2-\alpha }=\left\{\begin{array}{c}{\displaystyle \frac{{(l+\frac{1}{2})}^{3-\alpha }-{(l+1+\frac{1}{2})}^{3-\alpha }}{3-\alpha }-\frac{(l+1)({(l+\frac{1}{2})}^{2-\alpha }-{(l+1+\frac{1}{2})}^{2-\alpha })}{2-\alpha },l\ge 0,}\hfill \\ {\displaystyle 0,l=-1,}\hfill \\ {\displaystyle \frac{{(-l-\frac{1}{2})}^{3-\alpha }-{(-l-1-\frac{1}{2})}^{3-\alpha }}{3-\alpha }-\frac{(-l-1)({(-l-\frac{1}{2})}^{2-\alpha }-{(-l-1-\frac{1}{2})}^{2-\alpha })}{2-\alpha },l\le -2.}\hfill \end{array}\right.}\end{array}$$

When $\alpha =1$, the integral operator ${\mathcal{J}}^{\alpha }(x_{n+1/2})$ can be expressed by

$$\begin{array}{cc}\hfill {\mathcal{J}}^{\alpha }(x_{n+1/2})\approx {\mathcal{J}}_h^{\alpha }(x_{n+1/2})=& {\int }_{x_0}^{x_1}ln(x_{n+1/2}-y){({\pi }_{1,1}u(y))}^{\prime }dy+\sum _{k=2}^n{\int }_{x_{k-1}}^{x_k}ln(x_{n+1/2}-y){({\pi }_{2,k}u(y))}^{\prime }dy\hfill \\ \hfill & +{\int }_{x_n}^{x_{n+1/2}}ln(y-x_{n+1/2}){({\pi }_{2,k}u(y))}^{\prime }dy+{\int }_{x_{n+1/2}}^{x_{n+1}}ln(y-x_{n+1/2}){({\pi }_{2,k}u(y))}^{\prime }dy\hfill \\ \hfill & +\sum _{k=n+2}^{N-1}{\int }_{x_{k-1}}^{x_k}ln(y-x_{n+1/2}){({\pi }_{2,k}u(y))}^{\prime }dy+{\int }_{x_{N-1}}^{x_N}ln(y-x_{n+1/2}){({\pi }_{1,N}u(y))}^{\prime }dy\hfill \\ \hfill =& \sum _{k=1}^N{b}_{n-k}\frac{u_k-u_{k-1}}{h}+\sum _{k=1}^N{a}_{n-k}^{2-\alpha }\frac{u_k-2u_{k-1}+u_{k-2}}{h^2}\hfill \\ \hfill =& \sum _{k=1}^{N-1}\frac{b_{n-k}-b_{n-k-1}}{h}{u}_k+\sum _{k=1}^N\frac{a_{n-k}^{2-\alpha }-2a_{n-k-1}^{2-\alpha }+a_{n-k-2}^{2-\alpha }}{h^2}{u}_k,\hfill \end{array}$$

(48)

where

$$\begin{array}{c}\hfill {\displaystyle {\widehat{b}}_{n-k}^{2-\alpha }=\left\{\begin{array}{c}{\displaystyle \frac{{\alpha }_1}{h^{a_1-1}}{\int }_{x_0}^{x_1}ln|x_{n+1/2}-y|{(y-x_0)}^{{\alpha }_1-1}dy,k=1,}\hfill \\ {\displaystyle \frac{{\alpha }_1}{h^{a_1-1}}{\int }_{x_{N-1}}^{x_N}ln|y-x_{n+1/2}|{(y-x_N)}^{{\alpha }_1-1}dy,k=N,}\hfill \\ {\displaystyle b_{n-k}^{2-\alpha },1<k<N,}\hfill \end{array}\right.}\end{array}$$

and

$$\begin{array}{c}\hfill {\displaystyle a_l=\left\{\begin{array}{c}{\displaystyle (l+1)[(l+1+\frac{1}{2})hln(l+1+\frac{1}{2})h-(l++\frac{1}{2})hln(l+\frac{1}{2})h-h]}\hfill \\ {\displaystyle +\frac{1}{2}ln(l+\frac{1}{2})h{((l+\frac{1}{2})h)}^2-\frac{1}{2}ln(l+1+\frac{1}{2})h{((l+1+\frac{1}{2})h)}^2+\frac{1}{4}({((l+1+\frac{1}{2})h)}^2-{((l+\frac{1}{2})h)}^2),l\ge 1,}\hfill \\ {\displaystyle (l+1)[(l+1+\frac{1}{2})hln(l+1+\frac{1}{2})h-h]-\frac{1}{2}ln(l+1+\frac{1}{2})h{((l+1+\frac{1}{2})h)}^2+\frac{1}{4}{((l+1+\frac{1}{2})h)}^2,l=0,}\hfill \\ {\displaystyle (l+1)[((-l-\frac{1}{2})h)ln((-l-\frac{1}{2})h)-h]+\frac{1}{2}ln(-lh){((-l-\frac{1}{2})h)}^2-\frac{1}{4}{((-l-\frac{1}{2})h)}^2,l=-1,}\hfill \\ {\displaystyle (l+1)[((-l-\frac{1}{2})h)ln((-l-\frac{1}{2})h)-(-l-1-\frac{1}{2})hln(-l-1-\frac{1}{2})h-h]}\hfill \\ {\displaystyle +\frac{1}{2}ln((-l-\frac{1}{2})h){((-l-\frac{1}{2})h)}^2-\frac{1}{2}ln(-l-1-\frac{1}{2})h{((-l-1-\frac{1}{2})h)}^2+\frac{1}{4}({((-l-1-\frac{1}{2})h)}^2-{((-l-\frac{1}{2})h)}^2),l<-1.}\hfill \end{array}\right.}\end{array}$$

It follows from (47)–(48) that

$$\begin{array}{cc}\hfill & {\mathcal{J}}_h^{\alpha }(x_{n+1/2})-{\mathcal{J}}_h^{\alpha }(x_{n-1/2})=\sum _{k=1}^{N-1}\frac{{\widehat{b}}_{n-k}^{2-\alpha }-2{\widehat{b}}_{n-k-1}^{2-\alpha }+{\widehat{b}}_{n-k-2}^{2-\alpha }}{h^{\alpha -1}}{u}_k+\sum _{k=1}^N\frac{a_{n-k}^{2-\alpha }-3a_{n-k-1}^{2-\alpha }+3a_{n-k-2}^{2-\alpha }-a_{n-k-3}^{2-\alpha }}{h^{\alpha -1}}{u}_k,0<\alpha <2,\alpha \ne 1,\hfill \\ \hfill & {\mathcal{J}}_h^{\alpha }(x_{n+1/2})-{\mathcal{J}}_h^{\alpha }(x_{n-1/2})=\sum _{k=1}^{N-1}\frac{{\widehat{b}}_{n-k}-2{\widehat{b}}_{n-k-1}+{\widehat{b}}_{n-k-2}}{h}{u}_k+\sum _{k=1}^N\frac{a_{n-k}-3a_{n-k-1}+3a_{n-k-2}-a_{n-k-3}}{h^2}{u}_k,\alpha =1.\hfill \end{array}$$

Now, we compute the integral ${\int }_{x_{i-1/2}}^{x_{i+1/2}}u(x)dx$. When $i=1$, the integral can be approximated by

$$\begin{array}{cc}\hfill {\int }_{x_{1/2}}^{x_{3/2}}u(x)dx=& {\int }_{x_{1/2}}^{x_1}{\pi }_{{\alpha }_1,1}u(x)dx+{\int }_{x_1}^{x_{3/2}}{\pi }_{2,2}u(x)dx\hfill \\ \hfill =& {\int }_{x_{1/2}}^{x_1}\frac{{(x-x_0)}^{{\alpha }_1}}{h^{{\alpha }_1}}{u}_1+(1-\frac{{(x-x_0)}^{{\alpha }_1}}{h^{{\alpha }_1}})u_{0}dx\hfill \\ \hfill & +{\int }_{x_1}^{x_{3/2}}\frac{(x-x_2)(x-x_1)}{2h^2}{u}_0+\frac{(x-x_2)(x-x_0)}{-h^2}{u}_1+\frac{(x-x_1)(x-x_0)}{2h^2}{u}_{2}dx\hfill \\ \hfill =& (\frac{h}{2}-\frac{1}{{\alpha }_1+1}+\frac{1}{({\alpha }_1+1)2^{{\alpha }_1+1}})u_0+(\frac{1}{{\alpha }_1+1}-\frac{1}{({\alpha }_1+1)2^{{\alpha }_1+1}})u_1-\frac{h}{24}{u}_0+\frac{11h}{24}{u}_1+\frac{h}{12}{u}_2\hfill \\ \hfill =& (\frac{h}{2}-\frac{1}{{\alpha }_1+1}+\frac{1}{({\alpha }_1+1)2^{{\alpha }_1+1}}-\frac{h}{24})u_0+(\frac{1}{{\alpha }_1+1}-\frac{1}{({\alpha }_1+1)2^{{\alpha }_1+1}}+\frac{11h}{24})u_1+\frac{h}{12}{u}_2.\hfill \end{array}$$

When $i=N-1$, the integral can be approximated by

$$\begin{array}{cc}\hfill {\int }_{x_{N-3/2}}^{x_{N-1/2}}u(x)dx=& {\int }_{x_{N-1}}^{x_{N-1/2}}{\pi }_{{\alpha }_1,N}u(x)dx+{\int }_{x_{N-3/2}}^{x_{N-1}}{\pi }_{2,N-1}u(x)dx\hfill \\ \hfill =& {\int }_{x_{N-1}}^{x_{N-1/2}}\frac{{(x-x_N)}^{{\alpha }_1}}{h^{{\alpha }_1}}{u}_{N-1}+(1-\frac{{(x-x_N)}^{{\alpha }_1}}{h^{{\alpha }_1}})u_{N}dx\hfill \\ \hfill & +{\int }_{x_{N-3/2}}^{x_{N-1}}\frac{(x-x_N)(x-x_{N-1})}{2h^2}{u}_{N-2}+\frac{(x-x_N)(x-x_{N-2})}{-h^2}{u}_{N-1}+\frac{(x-x_{N-1})(x-x_{N-2})}{2h^2}{u}_{N}dx\hfill \\ \hfill =& (\frac{h}{2}-\frac{1}{{\alpha }_1+1}+\frac{1}{({\alpha }_1+1)2^{{\alpha }_1+1}})u_N+(\frac{1}{{\alpha }_1+1}-\frac{1}{({\alpha }_1+1)2^{{\alpha }_1+1}})u_{N-1}+\frac{h}{12}{u}_{N-2}+\frac{11h}{24}{u}_{N-1}-\frac{h}{24}{u}_N\hfill \\ \hfill =& (\frac{h}{2}-\frac{1}{{\alpha }_1+1}+\frac{1}{({\alpha }_1+1)2^{{\alpha }_1+1}}-\frac{h}{24})u_N+(\frac{1}{{\alpha }_1+1}-\frac{1}{({\alpha }_1+1)2^{{\alpha }_1+1}}+\frac{11h}{24})u_{N-1}+\frac{h}{12}{u}_{N-2}.\hfill \end{array}$$

When $1<i<N-1$, the integral can be approximated by

$$\begin{array}{cc}\hfill {\int }_{x_{k-1/2}}^{x_{k+1/2}}u(x)dx=& {\int }_{x_{k-1/2}}^{x_{k+1/2}}{\pi }_{2,k}u(x)dx\hfill \\ \hfill =& {\int }_{x_{k-1/2}}^{x_{k+1/2}}\frac{(x-x_{k+1})(x-x_k)}{2h^2}{u}_{k-1}+\frac{(x-x_{k+1})(x-x_{k-1})}{-h^2}{u}_k+\frac{(x-x_k)(x-x_{k-1})}{2h^2}{u}_{k+1}dx\hfill \\ \hfill =& \frac{h}{24}{u}_{k-1}+\frac{11h}{12}{u}_k+\frac{h}{24}{u}_{k+1}.\hfill \end{array}$$

Applying numerical schemes (47)–(48) of the integral operator ${\mathcal{J}}^{\alpha }(x_{n+1/2})$ to fractional diffusion Equation (24), we can obtain the following discrete numerical schemes:

$$\begin{array}{cc}\hfill & \mu BU+\frac{C_{1,\alpha }}{h^{\alpha -1}}{A}^{\alpha }U=F,0<\alpha <2,\alpha \ne 1,\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill & \mu BU+\frac{1}{\pi }{A}^{\alpha }U=F,\alpha =1,\hfill \end{array}$$

(50)

where

$$\begin{array}{c}\hfill B=\left[\begin{array}{ccccccc}5h/4& h/12& 0& \cdots & 0& 0& 0\\ h/12& 11h/12& h/12& \cdots & 0& 0& 0\\ 0& h/12& 11h/12& \cdots & 0& 0& 0\\ \cdots & \cdots & \cdots & \ddots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & 11h/12& h/12& 0\\ 0& 0& 0& \cdots & h/12& 11h/12& h/12\\ 0& 0& 0& \cdots & 0& h/12& 5h/4\end{array}\right].\end{array}$$

When $0<\alpha <2,\alpha \ne 1$, then

$$\begin{array}{c}\hfill {\displaystyle A_{ij}^{\alpha }=\left\{\begin{array}{c}{\displaystyle 2{\widehat{b}}_0^{2-\alpha }-2{\widehat{b}}_{-1}^{2-\alpha }-2a_0^{2-\alpha }+a_1^{2-\alpha },i=j,}\hfill \\ {\displaystyle {\widehat{b}}_1^{2-\alpha }-2{\widehat{b}}_0^{2-\alpha }+{\widehat{b}}_{-1}^{2-\alpha }+a_1^{2-\alpha }-2a_0^{2-\alpha },i-j=1,}\hfill \\ {\displaystyle {\widehat{b}}_{-1}^{2-\alpha }-2{\widehat{b}}_{-2}^{2-\alpha }+{\widehat{b}}_{-3}^{2-\alpha }+3a_0^{2-\alpha }-3a_1^{2-\alpha }+a_2^{2-\alpha },i-j=-1,}\hfill \\ {\displaystyle {\widehat{b}}_k^{2-\alpha }-2{\widehat{b}}_{k-1}^{2-\alpha }+{\widehat{b}}_{k+1}^{2-\alpha }+a_k^{2-\alpha }-3a_{k-1}^{2-\alpha }+3a_{k-2}^{2-\alpha }-a_{k-3}^{2-\alpha },i-j=k>1,}\hfill \\ {\displaystyle {\widehat{b}}_{-k}^{2-\alpha }-2{\widehat{b}}_{-k-1}^{2-\alpha }+{\widehat{b}}_{-k-2}^{2-\alpha }+a_{-k}^{2-\alpha }-3a_{-k-1}^{2-\alpha }+3a_{-k-2}^{2-\alpha }-a_{-k-3}^{2-\alpha },i-j=-k<-1.}\hfill \end{array}\right.}\end{array}$$

(51)

when $\alpha =1$, then

$$\begin{array}{c}\hfill {\displaystyle A_{ij}=\left\{\begin{array}{c}{\displaystyle \frac{1}{h}(2{\widehat{b}}_0-2{\widehat{b}}_{-1})+\frac{1}{h^2}(-2a_0+a_1),i=j,}\hfill \\ {\displaystyle \frac{1}{h}({\widehat{b}}_1-2{\widehat{b}}_0+{\widehat{b}}_{-1})+\frac{1}{h^2}(a_1-2a_0),i-j=1,}\hfill \\ {\displaystyle \frac{1}{h}({\widehat{b}}_{-1}-2{\widehat{b}}_{-2}+{\widehat{b}}_{-3})+\frac{1}{h^2}(3a_0-3a_1+a_2),i-j=-1,}\hfill \\ {\displaystyle \frac{1}{h}({\widehat{b}}_k-2{\widehat{b}}_{k-1}+{\widehat{b}}_{k+1})+\frac{1}{h^2}(a_k-3a_{k-1}+3a_{k-2}-a_{k-3}),i-j=k>1,}\hfill \\ {\displaystyle \frac{1}{h}({\widehat{b}}_{-k}-2{\widehat{b}}_{-k-1}+{\widehat{b}}_{-k-2})+\frac{1}{h^2}(a_{-k}-3a_{-k-1}+3a_{-k-2}-a_{-k-3}),i-j=-k<-1.}\hfill \end{array}\right.}\end{array}$$

(52)

4. Numerical Example

In this section, we use the above finite difference scheme and finite volume scheme to solve some fractional diffuse equations with zero boundary conditions. The novelty of our method is that we deal with the hypersingular integral representation of the fractional Laplacian operator as a weak singular integral using an integral operator ${\mathcal{J}}^{\alpha }(x)$ so as to avoid directly discretizing the hypersingular integral. Moreover, it is easy to extend the numerical scheme for nonuniform dissection by a similar approach. First, we check the numerical errors of the finite difference scheme and finite volume scheme by fractional diffusion Equation (24) and compare the algorithms of this paper with those from the literature [11]. Second, we apply the resulting numerical scheme to solve other complex space fractional problems, such as the fractional Allen–Cahn system.

4.1. Example A

In this subsection, we apply our numerical schemes to solve the fractional diffuse Equation (24) with zero boundary conditions. We choose the function

$$\begin{array}{c}\hfill f(x)=\frac{2^{\alpha }\mathsf{\Gamma }\frac{\alpha +1}{2}\mathsf{\Gamma }(s+1+\frac{\alpha }{2})}{\sqrt{\pi }\mathsf{\Gamma }(\alpha +1)}{}_2{F}_1(\frac{\alpha +1}{2},-s;\frac{1}{2};x^2)+{(1-x^2)}^{s+\frac{\alpha }{2}},\mu =1,\end{array}$$

then the exact solution is given by $u(x)={(1-x^2)}^{s+\frac{\alpha }{2}}$.

In this example, we solve fractional diffuse Equation (24) by a finite difference scheme and finite volume scheme with zero boundary conditions. We first verify the convergence orders and numerical errors in $l_h^{\infty }$ norms by finite difference schemes (26)–(27) for $0<\alpha <2,\alpha \ne 1$ with $s=6,3,2,1$, respectively. The results are listed in Figure 1. The dates in Figure 1 indicate that the convergence rates of the finite difference schemes (26)–(27) are of second order for $u\in C^2(R)$. The above results indicate that the convergence rates will fail to achieve second order if $s\le 1$ for finite difference schemes (26)–(27). When $s\le 1$, it is easy to show that the solution $u\in C^{\gamma }(R),\gamma \le 1$, which has lower regularity. Second, we show the convergence orders and numerical errors in $l_h^{\infty }$ norms by finite volume schemes (39)–(40) for $0<\alpha <2,\alpha \ne 1$ with $s=6,3,2,1$, respectively. The results are listed in Figure 2. The dates in Figure 2 indicate that the convergence rates of the finite volume scheme are higher than those of the finite difference scheme but have no more than three successive orders. Figure 1 and Figure 2 indicate that the convergence rates of the finite difference scheme and finite volume scheme are related to $\alpha$ for $u\in C^1(R)$.

Third, we apply the finite difference schemes (28)–(29) and finite volume schemes (49)–(50) to solve the fractional diffuse Equation (24) with zero boundary conditions, and we compare the numerical errors with finite difference schemes (26)–(27) and finite volume method (39)–(40). Then, we present the numerical errors of the finite difference schemes (26)–(27) and (28)–(29) for $0<\alpha <2,\alpha \ne 1$ with $\alpha =1.9,1.5$ and $s=4,3,2,1$, respectively. The results are listed in Figure 3 and Figure 4, where FDM I and FDM II represent numerical schemes (26)–(27) and (28)–(29). The dates in Figure 3 and Figure 4 indicate that the error of finite difference schemes (28)–(29) is less than that of finite difference schemes (26)–(27), and finite difference schemes (26)–(27) and (28)–(29) produce numerical oscillations when s is smaller. Then, we present the numerical errors of the finite volume schemes (39)–(40) and (49)–(50) for $0<\alpha <2,\alpha \ne 1$ with $\alpha =1.9,1.5$ and $s=4,3,2,1$, respectively. The results are listed in Figure 5 and Figure 6, where FVM I and FVM II represent numerical schemes (39)–(40) and (49)–(50). The dates in Figure 5 and Figure 6 indicate that finite volume schemes (49)–(50) are fewer than finite volume schemes (39)–(40), and, in finite volume schemes (39)–(40) and (49)–(50), no numerical oscillations will occur when s is smaller.

Finally, we solve fractional diffuse Equation (24) by finite difference schemes (28)–(29) and the fractional central difference scheme in [11] with zero boundary conditions. The results are listed in Figure 7, where scheme I and scheme II represent the fractional central difference scheme and finite difference schemes (28)–(29). The dates in Figure 7 indicate that finite difference schemes (28)–(29) are fewer than the fractional central difference schemes.

4.2. Example B

The algorithms in this paper can be used to solve other space fractional problems, such as space fractional Schrödinger, Klein–Gordon–Schrödinger equations, strongly coupled nonlinear fractional Schrödinger equations, etc. In this subsection, we show the numerical approximation for the space fractional Allen–Cahn equation

$$\begin{array}{cc}\hfill & u_t=-{ϵ}^2{(-\Delta )}^{\alpha /2}u-f(u),(x,t)\in (a,b)\times [0,T],\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill & u(x,0)=u_0,x\in (a,b),\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill & u(x,t)=0,(x,t)\in {(a,b)}^c\times [0,T],\hfill \end{array}$$

(55)

where $f(u)=u^3-u.$ The space fractional Allen–Cahn equation is a kind of important fractional-order model, which has important application prospects in mathematics, physics, and engineering. The above space fractional Allen–Cahn equation has been studied both theoretically and numerically in recent years. In this example, we solve the space fractional Allen–Cahn Equation (53) by finite difference schemes (28)–(29) with zero boundary conditions. It follows from numerical scheme (22) that we can obtain the following semidiscrete numerical scheme:

$$\begin{array}{c}\hfill \frac{dU}{dt}={ϵ}^{2}AU+U-U^3.\end{array}$$

(56)

Applying an implicit scheme and the Crank–Nicolson scheme in time to a semidiscrete scheme, we can obtain the following fully discrete schemes:

$$\begin{array}{cc}\hfill \mathrm{Implicit}:& \frac{U^{n+1}-U^n}{\Delta t}=U^{n+1}-{(U^{n+1})}^3+{ϵ}^{2}A{U}^{n+1},\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill \mathrm{Crank–Nicolson\; I}:& \frac{U^{n+1}-U^n}{\Delta t}=\frac{U^n-{(U^n)}^3+U^{n+1}-{(U^{n+1})}^3}{2}+{ϵ}^{2}A\frac{U^n+U^{n+1}}{2},\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill \mathrm{Crank–Nicolson\; II}:& \frac{U^{n+1}-U^n}{\Delta t}=\frac{(U^n+U^{n+1})}{2}+\frac{(U^n+U^{n+1})({(U^n)}^2+{(U^{n+1})}^2)}{4}+{ϵ}^{2}A\frac{U^n+U^{n+1}}{2}.\hfill \end{array}$$

(59)

In this example, we solve fractional Allen–Cahn systems (53)–(55) with zero boundary conditions by finite difference schemes (28)–(29) in space and implicit scheme and Crank–Nicolson scheme in time, respectively. Consider the initial value $u_0(x)=1$ on $[-2,0]$, or zero elsewhere, and simulate the numerical solution with $[-10,10],\tau =0.001,h=0.1$. First, we display the waveform of the numerical solution at the difference $\alpha$ and time. The results are listed in Figure 8 and Figure 9. The dates in Figure 8 and Figure 9 indicate that the $\alpha$ affects the propagation velocity of the solitary wave. For a smaller $\alpha$, the propagation of the soliton becomes slower, thus indicating the presence of quantum subdiffusion. Second, we display the evolution of discrete energy over time by implicit scheme and Crank–Nicolson scheme. The results are listed in Figure 10. The dates in Figure 10 indicate that the energy of the numerical scheme is dissipated, which is consistent with the nature of the original problem.

5. Conclusions

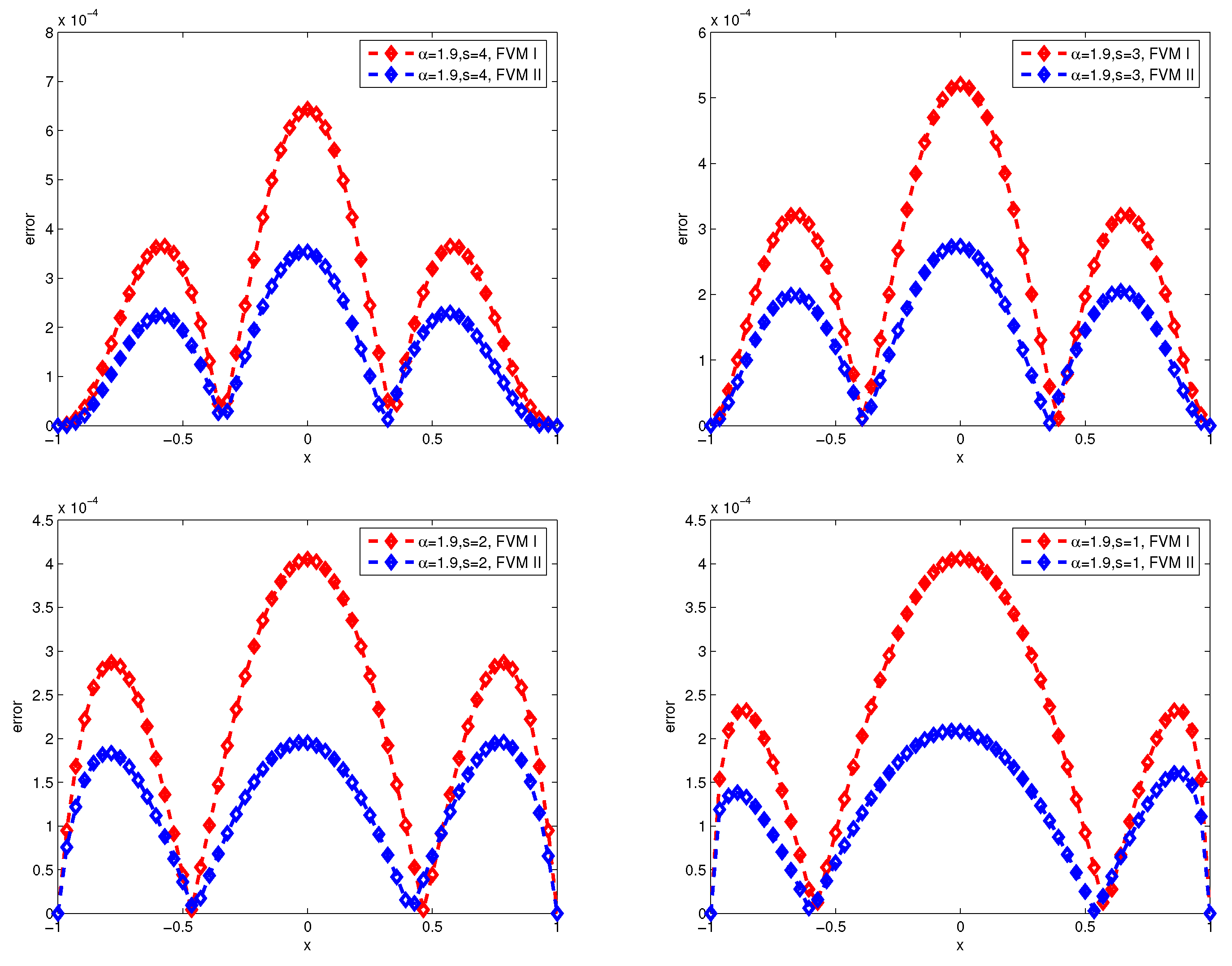
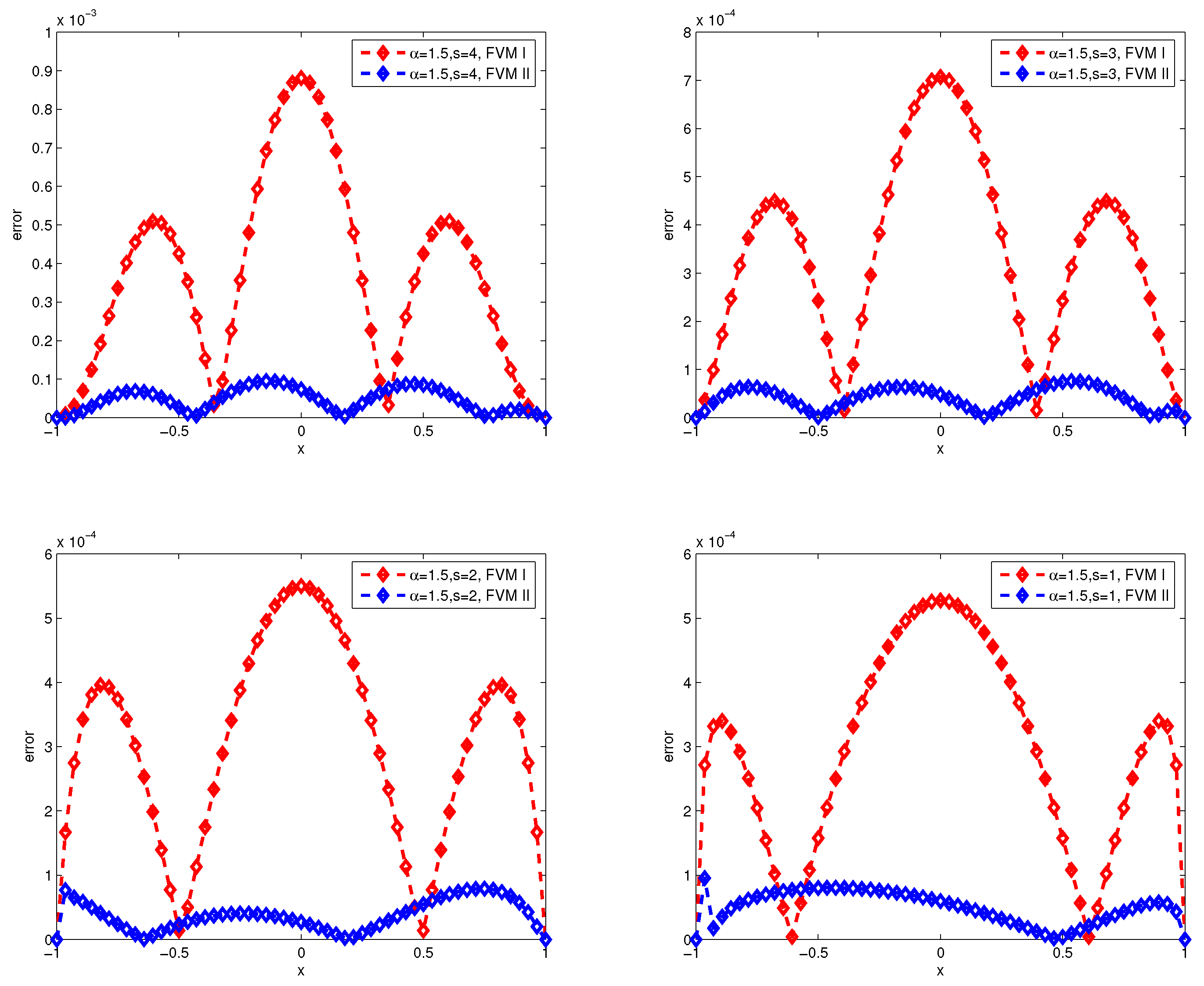
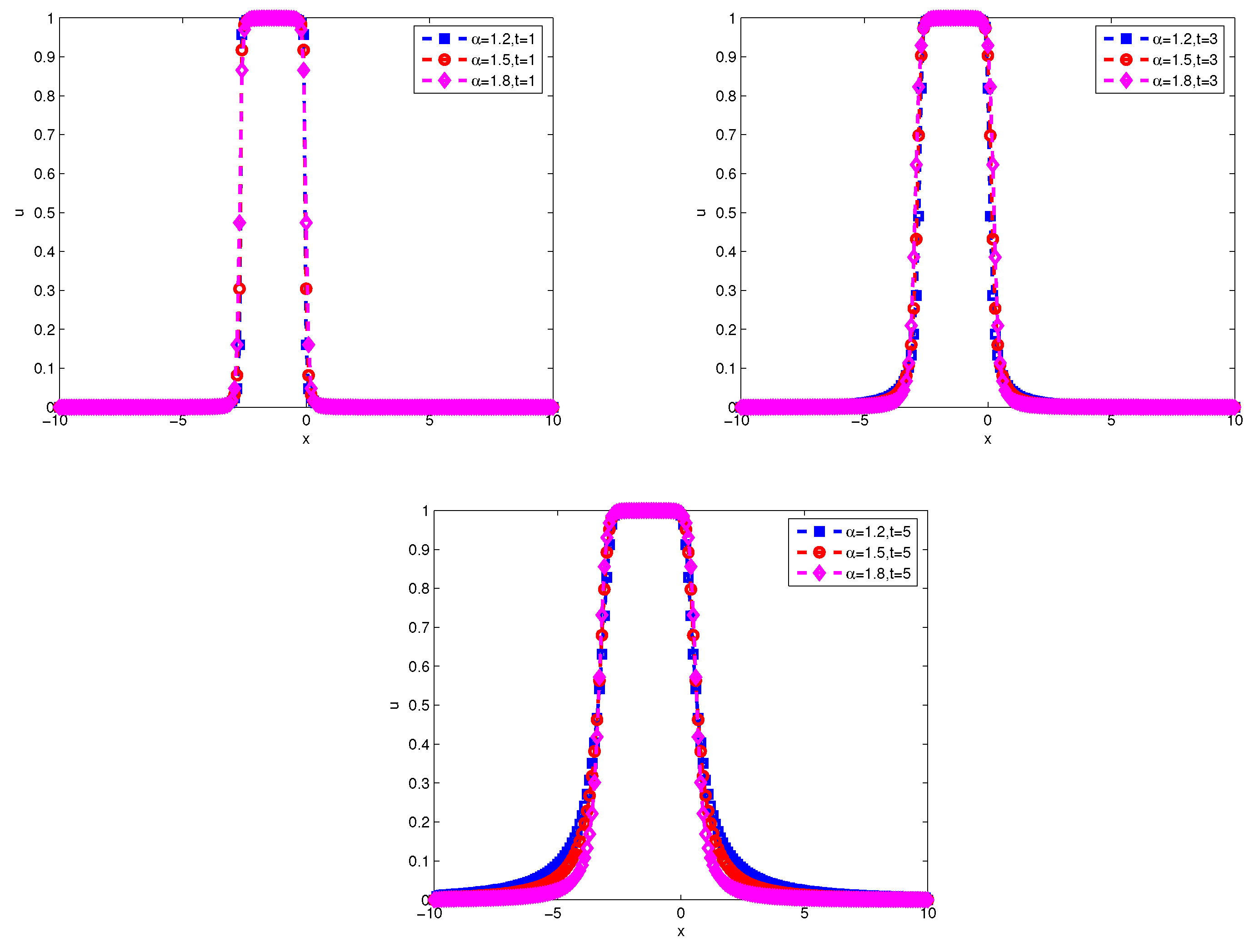
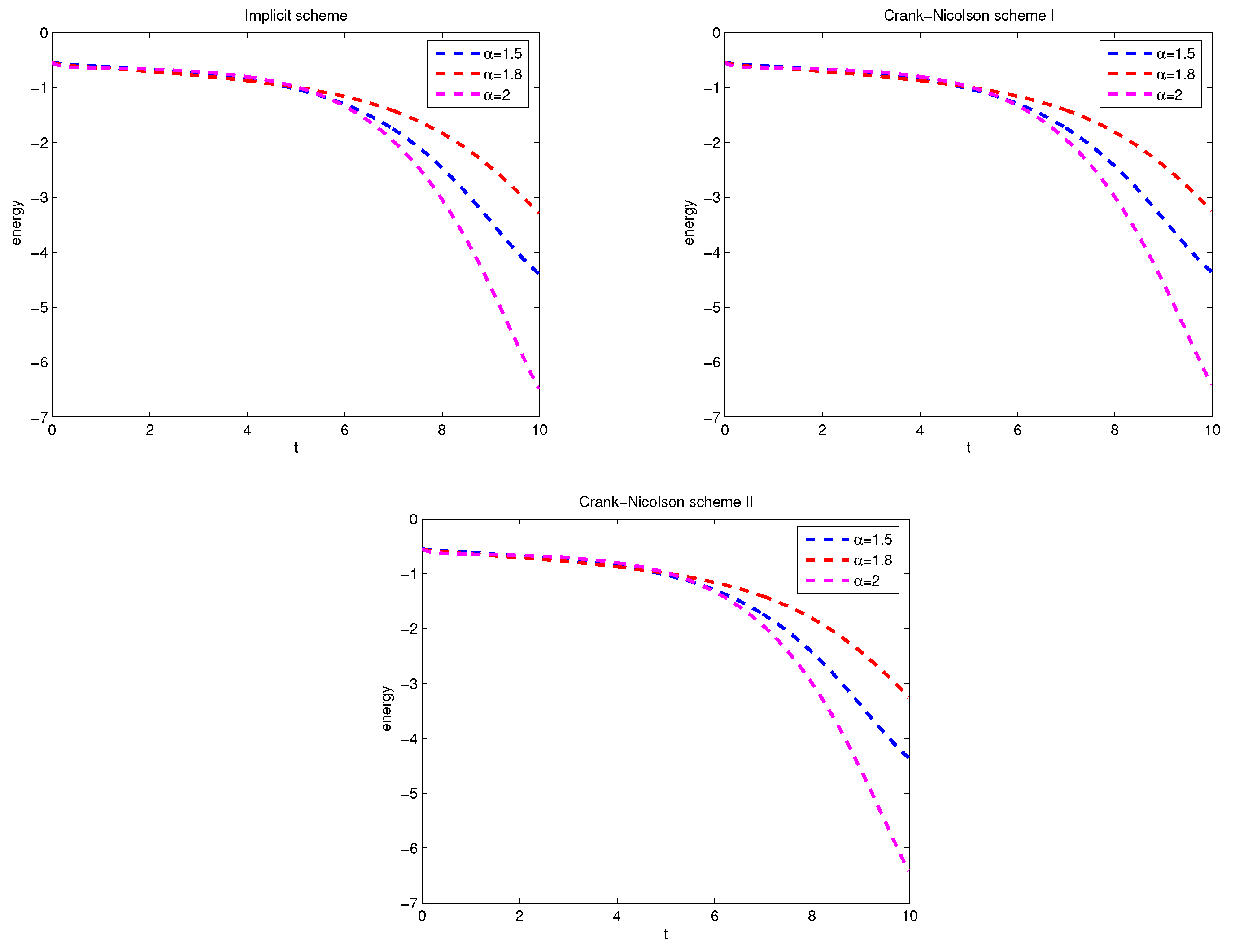
In the paper, we show the finite difference method and finite volume method for fractional diffuse equations by fractional interpolation function and classical interpolation function with zero boundary conditions. The novelty of our method is that we deal with the hypersingular integral representation of the fractional Laplacian operator as a weak singular integral by an integral operator ${\mathcal{J}}^{\alpha }(x)$. Because the solution of the fractional diffusion equation is usually singular near the boundary, we use the fractional interpolation function in the boundary region to approach the fractional Laplacian operator based on some lemmas, and we use the classical interpolation function in the inner region. Then, it is found that the differential matrix of the above scheme is a symmetric matrix and strictly row-wise diagonally dominant in special fractional interpolation functions. Moreover, it is easy to extend the numerical scheme for nonuniform dissection by a similar approach. Finally, several numerical examples are considered to demonstrate the validity and applicability of the numerical scheme to approximate fractional diffusion equations.

In future work, this method will be extended to solve fractional nonlinear Schröinger, Klein–Gordon–Schrödinger equations, etc., with zero boundary conditions. Moreover, we will also try to extend the method to solve the high-dimensional diffuse equation with zero boundary conditions.