Study on the Influence of Sample Size on the Mechanical and Integrity Characteristics of Coal Measure Sandstone under High Strain Rate
Abstract
:1. Introduction
2. Experiment
2.1. Experiment Design
- (a)
- Impact compression test
- (b)
- Mercury injection test
- (c)
- Scanning electron microscope (SEM) test
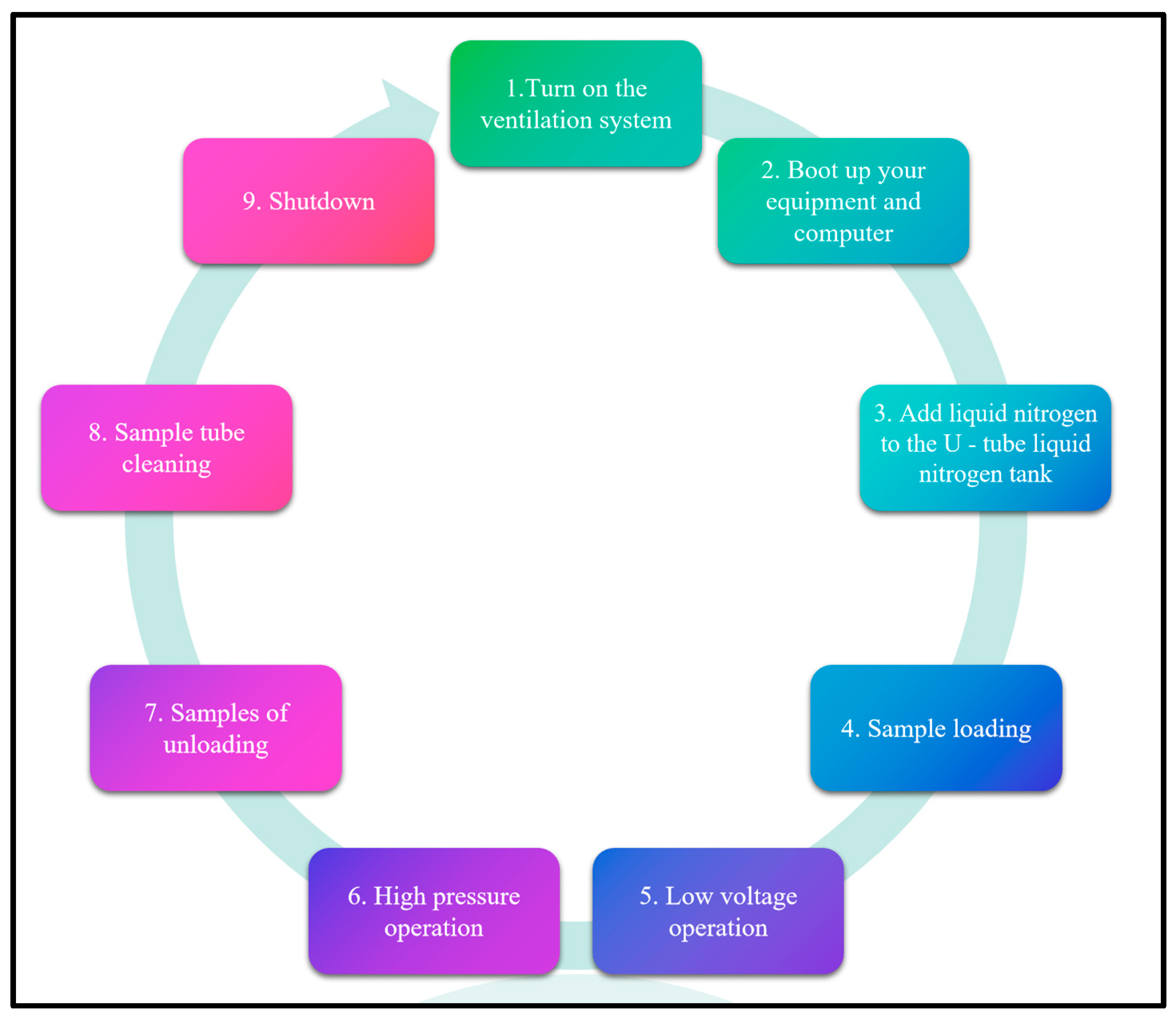
2.2. Test Equipment
- (a)
- The Hopkinson Pressure rod test system (SHPB)
- (b)
- Mercury injection test system
- (c)
- Electron microscope scanning test (SEM)
2.3. Sample Preparation
- (a)
- Preparation of samples for impact compression tests
- (b)
- Preparation of samples for mercury injection test
- (c)
- Preparation of samples for scanning electron microscope (SEM) test
3. Results
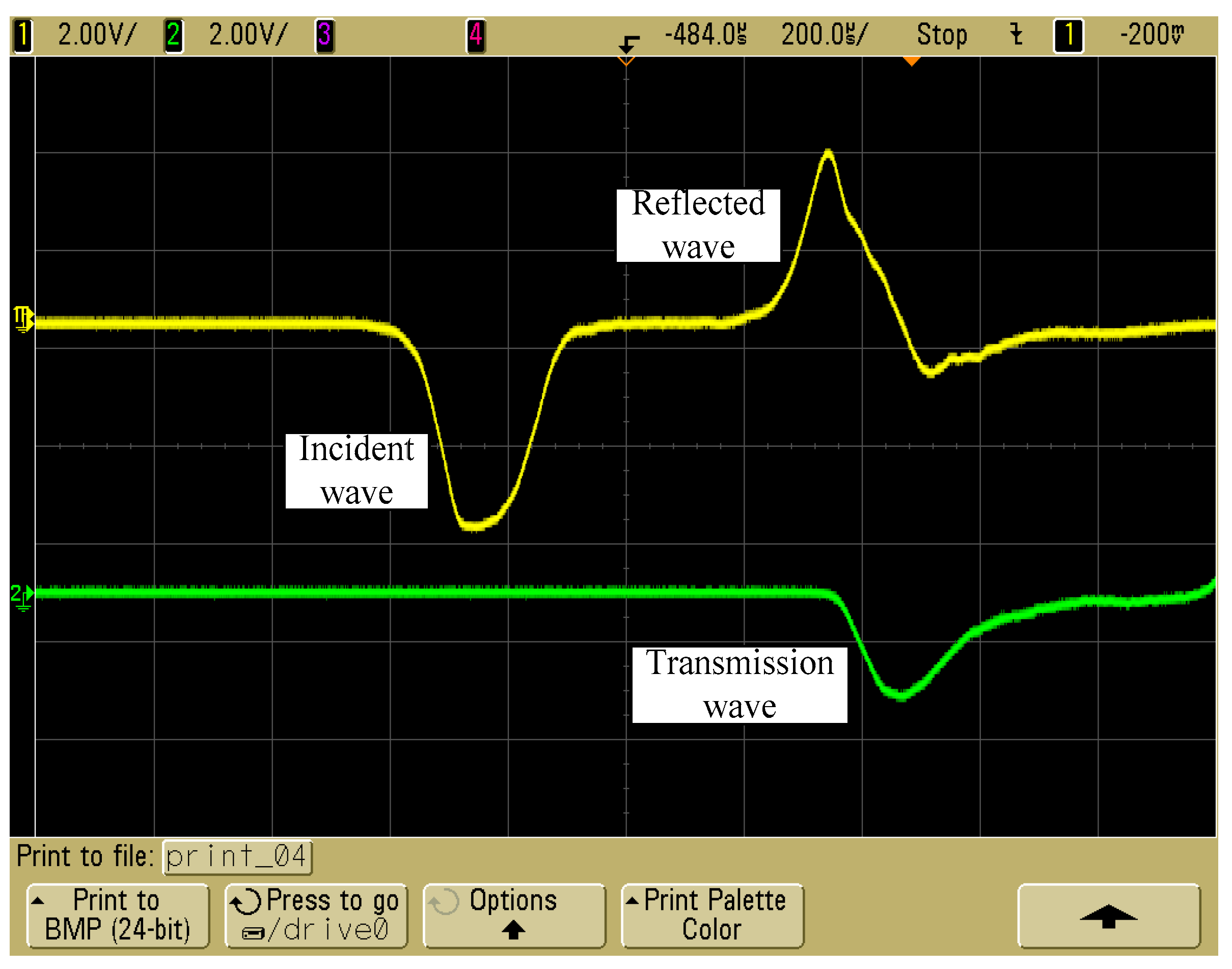
3.1. Data Processing Method
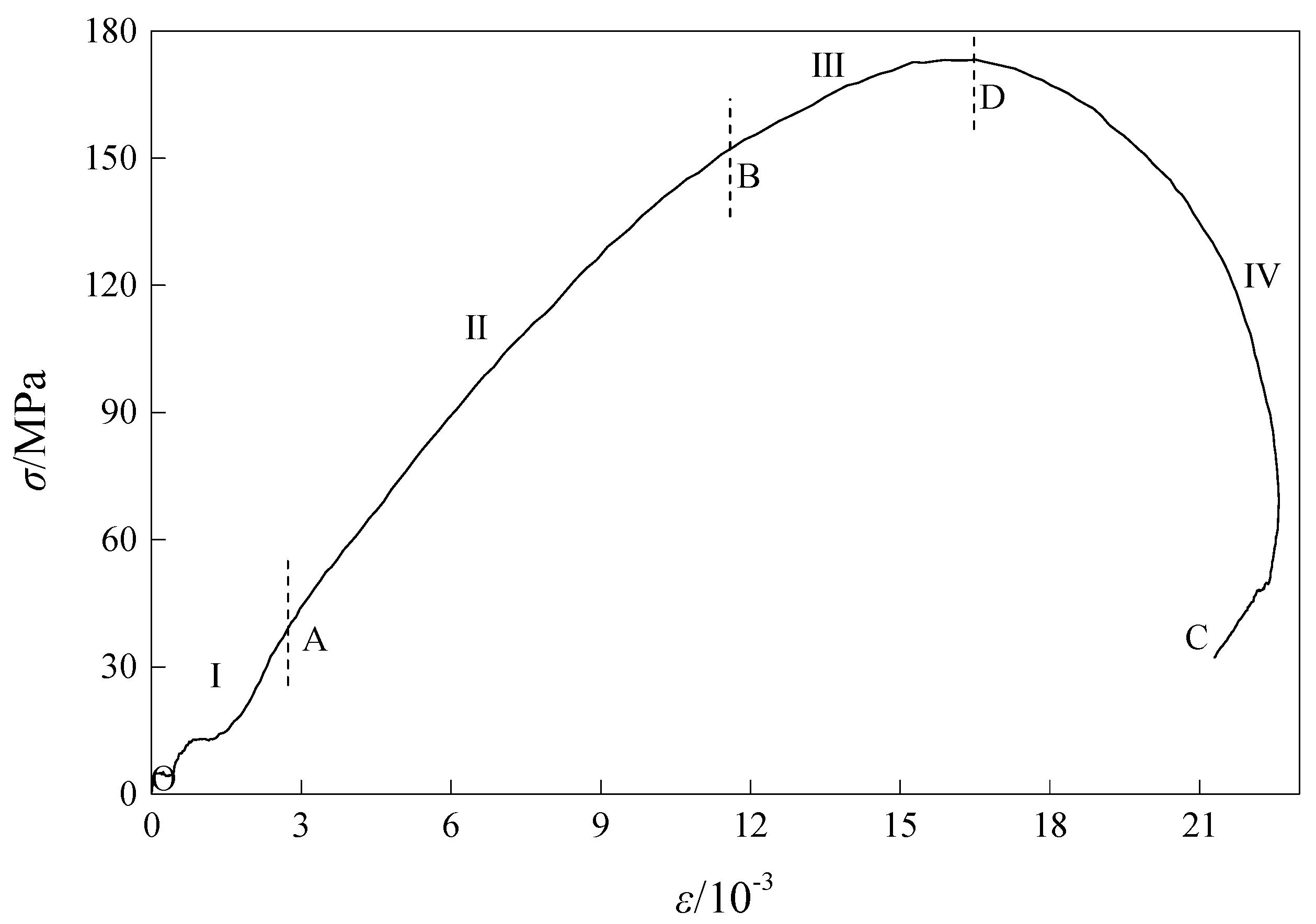
3.2. Stress–Strain Curve Characteristics
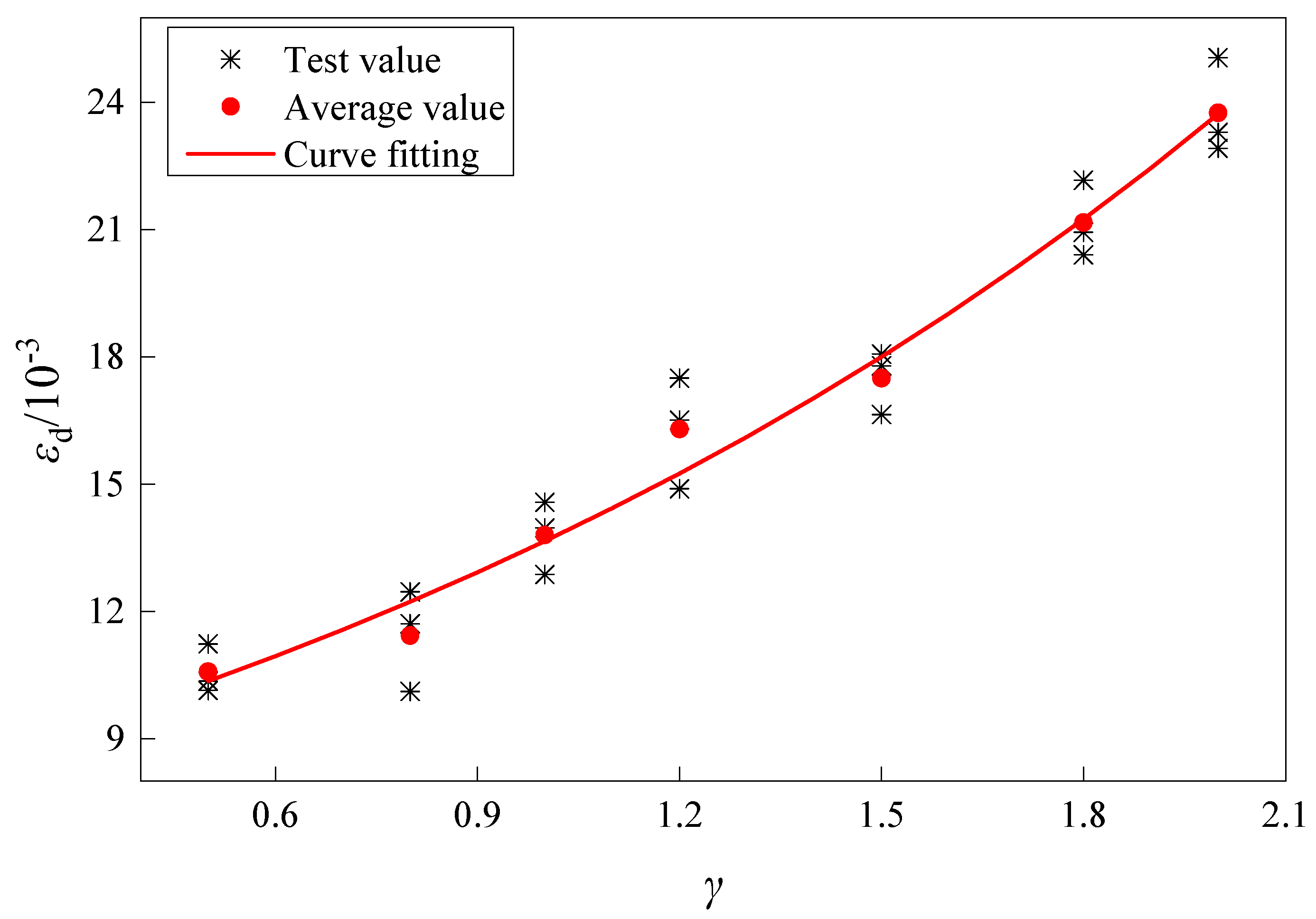
3.3. The Influence of Size Effect on the Variation in Mechanical Property Parameters of Samples
4. Energy Dissipation Characteristics
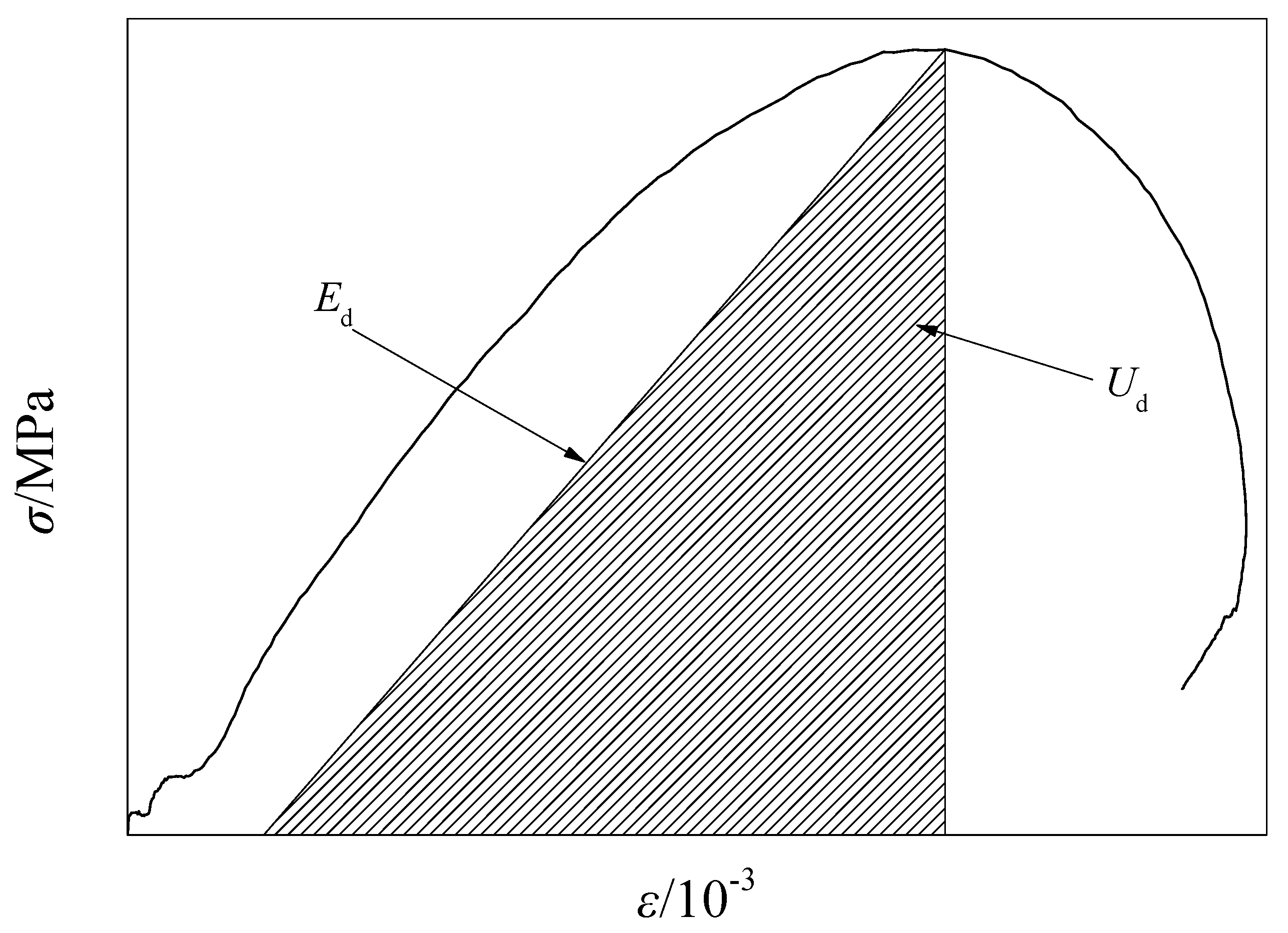
4.1. The Calculation Principle of Energy
4.2. The Law of Energy Change
5. Size Effect of Intact Characteristics of Sandstone
5.1. Variation in Porosity of Coal-Bearing Sandstone under Different Length–Diameter Ratios
5.2. Micromorphologic Characteristics of Coal-Bearing Sandstone under Different Length–Diameter Ratio
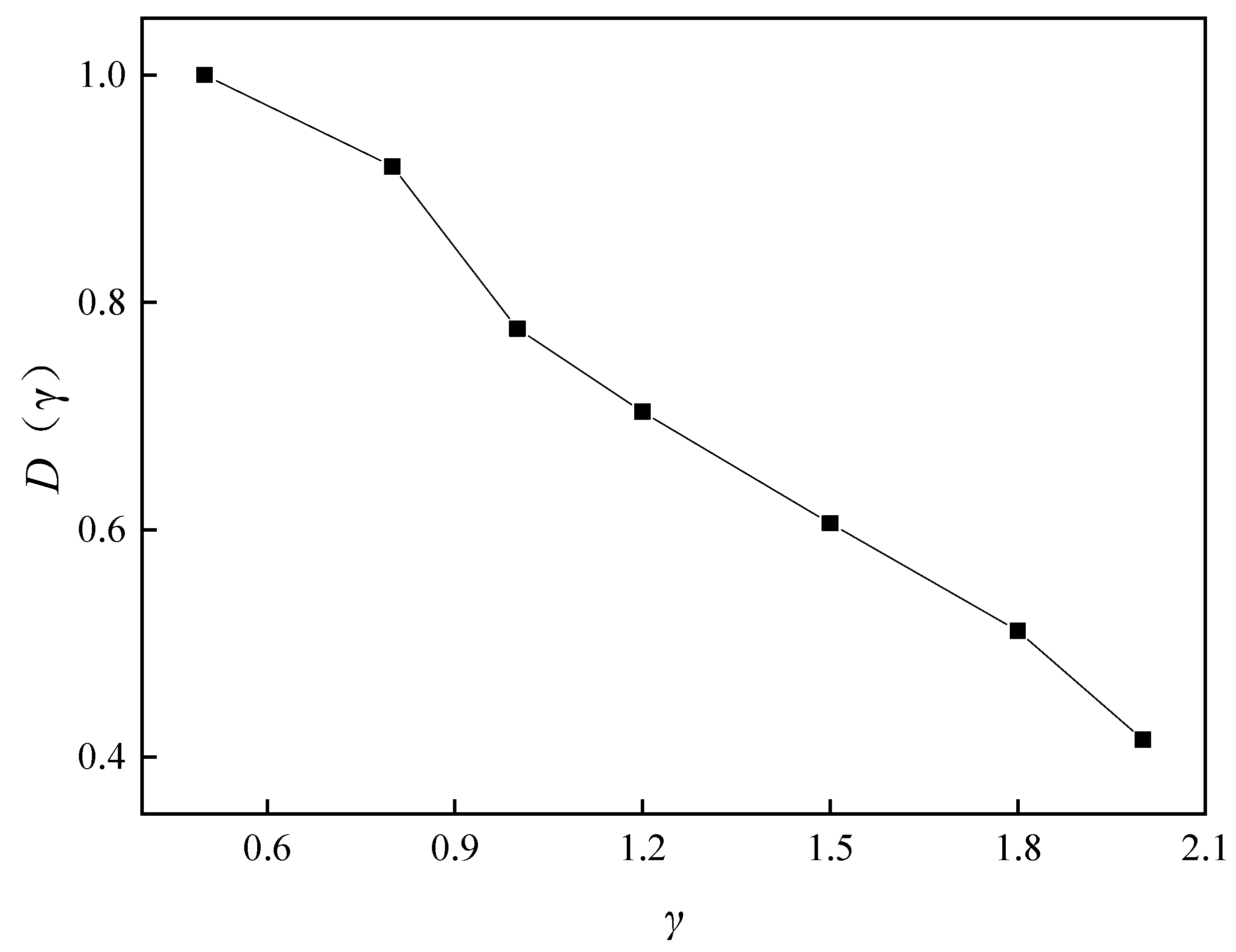
5.3. Size Effect on Integrity of Coal-Bearing Sandstone
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jackson, R.; Lau, J.S.O. The effect of specimen size on the laboratory mechanical properties of Lac du Bonnet grey granite. In Proceedings of the International Workshop on Scale Effects in Rock Masses, Loen, Norway, 7–8 June 1990; pp. 165–174. [Google Scholar]
- Yiouta–Mitra, P.; Dimitriadis, G.; Nomikos, P. Size effect on triaxial strength of randomly fractured rock mass with discrete fracture network. Bull. Eng. Geol. Environ. 2023, 82, 8. [Google Scholar] [CrossRef]
- Hudson John, A.; Crouch Steven, L.; Charles, F. Soft, stiff and servo-controlled testing machines: A review with reference to rock failure. Eng. Geol. 1972, 6, 155–189. [Google Scholar] [CrossRef]
- You, M.; Hua, A. The size effect of uniaxial compression of rock specimen and support capacity of ore pillar. J. China Coal Soc. 1997, 22, 37–41. (In Chinese) [Google Scholar]
- Lu, Z.; Feng, Z.; Zhao, Y. Influence of rock inhomogeneity on strength-size effect of rock materials. J. China Coal Soc. 2007, 32, 917–920. [Google Scholar]
- Sun, C.; Liu, F.; Jiang, M.; Chen, H. Size effect of compression strength and end constraint of rocks by distinct element simulation. Chin. J. Rock Mech. Eng. 2014, 33, 3421–3428. [Google Scholar]
- Yang, S.; Su, C.; Xu, W. Experimental and theoretical study of size effect of rock material. Eng. Mech. 2005, 22, 112–118. [Google Scholar] [CrossRef]
- Zhang, M.; Lu, Y.; Yang, Q. Failure probability and strength size effect of quasi-brittle materials. Chin. J. Rock Mech. Eng. 2010, 29, 1782–1789. [Google Scholar]
- Zhao, T.; Hu, G.; Wang, T.; Zhang, H. Influence of Parallel Joint Spacing and Rock Size on Rock Bulk Modulus. Adv. Civ. Eng. 2022. [Google Scholar] [CrossRef]
- Han, Q.; Gao, Y.; Zhang, Y. Experimental Study of Size Effects on the Deformation Strength and Failure Characteristics of Hard Rocks under True Triaxial Compression. Adv. Civ. Eng. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- You, M.; Zou, Y. Discussion on heterogeneity of rock material and size effect on specimen strength. Chin. J. Rock Mech. Eng. 2000, 19, 391–395. [Google Scholar]
- Liang, Z.; Zhang, Y.; Tang, S.; Li, L. Size effect of rock messes and associated representative element properties. Chin. J. Rock Mech. Eng. 2013, 32, 1157–1166. [Google Scholar]
- Su, H.; Jing, H.; Zhao, H.; Yin, Q. Study on tensile strength and size effect of red sandstone after high temperature treatment. Chin. J. Rock Mech. Eng. 2015, 34, 2879–2887. [Google Scholar]
- Yang, S.; Wen, S. Method for strength parameters of coal samples with different diameters. Chin. J. Geotech. Eng. 2010, 32, 881–891. [Google Scholar]
- Masoumi, H.; Roshan, H.; Hagan, P.C. Size-dependent Hoek-Brown failure criterion. Int. J. Geomech. 2017, 17, 04016048. [Google Scholar] [CrossRef]
- Chang-yu, L.; Xiao, L.I.; Shu-ren, W.U. Research on energy characteristics of size effect of granite under low/intermediate strain rates. Rock Soil Mech. 2016, 37, 3472–3480. [Google Scholar]
- Li, M.; Mao, X.; Lu, A.; Tao, J.; Zhang, G.; Zhang, L.; Li, C. Effect of specimen size on energy dissipation characteristics of red sandstone under high strain rate. Int. J. Min. Sci. Technol. 2014, 24, 151–156. [Google Scholar] [CrossRef]
- Meng, Q.B.; Han, L.J.; Pu, H.; Wen, S.-Y. Experimental on the effect of strain rate and size on the energy accumulation and dissipation of rock. J. China Coal Soc. 2015, 40, 2386–2398. [Google Scholar]
- Li, X.; Ni, X.; Sun, B.; Zhu, Z.; Du, S. Quantitative study on meso-damage characteristics of siltstone under triaxial compression. J. China Coal Soc. 2012, 37, 590–595. [Google Scholar]
- Xia, Y.-Y.; Lin, M.-Q.; Liao, L.; Xiong, W.; Wang, Z.D. Fractal characteristics analysis of fragments from rockburst tests of large-diameter specimens. Chin. J. Rock Mech. Eng. 2014, 33, 1358–1365. [Google Scholar]
- Zhou, J.; Zhao, G.; Meng, X.; Liu, C.; Ma, L.; Xu, W.; Cheng, X. Experimental Investigation of the Size Effect of Rock under Impact Load. Minerals 2022, 13, 43. [Google Scholar] [CrossRef]
- Li, K.; Yin, Z.-Y.; Han, D.; Fan, X.; Cao, R.; Lin, H. Size effect and anisotropy in a transversely isotropic rock under compressive conditions. Rock Mech. Rock Eng. 2021, 54, 4639–4662. [Google Scholar] [CrossRef]
- Li, K.; Cheng, Y.; Yin, Z.-Y.; Han, D.; Meng, J. Size effects in a transversely isotropic rock under brazilian tests: Laboratory testing. Rock Mech. Rock Eng. 2020, 53, 2623–2642. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, X.J.; Liu, F.; Luo, W.-C. Propagation of stress wave in porous material. Explos. Shock. Waves 2011, 31, 107–112. [Google Scholar]
- Gong, F.Q.; Li, X.B.; Rao, Q.H.; Liu, X. Reference method for determining sample size in SHPB tests of rock materials. J. Vib. Shock. 2013, 32, 24–28. [Google Scholar]
- Jing, H.W.; Su, H.J.; Yang, D.L.; Meng, B. Study of strength degradation law of damaged rock sample and its size effect. Chin. J. Rock Mech. Eng. 2012, 31, 543–549. [Google Scholar]
- Li, D.; Xiao, P.; Xie, T.; Li, X. On the effect of length to diameter ratio of rock specimen subjected to dynamic and static compression. J. Exp. Mech. 2018, 33, 93–100. [Google Scholar]
- Wang, W.H.; Li, X.B.; Zhou, Z.L.; Zhang, Y.P. Energy-transmitted rule of various stress waves across open joint. J. Cent. South Univ. Sci. Technol. 2006, 37, 376–380. [Google Scholar]
- Ma, D.; Wang, J.; Cai, X.; Ma, X.; Zhang, J.; Zhou, Z.; Tao, M. Effects of height/diameter ratio on failure and damage properties of granite under coupled bending and splitting deformation. Eng. Fract. Mech. 2019, 220, 106640. [Google Scholar] [CrossRef]
- TB 10099-2017; Code for Design of Railway Station and Terminal. China Railway Publishing House: Beijing, China, 2017.
- Yi, E. The Influence of Fly Ash Contents on Mechanical Properties and Energy Response of Concrete at a High Strain Rate. Adv. Civ. Eng. 2023, 2023. [Google Scholar] [CrossRef]
- Lu, A.; Hu, S.; Li, M.; Duan, T.; Li, B.; Chang, X. Impact of Moisture Content on the Dynamic Failure Energy Dissipation Characteristics of Sandstone. Shock. Vib. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Hu, Y.; Duan, T.; Xian, P.; Chen, L. Freeze-Thaw Cycle Effect on Sputtering Rate of Water-Saturated Yellow Sandstone under Impact Loading. Adv. Civ. Eng. 2019, 2019, 2549603. [Google Scholar] [CrossRef]
- Zhang, Z. Energy Evolution Mechanism during Rock Deformation and Failure. China University of Mining and Technology. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CDFD1214&filename=1013030078.nh (accessed on 6 November 2023).
- Hu, S. Study on Mechanical Properties and Energy Response Characteristics of High-Porosity Concrete under Cyclic Loading and Unloading. China University of Mining and Technology. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201901&filename=1018826818.nh (accessed on 6 November 2023).
- Belak, J. On the nucleation and growth of voids at high strain-rates. J. Comput. Aided Mater. Des. 1998, 5, 193–206. [Google Scholar] [CrossRef]
- Song, Y.; Yang, H.; Tan, H.; Reng, J. Study on damage evolution characteristics of sandstone with different saturations in freeze-thaw environment. Chin. J. Rock Mech. Eng. 2021, 40, 1513–1524. [Google Scholar]
- Song, Y.; Yang, H.; Tan, H. Research on Digital Core Pore-Level Network Modeling Based on Micro-CT Images; Jilin University: Changchun, China, 2015. [Google Scholar]
- Jia, H.L.; Liu, Q.B.; Xiang, W.; Zhang, W. Damage evolution model of saturated sandstone under freeze-thaw cycles. Chin. J. Rock Mech. Eng. 2013, 32, 3049–3055. [Google Scholar]











| NO. | Density/kg·m−3 | Longitudinal Wave Velocity/m·s−1 | Uniaxial Compressive Strength/MPa | Elasticity Modulus/GPa | Poisson’s Ratio | Porosity/% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tv | Av | Tv | Av | Tv | Av | Tv | Av | Tv | Av | Tv | Av | |
| 1-1 | 2649 | 2629.33 | 3856 | 3873.76 | 117.24 | 112.85 | 7.05 | 7.15 | 0.22 | 0.21 | 2.35 | 2.31 |
| 1-2 | 2611 | 3942 | 109.36 | 7.30 | 0.20 | 2.27 | ||||||
| 1-3 | 2628 | 3823 | 111.95 | 7.11 | 0.21 | 2.32 | ||||||
| γ | σd/MPa | εd/10−3 | Ed/GPa | |||
|---|---|---|---|---|---|---|
| Tv | Av | Tv | Av | Tv | Av | |
| 0.5 | 66.11 | 64.04 | 10.14 | 10.58 | 10.73 | 9.64 |
| 62.64 | 11.23 | 8.61 | ||||
| 63.38 | 10.36 | 9.57 | ||||
| 0.8 | 108.09 | 108.70 | 11.71 | 11.43 | 12.72 | 12.78 |
| 109.28 | 10.11 | 13.17 | ||||
| 108.74 | 12.46 | 12.44 | ||||
| 1.0 | 140.86 | 141.91 | 13.97 | 13.80 | 15.33 | 15.79 |
| 139.44 | 14.57 | 14.79 | ||||
| 145.42 | 12.87 | 17.26 | ||||
| 1.2 | 173.20 | 172.76 | 16.51 | 16.30 | 15.13 | 16.21 |
| 176.65 | 14.89 | 18.66 | ||||
| 168.43 | 17.50 | 14.84 | ||||
| 1.5 | 132.78 | 133.93 | 17.79 | 17.50 | 11.42 | 11.03 |
| 141.14 | 18.07 | 9.66 | ||||
| 127.88 | 16.64 | 12.00 | ||||
| 1.8 | 111.01 | 112.30 | 20.41 | 21.17 | 7.82 | 8.06 |
| 115.10 | 20.94 | 8.91 | ||||
| 110.78 | 22.17 | 7.44 | ||||
| 2.0 | 98.91 | 96.40 | 22.92 | 23.76 | 7.17 | 6.73 |
| 93.83 | 25.06 | 6.40 | ||||
| 96.45 | 23.30 | 6.62 | ||||
| γ | Total Absorbed Energy | Elastic Energy | Dissipated Energy | |||
|---|---|---|---|---|---|---|
| Tv | Av | Tv | Av | Tv | Av | |
| 0.5 | 29.95 | 29.64 | 9.99 | 10.49 | 8.35 | 7.46 |
| 25.75 | 11.18 | 7.98 | ||||
| 33.21 | 10.30 | 6.04 | ||||
| 0.8 | 86.74 | 76.42 | 36.05 | 36.32 | 24.36 | 23.06 |
| 71.91 | 35.59 | 22.09 | ||||
| 70.62 | 37.31 | 22.72 | ||||
| 1.0 | 120.58 | 111.63 | 63.50 | 62.70 | 44.55 | 48.75 |
| 126.34 | 64.50 | 48.79 | ||||
| 87.96 | 60.11 | 52.91 | ||||
| 1.2 | 306.57 | 255.19 | 116.73 | 109.25 | 72.83 | 73.59 |
| 257.32 | 98.46 | 79.22 | ||||
| 201.69 | 112.55 | 68.73 | ||||
| 1.5 | 315.35 | 277.92 | 109.07 | 117.01 | 78.93 | 83.26 |
| 267.61 | 145.69 | 87.25 | ||||
| 250.81 | 96.28 | 83.61 | ||||
| 1.8 | 337.20 | 310.00 | 139.17 | 138.72 | 101.1 | 102.45 |
| 305.39 | 131.31 | 97.79 | ||||
| 287.41 | 145.67 | 108.47 | ||||
| 2.0 | 332.37 | 306.59 | 133.89 | 135.59 | 106.59 | 109.43 |
| 243.55 | 134.98 | 112.39 | ||||
| 343.84 | 137.89 | 109.3 | ||||
| Length–Diameter Ratio | The Porosity Values of Coal-Bearing Sandstone at Each Position F (%) | ||||
|---|---|---|---|---|---|
| The End of the Incident Bar | 1/4 Length of the Sample | 1/2 Length of Sample | 3/4 Length of Sample | The End of the Transmission Bar | |
| 0.5 | 2.91 | 2.89 | 2.92 | 2.9 | 2.9 |
| 0.8 | 2.92 | 2.9 | 2.86 | 2.82 | 2.78 |
| 1 | 2.89 | 2.85 | 2.76 | 2.71 | 2.65 |
| 1.2 | 2.95 | 2.8 | 2.69 | 2.64 | 2.6 |
| 1.5 | 2.92 | 2.78 | 2.62 | 2.56 | 2.51 |
| 1.8 | 2.91 | 2.69 | 2.58 | 2.49 | 2.46 |
| 2 | 2.81 | 2.63 | 2.52 | 2.45 | 2.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, E.; Li, Z. Study on the Influence of Sample Size on the Mechanical and Integrity Characteristics of Coal Measure Sandstone under High Strain Rate. Fractal Fract. 2023, 7, 869. https://doi.org/10.3390/fractalfract7120869
Yi E, Li Z. Study on the Influence of Sample Size on the Mechanical and Integrity Characteristics of Coal Measure Sandstone under High Strain Rate. Fractal and Fractional. 2023; 7(12):869. https://doi.org/10.3390/fractalfract7120869
Chicago/Turabian StyleYi, Enbing, and Zhenhua Li. 2023. "Study on the Influence of Sample Size on the Mechanical and Integrity Characteristics of Coal Measure Sandstone under High Strain Rate" Fractal and Fractional 7, no. 12: 869. https://doi.org/10.3390/fractalfract7120869
APA StyleYi, E., & Li, Z. (2023). Study on the Influence of Sample Size on the Mechanical and Integrity Characteristics of Coal Measure Sandstone under High Strain Rate. Fractal and Fractional, 7(12), 869. https://doi.org/10.3390/fractalfract7120869






