The Analytical Stochastic Solutions for the Stochastic Potential Yu–Toda–Sasa–Fukuyama Equation with Conformable Derivative Using Different Methods
Abstract
:1. Introduction
2. Wave Equation for SPYTSFE
3. Exact Solutions of SPYTSFE
3.1. He’s Semi-Inverse Method
3.2. Improved -Expansion Method
| No | |
| 1 | orif |
| 2 | ifand |
| 3 | orifand |
| 4 | ifand |
| 5 | orifand |
| 6 | orifand |
| 7 | if |
| 8 | orifand |
| 9 | if and |
| 10 | if and |
| where | |
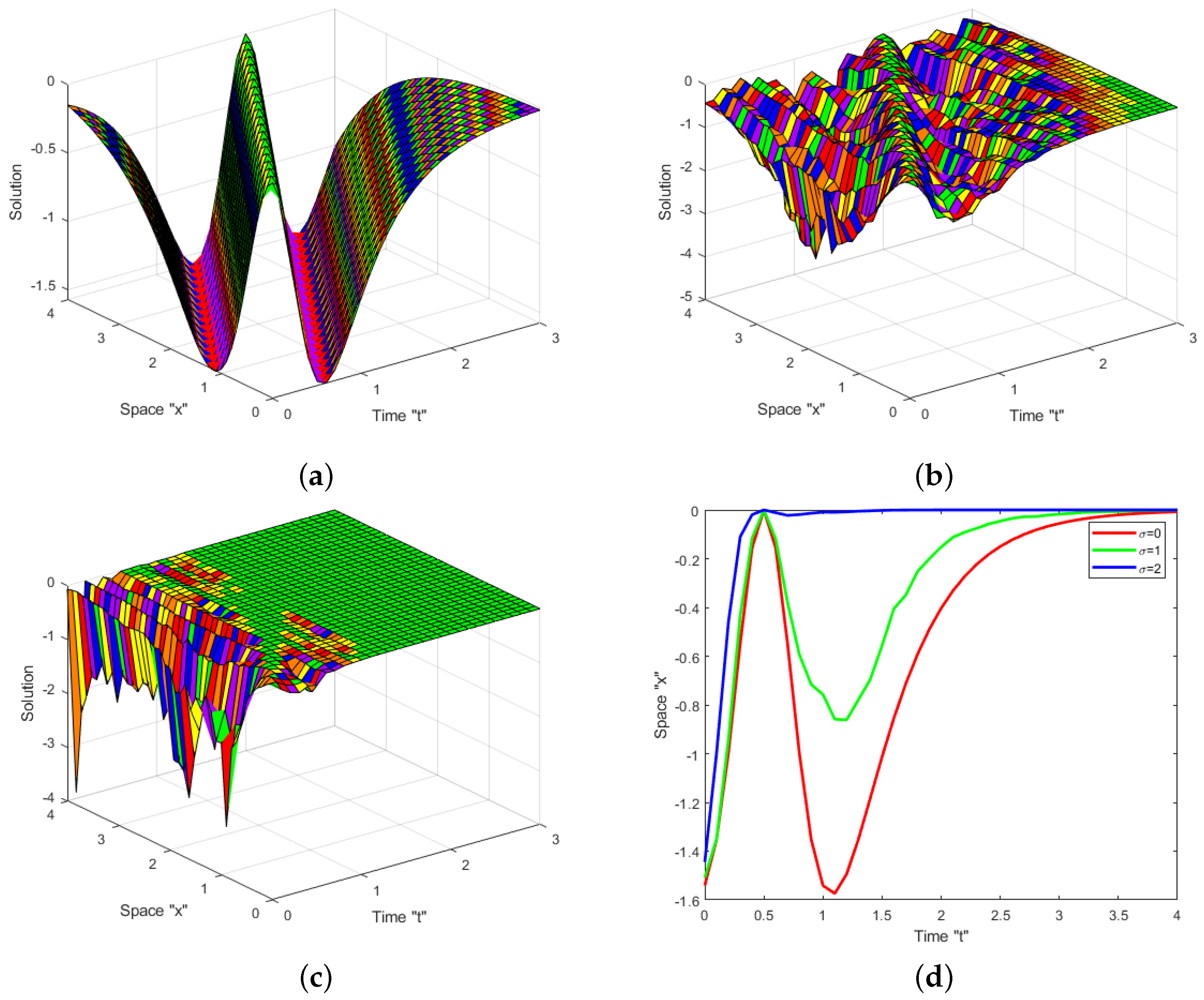
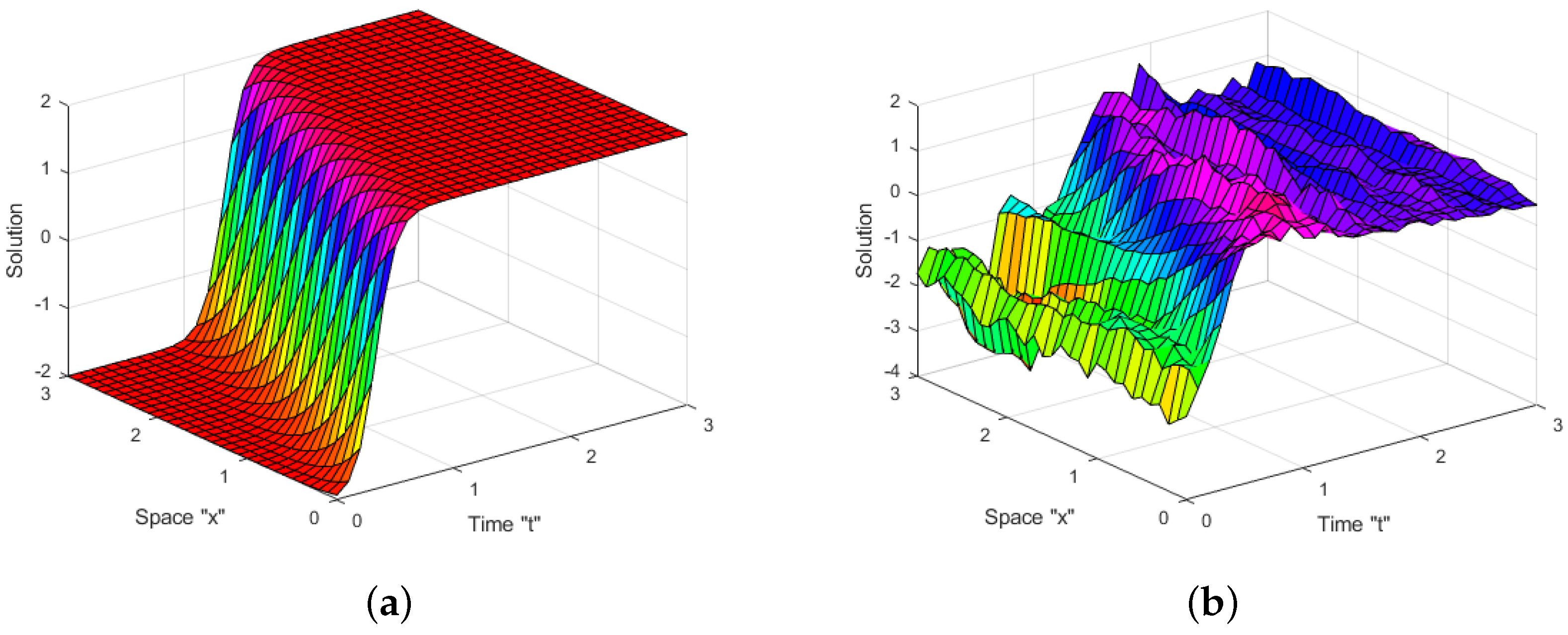
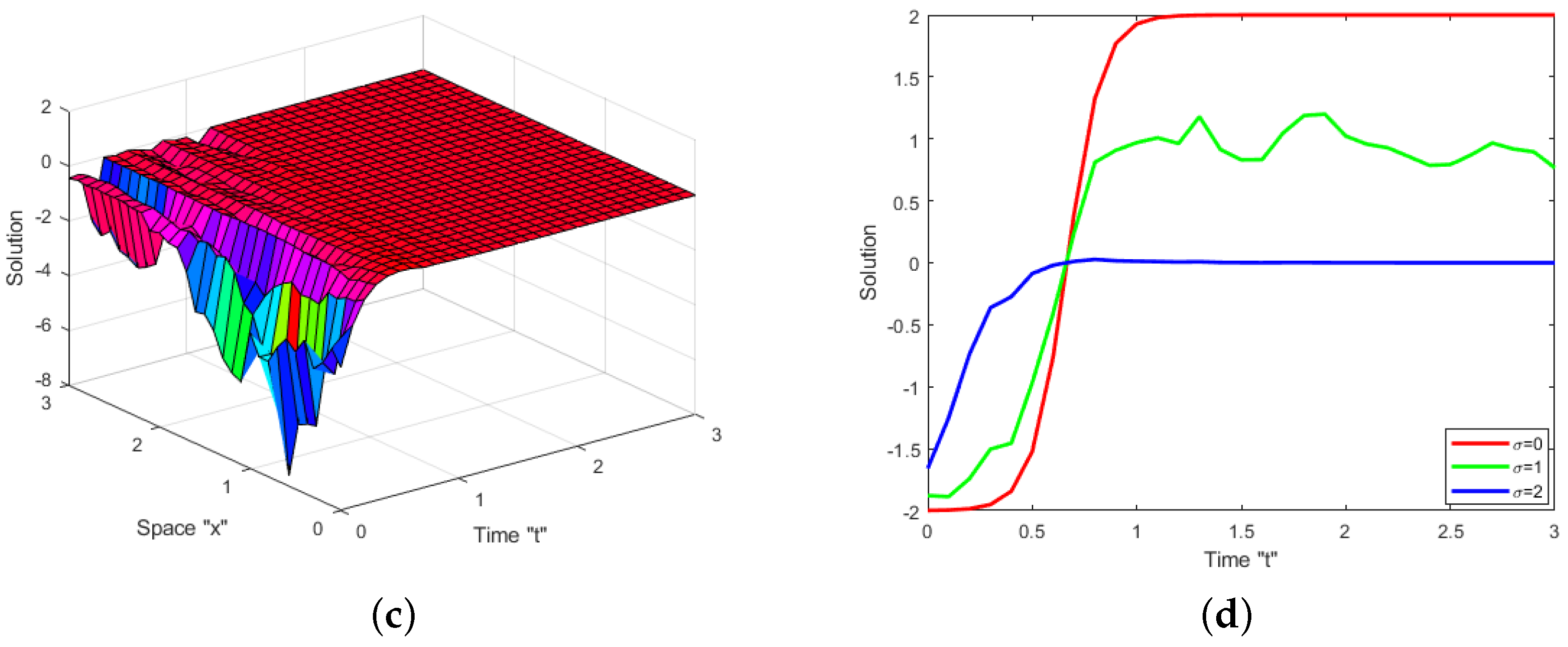
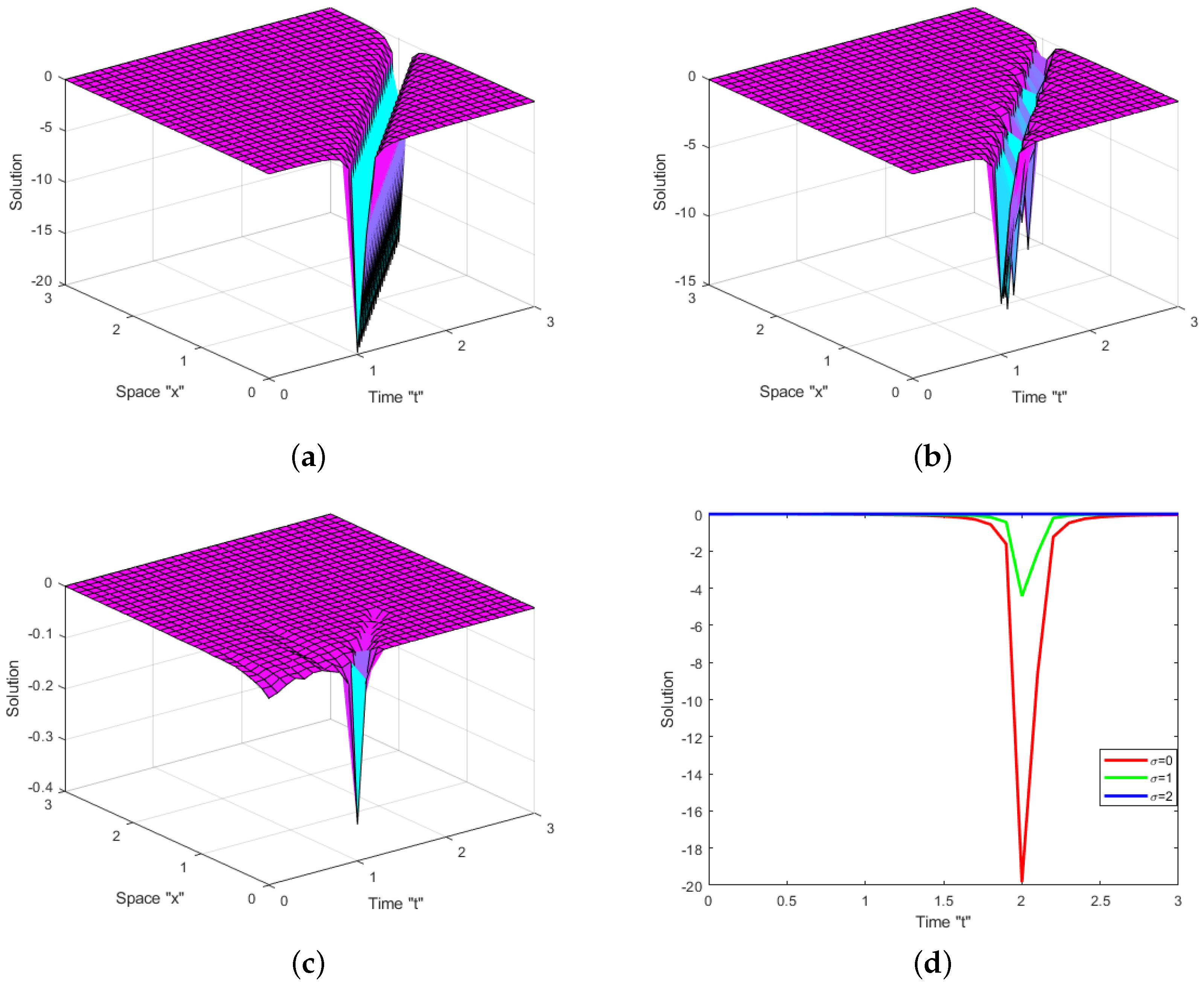
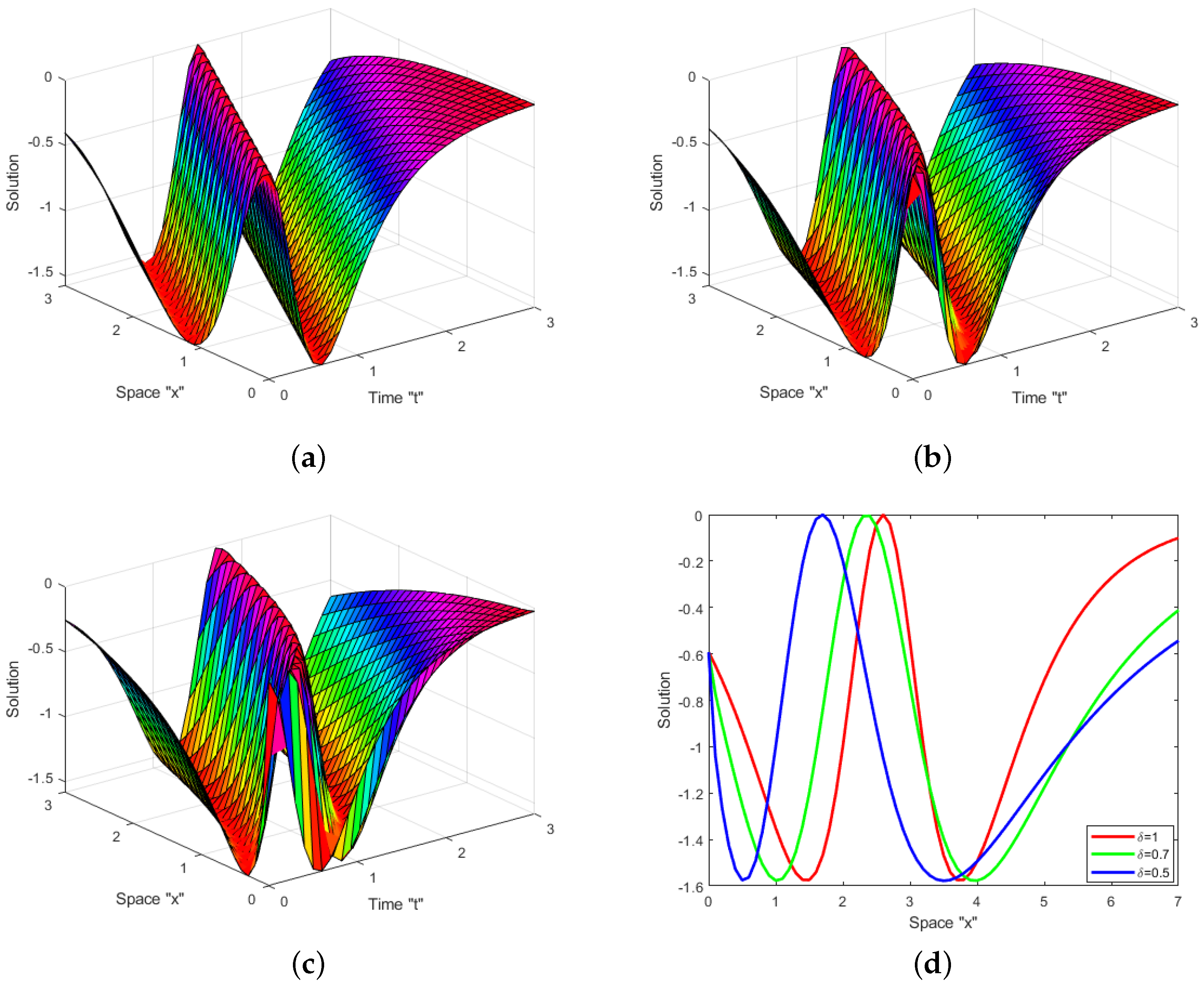
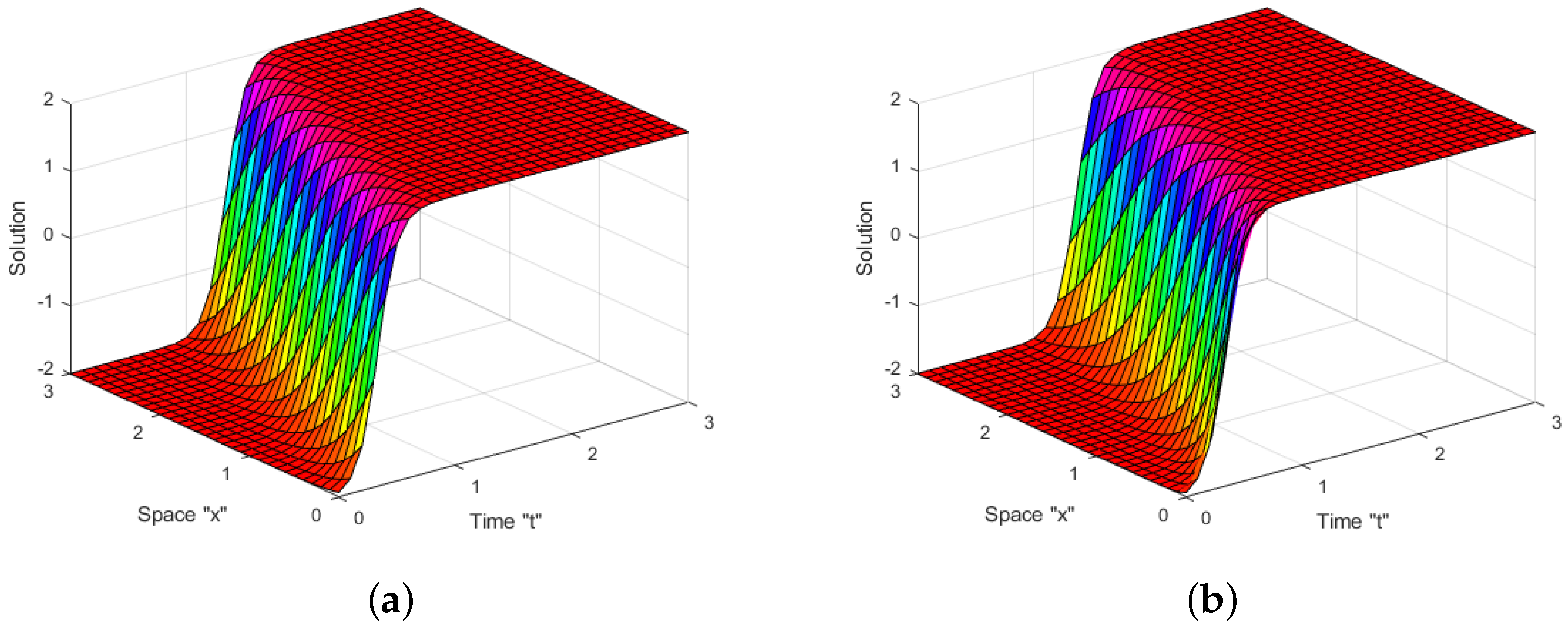
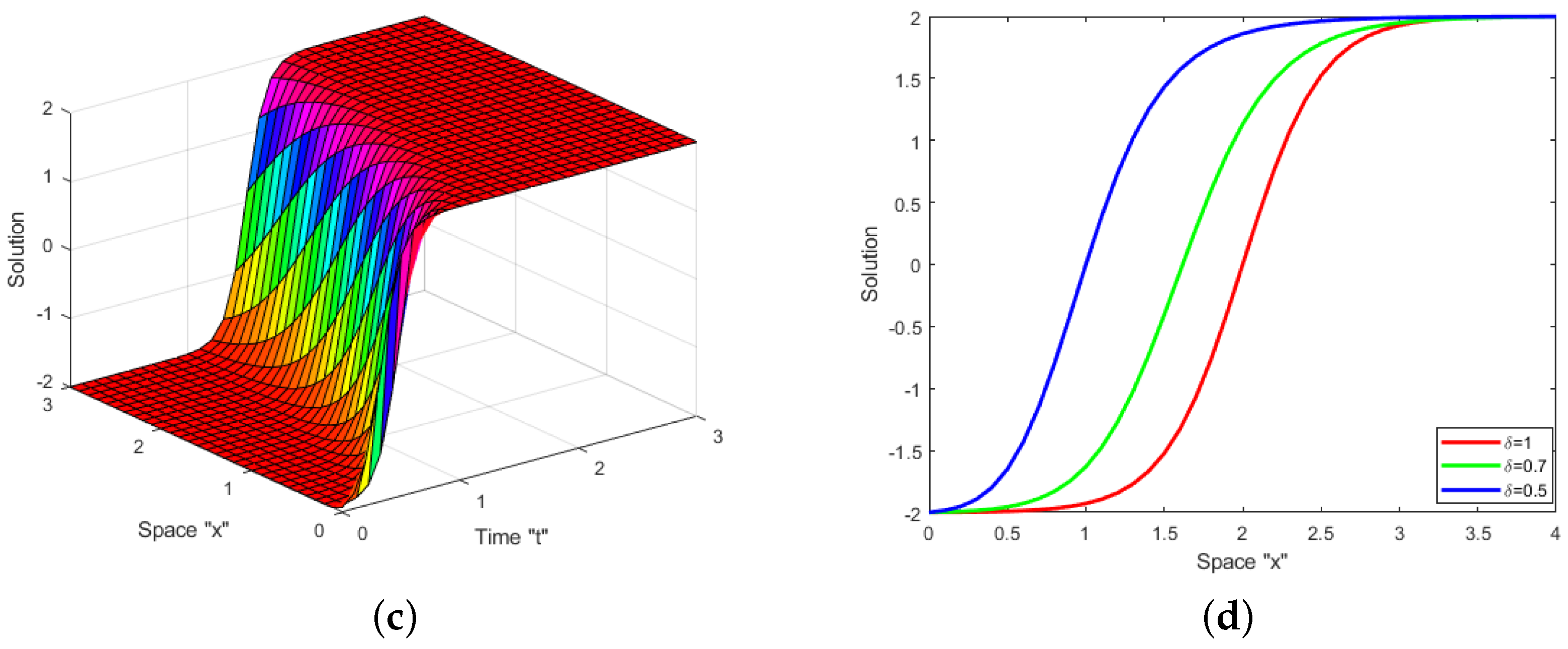
4. Impacts of White Noise and CD
4.1. Impact of White Noise
4.2. Impact of CD
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, S.; Toda, K.; Sasa, N.; Fukuyama, T. N soliton solutions to the Bogoyavlenskii-Schiff equation and a quest for the soliton solution in (3+1) dimensions. J. Phys. A 1998, 31, 3337–3347. [Google Scholar] [CrossRef]
- Yan, Z.Y. New families of non-travelling wave solutions to a new (3+1)-dimensional potential-YTSF equation. Phys. Lett. A 2003, 318, 78–83. [Google Scholar] [CrossRef]
- Yin, H.M.; Tian, B.; Chai, J.; Wu, X.Y.; Sun, W.R. Solitons and bilinear Bäcklund transformations for a (3+1) mathcontainer loading mathjax-dimensional Yu–Toda–Sasa–Fukuyama equation in a liquid or lattice. Appl. Math. Lett. 2016, 58, 178–183. [Google Scholar] [CrossRef]
- Hu, Y.J.; Chen, H.; Dai, Z.D. New kink multi-soliton solutions for the (3+1)-dimensional potential-Yu–Toda–Sasa–Fukuyama equation. Appl. Math. Comput. 2014, 234, 548–556. [Google Scholar] [CrossRef]
- Tan, W.; Dai, Z.D. Dynamics of kinky wave for (3+1)-dimensional potential Yu–Toda–Sasa–Fukuyama equation. Nonlinear Dyn. 2016, 85, 817–823. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple-soliton solutions for the Calogero–Bogoyavlenskii–Schiff, Jimbo–Miwa and YTSF equations. Appl. Math. Comput. 2008, 203, 592–597. [Google Scholar] [CrossRef]
- Fang, T.; Wang, Y.H. Lump-stripe interaction solutions to the potential Yu–Toda–Sasa–Fukuyama equation. Anal. Math. Phys. 2019, 9, 1481–1495. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.U. A transformed rational function method for (3+1)-dimensional potential Yu–Toda–Sasa–Fukuyama equation. Pramana-J. Phys. 2011, 76, 561–571. [Google Scholar] [CrossRef]
- Roshid, H.O.; Akbar, M.A.; Alam, M.N.; Hoque, M.F.; Rahman, N. New extended (G′/G)-expansion method to solve nonlinear evolution equation: The (3+1)-dimensional potential-YTSF equation. SpringerPlus 2014, 3, 122. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Katugampola, U.N. New approach to a generalized fractional integral. Appl. Math. Comput. 2011, 218, 860–865. [Google Scholar] [CrossRef]
- Alshammari, M.; Hamza, A.E.; Cesarano, C.; Aly, E.S.; Mohammed, W.W. The Analytical Solutions to the Fractional Kraenkel–Manna–Merle System in Ferromagnetic Materials. Fractal Fract. 2023, 7, 523. [Google Scholar] [CrossRef]
- Mouy, M.; Boulares, H.; Alshammari, S.; Alshammari, M.; Laskri, Y.; Mohammed, W.W. On Averaging Principle for Caputo-Hadamard Fractional Stochastic Differential Pantograph Equation. Fractal. Fract. 2023, 7, 31. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Cesarano, C.; Al-Askar, F.M. Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative. Mathematics 2023, 11, 194. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. Abundant Solitary Wave Solutions for the Boiti–Leon–Manna–Pempinelli Equation with M-Truncated Derivative. Axioms 2023, 12, 466. [Google Scholar] [CrossRef]
- He, J.-H. Variational principles for some nonlinear partial dikerential equations with variable coencients. Chaos Solitons Fractals 2004, 19, 847–851. [Google Scholar] [CrossRef]
- Hamza, A.E.; Alshammari, M.; Atta, D.; Mohammed, W.W. Fractional-stochastic shallow water equations and its analytical solutions. Results Phys. 2023, 53, 106953. [Google Scholar] [CrossRef]
- Ye, Y.H.; Mo, L.F. He’s variational method for the Benjamin–Bona–Mahony equation and the Kawahara equation. Comput. Math. Appl. 2009, 58, 2420–2422. [Google Scholar] [CrossRef]
- Yomba, E. A generalized auxiliary equation method and its application to nonlinear Klein–Gordon and generalized nonlinear Camassa–Holm equations. Phys. Lett. A 2008, 372, 1048–1060. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, T.C. A generalized new auxiliary equation method and its applications to nonlinear partial differential equations. Phys. Lett. A 2007, 363, 356–360. [Google Scholar] [CrossRef]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albosaily, S.; Elsayed, E.M.; Albalwi, M.D.; Alesemi, M.; Mohammed, W.W. The Analytical Stochastic Solutions for the Stochastic Potential Yu–Toda–Sasa–Fukuyama Equation with Conformable Derivative Using Different Methods. Fractal Fract. 2023, 7, 787. https://doi.org/10.3390/fractalfract7110787
Albosaily S, Elsayed EM, Albalwi MD, Alesemi M, Mohammed WW. The Analytical Stochastic Solutions for the Stochastic Potential Yu–Toda–Sasa–Fukuyama Equation with Conformable Derivative Using Different Methods. Fractal and Fractional. 2023; 7(11):787. https://doi.org/10.3390/fractalfract7110787
Chicago/Turabian StyleAlbosaily, Sahar, Elsayed M. Elsayed, M. Daher Albalwi, Meshari Alesemi, and Wael W. Mohammed. 2023. "The Analytical Stochastic Solutions for the Stochastic Potential Yu–Toda–Sasa–Fukuyama Equation with Conformable Derivative Using Different Methods" Fractal and Fractional 7, no. 11: 787. https://doi.org/10.3390/fractalfract7110787
APA StyleAlbosaily, S., Elsayed, E. M., Albalwi, M. D., Alesemi, M., & Mohammed, W. W. (2023). The Analytical Stochastic Solutions for the Stochastic Potential Yu–Toda–Sasa–Fukuyama Equation with Conformable Derivative Using Different Methods. Fractal and Fractional, 7(11), 787. https://doi.org/10.3390/fractalfract7110787





