Fixed-Time Fractional-Order Sliding Mode Control for UAVs under External Disturbances
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Related Works
1.3. Contributions
- The suggested FTFOSMC can achieve the benefits of the SMC with a quick response and robustness. In addition, fractional calculus can provide the proposed control with more flexibility in parameter adjustment and perform an improved task of removing the chattering problem associated with the standard SMC.
- The proposed control approach has been applied to quadrotor systems and compared to the two existing techniques.
- With the suggested FTFOSMC, the Lyapunov function is used to analyze the fixed-time stability of the quadrotor system. Simulations are also used to confirm the effectiveness of the proposed control for the quadrotor system.
1.4. Outline
2. Problem Formulation and Preliminaries
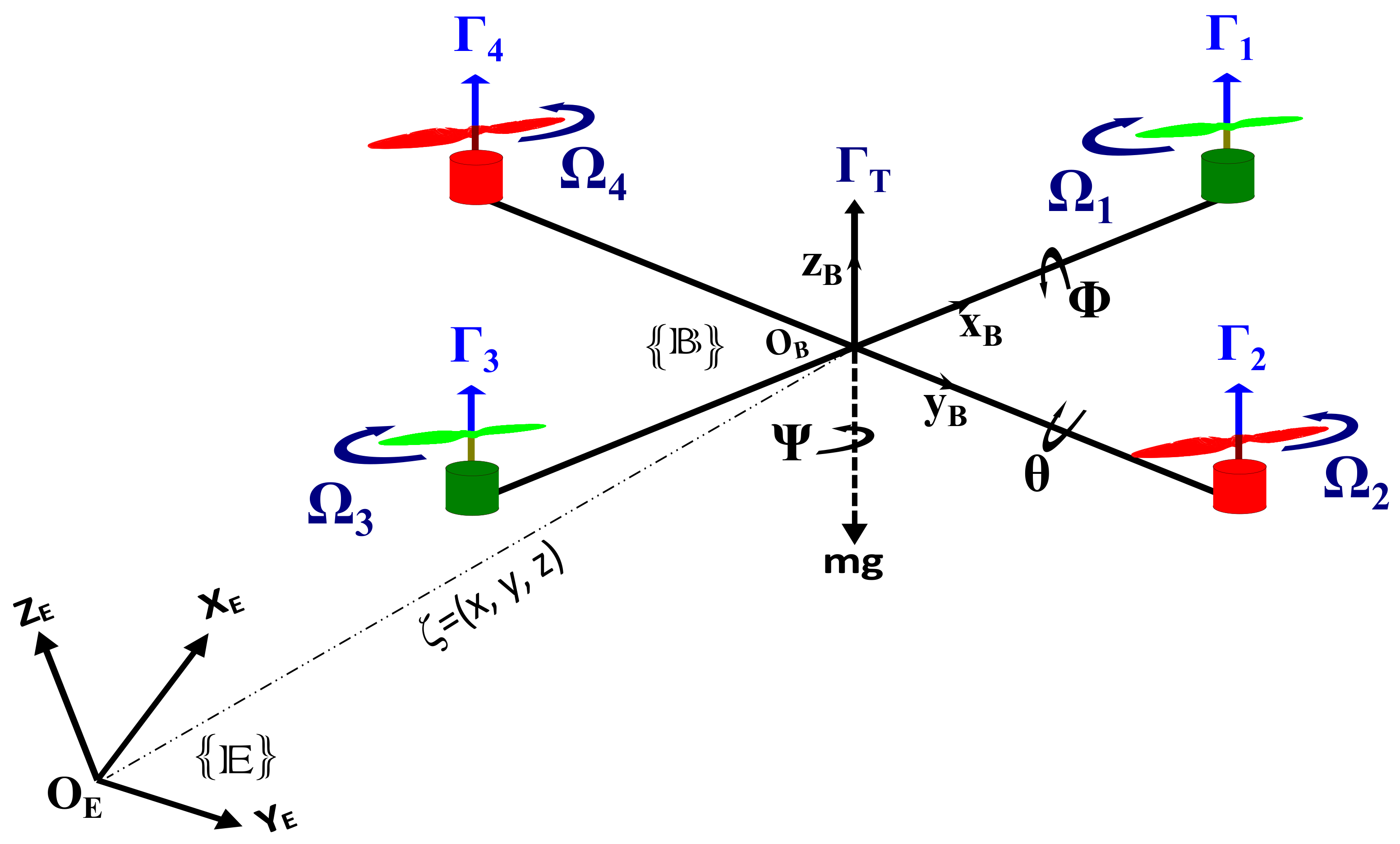
2.1. Problem Definition and Formulation
2.2. Fixed-Time Stability
2.3. Fractional-Order Calculus
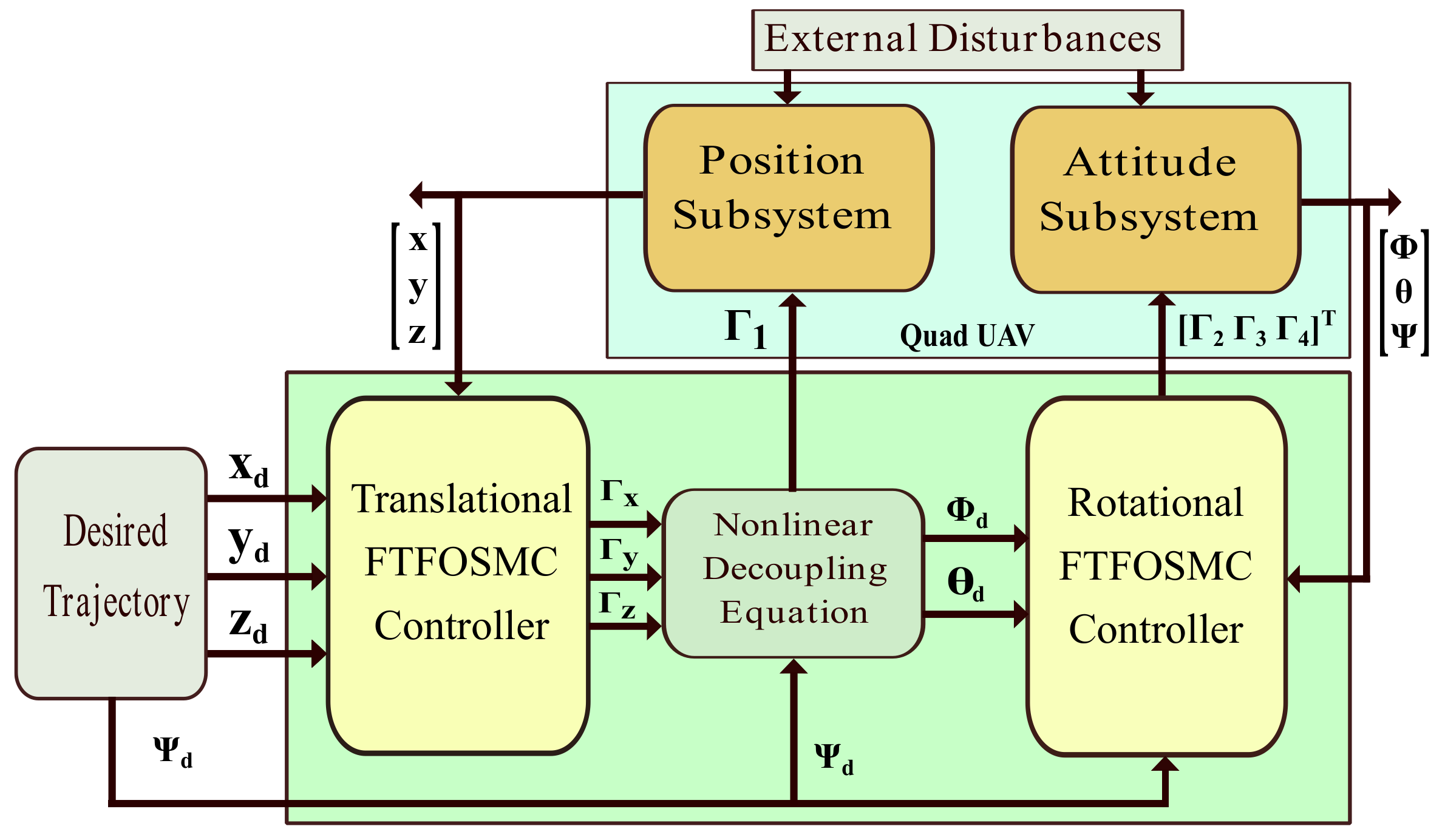
3. Control Design
3.1. External Disturbances
3.2. Fractional-Order Fixed Time Sliding Mode Control
3.3. Stability Analysis
3.4. Proposed Control Laws for Quadrotor
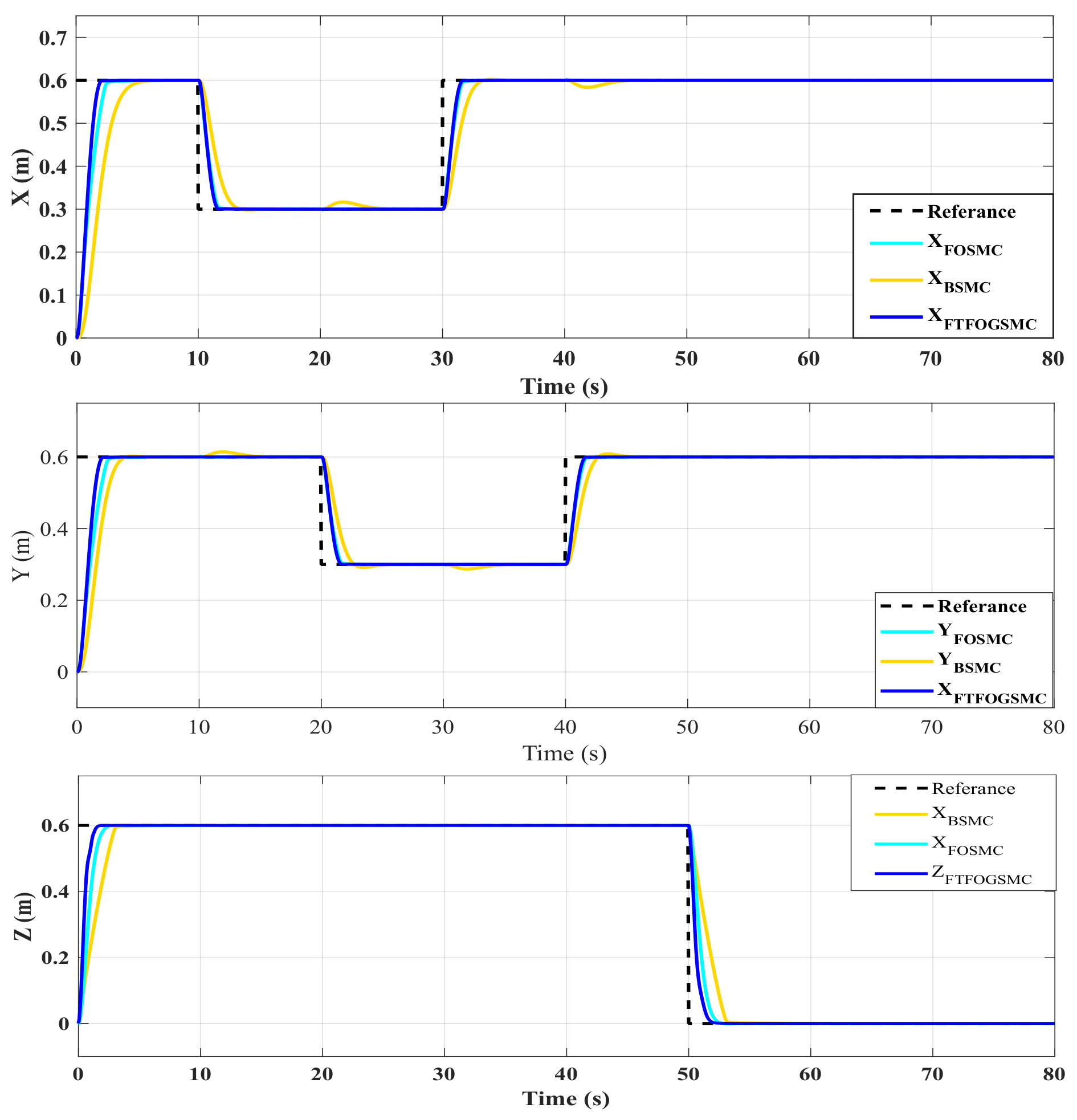
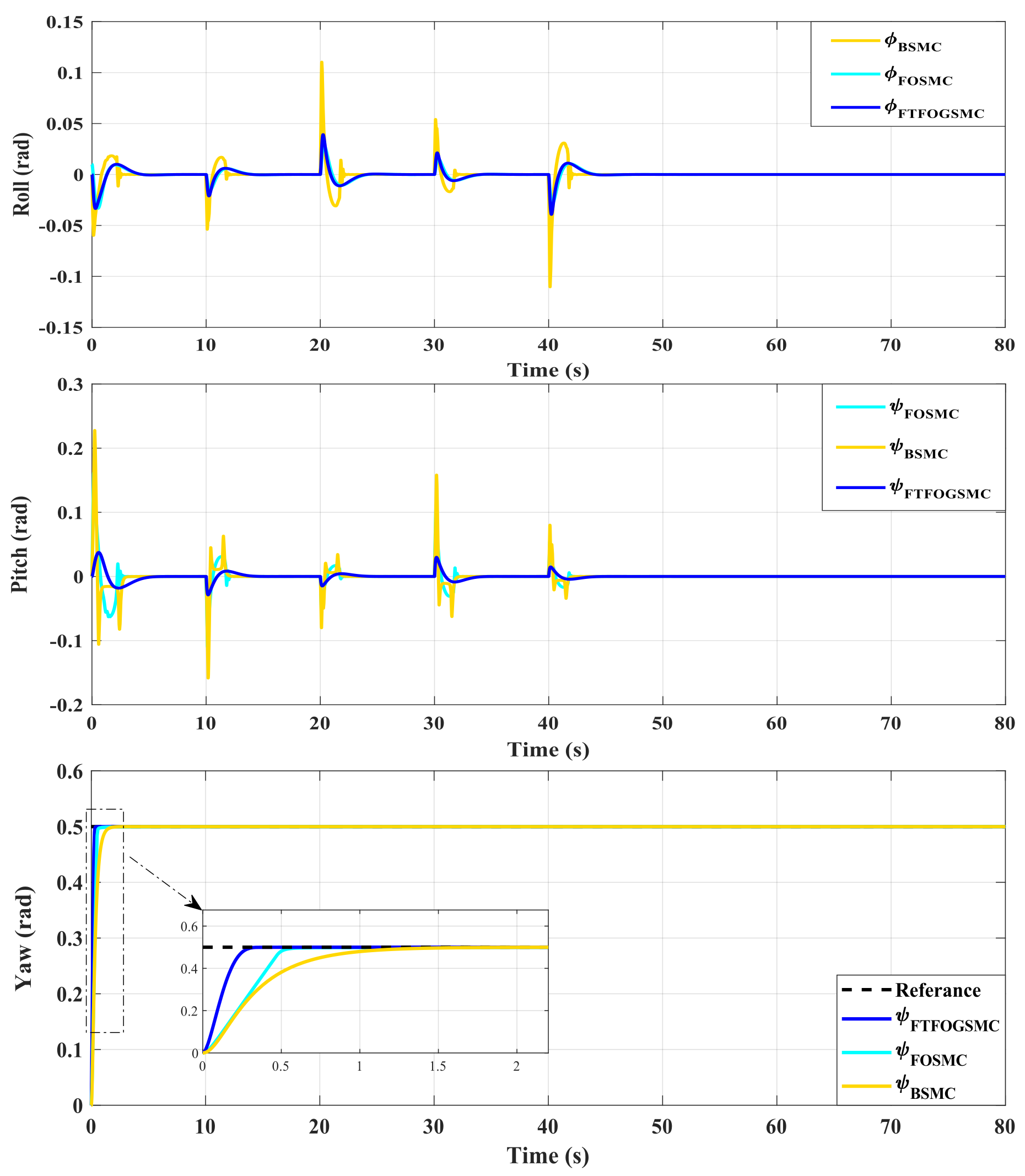
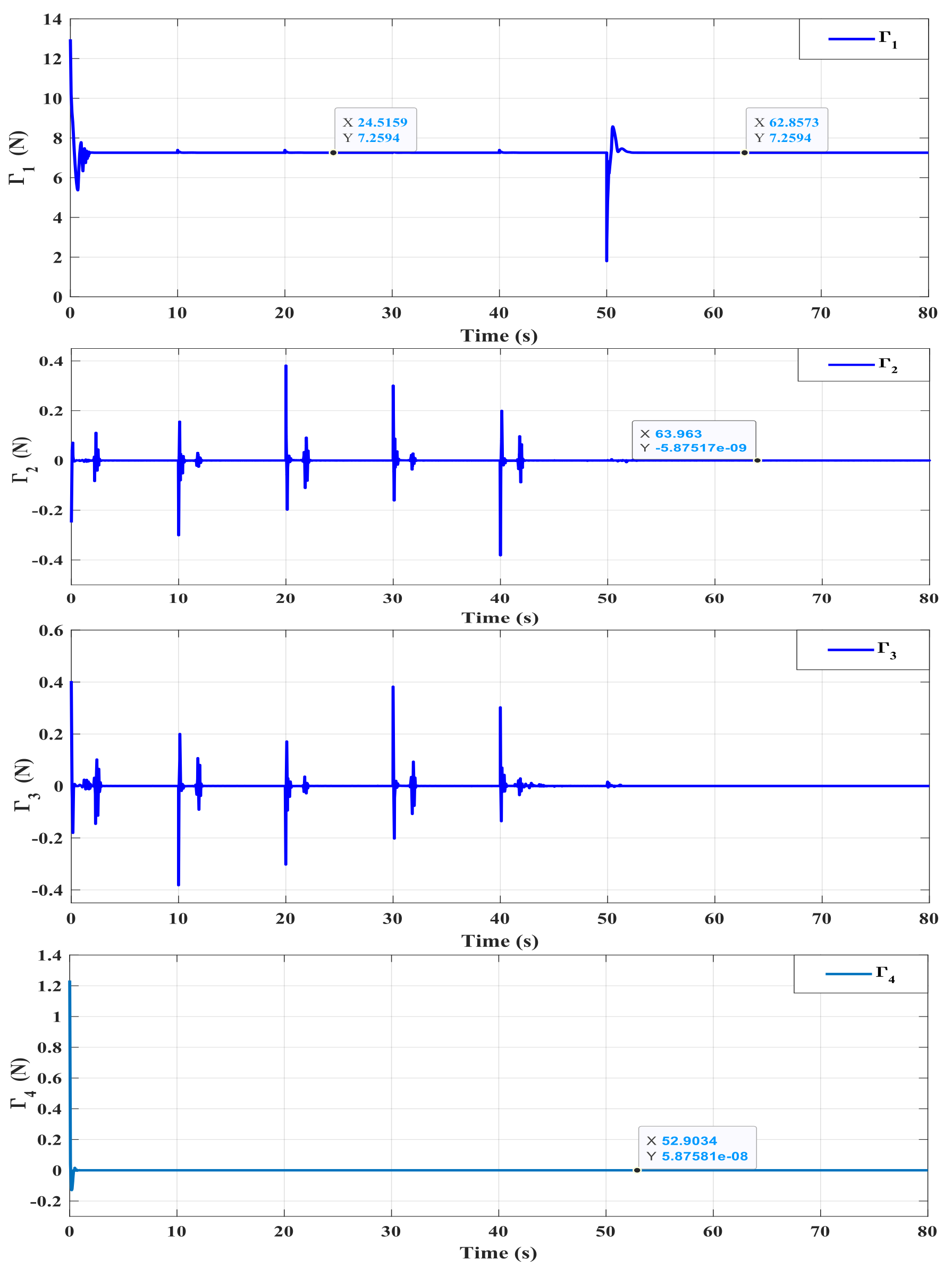
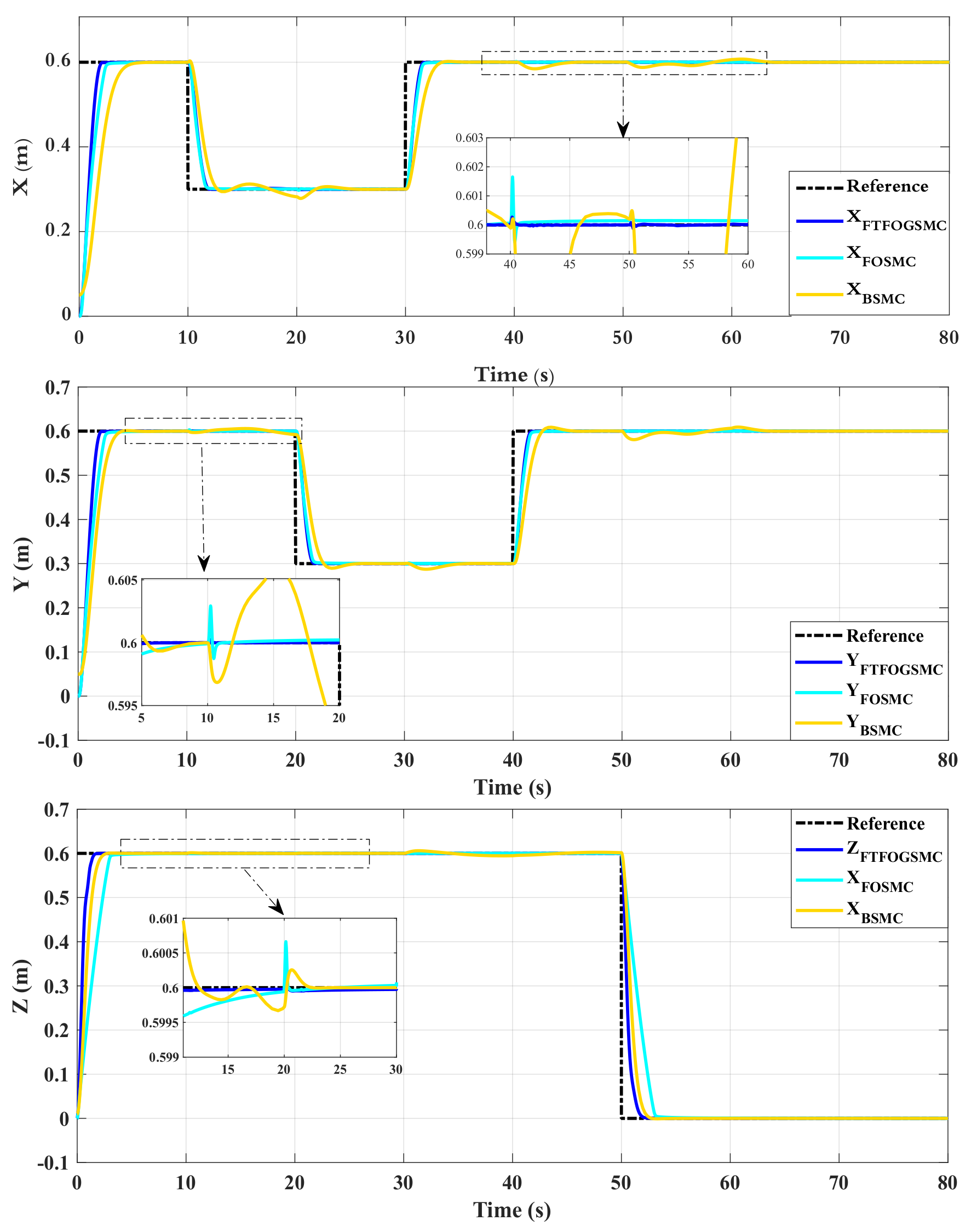
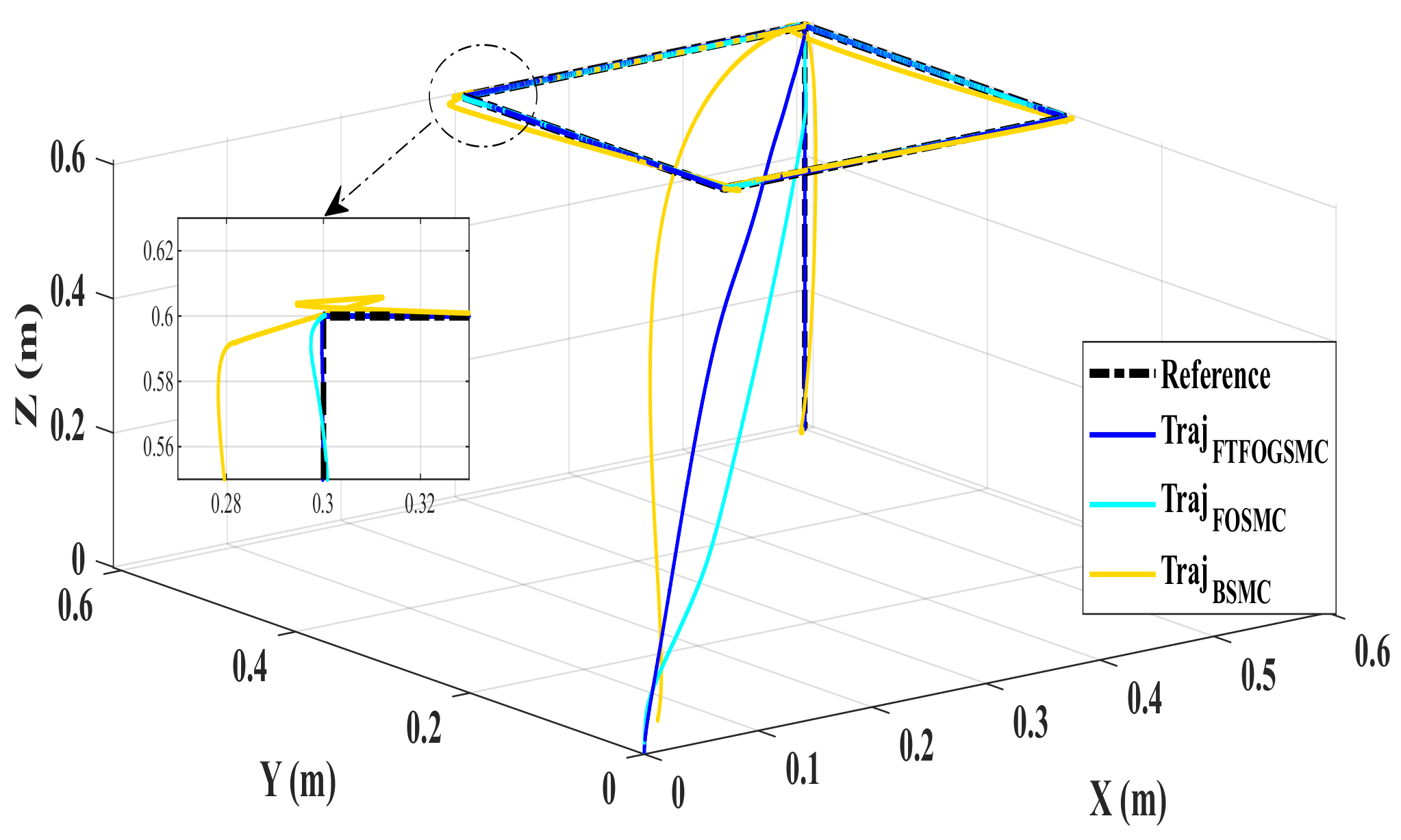
4. Simulation Results
- The Inertial Measurement Unit (IMU) consists of a gyroscope, a three-axis magnetometer, and an accelerometer.
- The GPS module uses horizontal plane measurements to determine the position and velocity. The altitude is measured via a magnetometer and a barometer.
- Communication between the quadrotor and the ground control station (GCS) is ensured by two Zigbee wireless modules.
- Digital signal processing (DSP) is used in the flight control system. The wind is generated by a fan and then applied as an external disturbance to the quadrotor.
- The flight parameters are saved onboard using a micro SD card.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, K.; Xia, Y. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence. Automatica 2013, 49, 3591–3599. [Google Scholar] [CrossRef]
- Xu, B. Composite learning finite-time control with application to quadrotors. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1806–1815. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Adaptive Fractional-Order Nonsingular Fast Terminal Sliding Mode Based Robust Tracking Control of Quadrotor UAV With Gaussian Random Disturbances and Uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2265–2277. [Google Scholar] [CrossRef]
- Labbadi, M.; Boukal, Y.; Cherkaoui, M.; Djemai, M. Fractional-order global sliding mode controller for an uncertain quadrotor UAVs subjected to external disturbances. J. Frankl. Inst. 2021, 358, 4822–4847. [Google Scholar] [CrossRef]
- Labbadi, M.; Boubaker, S.; Djemai, M.; Mekni, S.K.; Bekrar, A. Fixed-Time Fractional-Order Global Sliding Mode Control for Nonholonomic Mobile Robot Systems under External Disturbances. Fractal Fract. 2022, 6, 177. [Google Scholar] [CrossRef]
- Liu, D.; Li, T.; He, X. Fixed-Time Multi-Switch Combined–Combined Synchronization of Fractional-Order Chaotic Systems with Uncertainties and External Disturbances. Fractal Fract. 2023, 7, 281. [Google Scholar] [CrossRef]
- Idrissi, M.; Salami, M.; Annaz, F. A Review of Quadrotor Unmanned Aerial Vehicles: Applications, Architectural Design and Control Algorithms. J. Intell. Robot. Syst. 2022, 104, 22. [Google Scholar] [CrossRef]
- Huang, S.; Wang, J. Fixed-time fractional-order sliding mode control for nonlinear power systems. J. Vib. Control 2020, 26, 1425–1434. [Google Scholar] [CrossRef]
- Chen, L.; Fang, J. Adaptive Continuous Sliding Mode Control for Fractional-order Systems with Uncertainties and Unknown Control Gains. Int. J. Control Autom. Syst. 2022, 20, 1509–1520. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Fernández-Anaya, G.; Sánchez-Torres, J.D. Adaptive parallel fractional sliding mode control. Int. J. Adapt. Control Signal Process. 2021, 36, 751–759. [Google Scholar] [CrossRef]
- Nikdel, N.; Badamchizadeh, M.; Azimirad, V. Fractional-order adaptive backstepping control of robotic manipulators in the presence of model uncertainties and external disturbances. IEEE Trans. Ind. Electron. 2016, 63, 6249–6256. [Google Scholar] [CrossRef]
- Wang, J.; Ma, X.; Li, H.; Tian, B. Self-triggered sliding mode control for distributed formation of multiple quadrotors. J. Frankl. Inst. 2020, 357, 12223–12240. [Google Scholar] [CrossRef]
- Singh, P.; Gupta, S.; Behera, L.; Verma, N.K.; Nahavandi, S. Perching of Nano-Quadrotor Using Self-Trigger Finite-Time Second-Order Continuous Control. IEEE Syst. J. 2021, 15, 4989–4999. [Google Scholar] [CrossRef]
- Benaddy, A.; Labbadi, M.; Bouzi, M. Robust flight control for a quadrotor under external disturbances based on generic second order sliding mode control. IFAC-PapersOnLine 2022, 55, 270–275. [Google Scholar] [CrossRef]
- Giap, V.; Vu, H.; Nguyen, Q.; Huang, S.C. Chattering-free sliding mode control-based disturbance observer for MEMS gyroscope system. Microsyst. Technol. 2022, 28, 1867–1877. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X. Fractional order fixed-time nonsingular terminal sliding mode synchronization and control of fractional order chaotic systems. Nonlinear Dyn. 2017, 89, 2065–2083. [Google Scholar] [CrossRef]
- Aghababa, M.P. A fractional sliding mode for finite-time control scheme with application to stabilization of electrostatic and electromechanical transducers. Appl. Math. Model. 2015, 39, 6103–6113. [Google Scholar] [CrossRef]
- Lee, J.; Haddad, W.M. Fixed time stability and optimal stabilisation of discrete autonomous systems. Int. J. Control 2022, 96, 2341–2355. [Google Scholar] [CrossRef]
- Olguin-Roque, J.; Salazar, S.; Gonzalez-Hernandez, I.; Lozano, R. A Robust Fixed-Time Sliding Mode Control for Quadrotor UAV. Algorithms 2023, 16, 229. [Google Scholar] [CrossRef]
- Giap, V.N.; Nguyen, Q.D.; Trung, N.K.; Huang, S.C. Time-varying disturbance observer based on sliding-mode observer and double phases fixed-time sliding mode control for a T-S fuzzy micro-electro-mechanical system gyroscope. J. Vib. Control 2022, 29, 1927–1942. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X.; Li, S. Fast Fixed-Time Nonsingular Terminal Sliding Mode Control and Its Application to Chaos Suppression in Power System. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 151–155. [Google Scholar] [CrossRef]
- Su, Y. Comments on “Fixed-time sliding mode control with mismatched disturbances” [Automatica 136 (2022) 110009]. Automatica 2023, 151, 110916. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Scala, M.L. A Novel Distributed-Decentralized Fixed-Time Optimal Frequency and Excitation Control Framework in a Nonlinear Network-Preserving Power System. IEEE Trans. Power Syst. 2021, 36, 1285–1297. [Google Scholar] [CrossRef]
- Zeng, T.; Ren, X.; Zhang, Y. Fixed-Time Sliding Mode Control and High-Gain Nonlinearity Compensation for Dual-Motor Driving System. IEEE Trans. Ind. Informatics 2020, 16, 4090–4098. [Google Scholar] [CrossRef]
- Shirkavand, M.; Pourgholi, M. Robust fixed-time synchronization of fractional order chaotic using free chattering nonsingular adaptive fractional sliding mode controller design. Chaos Solitons Fractals 2018, 113, 135–147. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Fernández-Anaya, G.; Sánchez-Torres, J.D.; Meléndez-Vázquez, F. Predefined-time control of distributed-order systems. Nonlinear Dyn. 2021, 103, 2689–2700. [Google Scholar] [CrossRef]
- Huang, S.; Xiong, L.; Wang, J.; Li, P.; Wang, Z.; Ma, M. Fixed-Time Fractional-Order Sliding Mode Controller for Multimachine Power Systems. IEEE Trans. Power Syst. 2021, 36, 2866–2876. [Google Scholar] [CrossRef]
- Podlubny, I.; Ivo, P.; Blas, M.; Paul, O.; Dorcak, L. Analogue realizations of fractional-order controllers. Nonlinear Dyn. 2002, 29, 281–296. [Google Scholar] [CrossRef]
- Asignacion, A.; Suzuki, S.; Noda, R.; Nakata, T.; Liu, H. Frequency-Based Wind Gust Estimation for Quadrotors Using a Nonlinear Disturbance Observer. IEEE Robot. Autom. Lett. 2022, 7, 9224–9231. [Google Scholar] [CrossRef]
- Sanchez-Cuevas, P.; Heredia, G.; Ollero, A. Characterization of the Aerodynamic Ground Effect and Its Influence in Multirotor Control. Int. J. Aerosp. Eng. 2017, 2017, 1823056. [Google Scholar] [CrossRef]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-Varying Formation Tracking for Second-Order Multi-Agent Systems Subjected to Switching Topologies With Application to Quadrotor Formation Flying. IEEE Trans. Ind. Electron. 2017, 64, 5014–5024. [Google Scholar] [CrossRef]



| Symbol | Value | Unit |
|---|---|---|
| m | ||
| g | ||
| l | ||
| Symbol | Value | Symbol | Value | Symbol | Value |
|---|---|---|---|---|---|
| 12 | |||||
| ℵ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benaddy, A.; Labbadi, M.; Elyaalaoui, K.; Bouzi, M. Fixed-Time Fractional-Order Sliding Mode Control for UAVs under External Disturbances. Fractal Fract. 2023, 7, 775. https://doi.org/10.3390/fractalfract7110775
Benaddy A, Labbadi M, Elyaalaoui K, Bouzi M. Fixed-Time Fractional-Order Sliding Mode Control for UAVs under External Disturbances. Fractal and Fractional. 2023; 7(11):775. https://doi.org/10.3390/fractalfract7110775
Chicago/Turabian StyleBenaddy, Abdellah, Moussa Labbadi, Kamal Elyaalaoui, and Mostafa Bouzi. 2023. "Fixed-Time Fractional-Order Sliding Mode Control for UAVs under External Disturbances" Fractal and Fractional 7, no. 11: 775. https://doi.org/10.3390/fractalfract7110775
APA StyleBenaddy, A., Labbadi, M., Elyaalaoui, K., & Bouzi, M. (2023). Fixed-Time Fractional-Order Sliding Mode Control for UAVs under External Disturbances. Fractal and Fractional, 7(11), 775. https://doi.org/10.3390/fractalfract7110775








