Adaptive Fault-Tolerant Control for Consensus of Nonlinear Fractional-Order Multi-Agent Systems with Diffusion
Abstract
:1. Introduction
2. Problem Formulation
2.1. System Dynamics Model
2.2. Actuator Fault Model
3. Consensus of Leaderless the PDEFOMAS through Adaptive Fault-Tolerant Control Protocol
4. Consensus of the Leader-Following PDEFOMAS through Adaptive Fault-Tolerant Control Protocols
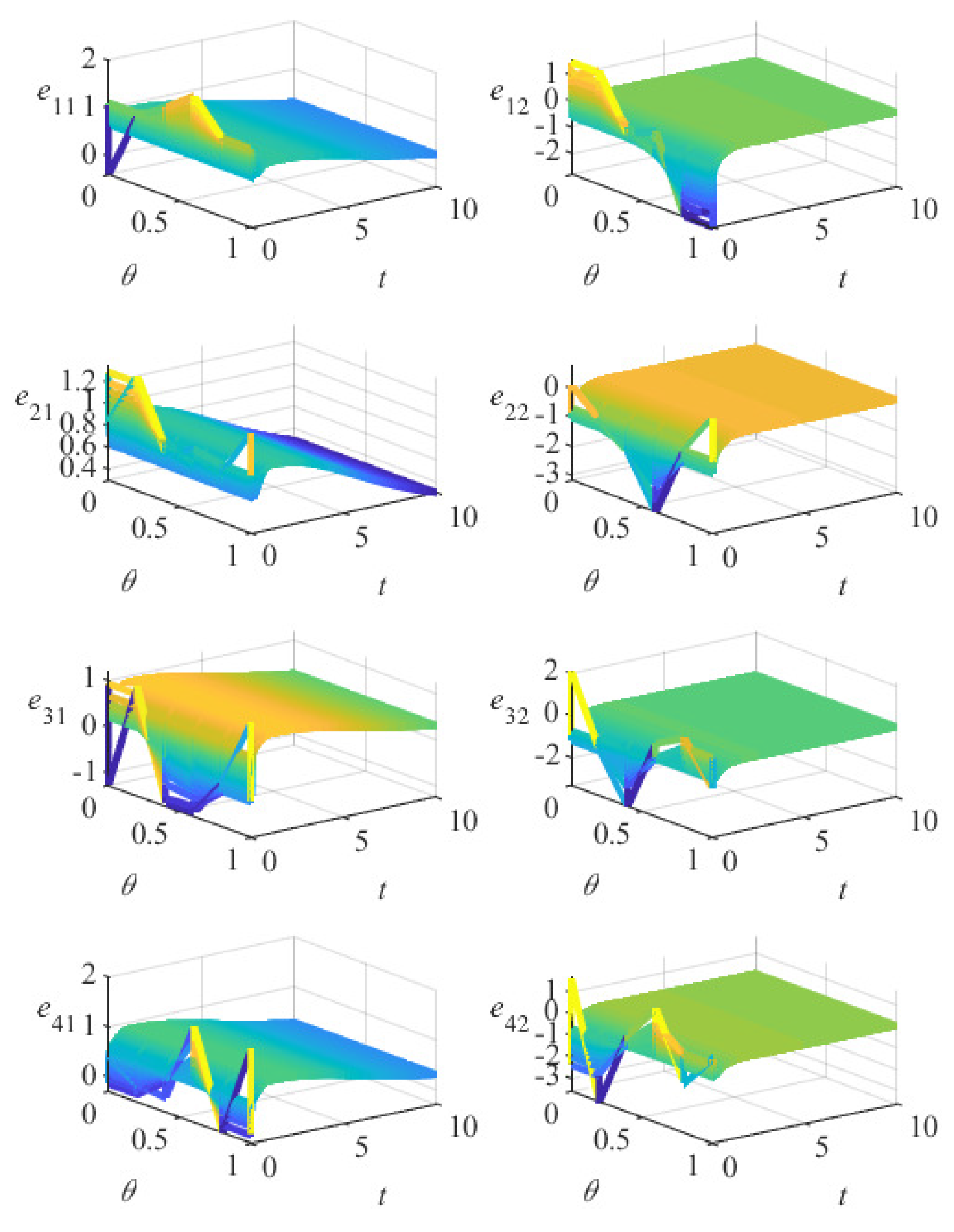
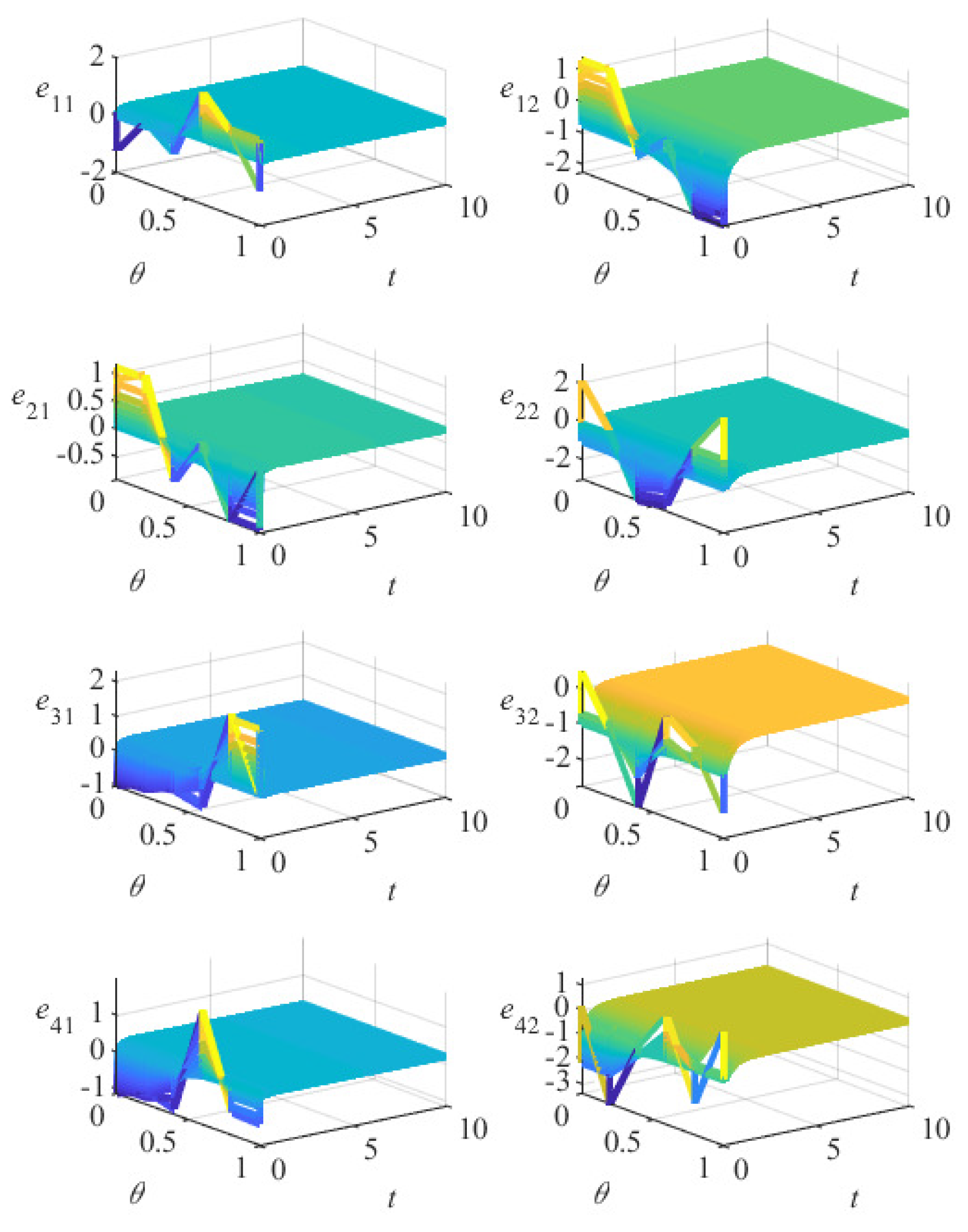
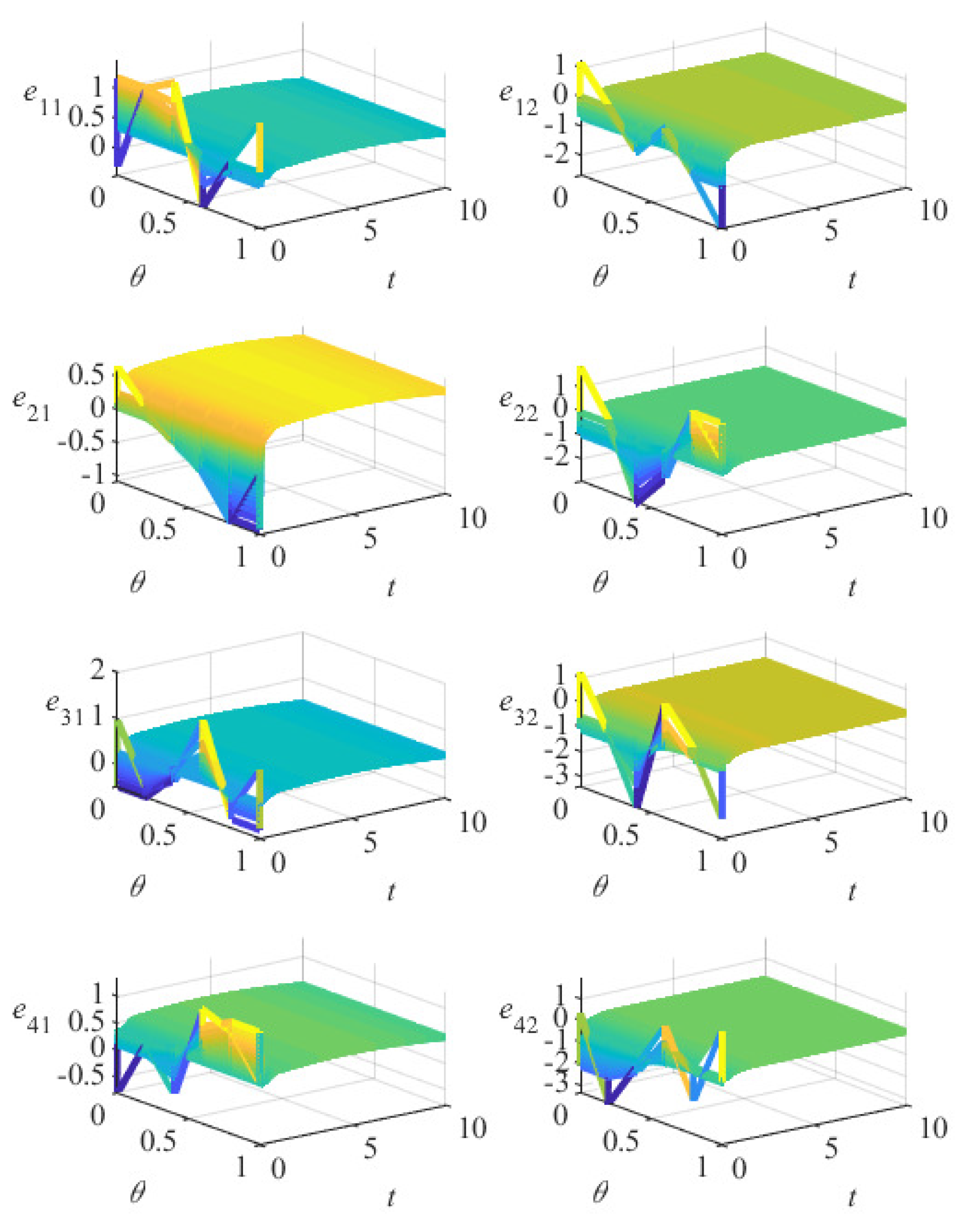
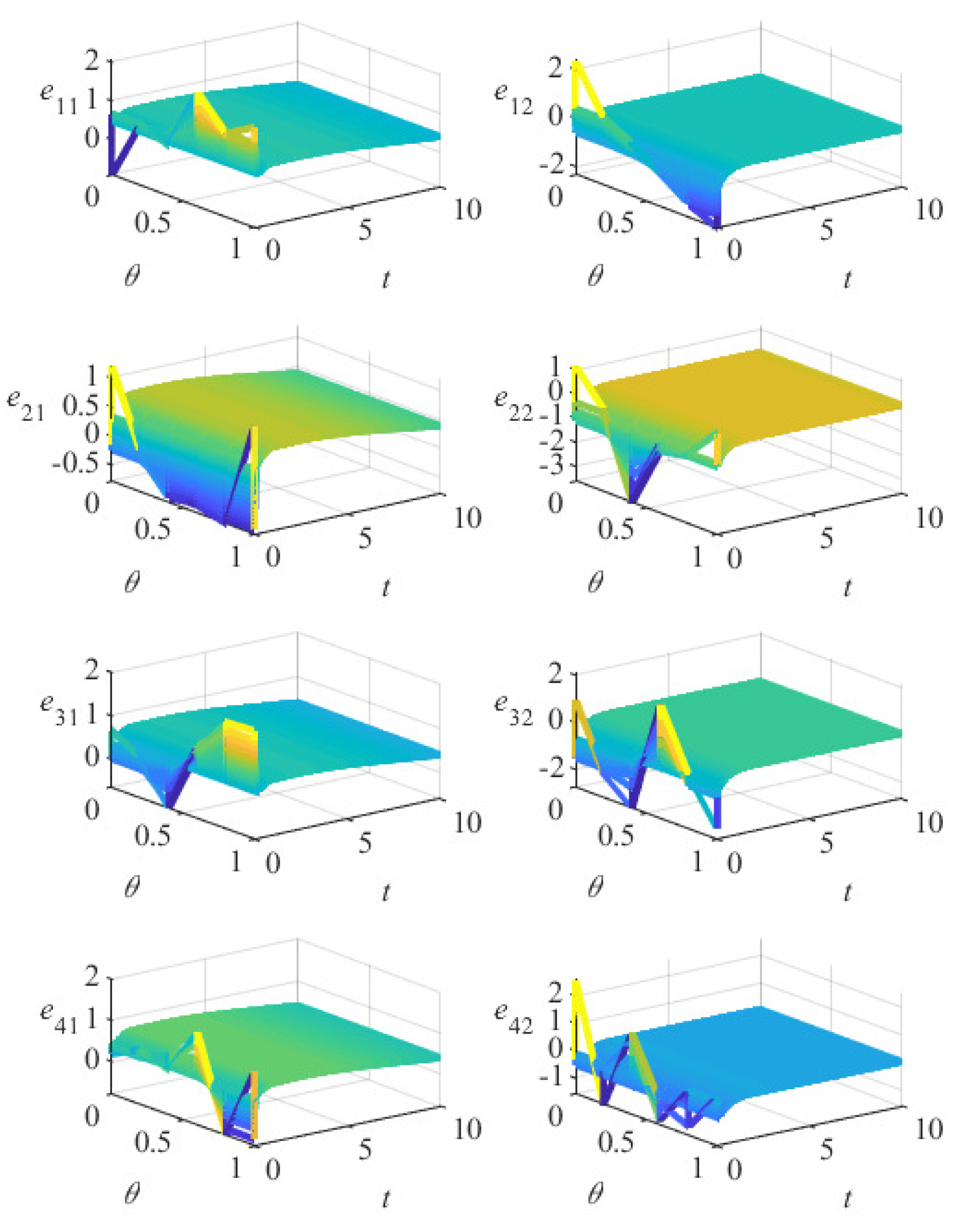
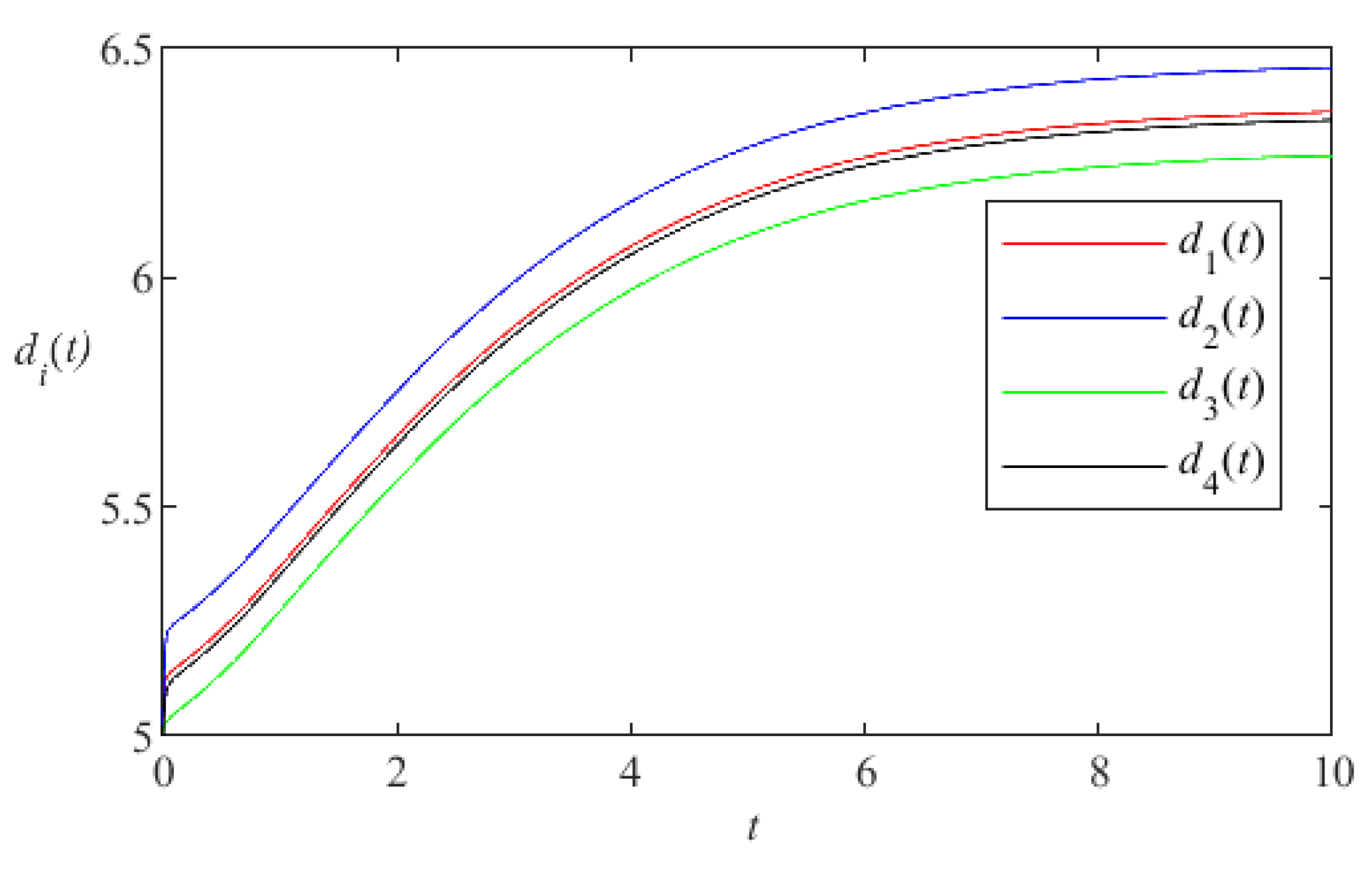
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Y.; Peng, S.; Dong, X.; Li, Q.; Ren, Z. UIF-based cooperative tracking method for multi-agent systems with sensor faults. Sci. China Inf. Sci. 2019, 62, 10202. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Guo, Y. Relative position coordinated control for spacecraft formation flying with obstacle/collision avoidance. Nonlinear Dyn. 2021, 104, 1329–1342. [Google Scholar] [CrossRef]
- Wang, C.; Yan, C.; Liu, Z. Leader-following consensus for second-order nonlinear multi-agent systems under Markovian switching topologies with application to ship course-keeping. Int. J. Control. Autom. Syst. 2021, 19, 54–62. [Google Scholar] [CrossRef]
- Yuchao, Z.; Yuan, J.; Jiyang, D. Dynamic Obstacle Avoidance Control of Three-order Multi-robot Cooperative Formation. J. Syst. Simul. 2022, 34, 1762. [Google Scholar]
- Zhao, Q.; Jiang, J. Reliable state feedback control system design against actuator failures. Automatica 1998, 34, 1267–1272. [Google Scholar] [CrossRef]
- Bounemeur, A.; Chemachema, M.; Essounbouli, N. Indirect adaptive fuzzy fault-tolerant tracking control for MIMO nonlinear systems with actuator and sensor failures. ISA Trans. 2018, 79, 45–61. [Google Scholar] [CrossRef]
- Maybeck, P.S. Multiple model adaptive algorithms for detecting and compensating sensor and actuator/surface failures in aircraft flight control systems. Int. J. Robust Nonlinear Control 1999, 9, 1051–1070. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M.; Schröder, J. Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Yin, S.; Luo, H.; Ding, S.X. Real-time implementation of fault-tolerant control systems with performance optimization. IEEE Trans. Ind. Electron. 2013, 61, 2402–2411. [Google Scholar] [CrossRef]
- Khalili, M.; Zhang, X.; Polycarpou, M.M.; Parisini, T.; Cao, Y. Distributed adaptive fault-tolerant control of uncertain multi-agent systems. Automatica 2018, 87, 142–151. [Google Scholar] [CrossRef]
- Deng, C.; Yang, G.H. Distributed adaptive fault-tolerant control approach to cooperative output regulation for linear multi-agent systems. Automatica 2019, 103, 62–68. [Google Scholar] [CrossRef]
- Liu, F.; Hua, Y.; Dong, X.; Li, Q.; Ren, Z. Adaptive fault-tolerant time-varying formation tracking for multi-agent systems under actuator failure and input saturation. ISA Trans. 2020, 104, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, J. Fault-tolerant tracking control for a class of nonlinear multi-agent systems. Syst. Control Lett. 2020, 135, 104576. [Google Scholar] [CrossRef]
- Dong, S.; Chen, G.; Liu, M.; Wu, Z.G. Cooperative neural-adaptive fault-tolerant output regulation for heterogeneous nonlinear uncertain multiagent systems with disturbance. Sci. China Inf. Sci. 2021, 64, 172212. [Google Scholar] [CrossRef]
- Yadegar, M.; Meskin, N. Fault-tolerant control of nonlinear heterogeneous multi-agent systems. Automatica 2021, 127, 109514. [Google Scholar] [CrossRef]
- Wang, J.W.; Wang, J.M. Spatiotemporal adaptive state feedback control of a linear parabolic partial differential equation. Int. J. Robust Nonlinear Control 2023, 33, 3850–3873. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Y.; Wang, J.W.; Li, H.X. Backstepping-based distributed abnormality localization for linear parabolic distributed parameter systems. Automatica 2022, 135, 109930. [Google Scholar] [CrossRef]
- Christofides, P.D.; Chow, J. Nonlinear and robust control of PDE systems: Methods and applications to transport-reaction processes. Appl. Mech. Rev. 2002, 55, B29–B30. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, X.; Liu, Q. Model predictive control of a dynamic nonlinear PDE system with application to continuous casting. J. Process Control 2018, 65, 41–55. [Google Scholar] [CrossRef]
- Lou, Y.; Christofides, P.D. Nonlinear feedback control of surface roughness using a stochastic PDE: Design and application to a sputtering process. Ind. Eng. Chem. Res. 2006, 45, 7177–7189. [Google Scholar] [CrossRef]
- Sidhu, H.S.; Narasingam, A.; Siddhamshetty, P.; Kwon, J.S.I. Model order reduction of nonlinear parabolic PDE systems with moving boundaries using sparse proper orthogonal decomposition: Application to hydraulic fracturing. Comput. Chem. Eng. 2018, 112, 92–100. [Google Scholar] [CrossRef]
- Panjapornpon, C.; Limpanachaipornkul, P.; Charinpanitkul, T. Control of coupled PDEs–ODEs using input–output linearization: Application to a cracking furnace. Chem. Eng. Sci. 2012, 75, 144–151. [Google Scholar] [CrossRef]
- Dai, J.; Yang, C.; Yan, X.; Wang, J.; Zhu, K.; Yang, C. Leaderless consensus control of nonlinear PIDE-type multi-agent systems with time delays. IEEE Access 2022, 10, 21211–21218. [Google Scholar] [CrossRef]
- Yang, C.; Huang, T.; Li, Z.; Zhang, A.; Qiu, J.; Alsaadi, F.E. Boundary control for exponential stabilization of nonlinear distributed parameter systems modeled by PIDEs. IEEE Access 2018, 6, 47889–47896. [Google Scholar] [CrossRef]
- Yang, C.; Li, Z.; Chen, X.; Zhang, A.; Qiu, J. Boundary control for exponential synchronization of reaction-diffusion neural networks based on coupled PDE-ODEs. IFAC-PapersOnLine 2020, 53, 3415–3420. [Google Scholar] [CrossRef]
- Li, Y.X.; Wang, Q.Y.; Tong, S. Fuzzy adaptive fault-tolerant control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1372–1379. [Google Scholar] [CrossRef]
- Gong, P.; Lan, W.; Han, Q.L. Robust adaptive fault-tolerant consensus control for uncertain nonlinear fractional-order multi-agent systems with directed topologies. Automatica 2020, 117, 109011. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, F.; Che, W.W. Distributed adaptive fuzzy fault-tolerant control for multi-agent systems with node faults and denial-of-service attacks. Inf. Sci. 2023, 631, 385–395. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, S.; Ahn, C.K.; Xie, Y. Adaptive neural consensus for fractional-order multi-agent systems with faults and delays. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7873–7886. [Google Scholar] [CrossRef]
- Zhang, J.; Tong, S. Event-triggered fuzzy adaptive output feedback containment fault-tolerant control for nonlinear multi-agent systems against actuator faults. Eur. J. Control 2023, In Press, 100887. [Google Scholar] [CrossRef]
- Ferdi, Y. Some applications of fractional order calculus to design digital filters for biomedical signal processing. J. Mech. Med. Biol. 2012, 12, 1240008. [Google Scholar] [CrossRef]
- Ma, C.; Hori, Y. Fractional-order control: Theory and applications in motion control past and present. IEEE Ind. Electron. Mag. 2007, 1, 6–16. [Google Scholar] [CrossRef]
- Kumar, S.; Saxena, R.; Singh, K. Fractional Fourier transform and fractional-order calculus-based image edge detection. Circuits Syst. Signal Process. 2017, 36, 1493–1513. [Google Scholar] [CrossRef]
- Jamil, A.A.; Tu, W.F.; Ali, S.W.; Terriche, Y.; Guerrero, J.M. Fractional-order PID controllers for temperature control: A review. Energies 2022, 15, 3800. [Google Scholar] [CrossRef]
- Yan, X.; Yang, C.; Cao, J.; Korovin, I.; Gorbachev, S.; Gorbacheva, N. Boundary consensus control strategies for fractional-order multi-agent systems with reaction-diffusion terms. Inf. Sci. 2022, 616, 461–473. [Google Scholar] [CrossRef]
- Yan, X.; Yang, C.; Yang, Y.; Wang, X.; Li, Z.; Huang, T. Boundary control for synchronization of fractional-order complex spatiotemporal networks based on PDEs with multiple delays and its application in image encryption. J. Frankl. Inst. 2023, 360, 5267–5291. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, C.; Yang, Y.; Li, N. Observer-based consensus of fractional order parabolic PDEs agents on directed networks via boundary communication. Chaos Solitons Fractals 2023, 170, 113332. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Tversky, A.; Gati, I. Similarity, separability, and the triangle inequality. Psychol. Rev. 1982, 89, 123. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, H. Bipartite consensus for multi-agent networks of fractional diffusion PDEs via aperiodically intermittent boundary control. Math. Biosci. Eng. 2023, 20, 12649–12665. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Qi, Q.; Hu, J.; Dai, J.; Yang, C. Adaptive Fault-Tolerant Control for Consensus of Nonlinear Fractional-Order Multi-Agent Systems with Diffusion. Fractal Fract. 2023, 7, 760. https://doi.org/10.3390/fractalfract7100760
Yang Y, Qi Q, Hu J, Dai J, Yang C. Adaptive Fault-Tolerant Control for Consensus of Nonlinear Fractional-Order Multi-Agent Systems with Diffusion. Fractal and Fractional. 2023; 7(10):760. https://doi.org/10.3390/fractalfract7100760
Chicago/Turabian StyleYang, Yuqian, Qingwen Qi, Jingyao Hu, Jiashu Dai, and Chengdong Yang. 2023. "Adaptive Fault-Tolerant Control for Consensus of Nonlinear Fractional-Order Multi-Agent Systems with Diffusion" Fractal and Fractional 7, no. 10: 760. https://doi.org/10.3390/fractalfract7100760
APA StyleYang, Y., Qi, Q., Hu, J., Dai, J., & Yang, C. (2023). Adaptive Fault-Tolerant Control for Consensus of Nonlinear Fractional-Order Multi-Agent Systems with Diffusion. Fractal and Fractional, 7(10), 760. https://doi.org/10.3390/fractalfract7100760






