Comparisons for Global Dynamics of a Geometrically Nonlinear Oscillator among Single-, Double- and Quadruple-Well Configurations
Abstract
1. Introduction
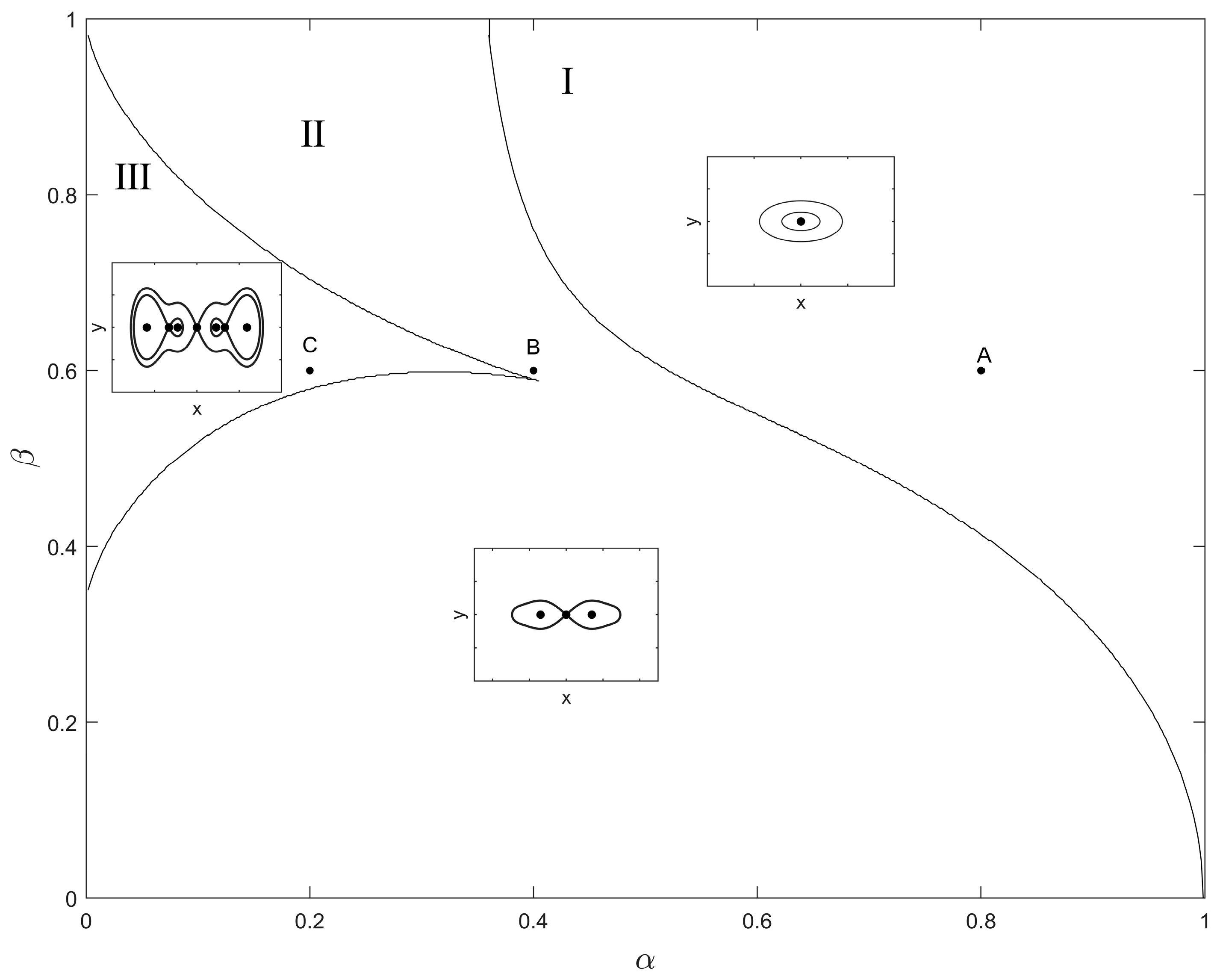
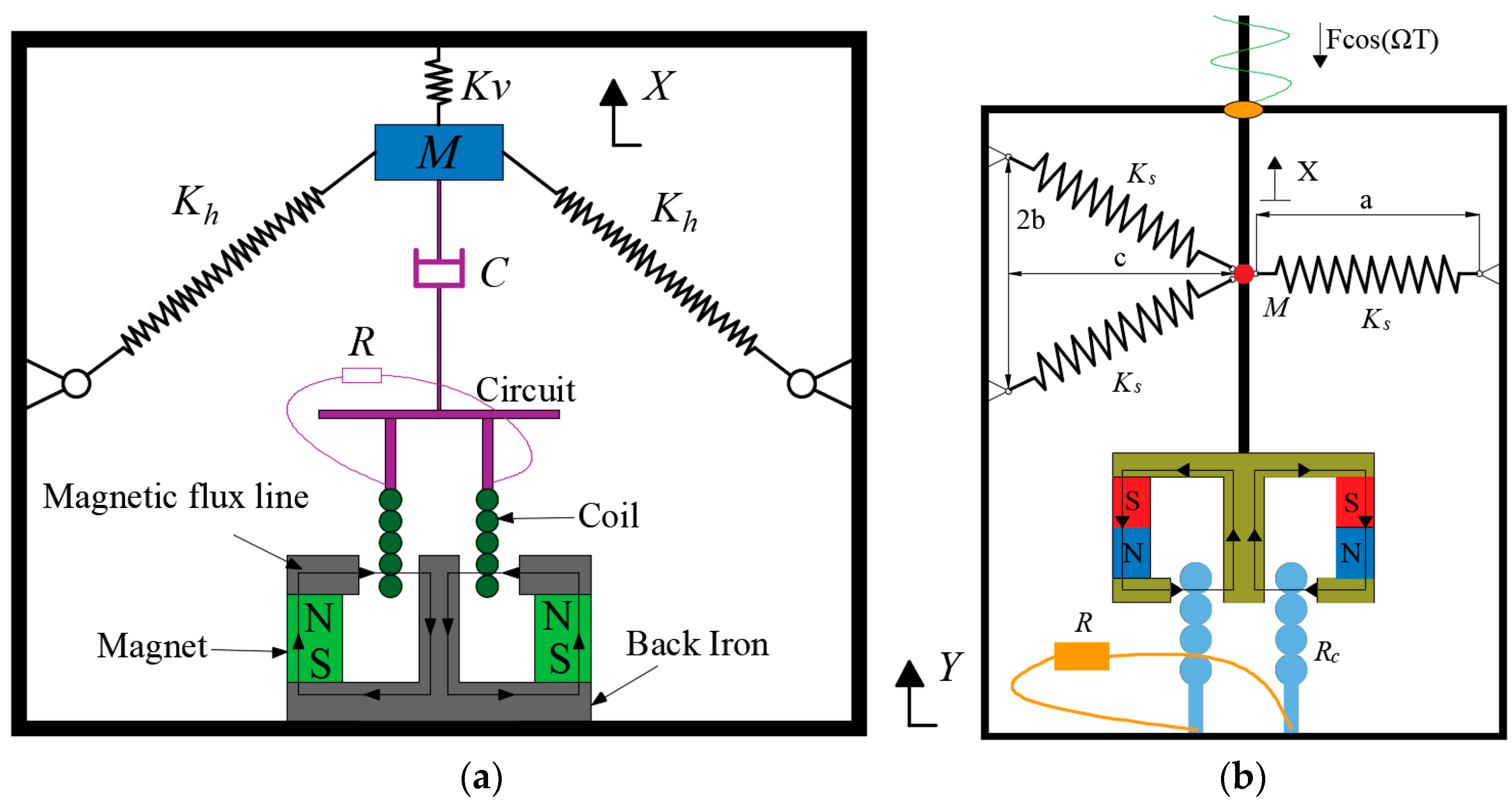
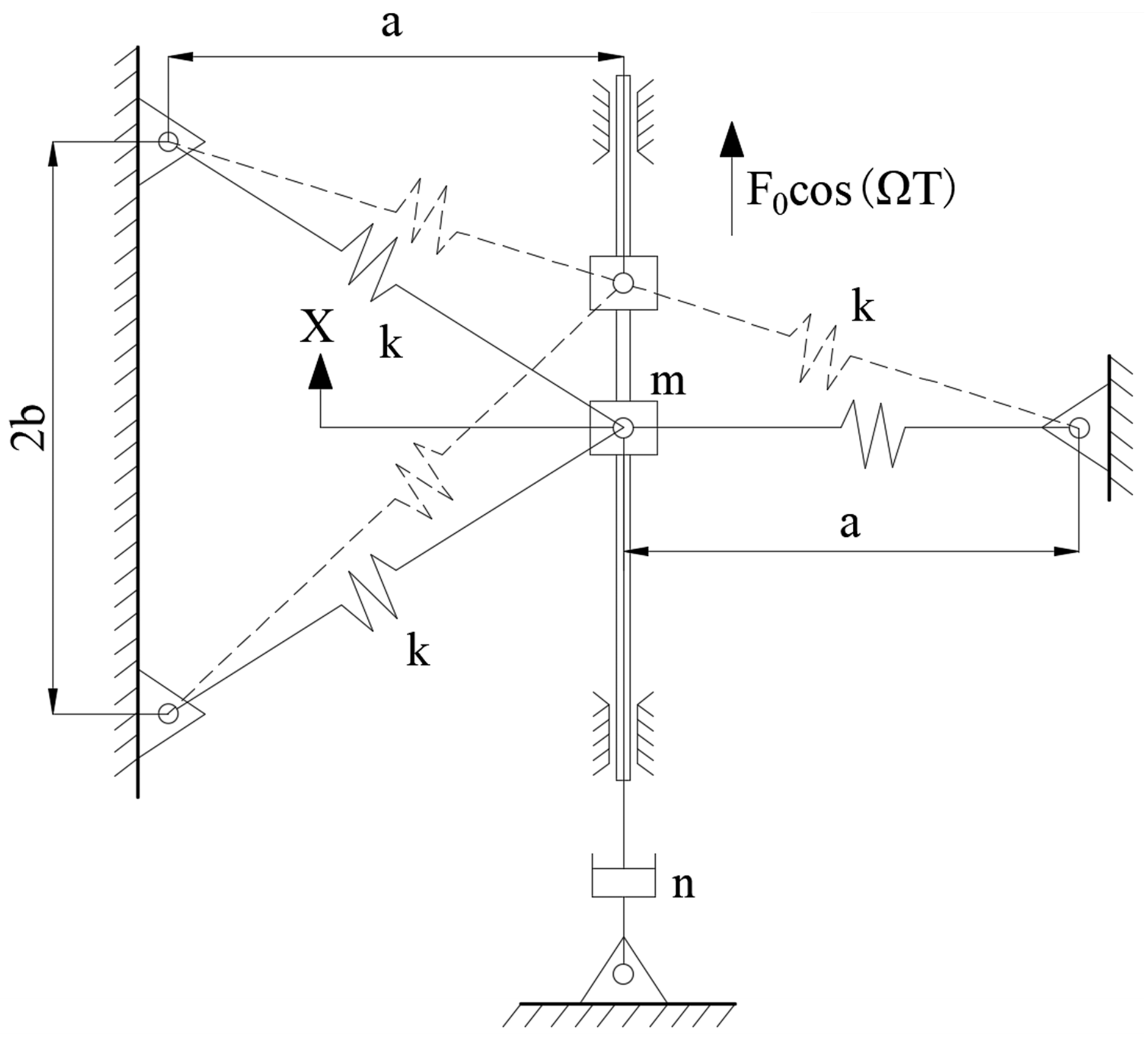
2. Dynamical Model and Unperturbed Dynamics
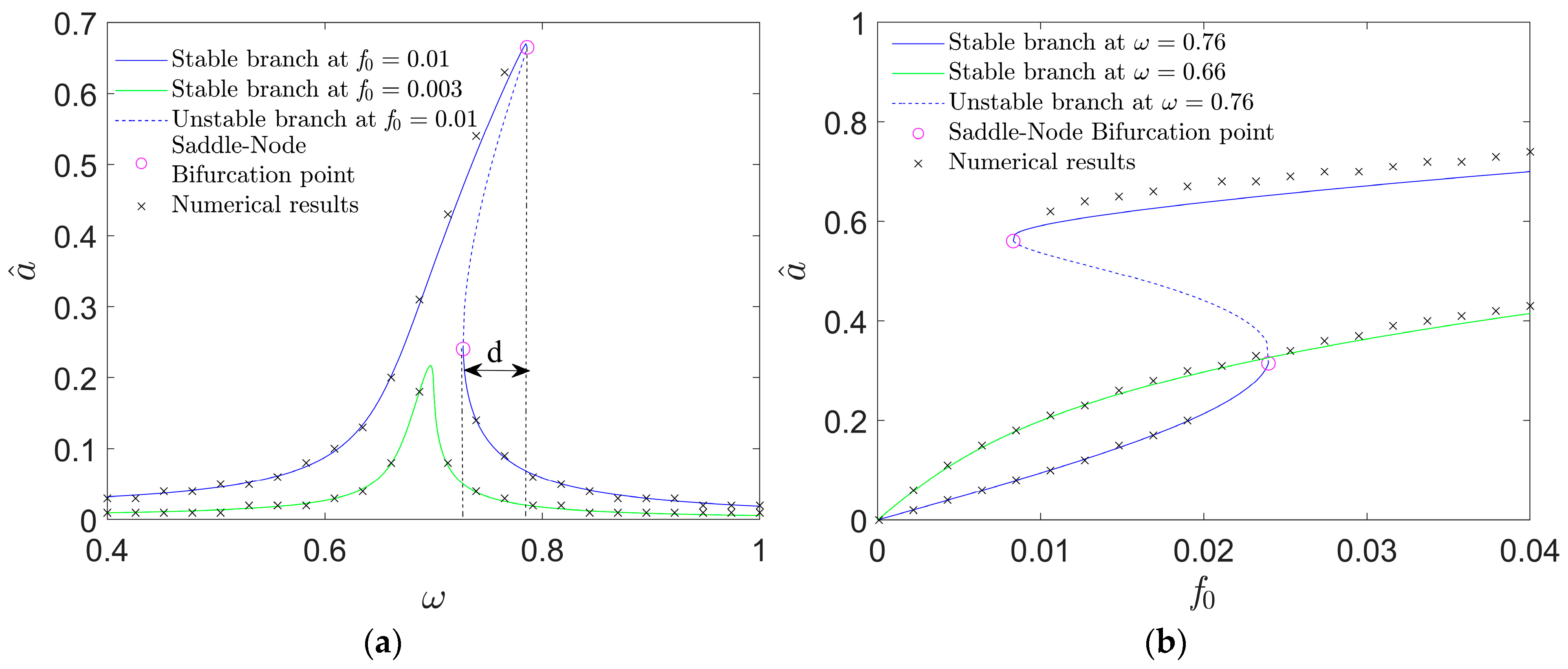
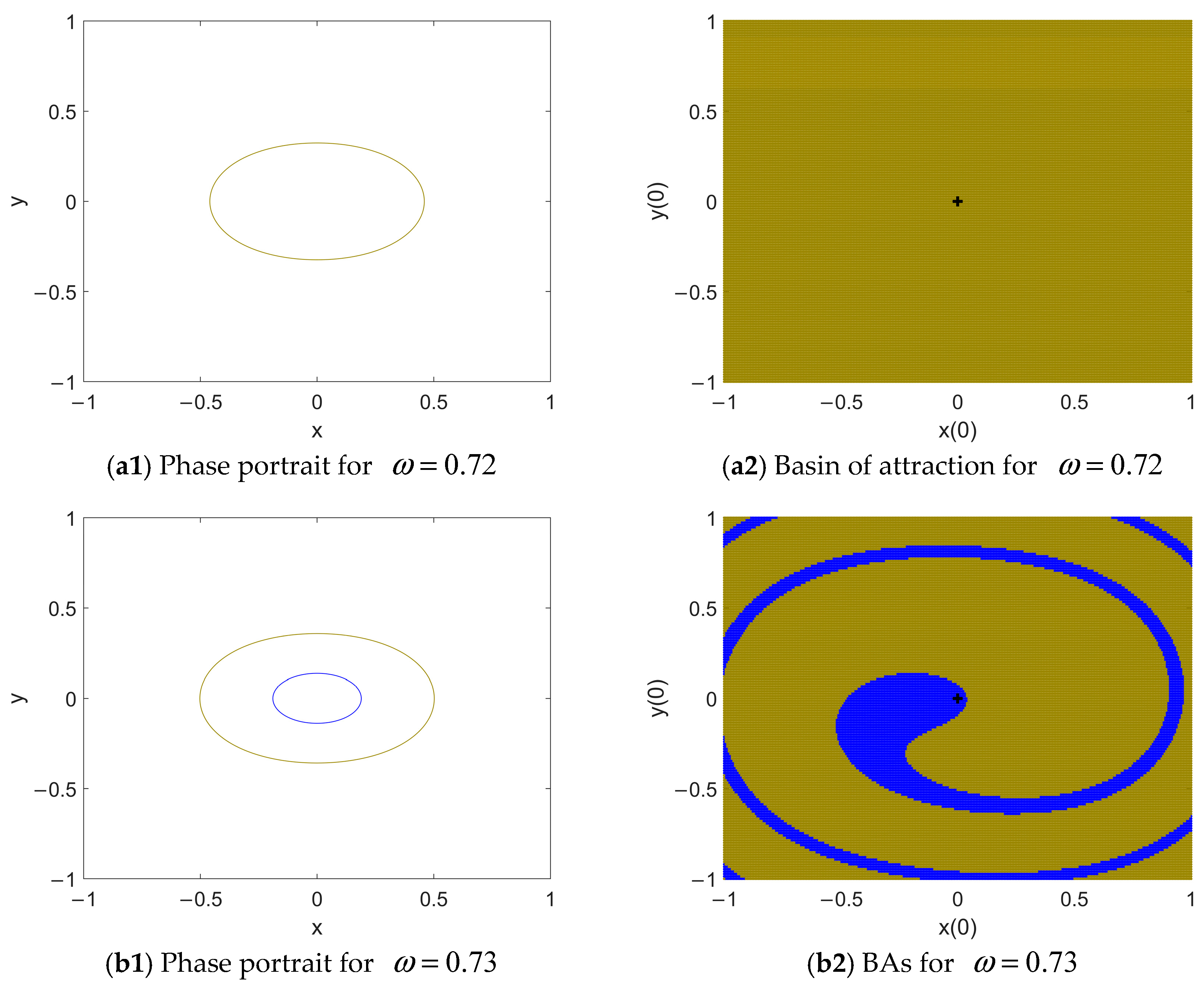
3. Periodic Responses in the Case of Single Potential Well
4. Periodic Responses in the Case of Double Potential Wells
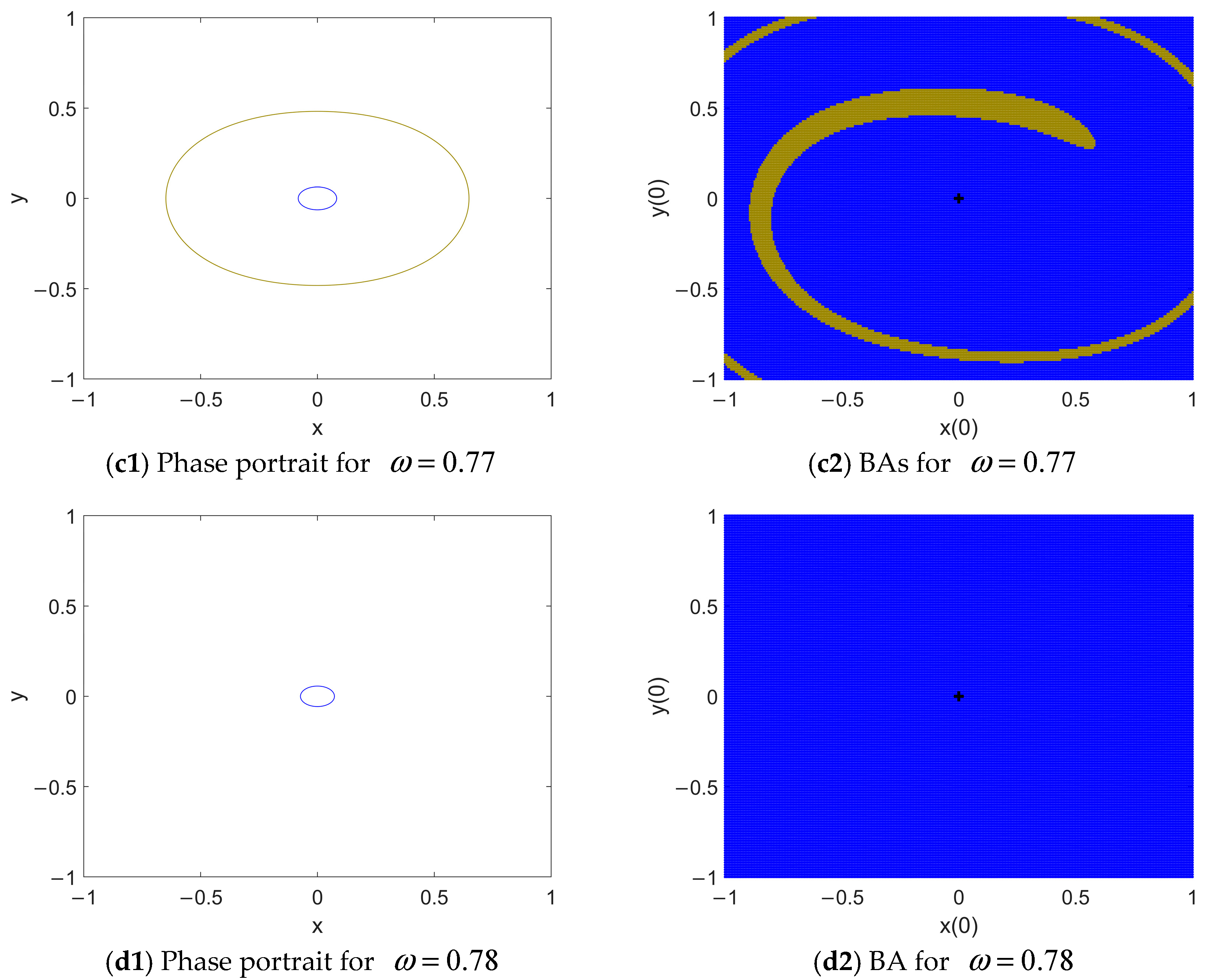
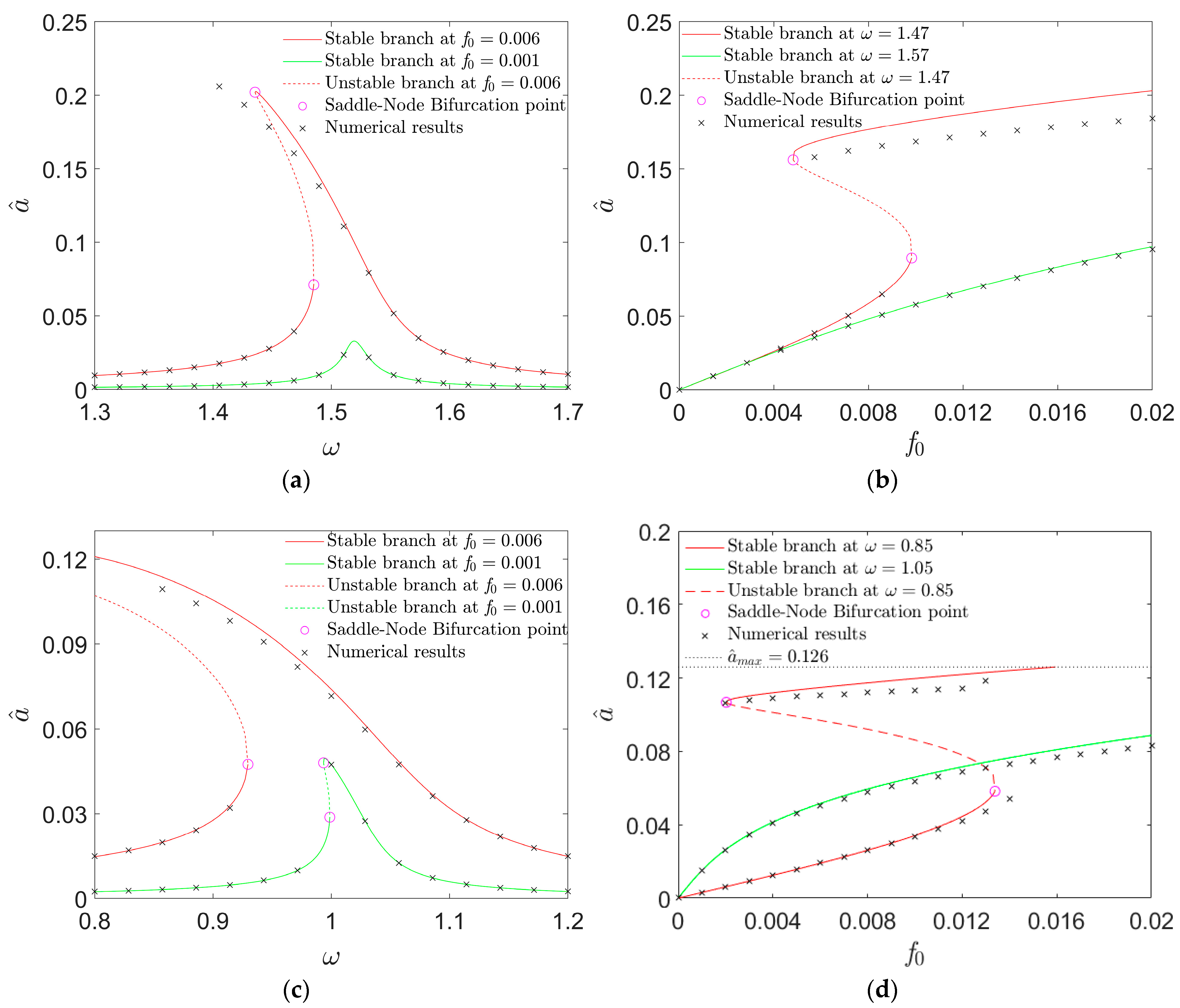
4.1. Intra-Well Resonant Responses
4.2. Inter-Well Periodic Solutions in the Case of Double Potential Wells
4.3. Coexisting Responses and Their Basins of Attraction
5. Periodic Responses in the Case of Quadruple Potential Wells
5.1. Resonant Responses around the Centers
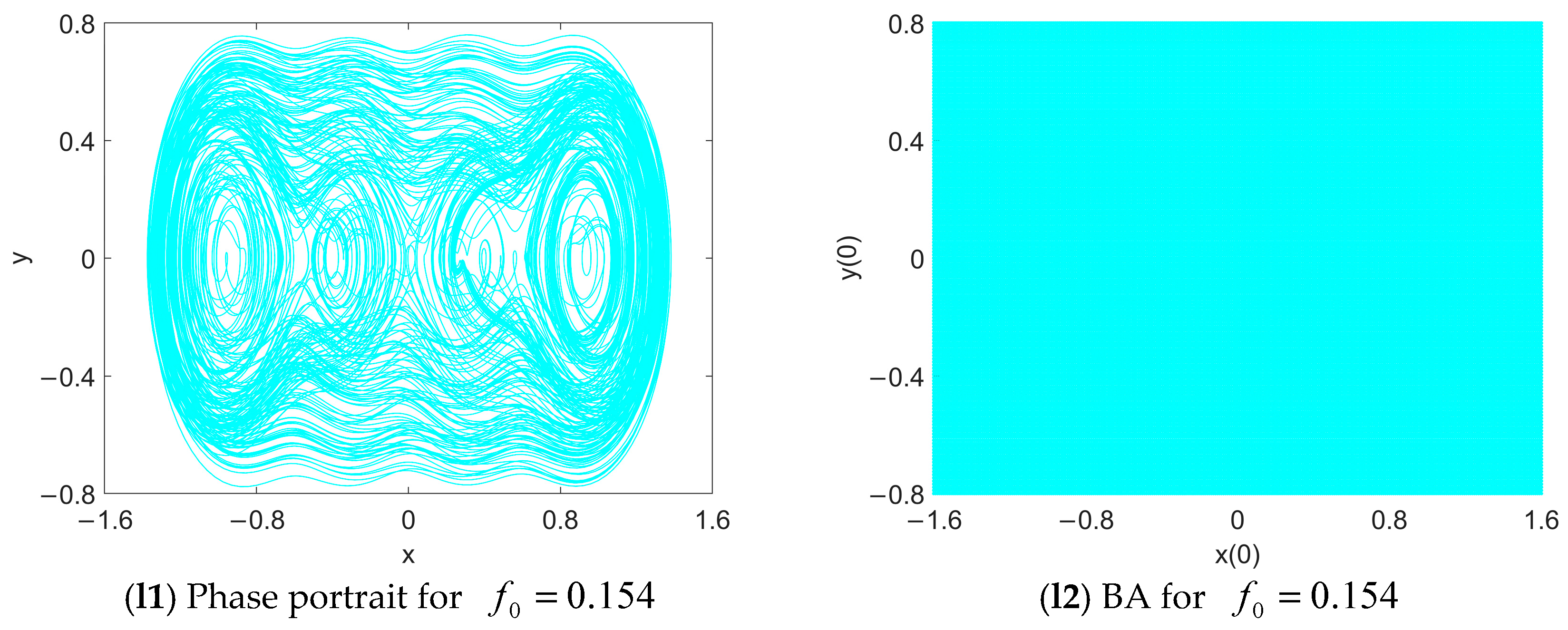
5.2. Coexisting Attractors and Their Basins of Attraction
6. Conclusions
- (1)
- With the decrease in the horizontal distance between the collar and each fixed pin, the system may undergo single, double and quadruple potential wells successively.
- (2)
- The resonant response in the case of single potential wells displays the stiffness–hardening characteristic, while the intra-well resonant responses in the cases of double and quadruple potential wells display the stiffness–softening characteristic.
- (3)
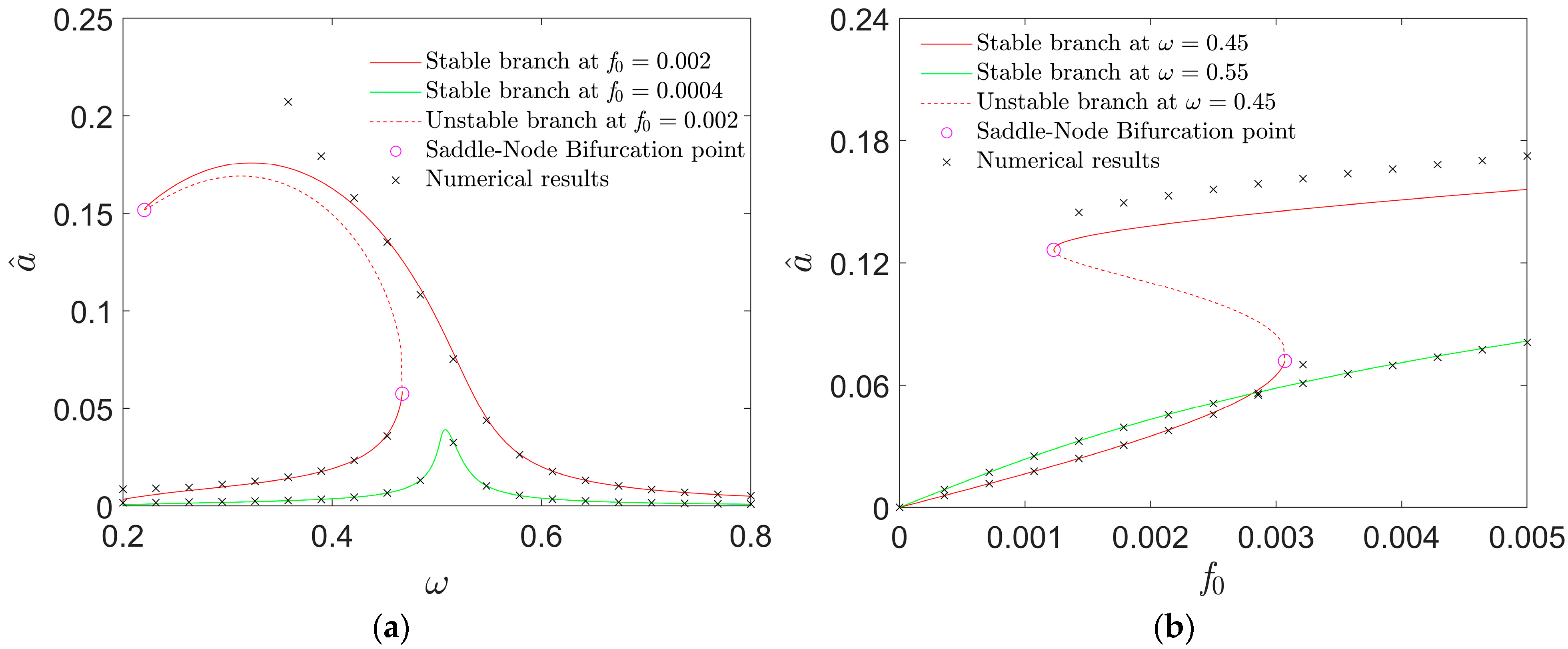
- Bistable responses in the vicinity of each well center can be triggered by the variation in the excitation frequency or level due to saddle-node bifurcations of the resonant solutions.
- (4)
- The double-well configuration is the most practical to achieving a high-amplitude intra-well response under a low-frequency ambient excitation, as the frequency band for the intra-well bi-stability, in this case, is much broader than in the cases of the other two configurations.
- (5)
- In the case of double potential wells, the increase in the excitation level can induce the inter-well resonant response and complicated dynamical behaviors, including period-3 attractors and chaos, coexisting with the intra-well responses. Their BAs intermingle with each other, showing another type of high initial sensitive phenomenon, unlike the phenomenon of chaos. When the excitation amplitude grows high enough, the inter-well periodic response definitely becomes the final response due to its global attraction.
- (6)
- In the case of quadruple potential wells, the excitation frequency in the vicinity of the resonant frequency within larger potential wells can help to achieve a higher amplitude final response. With the increase in the excitation level, apart from the periodic responses, various complex responses such as period-2 attractors, period-3 ones and chaos appear as hidden attractors. When the excitation level is high enough, the chaotic response is globally attractive.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, T.; Cao, Q. Novel multi-stable energy harvester by exploring the benefits of geometric nonlinearity. J. Stat. Mech. Theory Exp. 2019, 2019, 033405. [Google Scholar] [CrossRef]
- Naseer, R.; Dai, H.; Abdelkefi, A.; Wang, L. Comparative Study of Piezoelectric Vortex-Induced Vibration-Based Energy Harvesters with Multi-Stability Characteristics. Energies 2019, 13, 71. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56, 55–80. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Xu, D.; Bishop, S. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam–roller–spring mechanisms. J. Sound Vib. 2015, 346, 53–69. [Google Scholar] [CrossRef]
- Meng, Q.; Yang, X.; Li, W.; Lu, E.; Sheng, L. Research and Analysis of Quasi-Zero-Stiffness Isolator with Geometric Nonlinear Damping. Shock. Vib. 2017, 2017, 6719054. [Google Scholar] [CrossRef]
- Yang, T.; Liu, J.; Cao, Q. Response analysis of the archetypal smooth and discontinuous oscillator for vibration energy harvesting. Phys. A Stat. Mech. Its Appl. 2018, 507, 358–373. [Google Scholar] [CrossRef]
- Yang, T.; Cao, Q. Dynamics and high efficiency of a novel multi-stable energy harvesting system. Chaos Solitons Fractals 2020, 131, 109516. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Feng, X.; Li, R.; Dai, L.; Yang, K. A novel electromagnetic bistable vibration energy harvester with an elastic boundary: Numerical and experimental study. Mech. Syst. Signal Process. 2021, 160, 107937. [Google Scholar] [CrossRef]
- Kenmogne, F.; Wokwenmendam, M.L.; Simo, H.; Adile, A.D.; Noah, P.M.A.; Barka, M.; Nguiya, S. Effects of damping on the dynamics of an electromechanical system consisting of mechanical network of discontinuous coupled system oscillators with irrational nonlinearities: Application to sand sieves. Chaos Solitons Fractals 2022, 156, 111805. [Google Scholar] [CrossRef]
- Margielewicz, J.; Gąska, D.; Litak, G.; Wolszczak, P.; Yurchenko, D. Nonlinear dynamics of a new energy harvesting system with quasi-zero stiffness. Appl. Energy 2022, 307, 118159. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, Y.; Han, J.; Hao, S.; Wang, W. Dynamic design of a quad-Stable piezoelectric energy harvester via bifurcation theory. Sensors 2022, 22, 8453. [Google Scholar] [CrossRef]
- Von Kluge, P.N.; Sengha, G.G.; Kenfack, W.F.; Talla, L.L.; Kenmoé, G.D.; Kofané, T.C. Fractional dynamical behavior of a new nonlinear smooth and discontinuous (SD) oscillator for vibration energy harvesting with nonlinear magnetic coupling. Eur. Phys. J. Plus 2023, 138, 937. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, Q.; Han, J.; Wang, W.; Wang, T.; Cao, X.; Hao, S. Design and investigation of a quad-stable piezoelectric vibration energy harvester by using geometric nonlinearity of springs. J. Sound Vib. 2023, 547, 117484. [Google Scholar] [CrossRef]
- Wang, Z.; Shang, H. Multistability mechanisms for improving the performance of a piezoelectric energy harvester with geometric nonlinearities. Fractal Fract. 2024, 8, 41. [Google Scholar] [CrossRef]
- Sun, X.; Jing, X. Multi-direction vibration isolation with quasi-zero stiffness by employing geometrical nonlinearity. Mech. Syst. Signal Process. 2015, 62, 149–163. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, L.; Song, C.; Gu, H.; Ji, W. Dynamic characteristics of a quasi-zero stiffness vibration isolator with nonlinear stiffness and damping. Arch. Appl. Mech. 2019, 89, 1743–1759. [Google Scholar] [CrossRef]
- Chang, Y.; Zhou, J.; Wang, K.; Xu, D. A quasi-zero-stiffness dynamic vibration absorber. J. Sound Vib. 2021, 494, 115859. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Chang, Y.; Ouyang, H.; Xu, D.; Yang, Y. A nonlinear ultra-low-frequency vibration isolator with dual quasi-zero-stiffness mechanism. Nonlinear Dyn. 2020, 101, 755–773. [Google Scholar] [CrossRef]
- Xing, Z.-Y.; Yang, X.-D. A combined vibration isolation system with quasi-zero stiffness and dynamic vibration absorber. Int. J. Mech. Sci. 2023, 256, 108508. [Google Scholar] [CrossRef]
- Liu, R.; Shang, H. Global dynamics and bifurcations of an oscillator with symmetric irrational nonlinearities. Fractal Fract. 2023, 7, 888. [Google Scholar] [CrossRef]
- Kenmogne, F.; Noah, P.M.A.; Tafo, J.B.G.; Adoum, D.A.; Sali, M.; Abakar, M.T.; Eno, R.; Bell, E.Y. Stability of modulated signals in the damped mechanical network of discontinuous coupled system oscillators with irrational nonlinearities. Arch. Appl. Mech. 2022, 92, 3077–3091. [Google Scholar] [CrossRef]
- Chen, H.; Xie, J. Harmonic and subharmonic solutions of the SD oscillator. Nonlinear Dyn. 2016, 84, 2477–2486. [Google Scholar] [CrossRef]
- Wang, Z.; Shang, H. Multistability and Jump in the Harmonically Excited SD Oscillator. Fractal Fract. 2023, 7, 314. [Google Scholar] [CrossRef]
- Han, N.; Cao, Q. A parametrically excited pendulum with irrational nonlinearity. Int. J. Non-Linear Mech. 2017, 88, 122–134. [Google Scholar] [CrossRef]
- Yang, T.; Cao, Q. Delay-controlled primary and stochastic resonances of the SD oscillator with stiffness nonlinearities. Mech. Syst. Signal Process. 2018, 103, 216–235. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Q.; Nie, Z. Stick-slip vibrations of a self-excited SD oscillator with Coulomb friction. Nonlinear Dyn. 2020, 102, 1419–1435. [Google Scholar] [CrossRef]
- Han, Y.; Cao, Q.; Ji, J. Nonlinear dynamics of a smooth and discontinuous oscillator with multiple stability. Int. J. Bifurc. Chaos 2015, 25, 1530038. [Google Scholar] [CrossRef]
- Hao, Z.; Cao, Q.; Wiercigroch, M. Nonlinear dynamics of the quasi-zero-stiffness SD oscillator based upon the local and global bifurcation analyses. Nonlinear Dyn. 2016, 87, 987–1014. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Huang, L. Global dynamics and bifurcation for a discontinuous oscillator with irrational nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 2023, 119, 107073. [Google Scholar] [CrossRef]
- Dudkowski, D.; Prasad, A.; Kapitaniak, T. Perpetual points and hidden attractors in dynamical systems. Phys. Lett. A 2015, 379, 2591–2596. [Google Scholar] [CrossRef]
- Brezetskyi, S.; Dudkowski, D.; Kapitaniak, T. Rare and hidden attractors in Van der Pol-Duffing oscillators. Eur. Phys. J. Spec. Top. 2015, 224, 1459–1467. [Google Scholar] [CrossRef]



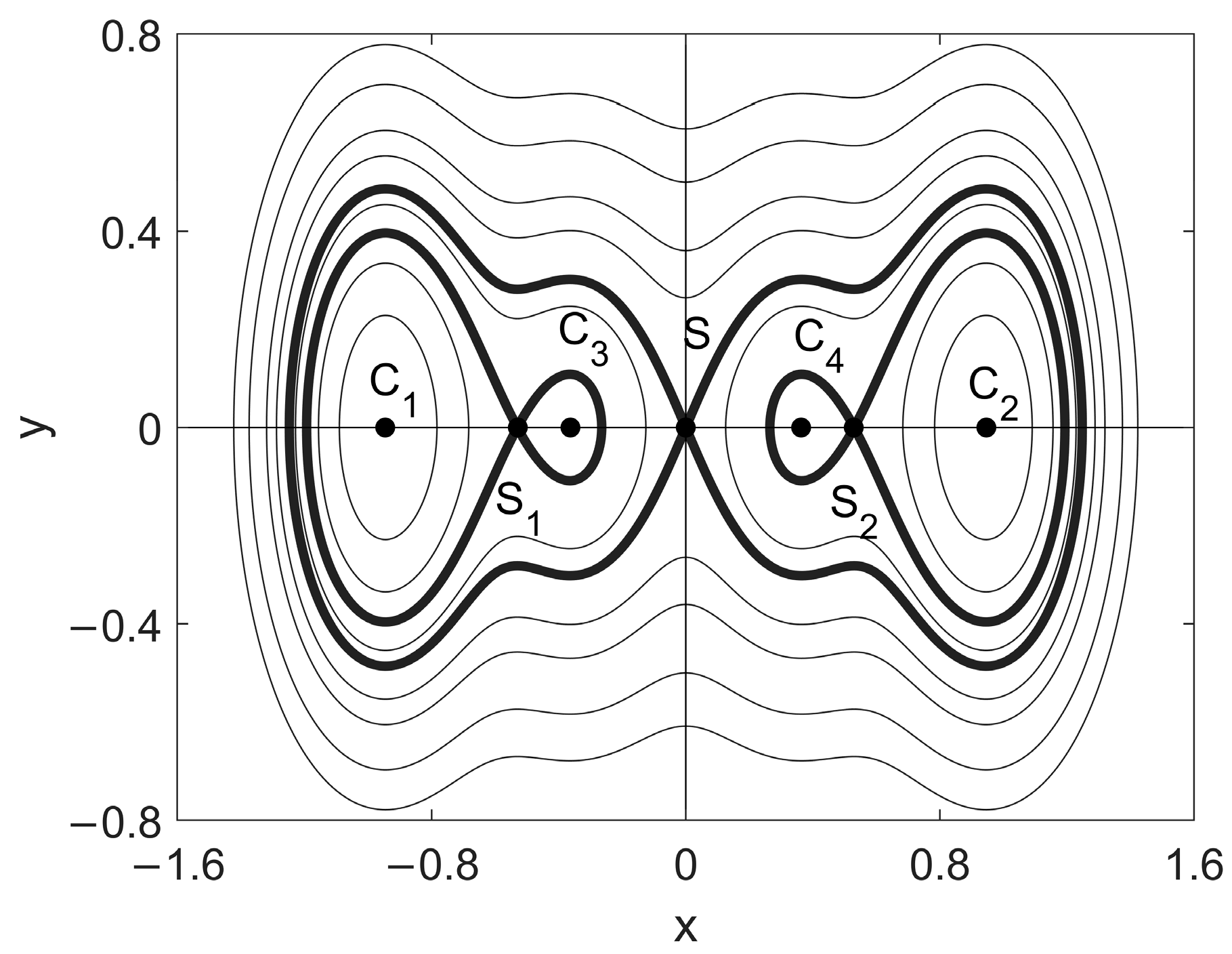


| Value of α | Number of Equilibria | Positions of Equilibria |
|---|---|---|
| 0.8 | 1 | O(0,0) |
| 0.4 | 3 | C±(±0.351,0), O(0,0) |
| 0.2 | 7 | C1,2(±0.945,0), S1,2(±0.530,0), C3,4(±0.365,0), O(0,0) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Shang, H. Comparisons for Global Dynamics of a Geometrically Nonlinear Oscillator among Single-, Double- and Quadruple-Well Configurations. Fractal Fract. 2024, 8, 202. https://doi.org/10.3390/fractalfract8040202
Sun H, Shang H. Comparisons for Global Dynamics of a Geometrically Nonlinear Oscillator among Single-, Double- and Quadruple-Well Configurations. Fractal and Fractional. 2024; 8(4):202. https://doi.org/10.3390/fractalfract8040202
Chicago/Turabian StyleSun, Huihang, and Huilin Shang. 2024. "Comparisons for Global Dynamics of a Geometrically Nonlinear Oscillator among Single-, Double- and Quadruple-Well Configurations" Fractal and Fractional 8, no. 4: 202. https://doi.org/10.3390/fractalfract8040202
APA StyleSun, H., & Shang, H. (2024). Comparisons for Global Dynamics of a Geometrically Nonlinear Oscillator among Single-, Double- and Quadruple-Well Configurations. Fractal and Fractional, 8(4), 202. https://doi.org/10.3390/fractalfract8040202







