Operator Kernel Functions in Operational Calculus and Applications in Fractals with Fractional Operators
Abstract
1. Introduction
2. Preliminaries
2.1. Function Space
- (i)
- The function has, at most, a finite number of discontinuity points in any finite interval.
- (ii)
- For arbitrary the integration of is bounded, i.e., .
2.2. Ring and Field
2.3. Notation of Operators
3. Operator Kernel Function Method
3.1. Uniqueness of Solutions of Operator Differential Equations
3.2. Translation Operator
3.3. The Equivalence of Operational Calculus and Integral Transformations
3.4. The Uniqueness of Operational Calculus and Integral Transformations
3.5. Relationship with Carson-Laplace Transform
4. Applications of Operator Kernel Function Method
4.1. The Heat Conduction Problem
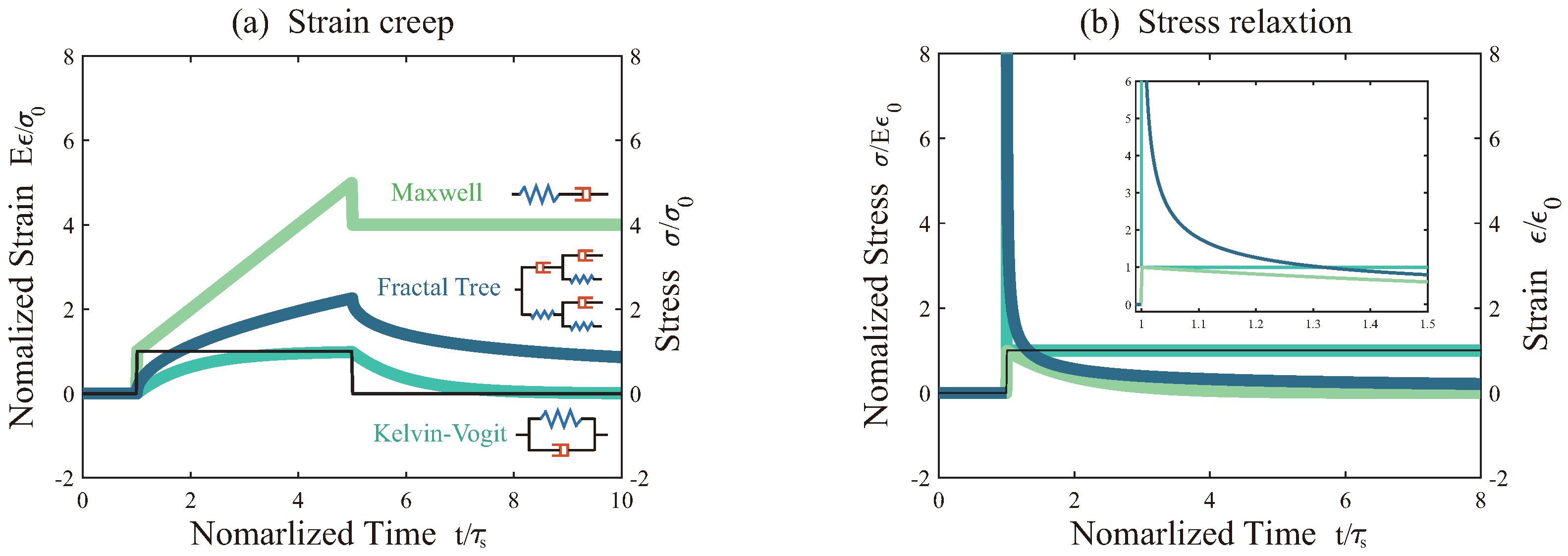
4.2. Fractional-Order Mechanics on a Fractal Tree
4.3. Fractional-Order Mechanics on a Fractal Loop
4.4. Hemodynamics on a Fractal Ladder
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OKF | Operator kernal funtion |
| OC | Operational Calculus |
| LHS | Left hand side |
| RHS | Right hand side |
Appendix A
References
- Carslaw, H.S. Operational Methods in Mathematical Physics. Math. Gaz. 1928, 14, 216–226. [Google Scholar] [CrossRef]
- Milne-Thomson, M.L. Operational methods in applied mathematics. Nature 1942, 150, 647. [Google Scholar] [CrossRef]
- Britton, J.R. Modern Operational Calculus for Undergraduates. Am. Math. Mon. 1949, 56, 295–300. [Google Scholar] [CrossRef]
- Cooper, J.L.B. Heaviside and the Operational Calculus. Math. Gaz. 1952, 36, 5–19. [Google Scholar] [CrossRef]
- Lützen, J. Heaviside’s operational calculus and the attempts to rigorise it. Arch. Hist. Exact Sci. 1979, 21, 161–200. [Google Scholar] [CrossRef]
- Hanna, L.A.M.; Al-Kandari, M.; Luchko, Y. Operational method for solving fractional differential equations with the left-and right-hand sided Erdélyi-Kober fractional derivatives. Fract. Calc. Appl. Anal. 2020, 23, 103–125. [Google Scholar] [CrossRef]
- Heaviside, O. On Operators in Physical Mathematics, Part I. Proc. R. Soc. Lond. Ser. A-Math. Phys. Eng. Sci. 1893, 52, 315–320. [Google Scholar] [CrossRef]
- Bengochea, G. Operational solution of fractional differential equations. Appl. Math. Lett. 2014, 32, 48–52. [Google Scholar] [CrossRef]
- Al-Kandari, M.; Hanna, L.A.M.; Luchko, Y. On an extension of the Mikusiński type operational calculus for the Caputo fractional derivative. Integral Transform. Spec. Funct. 2020, 32, 710–725. [Google Scholar] [CrossRef]
- Rani, N.; Fernandez, A. Mikusiński’s operational calculus for Prabhakar fractional calculus. Integral Transform. Spec. Funct. 2022, 33, 945–965. [Google Scholar] [CrossRef]
- McCullough-Benner, C. Applying unrigorous mathematics: Heaviside’s operational calculus. Stud. Hist. Philos. Sci. 2022, 91, 113–124. [Google Scholar] [CrossRef]
- Fernandez, A. Mikusiński’s operational calculus for general conjugated fractional derivatives. Bol. Soc. Mat. Mex. 2023, 29, 1–24. [Google Scholar] [CrossRef]
- Kochubei, A.N. General fractional calculus, evolution equations, and renewal processes. Integral Transform. Spec. Funct. 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Luchko, Y.; Srivastava, H.M. The exact solution of certain differential equations of fractional order by using operational calculus. Comput. Math. Appl. 1995, 29, 73–85. [Google Scholar] [CrossRef]
- Luchko, Y.; G, R. An operational method for solving fractional differential equations with the Caputo derivatives. Acta Math. Vietnam 1999, 24, 207–233. [Google Scholar]
- Fahad, H.M.; Fernandez, A. Operational calculus for Caputo fractional calculus with respect to functions and the associated fractional differential equations. Appl. Math. Comput. 2021, 409, 126400. [Google Scholar] [CrossRef]
- Hu, K.X.; Zhu, K.Q. Mechanical analogies of fractional elements. Chin. Phys. Lett. 2009, 26, 108301. [Google Scholar] [CrossRef]
- Butera, S.; Di-Paola, M. A physically based connection between fractional calculus and fractal geometry. Ann. Phys. 2014, 350, 146–158. [Google Scholar] [CrossRef]
- Guo, J.Q.; Yin, Y.J.; Hu, X.L.; Ren, G.X. Self-similar network model for fractional-order neuronal spiking: Implications of dendritic spine functions. Nonlinear Dyn. 2020, 100, 921–935. [Google Scholar] [CrossRef]
- Peng, G.; Guo, J.Q.; Yin, Y.J. Self-similar functional circuit models of arteries and deterministic fractal operators: Theoretical revelation for biomimetic materials. Int. J. Mol. Sci. 2021, 22, 12897. [Google Scholar] [CrossRef]
- Yin, Y.J.; Peng, G.; Yu, X.B. Algebraic equations and non-integer orders of fractal operators abstracted from biomechanics. Acta Mech. Sin. 2022, 38, 521488. [Google Scholar] [CrossRef]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics; John Wiley and Sons: New York, NY, USA, 1989; pp. 1–560. [Google Scholar]
- Carson, J.R. Theory and calculation of variable electrical systems. Phys. Rev. 1921, 17, 116–134. [Google Scholar] [CrossRef]
- Carson, J.R. The Heaviside operational calculus. Bell Syst. Tech. J. 1922, 1, 43–55. [Google Scholar] [CrossRef]
- Moore, D.H. Heaviside Operational Calculus; Elsevier: New York, NY, USA, 1971; p. xiii+152. [Google Scholar]
- Kullstam, P. Heaviside Operational Calculus—Oliver Revenge. IEEE Trans. Educ. 1991, 34, 155–166. [Google Scholar] [CrossRef]
- Bengochea, G.; López, G. Mikusiński’s operational calculus with algebraic foundations and applications to Bessel functions. Integral Transform. Spec. Funct. 2014, 25, 272–282. [Google Scholar] [CrossRef][Green Version]
- Luchko, Y. Operational calculus for the general fractional derivative and its applications. Fract. Calc. Appl. Anal. 2021, 24, 338–375. [Google Scholar] [CrossRef]
- Diethelm, K.; Kiryakova, V.; Luchko, Y.; Machado, J.A.T.; Tarasov, V.E. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. 2022, 107, 3245–3270. [Google Scholar] [CrossRef]
- Van-Der-Pol, B.; Bremmer, H. Operational Calculus: Based on the Two-Sided Laplace Integral; Chelsea: New York, NY, USA, 1987. [Google Scholar]
- Flegg, H.G. Mikusiński’s Operational Calculus. Int. J. Educ. Res. 1974, 5, 131–137. [Google Scholar] [CrossRef]
- Mikusiński, J. Operational Calculus; Pergamon Press: Oxford, UK, 1959. [Google Scholar]
- Prudnikov, A.P. Operational Calculus and Related Topics; Chapman and Hall/CRC: New York, NY, USA, 2006. [Google Scholar]
- Berg, L. Introduction to the Operational Calculus; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Durbin, J.R. Modern Algebra: An Introduction; John Wiley and Sons: New York, NY, USA, 2008. [Google Scholar]
- Hetnarski, R.B.; Eslami, M.R. Heat Conduction Problems; Springer: Dordrecht, The Netherlands, 2009; pp. 132–218. [Google Scholar]
- Heymans, N.; Bauwens, J. Fractal rheological models and fractional differential equations for viscoelastic behavior. Rheol. Acta 1994, 33, 210–219. [Google Scholar] [CrossRef]
- Schiessel, H.; Blumen, A. Mesoscopic Pictures of the Sol-Gel Transition Ladder Models and Fractal Networks. Macromolecules 1995, 28, 4013–4019. [Google Scholar] [CrossRef]
- Schiessel, H.; Metzler, R.; Blumen, A.; Nonnenmacher, T.F. Generalized viscoelastic models Their fractional equations with solutions. J. Phys. A Math. Gen 1995, 28, 6567–6584. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999; pp. 159–198. [Google Scholar]
- Noordergraaf, A. Circulatory Systems Dynamics; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Stergiopulos, N.; Westerhof, B.E.; Westerhof, N. Total arterial inertance as the fourth element of the windkessel model. Am. J. Physiol. Heart Circ. Physiol. 1999, 276, H81–H88. [Google Scholar] [CrossRef]
- Gul, R.; Schütte, C.; Bernhard, S. Mathematical modelling and sensitivity analysis of arterial anastomosis in the arm. Appl. Math. Model. 2016, 40, 7724–7738. [Google Scholar] [CrossRef]
- Baker, W.B.; Parthasarathy, A.B.; Gannon, K.P.; Kavuri, V.C.; Busch, D.R.; Abramson, K.; He, L.; Mesquita, R.C.; Mullen, M.T.; Detre, J.A.; et al. Noninvasive optical monitoring of critical closing pressure and arteriole compliance in human subjects. J. Cerebr. Blood. F. Met 2017, 37, 2691–2705. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Mao, B.; Feng, Y.; Liu, J.; Zhao, Z.; Duan, M.; Liu, Y. The hemodynamic mechanism of FFR-guided coronary artery bypass grafting. Front. Physiol. 2021, 12, 8. [Google Scholar] [CrossRef]


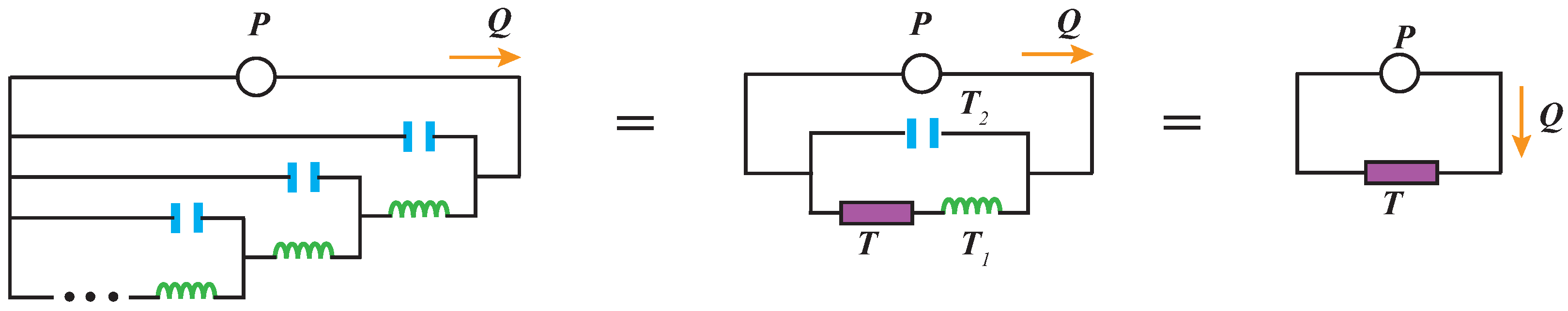
| Operator | Kernel Function |
|---|---|
| 1 | |
| 2 | |
| 3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Yin, Y. Operator Kernel Functions in Operational Calculus and Applications in Fractals with Fractional Operators. Fractal Fract. 2023, 7, 755. https://doi.org/10.3390/fractalfract7100755
Yu X, Yin Y. Operator Kernel Functions in Operational Calculus and Applications in Fractals with Fractional Operators. Fractal and Fractional. 2023; 7(10):755. https://doi.org/10.3390/fractalfract7100755
Chicago/Turabian StyleYu, Xiaobin, and Yajun Yin. 2023. "Operator Kernel Functions in Operational Calculus and Applications in Fractals with Fractional Operators" Fractal and Fractional 7, no. 10: 755. https://doi.org/10.3390/fractalfract7100755
APA StyleYu, X., & Yin, Y. (2023). Operator Kernel Functions in Operational Calculus and Applications in Fractals with Fractional Operators. Fractal and Fractional, 7(10), 755. https://doi.org/10.3390/fractalfract7100755





