Global Dynamic Analysis of a Typical Bistable Piezoelectric Cantilever Energy Harvesting System
Abstract
:1. Introduction
2. Dynamical Model and Unperturbed Dynamics
3. Multiple Intra-Well Responses
3.1. Dynamic Responses around the Potential Well Centers
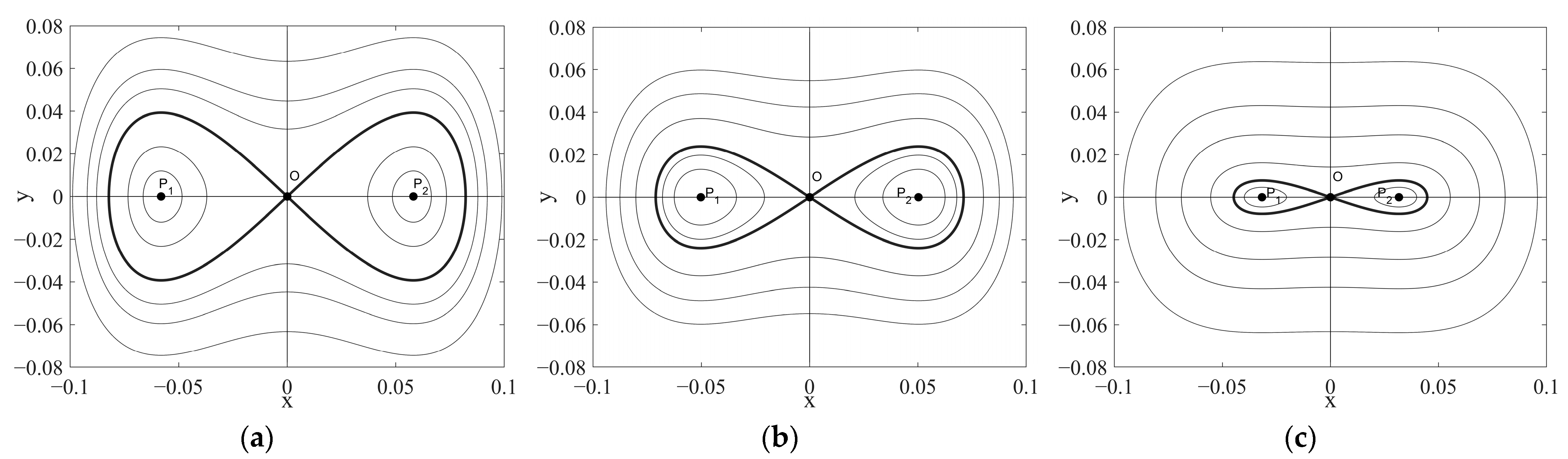
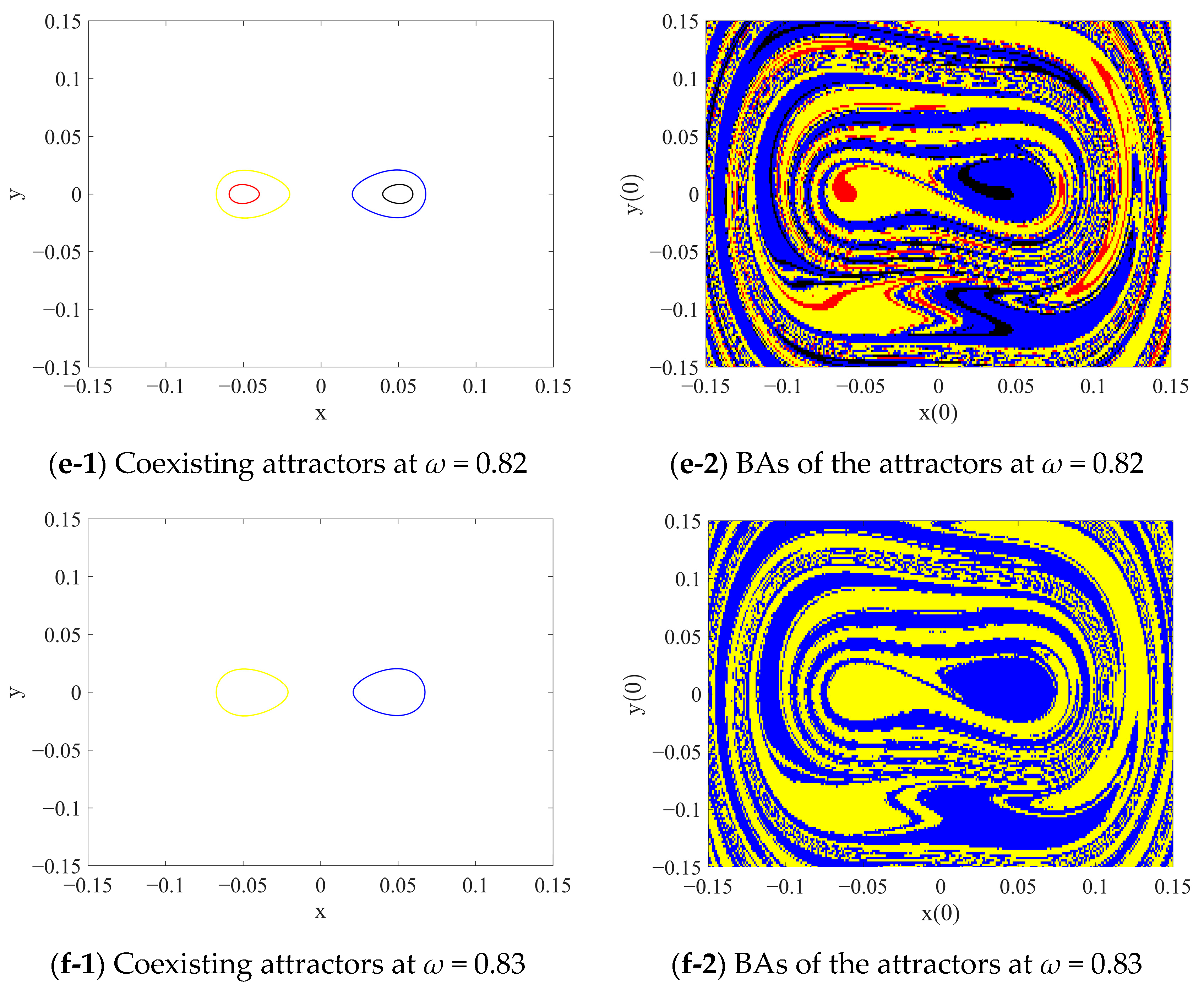
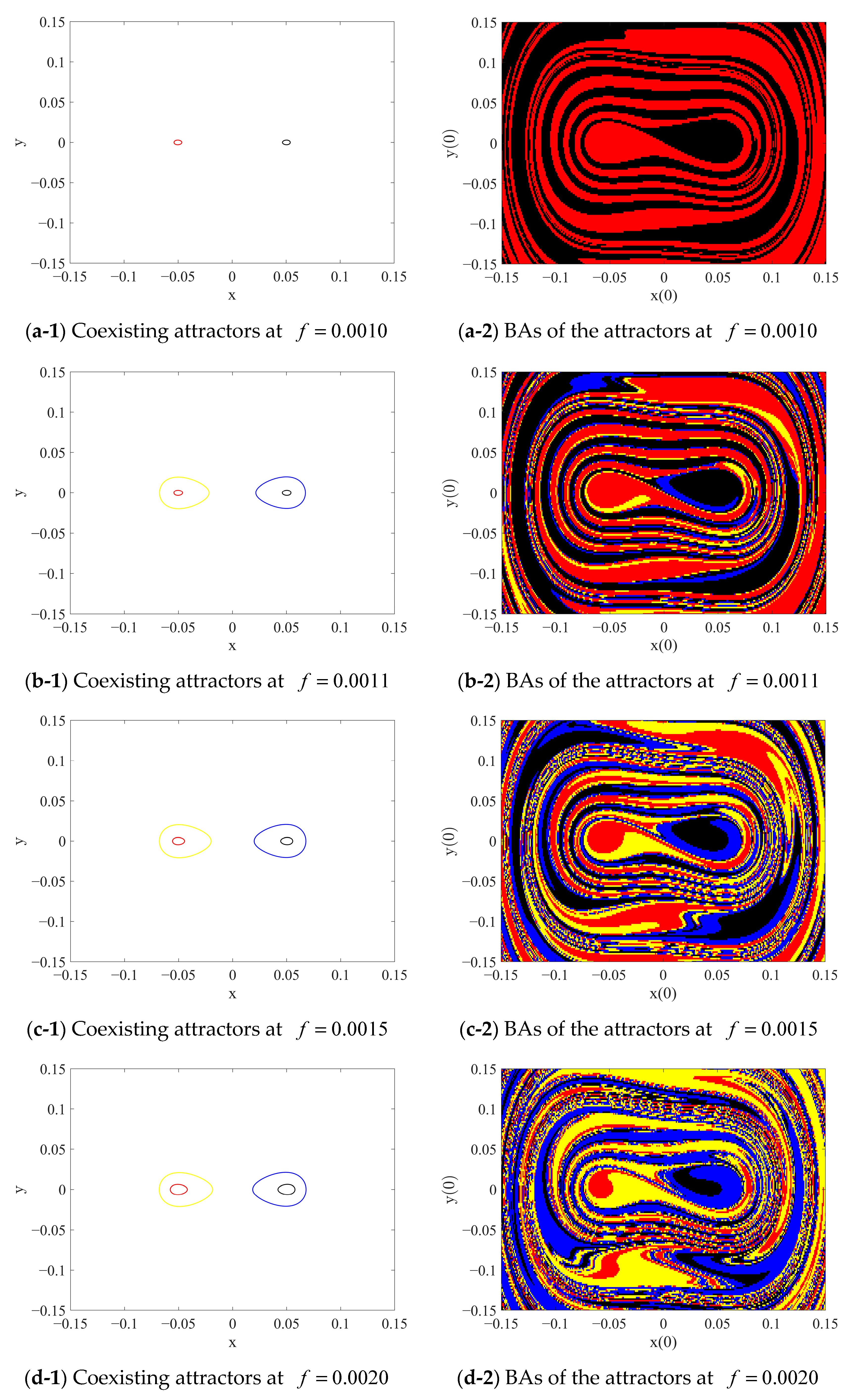
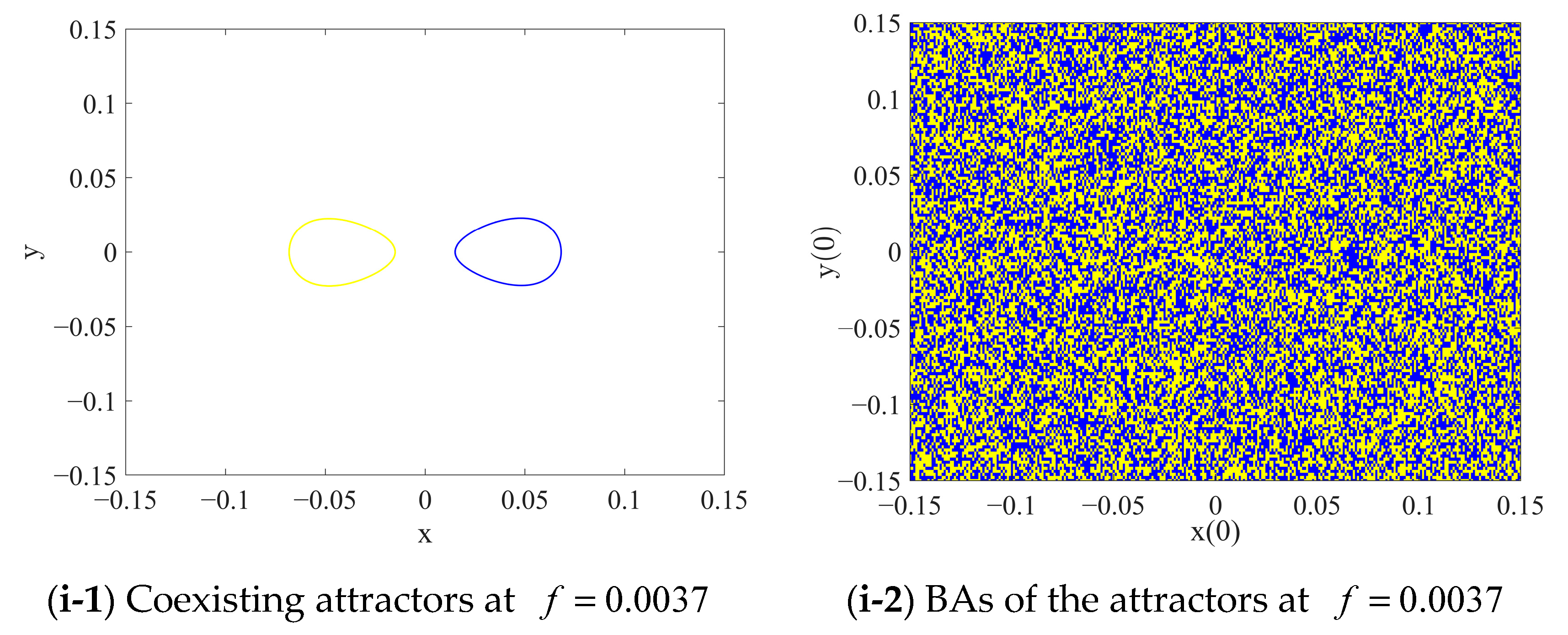
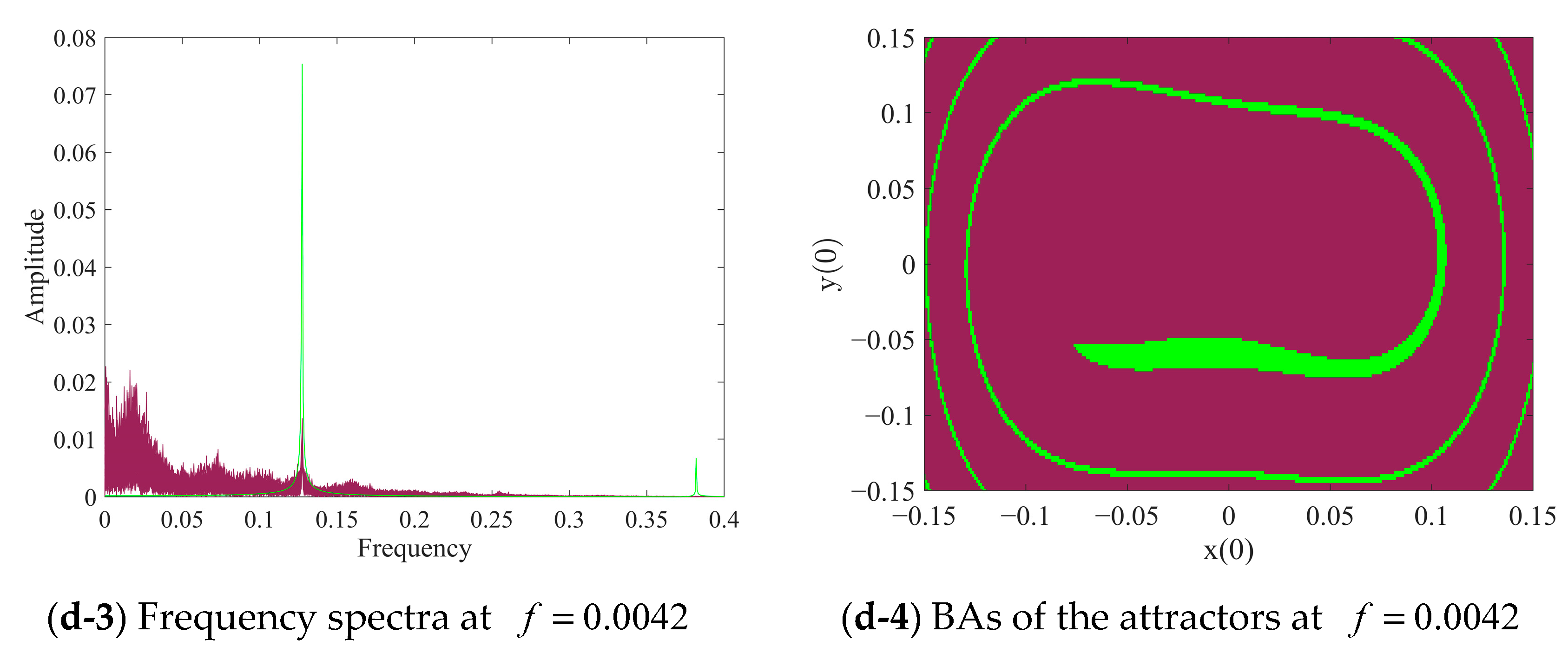
3.2. Coexistence of the Attractors
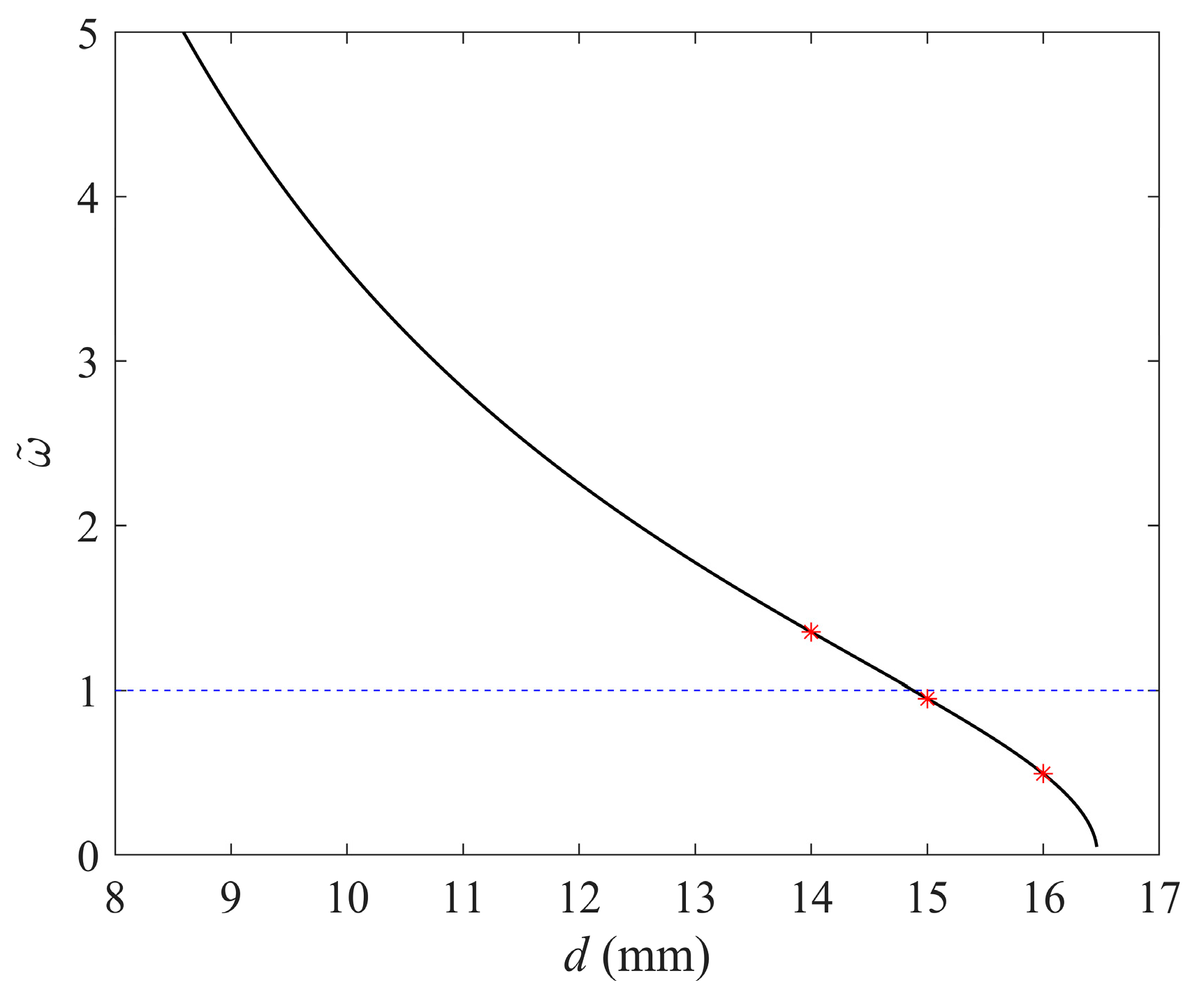
4. Global Bifurcation and Inter-Well Responses
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, D.; Shi, B.; Ouyang, S.; Fan, Y.; Wang, Z.L.; Zhou, L. Emerging implantable energy harvesters and self-powered implantable medical electronics. ACS Nano 2020, 14, 6436–6448. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.; Bao, B.; Wang, Q. Review on engineering structural designs for efficient piezoelectric energy harvesting to obtain high power output. Eng. Struct. 2021, 235, 112068. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Song, H.; Shan, X.; Li, R.; Hou, C. Review on the vibration suppression of cantilever beam through piezoelectric materials. Adv. Eng. Mater. 2022, 24, 2200408. [Google Scholar] [CrossRef]
- Fu, X.; Liao, W. Modeling and analysis of piezoelectric energy harvesting with dynamic plucking mechanism. J. Vib. Acoust.-Trans. ASME 2019, 141, 031002. [Google Scholar] [CrossRef]
- Zhou, S.; Yan, B.; Inman, D.J. A novel nonlinear piezoelectric energy harvesting system based on linear-element coupling: Design, modeling and dynamic analysis. Sensors 2018, 18, 1492. [Google Scholar] [CrossRef]
- Song, J.; Sun, G.; Zeng, X.; Li, X.; Bai, Q.; Zheng, X. Piezoelectric energy harvester with double cantilever beam undergoing coupled bending-torsion vibrations by width-splitting method. Sci. Rep. 2022, 12, 583. [Google Scholar] [CrossRef]
- Eshtehardiha, R.; Tikani, R.; Ziaei-Rad, S. Investigating the multiple scales method based on a new scaling for energy harvesting from a double cantilever beam with internal resonance. Meccanica 2022, 57, 1281–1306. [Google Scholar] [CrossRef]
- Peng, L.; Qi, Y.; Liu, J.; Sun, Y.; Zu, H.; Ru, X. Contact and non-contact dual-piezoelectric energy harvesting system driven by cantilever vibration. IEEE Access 2022, 10, 111974–111984. [Google Scholar] [CrossRef]
- Kumar, K.A.; Ali, S.F.; Arockiarajan, A. Exploring the benefits of an asymmetric monostable potential function in broadband vibration energy harvesting. Appl. Phys. Lett. 2018, 112, 233901. [Google Scholar] [CrossRef]
- Zhou, Z.; Qin, W.; Zhu, P. Harvesting acoustic energy by coherence resonance of a bi-stable piezoelectric harvester. Energy 2017, 126, 527–534. [Google Scholar] [CrossRef]
- Shah, V.; Kumar, R.; Talha, M.; Vaish, R. Piezoelectric materials for bistable energy harvester: A comparative study. Integr. Ferroelectr. 2016, 176, 73–84. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Erturk, A.; Lin, J. Enhanced broadband piezoelectric energy harvesting using rotatable magnets. Appl. Phys. Lett. 2013, 102, 173901. [Google Scholar] [CrossRef]
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear. Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Kumar, K.A.; Ali, S.F.; Arockiarajan, A. Piezomagnetoelastic broadband energy harvester: Nonlinear modeling and characterization. Eur. Phys. J.-Spec. Top. 2015, 224, 2803–2822. [Google Scholar] [CrossRef]
- Oumbé Tékam, G.T.O.; Kito Kwuimy, C.A.; Woafo, P. Analysis of tristable energy harvesting system having fractional order viscoelastic material. Chaos 2015, 25, 013112. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yang, Y. Stochastic resonance mechanism for wideband and low frequency vibration energy harvesting based on piezoelectric cantilever beams. Acta. Phys. Sin. 2011, 60, 074301. [Google Scholar] [CrossRef]
- Sun, S.; Leng, Y.; Hur, S.; Sun, F.; Su, X.; Song, H.; Kang, C. Energy harvesting performance of a novel nonlinear quad-stable piezoelectric energy harvester with only one external magnet. Machines 2022, 10, 803. [Google Scholar] [CrossRef]
- Sun, S.; Cao, S. Dynamic modeling and analysis of a bistable piezoelectric cantilever power generation system. Acta Phys. Sin. 2012, 61, 210505. [Google Scholar] [CrossRef]
- Tang, W.; Wang, X.; Cao, J. Modeling and analysis of piezoelectric vibration energy harvesting system using permanent magnetics. Acta Phys. Sin. 2014, 63, 240504. [Google Scholar] [CrossRef]
- Barbosa, W.O.V.; De Paula, A.S.; Savi, M.A.; Inman, D.J. Chao control applied to piezoelectric vibration-based energy harvesting systems. Eur. Phys. J. Special Topics 2015, 224, 2787–2801. [Google Scholar] [CrossRef]
- Shah, V.; Kumar, R.; Talha, M.; Twiefel, J. Numerical and experimental study of bistable piezoelectric energy harvester. Integr. Ferroelectr. 2018, 192, 38–56. [Google Scholar] [CrossRef]
- Litak, G.; Margielewicz, J.; Gaska, D.; Rysak, A.; Trigona, C. On Theoretical and numerical aspects of bifurcations and hysteresis effects in kinetic energy harvesters. Sensors 2022, 22, 381. [Google Scholar] [CrossRef]
- Zhu, Y.; Shang, H. Global dynamics of the vibrating system of a tristable piezoelectric energy harvester. Mathematics 2022, 10, 2894. [Google Scholar] [CrossRef]
- Jung, J.; Kim, P.; Lee, J.; Seok, J. Nonlinear dynamic and energetic characteristics of piezoelectric energy harvester with two rotatable external magnets. Int. J. Mech. Sci. 2015, 92, 206–222. [Google Scholar] [CrossRef]
- Cao, J.; Zhou, S.; Inman, D.J.; Chen, Y. Chaos in the fractionally damped broadband piezoelectric energy generator. Nonlinear. Dynamics 2015, 80, 1705–1719. [Google Scholar] [CrossRef]
- Ju, Y.; Li, Y.; Tan, J.; Zhao, Z.; Wang, G. Transition mechanism and dynamic behaviors of a multi-stable piezoelectric energy harvester with magnetic interaction. J. Sound Vib. 2021, 501, 116074. [Google Scholar] [CrossRef]
- Tan, D.; Leng, Y.; Fan, S.; Gao, Y. Magnetic force of piezoelectric cantilever energy harvesting system with an externally applied magnetic field based on magnetizing current method. Acta Phys. Sin. 2015, 64, 060502. [Google Scholar] [CrossRef]
- Dong, C.; Wang, J. Hidden and coexisting attractors in a novel 4D hyperchaotic system with no equilibrium point. Fractal Fract. 2022, 6, 306. [Google Scholar] [CrossRef]
- Sun, S.; Cao, S. Analysis of chaos behaviors of a bistable piezoelectric cantilever power generation system by the second-order Melnikov function. Acta Mech. Sin. 2017, 33, 200–207. [Google Scholar] [CrossRef]
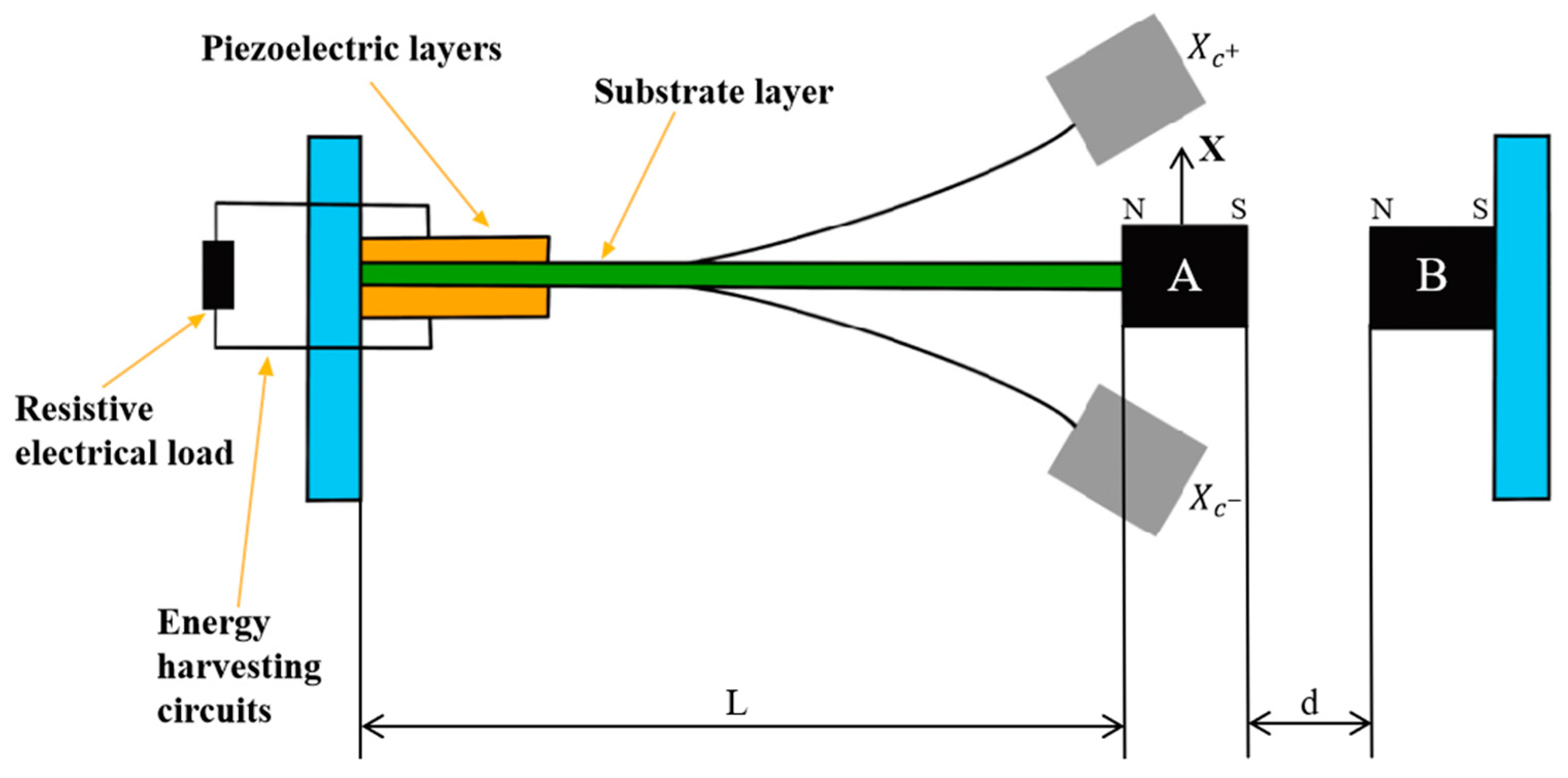



| Parameter | Symbol | Values |
|---|---|---|
| Equivalent mass of beam and magnet (g) | 25.9 | |
| Equivalent damping of the cantilever beam (N·s/m) | 0.01 | |
| Elastic constant of the cantilever beam (N/m) | 774.664 | |
| Vacuum permeability (H/m) | ||
| The magnetization of magnet A (A/m) | ||
| The volume of magnet A () | ||
| The magnetization of magnet B (A/m) | ||
| The volume of magnet B () | ||
| The horizontal distance between magnet A and the base of the beam (cm) | 7.4 | |
| Electromechanical coupling coefficient in relation to voltage (N/V) | ||
| Equivalent capacitance of piezoelectric ceramics (F) | ||
| Resistive electrical load () | 1000 | |
| Electromechanical coupling coefficient in relation to current (A·s/m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, D.; Shang, H. Global Dynamic Analysis of a Typical Bistable Piezoelectric Cantilever Energy Harvesting System. Fractal Fract. 2023, 7, 717. https://doi.org/10.3390/fractalfract7100717
Cui D, Shang H. Global Dynamic Analysis of a Typical Bistable Piezoelectric Cantilever Energy Harvesting System. Fractal and Fractional. 2023; 7(10):717. https://doi.org/10.3390/fractalfract7100717
Chicago/Turabian StyleCui, Diandian, and Huilin Shang. 2023. "Global Dynamic Analysis of a Typical Bistable Piezoelectric Cantilever Energy Harvesting System" Fractal and Fractional 7, no. 10: 717. https://doi.org/10.3390/fractalfract7100717
APA StyleCui, D., & Shang, H. (2023). Global Dynamic Analysis of a Typical Bistable Piezoelectric Cantilever Energy Harvesting System. Fractal and Fractional, 7(10), 717. https://doi.org/10.3390/fractalfract7100717







