A Family of Transformed Difference Schemes for Nonlinear Time-Fractional Equations

Abstract

In this paper, we present a class of finite difference methods for numerically solving fractional differential equations. Such numerical schemes are developed based on the change in variable and piecewise interpolations. Error analysis of the numerical schemes is obtained by using a Grönwall-type inequality. Numerical examples are given to confirm the theoretical results.

1. Introduction

We aim to develop a family of effective numerical methods for solving the following nonlinear time-fractional differential equations:

$$\begin{array}{c}\hfill D_{*}^{\alpha }y=f(t,y\left(t\right)),y\left(0\right)=y_0,t\in (0,T],\end{array}$$

(1)

where $0<\alpha <1$, $D_{*}^{\alpha }$ is the the differential operator in sense of Caputo, given by

$$D_{*}^{\alpha }y=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t{(t-r)}^{-\alpha }{y}^{\prime }\left(r\right)dr.$$

The fractional differential equations provide a powerful tool to describe many natural phenomena in the fields of physics [1,2,3], economics [4] and biology [5].

Developing and analyzing highly effective numerical methods for fractional differential equations has been one of the hot topics. The widely used numerical methods are the L1 schemes [6,7,8,9,10,11,12,13] and L2-schemes [14,15,16]. Such schemes are developed by using piecewise interpolations. The optimal convergence results of L1-type schemes for time-dependent partial equations can be obtained by using the fractional Grönwall type inequalities [17,18,19]. Moreover, L1-type schemes can be accelerated by using sum-of-exponentials approximations [20,21,22]. Other widely used schemes are the so-called backward differentiation formula (BDF) convolution quadrature (CQ) methods. The CQ methods were originally proposed in [23,24] and further investigated in [25,26,27]. That aside, some transformed finite difference methods were constructed based on some change in variables [28,29,30]. More numerical schemes as well as their numerical analysis can be found in an incomplete list of references [31,32,33].

It is widely accepted that Equation (1) is equivalent to the following Volterra integral equation [34]:

$$y\left(t\right)=y_0+\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-r)}^{\alpha -1}f(r,y\left(r\right))dr.$$

(2)

Here and below, we always assume that the function f is Lipschitz continuous with respect to the second argument on a suitable set G and the Lipschitz constant is L. Moreover, suppose $f\in {\mathcal{C}}^3\left(G\right)$. Then, there exists a function $\psi \in {\mathcal{C}}^2[0,T]$ and some $c_1,c_2,\cdots ,c_J\in \mathbb{R}$ and $d_1,d_2,\cdots ,d_{\widehat{J}}\in \mathbb{R}$ such that the solution to Equation (1) can be given by (see, e.g., [35,36,37,38])

$$y\left(t\right)=\psi \left(t\right)+\sum _{j=1}^J{c}_j{t}^{j\alpha }+\sum _{j=1}^{\widehat{J}}{d}_j{t}^{1+j\alpha },$$

(3)

where $J:=\lceil 2/\alpha \rceil -1$. Clearly, the typical solution to the problem in Equation (1) has an initial layer at the beginning, and $y_t$ blows up as $t\to 0^{+}$. In this paper, we aim to present effective numerical schemes to solve the fractional problems, taking the initial layer into account.

The new numerical schemes are developed based on the following changes in variables:

$$t=s^{\eta /\alpha },\eta \in {\mathbb{N}}^{+},$$

(4)

Equations (1) or (2) is equivalent to the following integral equation:

$$\begin{array}{ccc}\hfill y\left(s^{\eta /\alpha }\right)& =& y_0+\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^{s^{\eta /\alpha }}{(s^{\eta /\alpha }-r)}^{\alpha -1}f(r,y\left(r\right))dr\hfill \\ & =& y_0+\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^s{(s^{\eta /\alpha }-u^{\eta /\alpha })}^{\alpha -1}f(u^{\eta /\alpha },y(u^{\eta /\alpha }))\frac{\eta }{\alpha }{u}^{\eta /\alpha -1}du\hfill \\ & =& y_0+\frac{\eta }{\mathrm{\Gamma }(1+\alpha )}{\int }_0^s{(s^{\eta /\alpha }-r^{\eta /\alpha })}^{\alpha -1}{r}^{\eta /\alpha -1}f(r^{\eta /\alpha },y(r^{\eta /\alpha }))dr,\hfill \end{array}$$

(5)

Furthermore, let

$$z\left(s\right)=y(s^{\eta /\alpha }),$$

(6)

Equation (5) becomes

$$\begin{array}{c}\hfill z\left(s\right)=y_0+\frac{\eta }{\mathrm{\Gamma }(1+\alpha )}{\int }_0^s{(s^{\eta /\alpha }-r^{\eta /\alpha })}^{\alpha -1}{r}^{\eta /\alpha -1}f(r^{\eta /\alpha },z(r))dr,0\le s\le T^{\alpha /\eta }.\end{array}$$

(7)

Then, the solution to Equation (7) has the form

$$z\left(s\right)=\psi (s^{\eta /\alpha })+\sum _{j=1}^J{c}_j{s}^{j\eta }+\sum _{j=1}^{\widehat{J}}{s}^{\frac{\eta (1+j\alpha )}{\alpha }},$$

(8)

where $\psi \in {\mathcal{C}}^2[0,T]$. Clearly, by the changes in variables, the initial layer will vanish, and the exact solution will become smoother. Then, the idea of developing effective numerical methods for solving Equation (1) is as follows:

• Apply the change in Equation (4) with a suitable parameter $\eta$ to obtain Equation (7) and its regularity of the solution.
• Develop numerical methods based on the smoothness of the solution to Equation (7).
• Recover the numerical solution by using the simple inverse change $y\left(s\right)=z\left(s^{\alpha /\eta }\right)$.

The rest of the paper is organized as follows. In Section 2, we present a family of new numerical schemes and investigate the numerical schemes’ convergence results. In Section 3, we present some numerical results to confirm the theoretical findings. Finally, our conclusions are presented in Section 4.

2. Construction of the Numerical Methods

In this section, we develop some numerical methods and present the numerical results based on the change in variable. Here and below, we always set the step size $h={\displaystyle \frac{T^{\alpha /\eta }}{N}}$, with N being a given integer and $s_i=ih,i=0,1,2,\cdots ,N$. In what follows, we will present two numerical methods for solving Equation (7).

2.1. First-Order Accurate Methods

In this subsection, we present a numerical method based on the following change in variable:

$$t=s^{1/\alpha }$$

With Equations (7) and (8), one can check that its solution $z\left(s\right)\in C[0,T]$ with the change in variable. Therefore, we propose a first-order accurate method based on the product rectangle rule for every interval; in other words, we propose

$${\int }_{s_{m-1}}^{s_m}{(s_i^{1/\alpha }-r^{1/\alpha })}^{\alpha -1}{r}^{1/\alpha -1}f(r^{1/\alpha },z(r))dr\approx f(s_m^{1/\alpha },z(s_m)){\int }_{s_{m-1}}^{s_m}{(s_i^{1/\alpha }-r^{1/\alpha })}^{\alpha -1}{r}^{1/\alpha -1}dr.$$

Then, it follows from Equation (7) that

$$\begin{array}{ccc}\hfill z\left(s_i\right)& =& z_0+\frac{1}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{\int }_{s_{m-1}}^{s_m}{(s_i^{1/\alpha }-r^{1/\alpha })}^{\alpha -1}{r}^{1/\alpha -1}f(r^{1/\alpha },z(r))dr\hfill \\ & =& z_0+\frac{1}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^{i}f(s_m^{1/\alpha },z(s_m)){\int }_{s_{m-1}}^{s_m}{(s_i^{1/\alpha }-r^{1/\alpha })}^{\alpha -1}{r}^{1/\alpha -1}dr+R_1^i\hfill \\ & =& z_0+\frac{1}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{a}_m^{i}f(s_m^{1/\alpha },z(s_m))+R_1^i,\hfill \end{array}$$

(9)

where $z_0=y_0$ and the truncation error is

$$R_1^i=\frac{1}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{\int }_{s_{m-1}}^{s_m}{(s_i^{1/\alpha }-r^{1/\alpha })}^{\alpha -1}{r}^{1/\alpha -1}\left(f(r^{1/\alpha },z(r))-(f(s_m^{1/\alpha },z(s_m))\right)dr=\mathcal{O}(h),$$

while the coefficients are

$$a_m^i={\int }_{s_{m-1}}^{s_m}{(s_i^{1/\alpha }-r^{1/\alpha })}^{\alpha -1}{r}^{1/\alpha -1}dr.$$

(10)

Let $z_i$ be a numerical approximation to $z\left(s_i\right)$. By replacing $z\left(s_i\right)$ with $z_i$ and omitting the truncation error $R_i$, we have the following numerical scheme:

$$\begin{array}{ccc}\hfill \mathrm{Scheme}\mathrm{I}:z_i& =& z_0+\frac{1}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{a}_m^{i}f(s_m^{1/\alpha },z_m).\hfill \end{array}$$

(11)

Scheme I is an implicit method. At each step, iterative processes are required to solve the nonlinear equations. In order to reduce the computational cost, a linearized scheme can be developed as follows:

$$\begin{array}{ccc}\hfill \mathrm{Scheme}\mathrm{II}:z_i& =& z_0+\frac{1}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{a}_m^{i}f(s_m^{1/\alpha },z_{m-1}).\hfill \end{array}$$

(12)

The convergence results of the proposed schemes rely heavily on the following lemmas:

Lemma 1 ([39]).

Let $x_i,0\le i\le N$ be a sequence of non-negative real numbers. If

$$x_i\le {\psi }_i+M{h}^{\sigma +1-\alpha \beta }\sum _{j=0}^{i-1}\frac{j^{\sigma }{x}_j}{{(i^{\beta }-j^{\beta })}^{\alpha }},0\le i\le N,$$

where $0<\alpha <1,1\le \beta \le \sigma +1,\sigma \ge 0,M$ is a positive constant, and ${\psi }_i,0\le i\le N$, is a monotonic increasing sequence of non-negative real numbers, then

$$x_i\le {\psi }_i\sum _{n=0}^{\infty }{(\frac{M{\left(ih\right)}^{\sigma +1-\alpha \beta }}{\beta })}^n{\widehat{B}}_n(\alpha ,\beta ,\sigma ),0\le i\le N.$$

$${\widehat{B}}_n(\alpha ,\beta ,\sigma )=\left\{\begin{array}{c}1,n=0,\hfill \\ {\mathrm{\Pi }}_{l=1}^{n}B(\frac{l}{\beta }(\sigma +1-\alpha \beta )+\alpha ,(1-\alpha )),n\ge 1,\hfill \end{array}\right.$$

where B is the Beta function.

When $\sigma +1-\beta =0$, the following is true:

$$x_i\le {\psi }_i{E}_{1-\alpha }(\frac{M\mathrm{\Gamma }(1-\alpha )}{\beta }{(ih)}^{\beta (1-\alpha )}),0\le i\le N,$$

where $E_{\alpha }\left(z\right)={\sum }_{k=0}^{\infty }\frac{z^k}{\mathrm{\Gamma }(1+k\alpha )}$ is the Mittag-Leffler function.

Now, we have the following convergence results:

Theorem 1.

Suppose $f\in {\mathcal{C}}^3\left(G\right)$. Then, the schemes in Equations (11) and (12) are first-order accurate.

Proof. 

Let $e_i=z\left(s_i\right)-z_i$. Subtracting Equation (11) from Equation (9) gives

$$\begin{array}{ccc}\hfill |e_i|& =& |e_0+\frac{1}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{a}_m^i(f(s_m^{1/\alpha },z(s_m))-f(s_m^{1/\alpha },z_m))+R_1^i|\hfill \\ & \le & |e_0|+\frac{L}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{a}_m^i|e_i|+|R_1^i|.\hfill \end{array}$$

(13)

It follows from Equation (10) that, for $1\le m\le i-1$, we have

$$\begin{array}{ccc}\hfill a_m^i& =& {\int }_{s_{m-1}}^{s_m}\frac{r^{\frac{1}{\alpha }-1}}{{(s_i^{\frac{1}{\alpha }}-r^{\frac{1}{\alpha }})}^{1-\alpha }}=h\frac{{\zeta }^{\frac{1}{\alpha }-1}}{{(s_i^{\frac{1}{\alpha }}-{\zeta }^{\frac{1}{\alpha }})}^{1-\alpha }}\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& \le & h\frac{s_m^{\frac{1}{\alpha }-1}}{{(s_i^{\frac{1}{\alpha }}-s_m^{\frac{1}{\alpha }})}^{1-\alpha }}=h\frac{m^{\frac{1}{\alpha }-1}}{{(i^{\frac{1}{\alpha }}-m^{\frac{1}{\alpha }})}^{\alpha -1}},\hfill \end{array}$$

(15)

where $\zeta$ belongs to the interval $[s_{m-1},s_m]$ and the mean value theorem of the integral is used. Noting that

$$\begin{array}{c}\hfill a_i^i={(s_i^{1/\alpha }-s_{i-1}^{1/\alpha })}^{\alpha }={\xi }^{1/\alpha -1}h,(\xi \in (s_{i-1},s_i)).\end{array}$$

(16)

then $a_i^i\left|e^i\right|$ can be absorbed by the left-hand side of the inequality when h is sufficiently small. By combining Equations (14) and (15) with the truncation error $R_1^i$, we can obtain

$$\begin{array}{cc}\hfill |e_i|& \le |e_0|+\frac{C_{0}L}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^{i-1}h\frac{m^{\frac{1}{\alpha }-1}}{{(i^{\frac{1}{\alpha }}-m^{\frac{1}{\alpha }})}^{1-\alpha }}+\frac{L}{\mathrm{\Gamma }(1+\alpha )}{\xi }^{\frac{1}{\alpha }-1}h+C_{2}h\hfill \\ \hfill & \le C_{3}h+\frac{C_{0}L}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^{i-1}h\frac{m^{\frac{1}{\alpha }-1}}{{(i^{\frac{1}{\alpha }}-m^{\frac{1}{\alpha }})}^{1-\alpha }},\hfill \end{array}$$

where $C_2$ and $C_3$ are two constants independent on h. When applying Lemma 1, the above inequality yields that

$$e_i\le C_{3}h{E}_{1-\alpha }(\frac{\alpha C_0\mathrm{\Gamma }(1-\alpha )}{\mathrm{\Gamma }(1+\alpha )}{\left(ih\right)}^{\frac{1-\alpha }{\alpha }}).$$

Now, we conclude that Scheme I is first-order accurate. The convergence of Scheme II can be obtained in a similar fashion. □

2.2. Second-Order Accurate Methods

In this subsection, we present the numerical methods based on the following change in variable:

$$t=s^{2/\alpha }.$$

Again, through Equations (7) and (8), one can check that its solution $z(s)\in C^2[0,T]$ with the change in variable. Therefore, we propose a second-order accurate method based on the product trapezoidal quadrature rule; in other words, we have

$$\begin{array}{ccc}& & {\int }_{s_m}^{s_{m+1}}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}f(r^{2/\alpha },z\left(r\right))dr\hfill \\ \hfill & \approx & {\int }_{s_m}^{s_{m+1}}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\left(\frac{s_{m+1}-r}{h}f(s_m^{2/\alpha },z(s_m))+\frac{r-s_m}{h}f(s_{m+1}^{2/\alpha },z(s_m+1))\right)dr.\hfill \end{array}$$

Then, it follows from Equation (7) again that

$$\begin{array}{ccc}\hfill z\left(s_i\right)& =& z_0+\frac{2}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=0}^{i-1}{\int }_{s_m}^{s_{m+1}}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}f(r^{2/\alpha },z(r))dr\hfill \\ & =& z_0+\frac{2}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=0}^{i-1}{\int }_{s_m}^{s_{m+1}}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}(\frac{s_{m+1}-r}{h}f(s_m^{2/\alpha },z(s_m))+\hfill \\ & & \frac{r-s_m}{h}f(s_{m+1}^{2/\alpha },z(s_m+1)))dr+R_2^i\hfill \\ & =& z_0+\frac{2}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=0}^i{b}_m^{i}f(s_m^{2/\alpha },z(s_m))+R_2^i,\hfill \end{array}$$

(17)

where the truncation error is

$$\begin{array}{ccc}\hfill R_2^i& =& \frac{2}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=0}^{i-1}{\int }_{s_m}^{s_{m+1}}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}(f(r^{2/\alpha },z(r))-\frac{s_{m+1}-r}{h}f(s_m^{2/\alpha },z(s_m))-\hfill \\ & & \frac{r-s_m}{h}f(s_{m+1}^{2/\alpha },z(s_m+1)))dr=\mathcal{O}(h^2),\hfill \end{array}$$

and the coefficient is

$$\begin{array}{ccc}\hfill b_0^i& =& {\int }_{s_0}^{s_1}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\frac{s_1-r}{h}dr=\frac{1}{2}{s}_i^2-\frac{1}{2}{(s_i^{2/\alpha }-s_1^{2/\alpha })}^{\alpha }-\frac{1}{h}{\int }_{s_0}^{s_1}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha }dr\hfill \\ & =& \frac{1}{2}{s}_i^2-\frac{1}{2}{(s_i^{2/\alpha }-s_1^{2/\alpha })}^{\alpha }-\frac{\alpha }{2h}{\int }_{s_0^{2/\alpha }}^{s_1^{2/\alpha }}{(s_i^{2/\alpha }-u)}^{\alpha -1}{u}^{\alpha /2}du\hfill \\ & =& \frac{1}{2}{s}_i^2-\frac{1}{2}{(s_i^{2/\alpha }-s_1^{2/\alpha })}^{\alpha }-\frac{\alpha s_i^{2+1}}{2h}{\int }_0^{{(s_1/s_i)}^{2/\alpha }}{(1-r)}^{\alpha -1}{r}^{\alpha /2}dr\hfill \\ & =& \frac{1}{2}{s}_i^2-\frac{1}{2}{(s_i^{2/\alpha }-s_1^{2/\alpha })}^{\alpha }-\frac{\alpha s_i^{2+1}}{2h}\mathbf{B}(i^{-2/\alpha },\alpha /2+1,\alpha ),\hfill \end{array}$$

where $\mathbf{B}(i^{-2/\alpha },\alpha /2+1,\alpha )$ is the product of an incomplete beta function and beta function. For $1\le m\le i-1$, we have

$$\begin{array}{ccc}\hfill b_m^i& =& {\int }_{s_m}^{s_{m+1}}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\left(\frac{s_{m+1}-r}{h}\right)dr+{\int }_{s_{m-1}}^{s_m}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\left(\frac{r-s_{m-1}}{h}\right)dr\hfill \\ & =& \frac{m+1}{2}\left({(s_i^{2/\alpha }-s_m^{2/\alpha })}^{\alpha }-{(s_i^{2/\alpha }-s_{m+1}^{2/\alpha })}^{\alpha }\right)-\frac{m-1}{2}\left({(s_i^{2/\alpha }-s_{m-1}^{2/\alpha })}^{\alpha }-{(s_i^{2/\alpha }-s_m^{2/\alpha })}^{\alpha }\right)\hfill \\ & & -\frac{\alpha s_i^{2+1}}{2h}{\int }_{{\left(s_m/s_i\right)}^{2/\alpha }}^{{\left(s_{m+1}/s_i\right)}^{2/\alpha }}{(1-r)}^{\alpha -1}{r}^{\alpha /2}dr+\frac{\alpha s_i^{2+1}}{2h}{\int }_{{\left(s_{m-1}/s_i\right)}^{2/\alpha }}^{{\left(s_m/s_i\right)}^{2/\alpha }}{(1-r)}^{\alpha -1}{r}^{\alpha /2}dr\hfill \\ & =& \frac{m+1}{2}\left({(s_i^{2/\alpha }-s_m^{2/\alpha })}^{\alpha }-{(s_i^{2/\alpha }-s_{m+1}^{2/\alpha })}^{\alpha }\right)-\frac{m-1}{2}\left({(s_i^{2/\alpha }-s_{m-1}^{2/\alpha })}^{\alpha }-{(s_i^{2/\alpha }-s_m^{2/\alpha })}^{\alpha }\right)\hfill \\ & & -\frac{\alpha s_i^{2+1}}{2h}\mathbf{B}({(m+1/i)}^{2/\alpha },\alpha /2+1,\alpha )+2\frac{\alpha s_i^{2+1}}{2h}\mathbf{B}({(m/i)}^{2/\alpha },\alpha /2+1,\alpha )\hfill \\ & & -\frac{\alpha s_i^{2+1}}{2h}\mathbf{B}({((m-1)/i)}^{2/\alpha },\alpha /2+1,\alpha ).\hfill \end{array}$$

In addition, we have

$$\begin{array}{ccc}\hfill b_i^i& =& {\int }_{s_{i-1}}^{s_i}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\frac{r-s_{i-1}}{h}dr\hfill \\ & =& \frac{\alpha s_i^{2+1}}{2h}\mathbf{B}(1,\frac{\alpha }{2}+1,\alpha )-\frac{\alpha s_i^{2+1}}{2h}\mathbf{B}({((i-1)/i)}^{2/\alpha },\frac{\alpha }{2}+1,\alpha )-\frac{i-1}{2}{(s_i^{2/\alpha }-s_{i-1}^{2/\alpha })}^{\alpha }.\hfill \end{array}$$

Again, by replacing $z(s_i)$ with $z_i$ and omitting the truncation error $R_i$ in Equation (9), we have the following numerical scheme:

$$\begin{array}{ccc}\hfill \mathrm{Scheme}\mathrm{III}:z_i& =& z_0+\frac{2}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=0}^i{b}_m^{i}f(s_m^{2/\alpha },z_m).\hfill \end{array}$$

(18)

By applying the Newton linearized method to approximate the nonlinear term, we have the following linearized scheme:

$$\begin{array}{c}\hfill \mathrm{Scheme}\mathrm{IV}:z_i=z_0+\frac{2}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=0}^{i-1}{b}_m^{i}f(s_m^{2/\alpha },z_m)+\frac{2}{\mathrm{\Gamma }(1+\alpha )}{b}_i^i\left(f(s_i^{2/\alpha },z_{i-1})+f_2(s_i^{2/\alpha },z_{i-1})(z_i-z_{i-1})\right).\end{array}$$

(19)

where $f_2(s_i^{2/\alpha },z_{i-1})=\frac{\partial }{\partial y}f(s,y){|}_{s=s_i^{2/\alpha },y=z_{i-1}}$.

By applying the extrapolation to approximate the nonlinear term, we obtain the following linearized scheme:

$$\begin{array}{ccc}\hfill \mathrm{Scheme}\mathrm{V}:z_0& =& z_0,\hfill \\ \hfill z_1& =& z_0+\frac{2}{\mathrm{\Gamma }(1+\alpha )}{b}_0^{1}f(s_0^{2/\alpha },z_0)+\frac{2}{\mathrm{\Gamma }(1+\alpha )}{b}_1^1\left(f(s_1^{2/\alpha },z_0)+f_2(s_1^{2/\alpha },z_0)(z_1-z_0)\right),\hfill \\ \hfill z_i& =& z_0+\frac{2}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=0}^{i-1}{b}_m^{i}f(s_m^{2/\alpha },z_m)+\frac{2}{\mathrm{\Gamma }(1+\alpha )}{b}_i^{i}f(s_i^{2/\alpha },2z_{i-1}-z_{i-2}),i\ge 2.\hfill \end{array}$$

(20)

Next, we have the following convergence results:

Theorem 2.

Suppose $f\in {\mathcal{C}}^3\left(G\right)$. Then, the schemes in Equations (18)–(20) are second-order accurate.

Proof. 

Let $e_i=z\left(s_i\right)-z_i$. Subtracting Equation (11) from Equation (9) gives

$$\begin{array}{ccc}\hfill |e_i|& =& |e_0+\frac{1}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{b}_m^i(f(s_m^{1/\alpha },z_m)-f(s_m^{1/\alpha },z_m))+R_2^i|\hfill \\ & \le & |e_0|+\frac{L}{\mathrm{\Gamma }(1+\alpha )}\sum _{m=1}^i{b}_m^i|e_i|+|R_2^i|.\hfill \end{array}$$

(21)

Now, we present some estimates for the coefficients $b_m^i$. First, it holds that

$$\begin{array}{ccc}\hfill b_0^i& =& {\int }_{s_0}^{s_1}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\frac{s_1-r}{h}dr=\frac{1}{2}{s}_i^2-\frac{1}{2}{(s_i^{2/\alpha }-s_1^{2/\alpha })}^{\alpha }\le C_1{h}^2\hfill \end{array}$$

For $1\le m\le i-1$, it holds that

$$\begin{array}{ccc}\hfill b_m^i& =& {\int }_{s_m}^{s_{m+1}}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\left(\frac{s_{m+1}-r}{h}\right)dr+{\int }_{s_{m-1}}^{s_m}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\left(\frac{r-s_{m-1}}{h}\right)dr\hfill \\ & =& {(s_i^{2/\alpha }-{\xi }_m^{2/\alpha })}^{\alpha -1}{\xi }_m^{2/\alpha -1}(s_{m+1}-{\xi }_m)+{(s_i^{2/\alpha }-{\tilde{\xi }}_m^{2/\alpha })}^{\alpha -1}{\tilde{\xi }}_m^{2/\alpha -1}({\tilde{\xi }}_m-s_{m-1})\hfill \\ & \le & C_2{h}^2{(i^{2/\alpha }-m^{2/\alpha })}^{\alpha -1}{m}^{2/\alpha -1},\hfill \end{array}$$

where $C_2$ is a constant independent of h, ${\xi }_m\in (s_m,s_{m+1})$, and ${\xi }_m\in (s_{m-1},s_m)$. Noting that

$$\begin{array}{ccc}\hfill b_i^i& =& {\int }_{s_{i-1}}^{s_i}{(s_i^{2/\alpha }-r^{2/\alpha })}^{\alpha -1}{r}^{2/\alpha -1}\frac{r-s_{i-1}}{h}dr\le h{(s_i^{2/\alpha }-s_{i-1}^{2/\alpha })}^{\alpha -1}{s}_i^{2/\alpha -1}\hfill \end{array}$$

then $b_i^i|e^i|$ can be absorbed by the left-hand side of the inequality when h is sufficiently small.

Now, together with the estimates for $b_m^i$ and Lemma 1, we conclude that Scheme III is second-order accurate. The rest of the results can be obtained in a similar manner. □

3. Applications

In this section, several numerical examples are given to illustrate the convergence results, and the $L^{\infty }$ norm of the error is computed with different $\alpha$. All numerical examples are calculated by using the software MATLAB, and $T=1$.

Example 1.

We consider the nonlinear time fractional ODEs as follows:

$$D_{*}^{\alpha }u-(u^2-u)=g,t\in (0,T],$$

(22)

where $g\left(t\right)$ satisfies the exact solution $u=t+t^{\alpha },0<\alpha <1.$

We solve Equation (22) by using Schemes I–V. To verify the numerical errors and convergence orders, we use the temporal step sizes $d_s=1/1000,1/2000,1/3000,1/4000$ with different $\alpha$ in the first-order scheme. The results presented in

Table 1. Errors and orders in temporal direction for Scheme I (Example 1).

	$\mathit{\alpha }=0.4$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
$\mathit{N}$	Errors	Orders	Errors	Orders	Errors	Orders
1000	$3.4639\times {10}^{-1}$	*	$6.7655\times {10}^{-3}$	*	$2.2863\times {10}^{-3}$	*
2000	$1.3343\times {10}^{-1}$	$1.3763$	$3.3359\times {10}^{-3}$	$1.0201$	$1.8669\times {10}^{-3}$	$1.0731$
3000	$8.3082\times {10}^{-2}$	$1.1685$	$2.2133\times {10}^{-3}$	$1.012$	$7.0564\times {10}^{-4}$	$1.0649$
4000	$6.0391\times {10}^{-2}$	$1.1088$	$1.6559\times {10}^{-3}$	$1.0086$	$5.2011\times {10}^{-4}$	$1.0643$

and

Table 2. Errors and orders in temporal direction for Scheme II (Example 1).

	$\mathit{\alpha }=0.4$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
$\mathit{N}$	Errors	Orders	Errors	Orders	Errors	Orders
1000	$4.3014\times {10}^{-1}$	*	$2.7604\times {10}^{-2}$	*	$7.1714\times {10}^{-3}$	*
2000	$2.7749\times {10}^{-1}$	$0.6324$	$1.4006\times {10}^{-2}$	$0.9788$	$3.5936\times {10}^{-3}$	$0.9968$
3000	$2.0582\times {10}^{-1}$	$0.7368$	$9.3831\times {10}^{-3}$	$0.9879$	$2.3972\times {10}^{-3}$	$0.9985$
4000	$1.6379\times {10}^{-1}$	$0.7941$	$1.6559\times {10}^{-3}$	$1.0086$	$1.7983\times {10}^{-3}$	$0.9991$

indicate that the convergence order was one, which coincided with our theoretical results. In

Table 3. Errors and orders in temporal direction for Scheme III (Example 1).

	$\mathit{\alpha }=0.4$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
$\mathit{N}$	Errors	Orders	Errors	Orders	Errors	Orders
100	$1.8761\times {10}^{-2}$	*	$7.2753\times {10}^{-5}$	*	$2.6841\times {10}^{-5}$	*
200	$3.7660\times {10}^{-3}$	$2.3167$	$1.8112\times {10}^{-5}$	$2.0060$	$6.6615\times {10}^{-6}$	$2.0105$
400	$9.0495\times {10}^{-4}$	$2.0571$	$4.5335\times {10}^{-6}$	$1.9983$	$1.6600\times {10}^{-6}$	$2.0046$
800	$2.2606\times {10}^{-4}$	$2.0012$	$1.1354\times {10}^{-6}$	$1.9974$	$4.1439\times {10}^{-6}$	$2.0021$

,

Table 4. Errors and orders in temporal direction for Scheme IV (Example 1).

	$\mathit{\alpha }=0.4$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
$\mathit{N}$	Errors	Orders	Errors	Orders	Errors	Orders
100	$1.5948\times {10}^{-1}$	*	$2.2079\times {10}^{-3}$	*	$2.4690\times {10}^{-4}$	*
200	$3.1524\times {10}^{-2}$	$2.3388$	$3.6106\times {10}^{-4}$	$2.6123$	$3.8513\times {10}^{-5}$	$2.6805$
400	$5.7871\times {10}^{-3}$	$2.4455$	$5.8291\times {10}^{-5}$	$2.6309$	$6.2528\times {10}^{-6}$	$2.6228$
800	$1.0401\times {10}^{-3}$	$2.4761$	$9.2534\times {10}^{-6}$	$2.6552$	$1.0753\times {10}^{-6}$	$2.5998$

and

Table 5. Errors and orders in temporal direction for Scheme V (Example 1).

	$\mathit{\alpha }=0.4$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
$\mathit{N}$	Errors	Orders	Errors	Orders	Errors	Orders
100	$8.7281\times {10}^{-2}$	*	$1.9757\times {10}^{-3}$	*	$2.0034\times {10}^{-4}$	*
200	$2.7388\times {10}^{-2}$	$1.6721$	$3.2896\times {10}^{-4}$	$2.5864$	$3.1694\times {10}^{-5}$	$2.6602$
400	$6.2592\times {10}^{-3}$	$2.1295$	$5.3119\times {10}^{-5}$	$2.6302$	$5.2614\times {10}^{-6}$	$2.5907$
800	$1.2079\times {10}^{-3}$	$2.3735$	$8.3960\times {10}^{-6}$	$2.6615$	$9.3199\times {10}^{-7}$	$2.4971$

, we give the maximum error and the convergence orders for the Newton iterative and Newton linearized methods and the extrapolation skills, respectively. In all these cases, the time steps chosen were $d_s=1/100,1/200,1/400,1/800$, and we can see from Table 3 that the convergence order was two, which is consistent with the theoretical findings. The results illustrated in Table 4 and Table 5 indicate that the numerical experiment performed better than the theoretical conclusions. Here, we also compared our methods with some classical ones, and the results in

Table 6. Errors and orders in temporal direction.

		$\mathit{\alpha }=0.4$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
	$\mathit{N}$	Errors	Orders	Errors	Orders	Errors	Orders
Euler	1000	$5.8753\times {10}^{-3}$	*	$2.5839\times {10}^{-3}$	*	$5.9704\times {10}^{-4}$	*
	2000	$4.9689\times {10}^{-3}$	$0.2418$	$1.7779\times {10}^{-3}$	$0.5394$	$3.5089\times {10}^{-4}$	$0.7668$
	4000	$4.0802\times {10}^{-3}$	$0.2843$	$1.2407\times {10}^{-3}$	$0.5614$	$2.0410\times {10}^{-4}$	$0.7817$
	8000	$3.2811\times {10}^{-3}$	$0.3145$	$8.0860\times {10}^{-4}$	$0.5752$	$1.1806\times {10}^{-4}$	$0.7898$
L1	1000	$8.3161\times {10}^{-3}$	*	$2.8395\times {10}^{-3}$	*	$6.2471\times {10}^{-4}$	*
	2000	$6.4074\times {10}^{-3}$	$0.3762$	$1.8880\times {10}^{-3}$	$0.5888$	$3.5977\times {10}^{-4}$	$0.7961$
	4000	$4.9231\times {10}^{-3}$	$0.3802$	$1.2522\times {10}^{-3}$	$0.5924$	$2.0696\times {10}^{-4}$	$0.7977$
	8000	$3.7727\times {10}^{-3}$	$0.3840$	$8.2909\times {10}^{-4}$	$0.5949$	$1.1897\times {10}^{-4}$	$0.7987$
CQBDF1	10	$6.6267\times {10}^{-3}$	*	$1.5370\times {10}^{-3}$	*	$1.8332\times {10}^{-4}$	*
	20	$5.1092\times {10}^{-3}$	$0.3752$	$1.0393\times {10}^{-3}$	$0.5646$	$1.1208\times {10}^{-4}$	$0.7099$
	40	$3.9323\times {10}^{-3}$	$0.3810$	$6.9808\times {10}^{-4}$	$0.5741$	$6.7741\times {10}^{-4}$	$0.7264$
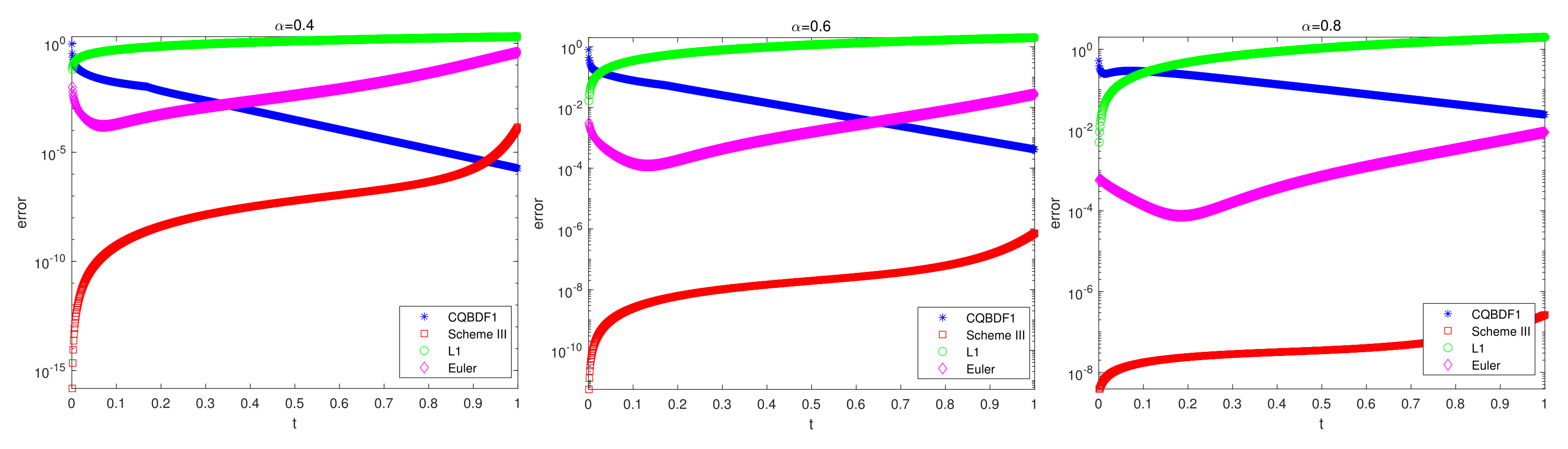
	80	$3.0031\times {10}^{-3}$	$0.3856$	$4.6667\times {10}^{-4}$	$0.5810$	$4.0584\times {10}^{-5}$	$0.7391$

indicate that these methods’ orders were $\alpha$. Moreover, we present the evolution of the maximum norm of the error, and the results found in Figure 1 indicate that our method performed well at the beginning.

Example 2.

We consider the nonlinear time fractional Allen–Cahn equation

$$D_{*}^{\alpha }u-u_{xx}-(u-u^3)=g,(x,t)\in \mathrm{\Omega }\times (0,T],$$

(23)

where $\mathrm{\Omega }=[0,\pi ]$ and $g(x,t)$ satisfies the exact solution is $u(x,t)=(t+t^{\alpha })sinx$.

Similarly, we solve the time-fractional Allen–Cahn equation by using Scheme III based on a variable transform. We take $M=1000$ with $N=8,16,32,64$ to find the maximum of the errors and orders in the temporal direction. Moreover, we consider different spatial step sizes $d_x=\frac{\pi }{M}$, where $M=8,16,32,64$ with $N=1000$ for different $\alpha$. The numerical errors are shown in

Table 7. Errors and orders in temporal direction for Scheme III (Example 2).

	$\mathit{\alpha }=0.4$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
$\mathit{N}$	Errors	Orders	Errors	Orders	Errors	Orders
8	$1.5343\times {10}^{-3}$	*	$3.4241\times {10}^{-4}$	*	$7.3544\times {10}^{-4}$	*
16	$4.3389\times {10}^{-4}$	$1.8222$	$8.7884\times {10}^{-5}$	$1.9459$	$1.6378\times {10}^{-4}$	$2.1669$
32	$1.1709\times {10}^{-4}$	$1.8897$	$2.2818\times {10}^{-5}$	$1.9616$	$3.8450\times {10}^{-5}$	$2.0907$
64	$3.0965\times {10}^{-5}$	$1.9189$	$5.8943\times {10}^{-6}$	$1.9527$	$9.2644\times {10}^{-6}$	$2.0532$

and

Table 8. Numerical spatial accuracy of Scheme III for different $\alpha$ (Example 2).

	$\mathit{\alpha }=0.4$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
$\mathit{M}$	Errors	Orders	Errors	Orders	Errors	Orders
8	$3.4258\times {10}^{-3}$	*	$3.3368\times {10}^{-3}$	*	$3.2843\times {10}^{-3}$	*
16	$8.6220\times {10}^{-4}$	$1.9903$	$8.4019\times {10}^{-4}$	$1.9897$	$8.2728\times {10}^{-4}$	$1.9891$
32	$2.1600\times {10}^{-4}$	$1.9970$	$2.1043\times {10}^{-4}$	$1.9974$	$2.0720\times {10}^{-4}$	$1.9974$
64	$5.4114\times {10}^{-5}$	$1.9969$	$5.2643\times {10}^{-5}$	$1.9990$	$5.1812\times {10}^{-5}$	$1.9997$

, respectively, where it can clearly be seen that the convergence orders in the temporal and spatial directions are both two.

4. Conclusions

In this paper, we presented a family of transformed finite difference methods for numerically solving fractional differential equations while taking the initial singularities of the solutions into account. The convergence results were obtained by using a fractional Grönwall-type inequality. The numerical results were given to illustrate the theoretical results.