Non-Linear Analysis of Novel Equivalent Circuits of Single-Diode Solar Cell Models with Voltage-Dependent Resistance

Abstract

The most commonly used model of solar cells is the single-diode model, with five unknown parameters. First, this paper proposes three variants of the single-diode model, which imply the voltage dependence of the series resistance, parallel resistance, and both resistors. Second, analytical relationships between the current and the voltage expressed were derived using the Lambert W function for each proposed model. Third, the paper presents a hybrid algorithm, Chaotic Snake Optimization (Chaotic SO), combining chaotic sequences with the snake optimization algorithm. The application of the proposed models and algorithm was justified on two well-known solar photovoltaic (PV) cells—RTC France solar cell and Photowatt-PWP201 module. The results showed that the root-mean-square-error (RMSE) values calculated by applying the proposed equivalent circuit with voltage dependence of both resistors are reduced by 20% for the RTC France solar cell and 40% for the Photowatt-PWP201 module compared to the standard single-diode equivalent circuit. Finally, an experimental investigation was conducted into the applicability of the proposed models to a solar laboratory module, and the results obtained proved the relevance and effectiveness of the proposed models.

1. Introduction

1.1. Background

In the near future, energy demand will almost double for many reasons, while water and food demand is expected to increase significantly. Unfortunately, countries’ economies are greatly affected by energy shortages, especially when energy resources are not independent, as evidenced by the Russian-Ukrainian war and the COVID-19 pandemic. Thus, on the one hand, all states aspire to harness their natural resources to serve them and to be economically independent. On the other hand, industrial development and environmental pollution are increasingly affecting the world’s decarbonization [1,2]. The use of renewable energy sources and energy storage technologies can help reduce this pressure on the planet. In this regard, very high expectations and growth in energy use rely on solar energy as a promising player in the carbon-free independent energy mix [3].

In this context, any energy analysis that looks at how a solar power plant connects to the grid has to know how powerful the solar panels are. However, power calculation is directly related to solar power plant management to maximize solar energy, based on the regulation of output voltage and current to obtain maximum power. The knowledge of the solar panel’s mathematical model, i.e., its solar cells’ electrical properties, is fundamental to understanding the challenges of power regulation of the solar panel or the so-called maximum power point tracking (MPPT) [4]. Because of this, estimating the parameters of solar models while creating new models to represent solar cells’ performance is of considerable interest in energy-based research works.

Single-diode, double-diode, and triple-diode models are used in the literature to simulate solar cells electrically. Each of these models consists of a single current generator acting as the source of photocurrent (I_PV) and two resistances, R_S and R_P, which are connected in series and parallel, respectively. The number of diodes in an equivalent circuit can be determined using the triple-diode, double-diode, and single-diode models. The electrical parameters of the diodes employed in the triple-diode and double-diode models—the ideal factor (n) and reverse saturation current (I₀)—are different. The traditional single-diode model has five parameters, the double-diode model has seven parameters, and the triple-diode model has nine parameters [5,6].

1.2. Motivation

At the beginning of the 2000s, several works were presented to investigate new equivalent circuits of solar cell models, which have additional resistors and capacitors [5,6,7,8]. In addition, in the last few years, several works have also been published in which modified equivalent circuits of solar models have been proposed, where additional resistors are added in series with the diode [7]. Specifically, a modification of the triple-diode equivalent circuit has been proposed in [7], and the single-diode equivalent circuit in [8]. However, based on the presented results in these works, it was clear that the proposed modifications in the equivalent circuits have not significantly improved the estimation accuracy of the solar cell parameters, which represents the main motivation for this research. Therefore, the need for an accurate but simple model of solar cells is still an important and trendy research goal. It should be emphasized that in one-diode models and their modified variants [8], there is an analytical dependence between current and voltage, which is not the case in the double-diode and triple-diode models.

1.3. Methodology

In the literature, the authors in [9] presented a modified single-diode model of solar cells in which the series resistance is represented as a voltage-dependent component. The findings of multiple experiments and techniques for modeling this voltage dependency were provided in the paper. Based on [9], emphasis will be placed on creating a novel model in this study that considers both series and parallel resistance and voltage dependency. The primary cause of this is that it was observed while studying solar cell model designs that their characteristics limit the accurate fitting of the simulated and measured curves at high voltage values.

From the point of view of parameter estimation methods, it can be said that the application of metaheuristic algorithms dominates in scientific publications [10,11,12,13,14,15,16,17,18]. These algorithms have a straightforward application, fast search, and adaptability for the range of parameter changes. The list of metaheuristic algorithms and the data source is given in the Appendix A in Table A1 and Table A2. The mentioned tables describe the algorithms used for estimating the parameters in the literature known as solar cells RTC France and PWP Photowatt cell [19,20]. In addition, classical numerical methods were used to estimate the parameters of solar cells, especially those based on iterative methods. Besides, there are analytical methods, which, unlike others, involve many approximate solutions and are the least accurate [8]. To sum up, the most efficient model has not yet been found, nor has the approach for estimating the parameters of solar cells. For this reason, a new hybrid variant of a metaheuristic algorithm is proposed in this work. Namely, it was learned from the literature that the hybridization of algorithms supports the speed of convergence and the obtained solutions [8].

1.4. Novelty and Contributions

The single-diode model is modified in three ways in this study, implying that the series resistance, parallel resistance, and both resistances are all voltage-dependent. Analytical relationships between the expressed current and voltage were developed using the Lambert W function for each suggested model. The paper also introduces a hybrid approach called Chaotic Snake Optimization (Chaotic SO), which combines the snake optimization algorithm and chaotic sequences. The application of the proposed models and algorithm was justified on two well-known solar PV cells–RTC France solar cell and Photowatt-PWP201 module. The findings demonstrated that the suggested equivalent circuit with voltage dependency of both series and parallel resistance has much lower root-mean-square-error (RMSE) values than the conventional single-diode equivalent circuit. Finally, experimental research was carried out to see whether the suggested models could be used in a solar laboratory module, and the outcomes demonstrated the adaptability and efficacy of the proposed models.

The primary contributions of this work are briefed as follows:

• Three new variants of the single-diode model of solar cells are proposed.
• The voltage dependence of the series resistance, parallel resistance and both of them are considered.
• Analytical expressions for current-voltage dependences of the proposed solar cell models are derived using the Lambert W function.
• An improved snake optimization algorithm using chaotic sequences is presented in this work for estimating the parameters of the investigated solar cell and module.
• The results of comparing the proposed algorithm and numerous literature-known algorithms are presented.
• An experimental investigation was conducted into the applicability of the proposed models to a solar laboratory module, and the results obtained proved the relevance and effectiveness of the proposed models.

1.5. Organization

The paper was divided into several sections to present the research results better. In Section 2, a mathematical description of the standard single-diode model of solar cells is given, as well as the results of calculating current-voltage characteristics for two literature-known cells whose parameters were determined by applying different optimization methods. In Section 3, new single-diode equivalent circuits of solar cells are proposed, and the analytical relationships of their current and voltage expressions are presented. Section 4 presents a novel hybrid metaheuristic algorithm called chaotic snake optimization (Chaotic SO). Section 5 presents the results of estimating the parameters of the investigated solar cells using the standard and the proposed equivalent circuits. Section 6 presents the experimental results conducted on a laboratory solar cell. The concluding remarks and future research directions are given at the end of the paper in Section 7, followed by the appendices.

2. Single-Diode Solar Cell Model and Discussion of the Related Literature

This section is divided into two subsections—basic information about the standard single-diode solar cell model and a discussion of the related literature review.

2.1. Basic Information about the Standard Single-Diode Solar Cell Model

The standard single-diode solar cell model (SDM) is a commonly used model for solar cell representation [3]. The equivalent circuit of the SDM is explored in Figure 1. In this figure, the labels are given as follows: R_S is the series resistance, R_P is the parallel resistance, I_pv represents the photo-generated current, and D is the diode.

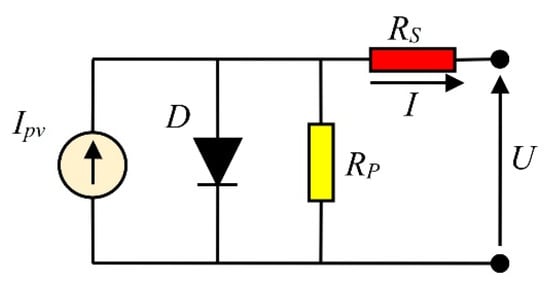
Figure 1. Equivalent circuit of the standard single-diode solar cell model.

The current-voltage relationship of this model is formulated as follows [3]:

$$I=I_{pv}-I_0\left(e^{\frac{U+I{R}_S}{n{V}_t}}-1\right)-\frac{U+I{R}_S}{R_P}$$

(1)

where I is the output current, U denotes the voltage, n is the ideality factor of the diode, and V_t = K_BT/q is the thermal voltage (K_B is the Boltzmann constant, T is the temperature, and q is the electron’s charge).

In SDM, the analytical solution for the current as a function of the voltage is given as follows [3]:

$$I=\frac{R_P\left(I_{pv}+I_0\right)-U}{R_S+R_P}-\frac{n{V}_t}{R_S}W(\beta )$$

(2)

so that

$$\beta =\frac{I_0{R}_P{R}_S}{n{V}_t\left(R_S+R_P\right)}{\mathrm{e}}^{\frac{R_P\left(R_S{I}_{pv}+R_S{I}_0+U\right)}{n{V}_t\left(R_S+R_P\right)}}$$

(3)

where W(β) represents the solution of the Lambert W function, a function of the type W(β) = β∙exp(−W(β)) that can be solved using several methods. Regarding the analytical solution of this equation, it is evident that the special trans function theory (STFT) is the most efficient and accurate method over other analytical solutions in the available literature [3,5]. Therefore, using the STFT, the analytical closed-form solution for the current has the following form:

$$I=\frac{R_P\left(I_{pv}+I_0\right)-U}{R_S+R_P}-\frac{n{V}_t\beta }{R_S}\frac{{{\displaystyle \sum }}_{k=0}^M\frac{{\beta }^k{\left(M-k\right)}^k}{k!}}{{{\displaystyle \sum }}_{k=0}^{M+1}\frac{{\beta }^k{\left(M+1-k\right)}^k}{k!}}$$

(4)

where M represents a positive integer, and the mathematical genesis of the analytical closed-form solution of the Lambert W function, in addition to the theoretical derivation and proofs, are derived in [21].

2.2. Discussion of the Related Literature Review

Table A1 and Table A2 are given in Appendix A, in which a literature review of the estimated parameters using several literature-known approaches that investigated the RTC France solar cell and the Photowatt-PWP201 module are presented. In these tables, values of the root-mean-square-error (RMSE) are calculated as follows:

$$RMSE=\sqrt{\frac{1}{N_{mes}}{\displaystyle \sum _{k=1}^{N_{mes}}{\left(I_k^{meas}-I_k^{sim}\right)}^2}}$$

(5)

N_mes represents the total number of the measured points, while the simulated current values are calculated using (2)–(5). Therefore, this metric defines the degree of matching between measured and simulated curves value. All calculations were carried out in the MATLAB software package, 2018 version.

The graphical presentation of the calculated RMSE values is given in Figure 2a,b for the solar cells investigated. The 3D graph, which illustrates the voltage-method-current and voltage-method-power for both cells, is given in Figure 3, Figure 4, Figure 5 and Figure 6.

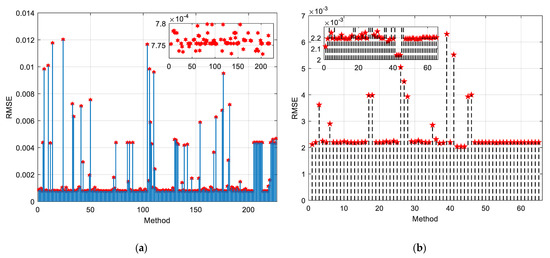
Figure 2. RMSE calculated for: (a) RTC France solar cell; (b) Photowatt-PWP201 module.

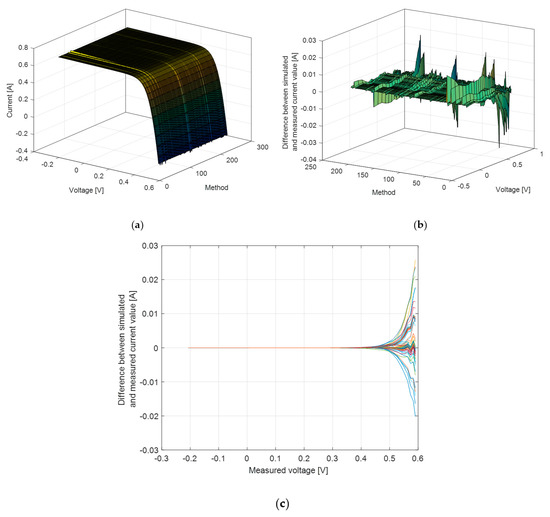
Figure 3. RTC France solar cell: (a) current-voltage characteristics; (b) the corresponding error; (c) error in the current values versus the measured voltage for all methods.

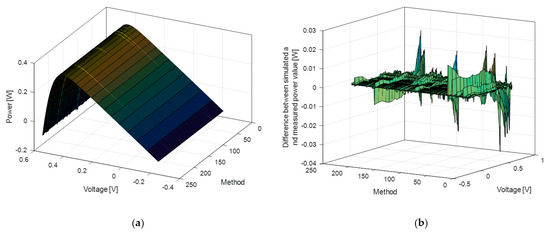
Figure 4. RTC France solar cell: (a) power-voltage characteristics; (b) the corresponding error.

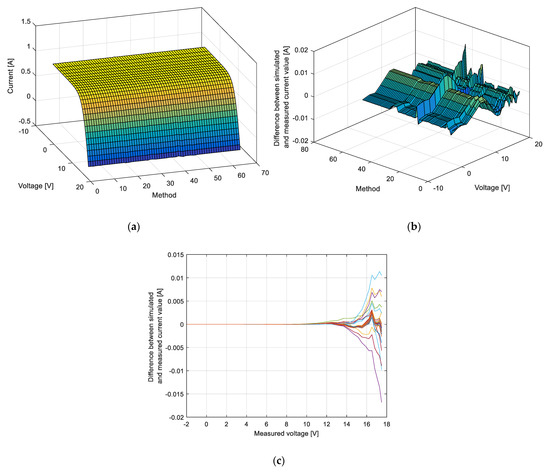
Figure 5. Photowatt-PWP201 module: (a) current-voltage characteristics; (b) the corresponding error; (c) error in the current values versus the measured voltage for all methods.

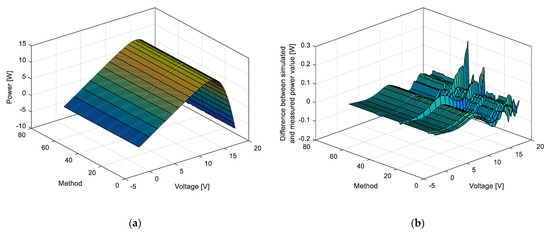
Figure 6. Photowatt-PWP201 module: (a) power-voltage characteristics; (b) the corresponding error.

Based on the presented results, it is clear that many methods enable almost the same results (e.g., values of the estimated parameters) and almost equal RMSE values. This remark is also apparent in the presented 3D graphs. The minimum value of RMSE for the RTC France solar cell was provided by Method 204 [13] in Table A1—application of the GAMS program. The minimum value of RMSE for the Photowatt-PWP201 module was provided by Method 43 [13] in Table A2—application of the guaranteed convergence particle swarm optimization (GCPSO). For RTC France solar cell, the minimum RMSE value is 7.730068 ∙ 10⁻⁴, whilst the minimum RMSE value is 2.040452 ∙ 10⁻³ for the Photowatt-PWP201 module.

3. Equivalent Circuits Proposed

The modified SDM with voltage-dependent series resistance was proposed in [9] to elucidate the electrical behavior of organic solar cells while enhancing the modeling accuracy and benefiting from the simplicity of the equivalent circuit. The reasons for introducing the voltage-dependent series resistance and its physical interpretation were described in [9], in which the modification was mainly related to the internal processes of charge extraction and charge transport. Besides, in [9], it was concluded that a voltage-dependent series resistance provides good knowledge about the behavior of the organic solar cells at different applied voltage regions.

Based on [9], in this section, three novel SDM circuits, shown in Figure 7, are proposed. Unlike the standard SDM, these circuits have voltage-dependent series resistance called SDM_RS (shown in Figure 7a), voltage-dependent parallel resistance called SDM_RP (shown in Figure 7b), and voltage dependence of both resistances called SDM_RPRS (shown in Figure 7c).

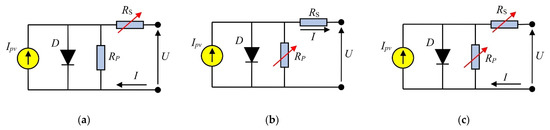
Figure 7. Proposed equivalent circuit non-linear single diode models of solar cells: (a) SDM_RS; (b) SDM_RP; (c) SDM_RPRS.

In SDM_RS, the analytical solution for the current ($I_{n-R_S}$) as a function of the voltage is formulated as follows:

$$I_{n-R_s}=\frac{R_P\left(I_{pv}+I_0\right)-U}{R_{S0}\left(1+k_{n-R_s}U\right)+R_P}-\frac{n{V}_t}{R_{S0}\left(1+k_{n-R_s}U\right)}W\left({\beta }_{n-R_s}\right)$$

(6)

where

$${\beta }_{n-R_s}=\frac{I_0{R}_P{R}_{S0}\left(1+k_{n-R_s}U\right)}{n{V}_t\left(R_{S0}\left(1+k_{n-R_s}U\right)+R_P\right)}{\mathrm{e}}^{\frac{R_P\left(R_{S0}\left(1+k_{n-R_s}U\right)I_{pv}+R_{S0}\left(1+k_{n-R_s}U\right)I_0+U\right)}{n{V}_t\left(R_{S0}\left(1+k_{n-R_s}U\right)+R_P\right)}}$$

(7)

where R_S0 is the series resistance at zero voltage (Ω), while $k_{n-R_s}$ is the series resistance- voltage coefficient (1/V), applying the STFT [22], the current-voltage expression for this model, derived as follows:

$$I_{n-R_s}=\frac{R_P\left(I_{pv}+I_0\right)-U}{R_{S0}\left(1+k_{n-R_s}U\right)+R_P}-\frac{n{V}_t{\beta }_{n-R_s}}{R_{S0}\left(1+k_{n-R_s}U\right)}\left(\frac{{{\displaystyle \sum }}_{k=0}^M\frac{{\beta }_{n-R_s}{}^k{\left(M-k\right)}^k}{k!}}{{{\displaystyle \sum }}_{k=0}^{M+1}\frac{{\beta }_{n-R_s}{}^k{\left(M+1-k\right)}^k}{k!}}\right)$$

(8)

In SDM_RP, the analytical solution for the current $(I_{n-R_P}$) as a function of the voltage is formulated as follows:

$$I_{n-R_P}=\frac{R_{P0}\left(1+k_{n-R_P}U\right)\left(I_{pv}+I_0\right)-U}{R_S+R_{P0}\left(1+k_{n-R_P}U\right)}-\frac{n{V}_t}{R_S}W\left({\beta }_{n-R_P}\right)$$

(9)

where

$${\beta }_{n-R_P}=\frac{I_0{R}_S{R}_{P0}\left(1+k_{n-R_P}U\right)}{n{V}_t\left(R_S+R_{P0}\left(1+k_{n-R_P}U\right)\right)}{\mathrm{e}}^{\frac{R_{P0}\left(1+k_{n-R_P}U\right)\left(R_S{I}_{pv}+R_S{I}_0+U\right)}{n{V}_t\left(R_S+R_{P0}\left(1+k_{n-R_P}U\right)\right)}}$$

(10)

where R_P0 is the parallel resistance at zero voltage (Ω), while $k_{n-R_P}$ is the parallel resistance-voltage coefficient (1/V), and applying the STFT [22], the current-voltage expression is derived for this model as follows:

$$I_{n-R_P}=\frac{R_{P0}\left(1+k_{n-R_P}U\right)\left(I_{pv}+I_0\right)-U}{R_S+R_{P0}\left(1+k_{n-R_P}U\right)}-\frac{n{V}_t{\beta }_{n-R_P}}{R_S}\left(\frac{{{\displaystyle \sum }}_{k=0}^M\frac{{\beta }_{n-R_P}{}^k{\left(M-k\right)}^k}{k!}}{{{\displaystyle \sum }}_{k=0}^{M+1}\frac{{\beta }_{n-R_P}{}^k{\left(M+1-k\right)}^k}{k!}}\right)$$

(11)

In SDM_RPRS, the analytical solution for the current $(I_{n-R_P{R}_S}$) as a function of the voltage is formulated as follows:

$$I_{n-R_P{R}_S}=\frac{R_{P0}\left(1+k_{n-R_P}U\right)\left(I_{pv}+I_0\right)-U}{R_{S0}\left(1+k_{n-R_s}U\right)+R_{P0}\left(1+k_{n-R_P}U\right)}-\frac{n{V}_t}{R_{S0}\left(1+k_{n-R_s}U\right)}W\left({\beta }_{n-R_P{R}_S}\right)$$

(12)

where

$${\beta }_{n-R_P{R}_S}=\frac{I_0{R}_{S0}{R}_{P0}\left(1+k_{n-R_P}U\right)\left(1+k_{n-R_s}U\right)}{n{V}_t\left(R_{S0}\left(1+k_{n-R_s}U\right)+R_{P0}\left(1+k_{n-R_P}U\right)\right)}{\mathrm{e}}^{\frac{R_{P0}\left(1+k_{n-R_P}U\right)\left(R_{S0}\left(1+k_{n-R_s}U\right)I_{pv}+R_{S0}\left(1+k_{n-R_s}U\right)I_0+U\right)}{n{V}_t\left(R_{S0}\left(1+k_{n-R_s}U\right)+R_{P0}\left(1+k_{n-R_P}U\right)\right)}}$$

(13)

Applying the STFT [22], the current-voltage expression is derived as follows:

$$I_{n-R_P{R}_S}=\frac{R_{P0}\left(1+k_{n-R_P}U\right)\left(I_{pv}+I_0\right)-U}{R_{S0}\left(1+k_{n-R_s}U\right)+R_{P0}\left(1+k_{n-R_P}U\right)}-\frac{n{V}_t{\beta }_{n-R_P{R}_S}}{R_S}\left(\frac{{{\displaystyle \sum }}_{k=0}^M\frac{{\beta }_{n-R_P{R}_S}{}^k{\left(M-k\right)}^k}{k!}}{{{\displaystyle \sum }}_{k=0}^{M+1}\frac{{\beta }_{n-R_P{R}_S}{}^k{\left(M+1-k\right)}^k}{k!}}\right)$$

(14)

4. Chaotic SO Algorithm Proposed

The snake optimization (SO) algorithm [23] is inspired by the behavior of snakes, which can be explained in several phases. If the temperature is low and the food is available, the snakes’ mating occurs. Otherwise, snakes will search for food or eat the existing food, depending on the remaining quantity of food.

Like all metaheuristic algorithms, the original version of the SO algorithm starts by generating a random population to begin the optimization process. This process is carried out as represented in (15):

$$X_i=X_{min}+rand\left(X_{max}-X_{min}\right),$$

(15)

where X_i denotes the position of the i-th individual, rand is a random number between 0 and 1, while X_max and X_min are the upper and lower boundaries of the design variables.

This paper proposes a chaotic version of the SO algorithm, named the chaotic-snake optimization (C-SO) algorithm. The proposed algorithm initializes the population using chaotic Gauss mapping [24] instead of conventional random initialization. The equations that describe the initialization process using chaotic Gauss mapping are given as follows:

$$\begin{gathered} y_1=rand, \\ {y}_{i+1}=exp\left(-\alpha y_i{}^2\right)+\beta , \\ {X}_i=X_{min}+y_i\left(X_{max}-X_{min}\right). \end{gathered}$$

(16)

The parameters α and β are related to the width and height of the Gaussian curve, respectively. Interesting chaotic properties occur around −1 ≤ β ≤ 1 on the Gauss map, where the map’s value asymptotically oscillates around −1 and 1.25. The parameters α and β are set to 4.9 and −0.58, according to the original version of Gauss chaotic maps. The main advantage of embedding chaotic maps into the initialization process is obtaining an optimal initial population for the optimization process. Obtaining a good starting population ensures that the proposed chaotic version of the algorithm will converge to the optimal solution faster than the original version.

The iterative process starts with dividing the population into male and female snakes. Assuming an equal number of male and female snakes in the population, if we denote the total number of individuals in the population as N, the number of male snakes as N_m, and the number of female snakes as N_f, the following equations can be applied:

$$\begin{gathered} N_m\approx N/2, \\ {N}_f=N-N_m. \end{gathered}$$

(17)

Afterward, the temperature T and food quantity Q must be calculated:

$$\begin{gathered} T=exp\left(-\frac{ite}{ma{x}_{ite}}\right), \\ Q=c_1 exp\left(\frac{ite-ma{x}_{ite}}{ma{x}_{ite}}\right). \end{gathered}$$

(18)

where ite stands for the current iteration, $ma{x}_{ite}$ denotes the maximum number of iterations, and c₁ is a constant that equals 0.5 [23].

If the Q value is less than the selected threshold (0.25 in [23]), the snakes do not have enough food and must search for it. This phase is called the exploration phase, and the positions of male and female snakes are updated according to the following equations:

$$\begin{gathered} X_{i,m}\left(ite+1\right)=X_{rand,m}\left(ite\right)\pm c_2{A}_m\left(\left(X_{max}-X_{min}\right)rand+X_{min}\right), \\ {X}_{i,f}\left(ite+1\right)=X_{rand,f}\left(ite\right)\pm c_2{A}_f\left(\left(X_{max}-X_{min}\right)rand+X_{min}\right). \end{gathered}$$

(19)

where X_i,m and X_i,f denote the positions of the i-th male and female snakes, while X_rand,m and X_rand,f stand for random male and female snakes, respectively. In the previous equations, A_m and A_f denote the male and female ability to find food and can be calculated as follows:

$$\begin{gathered} A_m=exp\left(-\frac{f_{rand,m}}{f_{i,m}}\right), \\ {A}_f=exp\left(-\frac{f_{rand,f}}{f_{i,f}}\right). \end{gathered}$$

(20)

where f_rand,m and f_rand,f stand for the fitness function values for individuals X_rand,m and X_rand,f. Like this, f_i,m and f_i,f denote the fitness function values for individuals X_i,m(ite) and X_i,f(ite).

Otherwise, if Q is higher than the threshold value, the food exists, and the exploitation phase occurs. Furthermore, it is necessary to examine the temperature T. If T is higher than a certain temperature threshold (selected to be 0.6 as in [23]), the weather is hot, and the snakes will move to the food. In that case, the position of the i-th snake X_i,j is updated according to the following equation:

$$X_{i,j}\left(t+1\right)=X_{food}\pm c_{3}T.rand\left(X_{food}-X_{i,j}\left(t\right)\right),$$

(21)

where c₃ is a constant set to 2 [23], and X_food is the position of the best snake, i.e., the snake whose fitness function has the lowest value. On the other hand, if the temperature T is lower than the threshold, the snakes will fight or mate. In the fight mode, the positions of X_i,m and X_i,f are updated as follows:

$$\begin{gathered} X_{i,m}\left(t+1\right)=X_{i,m}\left(t\right)\pm c_{3}FM.rand\left(X_{best,f}-X_{i,m}\left(t\right)\right), \\ {X}_{i,f}\left(t+1\right)=X_{i,f}\left(t\right)\pm c_{3}FF.rand\left(X_{best,m}-X_{i,f}\left(t\right)\right). \end{gathered}$$

(22)

In the previous equations, X_best,f and X_best,m are the best snakes selected from the female and male populations, respectively. Additionally, FM and FF denote the fighting ability of male and female snakes:

$$\begin{gathered} FM=exp\left(-\frac{f_{best,f}}{f_i}\right), \\ FF=exp\left(-\frac{f_{best,m}}{f_i}\right). \end{gathered}$$

(23)

where f_best,f and f_best,m stand for the fitness function value of the best female and male snakes. Additionally, f_i denotes the fitness function value of the i-th individual.

In the mating mode, the positions of the male and female snakes can be calculated using the following equations:

$$\begin{gathered} X_{i,m}\left(t+1\right)=X_{i,m}\left(t\right)\pm c_3{M}_m.rand\left(Q{X}_{i,f}\left(t\right)-X_{i,m}\left(t\right)\right), \\ {X}_{i,f}\left(t+1\right)=X_{i,f}\left(t\right)\pm c_3{M}_f.rand\left(Q{X}_{i,m}\left(t\right)-X_{i,f}\left(t\right)\right). \end{gathered}$$

(24)

where M_m and M_f denote the mating abilities of male and female snakes, respectively. Thus:

$$\begin{gathered} M_m=exp\left(-\frac{f_{i,f}}{f_{i,m}}\right), \\ {M}_f=exp\left(-\frac{f_{i,m}}{f_{i,f}}\right). \end{gathered}$$

(25)

In the previous equations, f_i,f and f_i,m are the fitness function values of X_i,f(ite) and X_i,m(ite). Finally, the last step of the iteration is to select the worst male snake X_worst,m and the worst female snake X_worst,f and replace them as follows:

$$\begin{gathered} X_{worst,m}=X_{min}+rand\left(X_{max}-X_{min}\right), \\ {X}_{worst,f}=X_{min}+rand\left(X_{max}-X_{min}\right). \end{gathered}$$

(26)

The steps of the proposed C-SO algorithm are summarized in the pseudo-code given in Algorithm 1. Additionally, the flowchart shown in Figure 8 depicts the steps of the C-SO algorithm.

Algorithm 1 Procedure of the Proposed C-SO Algorithm

1: Set parameters N, $ma{x}_{ite}$, Xmin, Xmax, and dimension 2: Initialize the population using Gauss chaotic maps 3: Divide the population N into 2 equal groups–male and female 4: forite = 1 to $ma{x}_{ite}$ 5:   Evaluate each snake from the male and female group 6:   Find the best male fbest,m and best female fbest,f snake 7:   Define temperature T and food quantity Q 8:   if (Q < 0.25) 9:      Perform the exploration phase 10: else if (T > 0.6) 11:       The snakes will move to the food-exploitation phase 12: else 13:       if (rand > 0.6) 14:        Perform the fighting mode of the snakes 15:       else 16:         Perform mating of the snakes 17:         Find the worst male and female snake and update them 18:       end if 19:   end if 20: end for 21: Return the best solution

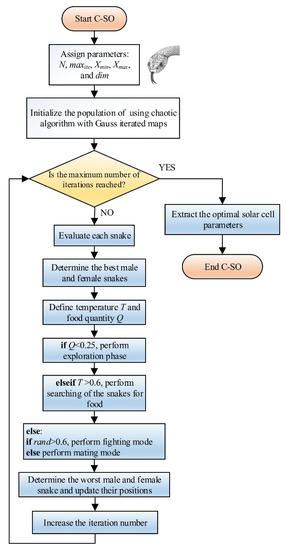
Figure 8. Flowchart of the C-SO algorithm.

5. Numerical Results

This section presents the results of applying the C-SO algorithm to estimate the parameters for standard and proposed solar cell models. The estimation process is used for RTC France solar cell and the Photowatt-PWP201 module. The goal of the estimation process was the minimization of the RMSE represented in Equation (5). However, the current for the proposed circuit was calculated using Equations (8), (11) and (14) based on the circuit type. The results are presented in Table 1 for RTC France solar cell and Table 2 for the Photowatt-PWP201 module. Besides, in Table 1 and Table 2, the values of RMSE calculated for all SDM circuits are also given.

Table 1. Estimated parameters value for the proposed equivalent circuits for the investigated RTC France solar cell.

Parameter	Standard SDM	SDMRS	SDMRP	SDMRPRS
Ipv (A)	0.7607879665080	0.7608049248859	0.7610468429411	0.7613631203879
I0 (μA)	0.3106846042013	0.2991003927335	0.2310892217190	0.0409996462319
n	1.4772677889166	1.4734669046357	1.4488935673420	1.3045585894008
RS (Ω)	0.0365469451928	-	0.0373848509444
RP (Ω)	52.8897883285066	52.6797662689792	-
RS0 (Ω)	-	0.0376221542230	-	0.0618725707814
RP0 (Ω)	-		66.7442335923146	83.3942065127408
kn − Rs	-	0.0440721596083	-	0.5094232140590
kn − Rp	-	-	0.8898254600473	1.5685793413223
RMSE × 10−4	7.7300626899432	7.7289464947487	6.9494430170526	6.1899974615364

Table 2. Estimated parameters value for the proposed equivalent circuits for the investigated Photowatt-PWP201 module.

Parameter	Standard SDM	SDMRS	SDMRP	SDMRPRS
Ipv (A)	1.0323575940489	1.0342899634638	1.0336560526298	1.0385507500932
I0 (μA)	2.4965956963769	0.5898019648459	3.1895652071363	0.1402290648789
n	47.3985550384409	42.6481872737510	48.2903258581200	38.7679613812771
RS (Ω)	1.2405473296235	-	1.2205195472483	-
RP (Ω)	748.323004851098	636.813538190211	-	-
RS0 (Ω)	-	2.1086757391782	-	2.8316185090761
RP0 (Ω)	-	-	414.225359045698	404.119541040858
kn − Rs	-	0.0211826846962	-	0.0288655047700
kn − Rp	-	-	−0.0848837309056	−0.0270864444391
RMSE	0.0020399922732	0.0015210625963	0.0018322922805	0.0012129409135

The current-voltage characteristics, power-voltage characteristics, corresponding current-voltage errors, corresponding power-voltage errors, series resistance–voltage, and parallel resistance–voltage characteristics for both RTC France solar cell and Photowatt-PWP201 module are explored in Figure 9 and Figure 10. Several conclusions can be derived based on the presented results in Table 1 and Table 2 and Figure 9 and Figure 10 for both RTC France solar cell and the Photowatt-PWP201 module.

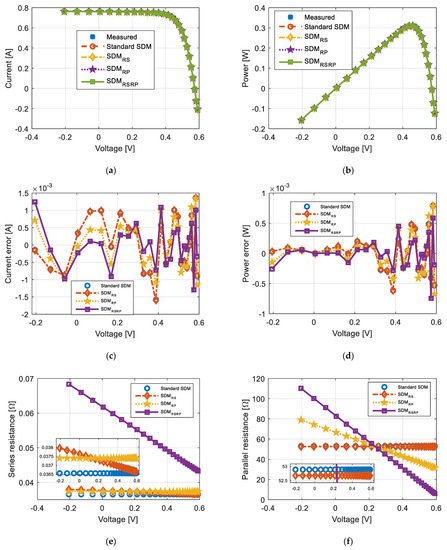
Figure 9. RTC France solar cell: (a) current-voltage characteristics; (b) power-voltage characteristics; (c) corresponding current-voltage errors; (d) corresponding power-voltage errors; (e) series resistance–voltage dependence characteristics; (f) parallel resistance–voltage dependence characteristics.

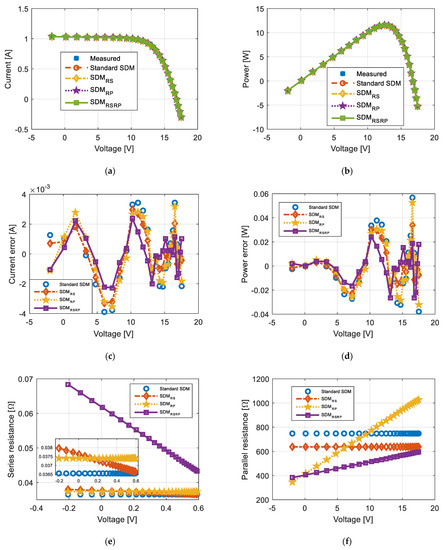
Figure 10. Photowatt-PWP201 module: (a) current-voltage characteristics; (b) power-voltage characteristics; (c) corresponding current-voltage errors; (d) corresponding power-voltage errors; (e) series resistance–voltage dependence characteristics; (f) parallel resistance–voltage dependence characteristics.

• The proposed algorithm is very efficient in estimating parameters for RTC France solar cell and the Photowatt-PWP201 module, as it enables parameters determination with a lower RMSE value than methods listed in Table A1 and Table A2.
• Recalling Section 2, the RMSE for RTC France solar cell determined for standard SDM is 7.730062689943169 × 10⁻⁴, slightly better than the results available in the literature. For the Photowatt-PWP201 module, the RMSE is 0.002039992273216, which is a better result than the results available in the literature.
• Additionally, the voltage dependence of R_P or R_S or both enables better fitting between the measured and simulated characteristics for both investigated solar cells/modules.
• The impact of voltage dependence on individual series or parallel resistance cannot be generally guaranteed as a better effect of the voltage dependence of series resistance for the Photowatt-PWP201 module on the results was observed in Table 2. In contrast, a better impact of the voltage dependence of the parallel resistance for the RTC France solar cell was observed in Table 1.
• The value of RMSE can be reduced by 40% for the Photowatt-PWP201 module and 20% for RTC France solar cell, considering the voltage dependence of both resistances in the solar cell model. Therefore, the matching between measured and simulated curves is significantly improved.

Finally, to test the proposed algorithm’s efficiency over other known algorithms, we compared the original variant of the SO algorithm, the proposed C-SO, particle swarm optimization (PSO), the Aquila optimizer (AO) algorithm and henry gas solubility optimization (HGSO). The results were compared using the same starting conditions and the number of iterations. The algorithm ran 30 independent times, and the best, worst, mean, median, and standard deviation (STD) results were calculated for the same number of iterations. A summary of the results obtained is presented in Table 3.

Table 3. Statistical measures for the obtained results using different algorithms over 30 independent runs.

Measure	C-SO Proposed	Original SO	PSO	AO	HGSO
Best	7.730066720825 × 10−4	7.730112887551 × 10−4	7.757602348738 × 10−4	0.00288037656117	0.00526106472624
Worst	8.468025234636 × 10−4	8.322080126651 × 10−4	0.00198685445976	0.00851885985240	0.01474037311829
Mean	7.826453665352 × 10−4	7.831299232730 × 10−4	0.00105448589746	0.00556610811629	0.01091282953358
Median	7.784837234895 × 10−4	7.786564960706 × 10−4	9.853004240075 × 10−4	0.00574743127044	0.01118504603992
Std	1.408324862610 × 10−5	1.234187862853 × 10−5	3.249036540248 × 10−4	0.00145918070830	0.00250149664426

Additionally, using the collected data, we performed the Wilcoxon p-value test, and the results obtained are given in Table 4. Based on these results, it is evident that the C-SO algorithm enables improvement of the original SO algorithm, outperforming the other algorithms. Additionally, based on the Wilcoxon p-value test, chaotic sequence improved the repeatability of the results. The convergence curve for the algorithms considered in the Wilcoxon p-value test is presented in Figure 11. Based on these results, it is evident that the proposed C-SO algorithm is superior to other literature-known algorithms.

Table 4. Wilcoxon test results.

C-SO Versus SO	C-SO Versus AO	C-SO Versus HGSO	C-SO Versus PSO
6.84322586762450 × 10−3	3.019859359162151 × 10−11	3.019859359162151 × 10−11	1.856733730733403 × 10−9

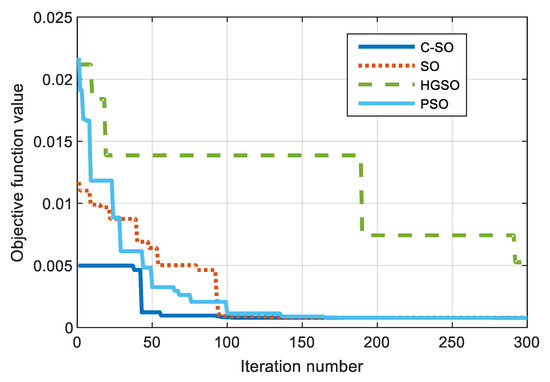
Figure 11. Convergence curve of C-SO versus different algorithms.

6. Experimental Verification

The usefulness of using the new equivalent schemes and the new algorithm to estimate solar cell parameters was covered in the previous section. The applicability of the modified models to a solar laboratory module (part of the laboratory set Clean Energy Trainer) is examined in this section. The method of measurement is as follows. Connect the PC device first, then the USB data monitor, solar cells, and then the USB data monitor. A PC and an active component, such as a solar cell, are connected via a power-electronic device called a USB data monitor. This tool makes it possible to test voltages and currents and scales the results on the computer. Solar cells must also be connected in parallel or in series. After that, we measured the solar module’s temperature, activated solar measurement equipment (in our case, the TES 133R), and set solar lamps at a specific distance. It is required to specify the current and measure the voltage values using the Clean Energy Trainer program loaded on the PC, checking the temperature and insolation of the solar cell or module during all measurements. Figure 12 shows a block diagram of all devices connected.

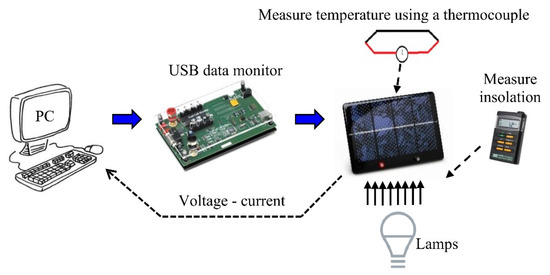
Figure 12. Experimental setup of the solar laboratory module.

Measurements were carefully performed, monitoring all variables (irradiance—1335 W/m², temperature 44 °C, voltage and current measures). The obtained results are then used for solar cell parameters estimation. Furthermore, we determined solar cell parameters for all equivalent circuits proposed. The results are summarized in Table 5. The measured and estimated characteristics of current, power, current error, power error, series resistance-voltage, and parallel resistance-voltage versus voltage are depicted in Figure 13.

Table 5. Estimated parameters value for proposed equivalent circuits for the observed solar laboratory module.

Parameter	Standard SDM	SDMRS	SDMRP	SDMRPRS
Ipv (A)	0.573103853383459	0.574513627819549	0.573197838345865	0.573000469924812
I0 (μA)	0.306664697651680	0.303792633051805	0.303290021746827	0.302816131087847
n	0.388241333333333	0.388215384615385	0.388215384615385	0.388214999538461
RS (Ω)	0.058300000000000	-	0.0570	-
RP (Ω)	120.79060	116.907	-	-
RS0 (Ω)	-	0.0581	-	0.057
RP0 (Ω)	-	-	117.227264	116.8833792
kn − Rs	-	−0.0111	-	− 0.0125
kn − Rp	-	-	0.013110	0.023110
RMSE	0.001940250703697	0.001605316586546	0.001583230030742	0.001504856980387

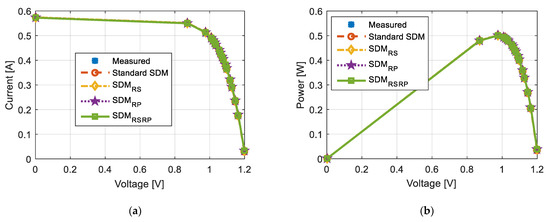
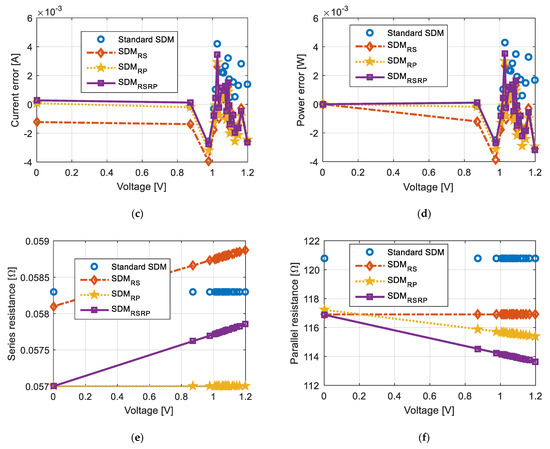
Figure 13. Solar laboratory module: (a) current-voltage characteristics; (b) power-voltage characteristics; (c) corresponding current-voltage errors; (d) corresponding power-voltage errors; (e) series resistance–voltage dependence characteristics; (f) parallel resistance–voltage dependence characteristics.

The first conclusion from all the results presented is that the results are close to each other (as evident in Figure 13 and current and voltage errors in Table 5). Second, the agreement between measured and estimated characteristics is remarkable for all figures. Third, the lowest value of RMSE gives the usage of the equivalent circuit with both resistance variables as a function of voltage. Therefore, for this example it is evident that the proposed equivalent circuits are effective for the current-voltage representation of solar cells. Additionally, the proposed algorithm enables effective solar cell parameter determination.

7. Conclusions

The selection of an appropriate equivalent circuit and the calculation of its parameters are necessary for modeling PV solar cells. In this regard, three new PV equivalent circuits are proposed in this study, in contrast to the many methods proposed in the literature, typically based on basic PV equivalent circuits and modified versions with added resistance. The definition of appropriate resistance as a voltage function gives the proposed schemes their originality.

The analytical equations for all three equivalent circuits are included in the study. The Lambert W function was used to express the current-voltage dependence solution. The C-SO algorithm for determining the solar cell equivalent circuit’s parameters was also put forth in this work.

The RTC France solar cell and the Photowatt-PWP201 module’s parameter estimates were carried out utilizing the proposed algorithm and the proposed equivalent circuits. The findings demonstrated that using the suggested methods, as opposed to conventional equivalent circuits, significantly reduces the RMSE between the measured and estimated values. Additionally, the error can be decreased by up to 20% with RTC France and up to 40% with the Photowatt-PWP201 module. The Clean Energy Trainer setup laboratory cell underwent the same analysis.

Future works will consider the voltage-dependent resistance of double and triple solar cell models for careful investigation of the mathematical analysis of these equivalent solar cell circuit designs. Additionally, new techniques for estimating the characteristics of solar cells will be developed with a specific focus on new hybrid optimization techniques.