Abstract
This research analyzes asymmetric volatility and multifractality in four representative cryptocurrencies using index-based asymmetric multifractal detrended fluctuation analysis. We suggest investigating an idiosyncratic risk premium, which can be obtained by removing the market influence in the cryptocurrency return series. We call the process a capital asset pricing model filter. The analyses on the original return series showed no significant sign of asymmetric volatility. However, the filter revealed a distinct asymmetric volatility, distinguishing the uptrend and downtrend fluctuations. Furthermore, the analyses on the idiosyncratic risk premium detected some cases of asymmetry in the degree and source of multifractality, whereas that on the original return series failed to detect the asymmetry. In conclusion, in a highly volatile market, the capital asset pricing model filter can improve an investigation of the asymmetric multifractality in cryptocurrencies.
1. Introduction
For decades, the characteristics of financial markets and time series have been widely studied. In 1970, Eugene F. Fama proposed the efficient market hypothesis (EMH), claiming that a financial market is efficient when the market price of an asset reflects all available information [1]. Specifically, all available information includes past prices, public information, and inside information. In the weak form of the EMH, all the prices from the past are reflected in the market price where the Markov property of the asset prices holds. Hence, the asset price should follow a random walk. However, many studies have discovered that some events in the financial market are inexplicable with the EMH [2,3]. Such events led to the advent of the fractal market hypothesis (FMH) based on complex theory [4]. The FMH claims that the fractal property exists within the price dynamics of an asset. Note that the fractal property indicates a self-similarity in the financial time series. Especially, the FMH explains the long-memory property of financial time series that the EMH fails to account for. Autocorrelation and fractal properties within a financial time series have been analyzed with the detrended fluctuation analysis (DFA) and multifractal detrended fluctuation analysis (MF-DFA) [5]. Furthermore, the variants of MF-DFA models have been developed to analyze the financial time series [6,7], including the stock market [8,9,10,11,12,13], market efficiency [14,15,16,17,18,19,20], and the commodity market [21,22,23,24].
Financial markets can be classified into two trends: bull and bear markets. The work of [25] stated that each trend should be explained separately. Especially, the asymmetric volatility and multifractality provide evidence of market efficiency and participants’ behavioral aspects toward the positive and negative shocks, which can be utilized to control the financial market. In this context, a method to explore the asymmetry in volatility and multifractality is required. From the perspective of Econophysics, the work of [26] presented the asymmetric DFA (A-DFA), identifying the asymmetric correlation of the time series based on DFA, while the work of [9] presented an asymmetric multifractal DFA (A-MFA) extending the A-DFA. Furthermore, many studies have analyzed asymmetric multifractality using the multifractal detrended moving average [27,28,29]. The aforementioned methods explained the asymmetry in time series with return dynamics. Recently, the work of [30] proposed an index-based A-MFDFA that uses the cumulative return (a.k.a. index dynamics) to determine the trend of time series. Using index dynamics, the work of [30] showed more distinct asymmetric multifractality in the U.S. stock market than the return-based A-MFDFA.
The cryptocurrency market is a new emerging financial market that has received considerable attention after the development of Bitcoin in 2008 [31]. Especially, the market size has been exponentially growing in recent years, and various altcoins have been created. Similar to the traditional financial market, the cryptocurrency market shows a cyclic pattern of bull and bear markets [32,33] with extreme volatility [34] and a fat-tailed return distribution [35]. Dealing with extreme volatility in the market, many researchers have explored the multifractality of cryptocurrencies [36,37,38,39,40], but a limited number of studies have investigated their asymmetric volatility and multifractality. Furthermore, analyses of the multifractal properties of a cryptocurrency’s return series using the method developed for the traditional financial asset might be difficult due to particularly extreme volatility in the market. For instance, the work of [41] showed that the idiosyncratic aspects of the cryptocurrency returns are hard to distinguish due to high correlation and comovement with extreme volatility among them.
Therefore, this research analyzes the asymmetric volatility and multifractality in the cryptocurrency market in recent years using the index-based A-MFDFA. Specifically, we utilize the idiosyncratic risk premium by removing the linear influence of the market on cryptocurrency [41,42]. The removal of market influence is expected to filter the noise from the comovement and reveal the idiosyncratic aspect of each cryptocurrency’s asymmetric volatility and multifractality. Investigating four representative cryptocurrencies from 2018 to 2021, we found that the removal of market influence successfully detected asymmetric volatility. The work of [43] showed the existence of asymmetric volatility in cryptocurrency from 2013 to 2018, in which the market volatility was much less than in recent years. Interestingly, the index-based A-MFDFA on a return series failed to detect distinct asymmetric volatility, while that on an idiosyncratic risk premium detected the property well. Additionally, the removal of market influence was helpful in analyzing the degree and source of asymmetric multifractality. Specifically, the return series showed no asymmetry in the degree and sources, whereas the idiosyncratic risk premium showed asymmetry in Bitcoin and Cardano.
2. Method
2.1. CAPM Filtering
CAPM derives the market equilibrium return of an individual asset under risk in the equilibrium market. First, the Markowitz model provides an efficient frontier using risky assets [44]. If a risk-free asset is included in the investment universe, the optimal portfolio can be obtained by combining a tangent portfolio in an efficient frontier and a risk-free asset, leading to the formulation of CAPM. Let be the daily closing price of an asset i at time t; then, the return, , is
Note that we changed a logarithmic return in [30] to a simple return due to exceptionally high volatility in the cryptocurrency market. Then, CAPM can be defined as a relationship between the sets of the expected excess returns of the market portfolio and individual asset such that
where , , , and are the expected returns of asset i, the expected returns of the associated market, a risk-free rate, and the sensitivity of an excess return of asset i to the market, respectively. Note that indicates an expected excess return on the asset, representing the market risk premium. For simplicity, we set the risk-free rate to zero.
This study focuses on the asymmetric multifractal properties of an asset’s idiosyncratic risk premium that is unique to an individual asset. It implies the specific risk information of a financial asset. In this context, we used a CAPM to filter the market risk from a financial time series. Considering CAPM as a simple factor model, we can obtain the idiosyncratic risk premium of an asset i with the ordinary least squares method as follows:
where and indicate an expected return of an asset i and the associated market index, respectively. Note that is set to zero. and are the intercept and the coefficient of the CAPM filter, respectively. Hence, can be considered an idiosyncratic risk premium since the linear influence of the market return is removed from the original return series. In this study, we investigate the asymmetric multifractal behavior of and simultaneously.
2.2. Index-Based A-MFDFA
The A-MFDFA method can be used to investigate an asymmetric multifractal scaling property in the uptrend and downtrend markets simultaneously. The work of [30] proposed the index-based A-MFDFA that utilizes the cumulative return as a criterion for market classification. Suppose that there exists a time series . Then, the index-based A-MFDFA consists of the following steps:
- Step 1: Determine the profile.where .
- Step 2: Divide the time series into nonoverlapping subtime series.Let as for , where . Note that is an indexing proxy for return series, which can be determined by or . Then, and are divided into nonoverlapping subtime series of equal length n. The number of resulting subtime series is , where is the largest integer less than or equal to . This procedure is repeated from both ends of and , creating subtime series. Suppose : is the jth subtime series of with length n and ; then is the length n subtime series of in the jth time interval. Both and have . Finally, the elements of and areand for , we have
- Step 3: Calculate a local trend and construct the fluctuation function.For each subperiod and , we use the ordinary least squares method to estimateNote that divides the trend of , whereas detrends the time series . In this regard, we define the fluctuation function as follows:
- Step 4: Identify the trend of subtime series.The sign of the slope, , determines the trend for each subperiod and . If (), the subtime series of is classified as an uptrend (downtrend).
- Step 5: Construct q-order average fluctuation functions.Assuming that and , we construct the directional q-order average fluctuation functions for uptrends and downtrends as follows:where ; ; and is a sign of arbitrary value x. Note that the average fluctuation function that does not discriminate the trend of the subtime series can be computed as
- Step 6: Calculate the generalized Hurst exponent.The Hurst exponent is related to the autocorrelation of a time series, claiming the long-term memory property. Let and be the generalized Hurst exponents of the overall trend, uptrend, and downtrend, respectively. These values satisfy the following power-law scaling of , , and , respectively. of a monofractal time series is a constant function of q, whereas that of a multifractal time series is a nonconstant function of q. In addition, a time series is persistent when , whereas it is antipersistent when . Note that a time series follows a random walk when . Furthermore, an asymmetric behavior in time series can be analyzed by comparing the values of and . A time series is symmetric when two values are the same, whereas a time series is asymmetric otherwise.
3. Results and Discussion
3.1. Data
Figure 1 shows the dynamics of the min–max scaled closing price of five representative cryptocurrencies, including Bitcoin (BTC), Ethereum (ETH), Cardano (ADA), Ripple (XRP), and the Cryptocurrency LargeCap Index (INDEX). The closing prices of the cryptocurrencies were obtained from coinmarketcap.com, whereas that of the INDEX was obtained from spglobal.com. The experiment period was from 1 January 2018 to 1 December 2021, consisting of bearish, sideways, and bull markets in chronological order. The period that includes various market conditions can produce comprehensive results of asymmetric multifractal behavior. Cryptocurrencies are traded 24/7, but the market index provided by the S&P is only traded on business days. Thus, we utilized 1023 daily closing prices limited to business days. The daily price dynamics of all cryptocurrencies varied with the same trend. Interestingly, the price of the INDEX represented the weighted average of the prices of all cryptocurrencies well. The price change in the INDEX appeared to be highly affected by that of BTC, consistent with the fact that the market capitalization of BTC overwhelmed that of others.
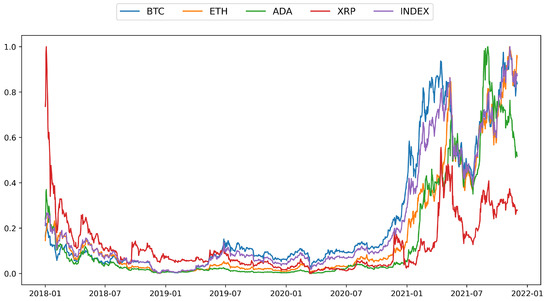
Figure 1.
BTC, ETH, ADA, XRP, and INDEX price dynamics on the same scale.
Figure 2 shows the CAPM filtering of the market returns on the cryptocurrency returns. The gray circles represent the returns of the market and the individual cryptocurrency on the x and y axes, respectively. The solid red line represents a fitted regression line. The slopes of BTC, ETH, ADA, and XRP are 0.838, 0.991, 0.947, and 0.848, respectively, indicating the effectiveness of filtering the linear influence from the returns of the INDEX to that of cryptocurrencies. Therefore, as in Equation (3), of four cryptocurrencies can represent an idiosyncratic risk premium.
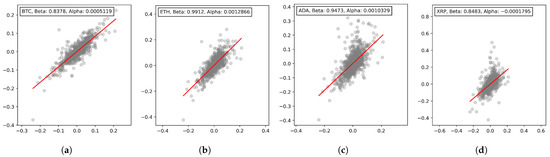
Figure 2.
CAPM filtering on the returns of cryptocurrencies with INDEX. (a) BTC. (b) ETH. (c) ADA. (d) XRP.
Figure 3 represents the original return series on the left and the idiosyncratic risk premium on the right. Since the influence of BTC is critical in the cryptocurrency market with its massive market capitalization, the idiosyncratic risk premium of BTC showed the least volatile dynamics with small peaks compared to those of other cryptocurrencies. Still, the idiosyncratic risk premia of ETH, ADA, and XRP also showed less volatile dynamics than their original series.
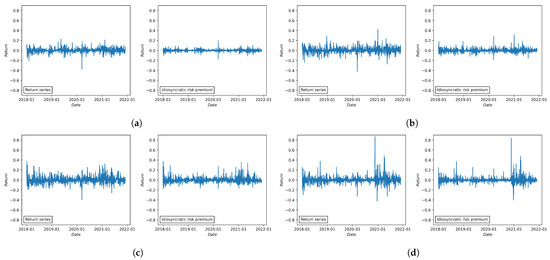
Figure 3.
Daily return series and idiosyncratic risk premium of each cryptocurrency. (a) BTC. (b) ETH. (c) ADA. (d) XRP.
3.2. Asymmetric Volatility
Figure 4 shows a change in with respect to the change in using the index-based A-MFDFA on the original return series and idiosyncratic risk premium of each cryptocurrency when . Note that the red, yellow, and blue dots indicate the uptrend, downtrend, and overall trend, respectively. In the case of the original return series, the fluctuation of each trend was not clearly distinguished except for XRP. Specifically, BTC and ETH showed a larger downtrend fluctuation than uptrend fluctuation, whereas ADA and XRP showed the opposite. Unlike the stock market as in [9,30], the representative cryptocurrencies showed weak evidence of asymmetric volatility in the original return series. On the contrary, in the case of the idiosyncratic risk premium, the fluctuation of each trend was more clearly distinguished than the original return series for all cryptocurrencies. Specifically, all cryptocurrencies showed a larger uptrend fluctuation than a downtrend fluctuation. The results of the idiosyncratic risk premium was consistent with the work of [43], who discovered an increase in the volatility of cryptocurrency after positive shocks using the asymmetric threshold generalized autoregressive conditional heteroskedasticity and quantile regression.
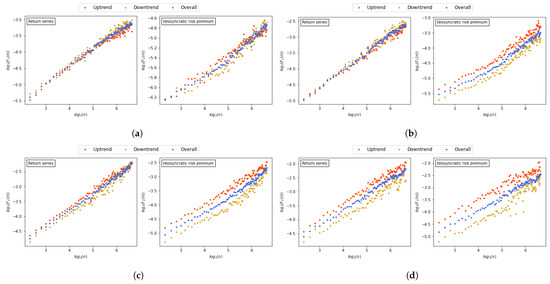
Figure 4.
Plots of vs. with index-based A-MFDFA. (a) BTC. (b) ETH. (c) ADA. (d) XRP.
The increase in volatility after positive shocks can be explained by the herding behavior of uninformed traders who buy assets because they fear missing out on the extreme bull market [43]. In this context, it is interesting that the experiment period of [43] was from 28 April 2013 to 8 August 2018, composed of a long bull market with small volatility. In contrast, the experiment period of this research dealt with the recent cryptocurrency market with much greater volatility. For example, the standard deviation of BTC returns in [43] and this research were 0.044 and 0.2251, respectively. Compared to the financial market, far more uninformed traders exist in the cryptocurrency market. In particular, since 2018, numerous traders have entered the market along with the dynamic increase in cryptocurrency prices, most of whom can be seen as uninformed noise traders. That is, asymmetric volatility should have been strengthened after 2018. However, such a phenomenon was not observed in analyzing the original return series. Interestingly, the aforementioned phenomenon was discovered in the analysis of the idiosyncratic risk premium from the CAPM filtering using the INDEX. The work of [41], who applied a similar filtering method to various cryptocurrencies, showed the difficulty in observing the idiosyncratic aspects of cryptocurrencies other than BTC due to the dominance of BTC in the cryptocurrency market. Therefore, we claim that the individual characteristics of each cryptocurrency’s asymmetric volatility can be analyzed in detail by limiting the influence of the market when the market volatility is severely high, as in this experiment. This claim coincides with the results of BTC, which showed a rather undistinguished fluctuation of each trend even after filtering. Note that the INDEX was highly correlated with BTC.
Figure 5 shows the difference in fluctuations, , of each cryptocurrency. Note that it implies the degree of asymmetry in the fluctuation. The larger the positive value, the larger the uptrend fluctuation is. On the contrary, the smaller the negative value, the larger the fluctuation of the downtrend. When , there is a symmetry between uptrend and downtrend fluctuations. The result of DF is consistent with Figure 4, showing that the DF of the original series of cryptocurrencies was moving around zero except for XRP. In contrast, the of the idiosyncratic risk premium showed positive values for most of n for ETH and ADA. Note that the DFs of BTC and XRP increased after CAPM filtering. Therefore, we claim that CAPM filtering enables an analysis of the asymmetric volatility in each cryptocurrency during the highly volatile market.
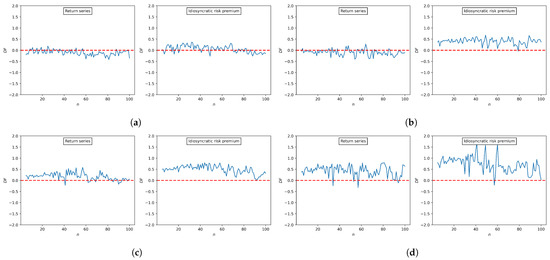
Figure 5.
Plots of with index-based A-MFDFA. (a) BTC. (b) ETH. (c) ADA. (d) XRP. Note that the red dashed horizontal line indicates a symmetry between uptrend and downtrend fluctuations.
3.3. Source of Asymmetric Multifractality
The generalized Hurst exponent varies along q when a time series is multifractal. The primary sources of multifractality are a long-range correlation and a fat-tailed distribution. A long-range correlation can be detected by comparing the original and shuffled time series, whereas a fat-tailed distribution can be detected by comparing the original and surrogate time series. Note that the surrogate time series follows the normal distribution. The processes of creating a randomly shuffled and surrogate financial time series are as follows:
- Randomly shuffled series
- When the length of the entire time series is N, two integers smaller than N are randomly extracted to produce () pairs.
- Swaps the xth value of the original time series with the yth value.
- Repeat 1 and 2 for 20N times.
- Surrogate series
- When the total time series has a length of N, we randomly extract from the Gaussian distribution generated using the mean and variance of the original time series.
- Rearrange to have the same rank pattern as .
The larger the difference between the minimum and maximum of generalized Hurst exponents, the stronger the multifractality is. According to the work of [45], the degree of multifractality is measured as . Let of the original, shuffled, and surrogate series be , , and , respectively. The main source of multifractality is a fat-tail distribution if , whereas it is a long-range correlation if .
At first, we investigated the generalized Hurst exponents of the overall trend(), uptrend(), and downtrend() for q in Figure 6. In the case of the original return series, , , and all decreased as q increased for all representative cryptocurrencies, which implies the existence of multifractal behavior. The asymmetric multifractality can be analyzed using differences between and along q. BTC showed an asymmetric multifractality in small fluctuations, but the asymmetry became subtle as q increased. In contrast, the asymmetry of XRP showed the opposite of BTC. ETH showed a subtle asymmetry for all q. ADA showed a strong multifractality in the uptrend but a relatively weak multifractality in the downtrend. In the case of the idiosyncratic risk premium, BTC and XRP showed a strong multifractality in an uptrend compared to the overall trend and downtrend, implying a significant asymmetry. However, ETH and ADA showed a subtle asymmetric multifractality.
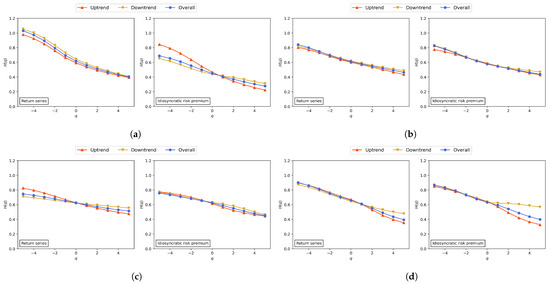
Figure 6.
Generalized Hurst exponent with index-based A-MFDFA. (a) BTC. (b) ETH. (c) ADA. (d) XRP.
The degree of asymmetric multifractality can be further investigated in Table 1. The degree of multifractality in the overall trend, uptrend, and downtrend in the original series explain the asymmetric multifractality in detail. As shown in Figure 6, BTC showed the highest degree of multifractality for the original return series. BTC showed a comparable degree of multifractality between the uptrend and downtrend, whereas ETH, ADA, and XRP showed a higher degree of multifractality in an uptrend than in a downtrend for the original return series. A significantly higher degree of multifractality was revealed through the CAPM filtering in an uptrend for BTC. A higher degree of multifractality in the uptrend was maintained for ADA and XRP after filtering. However, ETH showed a comparable degree of multifractality between the uptrend and downtrend after filtering.

Table 1.
of the original, shuffled, and surrogate series of cryptocurrencies.
The source of asymmetric multifractality can be analyzed in Table 1. The values in parentheses refer to the rate of value decrement against the original series for randomly shuffled, ()/, and surrogate, ()/, time series. Note that and are the average of 30 repetitions. In the case of the return series, each of the four representative cryptocurrencies showed a consistent pattern in the source of multifractality for the overall trend, uptrend, and downtrend, showing no asymmetry. BTC showed a long-range correlation as the source of multifractality for the overall trend, uptrend, and downtrend, whereas ETH, ADA, and XRP showed a fat-tailed distribution as the source. Interestingly, BTC showed significant rates of decrement for the shuffled and surrogate series for the overall trend, uptrend, and downtrend simultaneously. Hence, both the long-range correlation and fat-tail distribution are considerable sources in BTC, consistent with the works of [35,46]. On the contrary, the idiosyncratic risk premium detected an asymmetry in the sources of multifractality between the uptrend and downtrend of BTC and ADA. Unlike the return series, the fat-tailed distribution became the main source in BTC for the overall trend, uptrend, and downtrend. However, the uptrend in BTC showed significant rates of decrement for the shuffled and surrogate series simultaneously, whereas the downtrend showed a significant rate of decrement in the surrogate series only. ADA also showed comparable rates of decrement for the shuffled and surrogate series in a downtrend, but only a significant rate of decrement for the surrogate series in an uptrend.
4. Conclusions
In this study, we used the CAPM filter to investigate asymmetric volatility and multifractality in the cryptocurrency market. The CAPM filter allowed us to compare the original return series and idiosyncratic risk premium of four representative cryptocurrencies, including BTC, ETH, ADA, and XRP. Note that the CAPM filter removed the influence of the market from the cryptocurrency return series. We utilized the Cryptocurrency LargeCap Index provided by the S&P as the market index. We mainly focused on the experiment period from 1 January 2018 to 1 December 2021, which showed significantly higher market volatility than in the past with extreme bull and bear markets. To the best of our knowledge, this is the first attempt to analyze the multifractality of the idiosyncratic risk premium.
The first finding is the CAPM filter’s efficacy in analyzing asymmetric volatility in highly volatile markets. An increase in volatility after positive shocks is a well-known fact in the cryptocurrency market, caused by the herding behavior of uninformed noise traders. Since noise traders were abundant during the experiment period, the multifractal analysis should have identified the asymmetric volatility. However, the original return series analyses showed no significant sign of asymmetric volatility. On the other hand, the analyses on the idiosyncratic risk premium showed a distinct asymmetric volatility, which divides the uptrend and downtrend of ETH, ADA, and XRP. We confirmed the effectiveness of the CAPM filter with rather undistinguished fluctuation of each trend in BTC due to the dominance of BTC in the market index.
The second finding is the CAPM filter’s partial efficacy in analyzing asymmetric multifractality and its source. We found limited evidence of asymmetric multifractality in return series using the generalized Hurst exponent. However, the idiosyncratic risk premium succeeded in showing a significant asymmetry in BTC and XRP, whose uptrend showed a strong multifractality. Furthermore, a higher degree of multifractality in an uptrend was discovered in BTC, ADA, and XRP after the CAPM filtering. In the original return series, the main source of the multifractality in BTC was the long-range correlation, whereas those in ETH, ADA, and XRP were the fat-tailed distribution. The source of the multifractality of four representative cryptocurrencies showed a consistent pattern for the overall trend, uptrend, and downtrend, implying no asymmetry. In contrast, in the idiosyncratic risk premium, the fat-tailed distribution was the main source of the multifractality in all cryptocurrencies. Interestingly, BTC and ADA showed an inconsistent pattern of the sources, which revealed the asymmetry.
The asymmetric volatility and multifractality can be utilized as crucial evidence to understand the market participants and efficiency in different market conditions. However, extreme volatility in the market can blur the individual aspects of cryptocurrencies. Throughout the experiment, we claimed that the CAPM filter can clarify the asymmetric volatility and multifractality using the idiosyncratic risk premium. Despite its novelty, our approach has some limitations that should be addressed in future work. At first, the CAPM filter only removes a linear market influence. It is well known that asset and market returns exhibit a nonlinear relationship with a tail dependence. Additionally, the number of assets in the experiment should be increased, including many small-sized cryptocurrencies. Such research should use a different market index suitable for small-cap cryptocurrencies. From a modeling perspective, the MF-DFA has an advantage in analyzing the nonstationary time series, but its drawback lies in the fact that the periodic trend can affect the Hurst exponent estimation [47]. Furthermore, MF-DFA only handles the local polynomial trend of constant order in detrending, such as linear, quadratic, cubic, or higher order [7]. It is well known that the cryptocurrency market is a nonlinear system with higher complexity than the traditional financial market [48], which could incur a flaw in detrending. We suggest utilizing a set of polynomial and trigonometric functions as in [7] to overcome this limitation.
Author Contributions
Conceptualization, M.L. and J.W.S.; methodology, M.L. and J.W.S.; software, M.L., Y.C. and S.E.O.; data curation, Y.C. and S.E.O.; writing—original draft preparation, M.L., Y.C. and S.E.O.; writing—review and editing, J.W.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2021R1I1A3049656).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fama, E.F. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Wachtel, S.B. Certain observations on seasonal movements in stock prices. J. Bus. Univ. Chic. 1942, 15, 184–193. [Google Scholar] [CrossRef]
- Ball, R. The global financial crisis and the efficient market hypothesis: What have we learned? J. Appl. Corp. Financ. 2009, 21, 8–16. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons: Hoboken, NJ, USA, 1994; Volume 24. [Google Scholar]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.Y.; Gu, G.F.; Zhou, W.X. Modified detrended fluctuation analysis based on empirical mode decomposition for the characterization of anti-persistent processes. Phys. A Stat. Mech. Its Appl. 2011, 390, 4388–4395. [Google Scholar] [CrossRef]
- Morales Martínez, J.L.; Segovia-Domínguez, I.; Rodríguez, I.Q.; Horta-Rangel, F.A.; Sosa-Gómez, G. A modified multifractal detrended fluctuation analysis (MFDFA) approach for multifractal analysis of precipitation. Phys. A Stat. Mech. Its Appl. 2021, 565, 125611. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Disturbances and complexity in volatility time series. Chaos Solitons Fractals 2017, 105, 38–42. [Google Scholar] [CrossRef]
- Cao, G.; Cao, J.; Xu, L. Asymmetric multifractal scaling behavior in the Chinese stock market: Based on asymmetric MF-DFA. Phys. A Stat. Mech. Its Appl. 2013, 392, 797–807. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Bouri, E.; Kayani, G.M.; Nasir, R.M.; Kristoufek, L. Are clean energy stocks efficient? Asymmetric multifractal scaling behaviour. Phys. A Stat. Mech. Its Appl. 2020, 550, 124519. [Google Scholar] [CrossRef]
- Aslam, F.; Mohti, W.; Ferreira, P. Evidence of intraday multifractality in European stock markets during the recent coronavirus (COVID-19) outbreak. Int. J. Financ. Stud. 2020, 8, 31. [Google Scholar] [CrossRef]
- Xu, M.; Shang, P.; Lin, A. Cross-correlation analysis of stock markets using EMD and EEMD. Phys. A Stat. Mech. Its Appl. 2016, 442, 82–90. [Google Scholar] [CrossRef]
- Xu, C.; Ke, J.; Peng, Z.; Fang, W.; Duan, Y. Asymmetric Fractal Characteristics and Market Efficiency Analysis of Style Stock Indices. Entropy 2022, 24, 969. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, A.K.; Aye, G.C.; Gupta, R. Stock market efficiency analysis using long spans of data: A multifractal detrended fluctuation approach. Financ. Res. Lett. 2019, 28, 398–411. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Kim, S.; Chang, W. Asymmetric market efficiency using the index-based asymmetric-MFDFA. Phys. A Stat. Mech. Its Appl. 2018, 512, 1278–1294. [Google Scholar] [CrossRef]
- Zhuanga, X.; Wei, D. Asymmetric multifractality, comparative efficiency analysis of green finance markets: A dynamic study by index-based model. Phys. A Stat. Mech. Its Appl. 2022, 604, 127949. [Google Scholar] [CrossRef]
- Choi, S.Y. Analysis of stock market efficiency during crisis periods in the US stock market: Differences between the global financial crisis and COVID-19 pandemic. Phys. A Stat. Mech. Its Appl. 2021, 574, 125988. [Google Scholar] [CrossRef]
- Mnif, E.; Jarboui, A. COVID-19, bitcoin market efficiency, herd behaviour. Rev. Behav. Financ. 2021, 13, 69–84. [Google Scholar] [CrossRef]
- Aslam, F.; Ferreira, P.; Mohti, W. Investigating efficiency of frontier stock markets using multifractal detrended fluctuation analysis. Int. J. Emerg. Mark. 2021. [Google Scholar] [CrossRef]
- Gaio, L.E.; Stefanelli, N.O.; Júnior, T.P.; Bonacim, C.A.G.; Gatsios, R.C. The impact of the Russia-Ukraine conflict on market efficiency: Evidence for the developed stock market. Financ. Res. Lett. 2022, 50, 103302. [Google Scholar] [CrossRef]
- Lahmiri, S.; Uddin, G.S.; Bekiros, S. Nonlinear dynamics of equity, currency and commodity markets in the aftermath of the global financial crisis. Chaos Solitons Fractals 2017, 103, 342–346. [Google Scholar] [CrossRef]
- Stosic, T.; Nejad, S.A.; Stosic, B. Multifractal analysis of Brazilian agricultural market. Fractals 2020, 28, 2050076. [Google Scholar] [CrossRef]
- Arshad, S.; Rizvi, S.A.R.; Haroon, O.; Mehmood, F.; Gong, Q. Are oil prices efficient? Econ. Model. 2021, 96, 362–370. [Google Scholar] [CrossRef]
- Fernandes, L.H.; Silva, J.W.; de Araujo, F.H.; Ferreira, P.; Aslam, F.; Tabak, B.M. Interplay multifractal dynamics among metal commodities and us-epu. Phys. A Stat. Mech. Its Appl. 2022, 606, 128126. [Google Scholar] [CrossRef]
- Pagan, A.R.; Sossounov, K.A. A simple framework for analysing bull and bear markets. J. Appl. Econom. 2003, 18, 23–46. [Google Scholar] [CrossRef]
- Alvarez-Ramirez, J.; Rodriguez, E.; Echeverria, J.C. A DFA approach for assessing asymmetric correlations. Phys. A Stat. Mech. Its Appl. 2009, 388, 2263–2270. [Google Scholar] [CrossRef]
- Gu, G.F.; Zhou, W.X. Detrending moving average algorithm for multifractals. Phys. Rev. E 2010, 82, 011136. [Google Scholar] [CrossRef]
- Zhang, C.; Ni, Z.; Ni, L.; Li, J.; Zhou, L. Asymmetric multifractal detrending moving average analysis in time series of PM2. 5 concentration. Phys. A Stat. Mech. Its Appl. 2016, 457, 322–330. [Google Scholar] [CrossRef]
- Alessio, E.; Carbone, A.; Castelli, G.; Frappietro, V. Second-order moving average and scaling of stochastic time series. Eur. Phys. J. B-Condens. Matter Complex Syst. 2002, 27, 197–200. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Park, J.H.; Chang, W. Asymmetric multi-fractality in the US stock indices using index-based model of A-MFDFA. Chaos Solitons Fractals 2017, 97, 28–38. [Google Scholar] [CrossRef]
- Nakamoto, S.; Bitcoin, A. A peer-to-peer electronic cash system. Bitcoin 2008, 4. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 13 February 2016).
- Kristjanpoller, W.; Bouri, E. Asymmetric multifractal cross-correlations between the main world currencies and the main cryptocurrencies. Phys. A Stat. Mech. Its Appl. 2019, 523, 1057–1071. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Bouri, E.; Takaishi, T. Cryptocurrencies and equity funds: Evidence from an asymmetric multifractal analysis. Phys. A Stat. Mech. Its Appl. 2020, 545, 123711. [Google Scholar] [CrossRef]
- Begušić, S.; Kostanjčar, Z.; Stanley, H.E.; Podobnik, B. Scaling properties of extreme price fluctuations in Bitcoin markets. Phys. A Stat. Mech. Its Appl. 2018, 510, 400–406. [Google Scholar] [CrossRef]
- Takaishi, T. Statistical properties and multifractality of Bitcoin. Phys. A Stat. Mech. Its Appl. 2018, 506, 507–519. [Google Scholar] [CrossRef]
- da Silva Filho, A.C.; Maganini, N.D.; de Almeida, E.F. Multifractal analysis of Bitcoin market. Phys. A Stat. Mech. Its Appl. 2018, 512, 954–967. [Google Scholar] [CrossRef]
- Stavroyiannis, S.; Babalos, V.; Bekiros, S.; Lahmiri, S.; Uddin, G.S. The high frequency multifractal properties of Bitcoin. Phys. A Stat. Mech. Its Appl. 2019, 520, 62–71. [Google Scholar] [CrossRef]
- Mnif, E.; Jarboui, A.; Mouakhar, K. How the cryptocurrency market has performed during COVID 19? A multifractal analysis. Financ. Res. Lett. 2020, 36, 101647. [Google Scholar] [CrossRef]
- Wątorek, M.; Drożdż, S.; Kwapień, J.; Minati, L.; Oświęcimka, P.; Stanuszek, M. Multiscale characteristics of the emerging global cryptocurrency market. Phys. Rep. 2021, 901, 1–82. [Google Scholar] [CrossRef]
- Ghazani, M.M.; Khosravi, R. Multifractal detrended cross-correlation analysis on benchmark cryptocurrencies and crude oil prices. Phys. A Stat. Mech. Its Appl. 2020, 560, 125172. [Google Scholar] [CrossRef]
- Song, J.Y.; Chang, W.; Song, J.W. Cluster analysis on the structure of the cryptocurrency market via bitcoin–ethereum filtering. Phys. A Stat. Mech. Its Appl. 2019, 527, 121339. [Google Scholar] [CrossRef]
- Song, J.W.; Ko, B.; Cho, P.; Chang, W. Time-varying causal network of the Korean financial system based on firm-specific risk premiums. Phys. A Stat. Mech. Its Appl. 2016, 458, 287–302. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T. Asymmetric volatility in cryptocurrencies. Econ. Lett. 2018, 173, 148–151. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Yuan, Y.; Zhuang, X.T.; Jin, X. Measuring multifractality of stock price fluctuation using multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2009, 388, 2189–2197. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, L.; Zhu, Y. Analysis of multifractal characterization of Bitcoin market based on multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2019, 523, 973–983. [Google Scholar] [CrossRef]
- Kracík, J.; Lavička, H. Fluctuation analysis of high frequency electric power load in the Czech Republic. Phys. A Stat. Mech. Its Appl. 2016, 462, 951–961. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, X.; Zhu, X. Cryptocurrency momentum effect: DFA and MF-DFA analysis. Phys. A Stat. Mech. Its Appl. 2019, 526, 120847. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).