On the Validation of a Fractional Order Model for Pharmacokinetics Using Clinical Data
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Calculus
2.2. Fractional Order Compartment Model
2.3. Sensitivity Analysis
3. Methodology
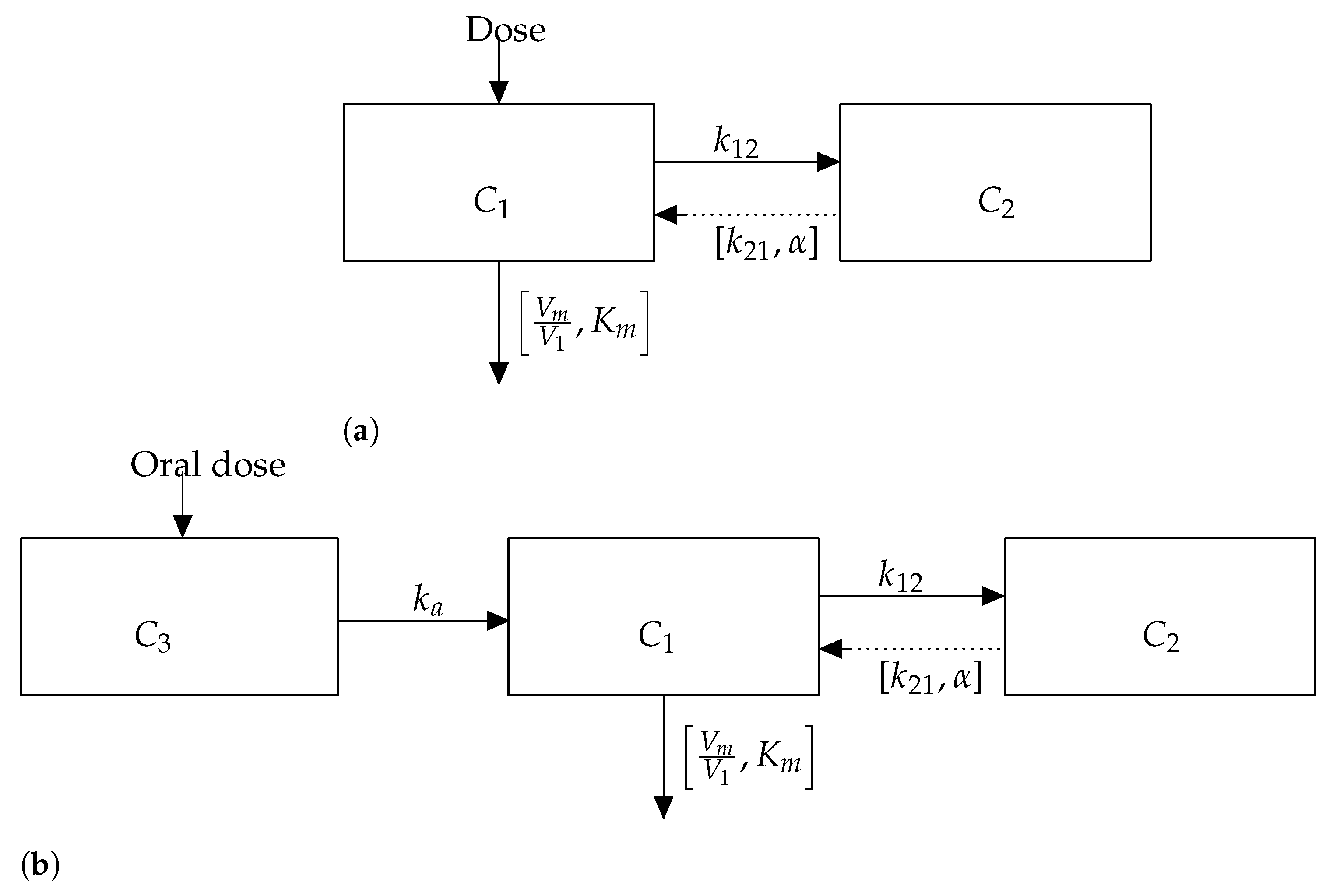
3.1. Model 1: Intravenous Bolus
3.2. Numerical Algorithm
3.2.1. The Grunwald–Letnikov
3.2.2. L1 Approximation
4. Model 2: Oral Absorption
Implementation: The Grunwald–Letnikov and L1 Approximations
- The GL Approximate Formula
- The L1 Approximation
5. Method of Manufactured Solution
- A solution is manufactured.
- The manufactured solution is passed through the governing equation to produce the new source term.
- The source term undergoes verification by being added to the governing equation.
- The code is run and compares the numerical solution to the solution manufactured in step 1 [21].
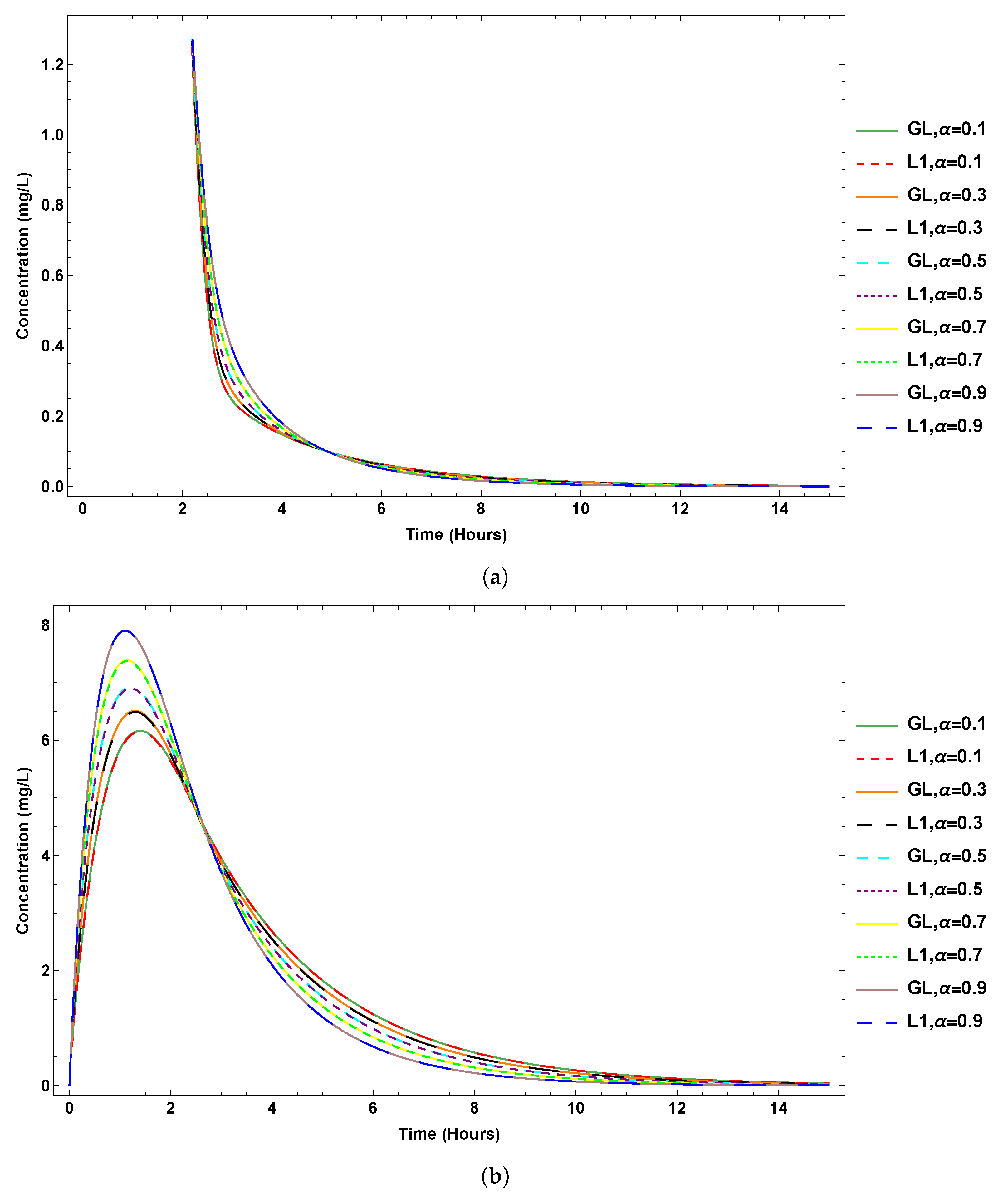
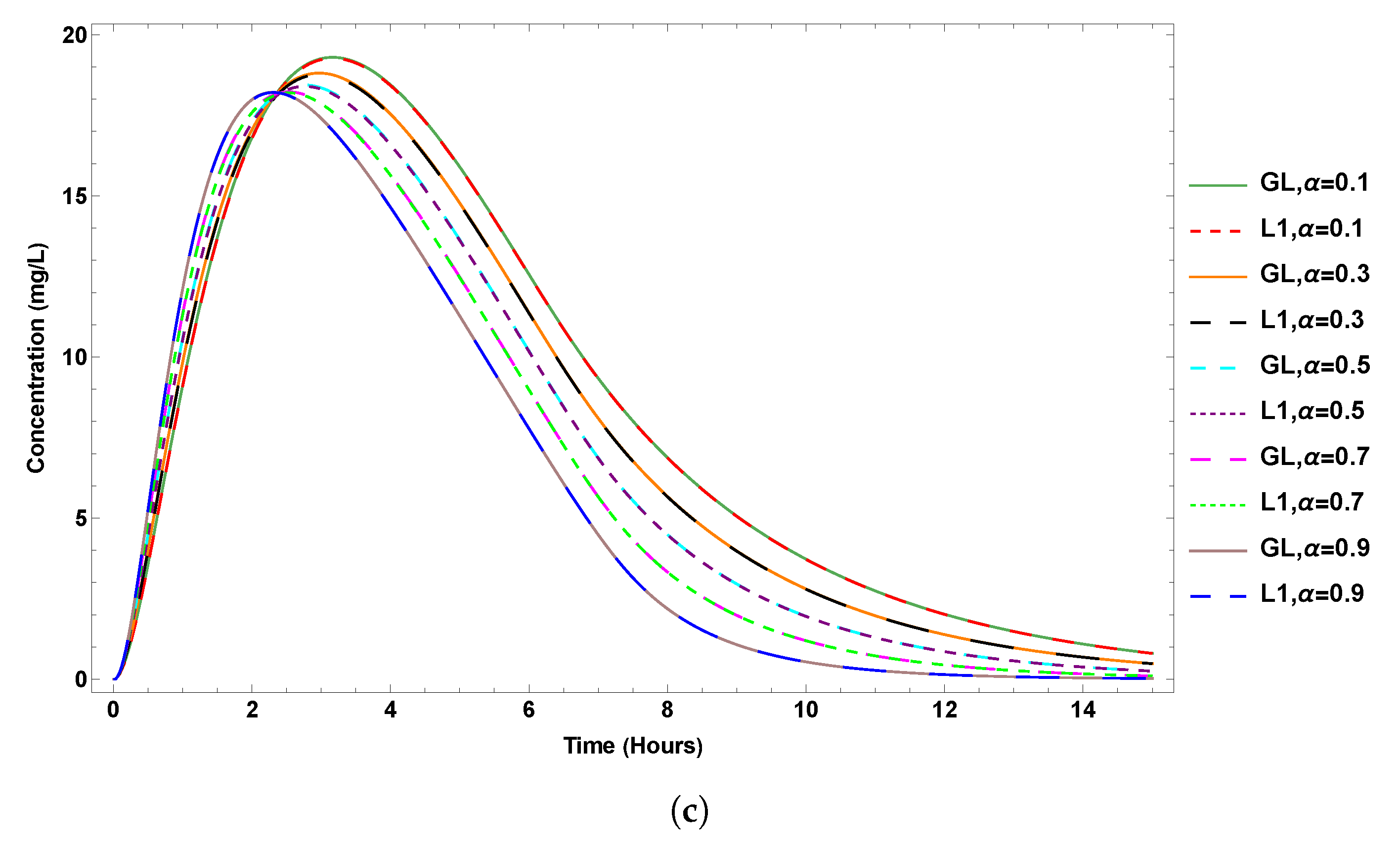
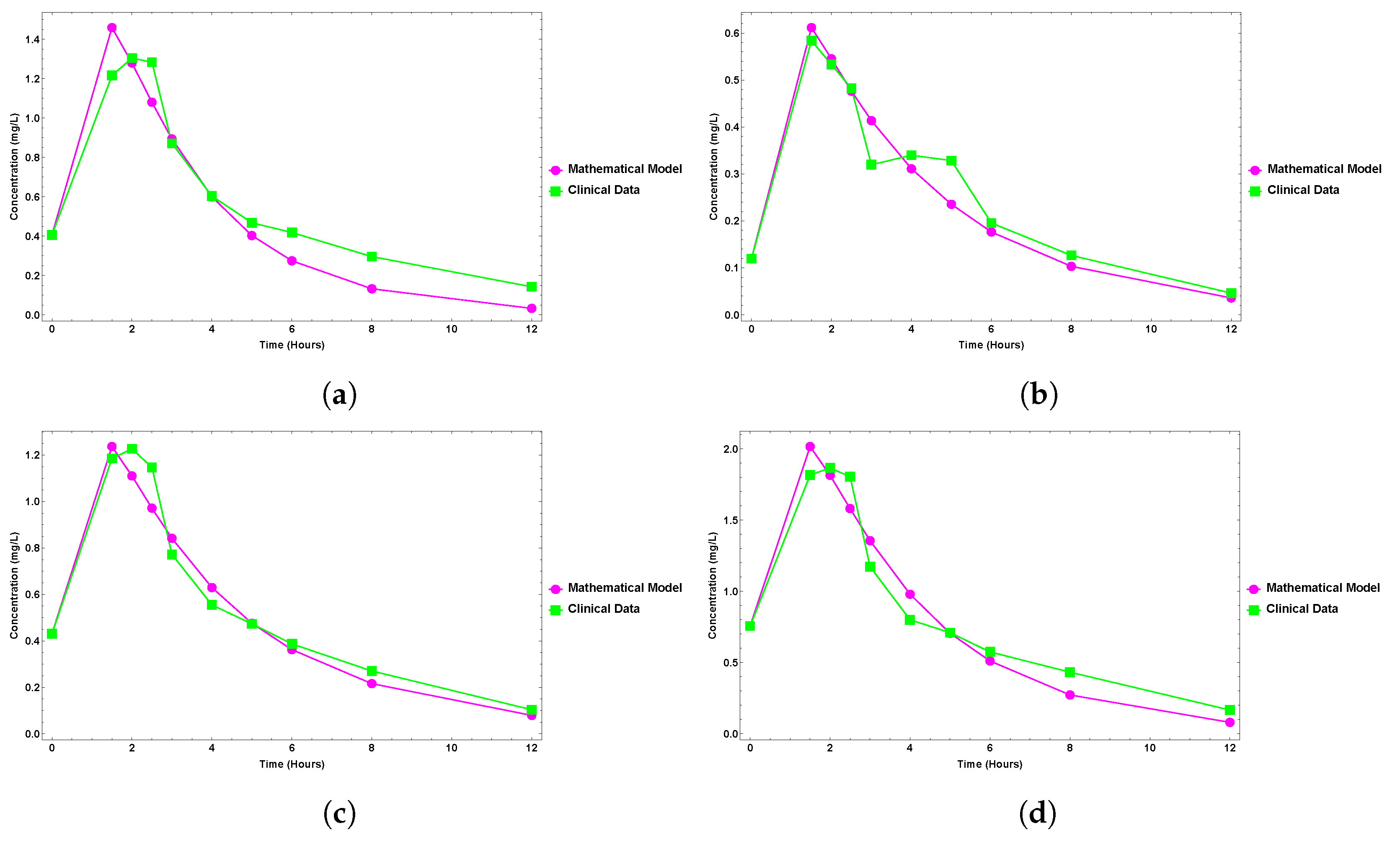
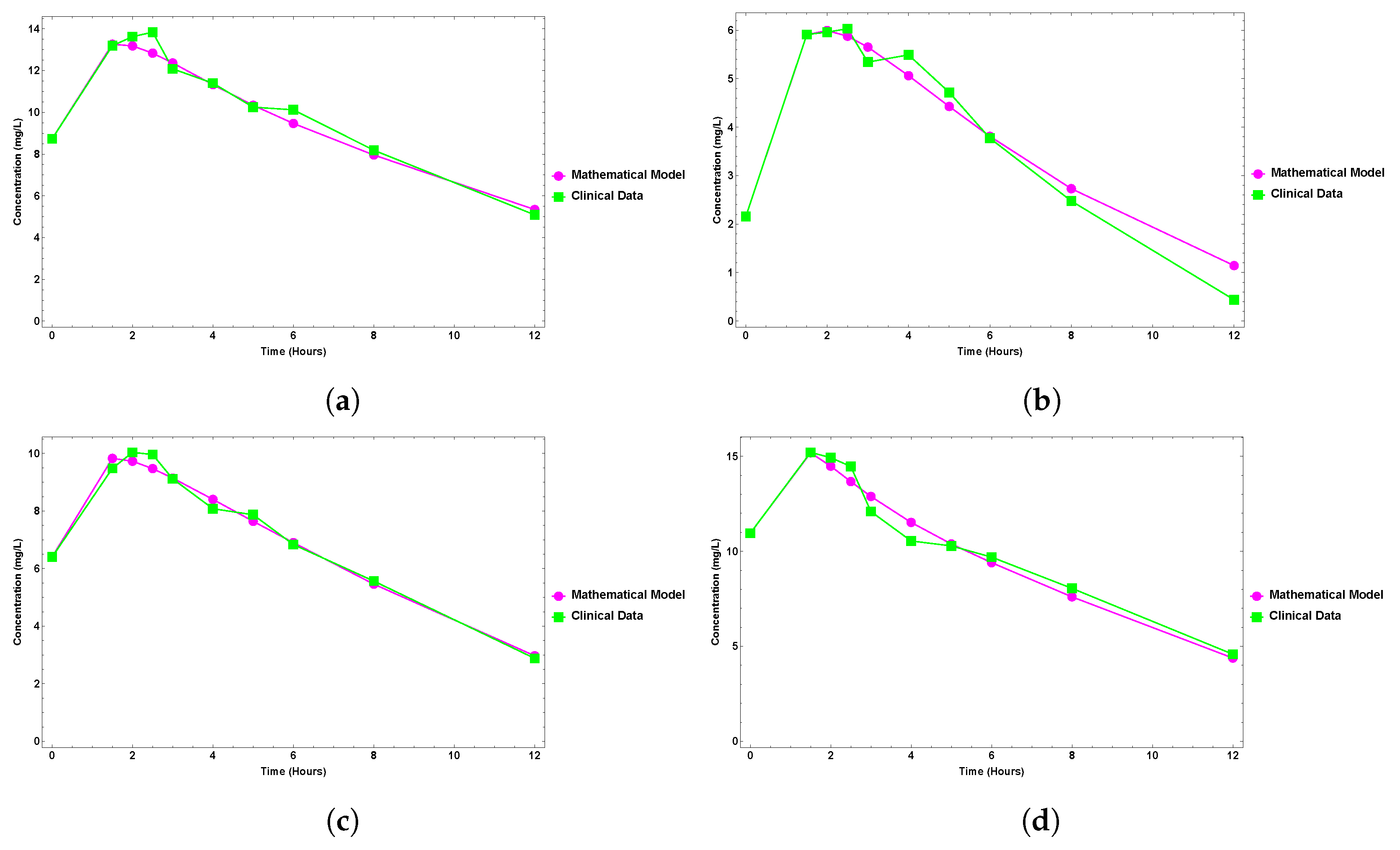
6. Results
7. Sensitivity Analysis
Clinical Data
8. Discussion
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Tatom, F.B. The relationship between fractional calculus and fractals. Fractals 1995, 3, 217–229. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Lazopoulos, A.K. On the mathematical formulation of fractional derivatives. Prog. Fract. Differ. Appl. 2019, 5, 261–267. [Google Scholar]
- Tarasov, V.E. No violation of the Leibniz rule. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2945–2948. [Google Scholar] [CrossRef]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. Fractional kinetics in multi-compartmental systems. J. Pharmacokinet. Pharmacodyn. 2010, 37, 507–524. [Google Scholar] [CrossRef] [PubMed]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. A commentary on fractionalization of multi-compartmental models. J. Pharmacokinet. Pharmacodyn. 2010, 37, 203–207. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; Jacobs, B.A.; McGann, A.V. An explicit numerical scheme for solving fractional order compartment models from the master equations of a stochastic process. Commun. Nonlinear Sci. Numer. Simul. 2019, 68, 188–202. [Google Scholar] [CrossRef]
- Qiao, Y.; Xu, H.; Qi, H. Numerical simulation of a two compartmental fractional model in pharmacokinetics and parameters estimation. Math. Methods Appl. Sci. 2021, 44, 11526–11536. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann–Liouville and caputo derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Kumar, P.; Agrawal, O.P. An approximate method for numerical solution of fractional differential equations. Signal Process. 2006, 86, 2602–2610. [Google Scholar] [CrossRef]
- Kang, Y.-M.; Xie, Y.; Lu, J.-C.; Jiang, J. On the nonexistence of non-constant exact periodic solutions in a class of the Caputo fractional-order dynamical systems. Nonlinear Dyn. 2015, 82, 1259–1267. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Li, C.; Deng, W. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Erickson, A.M.; Henry, B.I.; McGann, A.V.; Murray, J.M.; Nichols, J.A. Fractional order compartment models. SIAM J. Appl. Math. 2017, 77, 430–446. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A Fractional Order Recovery SIR Model from a Stochastic Process. Bull. Math. Biol. 2016, 78, 468–499. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Donnelly, I.C.; Henry, B.I.; Nichols, J.A. A Discrete Time Random Walk Model for Anomalous Diffusion. J. Comput. Phys. 2015, 293, 53–69. [Google Scholar] [CrossRef]
- Bateman, H. Higher Transcendental Functions [Volumes I–III]; McGraw-Hill Book Company: Columbus, OH, USA, 1953; p. 1. [Google Scholar]
- Rabitz, H.; Kramer, M.; Dacol, D. Sensitivity Analysis in Chemical Kinetics. Annu. Rev. Phys. Chem. 1983, 34, 419–461. [Google Scholar] [CrossRef]
- Sopasakis, P.; Sarimveis, H.; Macheras, P.; Dokoumetzidis, A. Fractional calculus in pharmacokinetics. J. Pharmacokinet. Pharmacodyn. 2018, 45, 107–125. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015; p. 24. [Google Scholar]
- Shunn, L.; Ham, F. Method of Manufactured Solutions Applied to Variable-Density Flow Solvers. Annual Research Briefs 2007 Center for Turbulence Research. 2007. pp. 155–168. Available online: https://web.stanford.edu/group/ctr/ResBriefs07/14_shunn_pp155_168.pdf (accessed on 1 October 2022).
- Brglez, Š. Code verification for governing equations with arbitrary functions using adjusted method of manufactured solutions. Eng. Comput. 2014, 30, 669–678. [Google Scholar] [CrossRef]
- Song, N.-N.; Zhang, S.-Y.; Liu, C.-X. Overview of factors affecting oral drug absorption. Asian J. Drug Metab. Pharmacokinet. 2004, 4, 167–176. [Google Scholar]
- Shewchuk, J.R. An Introduction to the Conjugate Gradient Method without the Agonizing Pain; Carnegie-Mellon University: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Decloedt, E.H.; McIlleron, H.; Smith, P.; Merry, C.; Orrell, C.; Maartens, G. Pharmacokinetics of lopinavir in HIV-infected adults receiving rifampin with adjusted doses of lopinavir-ritonavir tablets. Antimicrob. Agents Chemother. 2011, 55, 3195–3200. [Google Scholar] [CrossRef]
- Mtshali, S.; Jacobs, B.A. A Comparative Analysis of Physiologically Based Pharmacokinetic Models for Human Immunodeficiency Virus and Tuberculosis Infections. Antimicrob. Agents Chemother. 2022, 66, e00274-22. [Google Scholar] [CrossRef]
- Ahmed, T. Pharmacokinetics of drugs following IV Bolus, IV infusion, and oral administration. In Basic Pharmacokinetic Concepts and Some Clinical Applications; IntechOpen: London, UK, 2015; Volume 10. [Google Scholar]
- Martinez, M.N.; Amidon, G.L. A mechanistic approach to understanding the factors affecting drug absorption: A review of fundamentals. J. Clin. Pharmacol. 2002, 42, 620–643. [Google Scholar] [CrossRef] [PubMed]
- Unil Université Lausanne. Available online: https://sepia2.unil.ch/pharmacology/parameters/distributioneliminationphase/ (accessed on 18 December 2022).
- Grange, S.; Schutz, M.; Schmitt, C.; Riek, M.; Gaudeul-Ehrhart, E. Unexpected hepatotoxicity observed in a healthy volunteer study on the effects of multiple dose rifampicin on the steady-state pharmacokinetics of ritonavir-boosted saquinavir and vice versa. In Proceedings of the Sixth International Workshop on Clinical Pharmacology of HIV Therapy, Montreal, QC, Canada, 28–30 April 2005; Abstract 35. p. 28. [Google Scholar]
- La Porte, C.J.L.; Colbers, E.P.H.; Bertz, R.; Voncken, D.S.; Wikstrom, K.; Boeree, M.J.; Koopmans, P.P.; Hekster, Y.A.; Burger, D.M. Pharmacokinetics of adjusted-dose lopinavir-ritonavir combined with rifampin in healthy volunteers. Antimicrob. Agents Chemother. 2004, 48, 1553–1560. [Google Scholar] [CrossRef] [PubMed]


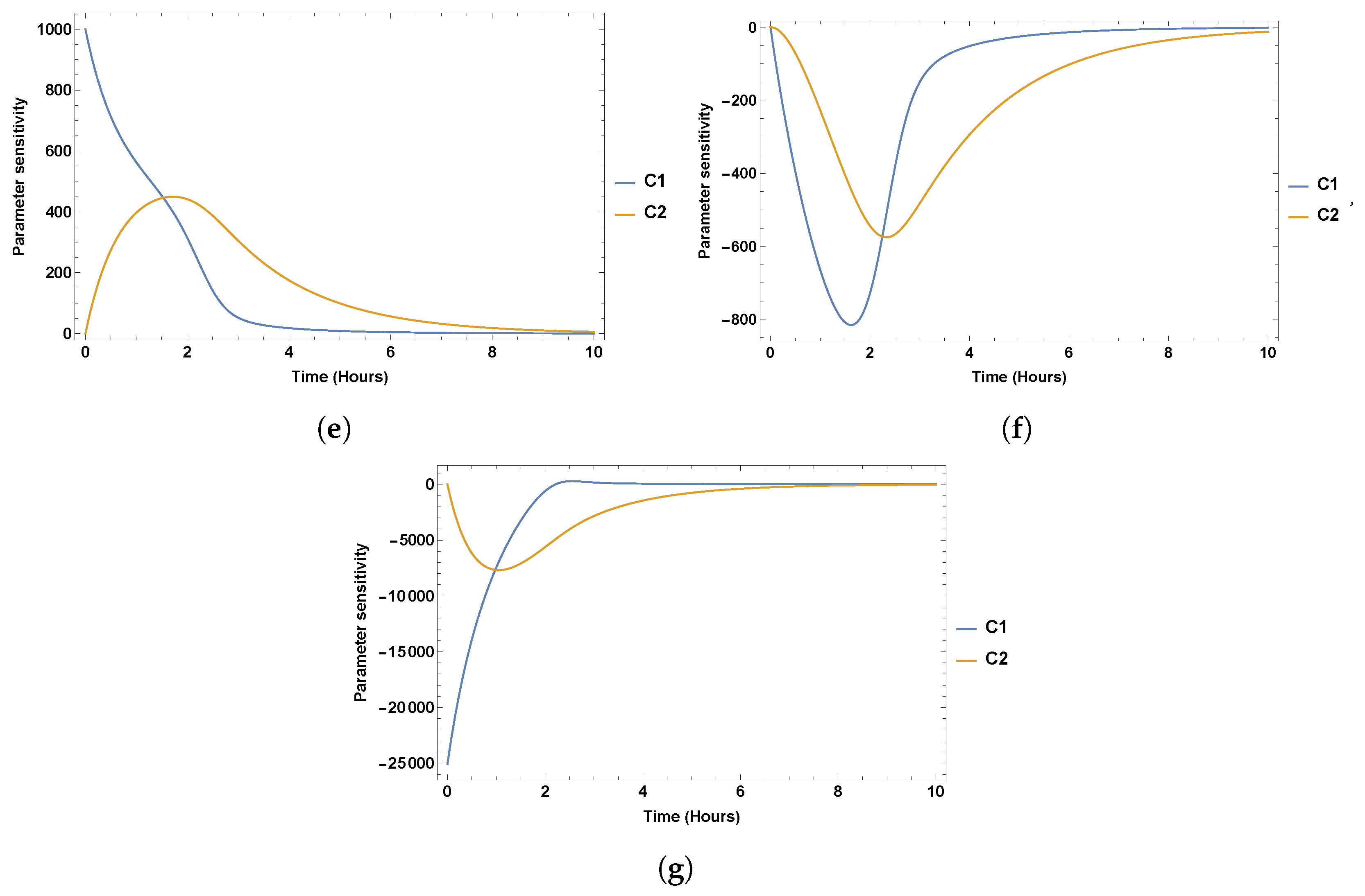
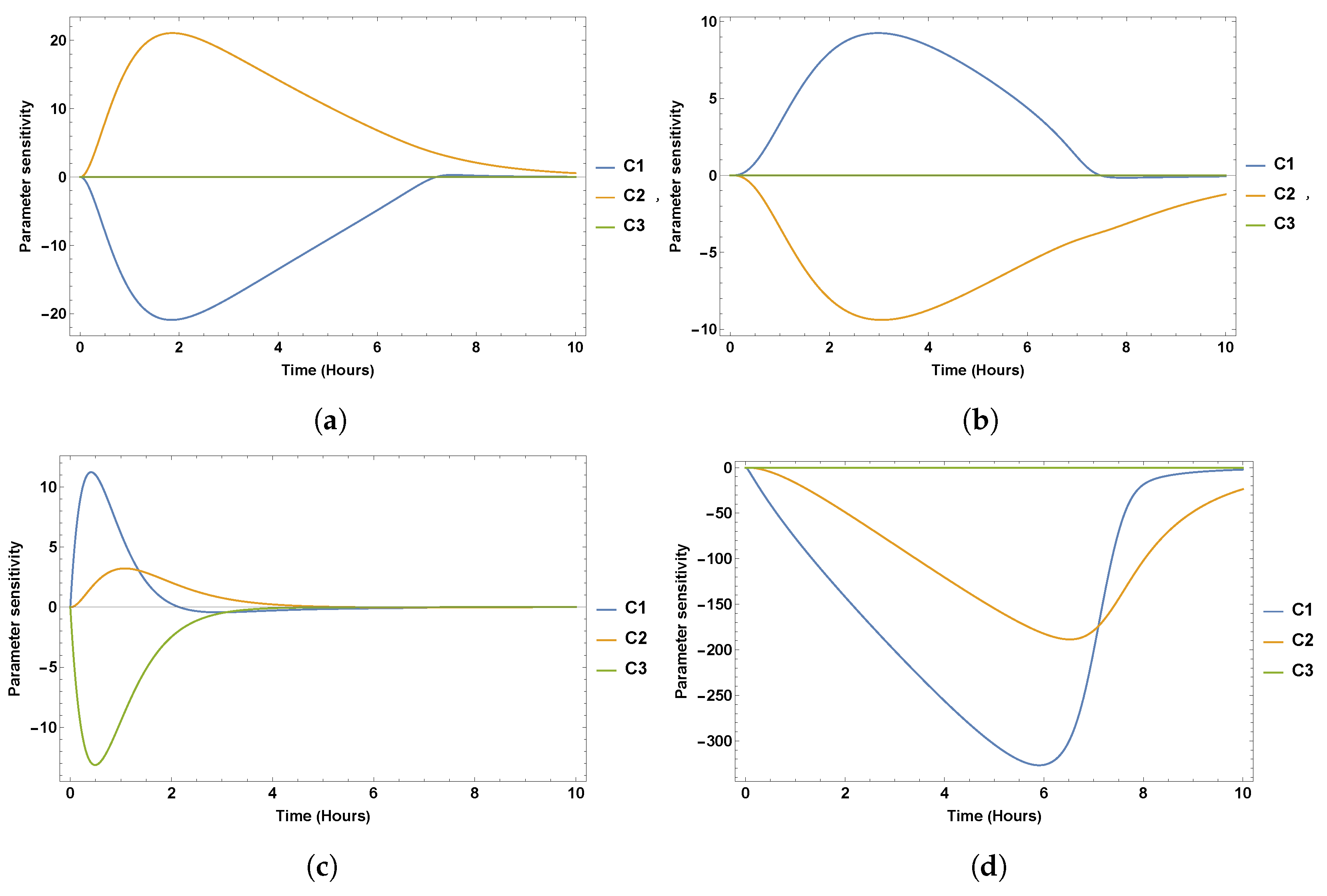

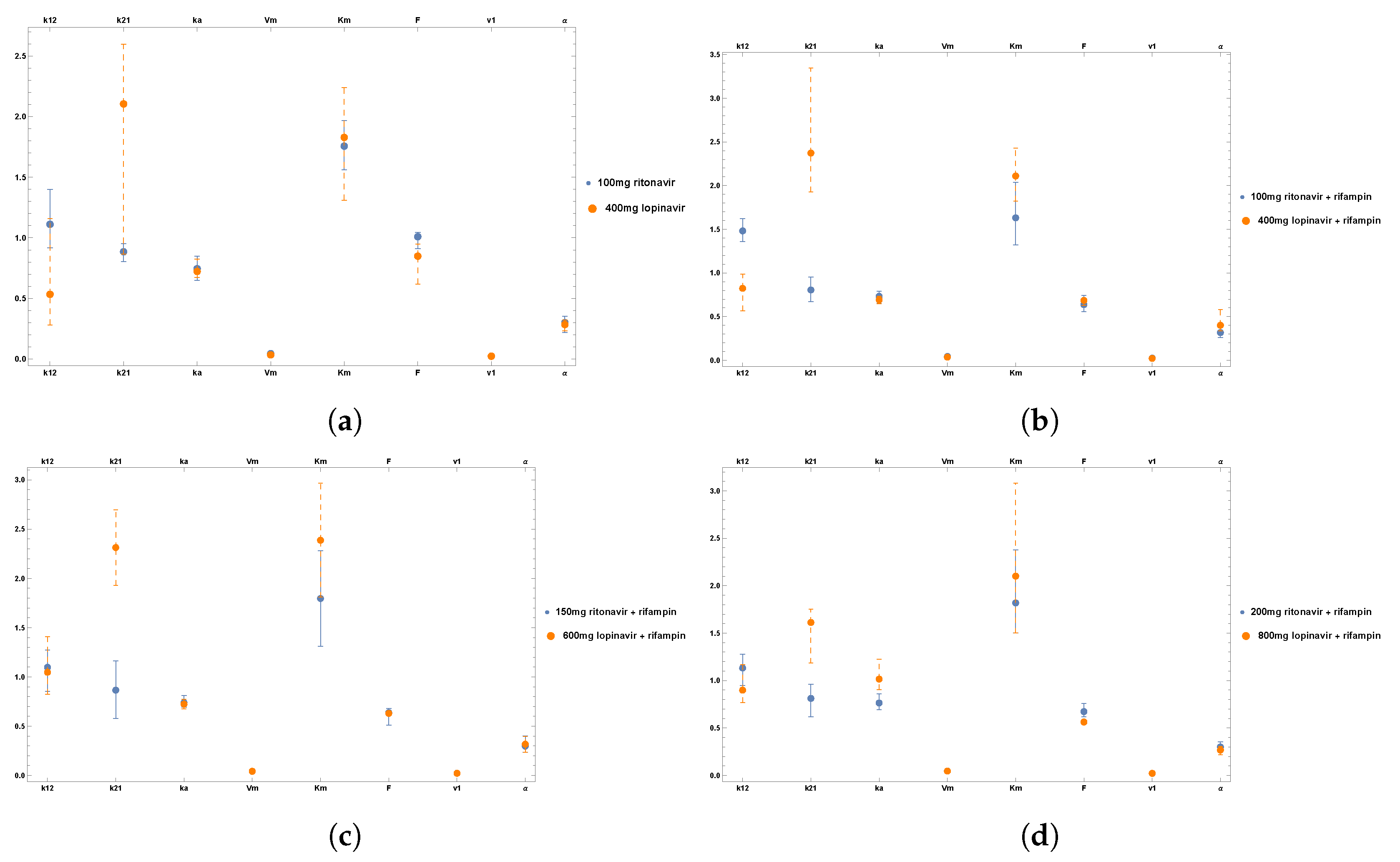
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mtshali, S.; Jacobs, B.A. On the Validation of a Fractional Order Model for Pharmacokinetics Using Clinical Data. Fractal Fract. 2023, 7, 84. https://doi.org/10.3390/fractalfract7010084
Mtshali S, Jacobs BA. On the Validation of a Fractional Order Model for Pharmacokinetics Using Clinical Data. Fractal and Fractional. 2023; 7(1):84. https://doi.org/10.3390/fractalfract7010084
Chicago/Turabian StyleMtshali, Sinenhlanhla, and Byron A. Jacobs. 2023. "On the Validation of a Fractional Order Model for Pharmacokinetics Using Clinical Data" Fractal and Fractional 7, no. 1: 84. https://doi.org/10.3390/fractalfract7010084
APA StyleMtshali, S., & Jacobs, B. A. (2023). On the Validation of a Fractional Order Model for Pharmacokinetics Using Clinical Data. Fractal and Fractional, 7(1), 84. https://doi.org/10.3390/fractalfract7010084







