A Second-Order Crank-Nicolson-Type Scheme for Nonlinear Space–Time Reaction–Diffusion Equations on Time-Graded Meshes
Abstract
1. Introduction
2. Numerical Scheme
2.1. Matrix Transfer Technique for Spatial Discretizations
2.2. Time Discretizations
3. Error and Stability Analysis
3.1. Error Analysis
3.2. Stability Analysis
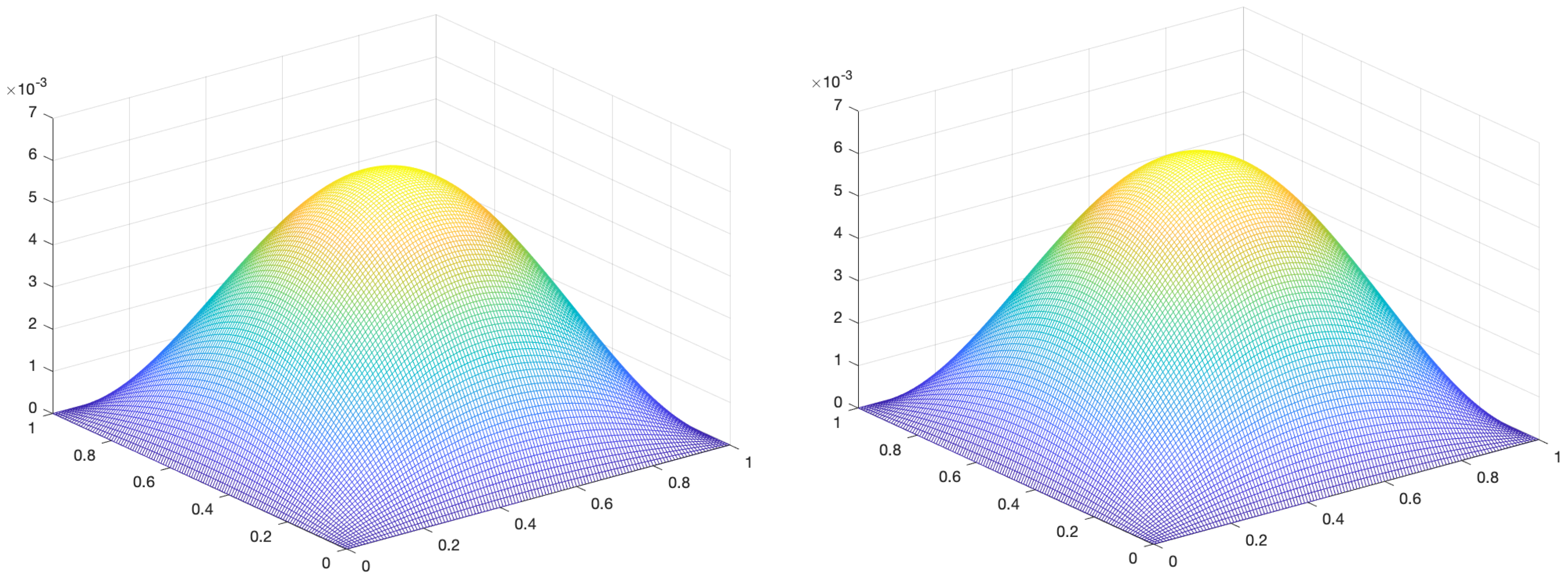
4. Numerical Illustrations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Di Giuseppe, E.; Moroni, M.; Caputo, M. Flux in porous media with memory: Models and experiments. Transp. Porous Media 2010, 83, 479–500. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016; Volume 5. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering 198; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar] [CrossRef]
- Fomin, S.; Chugunov, V.; Hashida, T. Mathematical modeling of anomalous diffusion in porous media. Fract. Differ. Calc. 2011, 1, 1–28. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Cloot, A.; Botha, J. A generalised groundwater flow equation using the concept of non-integer order derivatives. Water SA 2006, 32, 1–7. [Google Scholar] [CrossRef][Green Version]
- Iaffaldano, G.; Caputo, M.; Martino, S. Experimental and theoretical memory diffusion of water in sand. Hydrol. Earth Syst. Sci. Discuss. 2005, 2, 1329–1357. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and fractional-order controllers. Inst. Exp. Physics, Slovak Acad. Sci. Kosice 1994, 12, 1–18. [Google Scholar]
- Iyiola, O.; Oduro, B.; Zabilowicz, T.; Iyiola, B.; Kenes, D. System of time fractional models for COVID-19: Modeling, analysis and solutions. Symmetry 2021, 13, 787. [Google Scholar] [CrossRef]
- Biala, T.; Khaliq, A. A fractional-order compartmental model for the spread of the COVID-19 pandemic. Commun. Nonlinear Sci. Numer. Simul. 2021, 98, 1–19. [Google Scholar] [CrossRef]
- Biala, T.; Afolabi, Y.; Khaliq, A. How Efficient is Contact Tracing in Mitigating the Spread of COVID-19? A Mathematical Modeling Approach. Appl. Math. Model. 2022, 103, 714–730. [Google Scholar] [CrossRef]
- Furati, K.; Sarumi, I.; Khaliq, A. Fractional model for the spread of Covid-19 subject to government intervention and public perception. Appl. Math. Model. 2021, 95, 89–105. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Yu, Y.; Chen, Y.; Ren, G.; Xu, C.; Wang, S.; Yin, Z. A fractional-order SEIHDR model for COVID-19 with inter-city networked coupling effects. Nonlinear Dyn. 2020, 101, 1717–1730. [Google Scholar] [CrossRef] [PubMed]
- Ilic, M.; Liu, F.; Turner, I.; Anh, V. Numerical approximation of a fractional-in-space diffusion equation (II)- with nonhomogenous boundary conditions. Fract. Calc. Appl. Anal. 2006, 9, 333–349. [Google Scholar]
- Iyiola, O.; Wade, B. Exponential integrator methods for systems of non-linear space-fractional models with super-diffusion processes in pattern formation. Comput. Math. Appl. 2018, 75, 3719–3736. [Google Scholar] [CrossRef]
- Mustapha, K.; Abdallah, B.; Furati, K.M. A Discontinuous Petrov–Galerkin Method for Time-Fractional Diffusion Equations. SIAM J. Numer. Anal. 2014, 52, 2512–2529. [Google Scholar] [CrossRef]
- Biala, T.; Khaliq, A. Parallel algorithms for nonlinear time–space fractional parabolic PDEs. J. Comput. Phys. 2018, 375, 135–154. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, C. Finite Difference/Spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Iyiola, O.; Asante-Asamani, E.; Furati, K.; Khaliq, A.; Wade, B. Efficient time discretization scheme for nonlinear space fractional reaction-diffusion equations. Int. J. Comput. Math. 2018, 95, 1–17. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Gao, G.; Sun, Z.; Zhang, H. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 2014, 259, 33–50. [Google Scholar] [CrossRef]
- Jin, B.; Li, B.; Zhou, Z. An analysis of the Crank-Nicolson method for subdiffusion. IMA J. Numer. Anal. 2017, 38, 518–541. [Google Scholar] [CrossRef]
- Brunner, H. The Numerical Solution of Weakly Singular Volterra Integral Equations by Collocation on Graded Meshes. Math. Comput. 1985, 45, 417–437. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z.; Liao, H. Finite difference methods for the time fractional diffusion equation on non-uniform meshes. J. Comput. Phys. 2014, 265, 195–210. [Google Scholar] [CrossRef]
- Lyu, P.; Vong, S. A high-order method with a temporal nonuniform mesh for a time-fractional Benjamin-Bona-Mahony equation. J. Sci. Comput. 2019, 80, 1607–1628. [Google Scholar] [CrossRef]
- Stynes, M.; OŔiordan, E.; Gracia, J.L. Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 2017, 55, 1057–1079. [Google Scholar] [CrossRef]
- Liao, H.; Li, D.; Zhang, J. Sharp error estimate of the nonuniform L1 formula for linear reaction-subdiffusion equations. SIAM J. Numer. Anal. 2018, 56, 1112–1133. [Google Scholar] [CrossRef]
- Kopteva, N. Error analysis of the L1 method on graded and uniform meshes for a fractional- derivative problem in two and three dimensions. Math. Comp. 2019, 88, 2135–2155. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, Z. High-Order Time-Stepping Schemes for semilinear subdiffusion equations. SIAM J. Numer. Anal. 2020, 58, 3226–3250. [Google Scholar] [CrossRef]
- Mustapha, K. An L1 Approximation for a Fractional Reaction-Diffusion Equation, a Second-Order Error Analysis over Time-Graded Meshes. SIAM J. Numer. Anal. 2020, 58, 1319–1338. [Google Scholar] [CrossRef]
- Simpson, D.P. Krylov Subspace Methods for Approximating Functions of Symmetric Positive Definite Matrices with Applications to Applied Statistics and Anomalous Diffusion. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2008. [Google Scholar]
- McLean, W.; Mustapha, K. A second-order accurate numerical method for a fractional wave equation. Numer. Math. 2007, 105, 481–510. [Google Scholar] [CrossRef]
- McLean, W. Regularity of solutions to a time-fractional diffusion equation. ANZIAM J. 2010, 52, 123–138. [Google Scholar] [CrossRef]
- Li, C.; Yi, Q.; Chen, A. Finite difference methods with non-uniform meshes for nonlinear fractional differential equations. J. Comput. Phys. 2016, 316, 614–631. [Google Scholar] [CrossRef]
- Yang, Q.; Turner, I.; Liu, F.; Ilić, M. Novel numerical methods for solving the time-space fractional diffusion equation in two dimensions. SIAM J. Sci. Comput. 2011, 33, 1159–1180. [Google Scholar] [CrossRef]
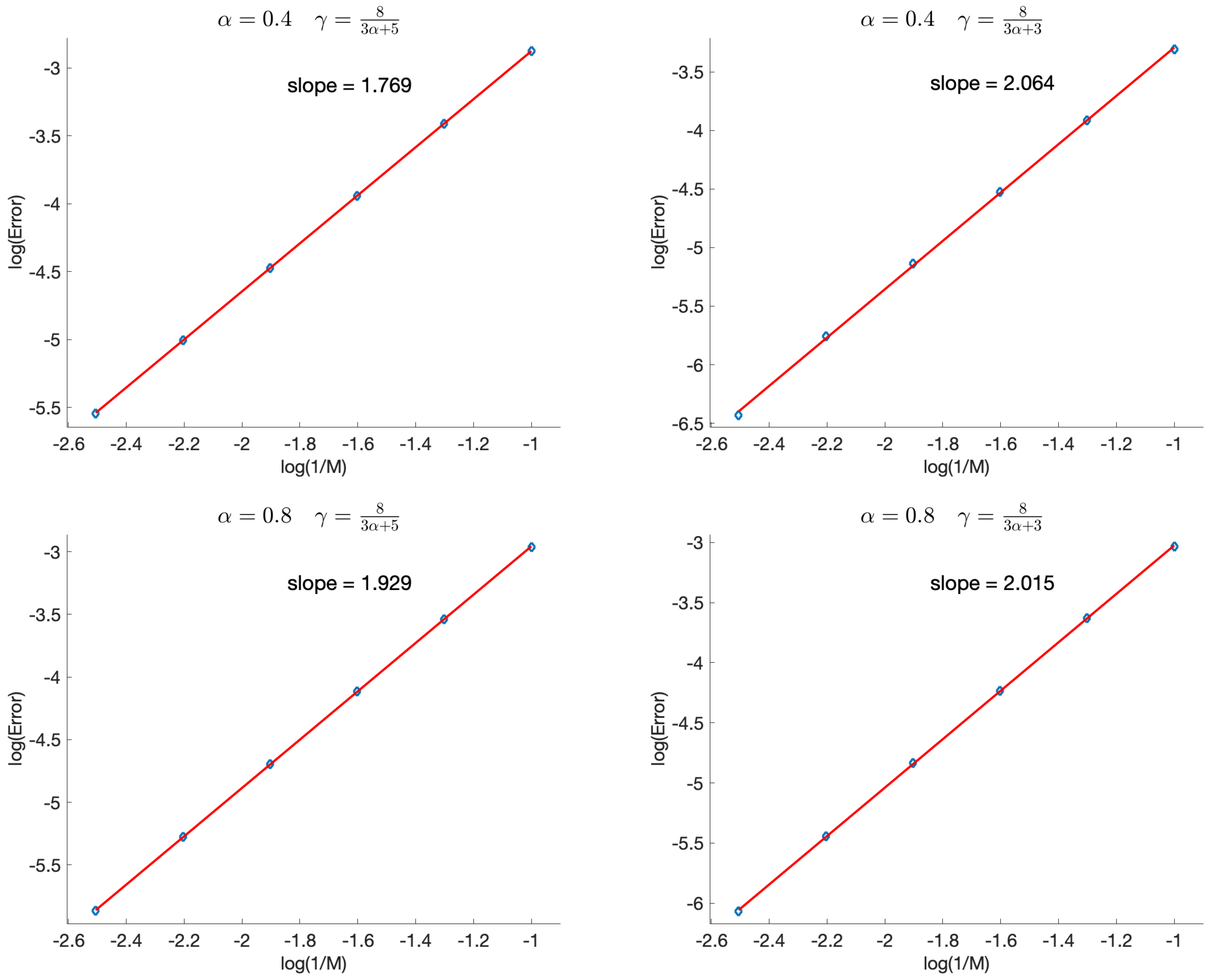
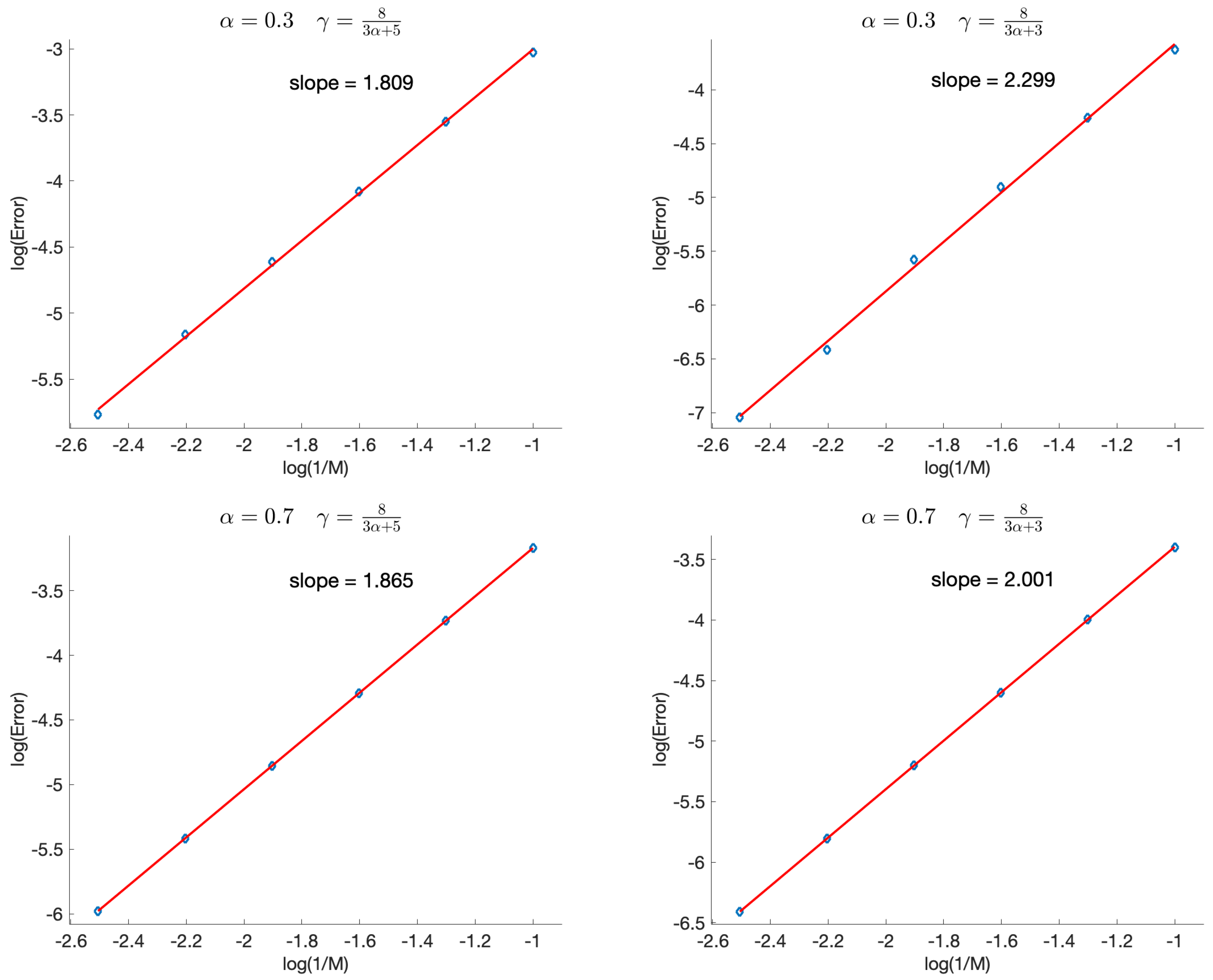
| Error | CR | Error | CR | Error | CR | Error | CR | |
| 10 | ||||||||
| 20 | 1.7690 | 2.0201 | 1.9167 | 1.9891 | ||||
| 40 | 1.7648 | 2.0217 | 1.9194 | 1.9989 | ||||
| 80 | 1.7629 | 2.0287 | 1.9216 | 2.0046 | ||||
| 160 | 1.7677 | 2.0656 | 1.9311 | 2.0193 | ||||
| 320 | 1.7901 | 2.2394 | 1.9684 | 2.0792 | ||||
| Error | CR | Error | CR | Error | CR | Error | CR | |
| 10 | ||||||||
| 20 | 1.7450 | 2.1002 | 1.8621 | 1.9823 | ||||
| 40 | 1.7482 | 2.1258 | 1.8649 | 1.9991 | ||||
| 80 | 1.7664 | 2.2456 | 1.8638 | 2.0051 | ||||
| 160 | 1.8276 | 2.7986 | 1.8646 | 2.0071 | ||||
| 320 | 2.0161 | 2.0728 | 1.8676 | 2.0090 | ||||
| Error | CR | Error | CR | Error | CR | Error | CR | |
| 10 | ||||||||
| 20 | 1.7126 | 2.2554 | 1.9352 | 2.1609 | ||||
| 40 | 1.7176 | 2.2886 | 1.8346 | 2.0209 | ||||
| 80 | 1.7395 | 2.7343 | 1.8556 | 2.1293 | ||||
| 160 | 1.8225 | 1.5829 | 1.9473 | 2.6424 | ||||
| Error | CR | Error | CR | Error | CR | Error | CR | |
| 10 | ||||||||
| 20 | 1.8250 | 3.2883 | 1.9312 | 4.1296 | ||||
| 40 | 1.7993 | 2.0278 | 1.9341 | 4.3404 | ||||
| 80 | 1.7937 | 2.0307 | 1.9556 | 2.2127 | ||||
| 160 | 1.7880 | 2.0244 | 1.9600 | 1.9933 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afolabi, Y.O.; Biala, T.A.; Iyiola, O.S.; Khaliq, A.Q.M.; Wade, B.A. A Second-Order Crank-Nicolson-Type Scheme for Nonlinear Space–Time Reaction–Diffusion Equations on Time-Graded Meshes. Fractal Fract. 2023, 7, 40. https://doi.org/10.3390/fractalfract7010040
Afolabi YO, Biala TA, Iyiola OS, Khaliq AQM, Wade BA. A Second-Order Crank-Nicolson-Type Scheme for Nonlinear Space–Time Reaction–Diffusion Equations on Time-Graded Meshes. Fractal and Fractional. 2023; 7(1):40. https://doi.org/10.3390/fractalfract7010040
Chicago/Turabian StyleAfolabi, Yusuf O., Toheeb A. Biala, Olaniyi S. Iyiola, Abdul Q. M. Khaliq, and Bruce A. Wade. 2023. "A Second-Order Crank-Nicolson-Type Scheme for Nonlinear Space–Time Reaction–Diffusion Equations on Time-Graded Meshes" Fractal and Fractional 7, no. 1: 40. https://doi.org/10.3390/fractalfract7010040
APA StyleAfolabi, Y. O., Biala, T. A., Iyiola, O. S., Khaliq, A. Q. M., & Wade, B. A. (2023). A Second-Order Crank-Nicolson-Type Scheme for Nonlinear Space–Time Reaction–Diffusion Equations on Time-Graded Meshes. Fractal and Fractional, 7(1), 40. https://doi.org/10.3390/fractalfract7010040









