Numerical Investigation on Effective Elastic Modulus of Multifractal Porous Materials
Abstract
1. Introduction
2. Multifractal Porous Materials
3. The Multiplicative Cascades Used for Synthesizing the Multifractal Fields
3.1. Paradigm of the Multiplicative Cascades
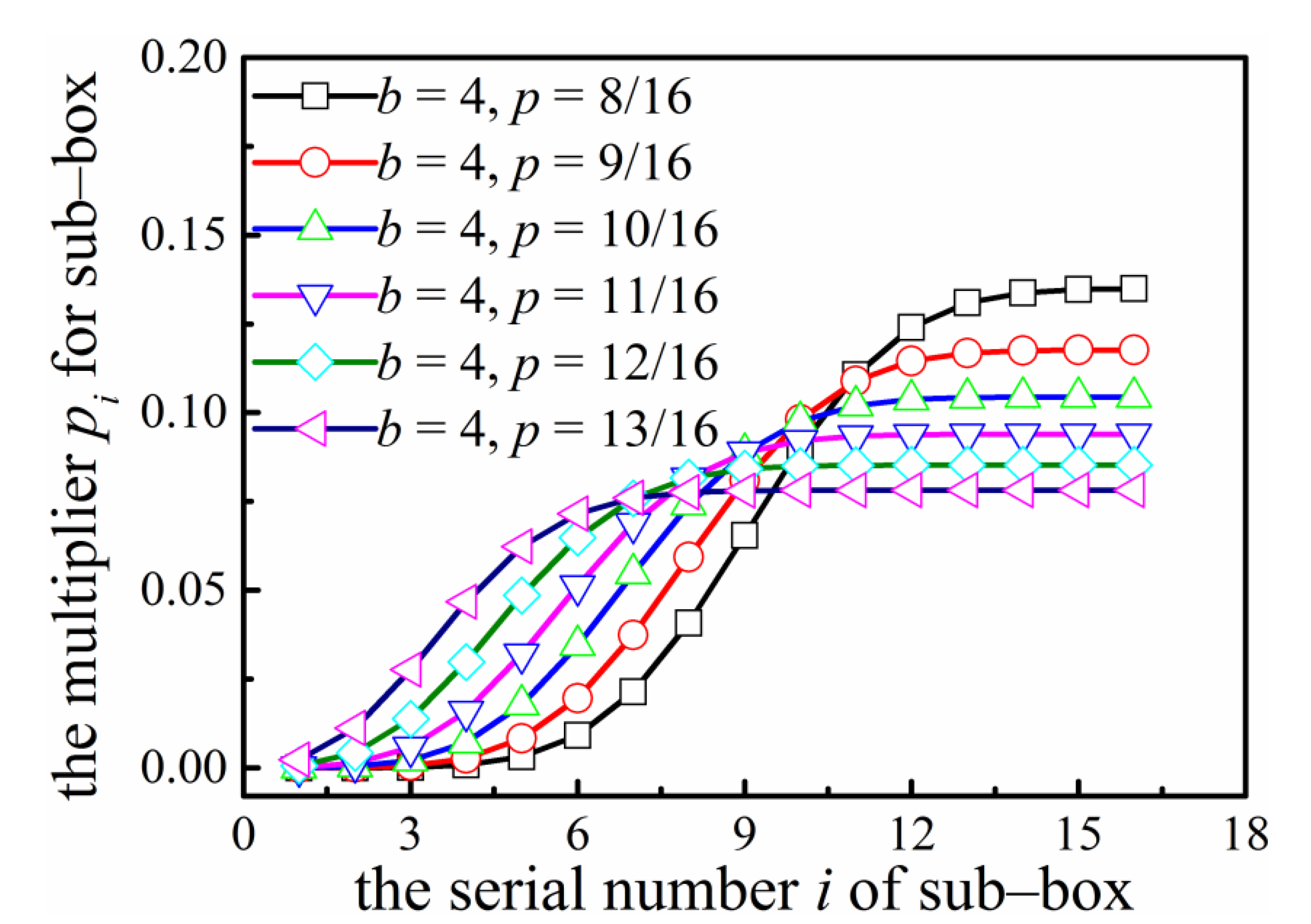
3.2. Two-Parameter Binomial Multiplicative Cascades
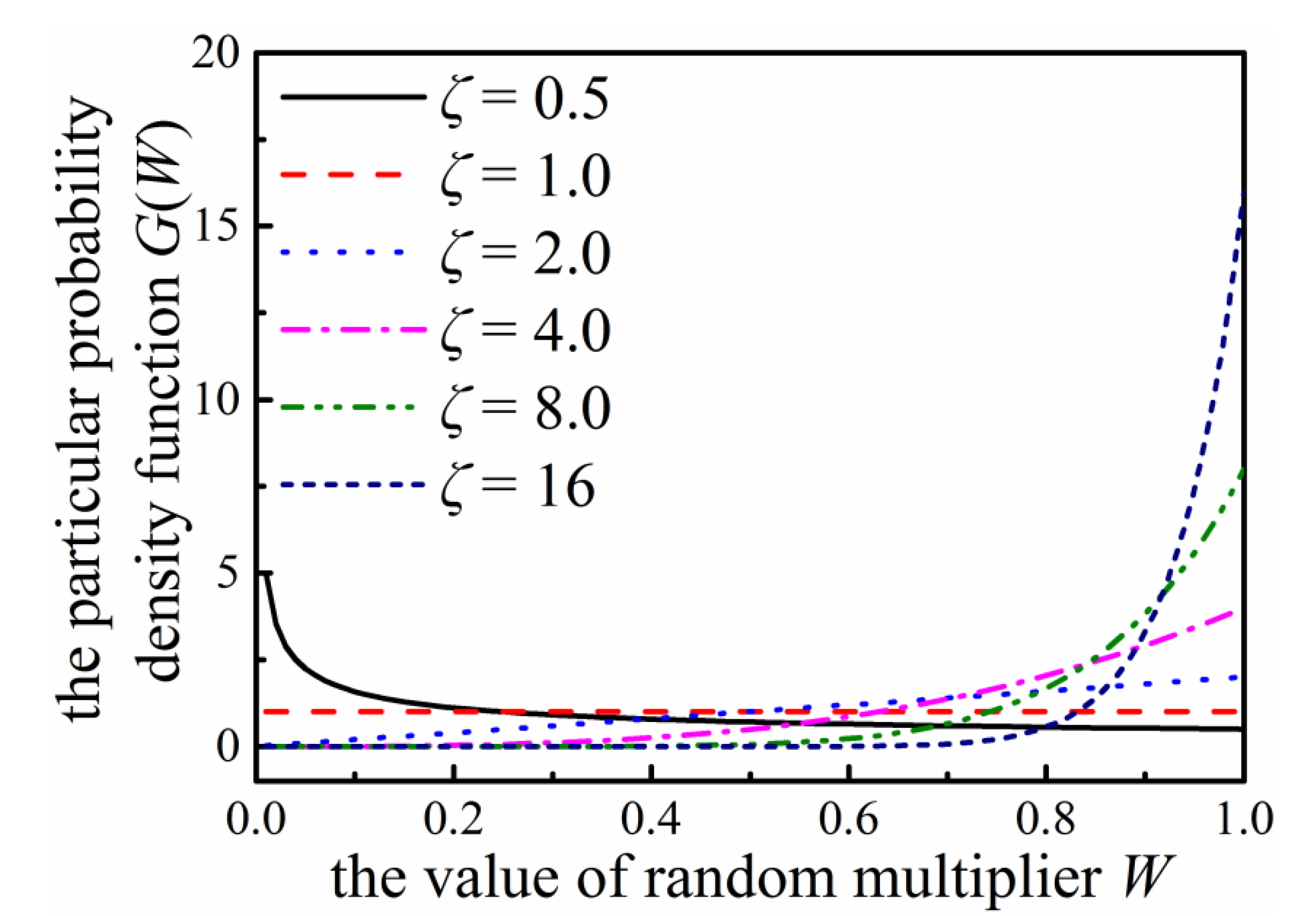
3.3. Compound Poisson Cascades
4. Conversion from the Intensity of a Multifractal Field to the Elastic Modulus
5. Finite Element Method for the Homogenization of Elastic Modulus
6. Results and Discussions
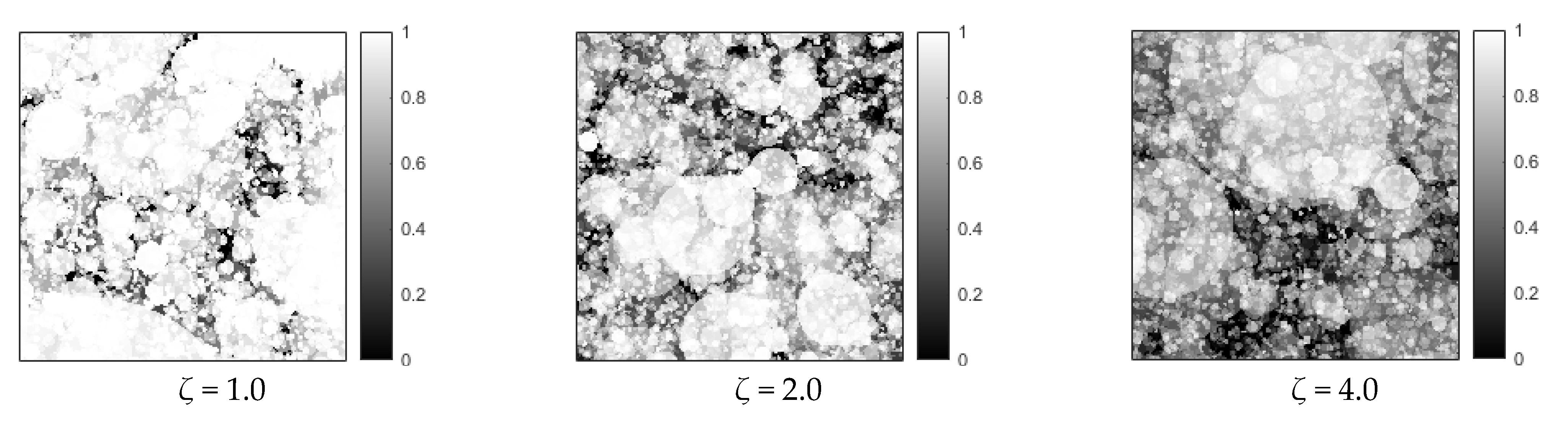
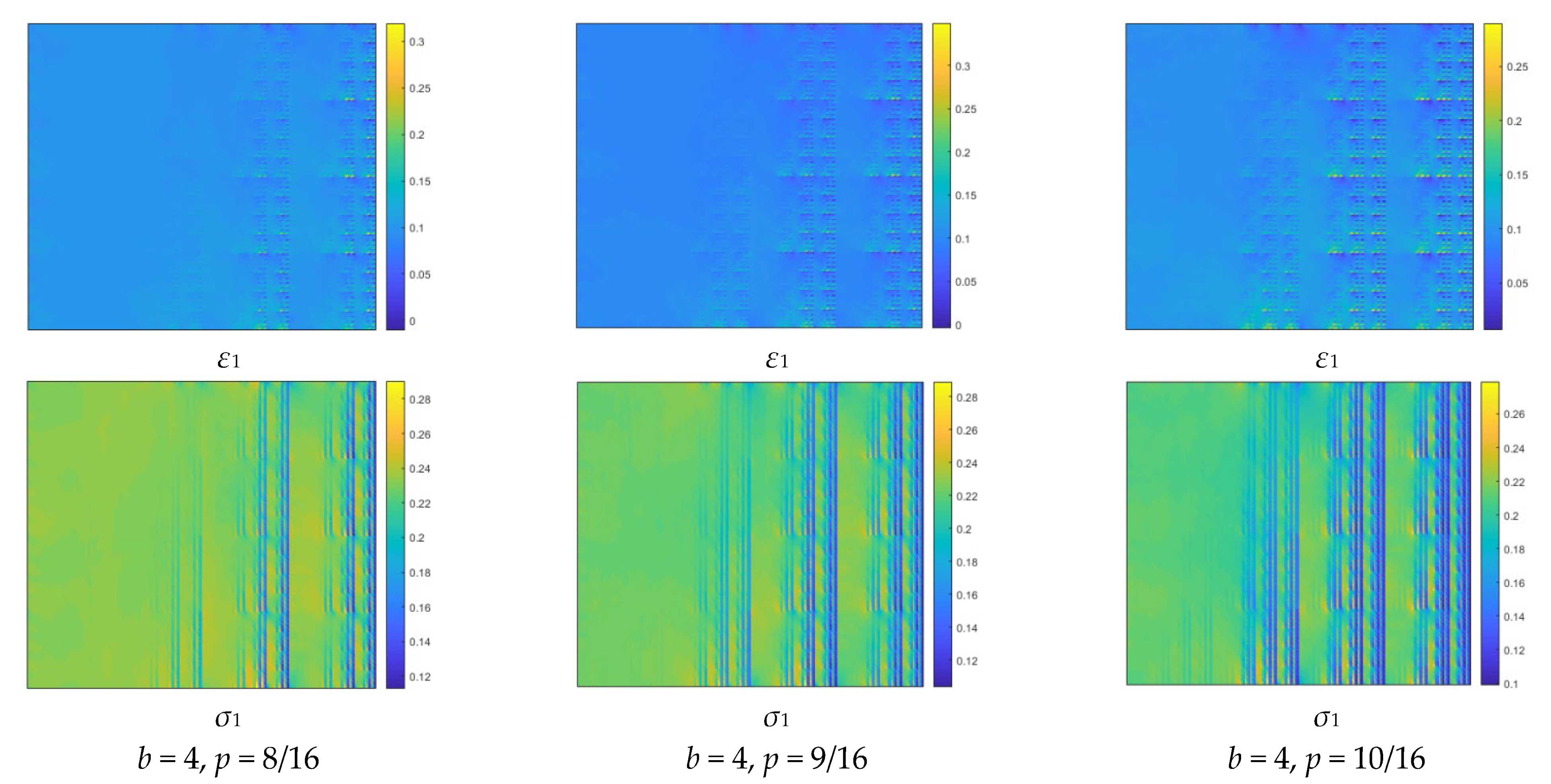
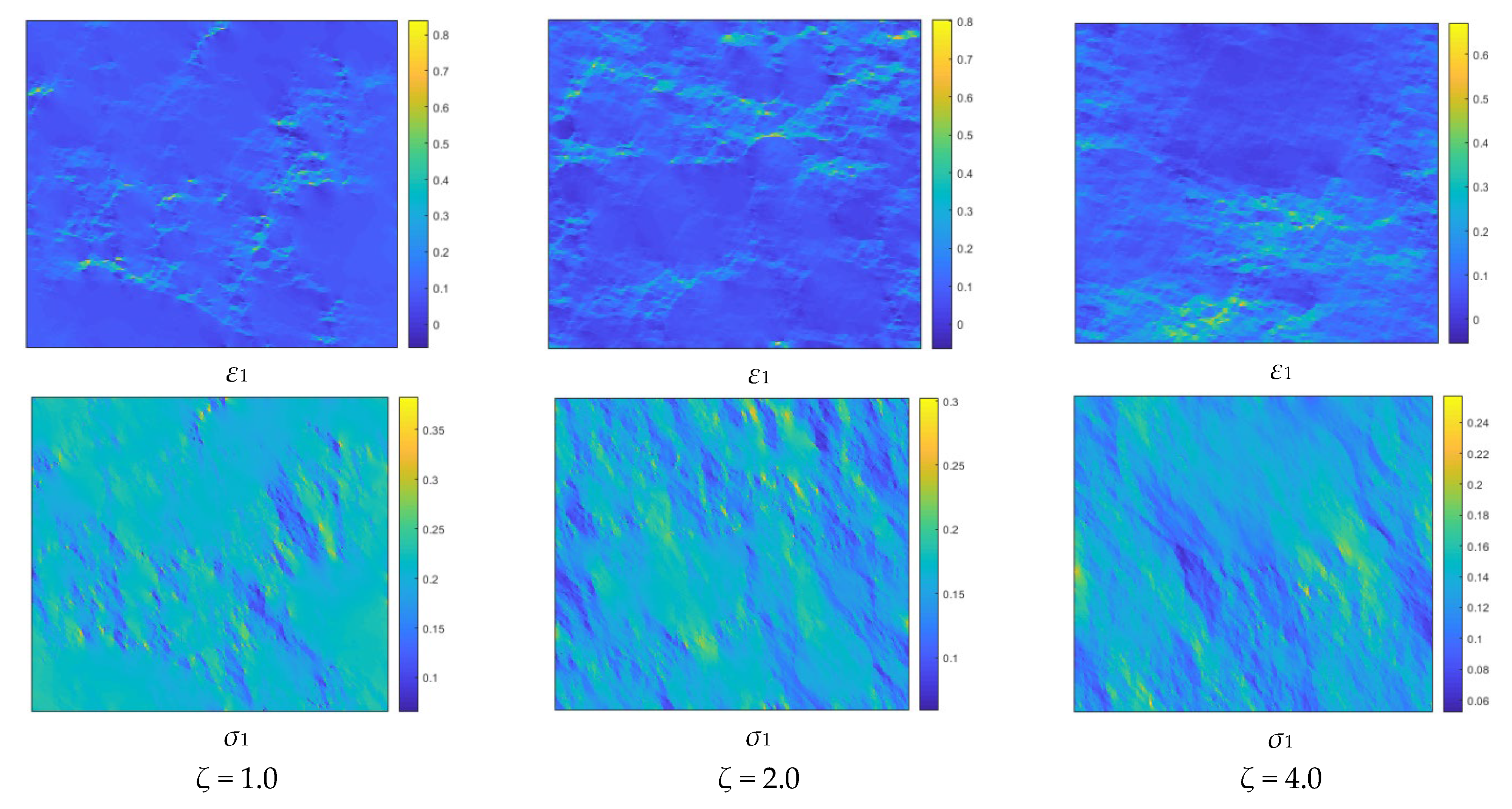
6.1. The Structural Heterogeneity of Multifractal Porous Materials
6.2. Finite Element Method Used to Determine the Effective Elastic Modulus
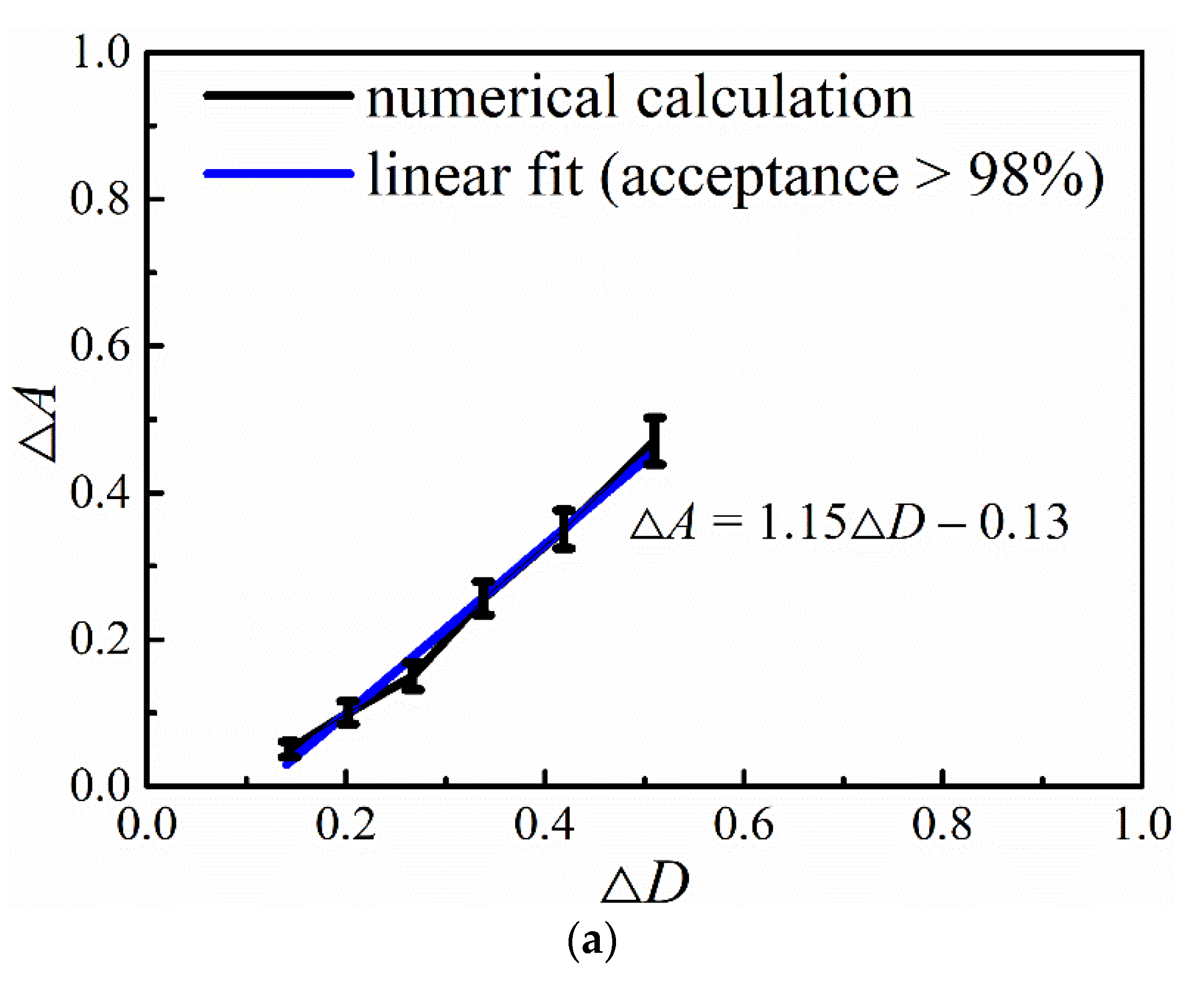
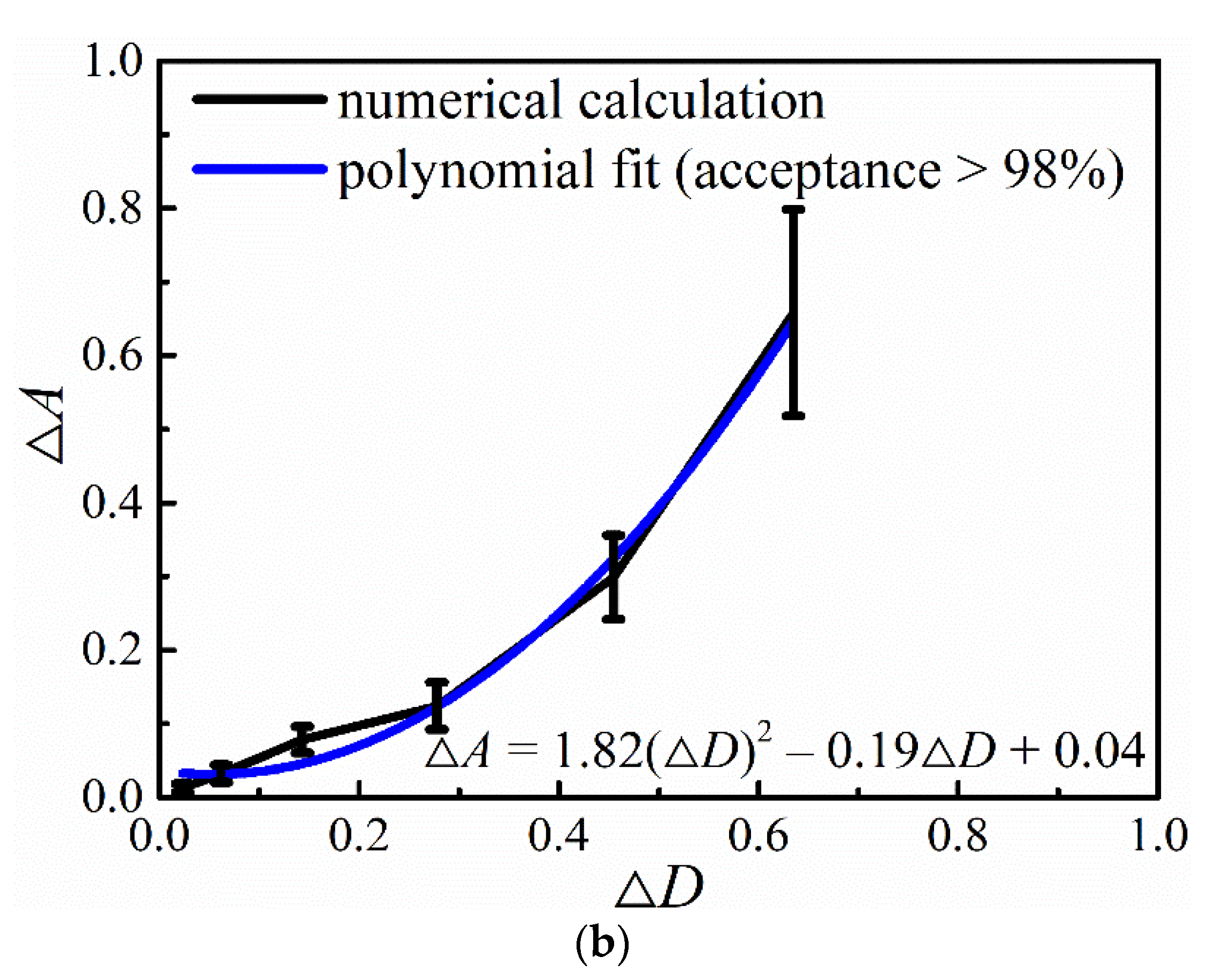
6.3. Dependence of the Effective Elastic Modulus on the Structural Heterogeneity
7. Concluding Remarks
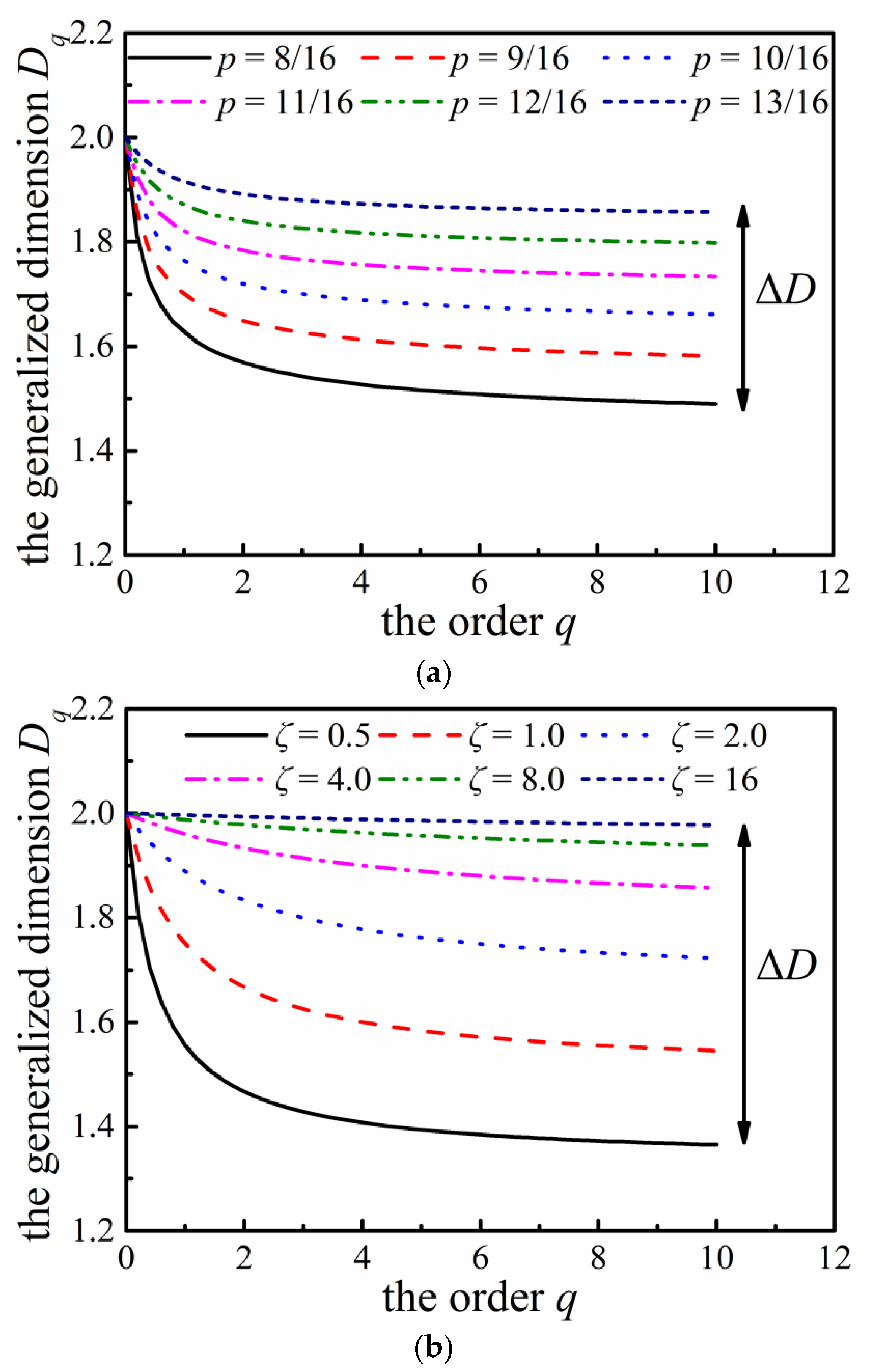
- Two types of cascading algorithms, i.e., two-parameter binomial multiplicative cascades (deterministic) and compound Poisson cascades (stochastic), are employed to synthesize the multifractal fields as well as the porous materials. The range of the Rényi dimension ΔD provides a novel means of quantifying the structural heterogeneity. As the parameter p → 1 (for the two-parameter binomial multiplicative cascades) or ζ >> 1 (for the compound Poisson cascades), one expects to observe rather homogeneous structures.
- A mathematical formula, written as E = E0 exp [–A (g–gmin)/(gmax–gmin)] or E = E0 exp [–Ag/gmax], is proposed to account for the conversion from the intensity g of a multifractal field to the local elastic modulus E of a multifractal porous material. The finite element method can achieve the homogenization of the local elastic modulus with great efficiency.
- For the synthesized multifractal porous materials as a whole, the mathematical formula for the macroscopic porosity <f> and the effective elastic modulus Eeff could be described as Eeff = E0 exp [–(A+ΔA)<f>]. ΔA > 0 is an auxiliary parameter used to quantify the dependence of the effective elastic modulus on the structural heterogeneity. A sound positive correlation exists between ΔA and ΔD, which can be fitted by a linear relation (for the two-parameter binomial multiplicative cascades) or a polynomial relation (for the compound Poisson cascades).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, C.; Kuang, Y.; Zhu, S.; Burgert, I.; Keplinger, T.; Gong, A.; Li, T.; Berglund, L.; Eichhorn, S.J.; Hu, L.B. Structure–property–function relationships of natural and engineered wood. Nat. Rev. Mater. 2020, 5, 642–666. [Google Scholar] [CrossRef]
- Roberts, A.P.; Knackstedt, M.A. Structure–property correlations in model composite materials. Phys. Rev. E 1996, 54, 2313–2328. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Marques, M.A.L.; Botti, S. Direct insight into the structure–property relation of interfaces from constrained crystal structure prediction. Nat. Commun. 2021, 12, 811. [Google Scholar] [CrossRef] [PubMed]
- Poutet, J.; Manzoni, D.; Hage Chehade, F.; Jacquin, C.J.; Bouteca, M.J.; Thovert, J.F.; Adler, P.M. The effective mechanical properties of random porous media. J. Mech. Phys. Solids 1996, 44, 1587–1620. [Google Scholar] [CrossRef]
- Diamond, S. The microstructure of cement paste and concrete—A visual primer. Cem. Concr. Compos. 2004, 26, 919–933. [Google Scholar] [CrossRef]
- Allen, A.J.; Thomas, J.J. Analysis of C–S–H gel and cement paste by small–angle neutron scattering. Cem. Concr. Res. 2007, 37, 319–324. [Google Scholar] [CrossRef]
- Bossa, N.; Chaurand, P.; Vicente, J.; Borschneck, D.; Levard, C.; Aguerre–Chariol, O.; Rose, J. Micro– and nano–X–ray computed–tomography: A step forward in the characterization of the pore network of a leached cement paste. Cem. Concr. Res. 2015, 67, 138–147. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, K.; Jiang, J.Y. Examination and modeling of fractality for pore–solid structure in cement paste: Starting from the mercury intrusion porosimetry test. Constr. Build. Mater. 2016, 124, 237–243. [Google Scholar] [CrossRef]
- Kim, J.S.; Chung, S.Y.; Stephan, D.; Han, T.S. Issues on characterization of cement paste microstructures from μ–CT and virtual experiment framework for evaluating mechanical properties. Constr. Build. Mater. 2019, 202, 82–102. [Google Scholar] [CrossRef]
- Song, Y.; Davy, C.A.; Troadec, D.; Bourbon, X. Pore network of cement hydrates in a high performance concrete by 3D FIB/SEM–implications for macroscopic fluid transport. Cem. Concr. Res. 2019, 115, 308–326. [Google Scholar] [CrossRef]
- Gao, Y.; Li, W.; Wu, K.; Yuan, Q. Modeling the elastic modulus of cement paste with X–ray computed tomography and a hybrid analytical–numerical algorithm: The effect of structural heterogeneity. Cem. Concr. Compos. 2021, 122, 104145. [Google Scholar] [CrossRef]
- Shah, H.A.; Yuan, Q.; Zuo, S.H. Air entrainment in fresh concrete and its effects on hardened concrete-a review. Constr. Build. Mater. 2021, 274, 121835. [Google Scholar] [CrossRef]
- Lopes, R.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef] [PubMed]
- San José Martínez, F.; Caniego, F.J.; García Gutiérrez, C.; Espejo, R. Representative elementary area for multifractal analysis of soil porosity using entropy dimension. Nonlin. Process. Geophys. 2007, 14, 503–511. [Google Scholar] [CrossRef]
- Soto Gómez, D.; Pérez Rodríguez, P.; Vázquez Juíz, L.; Paradelo, M.; Eugenio López Periago, J. 3D multifractal characterization of computed tomography images of soils under different tillage management: Linking multifractal parameters to physical properties. Geoderma 2020, 363, 114129. [Google Scholar] [CrossRef]
- Guan, M.; Liu, X.P.; Jin, Z.J.; Lai, J. The heterogeneity of pore structure in lacustrine shales: Insights from multifractal analysis using N2 adsorption and mercury intrusion. Mar. Pet. Geol. 2020, 114, 104150. [Google Scholar] [CrossRef]
- Duan, R.Q.; Xu, Z.F.; Dong, Y.H.; Liu, W.J. Characterization and classification of pore structures in deeply buried carbonate rocks based on mono– and multifractal methods. J. Pet. Sci. Eng. 2021, 203, 108606. [Google Scholar] [CrossRef]
- Stach, S.; Lamza, A.; Wróbel, Z. 3D image multifractal analysis and pore detection on a stereometric measurement file of a ceramic coating. J. Eur. Ceram. 2014, 34, 3427–3432. [Google Scholar] [CrossRef]
- Dănilăa, E.; Moraru, L.; Dey, N.; Ashour, A.S.; Shi, F.Q.; Fong, S.J.; Khan, S.; Biswas, A. Multifractal analysis of ceramic pottery SEM images in Cucuteni–Tripolye culture. Optik 2018, 164, 538–546. [Google Scholar] [CrossRef]
- Valentini, L.; Artioli, G.; Voltolini, M.; Dalconi, M.C. Multifractal analysis of calcium silicate hydrate (C–S–H) mapped by X–ray diffraction microtomography. J. Am. Ceram. Soc. 2012, 95, 2647–2652. [Google Scholar] [CrossRef]
- Gao, Y.; Gu, Y.H.; Mu, S.; Jiang, J.Y.; Liu, J.P. The multifractal property of heterogeneous microstructure in cement paste. Fractals 2021, 29, 2140006. [Google Scholar] [CrossRef]
- Bird, N.; Cruz Díaz, M.; Saa, A.; Tarquis, A.m. Fractal and multifractal analysis of pore–scale images of soil. J. Hydrol. 2006, 322, 211–219. [Google Scholar]
- Mendoza, F.; Verboven, P.; Ho, Q.T.; Kerckhofs, G.; Wevers, M.; Nicolaï, B. Multifractal properties of pore–size distribution in apple tissue using X–ray imaging. J. Food Eng. 2010, 99, 206–215. [Google Scholar] [CrossRef]
- Arnéodo, A.; Decoster, N.; Roux, S.G. A wavelet–based method for multifractal image analysis. I. Methodology and test applications on isotropic and anisotropic random rough surfaces. Eur. Phys. J. B 2000, 15, 567–600. [Google Scholar] [CrossRef]
- Decoster, N.; Roux, S.G.; Arnéodo, A. A wavelet–based method for multifractal image analysis. II. Applications to synthetic multifractal rough surfaces. Eur. Phys. J. B 2000, 15, 739–764. [Google Scholar]
- Saucier, A. Effective permeability of multifractal porous media. Physica A 1992, 183, 381–397. [Google Scholar] [CrossRef]
- Saucier, A. Scaling of the effective permeability in multifractal porous media. Physica A 1992, 191, 289–294. [Google Scholar] [CrossRef]
- Perfect, E.; Gentry, R.W.; Sukop, M.C.; Lawson, J.E. Multifractal Sierpinski carpets: Theory and application to upscaling effective saturated hydraulic conductivity. Geoderma 2006, 134, 240–252. [Google Scholar] [CrossRef]
- Cheng, Q. Generalized binomial multiplicative cascade processes and asymmetrical multifractal distributions. Nonlinear Process. Geophys. 2014, 21, 477–487. [Google Scholar] [CrossRef]
- Barral, J.; Mandelbrot, B. Multiplicative products of cylindrical pulses. Probab. Theory Relat. Fields 2002, 124, 409–430. [Google Scholar] [CrossRef]
- Muzy, J.; Bacry, E. Multifractal stationary random measures and multifractal random walks with log–infinitely divisible scaling laws. Phys. Rev. E 2002, 66, 056121. [Google Scholar] [CrossRef] [PubMed]
- Chainais, P. Multidimensional infinitely divisible cascades. Application to the modelling of intermittency in turbulence. Eur. Phys. J. B 2006, 51, 229–243. [Google Scholar] [CrossRef]
- Chainais, P. Infinitely divisible cascades to model the statistics of natural Images. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 2105–2119. [Google Scholar] [CrossRef] [PubMed]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Budiansky, B.; O'connell, R.J. Elastic moduli of a cracked solid. Int. J. Solids Struct. 1976, 12, 81–97. [Google Scholar]
- Zhao, Y.H.; Tandon, G.P.; Weng, G.J. Elastic moduli for a class of porous materials. Acta Mech. 1989, 76, 105–130. [Google Scholar] [CrossRef]
- Gong, S.; Li, Z.; Zhao, Y.Y. An extended Mori–Tanaka model for the elastic moduli of porous materials of finite size. Acta Mater. 2011, 59, 6820–6830. [Google Scholar] [CrossRef]
- Manoylov, A.V.; Borodich, F.M.; Evans, H.P. Modelling of elastic properties of sintered porous materials. Proc. R. Soc. A 2013, 469, 20120689. [Google Scholar] [CrossRef]
- Chen, Z.W.; Wang, X.; Giuliani, F.; Atkinson, A. Microstructural characteristics and elastic modulus of porous solids. Acta Mater. 2015, 89, 268–277. [Google Scholar] [CrossRef]
- Grigorenko, Y.M.; Savula, Y.G.; Mukha, I.S. Linear and nonlinear problems on the elastic deformation of complex shells and methods of their numerical solution. Int. Appl. Mech. 2000, 36, 979–1000. [Google Scholar] [CrossRef]
- Abbas, I.A.; Zenkour, A. Dual–phase–lag model on thermoelastic interactions in a semi–infinite medium subjected to a ramp-type heating. J. Comput. Theor. Nanosci. 2014, 11, 642–645. [Google Scholar]
- Abbas, I.A. Eigenvalue approach on fractional order theory of thermoelastic diffusion problem for an infinite elastic medium with a spherical cavity. Appl. Math. Model. 2015, 39, 6196–6206. [Google Scholar]
- Dyyak, I.I.; Rubino, B.; Savula, Y.H.; Styahar, A.O. Numerical analysis of heterogeneous mathematical model of elastic body with thin inclusion by combined BEM and FEM. Math. Model. Comput. 2019, 6, 239–250. [Google Scholar] [CrossRef]
- Balankin, A.S. The concept of multifractal elasticity. Phys. Lett. A 1996, 210, 51–59. [Google Scholar]
- Lashermes, B.; Abry, P.; Chainais, P. New insight in the estimation of scaling exponents. Int. J. Wavelets Multiresolut. Inf. Process. 2004, 2, 497–523. [Google Scholar]
- Wang, J. Young's modulus of porous materials, Part 1 Theoretical derivation of modulus–porosity correlation. J. Mater. Sci. 1984, 19, 801–808. [Google Scholar]
- Spriggs, R.M. Expression for effect of porosity on elastic modulus of polycrystalline refractory materials, particularly aluminum oxide. J. Am. Ceram. Soc. 1961, 44, 628–629. [Google Scholar]
- Kováčik, J. Correlation between Young’s modulus and porosity in porous materials. J. Mater. Sci. Lett. 1999, 18, 1007–1010. [Google Scholar]
- Roberts, A.P.; Garboczi, E.J. Elastic properties of model porous ceramics. J. Am. Ceram. Soc. 2000, 83, 3041–3048. [Google Scholar]
- Velez, K.; Maximilien, S.; Damidot, D.; Fantozzi, G.; Sorrentino, F. Determination by nanoindentation of elastic modulus and hardness of pure constituents of Portland cement clinker. Cem. Concr. Res. 2001, 31, 555–561. [Google Scholar]
- Šmilauer, V.; Bittnar, Z. Microstructure–based micromechanical prediction of elastic properties in hydrating cement paste. Cem. Concr. Res. 2006, 36, 1708–1718. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, P.; Jiang, J.Y. Analytical and numerical modeling of elastic moduli for cement based composites with solid mass fractal model. Constr. Build. Mater. 2018, 172, 330–339. [Google Scholar] [CrossRef]
- Wang, J. Young's modulus of porous materials, Part 2 Young's modulus of porous alumina with changing pore structure. J. Mater. Sci. 1984, 19, 809–814. [Google Scholar] [CrossRef]
- Garboczi, E.J.; Berryman, J.G. Elastic moduli of a material containing composite inclusions: Effective medium theory and finite element computations. Mech. Mater. 2001, 33, 455–470. [Google Scholar] [CrossRef]
- Huang, J.; Krabbenhoft, K.; Lyamin, A.V. Statistical homogenization of elastic properties of cement paste based on X-ray microtomography images. Int. J. Solids Struct. 2013, 50, 699–709. [Google Scholar] [CrossRef]
- Meille, S.; Garboczi, E.J. Linear elastic properties of 2–D and 3–D models of porous materials made from elongated objects. Mod. Sim. Mater. Sci. 2001, 9, 371–390. [Google Scholar] [CrossRef]





| Authors | Porous Materials | Experimental Techniques | Multifractal Parameters |
|---|---|---|---|
| San José Martínez et al. (2007) [14] | Soils from central Spain | Confocal microscope, digital camera | Entropy dimension |
| Soto-Gómez et al. (2020) [15] | Soils from northwestern Spain | X-ray-computed tomography | Rényi dimension, multifractal spectrum |
| Guan et al. (2020) [16] | Lacustrine shales from the Bohai Bay Basin of China | Gas adsorption, mercury intrusion porosimetry | Rényi dimension, multifractal spectrum |
| Duan et al. (2021) [17] | Carbonate rocks from the Tazhong Uplift of China | Gas adsorption, mercury intrusion porosimetry, nuclear magnetic resonance | Capacity dimension, Hölder exponent |
| Stach et al. (2014) [18] | Al2O3 coating deposited on an aluminum alloy disc | Confocal microscope | Hausdorff dimension spectra |
| Dănilă et al. (2018) [19] | Ceramic pottery in Cucuteni–Tripolye culture | Scanning electron microscopy | Rényi dimension, multifractal spectrum |
| Valentini et al. (2012) [20] | Ordinary Portland cement | X-ray powder diffraction microtomography | Multifractal spectrum |
| Gao et al. (2021) [21] | Ordinary Portland cement | X-ray-computed tomography | Multifractal spectrum |
| Parameter | <f> | Eeff/E0 | Error of Eeff/E0 |
|---|---|---|---|
| b = 4, p = 8/16 | 0.046 | 0.904 | 0.019 |
| b = 4, p = 9/16 | 0.080 | 0.848 | 0.023 |
| b = 4, p = 10/16 | 0.128 | 0.776 | 0.031 |
| b = 4, p = 11/16 | 0.197 | 0.692 | 0.035 |
| b = 4, p = 12/16 | 0.289 | 0.592 | 0.029 |
| b = 4, p = 13/16 | 0.409 | 0.484 | 0.021 |
| Parameter | <f> | Error of <f> | Eeff/E0 | Error of Eeff/E0 |
|---|---|---|---|---|
| ζ = 0.5 | 0.036 | 0.023 | 0.920 | 0.042 |
| ζ = 1.0 | 0.089 | 0.030 | 0.837 | 0.050 |
| ζ = 2.0 | 0.218 | 0.045 | 0.686 | 0.074 |
| ζ = 4.0 | 0.379 | 0.048 | 0.507 | 0.046 |
| ζ = 8.0 | 0.550 | 0.058 | 0.383 | 0.039 |
| ζ = 16 | 0.698 | 0.025 | 0.299 | 0.013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, Y.; Wang, L.; Gao, Y.; Lei, D. Numerical Investigation on Effective Elastic Modulus of Multifractal Porous Materials. Fractal Fract. 2023, 7, 3. https://doi.org/10.3390/fractalfract7010003
Xi Y, Wang L, Gao Y, Lei D. Numerical Investigation on Effective Elastic Modulus of Multifractal Porous Materials. Fractal and Fractional. 2023; 7(1):3. https://doi.org/10.3390/fractalfract7010003
Chicago/Turabian StyleXi, Yanan, Lijie Wang, Yun Gao, and Dong Lei. 2023. "Numerical Investigation on Effective Elastic Modulus of Multifractal Porous Materials" Fractal and Fractional 7, no. 1: 3. https://doi.org/10.3390/fractalfract7010003
APA StyleXi, Y., Wang, L., Gao, Y., & Lei, D. (2023). Numerical Investigation on Effective Elastic Modulus of Multifractal Porous Materials. Fractal and Fractional, 7(1), 3. https://doi.org/10.3390/fractalfract7010003







