Fractal Description of Rock Fracture Networks Based on the Space Syntax Metric
Abstract
:1. Introduction
2. Space Syntax Metrics
2.1. The Concept of Space Syntax Metrics
2.2. The Relationship between Space Syntax Metrics and Rock Fracture Networks
3. Methodology
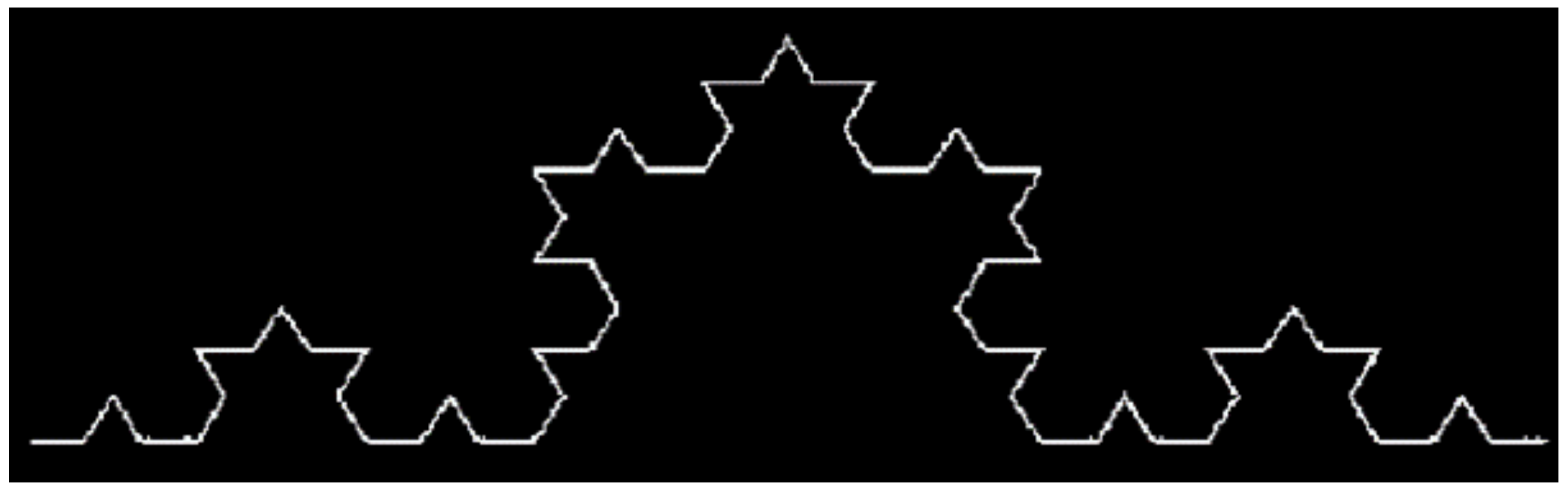
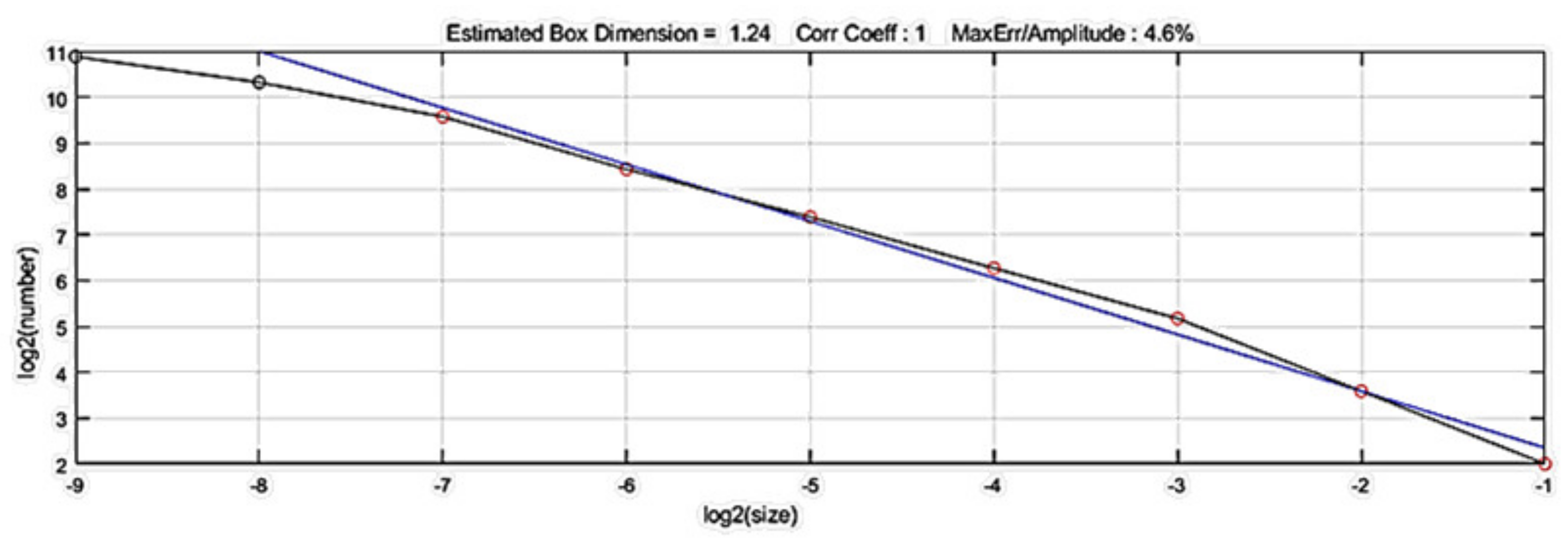
3.1. Traditional Fractal Calculation Method
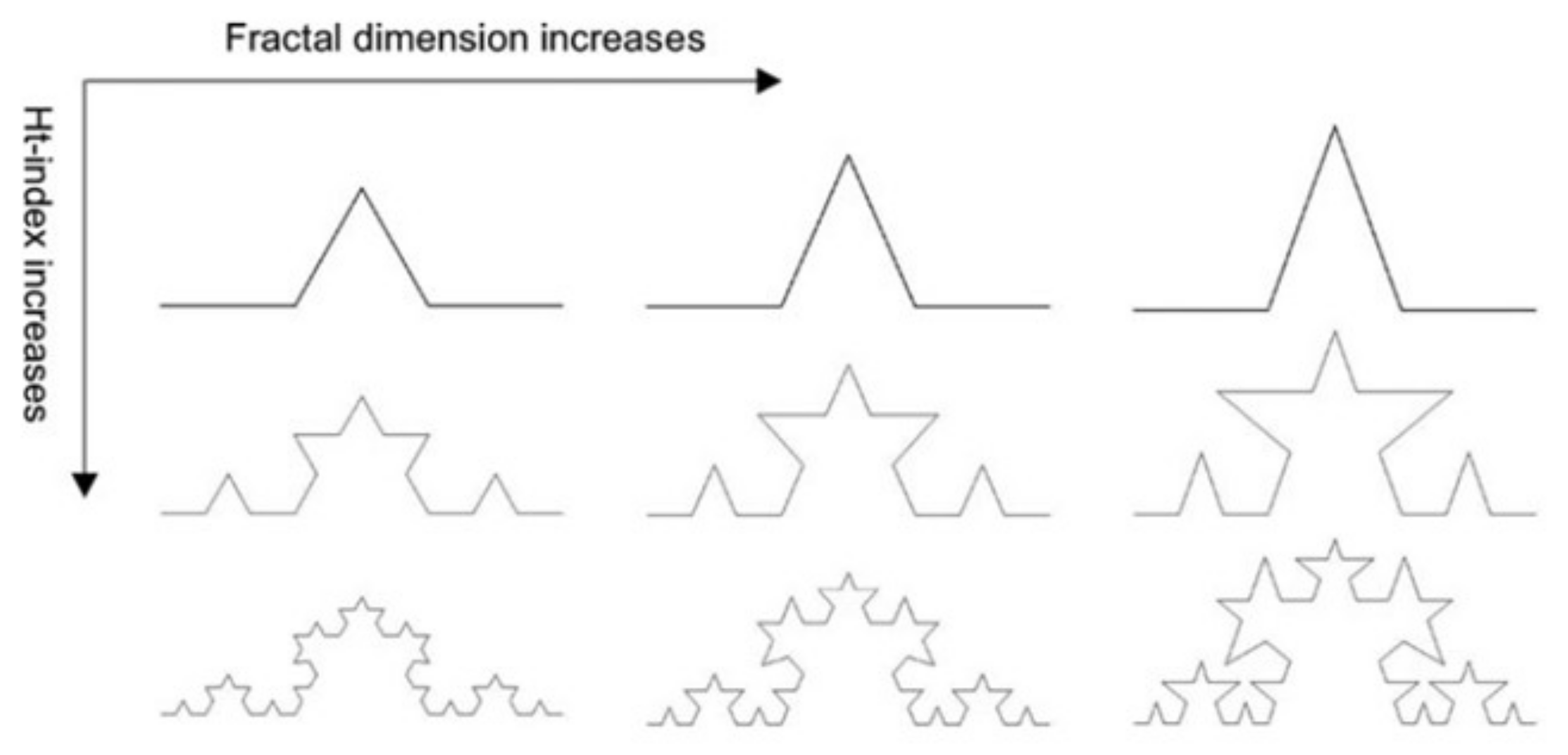
3.2. A Simple Method of Fractal Calculation
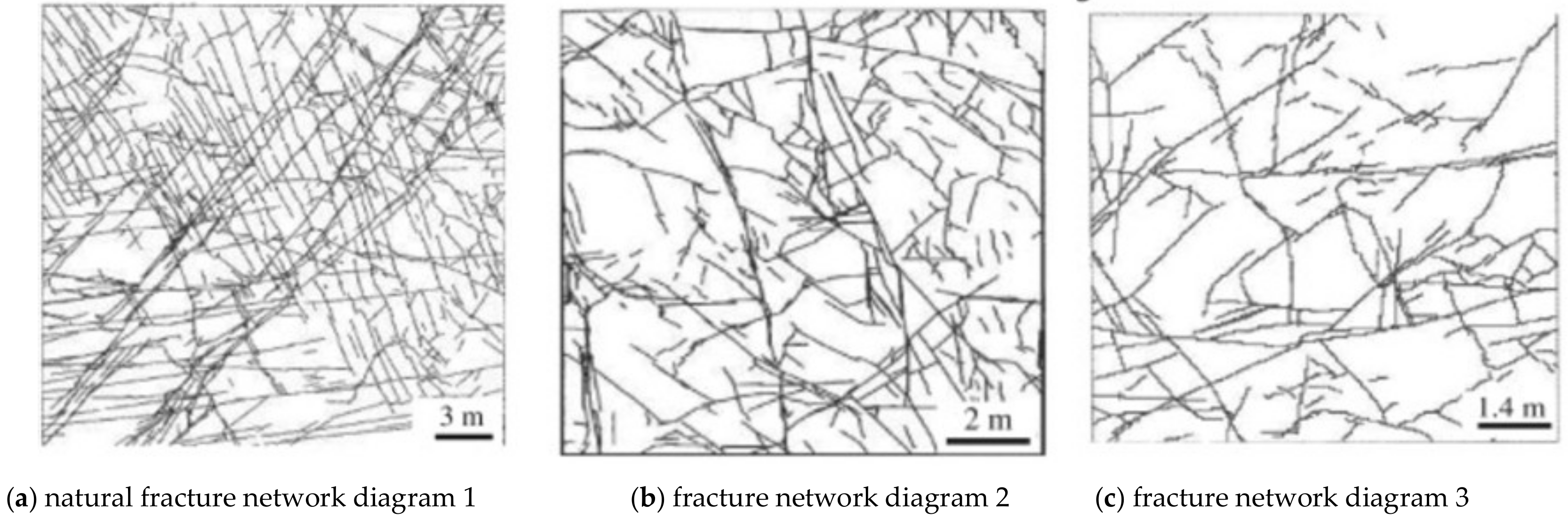
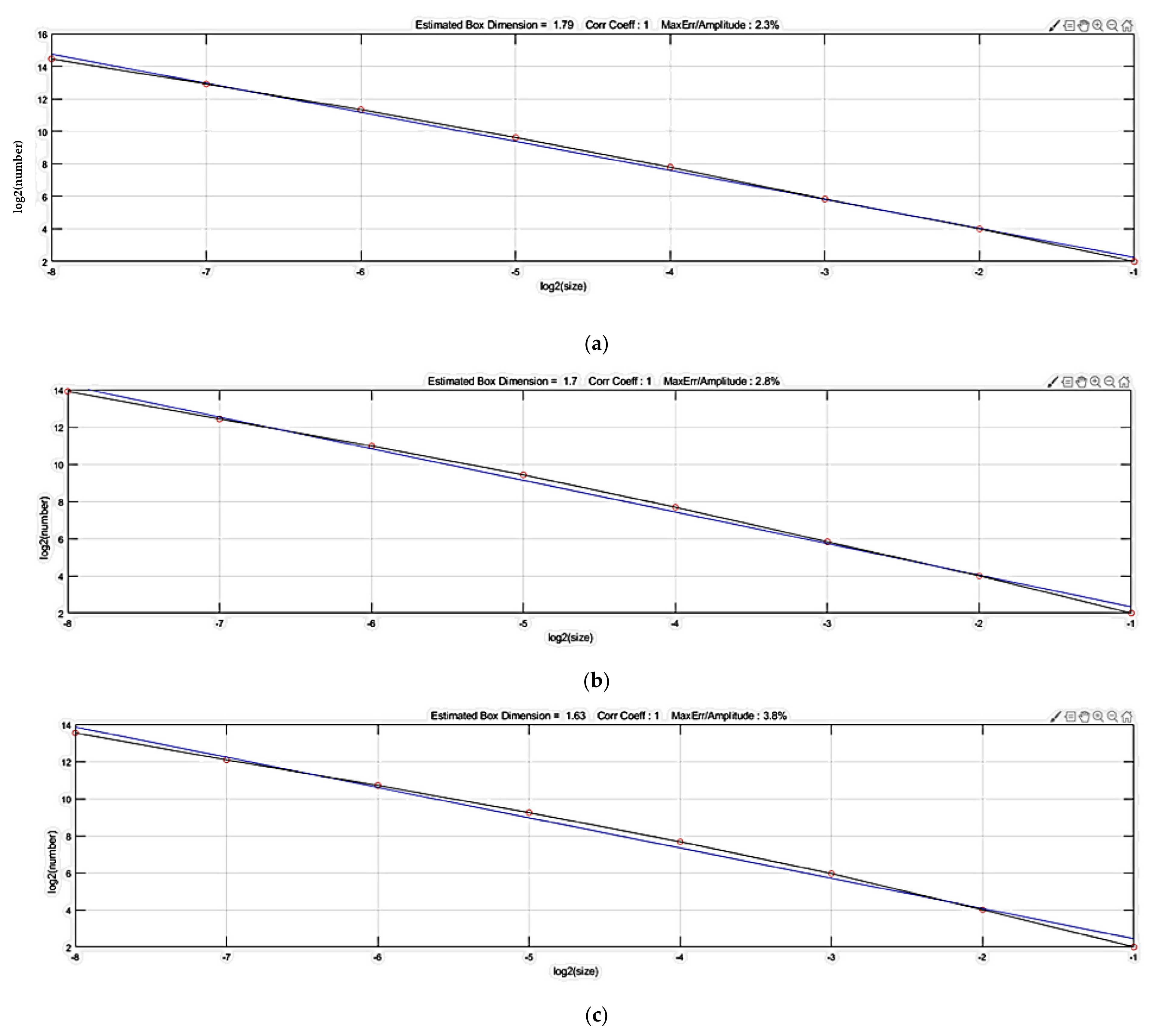
4. Comparison between Box-Counting Dimension Method and the Simple Method of Fractal Calculation
5. Comparison of Metric Parameter of Space Syntax and Length Fractal Dimension
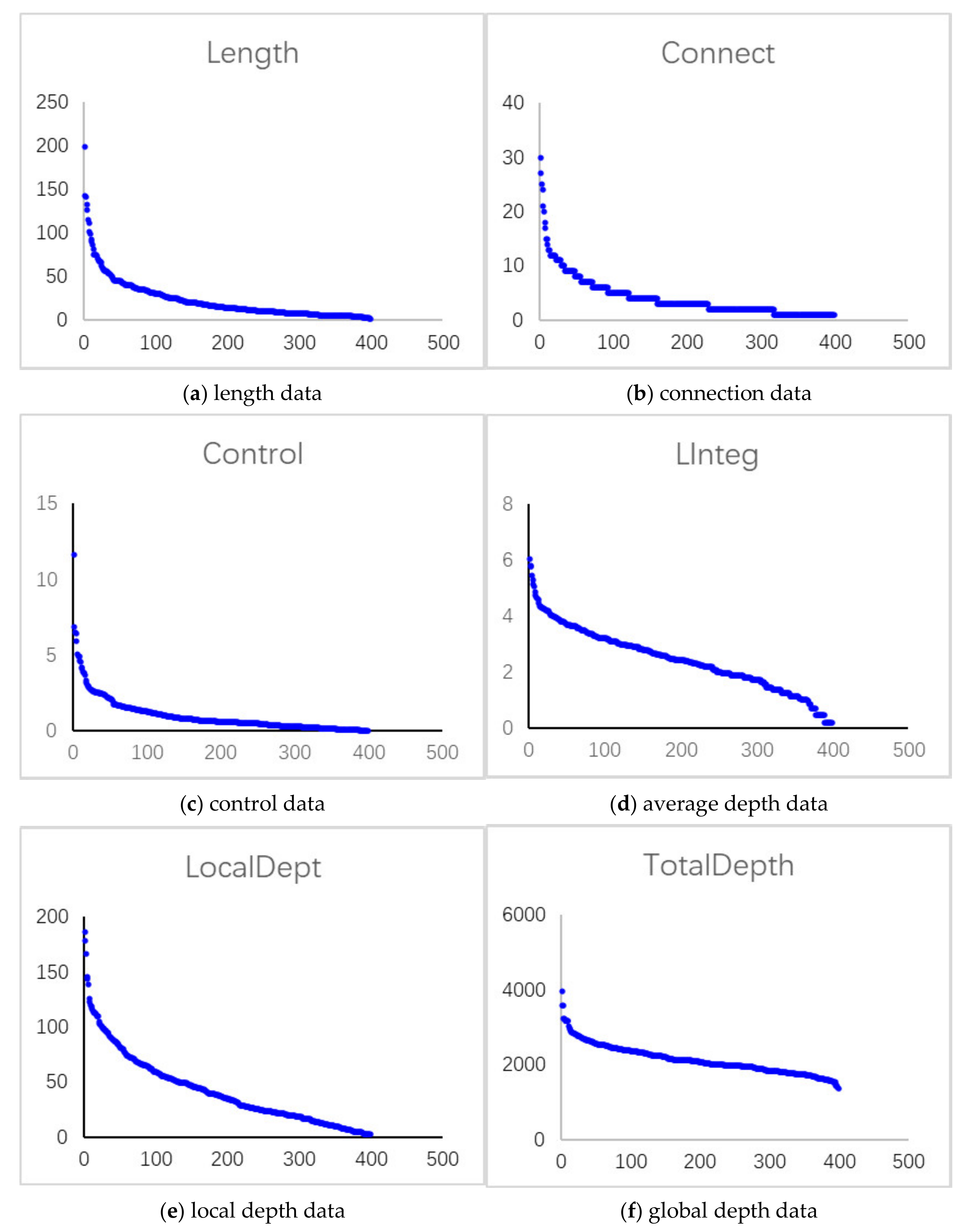
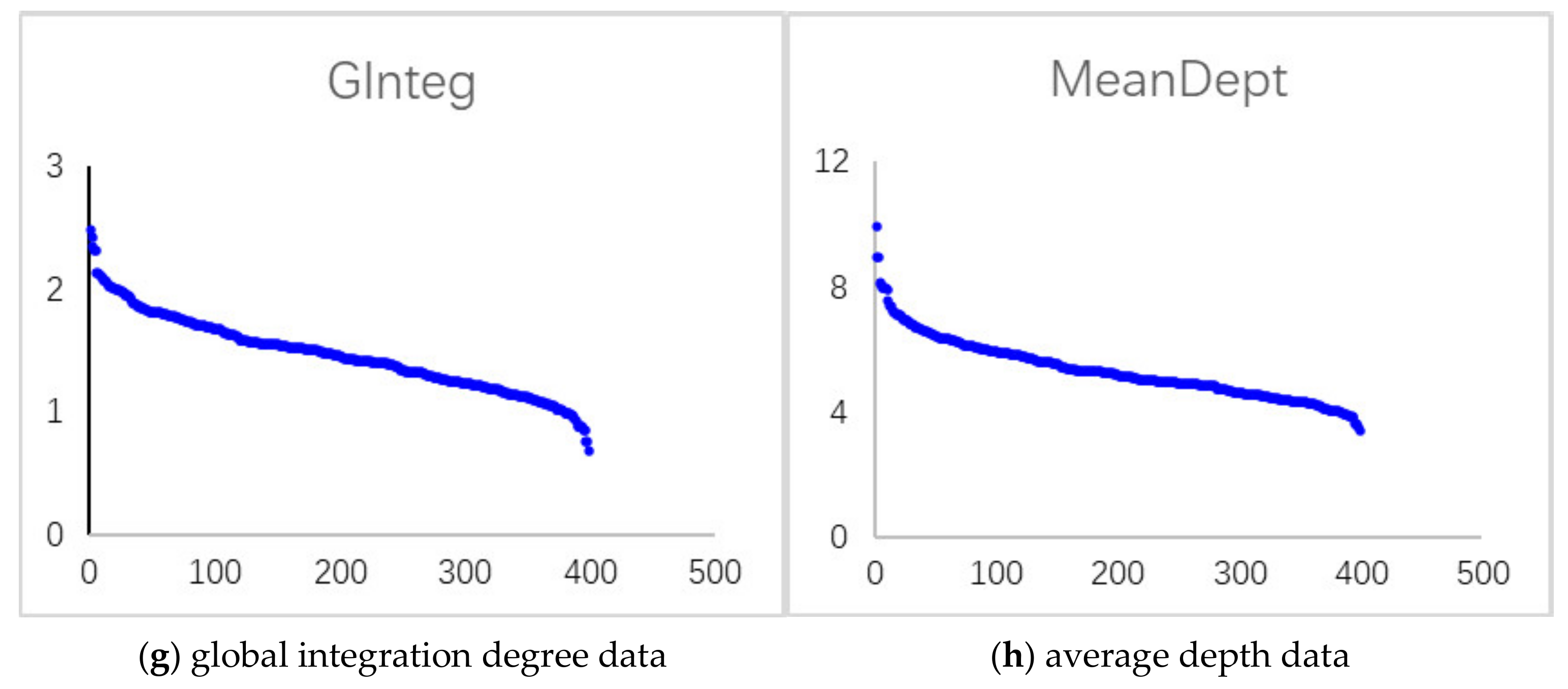
5.1. Parameter Selection
5.2. Comparison of Fractal Dimension Calculation
6. Conclusions
- (1)
- Based on the characteristics of self-similarity, heavy-tailed distribution, and being scale-free between the urban street networks and the rock fracture networks, we found that the space syntax metric of the urban street network can be effectively applied to rock fracture networks. Taking the rock fractures as the axis, there would be no dispute about the definition of the axis, which could better show the spatial structure of rock fracture networks.
- (2)
- Based on the traditional fractal theory and the head/tail breaks method, we proposed a new fractal dimension calculation method. The calculation process does not take the limit operation into consideration; the results are more stable than the previous fractal dimension calculation method. Because it combines the HT index and the traditional fractal dimension idea, the new calculation method can better and more effectively capture the fractal characteristics of a fractal set.
- (3)
- Through the calculation and analysis of three rock fracture network diagrams, the results of the simple fractal calculation method were found to be in the same order as the box-counting dimension results and the complexity of the rock fractures. This proves the effectiveness and accuracy of the fractal dimension calculation method.
- (4)
- The new quantification method was used to calculate the degrees of seven space syntax metrics. It was found that there were only two kinds of heavy-tailed distributions which meet the requirements of fractals—i.e., connection value and control value. By comparing the fractal dimension with the length fractal dimension, it was found that the trend of the length fractal dimension was the same as that of the control value fractal dimension, while the fractal dimension of the connection value was contrary to it. Compared with using the length fractal dimension as a parameter, it was also found that using the connection and control data as parameters to calculate the fractal dimension could better reflect the spatial characteristics of rock fracture networks. This also proves that space syntax has certain applicability in rock fracture networks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rahm, D. Regulating hydraulic fracturing in shale gas plays: The case of Texas. Energy Policy 2011, 39, 2974–2981. [Google Scholar] [CrossRef]
- Mark, Y.; Playton, S.; Paul, T.; Wayne, N.; Mike, S.; Robert, M. Petrophysical Challenges in Giant Carbonate Tengiz Field, Republic of Kazakhstan. Petrophysics 2015, 56, 615–647. [Google Scholar]
- Hu, X.; Yu, W.; Liu, M.; Wang, M.; Wang, W. A multiscale model for methane transport mechanisms in shale gas reservoirs. J. Pet. Sci. Eng. 2019, 172, 40–49. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.G.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Hobé, A.; Vogler, D.; Seybold, M.P.; Ebigbo, A.; Settgast, R.R.; Saar, M.O. Estimating fluid flow rates through fracture networks using combinatorial optimization. Adv. Water Resour. 2018, 122, 85–97. [Google Scholar] [CrossRef] [Green Version]
- Figueroa Pilz, F.; Dowey, P.J.; Fauchille, A.L.; Courtois, L.; Bay, B.; Ma, L.; Taylor, K.; Meckleburgh, J.; Lee, P. Synchrotron tomographic quantification of strain and fracture during simulated thermal maturation of an organic-rich shale, UK Kimmeridge Clay. J. Geophys. Res. Solid Earth 2017, 122, 2553–2564. [Google Scholar] [CrossRef] [Green Version]
- Le, T.D.; Murad, M.A. A new multiscale model for flow and transport in unconventional shale oil reservoirs. Appl. Math. Model. 2018, 64, 453–479. [Google Scholar] [CrossRef]
- Li, X.; Zuo, Y.; Zhuang, X.; Zhu, H. Estimation of fracture trace length distributions using probability weighted moments and L-moments. Eng. Geol. 2014, 168, 69–85. [Google Scholar] [CrossRef]
- Lu, J.; Ghassemi, A. Estimating natural fracture orientations using geomechanics based stochastic analysis of microseismicity related to reservoir stimulation. Geothermics 2019, 79, 129–139. [Google Scholar] [CrossRef]
- Kevin Bisdom, G.B.; Hamidreza, M.N. The impact of different aperture distribution models and critical stress criteria on equivalent permeability in fractured rocks. J. Geophys. Res. Solid Earth 2015, 10, 1002. [Google Scholar]
- El-Emam, H.; Elsisi, A.; Salim, H.; Sallam, H. Fatigue Crack Tip Plasticity for Inclined Cracks. Int. J. Steel Struct. 2018, 18, 443–455. [Google Scholar] [CrossRef]
- Roy, A.; Perfect, E.; Dunne, W.M.; McKay, L.D. A technique for revealing scale-dependent patterns in fracture spacing data. J. Geophys. Res. Solid Earth 2014, 119, 5979–5986. [Google Scholar] [CrossRef]
- Babanouri, N.; Nasab, S.K.; Sarafrazi, S. A hybrid particle swarm optimization and multi-layer perceptron algorithm for bivariate fractal analysis of rock fractures roughness. Int. J. Rock Mech. Min. Sci. 2013, 60, 66–74. [Google Scholar] [CrossRef]
- Geng, L.; Li, G.; Wang, M.; Li, Y.; Tian, S.; Pang, W.; Lyu, Z. A fractal production prediction model for shale gas reservoirs. J. Nat. Gas Sci. Eng. 2018, 55, 354–367. [Google Scholar] [CrossRef]
- Riley, P.; Tikoff, B.; Murray, A.B. Quantification of fracture networks in non-layered, massive rock using synthetic and natural data sets. Tectonophysics 2011, 505, 44–56. [Google Scholar] [CrossRef]
- Miao, T.; Yu, B.; Duan, Y.; Fang, Q. A fractal analysis of permeability for fractured rocks. Int. J. Heat Mass Transf. 2015, 81, 75–80. [Google Scholar] [CrossRef]
- Huang, S.; Yao, Y.; Zhang, S.; Ji, J.; Ma, R. Pressure transient analysis of multi-fractured horizontal wells in tight oil reservoirs with consideration of stress sensitivity. Arab. J. Geosci. 2018, 11, 285. [Google Scholar] [CrossRef]
- Wang, L.; Duan, K.; Zhang, Q.; Li, X.; Jiang, R. Study of the Dynamic Fracturing Process and Stress Shadowing Effect in Granite Sample with Two Holes Based on SCDA Fracturing Method. Rock Mech. Rock Eng. 2022, 55, 1537–1553. [Google Scholar] [CrossRef]
- Silberschmidt, V.V.; Silberschmidt, V.G. Fractal models in rock fracture analysis. Terra Nova 2010, 2, 483–488. [Google Scholar] [CrossRef]
- Koike, K.; Kaneko, K. Characterization and modeling of fracture distribution in rock mass using fractal theory. Geotherm. Sci. Technol. 1999, 6, 43–62. [Google Scholar]
- Zhou, Z.; Su, Y.; Wang, W.; Yan, Y. Integration of microseismic and well production data for fracture network calibration with an L-system and rate transient analysis. J. Unconv. Oil Gas Resour. 2016, 15, 113–121. [Google Scholar] [CrossRef]
- Liu, G.; Yu, B.; Ye, D.; Gao, F.; Liu, J. Study on Evolution of Fractal Dimension for Fractured Coal Seam under Multi-Field Cou-pling. Fractals 2020, 28, 2050072. [Google Scholar] [CrossRef]
- Mecholsky, J.J.; Passoja, D.E.; Feinberg-Ringel, K.S. Quantitative Analysis of Brittle Fracture Surfaces Using Fractal Geometry. J. Am. Ceram. Soc. 2010, 72, 1–12. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Wang, W.; Javadpour, F.; Tang, M. Application of Fractal Geometry in Evaluation of Effective Stimulated Reser-voir Volume in Shale Gas Reservoirs. Fractals 2017, 25, 1740007. [Google Scholar] [CrossRef] [Green Version]
- Sui, L.; Ju, Y.; Yang, Y.; Yang, Y.; Li, A. A quantification method for shale fracability based on analytic hierarchy process. Energy 2016, 115, 637–645. [Google Scholar] [CrossRef]
- Gillespie, P.A.; Walsh, J. Measurement and characterisation of fractures of space distributions. Tectonophysics 1993, 226, 113–141. [Google Scholar] [CrossRef]
- Walsh, J.; Watterson, J. Fractal analysis of fracture patterns using the standard box-counting technique: Valid and invalid methodologies. J. Struct. Geol. 1993, 15, 1509–1512. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T. Estimation of equivalent fracture network permeability using fractal and statistical network properties. J. Pet. Sci. Eng. 2012, 92–93, 110–123. [Google Scholar] [CrossRef]
- Space Syntax Network. Available online: https://www.spacesyntax.net/ (accessed on 17 January 2021).
- UCL. Space Syntax: Overview. Available online: https://www.spacesyntax.online/overview-2/ (accessed on 17 January 2021).
- Hillier, B.H.J. The Social Logic of Space; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Thomson, R.C. Bending the axial line smoothly continuous road centre-line segments as a basis for road network analysis. In Proceedings of the 4th International Space Syntax Symposium, London, UK, 17–19 June 2003. [Google Scholar]
- Liu, X.; Jiang, B. Defining and generating axial lines from street center lines for better understanding of urban morphologies. Int. J. Geogr. Inf. Sci. 2012, 26, 1521–1532. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. Topological Analysis of Urban Street Networks. Environ. Plan. B Plan. Des. 2004, 31, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Zhao, S.; Yin, J. Self-organized natural roads for predicting traffic flow: A sensitivity study. J. Stat. Mech. Theory Exp. 2008, 2008, P07008. [Google Scholar] [CrossRef] [Green Version]
- Jeong, S.-K.; Ban, Y.-U. Developing a topological information extraction model for space syntax analysis. Build. Environ. 2011, 46, 2442–2453. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, C. Street-based topological representations and analyses for predicting traffic flow in GIS. Int. J. Geogr. Inf. Sci. 2009, 23, 1119–1137. [Google Scholar] [CrossRef] [Green Version]
- Mustafa, F.A.; Rafeeq, D.A. Assessment of elementary school buildings in Erbil city using space syntax analysis and school teachers′ feedback. Alex. Eng. J. 2019, 58, 1039–1052. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B.; Qiu, S.; Cai, J. An analysis of the radial flow in the heterogeneous porous media based on fractal and constructal tree networks. Phys. A Stat. Mech. Its Appl. 2008, 387, 6471–6483. [Google Scholar] [CrossRef]
- Zheng, Q.; Yu, B.; Wang, S.; Luo, L. A diffusivity model for gas diffusion through fractal porous media. Chem. Eng. Sci. 2012, 68, 650–655. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, P.; Qiu, S.; Rao, B.; Yu, B. A generalized thermal conductivity model for unsaturated porous media with fractal ge-ometry. Int. J. Heat Mass Transf. 2020, 152, 119540. [Google Scholar] [CrossRef]
- Boming, Y.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar]
- Xu, P.; Yu, B. Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Miao, T.; Chen, A.; Zhang, L.; Yu, B. A novel fractal model for permeability of damaged tree-like branching networks. Int. J. Heat Mass Transf. 2018, 127, 278–285. [Google Scholar] [CrossRef]
- Sui, L.; Yu, J.; Cang, D.; Miao, W.; Wang, H.; Zhang, J.; Yin, S.; Chang, K. The fractal description model of rock fracture networks characterization. Chaos Solitons Fractals 2019, 129, 71–76. [Google Scholar] [CrossRef]
- Ding, M.; Jiang, B. A Smooth Curve as a Fractal under the Third Definition. Cartographica 2018, 53, 203–210. [Google Scholar]
- Jiang, B. Head/Tail Breaks: A New Classification Scheme for Data with a Heavy-Tailed Distribution. Prof. Geogr. 2013, 65, 482–494. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J. Ht-Index for Quantifying the Fractal or Scaling Structure of Geographic Features. Ann. Assoc. Am. Geogr. 2013, 104, 530–540. [Google Scholar] [CrossRef]
- Chelidze, T.; Gueguen, Y. Evidence of fractal fracture. Int. J. Rock Mech. Ming Sci. Geome-Chanics Abstr. 1990, 27, 223–225. [Google Scholar] [CrossRef]
- Jiang, B. A Recursive Definition of Goodness of Space for Bridging the Concepts of Space and Place for Sustainability. Sustainability 2019, 11, 4091. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B. Living Structure Down to Earth and Up to Heaven: Christopher Alexander. Urban Sci. 2019, 3, 96. [Google Scholar] [CrossRef] [Green Version]

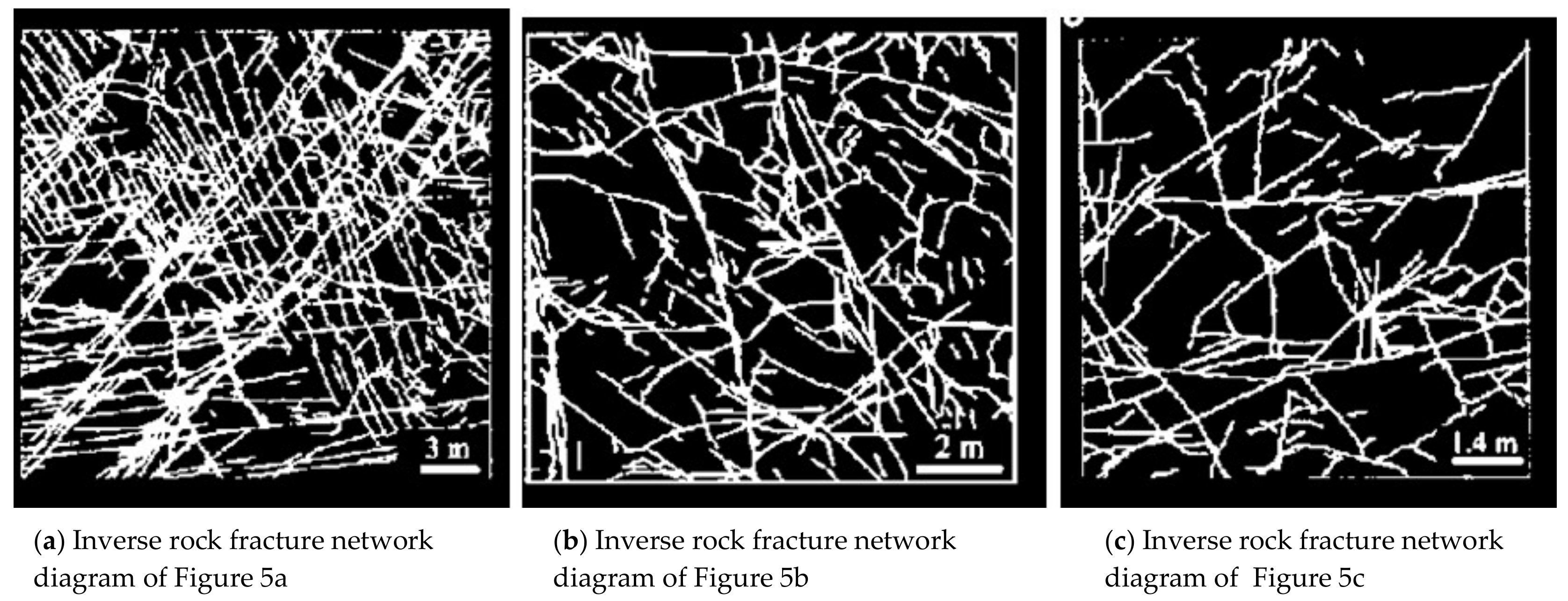
| Figure 5a | Figure 5b | Figure 5c | ||||
|---|---|---|---|---|---|---|
| N | M | N | M | N | M | |
| Total | 414.00 | 22.64 | 261.00 | 19.49 | 139.00 | 28.09 |
| H1 | 138.00 | 47.25 | 94.00 | 38.15 | 47.00 | 57.19 |
| T1 | 276.00 | 10.34 | 167.00 | 8.98 | 92.00 | 13.23 |
| H1 (%) | 0.33 | 0.36 | 0.34 | |||
| T1 (%) | 0.67 | 0.64 | 0.66 | |||
| H2 | 40.00 | 80.00 | 28.00 | 65.21 | 17.00 | 88.18 |
| T2 | 98.00 | 33.88 | 66.00 | 26.67 | 30.00 | 39.63 |
| H2 (%) | 0.29 | 0.30 | 0.36 | |||
| T2 (%) | 0.71 | 0.70 | 0.64 | |||
| H3 | 13.00 | 117.15 | 9.00 | 97.22 | 7.00 | 120.29 |
| T3 | 27.00 | 62.11 | 19.00 | 50.05 | 10.00 | 65.70 |
| H3 (%) | 0.33 | 0.32 | 0.41 | |||
| T3 (%) | 0.68 | 0.68 | 0.59 | |||
| H4 | 5.00 | 148.60 | 3.00 | 137.00 | 3.00 | 147.00 |
| T4 | 8.00 | 97.50 | 6.00 | 77.33 | 4.00 | 100.25 |
| H4 (%) | 0.38 | 0.33 | 0.43 | |||
| T4 (%) | 0.62 | 0.67 | 0.57 | |||
| H5 | 1.00 | 199.00 | 1.00 | 159.00 | 1.00 | 183.00 |
| T5 | 4.00 | 136.00 | 2.00 | 126.00 | 2.00 | 129.00 |
| H5 (%) | 0.20 | 0.33 | 0.33 | |||
| T5 (%) | 0.80 | 0.67 | 0.67 | |||
| Connect | Control | MeanDept | GInteg | LInteg | TotalDepth | LocalDept | Length | |
|---|---|---|---|---|---|---|---|---|
| HT Index | 4 | 6 | 1 | 1 | 1 | 1 | 1 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, L.; Wang, H.; Wu, J.; Zhang, J.; Yu, J.; Ma, X.; Sun, Q. Fractal Description of Rock Fracture Networks Based on the Space Syntax Metric. Fractal Fract. 2022, 6, 353. https://doi.org/10.3390/fractalfract6070353
Sui L, Wang H, Wu J, Zhang J, Yu J, Ma X, Sun Q. Fractal Description of Rock Fracture Networks Based on the Space Syntax Metric. Fractal and Fractional. 2022; 6(7):353. https://doi.org/10.3390/fractalfract6070353
Chicago/Turabian StyleSui, Lili, Heyuan Wang, Jinsui Wu, Jiwei Zhang, Jian Yu, Xinyu Ma, and Qiji Sun. 2022. "Fractal Description of Rock Fracture Networks Based on the Space Syntax Metric" Fractal and Fractional 6, no. 7: 353. https://doi.org/10.3390/fractalfract6070353
APA StyleSui, L., Wang, H., Wu, J., Zhang, J., Yu, J., Ma, X., & Sun, Q. (2022). Fractal Description of Rock Fracture Networks Based on the Space Syntax Metric. Fractal and Fractional, 6(7), 353. https://doi.org/10.3390/fractalfract6070353






