Application of Multifractal Analysis Theory to Interpret T2 Cutoffs of NMR Logging Data: A Case Study of Coarse Clastic Rock Reservoirs in Southwestern Bozhong Sag, China
Abstract
1. Introduction
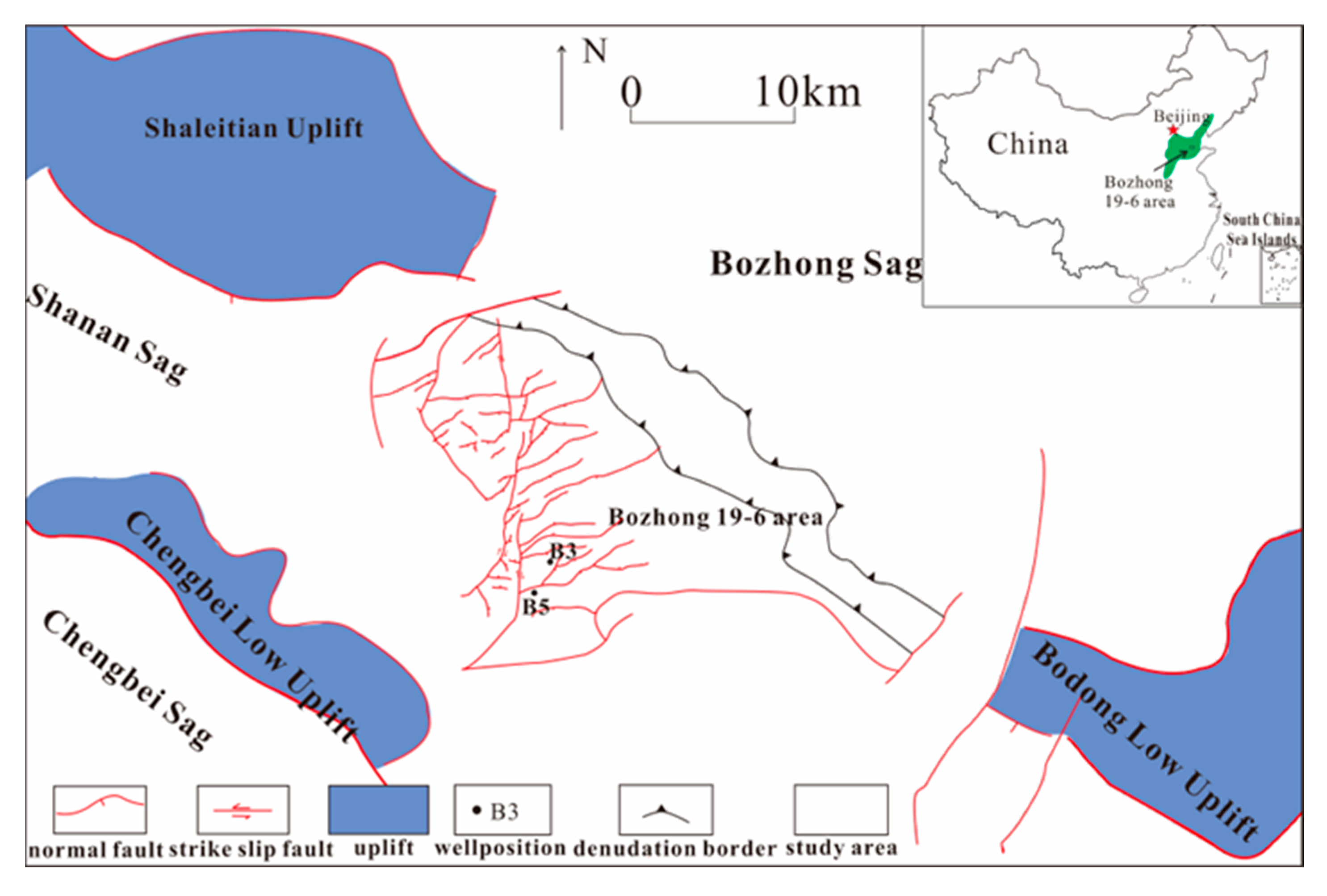
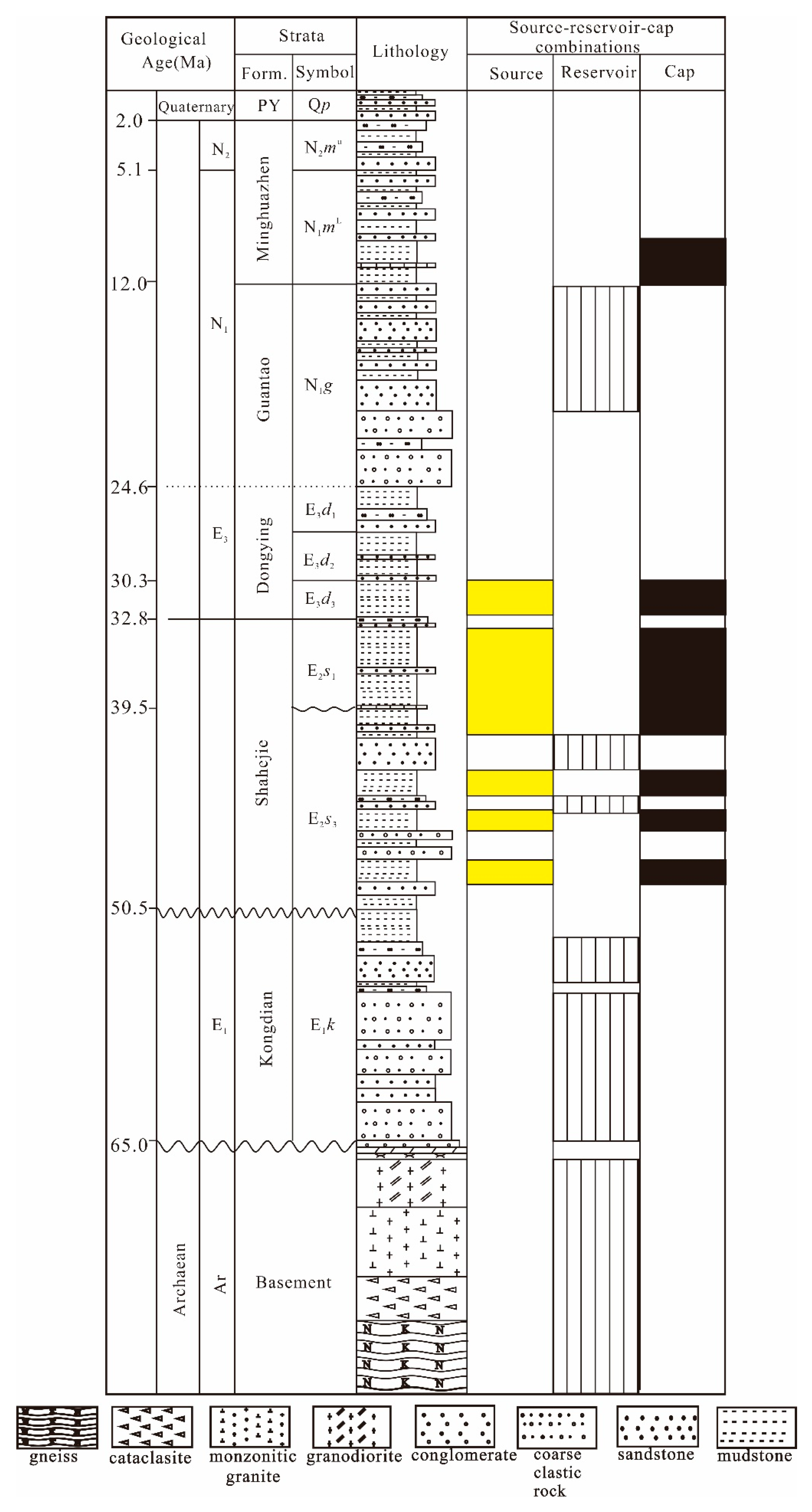
2. Geological Background
3. Samples and Methods
3.1. Samples
3.2. NMR and Centrifugal Experiments
3.3. Multifractal Analysis
4. Results
4.1. Porosity and Permeability
4.2. Calculation of T2C Based on Core Analysis
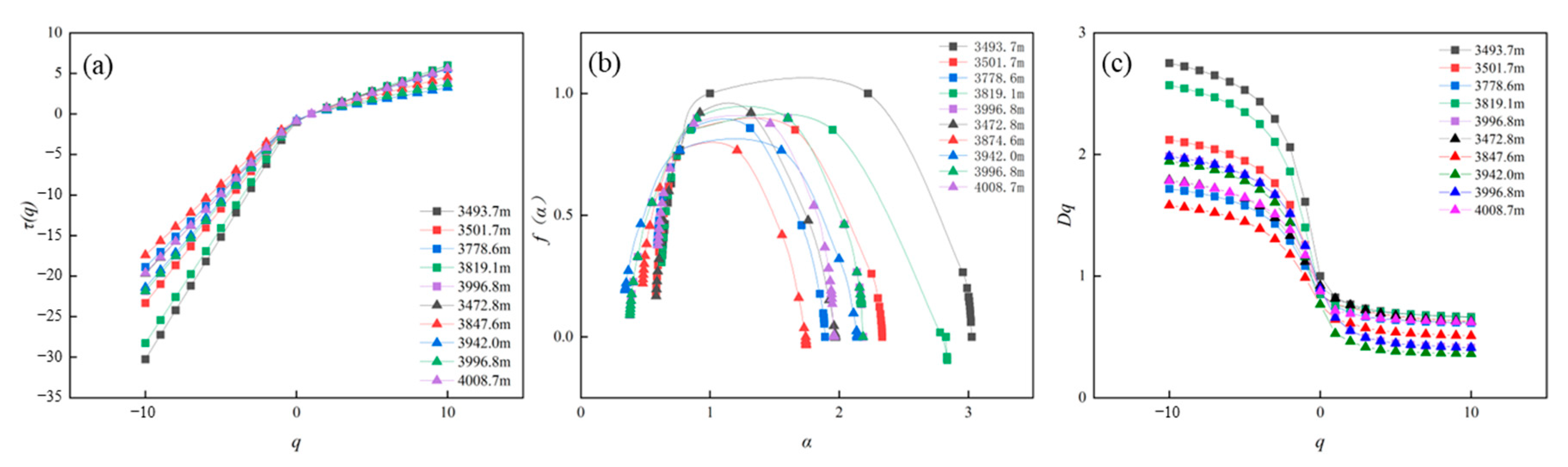
4.3. Multifractal Analysis of the NMR Data
5. Discussion
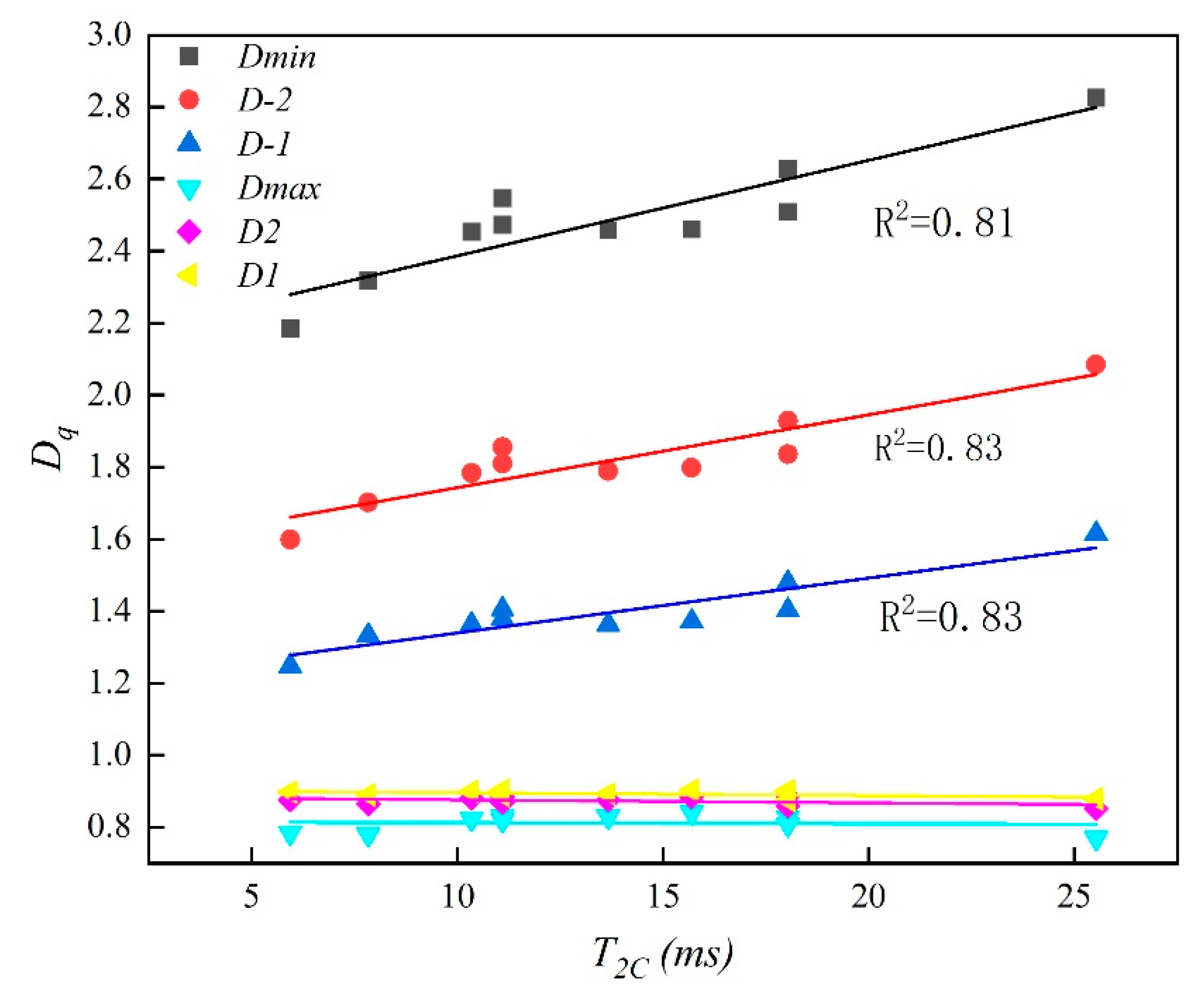
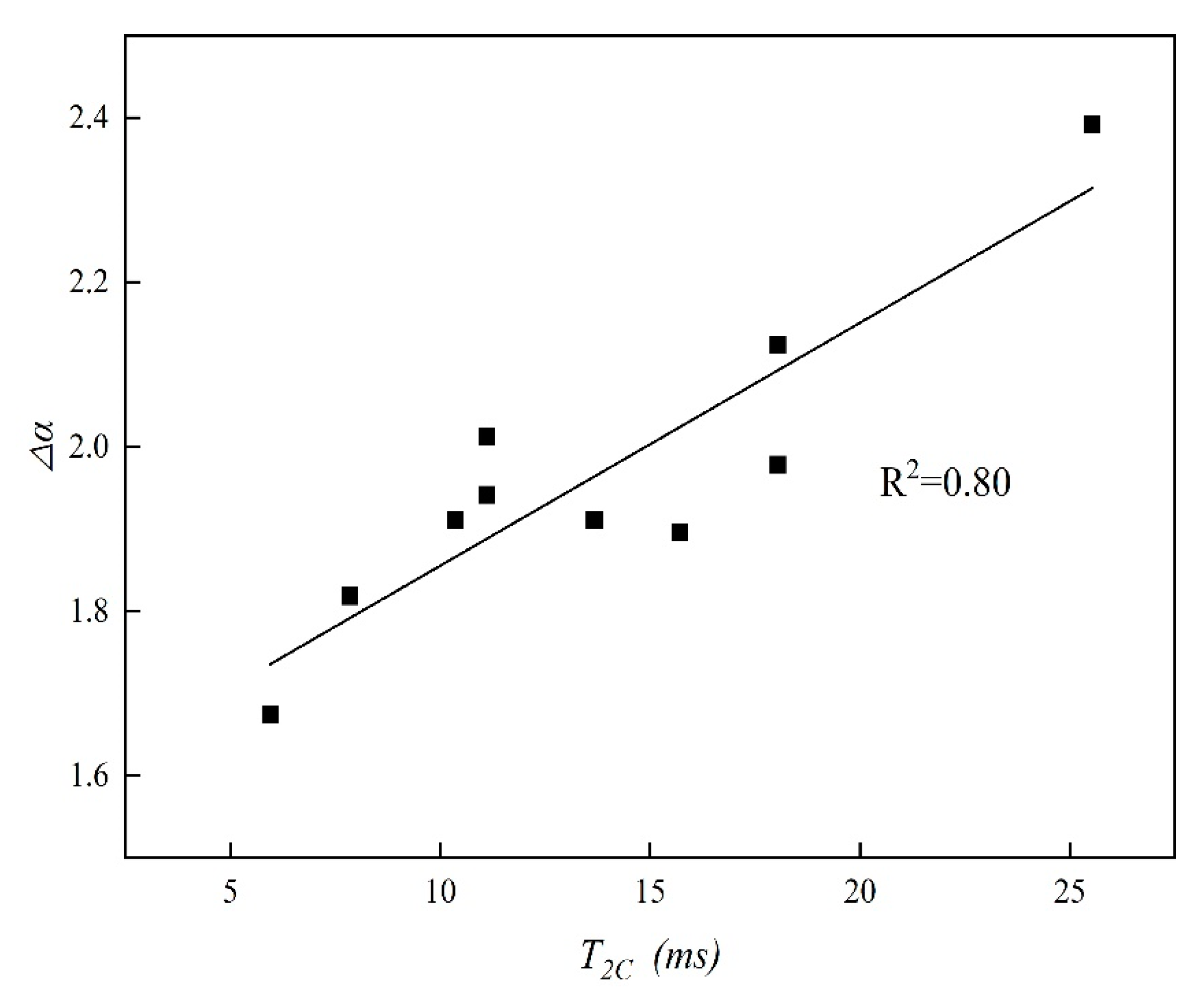
5.1. Relationships between T2C and Multifractal Parameters
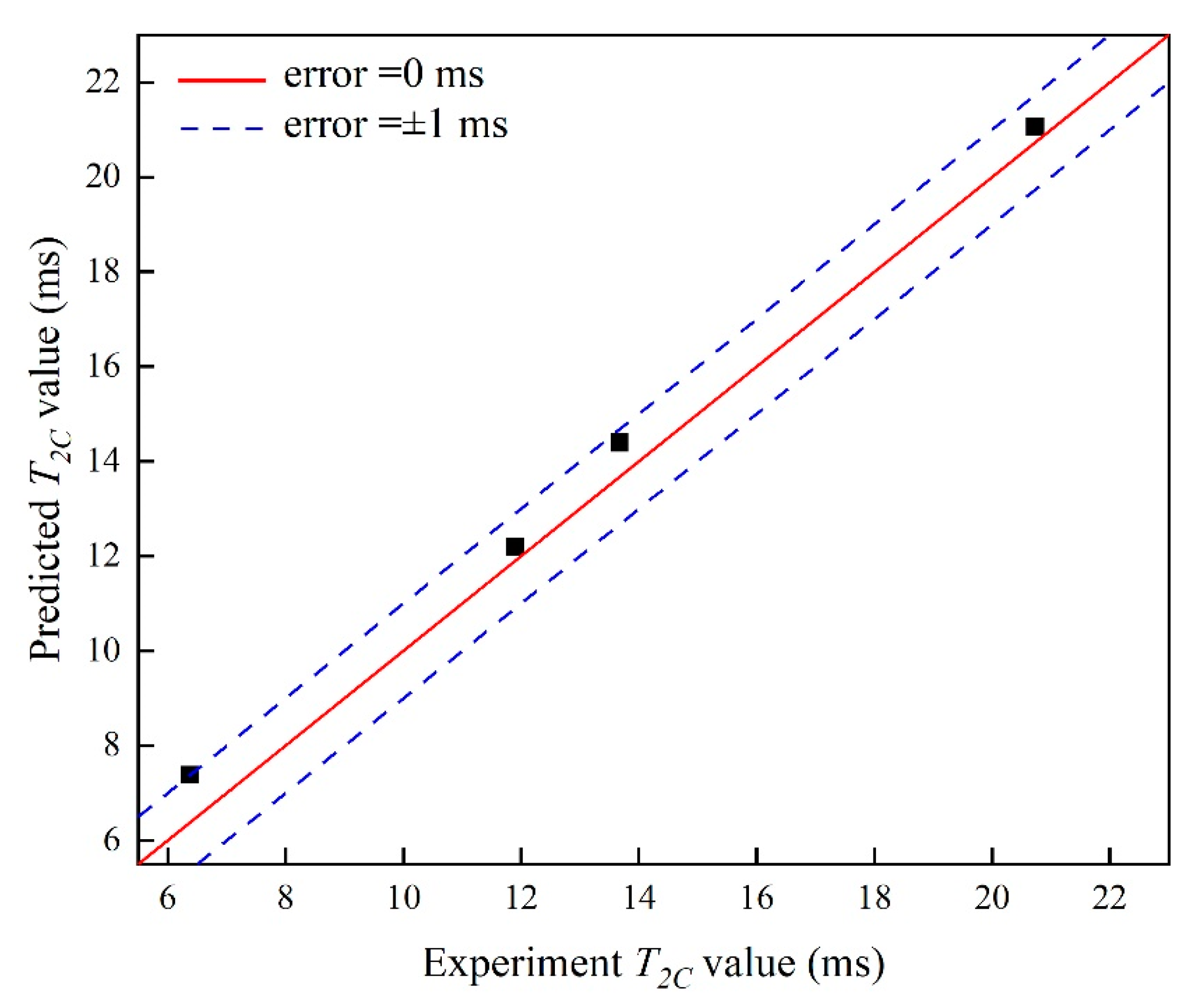
5.2. Model and Its Validation
5.3. Well Logs Applications
5.3.1. Expanding to Applications for NMR Logging
5.3.2. Model Correction from the Laboratory to the Field
5.3.3. Results of the Case Well
6. Conclusions
- (1)
- The saturated T2 spectra of the coarse clastic rock commonly show bimodal distributions, with measured T2C values of 5.94 ~ 25.53 ms for 14 samples.
- (2)
- Both the NMR logging T2 spectrum of the Kongdian Formation and the saturated T2 spectrum of the samples have typical multifractal characteristics. The multifractal parameters of the difference (D−q − Dq), the product (D−q/Dq), and Δα reveal strong correlations with the T2C value.
- (3)
- Based on the NMR experiment of 10 samples and multifractal theory, a prediction model for the T2C value was established, which was verified using the experimental results of 4 samples. The error between the predicted results and the experimental data is within 1 ms.
- (4)
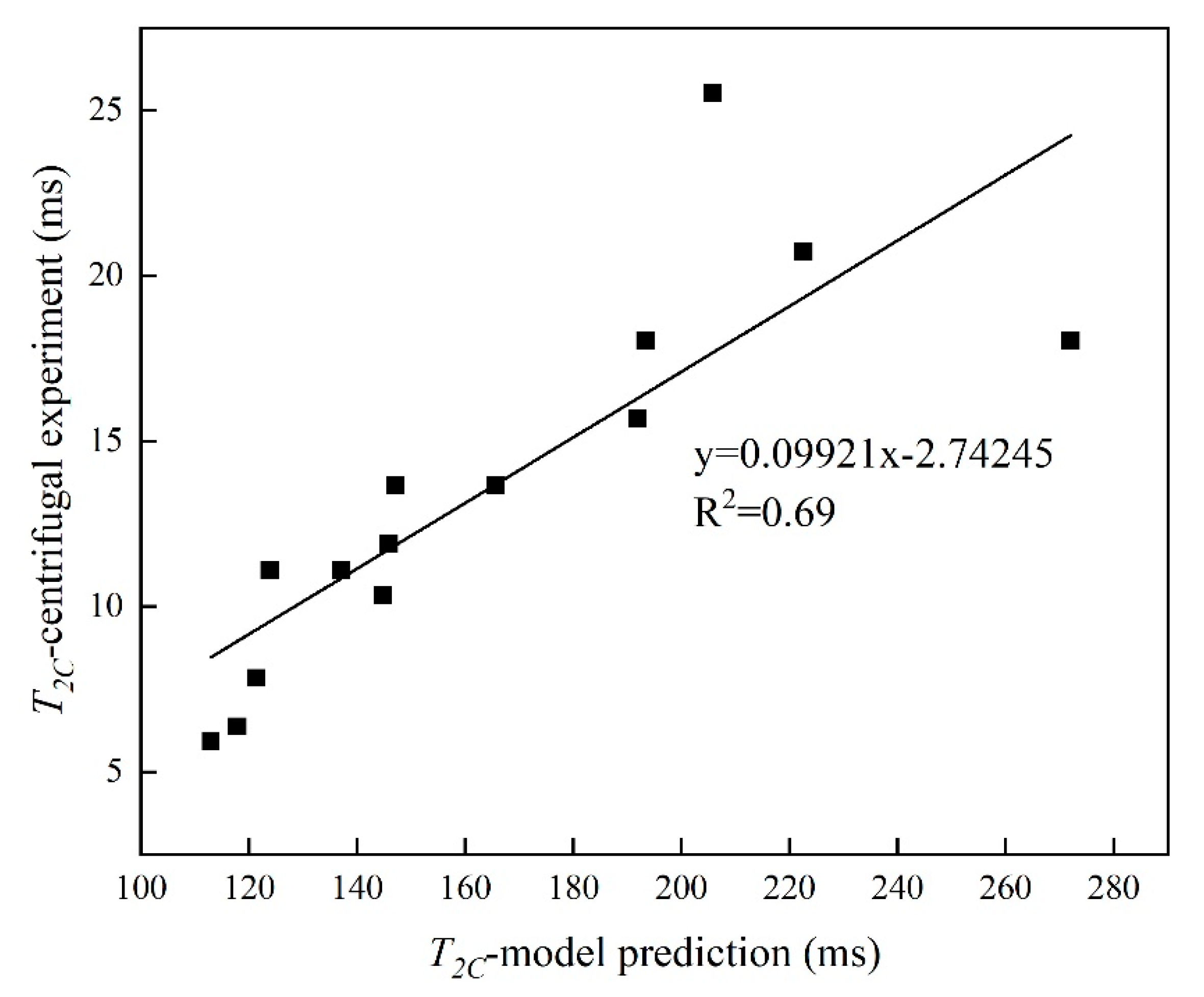
- The model built in the laboratory was expanded to be used in the field. The goodness of fit of the new model is 0.69, indicating a good matching degree.
- (5)
- This method was applied to Well-B5, and a continuous T2C value curve was obtained. The result of the interpretation is consistent with the production data, which indicates that the method is reliable.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qi, J.; Yang, Q. Cenozoic structural deformation and dynamic processes of the Bohai Bay basin province, China. Mar. Pet. Geol. 2010, 27, 757–771. [Google Scholar] [CrossRef]
- Guo, X.; He, S.; Liu, K.; Song, G.; Wang, X.; Shi, Z. Oil generation as the dominant overpressure mechanism in the Cenozoic Dongying depression, Bohai Bay Basin, China. Aapg Bull. 2010, 94, 1859–1881. [Google Scholar] [CrossRef]
- Du, X.; Wang, Q.; Zhao, M.; Liu, X. Sedimentary characteristics and mechanism analysis of a large-scale fan delta system in the Paleocene Kongdian Formation, Southwestern Bohai Sea, China. Interpretation 2020, 8, SF81–SF94. [Google Scholar] [CrossRef]
- Zeng, L.; Jiang, J.; Yang, Y. Fractures in the low porosity and ultra-low permeability glutenite reservoirs: A case study of the late Eocene Hetaoyuan formation in the Anpeng Oilfield, Nanxiang Basin, China. Mar. Pet. Geol. 2010, 27, 1642–1650. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, S.; Xiao, D.; Gu, M. Characterization of full pore size distribution and its significance to macroscopic physical parameters in tight glutenites. J. Nat. Gas Sci. Eng. 2017, 38, 434–449. [Google Scholar] [CrossRef]
- Li, L.; Meng, Q.; Wang, S.; Li, G.; Tang, C. A numerical investigation of the hydraulic fracturing behaviour of conglomerate in Glutenite formation. Acta Geotech. 2013, 8, 597–618. [Google Scholar] [CrossRef]
- Rui, Z.; Guo, T.; Feng, Q.; Qu, Z.; Qi, N.; Gong, F. Influence of gravel on the propagation pattern of hydraulic fracture in the glutenite reservoir. J. Pet. Sci. Eng. 2018, 165, 627–639. [Google Scholar] [CrossRef]
- Tian, W.; Lu, S.; Huang, W.; Wang, S.; Gao, Y.; Wang, W.; Li, J.; Xu, J.; Zhan, Z. Study on the Full-Range Pore Size Distribution and the Movable Oil Distribution in Glutenite. Energy Fuels 2019, 33, 7028–7042. [Google Scholar] [CrossRef]
- Ge, X.; Myers, M.T.; Liu, J.; Fan, Y.; Zahid, M.A.; Zhao, J.; Hathon, L. Determining the transverse surface relaxivity of reservoir rocks: A critical review and perspective. Mar. Pet. Geol. 2021, 126, 104934. [Google Scholar] [CrossRef]
- Singer, P.M.; Asthagiri, D.; Chapman, W.G.; Hirasaki, G.J. Molecular dynamics simulations of NMR relaxation and diffusion of bulk hydrocarbons and water. J. Magn. Reson. 2017, 277, 15–24. [Google Scholar] [CrossRef]
- Singer, P.M.; Chen, Z.; Wang, X.; Hirasaki, G.J. Diffusive coupling in heptane-saturated kerogen isolates evidenced by NMR T-1-T-2 and T-2-T-2 maps. Fuel 2020, 280, 118626. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, B.; You, J.; Liu, J.; Wang, D.; Lu, J.; Tong, J. Characterizing pore-level oil mobilization processes in unconventional reservoirs assisted by state-of-the-art nuclear magnetic resonance technique. Energy 2021, 236, 121549. [Google Scholar] [CrossRef]
- Ge, X.; Zhao, J.; Zhang, F.; Fan, Y.; Liu, J.; Cai, J.; Nie, S.; Wang, C. A Practical Method to Compensate for the Effect of Echo Spacing on the Shale NMR T-2 Spectrum. Earth Space Sci. 2019, 6, 1489–1497. [Google Scholar] [CrossRef]
- Siavashi, J.; Najafi, A.; Sharifi, M.; Fahimpour, J.; Shabani, M.; Liu, B.; Liu, K.; Yan, J.; Ostadhassan, M. An insight into core flooding experiment via NMR imaging and numerical simulation. Fuel 2022, 318, 123589. [Google Scholar] [CrossRef]
- Timur, A. Pulsed Nuclear Magnetic Resonance Studies of Porosity, Movable Fluid, and Permeability of Sandstones. J. Pet. Technol. 1969, 21, 775–786. [Google Scholar] [CrossRef]
- Gao, H.; Li, H. Determination of movable fluid percentage and movable fluid porosity in ultra-low permeability sandstone using nuclear magnetic resonance (NMR) technique. J. Pet. Sci. Eng. 2015, 133, 258–267. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, Y.; Liu, D.; Zheng, S.; Sun, G.; Chang, Y. Shale pore size classification: An NMR fluid typing method. Mar. Pet. Geol. 2018, 96, 591–601. [Google Scholar] [CrossRef]
- Oraby, M.; Chafai, N.; Hussing, R.B.; Massengill, D.R.; Pletcher, D. A New NMR Interpretation Technique Using Error Minimization with Variable T2 Cutoff. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE-38734-MS, San Antonio, TX, USA, 5 October 1997. [Google Scholar]
- Godefroy, S.; Fleury, M.; Deflandre, F.; Korb, J.P. Temperature Effect on NMR Surface Relaxation. In Proceedings of the SPE Annual Technical Conference and Exhibition, SPE71700, New Orleans, LA, USA, 30 September 2001. [Google Scholar]
- Nicot, B.; Ligneul, P.; Akbar, M. T2 Cutoff Determination Using Magnetic Susceptibility Measurements: U.S. Patent Application. U.S. Patent US20130265043A1, 23 August 2016. [Google Scholar]
- Wang, Z.H.; Zhang, C.G.; Xiao, C.W.; Chen, X.L.; Song, F. Experimental Study of T2 cutoff values in low-permeability reservoirs (in Chinese with English abstracts). Prog. Geophys. 2004, 19, 652–655. [Google Scholar]
- Parra, J.O.; Hackert, C.L.; Antonio, S.; Collier, T.; Bennet, M. NMR and Acoustic Signatures in Vuggy Carbonate Aquifers. In Proceedings of the SPWLA 42nd Annual Logging Symposium, SPWLA2001-II, Houston, TX, USA, 17 June 2001. [Google Scholar]
- Hutchinson, J.E. Fractals and Self Similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, D.; Chen, J.; Li, Q.; Dai, J. Fractal analysis of shale pore structure of continental shale gas reservoir in the Ordos Basin, NW China. Energy Fuels 2016, 30, 4676–4689. [Google Scholar] [CrossRef]
- Gould, D.J.; Vadakkan, T.J.; Poché, R.; Dickinson, M.E. Multifractal and Lacunarity Analysis of Microvascular Morphology and Remodeling. Microcirculation 2015, 18, 136–151. [Google Scholar] [CrossRef] [PubMed]
- Qu, K.; Guo, S. Investigation of the Pore Structure of Tight Sandstone Based on Multifractal Analysis from NMR Measurement: A Case from the Lower Permian Taiyuan Formation in the Southern North China Basin. Energies 2020, 13, 4067. [Google Scholar] [CrossRef]
- Peng, J.; Han, H.; Xia, Q.; Li, B. Evaluation of the pore structure of tight sandstone reservoirs based on multifractal analysis: A case study from the Kepingtage Formation in the Shuntuoguole uplift, Tarim Basin, NW China. J. Geophys. Eng. 2018, 15, 1122–1136. [Google Scholar] [CrossRef]
- Kai, J.; Ding, W.L.; Huang, W.H.; Zhang, Y.; Zhao, S. Fractures of lacustrine shale reservoirs, the Zhanhua Depression in the Bohai Bay Basin, eastern China. Mar. Pet. Geol. 2013, 48, 113–123. [Google Scholar] [CrossRef]
- Allen, M.B.; Macdonald, D.; Xun, Z.; Vincent, S.J.; Brouet-Menzies, C. Early Cenozoic two-phase extension and late Cenozoic thermal subsidence and inversion of the Bohai Basin, northern China. Mar. Pet. Geol. 1997, 14, 951–972. [Google Scholar] [CrossRef]
- Xu, C.; Yu, H.; Wang, J.; Liu, X. Formation conditions and accumulation characteristics of Bozhong 19-6 large condensate gas field in offshore Bohai Bay Basin. Pet. Explor. Dev. 2019, 46, 27–40. [Google Scholar] [CrossRef]
- Xu, C.; Du, X.; Zhu, H.; Jia, D.; Xu, W.; Lu, H. Source-to-sink system and its sedimentary records in the continental rift basins: An example from the Paleogene in the Bohai Sea Area, China. Interpretation 2017, 5, ST35–ST51. [Google Scholar] [CrossRef]
- Munn, K.; Smith, D.M. A NMR technique for the analysis of pore structure: Numerical inversion of relaxation measurements. J. Colloid Interface Sci. 1987, 119, 117–126. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Che, Y.; Tang, D.; Tang, S.; Huang, W. Petrophysical characterization of coals by low-field nuclear magnetic resonance (NMR). Fuel 2010, 89, 1371–1380. [Google Scholar] [CrossRef]
- Daigle, H.; Thomas, B.; Rowe, H.; Nieto, M. Nuclear magnetic resonance characterization of shallow marine sediments from the Nankai Trough, Integrated Ocean Drilling Program Expedition 333. J. Geophys. Res. Solid Earth 2014, 119, 2631–2650. [Google Scholar] [CrossRef]
- Kenyon, W. Petrophysical principles of applications of NMR logging. Log Anal. 1997, 38, SPWLA-1997-v38n2a4. [Google Scholar]
- Morriss, C.; Rossini, D.; Straley, C.; Tutunjian, P.; Vinegar, H. Core analysis by low-field NMR. Log Anal. 1997, 38, SPWLA-1997-v38n2a3. [Google Scholar]
- Martínez, F.; Martín, M.; Caniego, F.J.; Tuller, M.; Guber, A.; Pachepsky, Y.; García-Gutiérrez, C. Multifractal analysis of discretized X-ray CT images for the characterization of soil macropore structures. Geoderma 2010, 156, 32–42. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Zou, J.; Gentzis, T.; Rezaee, R.; Bubach, B.; Carvajal-Ortiz, H. Multifractal analysis of gas adsorption isotherms for pore structure characterization of the Bakken Shale. Fuel 2018, 219, 296–311. [Google Scholar] [CrossRef]
- Tarquis, A.; Giménez, D.; Saa, A.; Díaz, M.; Gascó, J.; Pachepsky, J.; Radcliffe, D.; Selim, H. Scaling and multiscaling of soil pore systems determined by image analysis. Scaling Methods Soil Phys. 2003, 19, 24–34. [Google Scholar]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141. [Google Scholar] [CrossRef]
- Chhabra, A.; Jensen, R.V. Direct determination of the f (α) singularity spectrum. Phys. Rev. Lett. 1989, 62, 1327. [Google Scholar] [CrossRef]
- Zheng, S.; Yao, Y.; Liu, D.; Cai, Y.; Liu, Y.; Li, X. Nuclear magnetic resonance T2 cutoffs of coals: A novel method by multifractal analysis theory. Fuel 2019, 241, 715–724. [Google Scholar] [CrossRef]
- Hou, X.; Zhu, Y.; Chen, S.; Wang, Y.; Liu, Y. Investigation on pore structure and multifractal of tight sandstone reservoirs in coal bearing strata using LF-NMR measurements. J. Pet. Sci. Eng. 2020, 187, 106757. [Google Scholar] [CrossRef]
- Gouyet, J.-F. Physics and Fractal Structures; Elsevier Masson: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Yao, Y.; Sun, X.; Zheng, S.; Wu, H.; Zhang, C.; Liu, Y.; Chang, Y. Methods for petrological and petrophysical characterization of gas shales. Energy Fuels 2021, 35, 11061–11088. [Google Scholar] [CrossRef]
- Sun, Y.; Zhai, C.; Zhao, Y.; Xu, J.; Cong, Y.; Zheng, Y.; Tang, W. Multifractal Analysis and Neural Network Prediction of Pore Structures in Coal Reservoirs Based on NMR T2 Spectra. Energy Fuels 2021, 35, 11306–11318. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Kong, L. Fractal and Multifractal Characteristics of Pore Throats in the Bakken Shale. Transp. Porous Media 2018, 126, 579–598. [Google Scholar] [CrossRef]
- Caniego, F.J.; Martin, M.A.; San Jose, F. Singularity features of pore-size soil distribution: Singularity strength analysis and entropy spectrum. Fractals-Complex Geom. Patterns Scaling Nat. Soc. 2001, 9, 305–316. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, X.; Cai, J.; Luo, M.; Zhang, J.; Liu, Y.; Rabiei, M.; Li, C. Multifractal analysis of pore structure of Middle Bakken formation using low temperature N-2 adsorption and NMR measurements. J. Pet. Sci. Eng. 2019, 176, 312–320. [Google Scholar] [CrossRef]
- Ge, X.; Fan, Y.; Zhu, X.; Chen, Y.; Li, R. Determination of nuclear magnetic resonance T2 cutoff value based on multifractal theory—An application in sandstone with complex pore structure. Geophysics 2014, 80, D11–D21. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, Y.; Zhang, J.; Shangguan, J.; Li, M.; Quan, F.; Li, G. A method to determine nuclear magnetic resonance T2 cutoff value of tight sandstone reservoir based on multifractal analysis. Energy Sci. Eng. 2020, 8, 1135–1148. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, B.; Liu, T.; Zheng, Y.; Sun, Y.; Zhang, G.; Li, Q. Multifractal analysis of coal pore structure based on NMR experiment: A new method for predicting T2 cutoff value. Fuel 2021, 283, 119338. [Google Scholar] [CrossRef]
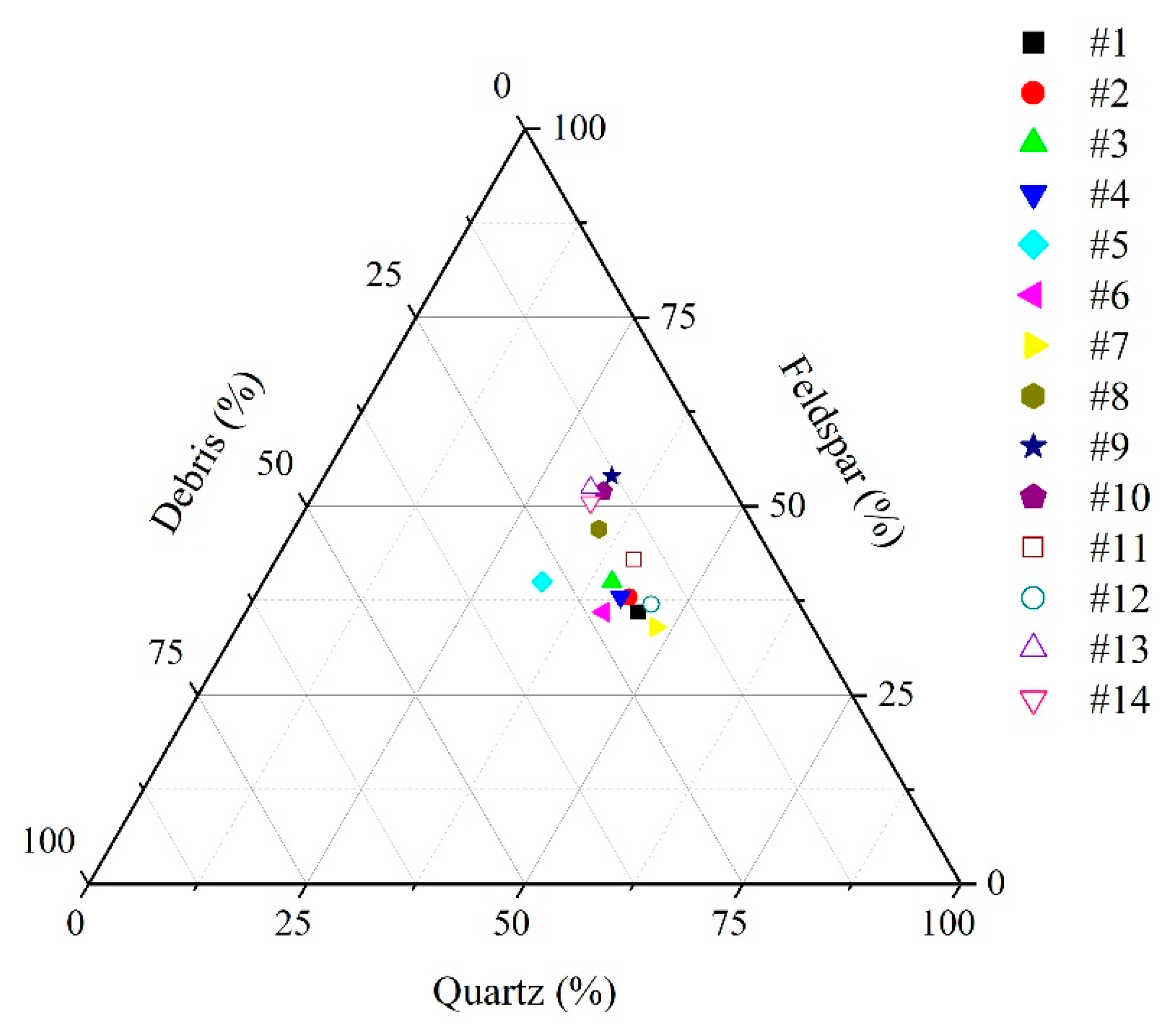

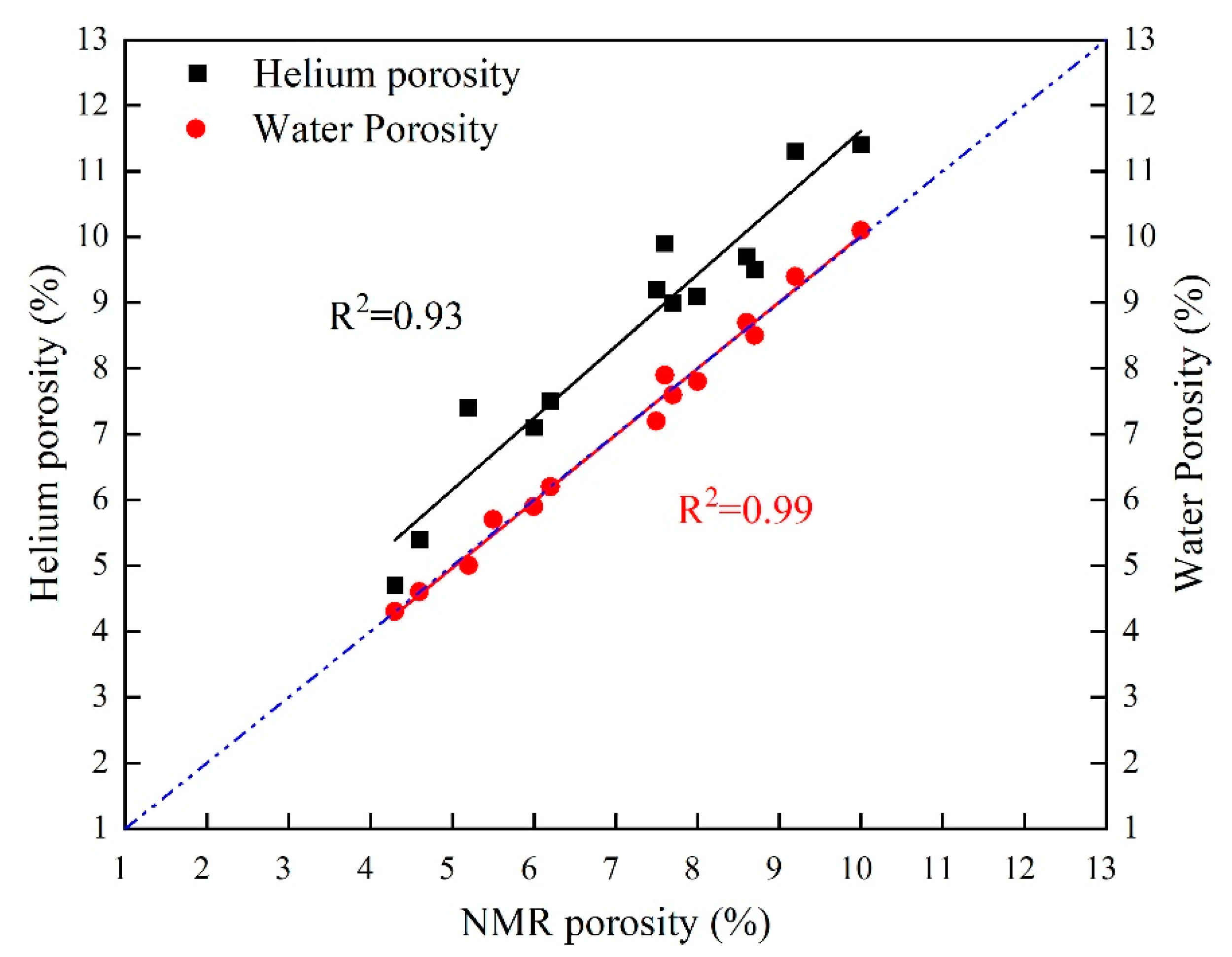
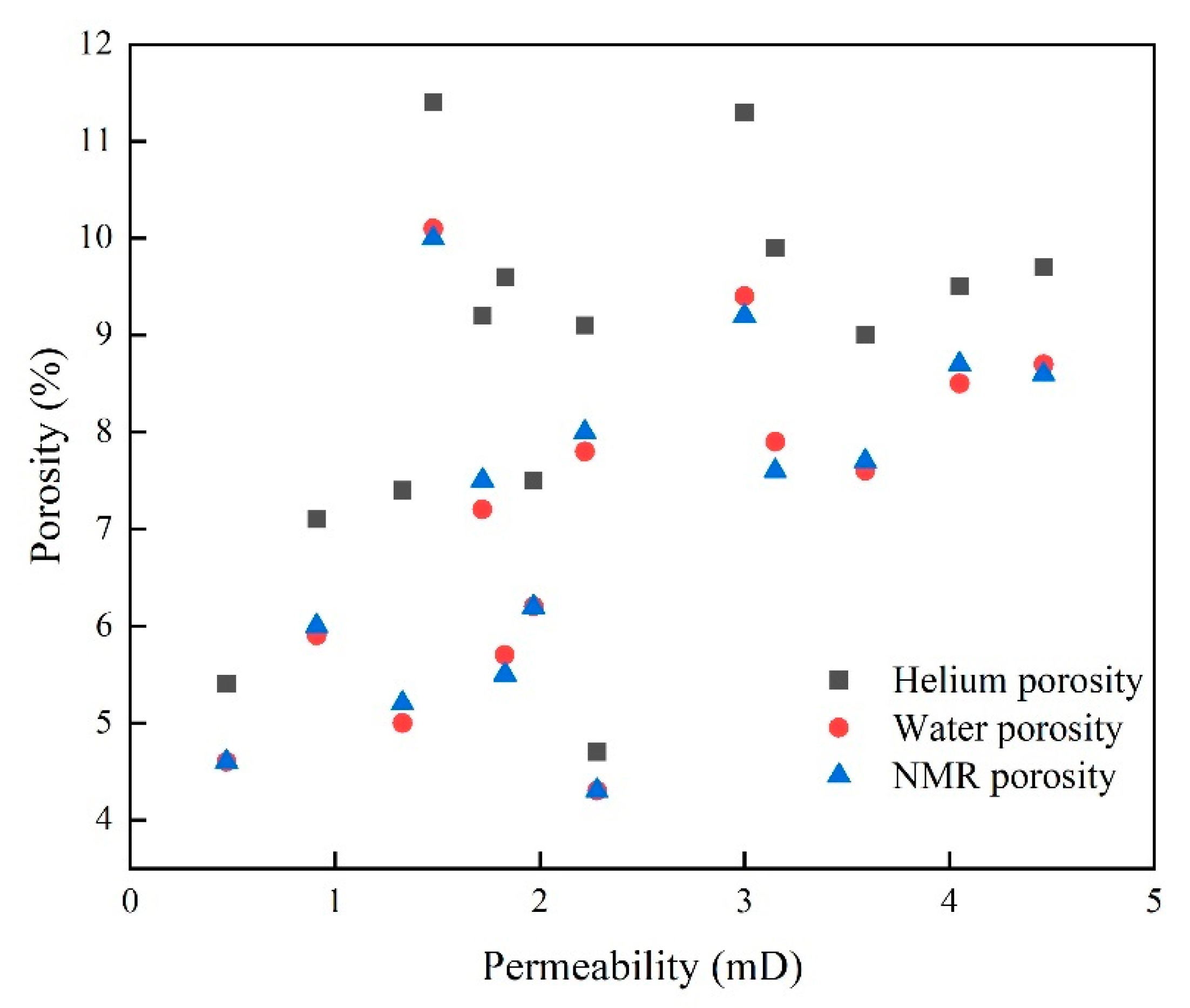

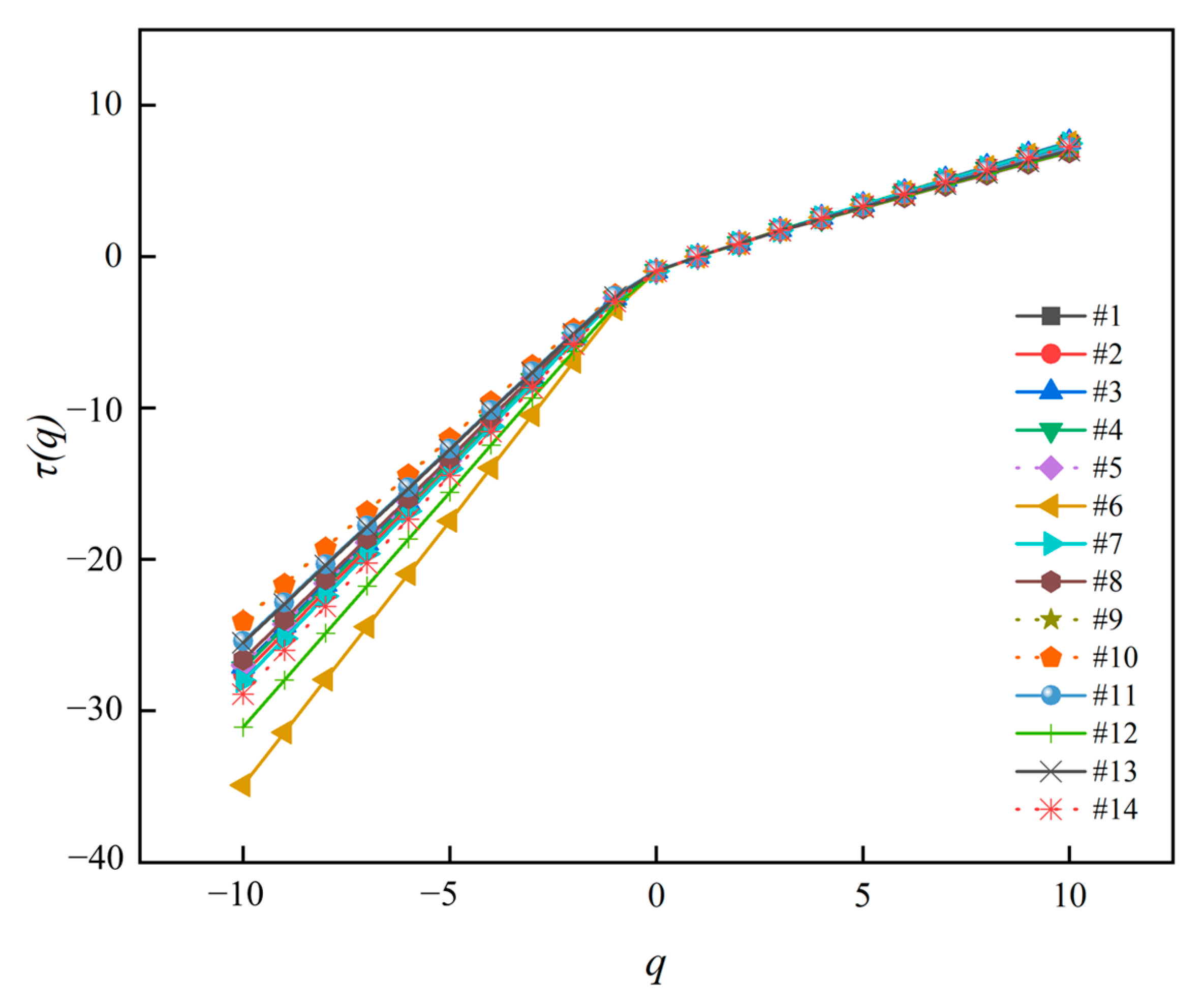
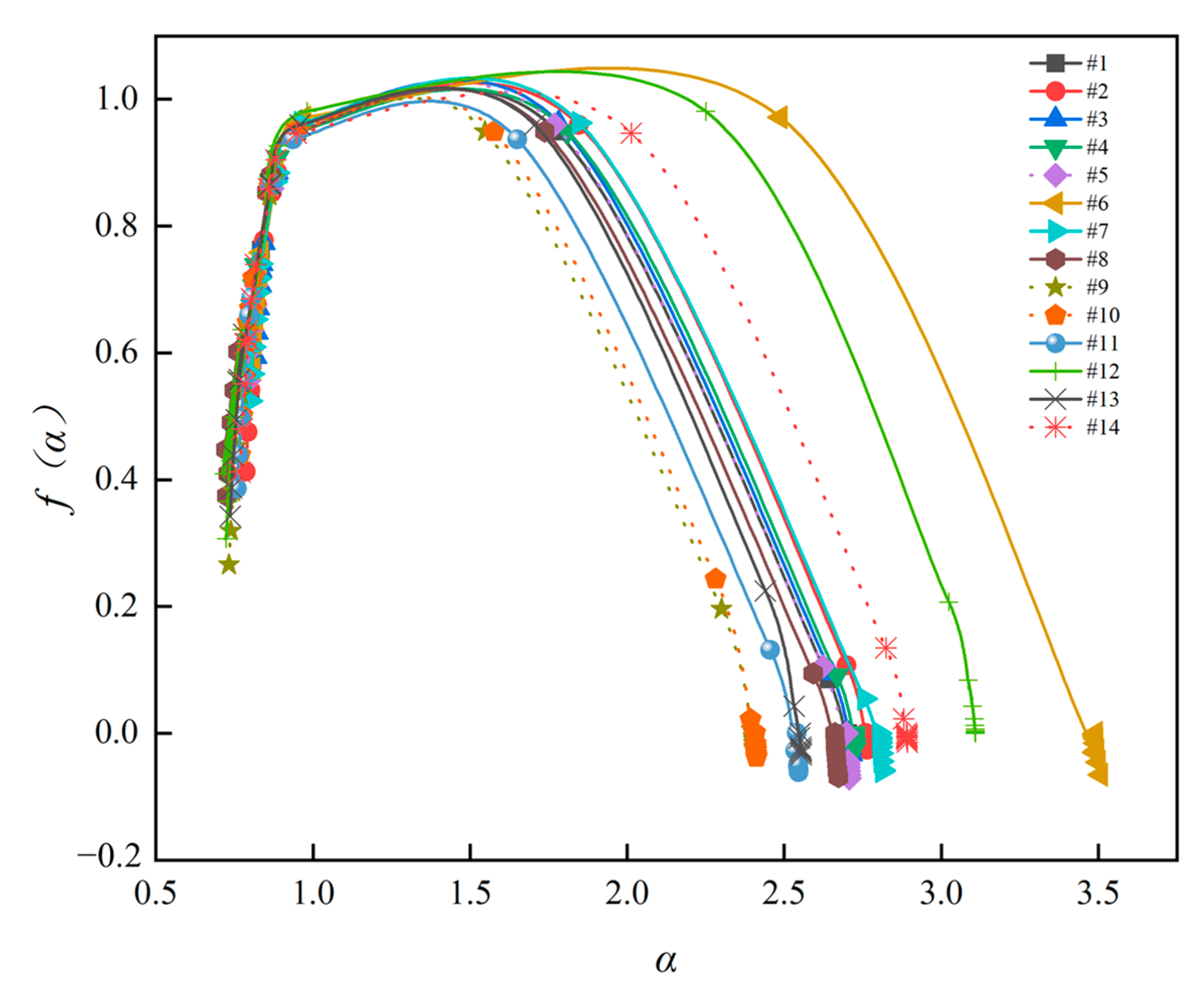
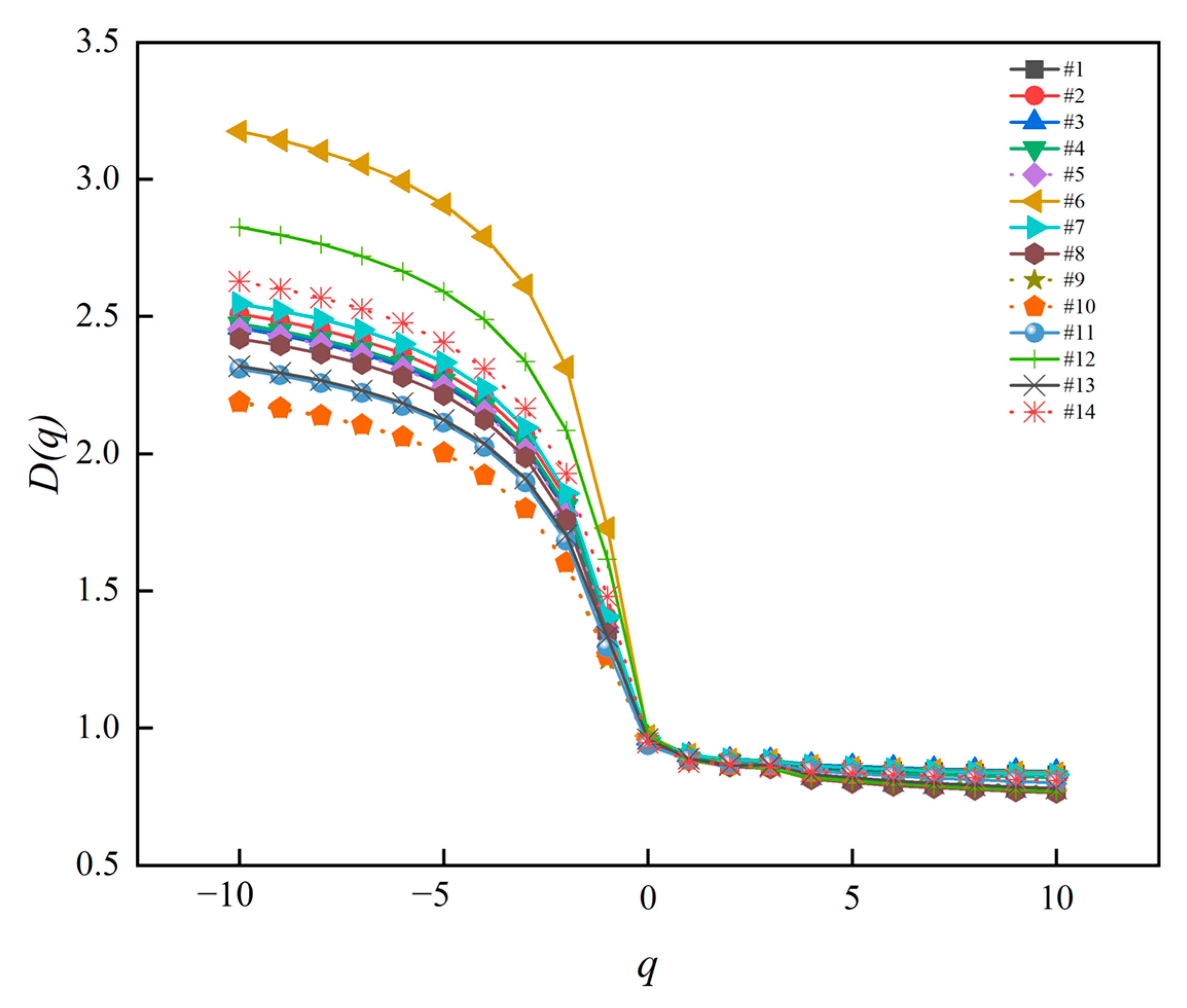


| Sample ID | Depth (m) | Φ-Helium (%) | Φ-Water (%) | Φ-NMR (%) | Permeability (mD) | T2C (ms) | Swiir (%) |
|---|---|---|---|---|---|---|---|
| #1 | 3853.15 | 9 | 7.6 | 7.7 | 3.59 | 13.67 | 41.40 |
| #2 | 3853.27 | 11.4 | 10.1 | 10 | 1.48 | 18.04 | 42.60 |
| #3 | 3853.97 | 9.5 | 8.5 | 8.7 | 4.05 | 15.70 | 38.30 |
| #4 | 3854.85 | 11.3 | 9.4 | 9.2 | 3.00 | 11.10 | 32.80 |
| #5 | 3855.71 | 9.2 | 7.2 | 7.5 | 1.72 | 10.35 | 40.20 |
| #6 | 3856.32 | 9.9 | 7.9 | 7.6 | 3.15 | 20.73 | 40.80 |
| #7 | 3857.21 | 9.7 | 8.7 | 8.6 | 4.46 | 11.10 | 37.30 |
| #8 | 4047.45 | 9.6 | 5.7 | 5.5 | 1.83 | 6.37 | 36.30 |
| #9 | 4048.15 | 4.7 | 4.3 | 4.3 | 2.28 | 5.94 | 58.10 |
| #10 | 4048.81 | 5.4 | 4.6 | 4.6 | 0.47 | 11.90 | 60.40 |
| #11 | 4050.46 | 7.1 | 5.9 | 6 | 0.91 | 13.67 | 49.70 |
| #12 | 4052.7 | 9.1 | 7.8 | 8 | 2.22 | 25.53 | 42.80 |
| #13 | 4054.64 | 7.5 | 6.2 | 6.2 | 1.97 | 7.84 | 40.70 |
| #14 | 4054.77 | 7.4 | 5.0 | 5.2 | 1.33 | 18.04 | 42.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yao, Y.; Ma, R.; Zhang, X.; Zhang, G. Application of Multifractal Analysis Theory to Interpret T2 Cutoffs of NMR Logging Data: A Case Study of Coarse Clastic Rock Reservoirs in Southwestern Bozhong Sag, China. Fractal Fract. 2023, 7, 57. https://doi.org/10.3390/fractalfract7010057
Wang Z, Yao Y, Ma R, Zhang X, Zhang G. Application of Multifractal Analysis Theory to Interpret T2 Cutoffs of NMR Logging Data: A Case Study of Coarse Clastic Rock Reservoirs in Southwestern Bozhong Sag, China. Fractal and Fractional. 2023; 7(1):57. https://doi.org/10.3390/fractalfract7010057
Chicago/Turabian StyleWang, Zefan, Yanbin Yao, Ruying Ma, Xiaona Zhang, and Guibin Zhang. 2023. "Application of Multifractal Analysis Theory to Interpret T2 Cutoffs of NMR Logging Data: A Case Study of Coarse Clastic Rock Reservoirs in Southwestern Bozhong Sag, China" Fractal and Fractional 7, no. 1: 57. https://doi.org/10.3390/fractalfract7010057
APA StyleWang, Z., Yao, Y., Ma, R., Zhang, X., & Zhang, G. (2023). Application of Multifractal Analysis Theory to Interpret T2 Cutoffs of NMR Logging Data: A Case Study of Coarse Clastic Rock Reservoirs in Southwestern Bozhong Sag, China. Fractal and Fractional, 7(1), 57. https://doi.org/10.3390/fractalfract7010057







