On Implicit Coupled Hadamard Fractional Differential Equations with Generalized Hadamard Fractional Integro-Differential Boundary Conditions

Abstract

This study is devoted to studying the existence and uniqueness of solutions for Hadamard implicit fractional differential equations with generalized Hadamard fractional integro-differential boundary conditions by utilizing the contraction principle of the Banach and Leray–Schauder fixed point theorems. Moreover, with two different approaches, the Hyers–Ulam stabilities are also discussed. Different ordinary differential equations of the third order with different boundary conditions (e.g., initial, anti periodic and integro-differential) can be obtained as a special case for our proposed model. Finally, for verification, an example is presented, and some graphs for the particular variables and particular functions are drawn using MATLAB.

1. Introduction

The notion of fractional derivatives was first introduced in 1695, when Leibniz used the notation $\frac{{\mathrm{d}}^{\mathrm{n}}}{\mathrm{d}{\chi }^{\mathrm{n}}}$ for the ${\mathrm{n}}^{\mathrm{t}\mathrm{h}}$ derivative and de L’Hospital questioned what this may imply when n is $\frac{1}{2}$ (see [1]). The generalization of integer-order derivatives and integration is actually the fractional order derivatives and integration. Riemann, Liouville, Caputo, Hadamard, Hilfer, Riesz, Erdelyi–Kober, Fourier and Laplace worked on non-integer-order fractional derivatives and made the fractional calculus more informative for mathematicians. An operator in the form of a fractional order is a global one which applies as a tool for many complicated applied phenomena (e.g., biological mathematical models [2], signal as well as image processes [3], mathematical chemistry [4], control theory [5] and processes involving dynamics [6]). For more details about fractional order differential equations ($\mathcal{FDE}\mathrm{s}$), see [7,8,9,10].

Among the qualitative properties of the nonlinear $\mathcal{FDE}\mathrm{s}$, the existence of solutions is the most important one and the first priority of researchers. As a result, $\mathcal{FDE}\mathrm{s}$ involving conditions on the boundary such as initial, anti-periodic ($\mathcal{AP}$) and periodic, integro-differential multi-points, have been investigated [11,12,13]. The idea of Hyers–Ulam stability ($\mathcal{HUS}$) began in 1940 [14]. Among other types, it is an important type of stability which guarantees an exact solution for each approximate solution within a specific boundary. Therefore, it can be required in a number of applications such as optimization, numerical analysis, error analysis, biology and economics [15,16,17]. Alqifiary et al. [18] investigated the generalized Hyers–Ulam stability $\left(\mathcal{GHUS}\right)$ for linear $\mathcal{DE}\mathrm{s}$. Razaei et al. [19] studied $\mathcal{HUS}$ by utilizing the approach of a Laplace transform for linear $\mathcal{DE}\mathrm{s}$. Wang et al. [20] obtained the $\mathcal{HUS}$ of two different kinds of $\mathcal{FDE}\mathrm{s}$. Liu et al. [21] achieved the $\mathcal{HUS}$ of linear Caputo–Fabrizio $\mathcal{FDE}\mathrm{s}$. Liu et al. [22] gave the $\mathcal{HUS}$ of linear Caputo–Fabrizio $\mathcal{FDE}\mathrm{s}$ by utilizing the property of a Mittag–Leffler kernel and using the method of Laplace transformation.

Luo et al. [23] discussed the existence, uniqueness ($\mathcal{EU}$) and $\mathcal{HUS}$ of

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)+\mu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))=0;\chi \in \mathcal{M},\hfill \\ & {\mathsf{v}\left(\chi \right)|}_{\chi =1}={}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\mathsf{v}\left(\chi \right){{|}_{\chi =1}=0,{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\mathsf{v}\left(\chi \right)|}_{\chi =2}=\alpha \left[\mathsf{v}\right]+{\int }_1^{\zeta }\phi \left(\chi \right){}_{\mathrm{H}}{\mathfrak{D}}^{\beta }\mathsf{v}\left(\chi \right)\mathrm{d}\chi ,\hfill \end{array}\right.\end{array}$$

They also extended their results to a system of the form

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)+\mu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))=0;\chi \in \mathcal{M},\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)+\nu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))=0;\chi \in \mathcal{M},\hfill \\ & {\mathsf{v}\left(\chi \right)|}_{\chi =1}={}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\mathsf{v}\left(\chi \right){{|}_{\chi =1}=0,{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\mathsf{v}\left(\chi \right)|}_{\chi =2}=\alpha \left[\mathsf{v}\right]+{\int }_1^{\zeta }{\phi }_{\kappa }\left(\chi \right){}_{\mathrm{H}}{\mathfrak{D}}^{\beta }\mathsf{v}\left(\chi \right)\mathrm{d}\chi ,\hfill \\ & {\mathsf{w}\left(\chi \right)|}_{\chi =1}={}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\mathsf{w}\left(\chi \right){{|}_{\chi =1}=0,{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\mathsf{w}\left(\chi \right)|}_{\chi =2}=\gamma \left[\mathsf{w}\right]+{\int }_1^{\xi }{\phi }_{\sigma }\left(\chi \right){}_{\mathrm{H}}{\mathfrak{D}}^{\delta }\mathsf{w}\left(\chi \right)\mathrm{d}\chi ,\hfill \end{array}\right.\end{array}$$

where $\kappa ,\sigma \in (2,3]$ and ${}_{\mathrm{H}}{\mathfrak{D}}^{(·)}$ are the Hadamard fractional derivative of the order $(·)$ with $\kappa -1-\beta >0$ and $\sigma -1-\delta >0$, ${\phi }_{\kappa },{\phi }_{\sigma }\in {\mathrm{L}}^1[1,2]$ is nonnegative and $\alpha \left[\mathsf{v}\right]$ and $\gamma \left[\mathsf{w}\right]$ are linear functions.

The above study motivated us to study the $\mathcal{EU}$ and at least one solution of the following coupled system ($\mathbb{CS}$) of $\mathcal{FDE}\mathrm{s}$ in the sense of Hadamard derivatives:

$$\left\{\begin{array}{cc}\hfill & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)-\mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))=0;\chi \in \mathcal{M},\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)-\nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))=0;\chi \in \mathcal{M},\hfill \end{array}\right.$$

(1)

having the generalized Hadamard fractional integro-differential boundary conditions

$$\left\{\begin{array}{cc}\hfill & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\mathsf{v}\left(1\right)={\mathsf{a}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\mathsf{v}\left(\mathrm{T}\right)+{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -1}\mathsf{v}\left(\mathrm{T}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\mathsf{v}\left(1\right)={\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\mathsf{v}\left(\mathrm{T}\right)+{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -2}\mathsf{v}\left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -3}\mathsf{v}\left(1\right)={\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -3}\mathsf{v}\left(\mathrm{T}\right)+{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -3}\mathsf{v}\left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\mathsf{w}\left(1\right)={\mathsf{a}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\mathsf{w}\left(\mathrm{T}\right)+{\eta }_4{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -1}\mathsf{w}\left(\mathrm{T}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\mathsf{w}\left(1\right)={\mathsf{b}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\mathsf{w}\left(\mathrm{T}\right)+{\eta }_5{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -2}\mathsf{w}\left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -3}\mathsf{w}\left(1\right)={\mathsf{c}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -3}\mathsf{w}\left(\mathrm{T}\right)+{\eta }_6{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -3}\mathsf{w}\left(\mathrm{T}\right),\hfill \end{array}\right.$$

(2)

where $2<\kappa ,\sigma \le 3,$$\mathcal{M}=[1,\mathrm{T}],\mathrm{T}>1$, ${\mathsf{a}}_{\mathrm{i}},{\mathsf{b}}_{\mathrm{i}},{\mathsf{c}}_{\mathrm{i}}\ne 1$ for $\mathrm{i}=0,1$ and ${\eta }_{\mathrm{j}}(\mathrm{j}=1,2,\cdots ,6)$ are coefficients of the integrals in boundary conditions (BCs). $\mu ,\nu :\mathcal{M}\times {\mathcal{R}}^2\to \mathcal{R}$ are continuous functions, and ${}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }/{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa }$ and ${}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }/{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma }$ are the Hadamard derivatives and integrals of the fractional orders $\kappa$ and $\sigma$, respectively.

The said system of Hadamard $\mathcal{FDE}\mathrm{s}$ (Equation (1)) is the generalization of third-order ordinary differential equations ($\mathcal{ODE}\mathrm{s}$), and according to our information, the proposed $\mathcal{ODE}\mathrm{s}$ have several uses in different engineering fields and the area of applied sciences [24,25,26,27]. It is attractive that some mathematical modeling of numerous physical phenomena gives systems in a form coupled with the aforementioned third-order $\mathcal{ODE}\mathrm{s}$. Such models are linked jerk-type equations, which are mainly used in the processes of manufacturing [28,29,30]. Additionally, for ${\eta }_{\mathrm{i}}=0(\mathrm{i}=1,2,\cdots ,6)$ and ${\mathsf{a}}_{\mathrm{i}}={\mathsf{b}}_{\mathrm{i}}={\mathsf{c}}_{\mathrm{i}}=-1(\mathrm{i}=0,1)$, we can acquire BCs in the form of $\mathcal{AP}$, which often occur in the models of different physical phenomena (e.g., in the partial, ordinary and $\mathcal{DE}\mathrm{s}$ with impulses, $\mathcal{AP}$ trigonometric polynomials in the investigation of the interpolation issues, $\mathcal{AP}$ wavelets and equations in the discrete form) [31,32,33,34].

2. Background Materials

Let $\mathcal{N}\left(\mathcal{M}\right)$ be the space of all continuous functions on $\mathcal{M}$, which is a Banach space with $\parallel \mathsf{v}\parallel ={max}_{\chi \in \mathcal{M}}\left|\mathsf{v}\left(\chi \right)\right|.$ Let $\mathcal{W}={\mathcal{N}}_r\left(\mathcal{M}\right)\subset \mathcal{N}\left(\mathcal{M}\right)$ be the space of all functions $\mathsf{v}$ such that for $\chi \in \mathcal{M}$ and $\mathrm{r}\ge 0$, we have ${\mathsf{v}}_{\mathrm{r}}\left(\chi \right)={(log\chi )}^{\mathrm{r}}\mathsf{v}\left(\chi \right)$. Obviously, $\mathcal{W}$ is a Banach space with

$${\parallel \mathsf{v}\parallel }_{\mathcal{W}}=max\{\underset{\chi \in \mathcal{M}}{sup}{(log\chi )}^{\mathrm{r}}|\mathsf{v}\left(\chi \right)|,\underset{\chi \in \mathcal{M}}{sup}{(log\chi )}^{\mathrm{r}}|{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)|\}.$$

Additionally, $\left(\mathcal{W}\times {\mathcal{W},\parallel (\mathsf{v},\mathsf{w})\parallel }_{\mathcal{W}\times \mathcal{W}}\right)$ is a Banach space with norm ${\parallel (\mathsf{v},\mathsf{w})\parallel }_{\mathcal{W}\times \mathcal{W}}={\parallel \mathsf{v}\parallel }_{\mathcal{W}}+{\parallel \mathsf{w}\parallel }_{\mathcal{W}}$:

Definition 1

([35]). The $\kappa >0$ order Hadamard integral for $\mathsf{v}:{\mathcal{R}}^{+}\to \mathcal{R}$ (continuous) is represented by

$${}_{\mathrm{H}}{\mathfrak{I}}^{\kappa }\mathsf{v}\left(\chi \right)=\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\chi -logs)}^{\kappa -1}\mathsf{v}\left(s\right)\frac{\mathit{ds}}{s}.$$

Definition 2

([35]). The Hadamard derivative of the order $\kappa >0$ for $\mathsf{v}:{\mathcal{R}}^{+}\to \mathcal{R}$ (continuous) is given by

$${}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)=\frac{1}{\mathrm{\Gamma }(\mathrm{n}-\kappa )}{(\chi \frac{d}{d\chi })}^{\mathrm{n}}{\int }_1^{\chi }{(log\chi -logs)}^{\mathrm{n}-\kappa +1}\mathsf{v}\left(s\right)\frac{\mathit{ds}}{s},$$

where $\mathrm{n}=\left[\kappa \right]+1$ and $\left[\kappa \right]$ is the integer value of κ.

It can be observed that for $\varrho >-1,\varrho \ne \kappa -1,\kappa -2,\cdots ,\kappa -\mathrm{n},$ we have

$${}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }log{\left(\chi \right)}^{\varrho }=\frac{\mathrm{\Gamma }(\varrho +1)}{\mathrm{\Gamma }(\varrho -\kappa +1)}log{\left(\chi \right)}^{\varrho -\kappa }$$

and

$${}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }log{\left(\chi \right)}^{\kappa -\mathrm{i}}=0,\mathrm{i}=1,2,\cdots ,\mathrm{n}.$$

In addition, we have

$${}_{\mathrm{H}}{\mathfrak{I}}^{\kappa }log{\left(\chi \right)}^{\varrho }=\frac{\mathrm{\Gamma }(\varrho +1)}{\mathrm{\Gamma }(\varrho +\kappa +1)}log{\left(\chi \right)}^{\varrho +\kappa }.$$

Lemma 1

([35]). For a Hadamard $\mathcal{FDE}$ of the order $\kappa >0$, we have

$${}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)=\mu \left(\chi \right),$$

which is

$${}_{\mathrm{H}}{\mathfrak{I}}^{\kappa }{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)={}_{\mathrm{H}}{\mathfrak{I}}^{\kappa }\mu \left(\chi \right)+{\mathrm{k}}_1{(log\chi )}^{\kappa -1}+{\mathrm{k}}_2{(log\chi )}^{\kappa -2}+\cdots +{\mathrm{k}}_{\mathrm{n}-1}{(log\chi )}^{\kappa -(\mathrm{n}-1)}+{\mathrm{k}}_{\mathrm{n}}{(log\chi )}^{\kappa -\mathrm{n}},$$

where ${\mathrm{k}}_1,{\mathrm{k}}_2,\cdots ,{\mathrm{k}}_{\mathrm{n}}$ are real constants.

3. Existence of Solutions

Lemma 2.

Assume that $\mu \in \mathcal{N}\left(\mathcal{M}\right)$ and $\kappa \in (2,3]$. Then, the solution of

$$\left\{\begin{array}{cc}& {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)=\mu \left(\chi \right);\chi \in \mathcal{M},\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\mathsf{v}\left(1\right)={\mathsf{a}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\mathsf{v}\left(\mathrm{T}\right)+{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -1}\mathsf{v}\left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\mathsf{v}\left(1\right)={\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\mathsf{v}\left(\mathrm{T}\right)+{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -2}\mathsf{v}\left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -3}\mathsf{v}\left(1\right)={\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -3}\mathsf{v}\left(\mathrm{T}\right)+{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -3}\mathsf{v}\left(\mathrm{T}\right),\hfill \end{array}\right.$$

is represented by

$$\mathsf{v}\left(\chi \right)={\int }_1^{\mathrm{T}}{\mathbf{G}}_{\kappa }(\chi ,s)\mu \left(s\right)\mathtt{d}s,$$

where

$${\mathbf{G}}_{\kappa }(\chi ,s)=\left\{\begin{array}{c}\frac{{(log\frac{\chi }{s})}^{\kappa -1}}{\mathrm{\Gamma }\left(\kappa \right)}-\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{a}}_0{\delta }_{11}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{a}}_0{\delta }_{21}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{a}}_0{\delta }_{31}}{\delta }\right]\hfill \\ -\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{b}}_0{\delta }_{12}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{b}}_0{\delta }_{22}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{b}}_0{\delta }_{32}}{\delta }\right]log\frac{\mathrm{T}}{s}\hfill \\ -\frac{1}{2}\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{c}}_0{\delta }_{13}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{c}}_0{\delta }_{23}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{c}}_0{\delta }_{33}}{\delta }\right]{(log\frac{\mathrm{T}}{s})}^2\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\kappa -1)}\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_1{\delta }_{11}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\eta }_1{\delta }_{21}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\eta }_1{\delta }_{31}}{\delta }\right]{(log\frac{\mathrm{T}}{s})}^{2\kappa -2}\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\kappa -2)}\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_2{\delta }_{12}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\eta }_2{\delta }_{22}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\eta }_2{\delta }_{32}}{\delta }\right]{(log\frac{\mathrm{T}}{s})}^{2\kappa -3}\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\kappa -3)}\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_3{\delta }_{13}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\eta }_3{\delta }_{23}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\eta }_3{\delta }_{33}}{\delta }\right]{(log\frac{\mathrm{T}}{s})}^{2\kappa -4},\hfill & & 1\le s<\chi \le \mathrm{T},\hfill \\ \\ -\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{a}}_0{\delta }_{11}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{a}}_0{\delta }_{21}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{a}}_0{\delta }_{31}}{\delta }\right]\hfill \\ -\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{b}}_0{\delta }_{12}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{b}}_0{\delta }_{22}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{b}}_0{\delta }_{32}}{\delta }\right]log\frac{\mathrm{T}}{s}\hfill \\ -\frac{1}{2}\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{c}}_0{\delta }_{13}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{c}}_0{\delta }_{23}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{c}}_0{\delta }_{33}}{\delta }\right]{(log\frac{\mathrm{T}}{s})}^2\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\kappa -1)}\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_1{\delta }_{11}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\eta }_1{\delta }_{21}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\eta }_1{\delta }_{31}}{\delta }\right]{(log\frac{\mathrm{T}}{s})}^{2\kappa -2}\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\kappa -2)}\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_2{\delta }_{12}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\eta }_2{\delta }_{22}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\eta }_2{\delta }_{32}}{\delta }\right]{(log\frac{\mathrm{T}}{s})}^{2\kappa -3}\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\kappa -3)}\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_3{\delta }_{13}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\eta }_3{\delta }_{23}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\eta }_3{\delta }_{33}}{\delta }\right]{(log\frac{\mathrm{T}}{s})}^{2\kappa -4},\hfill & & 1\le \chi <s\le \mathrm{T}.\hfill \end{array}\right.$$

(3)

Proof. 

By applying Lemma 1, we obtain

$$\mathsf{v}\left(\chi \right)={}_{\mathrm{H}}{\mathfrak{I}}^{\kappa }\mu \left(\chi \right)+{\mathrm{k}}_1{(log\chi )}^{\kappa -1}+{\mathrm{k}}_2{(log\chi )}^{\kappa -2}+{\mathrm{k}}_3{(log\chi )}^{\kappa -3}.$$

(4)

By utilizing the BCs, Equation (4) implies

$$\begin{array}{cc}\hfill & {\mathrm{k}}_1\mathrm{\Gamma }\left(\kappa \right)\left({\mathsf{a}}_0-1+\frac{{\eta }_1{(log\mathrm{T})}^{2\kappa -2}}{\mathrm{\Gamma }(2\kappa -1)}\right)+{\mathrm{k}}_2\frac{{\eta }_1\mathrm{\Gamma }(\kappa -1){(log\mathrm{T})}^{2\kappa -3}}{\mathrm{\Gamma }(2\kappa -2)}+{\mathrm{k}}_3\frac{{\eta }_1\mathrm{\Gamma }(\kappa -2){(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =-{\mathsf{a}}_0{}_{\mathrm{H}}\mathfrak{I}\mu \left(\mathrm{T}\right)-{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -1}\mu \left(\mathrm{T}\right),\hfill \\ \hfill & {\mathrm{k}}_1\mathrm{\Gamma }\left(\kappa \right)\left({\mathsf{b}}_{0}log\mathrm{T}+\frac{{\eta }_2{(log\mathrm{T})}^{2\kappa -3}}{\mathrm{\Gamma }(2\kappa -2)}\right)+{\mathrm{k}}_2\mathrm{\Gamma }(\kappa -1)\left({\mathsf{b}}_0-1+\frac{{\eta }_2{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}\right)\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & +{\mathrm{k}}_3\frac{{\eta }_2\mathrm{\Gamma }(\kappa -2){(log\mathrm{T})}^{2\kappa -5}}{\mathrm{\Gamma }(2\kappa -4)}=-{\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{I}}^2\mu \left(\mathrm{T}\right)-{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -2}\mu \left(\mathrm{T}\right),\hfill \\ \hfill & {\mathrm{k}}_1\mathrm{\Gamma }\left(\kappa \right)\left(\frac{{\mathsf{c}}_0{(log\mathrm{T})}^2}{2}+\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}\right)+{\mathrm{k}}_2\mathrm{\Gamma }(\kappa -1)\left({\mathsf{c}}_{0}log\mathrm{T}+\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -5}}{\mathrm{\Gamma }(2\kappa -4)}\right)\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & +{\mathrm{k}}_3\mathrm{\Gamma }(\kappa -2)\left({\mathsf{c}}_0-1+\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -6}}{\mathrm{\Gamma }(2\kappa -5)}\right)=-{\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{I}}^3\mu \left(\mathrm{T}\right)-{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -3}\mu \left(\mathrm{T}\right).\hfill \end{array}$$

(7)

We can write Equations (5)–(7) in matrix form:

$$\begin{array}{c}\hfill \mathrm{A}\mathrm{K}=\mathrm{I},\mathrm{implies}\mathrm{K}={\mathrm{A}}^{-1}\mathrm{I}\end{array}$$

where

$$\mathrm{A}=\left[\begin{array}{ccc}\mathrm{\Gamma }\left(\kappa \right)\left({\mathsf{a}}_0-1+\frac{{\eta }_1{(log\mathrm{T})}^{2\kappa -2}}{\mathrm{\Gamma }(2\kappa -1)}\right)& \frac{{\eta }_1\mathrm{\Gamma }(\kappa -1){(log\mathrm{T})}^{2\kappa -3}}{\mathrm{\Gamma }(2\kappa -2)}& \frac{{\eta }_1\mathrm{\Gamma }(\kappa -2){(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}\\ \mathrm{\Gamma }\left(\kappa \right)\left({\mathsf{b}}_{0}log\mathrm{T}+\frac{{\eta }_2{(log\mathrm{T})}^{2\kappa -3}}{\mathrm{\Gamma }(2\kappa -2)}\right)& \mathrm{\Gamma }(\kappa -1)\left({\mathsf{b}}_0-1+\frac{{\eta }_2{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}\right)& \frac{{\eta }_2\mathrm{\Gamma }(\kappa -2){(log\mathrm{T})}^{2\kappa -5}}{\mathrm{\Gamma }(2\kappa -4)}\\ \mathrm{\Gamma }\left(\kappa \right)\left(\frac{{\mathsf{c}}_0{(log\mathrm{T})}^2}{2}+\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}\right)& \mathrm{\Gamma }(\kappa -1)\left({\mathsf{c}}_{0}log\mathrm{T}+\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -5}}{\mathrm{\Gamma }(2\kappa -4)}\right)& \mathrm{\Gamma }(\kappa -2)\left({\mathsf{c}}_0-1+\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -6}}{\mathrm{\Gamma }(2\kappa -5)}\right)\end{array}\right],$$

$$\mathrm{K}=\left[\begin{array}{c}{\mathrm{k}}_1\\ \\ {\mathrm{k}}_2\\ \\ {\mathrm{k}}_3\end{array}\right],\mathrm{I}=\left[\begin{array}{c}-{\mathsf{a}}_0{}_{\mathrm{H}}\mathfrak{I}\mu \left(\mathrm{T}\right)-{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -1}\mu \left(\mathrm{T}\right)\\ \\ -{\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{I}}^2\mu \left(\mathrm{T}\right)-{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -2}\mu \left(\mathrm{T}\right)\\ \\ -{\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{I}}^3\mu \left(\mathrm{T}\right)-{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -3}\mu \left(\mathrm{T}\right)\end{array}\right]\mathrm{and}{\mathrm{A}}^{-1}=\frac{1}{det\left(\mathrm{A}\right)}\left[\begin{array}{ccc}{\delta }_{11}& {\delta }_{12}& {\delta }_{13}\\ {\delta }_{21}& {\delta }_{22}& {\delta }_{23}\\ {\delta }_{31}& {\delta }_{32}& {\delta }_{33}\end{array}\right].$$

Here, the determinant of matrix A is

$$\begin{array}{cc}\hfill det\left(\mathrm{A}\right)=& \mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -1)\mathrm{\Gamma }(\kappa -2)\left({\mathsf{a}}_0-1+\frac{{\eta }_1{(log\mathrm{T})}^{2\kappa -2}}{\mathrm{\Gamma }(2\kappa -1)}\right)[({\mathsf{b}}_0-1)\left({\mathsf{c}}_0-1+\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -6}}{\mathrm{\Gamma }(2\kappa -5)}\right)\hfill \\ \hfill & +\frac{({\mathsf{c}}_0(2\kappa -3)-1){\eta }_2{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -10}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -5)}+\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -10}}{\mathrm{\Gamma }(2\kappa -4)\mathrm{\Gamma }(2\kappa -4)}]\hfill \\ \hfill & -\mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -1)\mathrm{\Gamma }(\kappa -2)\frac{{\eta }_1{(log\mathrm{T})}^{2\kappa -3}}{\mathrm{\Gamma }(2\kappa -2)}[({\mathsf{c}}_0-1){\mathsf{b}}_{0}log\mathrm{T}+{\mathsf{b}}_{0}log\mathrm{T}\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -6}}{\mathrm{\Gamma }(2\kappa -5)}\hfill \\ \hfill & -\frac{[{\mathsf{c}}_0(4{\kappa }^2-14\kappa +10)+2]{\eta }_2{(log\mathrm{T})}^{2\kappa -3}}{2\mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -9}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -5)}-\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -9}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -4)}]\hfill \\ \hfill & +\mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -1)\mathrm{\Gamma }(\kappa -2)\frac{{\eta }_1{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}[\frac{({\mathsf{b}}_0+1){\mathsf{c}}_0{(log\mathrm{T})}^2}{2}-\frac{\left({\mathsf{c}}_0(2\kappa -5)\right){\eta }_2{(log\mathrm{T})}^{2\kappa -2}}{\mathrm{\Gamma }(2\kappa -2)}\hfill \\ \hfill & +\frac{({\mathsf{b}}_0(2\kappa -3)+1){\eta }_3{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -8}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -4)}-\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -8}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -3)}]=\delta \ne 0\hfill \end{array}$$

In addition, the co-factors are

$$\begin{array}{cc}\hfill {\delta }_{11}=& \mathrm{\Gamma }(\kappa -1)\mathrm{\Gamma }(\kappa -2)[({\mathsf{b}}_0-1)\left({\mathsf{c}}_0-1+\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -6}}{\mathrm{\Gamma }(2\kappa -5)}\right)+\frac{({\mathsf{c}}_0(2\kappa -3)-1){\eta }_2{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}\hfill \\ \hfill & +\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -10}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -5)}+\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -10}}{\mathrm{\Gamma }(2\kappa -4)\mathrm{\Gamma }(2\kappa -4)}],\hfill \\ \hfill {\delta }_{12}=& -\mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -2)[({\mathsf{c}}_0-1){\mathsf{b}}_{0}log\mathrm{T}+{\mathsf{b}}_{0}log\mathrm{T}\frac{{\eta }_3{(log\mathrm{T})}^{2\kappa -6}}{\mathrm{\Gamma }(2\kappa -5)}+\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -9}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -5)}\hfill \\ \hfill & +\frac{[{\mathsf{c}}_0(-4{\kappa }^2+14\kappa -10)-2]{\eta }_2{(log\mathrm{T})}^{2\kappa -3}}{2\mathrm{\Gamma }(2\kappa -2)}-\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -9}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -4)}],\hfill \\ \hfill {\delta }_{13}=& \mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -1)[\frac{({\mathsf{b}}_0+1){\mathsf{c}}_0{(log\mathrm{T})}^2}{2}-\frac{\left({\mathsf{c}}_0(2\kappa -5)\right){\eta }_2{(log\mathrm{T})}^{2\kappa -2}}{\mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -8}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -4)}\hfill \\ \hfill & +\frac{({\mathsf{b}}_0(2\kappa -3)+1){\eta }_3{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}-\frac{{\eta }_2{\eta }_3{(log\mathrm{T})}^{4\kappa -8}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -3)}],\hfill \\ \hfill {\delta }_{21}=& -\mathrm{\Gamma }(\kappa -1)\mathrm{\Gamma }(\kappa -2)\left[\frac{({\mathsf{c}}_0(4-2\kappa )-1){\eta }_1{(log\mathrm{T})}^{2\kappa -3}}{\mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_1{\eta }_3{(log\mathrm{T})}^{4\kappa -9}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -5)}-\frac{{\eta }_1{\eta }_3{(log\mathrm{T})}^{4\kappa -9}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -4)}\right],\hfill \\ \hfill {\delta }_{22}=& \mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -2)[({\mathsf{c}}_0-1)({\mathsf{a}}_0-1)+\frac{({\mathsf{a}}_0-1){\eta }_3{(log\mathrm{T})}^{2\kappa -6}}{\mathrm{\Gamma }(2\kappa -5)}\hfill \\ \hfill & -\frac{({\mathsf{c}}_0(4{\kappa }^2-10\kappa -4)+2){\eta }_1{(log\mathrm{T})}^{2\kappa -2}}{2\mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_1{\eta }_3{(log\mathrm{T})}^{4\kappa -8}}{\mathrm{\Gamma }(2\kappa -1)\mathrm{\Gamma }(2\kappa -5)}-\frac{{\eta }_1{\eta }_3{(log\mathrm{T})}^{4\kappa -8}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -3)}],\hfill \\ \hfill {\delta }_{23}=& -\mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -1)[({\mathsf{a}}_0-1){\mathsf{c}}_{0}log\mathrm{T}-\frac{{\mathsf{c}}_0\kappa {\eta }_1{(log\mathrm{T})}^{2\kappa -1}}{\mathrm{\Gamma }(2\kappa -1)}+\frac{({\mathsf{a}}_0-1){\eta }_3{(log\mathrm{T})}^{2\kappa -5}}{\mathrm{\Gamma }(2\kappa -4)}\hfill \\ \hfill & +\frac{{\eta }_1{\eta }_3{(log\mathrm{T})}^{4\kappa -7}}{\mathrm{\Gamma }(2\kappa -1)\mathrm{\Gamma }(2\kappa -4)}-\frac{{\eta }_1{\eta }_3{(log\mathrm{T})}^{4\kappa -7}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -3)}],\hfill \\ \hfill {\delta }_{31}=& -\mathrm{\Gamma }(\kappa -1)\mathrm{\Gamma }(\kappa -2)\left[\frac{({\mathsf{b}}_0-1){\eta }_1{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}-\frac{{\eta }_1{\eta }_2{(log\mathrm{T})}^{4\kappa -8}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -4)}+\frac{{\eta }_1{\eta }_2{(log\mathrm{T})}^{4\kappa -8}}{\mathrm{\Gamma }(2\kappa -3)\mathrm{\Gamma }(2\kappa -3)}\right],\hfill \\ \hfill {\delta }_{32}=& -\mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -2)[\frac{({\mathsf{a}}_0-1){\eta }_2{(log\mathrm{T})}^{2\kappa -5}}{\mathrm{\Gamma }(2\kappa -4)}-\frac{{\mathsf{b}}_0{\eta }_1{(log\mathrm{T})}^{2\kappa -3}}{\mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_1{\eta }_2{(log\mathrm{T})}^{4\kappa -7}}{\mathrm{\Gamma }(2\kappa -1)\mathrm{\Gamma }(2\kappa -4)}\hfill \\ \hfill & -\frac{{\eta }_1{\eta }_2{(log\mathrm{T})}^{4\kappa -7}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -3)}],\hfill \\ \hfill {\delta }_{33}=& \mathrm{\Gamma }\left(\kappa \right)\mathrm{\Gamma }(\kappa -1)[({\mathsf{a}}_0-1)({\mathsf{b}}_0-1)+\frac{({\mathsf{a}}_0-1){\eta }_2{(log\mathrm{T})}^{2\kappa -4}}{\mathrm{\Gamma }(2\kappa -3)}-\frac{({\mathsf{b}}_0(2\kappa -3)+1){\eta }_1{(log\mathrm{T})}^{2\kappa -2}}{\mathrm{\Gamma }(2\kappa -1)}\hfill \\ \hfill & +\frac{{\eta }_1{\eta }_2{(log\mathrm{T})}^{4\kappa -6}}{\mathrm{\Gamma }(2\kappa -1)\mathrm{\Gamma }(2\kappa -3)}-\frac{{\eta }_1{\eta }_2{(log\mathrm{T})}^{4\kappa -6}}{\mathrm{\Gamma }(2\kappa -2)\mathrm{\Gamma }(2\kappa -2)}].\hfill \end{array}$$

Hence, the unknowns are

$$\begin{array}{cc}\hfill {\mathrm{k}}_1=& \frac{{\delta }_{11}}{\delta }(-{\mathsf{a}}_0{}_{\mathrm{H}}\mathfrak{I}\mu \left(\mathrm{T}\right)-{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -1}\mu \left(\mathrm{T}\right))+\frac{{\delta }_{12}}{\delta }(-{\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{I}}^2\mu \left(\mathrm{T}\right)-{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -2}\mu \left(\mathrm{T}\right))\hfill \\ \hfill & +\frac{{\delta }_{13}}{\delta }(-{\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{I}}^3\mu \left(\mathrm{T}\right)-{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -3}\mu \left(\mathrm{T}\right)),\hfill \\ \hfill {\mathrm{k}}_2=& \frac{{\delta }_{21}}{\delta }(-{\mathsf{a}}_0{}_{\mathrm{H}}\mathfrak{I}\mu \left(\mathrm{T}\right)-{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -1}\mu \left(\mathrm{T}\right))+\frac{{\delta }_{22}}{\delta }(-{\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{I}}^2\mu \left(\mathrm{T}\right)-{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -2}\mu \left(\mathrm{T}\right))\hfill \\ \hfill & +\frac{{\delta }_{23}}{\delta }(-{\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{I}}^3\mu \left(\mathrm{T}\right)-{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -3}\mu \left(\mathrm{T}\right)),\hfill \\ \hfill {\mathrm{k}}_3=& \frac{{\delta }_{31}}{\delta }(-{\mathsf{a}}_0{}_{\mathrm{H}}\mathfrak{I}\mu \left(\mathrm{T}\right)-{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -1}\mu \left(\mathrm{T}\right))+\frac{{\delta }_{32}}{\delta }(-{\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{I}}^2\mu \left(\mathrm{T}\right)-{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -2}\mu \left(\mathrm{T}\right))\hfill \\ \hfill & +\frac{{\delta }_{33}}{\delta }(-{\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{I}}^3\mu \left(\mathrm{T}\right)-{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{2\kappa -3}\mu \left(\mathrm{T}\right)).\hfill \end{array}$$

By putting the values of ${\mathrm{k}}_0,{\mathrm{k}}_1$ and ${\mathrm{k}}_2$ into Equation (4), we obtain

$$\begin{array}{cc}\hfill \mathsf{v}\left(\chi \right)=& \frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}\mu \left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{a}}_0{\delta }_{11}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{a}}_0{\delta }_{21}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{a}}_0{\delta }_{31}}{\delta }\right]{\int }_1^{\mathrm{T}}\mu \left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{b}}_0{\delta }_{12}}{\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{b}}_0{\delta }_{22}}{\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{b}}_0{\delta }_{32}}{\delta }\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\mu \left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{(log\chi )}^{\kappa -1}{\mathsf{c}}_0{\delta }_{13}}{2\delta }+\frac{{(log\chi )}^{\kappa -2}{\mathsf{c}}_0{\delta }_{23}}{2\delta }+\frac{{(log\chi )}^{\kappa -3}{\mathsf{c}}_0{\delta }_{33}}{2\delta }\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\mu \left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_1{\delta }_{11}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{(log\chi )}^{\kappa -2}{\eta }_1{\delta }_{21}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{(log\chi )}^{\kappa -3}{\eta }_1{\delta }_{31}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}\mu \left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_2{\delta }_{12}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{(log\chi )}^{\kappa -2}{\eta }_2{\delta }_{22}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{(log\chi )}^{\kappa -3}{\eta }_2{\delta }_{32}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}\mu \left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{(log\chi )}^{\kappa -1}{\eta }_3{\delta }_{13}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{(log\chi )}^{\kappa -2}{\eta }_3{\delta }_{23}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{(log\chi )}^{\kappa -3}{\eta }_3{\delta }_{33}}{\delta \mathrm{\Gamma }(2\kappa -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}\mu \left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill =& {\int }_1^{\mathrm{T}}{\mathbf{G}}_{\kappa }(\chi ,\mathtt{s})\mu \left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}},\hfill \end{array}$$

where ${\mathbf{G}}_{\kappa }(\chi ,\mathtt{s})$ is given by Equation (3). □

Remark 1.

If in Equation (3), we place $\kappa =3$ and ${\mathsf{a}}_0={\mathsf{b}}_0={\mathsf{c}}_0=-1$, then the Green function ${\mathbf{G}}_{\kappa }(\chi ,\mathtt{s})$ for third-order $\mathcal{ODE}\mathrm{s}$ with $\mathcal{AP}$ BCs will be derived.

Remark 2.

If in Equation (3), we place $\kappa =3$ and ${\mathsf{a}}_0={\mathsf{b}}_0={\mathsf{c}}_0=0$, then the solution for the third-order $\mathcal{ODE}\mathrm{s}$ with the initial BCs can be derived.

Lemma 3.

Let $\nu \in \mathcal{N}\left(\mathcal{M}\right)$, $\sigma \in (2,3]$. Then, the following

$$\left\{\begin{array}{cc}& {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)=\nu \left(\chi \right);\chi \in \mathcal{M},\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\mathsf{w}\left(1\right)={\mathsf{a}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\mathsf{w}\left(\mathrm{T}\right)+{\eta }_4{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -1}\mathsf{w}\left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\mathsf{w}\left(1\right)={\mathsf{b}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\mathsf{w}\left(\mathrm{T}\right)+{\eta }_5{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -2}\mathsf{w}\left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -3}\mathsf{w}\left(1\right)={\mathsf{c}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -3}\mathsf{w}\left(\mathrm{T}\right)+{\eta }_6{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -3}\mathsf{w}\left(\mathrm{T}\right),\hfill \end{array}\right.$$

has a (unique) solution presented as

$$\mathsf{w}\left(\chi \right)={\int }_1^{\mathrm{T}}{\mathbf{G}}_{\sigma }(\chi ,s)\nu \left(s\right)\frac{\mathit{ds}}{s},$$

where ${\mathbf{G}}_{\sigma }(\chi ,s)$ is given by

$${\mathbf{G}}_{\sigma }(\chi ,s)=\left\{\begin{array}{c}\frac{{(log\frac{\chi }{s})}^{\sigma -1}}{\mathrm{\Gamma }\left(\sigma \right)}-\left[\frac{{(log\chi )}^{\sigma -1}{\mathsf{a}}_1{\delta }_{11}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\mathsf{a}}_1{\delta }_{21}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\mathsf{a}}_1{\delta }_{31}^{*}}{{\delta }^{*}}\right]\hfill \\ -\left[\frac{{(log\chi )}^{\sigma -1}{\mathsf{b}}_1{\delta }_{12}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\mathsf{b}}_1{\delta }_{22}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\mathsf{b}}_1{\delta }_{32}^{*}}{{\delta }^{*}}\right]log\frac{\mathrm{T}}{s}\hfill \\ -\frac{1}{2}\left[\frac{{(log\chi )}^{\sigma -1}{\mathsf{c}}_1{\delta }_{13}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\mathsf{c}}_1{\delta }_{23}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\mathsf{c}}_1{\delta }_{33}^{*}}{{\delta }^{*}}\right]{(log\frac{\mathrm{T}}{s})}^2\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\sigma -1)}\left[\frac{{(log\chi )}^{\sigma -1}{\eta }_4{\delta }_{11}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\eta }_4{\delta }_{21}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\eta }_4{\delta }_{31}^{*}}{{\delta }^{*}}\right]{(log\frac{\mathrm{T}}{s})}^{2\sigma -2}\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\sigma -2)}\left[\frac{{(log\chi )}^{\sigma -1}{\eta }_5{\delta }_{12}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\eta }_5{\delta }_{22}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\eta }_5{\delta }_{32}^{*}}{{\delta }^{*}}\right]{(log\frac{\mathrm{T}}{s})}^{2\sigma -3}\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\sigma -3)}\left[\frac{{(log\chi )}^{\sigma -1}{\eta }_6{\delta }_{13}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\eta }_6{\delta }_{23}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\eta }_6{\delta }_{33}^{*}}{{\delta }^{*}}\right]{(log\frac{\mathrm{T}}{s})}^{2\sigma -4},\hfill & & 1\le s<\chi \le \mathrm{T},\hfill \\ \\ -\left[\frac{{(log\chi )}^{\sigma -1}{\mathsf{a}}_1{\delta }_{11}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\mathsf{a}}_1{\delta }_{21}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\mathsf{a}}_1{\delta }_{31}^{*}}{{\delta }^{*}}\right]\hfill \\ -\left[\frac{{(log\chi )}^{\sigma -1}{\mathsf{b}}_1{\delta }_{12}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\mathsf{b}}_1{\delta }_{22}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\mathsf{b}}_1{\delta }_{32}^{*}}{{\delta }^{*}}\right]log\frac{\mathrm{T}}{s}\hfill \\ -\frac{1}{2}\left[\frac{{(log\chi )}^{\sigma -1}{\mathsf{c}}_1{\delta }_{13}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\mathsf{c}}_1{\delta }_{23}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\mathsf{c}}_1{\delta }_{33}^{*}}{{\delta }^{*}}\right]{(log\frac{\mathrm{T}}{s})}^2\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\sigma -1)}\left[\frac{{(log\chi )}^{\sigma -1}{\eta }_4{\delta }_{11}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\eta }_4{\delta }_{21}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\eta }_4{\delta }_{31}^{*}}{{\delta }^{*}}\right]{(log\frac{\mathrm{T}}{s})}^{2\sigma -2}\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\sigma -2)}\left[\frac{{(log\chi )}^{\sigma -1}{\eta }_5{\delta }_{12}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\eta }_5{\delta }_{22}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\eta }_5{\delta }_{32}^{*}}{{\delta }^{*}}\right]{(log\frac{\mathrm{T}}{s})}^{2\sigma -3}\hfill \\ -\frac{1}{\mathrm{\Gamma }(2\sigma -3)}\left[\frac{{(log\chi )}^{\sigma -1}{\eta }_6{\delta }_{13}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -2}{\eta }_6{\delta }_{23}^{*}}{{\delta }^{*}}+\frac{{(log\chi )}^{\sigma -3}{\eta }_6{\delta }_{33}^{*}}{{\delta }^{*}}\right]{(log\frac{\mathrm{T}}{s})}^{2\sigma -4},\hfill & & 1\le \chi <s\le \mathrm{T}.\hfill \end{array}\right.$$

Proof. 

The proof can be derived as in Lemma 2. □

For simplicity, let

$$\begin{array}{cc}\hfill {\mathfrak{R}}_{\kappa }=& max\left\{\right|\frac{{\mathsf{a}}_0{\delta }_{31}log\mathrm{T}}{\delta }|+|\frac{(2{\mathsf{a}}_0{\delta }_{21}+{\mathsf{b}}_0{\delta }_{32}){(log\mathrm{T})}^2}{2\delta }|+\frac{{(log\mathrm{T})}^3}{\mathrm{\Gamma }\left(\kappa \right)}\hfill \\ \hfill & +\left|\frac{(6{\mathsf{a}}_0{\delta }_{11}+3{\mathsf{b}}_0{\delta }_{22}+{\mathsf{c}}_0{\delta }_{33}){(log\mathrm{T})}^3}{6\delta }\right|+\left|\frac{(3{\mathsf{b}}_0{\delta }_{12}+{\mathsf{c}}_0{\delta }_{23}){(log\mathrm{T})}^4}{6\delta }\right|+\left|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\mathrm{T})}^5}{6\delta }\right|\hfill \\ \hfill & +\left|\frac{{\eta }_1{\delta }_{11}{(log\mathrm{T})}^{2\kappa +1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{({\eta }_1{\delta }_{21}+(2\kappa -1){\eta }_2{\delta }_{12}){(log\mathrm{T})}^{2\kappa }}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_1{\delta }_{31}+(2\kappa -1){\eta }_2{\delta }_{22}+(2\kappa -1)(2\kappa -2){\eta }_3{\delta }_{13}){(log\mathrm{T})}^{2\kappa -1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_2{\delta }_{32}+(2\kappa -2){\eta }_3{\delta }_{23}){(log\mathrm{T})}^{2\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right|+\left|\frac{{\eta }_3{\delta }_{33}{(log\mathrm{T})}^{2\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right|\}\hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill {\mathfrak{R}}_{\sigma }=& max\left\{\right|\frac{{\mathsf{a}}_1{\delta }_{31}^{*}log\mathrm{T}}{{\delta }^{*}}|+|\frac{(2{\mathsf{a}}_1{\delta }_{21}^{*}+{\mathsf{b}}_1{\delta }_{32}^{*}){(log\mathrm{T})}^2}{2{\delta }^{*}}|+\frac{{(log\mathrm{T})}^3}{\mathrm{\Gamma }\left(\sigma \right)}\hfill \\ \hfill & +\left|\frac{(6{\mathsf{a}}_1{\delta }_{11}^{*}+3{\mathsf{b}}_1{\delta }_{22}^{*}+{\mathsf{c}}_1{\delta }_{33}^{*}){(log\mathrm{T})}^3}{6{\delta }^{*}}\right|+\left|\frac{(3{\mathsf{b}}_1{\delta }_{12}^{*}+{\mathsf{c}}_1{\delta }_{23}^{*}){(log\mathrm{T})}^4}{6{\delta }^{*}}\right|+\left|\frac{{\mathsf{c}}_1{\delta }_{13}^{*}{(log\mathrm{T})}^5}{6{\delta }^{*}}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_4{\delta }_{11}^{*}{(log\mathrm{T})}^{2\sigma +1}}{{\delta }^{*}\mathrm{\Gamma }\left(2\sigma \right)}\right|+\left|\frac{({\eta }_4{\delta }_{21}^{*}+(2\sigma -1){\eta }_5{\delta }_{12}^{*}){(log\mathrm{T})}^{2\sigma }}{{\delta }^{*}\mathrm{\Gamma }\left(2\sigma \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_4{\delta }_{31}^{*}+(2\sigma -1){\eta }_5{\delta }_{22}^{*}+(2\sigma -1)(2\sigma -2){\eta }_6{\delta }_{13}^{*}){(log\mathrm{T})}^{2\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }\left(2\sigma \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_5{\delta }_{32}^{*}+(2\sigma -2){\eta }_6{\delta }_{23}^{*}){(log\mathrm{T})}^{2\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}\right|+\left|\frac{{\eta }_6{\delta }_{33}^{*}{(log\mathrm{T})}^{2\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}\right|\}.\hfill \end{array}$$

(9)

By letting $\mathsf{v},\mathsf{w}$ be the solutions to Equation (1) and $\chi \in \mathcal{M},$ then

$$\begin{array}{cc}\hfill \mathsf{v}\left(\chi \right)=& \frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^{\kappa -1}}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{21}{(log\chi )}^{\kappa -2}}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}{(log\chi )}^{\kappa -3}}{\delta }\right]{\int }_1^{\mathrm{T}}\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^{\kappa -1}}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{22}{(log\chi )}^{\kappa -2}}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}{(log\chi )}^{\kappa -3}}{\delta }\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^{\kappa -1}}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{23}{(log\chi )}^{\kappa -2}}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}{(log\chi )}^{\kappa -3}}{2\delta }\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_1{\delta }_{11}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{21}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{31}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_2{\delta }_{12}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{32}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_3{\delta }_{13}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{23}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill =& {\int }_1^{\mathrm{T}}{\mathbf{G}}_{\kappa }(\chi ,\mathtt{s})\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \mathsf{w}\left(\chi \right)=& \frac{1}{\mathrm{\Gamma }\left(\sigma \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\sigma -1}\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{a}}_1{\delta }_{11}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}}+\frac{{\mathsf{a}}_1{\delta }_{21}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}}+\frac{{\mathsf{a}}_1{\delta }_{31}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}\nu (\mathtt{s},\nu \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{b}}_1{\delta }_{12}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}}+\frac{{\mathsf{b}}_1{\delta }_{22}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}}+\frac{{\mathsf{b}}_1{\delta }_{32}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{c}}_1{\delta }_{13}^{*}{(log\chi )}^{\sigma -1}}{2{\delta }^{*}}+\frac{{\mathsf{c}}_1{\delta }_{23}^{*}{(log\chi )}^{\sigma -2}}{2{\delta }^{*}}+\frac{{\mathsf{c}}_1{\delta }_{33}^{*}{(log\chi )}^{\sigma -3}}{2{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_4{\delta }_{11}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}+\frac{{\eta }_4{\delta }_{21}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}+\frac{{\eta }_4{\delta }_{31}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -2}\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_5{\delta }_{12}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}+\frac{{\eta }_5{\delta }_{22}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}+\frac{{\eta }_5{\delta }_{32}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -3}\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_6{\delta }_{13}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}+\frac{{\eta }_6{\delta }_{23}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}+\frac{{\eta }_6{\delta }_{33}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -4}\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill =& {\int }_1^{\mathrm{T}}{\mathbf{G}}_{\sigma }(\chi ,\mathtt{s})\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}.\hfill \end{array}$$

For simplicity, we have

$$\begin{array}{cc}\hfill & \mathsf{u}\left(\chi \right)=\mu (\chi ,\mathsf{w}\left(\chi \right),{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))=\mu (\chi ,\mathsf{w}\left(\chi \right),\mathsf{u}\left(\chi \right)),\hfill \\ \hfill & \mathsf{x}\left(\chi \right)=\nu (\chi ,\mathsf{v}\left(\chi \right),{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))=\nu (\chi ,\mathsf{v}\left(\chi \right),\mathsf{x}\left(\chi \right)).\hfill \end{array}$$

To deal with Equation (1) as a problem of a fixed point, let $\mathfrak{U}:\mathcal{W}\times \mathcal{W}\to \mathcal{W}\times \mathcal{W}$ be an operator represented by

$$\mathfrak{U}(\mathsf{v},\mathsf{w})\left(\chi \right)=\left(\begin{array}{c}\underset{1}{\overset{\mathrm{T}}{\int }}{\mathbf{G}}_{\kappa }(\chi ,\mathtt{s})\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),\mathsf{u}\left(\mathtt{s}\right))\mathsf{d}\mathtt{s}\\ \underset{1}{\overset{\mathrm{T}}{\int }}{\mathbf{G}}_{\sigma }(\chi ,\mathtt{s})\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),\mathsf{x}\left(\mathtt{s}\right))\mathsf{d}\mathtt{s}\end{array}\right)=\left(\begin{array}{c}{\mathfrak{U}}_{\kappa }(\mathsf{w},\mathsf{u})\left(\chi \right)\\ {\mathfrak{U}}_{\sigma }(\mathsf{v},\mathsf{x})\left(\chi \right)\end{array}\right)=\left(\begin{array}{c}{\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left(\chi \right)\\ {\mathfrak{U}}_{\sigma }\left(\mathsf{w}\right)\left(\chi \right)\end{array}\right).$$

(10)

Then, obviously, the solution to Equation (1) is the fixed point of $\mathfrak{U}$, where

$$\begin{array}{cc}\hfill {\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left(\chi \right)=& \frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^{\kappa -1}}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{21}{(log\chi )}^{\kappa -2}}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}{(log\chi )}^{\kappa -3}}{\delta }\right]{\int }_1^{\mathrm{T}}\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^{\kappa -1}}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{22}{(log\chi )}^{\kappa -2}}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}{(log\chi )}^{\kappa -3}}{\delta }\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^{\kappa -1}}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{23}{(log\chi )}^{\kappa -2}}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}{(log\chi )}^{\kappa -3}}{2\delta }\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_1{\delta }_{11}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{21}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{31}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_2{\delta }_{12}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{32}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_3{\delta }_{13}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{23}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill =& {\int }_1^{\mathrm{T}}{\mathbf{G}}_{\kappa }(\chi ,\mathtt{s})\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\mathfrak{U}}_{\sigma }\left(\mathsf{w}\right)\left(\chi \right)=& \frac{1}{\mathrm{\Gamma }\left(\sigma \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\sigma -1}\mathsf{x}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{a}}_1{\delta }_{11}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}}+\frac{{\mathsf{a}}_1{\delta }_{21}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}}+\frac{{\mathsf{a}}_1{\delta }_{31}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}\mathsf{x}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{b}}_1{\delta }_{12}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}}+\frac{{\mathsf{b}}_1{\delta }_{22}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}}+\frac{{\mathsf{b}}_1{\delta }_{32}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\mathsf{x}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{c}}_1{\delta }_{13}^{*}{(log\chi )}^{\sigma -1}}{2{\delta }^{*}}+\frac{{\mathsf{c}}_1{\delta }_{23}^{*}{(log\chi )}^{\sigma -2}}{2{\delta }^{*}}+\frac{{\mathsf{c}}_1{\delta }_{33}^{*}{(log\chi )}^{\sigma -3}}{2{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\mathsf{x}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_4{\delta }_{11}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}+\frac{{\eta }_4{\delta }_{21}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}+\frac{{\eta }_4{\delta }_{31}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -2}\mathsf{x}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_5{\delta }_{12}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}+\frac{{\eta }_5{\delta }_{22}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}+\frac{{\eta }_5{\delta }_{32}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -3}\mathsf{x}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_6{\delta }_{13}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}+\frac{{\eta }_6{\delta }_{23}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}+\frac{{\eta }_6{\delta }_{33}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -4}\mathsf{x}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill =& {\int }_1^{\mathrm{T}}{\mathbf{G}}_{\sigma }(\chi ,\mathtt{s})\mathsf{x}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}.\hfill \end{array}$$

In the coming section, we utilize the Banach principle to obtain our first result:

Theorem 1.

Let $\mu ,\nu :\mathcal{M}\times {\mathcal{R}}^2\to \mathcal{R}$ be continuous such that the following condition holds true:

$\left[{\mathsf{H}}_1\right]$ For every $\chi \in \mathcal{M}$ and $\mathsf{w},\mathsf{v},\mathsf{u},\mathsf{x},\overline{\mathsf{w}},\overline{\mathsf{v}},\overline{\mathsf{x}},\overline{\mathsf{u}}:\mathcal{W}\to \mathcal{R}$, there are ${\mathcal{L}}_{\mu },{\mathcal{L}}_{\nu }>0$ and $0\le {\overline{\mathcal{L}}}_{\mu },{\overline{\mathcal{L}}}_{\nu }<1$ such that

$$|\mu (\chi ,\mathsf{w}\left(\chi \right),\mathsf{u}\left(\chi \right))-\mu (\chi ,\overline{\mathsf{w}}\left(\chi \right),\overline{\mathsf{u}}\left(\chi \right))|\le {\mathcal{L}}_{\mu }|\mathsf{w}\left(\chi \right)-\overline{\mathsf{w}}\left(\chi \right)|+{\overline{\mathcal{L}}}_{\mu }|\mathsf{u}\left(\chi \right)-\overline{\mathsf{u}}\left(\chi \right)|,$$

$$|\nu (\chi ,\mathsf{v}\left(\chi \right),\mathsf{x}\left(\chi \right))-\nu (\chi ,\overline{\mathsf{v}}\left(\chi \right),\overline{\mathsf{x}}\left(\chi \right))|\le {\mathcal{L}}_{\nu }|\mathsf{v}\left(\chi \right)-\overline{\mathsf{v}}\left(\chi \right)|+{\overline{\mathcal{L}}}_{\nu }|\mathsf{x}\left(\chi \right)-\overline{\mathsf{x}}\left(\chi \right)|.$$

Furthermore, suppose that

$$\begin{array}{c}\hfill \frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }(1-{\overline{\mathcal{L}}}_{\nu })+{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }(1-{\overline{\mathcal{L}}}_{\mu })}{(1-{\overline{\mathcal{L}}}_{\nu })(1-{\overline{\mathcal{L}}}_{\mu })}<1,\end{array}$$

where ${\mathfrak{R}}_{\kappa }$ and ${\mathfrak{R}}_{\sigma }$ are presented in Equations (8) and (9), respectively. Then, Equation (1) has a (unique) solution.

Proof. 

Let ${sup}_{\chi \in \mathcal{M}}\mu (\chi ,0,0)={\Phi }^{*}<\infty$ and ${sup}_{\chi \in \mathcal{M}}\nu (\chi ,0,0)={\Psi }^{*}<\infty$ such that

$$\begin{array}{cc}\hfill \mathrm{r}& \ge \frac{2{\mathfrak{R}}_{\kappa }{\Phi }^{*}(1-{\overline{\mathcal{L}}}_{\nu })+2{\mathfrak{R}}_{\sigma }{\Psi }^{*}(1-{\overline{\mathcal{L}}}_{\mu })}{2(1-{\overline{\mathcal{L}}}_{\mu })(1-{\overline{\mathcal{L}}}_{\nu })-{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }-{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}.\hfill \end{array}$$

We need to prove that $\mathfrak{U}\left({\mathcal{B}}_{\mathrm{r}}\right)\subset {\mathcal{B}}_{\mathrm{r}},$ where

$$\begin{array}{cc}\hfill {\mathcal{B}}_{\mathrm{r}}& =\left\{(\mathsf{v},\mathsf{w})\in \mathcal{W}\times {\mathcal{W}:\parallel (\mathsf{v},\mathsf{w})\parallel }_{\mathcal{W}\times \mathcal{W}}\le {r,\parallel \mathsf{v}\parallel }_{\mathcal{W}}\le \frac{\mathrm{r}}{2},{\parallel \mathsf{w}\parallel }_{\mathcal{W}}\le \frac{\mathrm{r}}{2}\right\}.\hfill \end{array}$$

For $(\mathsf{v},\mathsf{w})\in {\mathcal{B}}_{\mathrm{r}},$ we have

$$\begin{array}{cc}\hfill (log& {\chi )}^{3-\kappa }\left|{\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left(\chi \right)\right|\hfill \\ \hfill \le & \frac{{(log\chi )}^{3-\kappa }}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}\left[\right|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),\mathsf{u}\left(\mathtt{s}\right))-\mu (0,0,0)|+|\mu (0,0,0)\left|\right]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^2}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{21}log\left(\chi \right)}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}}{\delta }|{\int }_1^{\mathrm{T}}\left[\right|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),\mathsf{u}\left(\mathtt{s}\right))-\mu (0,0,0)|+|\mu (0,0,0)\left|\right]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^2}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{22}log\left(\chi \right)}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}}{\delta }|{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\left[\right|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),\mathsf{u}\left(\mathtt{s}\right))-\mu (0,0,0)|+|\mu (0,0,0)\left|\right]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^2}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{23}log\left(\chi \right)}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}}{2\delta }|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\left[\right|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),\mathsf{u}\left(\mathtt{s}\right))-\mu (0,0,0)|+|\mu (0,0,0)\left|\right]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_1{\delta }_{11}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{21}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{31}}{\delta \mathrm{\Gamma }(2\kappa -1)}|\hfill \\ \hfill & \times {\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}\left[\right|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),\mathsf{u}\left(\mathtt{s}\right))-\mu (0,0,0)|+|\mu (0,0,0)\left|\right]\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\eta }_2{\delta }_{12}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -2)}\hfill \\ \hfill & +\frac{{\eta }_2{\delta }_{32}}{\delta \mathrm{\Gamma }(2\kappa -2)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}\left[\right|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),\mathsf{u}\left(\mathtt{s}\right))-\mu (0,0,0)|+|\mu (0,0,0)\left|\right]\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\eta }_3{\delta }_{13}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -3)}\hfill \\ \hfill & +\frac{{\eta }_3{\delta }_{23}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}}{\delta \mathrm{\Gamma }(2\kappa -3)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}\left[\right|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),\mathsf{u}\left(\mathtt{s}\right))-\mu (0,0,0)|+|\mu (0,0,0)\left|\right]\frac{\mathtt{ds}}{\mathtt{s}}.\hfill \end{array}$$

(11)

Consider

$$\begin{array}{cc}\hfill \left|\mathsf{u}\right(\chi \left)\right|& \le \left|\mu \right(\chi ,\mathsf{w}\left(\chi \right),\mathsf{u}\left(\chi \right))-\mu (\chi ,0,0\left)\right|+\left|\mu \right(\chi ,0,0\left)\right|\hfill \\ \hfill & \le \left|\mu (\chi ,0,0)\right|+{\mathcal{L}}_{\mu }\left|\mathsf{w}\left(\chi \right)\right|+{\overline{\mathcal{L}}}_{\mu }\left|\mathsf{u}\left(\chi \right)\right|\hfill \\ \hfill & \le \frac{\left|\mu (\chi ,0,0)\right|+{\mathcal{L}}_{\mu }\left|\mathsf{w}\left(\chi \right)\right|}{1-{\overline{\mathcal{L}}}_{\mu }}.\hfill \end{array}$$

(12)

By substituting Equation (12) into Equation (11), we obtain

$$\begin{array}{cc}\hfill \parallel {\mathfrak{U}}_{\kappa }{\left(\mathsf{v}\right)\parallel }_{\mathcal{W}}\le & \left[\right|\frac{{\mathsf{a}}_0{\delta }_{31}log\mathrm{T}}{\delta }|+|\frac{(2{\mathsf{a}}_0{\delta }_{21}+{\mathsf{b}}_0{\delta }_{32}){(log\mathrm{T})}^2}{2\delta }|+|\frac{(6{\mathsf{a}}_0{\delta }_{11}+3{\mathsf{b}}_0{\delta }_{22}+{\mathsf{c}}_0{\delta }_{33}){(log\mathrm{T})}^3}{6\delta }|\hfill \\ \hfill & +\left|\frac{(3{\mathsf{b}}_0{\delta }_{12}+{\mathsf{c}}_0{\delta }_{23}){(log\mathrm{T})}^4}{6\delta }\right|+\left|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\mathrm{T})}^5}{6\delta }\right|+\frac{{(log\mathrm{T})}^3}{\mathrm{\Gamma }\left(\kappa \right)}+\left|\frac{{\eta }_1{\delta }_{11}{(log\mathrm{T})}^{2\kappa +1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_1{\delta }_{31}+(2\kappa -1){\eta }_2{\delta }_{22}+(2\kappa -1)(2\kappa -2){\eta }_3{\delta }_{13}){(log\mathrm{T})}^{2\kappa -1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{{\eta }_3{\delta }_{33}{(log\mathrm{T})}^{2\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_1{\delta }_{21}+(2\kappa -1){\eta }_2{\delta }_{12}){(log\mathrm{T})}^{2\kappa }}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{({\eta }_2{\delta }_{32}+(2\kappa -2){\eta }_3{\delta }_{23}){(log\mathrm{T})}^{2\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right|]\frac{2{\Phi }^{*}+{\mathcal{L}}_{\mu }\mathsf{r}}{2(1-{\overline{\mathcal{L}}}_{\mu })}.\hfill \end{array}$$

Hence, we have

$$\begin{array}{cc}\hfill \parallel {\mathfrak{U}}_{\kappa }{\left(\mathsf{v}\right)\parallel }_{\mathcal{W}}& \le {\mathfrak{R}}_{\kappa }\frac{2{\Phi }^{*}+{\mathcal{L}}_{\mu }\mathsf{r}}{2(1-{\overline{\mathcal{L}}}_{\mu })}.\hfill \end{array}$$

(13)

Equivalently, we have

$$\begin{array}{cc}\hfill \parallel {\mathfrak{U}}_{\sigma }{\left(\mathsf{w}\right)\parallel }_{\mathcal{W}}& \le {\mathfrak{R}}_{\sigma }\frac{2{\Psi }^{*}+{\mathcal{L}}_{\nu }\mathsf{r}}{2(1-{\overline{\mathcal{L}}}_{\nu })}.\hfill \end{array}$$

(14)

Equations (13) and (14) imply that

$$\begin{array}{c}\hfill {\parallel \mathfrak{U}(\mathsf{v},\mathsf{w})\parallel }_{\mathcal{W}\times \mathcal{W}}\le \mathrm{r}.\end{array}$$

For $({\mathsf{v}}_1,{\mathsf{w}}_1),({\mathsf{v}}_2,{\mathsf{w}}_2)\in \mathcal{W}\times \mathcal{W}$ and for any $\chi \in \mathcal{M},$ we obtain

$$\begin{array}{cc}\hfill (log& {\chi )}^{3-\kappa }|{\mathfrak{U}}_{\kappa }\left({\mathsf{v}}_1\right)\left(\chi \right)-{\mathfrak{U}}_{\kappa }\left({\mathsf{v}}_2\right)\left(\chi \right)|\hfill \\ \hfill \le & \frac{{(log\chi )}^{3-\kappa }}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}|\mu (\mathtt{s},{\mathsf{w}}_1\left(\mathtt{s}\right),{\mathsf{u}}_1\left(\mathtt{s}\right))-\mu (\mathtt{s},{\mathsf{w}}_2\left(\mathtt{s}\right),{\mathsf{u}}_2\left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^2}{\delta }\hfill \\ \hfill & +\frac{{\mathsf{a}}_0{\delta }_{21}log\left(\chi \right)}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}}{\delta }|{\int }_1^{\mathrm{T}}|\mu (\mathtt{s},{\mathsf{w}}_1\left(\mathtt{s}\right),{\mathsf{u}}_1\left(\mathtt{s}\right))-\mu (\mathtt{s},{\mathsf{w}}_2\left(\mathtt{s}\right),{\mathsf{u}}_2\left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^2}{\delta }\hfill \\ \hfill & +\frac{{\mathsf{b}}_0{\delta }_{22}log\left(\chi \right)}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}}{\delta }|{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}|\mu (\mathtt{s},{\mathsf{w}}_1\left(\mathtt{s}\right),{\mathsf{u}}_1\left(\mathtt{s}\right))-\mu (\mathtt{s},{\mathsf{w}}_2\left(\mathtt{s}\right),{\mathsf{u}}_2\left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^2}{2\delta }\hfill \\ \hfill & +\frac{{\mathsf{c}}_0{\delta }_{23}log\left(\chi \right)}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}}{2\delta }|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2|\mu (\mathtt{s},{\mathsf{w}}_1\left(\mathtt{s}\right),{\mathsf{u}}_1\left(\mathtt{s}\right))-\mu (\mathtt{s},{\mathsf{w}}_2\left(\mathtt{s}\right),{\mathsf{u}}_2\left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\eta }_1{\delta }_{31}}{\delta \mathrm{\Gamma }(2\kappa -1)}\hfill \\ \hfill & +\frac{{\eta }_1{\delta }_{21}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{11}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -1)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}|\mu (\mathtt{s},{\mathsf{w}}_1\left(\mathtt{s}\right),{\mathsf{u}}_1\left(\mathtt{s}\right))-\mu (\mathtt{s},{\mathsf{w}}_2\left(\mathtt{s}\right),{\mathsf{u}}_2\left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_2{\delta }_{12}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{32}}{\delta \mathrm{\Gamma }(2\kappa -2)}|\hfill \\ \hfill & \times {\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}|\mu (\mathtt{s},{\mathsf{w}}_1\left(\mathtt{s}\right),{\mathsf{u}}_1\left(\mathtt{s}\right))-\mu (\mathtt{s},{\mathsf{w}}_2\left(\mathtt{s}\right),{\mathsf{u}}_2\left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\eta }_3{\delta }_{13}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -3)}\hfill \\ \hfill & +\frac{{\eta }_3{\delta }_{23}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}}{\delta \mathrm{\Gamma }(2\kappa -3)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}|\mu (\mathtt{s},{\mathsf{w}}_1\left(\mathtt{s}\right),{\mathsf{u}}_1\left(\mathtt{s}\right))-\mu (\mathtt{s},{\mathsf{w}}_2\left(\mathtt{s}\right),{\mathsf{u}}_2\left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill \le & \left[\right|\frac{{\mathsf{a}}_0{\delta }_{31}log\mathrm{T}}{\delta }|+|\frac{(2{\mathsf{a}}_0{\delta }_{21}+{\mathsf{b}}_0{\delta }_{32}){(log\mathrm{T})}^2}{2\delta }|+|\frac{(6{\mathsf{a}}_0{\delta }_{11}+3{\mathsf{b}}_0{\delta }_{22}+{\mathsf{c}}_0{\delta }_{33}){(log\mathrm{T})}^3}{6\delta }|\hfill \\ \hfill & +\left|\frac{(3{\mathsf{b}}_0{\delta }_{12}+{\mathsf{c}}_0{\delta }_{23}){(log\mathrm{T})}^4}{6\delta }\right|+\left|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\mathrm{T})}^5}{6\delta }\right|+\frac{{(log\mathrm{T})}^3}{\mathrm{\Gamma }\left(\kappa \right)}+\left|\frac{{\eta }_1{\delta }_{11}{(log\mathrm{T})}^{2\kappa +1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_1{\delta }_{31}+(2\kappa -1){\eta }_2{\delta }_{22}+(2\kappa -1)(2\kappa -2){\eta }_3{\delta }_{13}){(log\mathrm{T})}^{2\kappa -1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{{\eta }_3{\delta }_{33}{(log\mathrm{T})}^{2\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_1{\delta }_{21}+(2\kappa -1){\eta }_2{\delta }_{12}){(log\mathrm{T})}^{2\kappa }}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{({\eta }_2{\delta }_{32}+(2\kappa -2){\eta }_3{\delta }_{23}){(log\mathrm{T})}^{2\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right|]\frac{{\mathcal{L}}_{\mu }}{1-{\overline{\mathcal{L}}}_{\mu }}{\parallel {\mathsf{w}}_1-{\mathsf{w}}_2\parallel }_{\mathcal{W}}\hfill \end{array}$$

Hence, we have

$$\begin{array}{cc}\hfill \parallel {\mathfrak{U}}_{\kappa }\left({\mathsf{v}}_1\right)-{\mathfrak{U}}_{\kappa }\left({\mathsf{v}}_2\right){\parallel }_{\mathcal{W}}& \le \frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }}{1-{\overline{\mathcal{L}}}_{\mu }}{\parallel {\mathsf{w}}_1-{\mathsf{w}}_2\parallel }_{\mathcal{W}}.\hfill \end{array}$$

(15)

Similarly, we have

$$\begin{array}{cc}\hfill \parallel {\mathfrak{U}}_{\sigma }\left({\mathsf{w}}_1\right)-{\mathfrak{U}}_{\sigma }\left({\mathsf{w}}_2\right){\parallel }_{\mathcal{W}}& \le \frac{{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}{1-{\overline{\mathcal{L}}}_{\nu }}{\parallel {\mathsf{v}}_1-{\mathsf{v}}_2\parallel }_{\mathcal{W}}.\hfill \end{array}$$

(16)

Equations (15) and (16) imply that

$$\begin{array}{cc}\hfill \parallel \mathfrak{U}({\mathsf{v}}_1,{\mathsf{w}}_1)-\mathfrak{U}({\mathsf{v}}_2,{\mathsf{w}}_2){\parallel }_{\mathcal{W}\times \mathcal{W}}& \le \frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }(1-{\overline{\mathcal{L}}}_{\nu })+{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }(1-{\overline{\mathcal{L}}}_{\mu })}{(1-{\overline{\mathcal{L}}}_{\nu })(1-{\overline{\mathcal{L}}}_{\mu })}{\parallel ({\mathsf{v}}_1,{\mathsf{w}}_1)-({\mathsf{v}}_2,{\mathsf{w}}_2)\parallel }_{\mathcal{W}\times \mathcal{W}}.\hfill \end{array}$$

Therefore, $\mathfrak{U}$ is a contraction. Thus, Equation (1) has a (unique) solution. □

In the sequel, we need the following theorem:

Theorem 2

([36]). Let $\mathfrak{U}:\mathcal{W}\to \mathcal{W}$ be a completely continuous operator, and let

$$\begin{array}{cc}\hfill \mathcal{B}\left(\mathfrak{U}\right)& =\left\{\mathsf{v}\in \mathcal{W}:\mathsf{v}=\lambda \mathfrak{U}\left(\mathsf{v}\right),\lambda \in [0,1]\right\}.\hfill \end{array}$$

Then either the set $\mathcal{B}\left(\mathfrak{U}\right)$ is unbounded or the operator $\mathfrak{U}$ has at least one fixed point.

Theorem 3.

Suppose the functions $\mu ,\nu :\mathcal{M}\times \mathcal{R}\times \mathcal{R}\to \mathcal{R}$ are continuous such that the following are true:

$\left[{\mathsf{H}}_2\right]$ For any $\chi \in \mathcal{M}$ and $\mathsf{w},\mathsf{u}:\mathcal{M}\to \mathcal{R}$, ∃${\varphi }_{\mathrm{i}}(\mathrm{i}=1,2,3):\mathcal{M}\to \mathcal{R}$, they satisfy

$$\left|\mu (\chi ,\mathsf{w}\left(\chi \right),\mathsf{u}\left(\chi \right))\right|\le {\varphi }_1\left(\chi \right)+{\varphi }_2\left(\chi \right)\left|\mathsf{w}\left(\chi \right)\right|+{\varphi }_3\left(\chi \right)\left|\mathsf{u}\left(\chi \right)\right|.$$

In addition, for $\chi \in \mathcal{M}$ and $\mathsf{v},\mathsf{x}:\mathcal{M}\to \mathcal{R}$, ∃${\phi }_{\mathrm{i}}(\mathrm{i}=1,2,3):\mathcal{M}\to \mathcal{R}$, they satisfy

$$\left|\nu (\chi ,\mathsf{v}\left(\chi \right),\mathsf{x}\left(\chi \right))\right|\le {\phi }_1\left(\chi \right)+{\phi }_2\left(\chi \right)\left|\mathsf{v}\left(\chi \right)\right|+{\phi }_3\left(\chi \right)\left|\mathsf{x}\left(\chi \right)\right|,$$

with ${sup}_{\chi \in \mathcal{M}}{\varphi }_{\mathrm{i}}\left(\chi \right)={\varphi }_{\mathrm{i}}^{*},{sup}_{\chi \in \mathcal{M}}{\phi }_{\mathrm{i}}\left(\chi \right)={\phi }_{\mathrm{i}}^{*}(\mathrm{i}=1,2,3)$.

Furthermore, the following is true:

$$\begin{array}{cc}\hfill {\mathfrak{R}}_0& =max\left\{\frac{{\mathfrak{R}}_{\sigma }{\phi }_2^{*}}{1-{\phi }_3^{*}},\frac{{\mathfrak{R}}_{\kappa }{\varphi }_2^{*}}{1-{\varphi }_3^{*}}\right\}<1\mathit{and}0\le {\varphi }_3^{*},{\phi }_3^{*}<1.\hfill \end{array}$$

(17)

Then, Equation (1) has at least one solution.

Proof. 

First, we prove that $\mathfrak{U}$ is completely continuous. As $\mu$ and $\nu$ are continuous, the operator $\mathfrak{U}$ is thus also continuous. Now, for $(\mathsf{v},\mathsf{w})\in {\mathcal{B}}_{\mathsf{r}}$, we obtain

$$\begin{array}{cc}\hfill (log& {\chi )}^{3-\kappa }\left|{\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left(\chi \right)\right|\hfill \\ \hfill \le & \frac{{(log\chi )}^{3-\kappa }}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}|\mathsf{u}\left(\mathtt{s}\right)|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^2}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{21}log\left(\chi \right)}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}}{\delta }|{\int }_1^{\mathrm{T}}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^2}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{22}log\left(\chi \right)}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}}{\delta }|{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^2}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{23}log\left(\chi \right)}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}}{2\delta }|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_1{\delta }_{11}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{21}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{31}}{\delta \mathrm{\Gamma }(2\kappa -1)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_2{\delta }_{12}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{32}}{\delta \mathrm{\Gamma }(2\kappa -2)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_3{\delta }_{13}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{23}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}}{\delta \mathrm{\Gamma }(2\kappa -3)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}.\hfill \end{array}$$

(18)

By applying $\left[{\mathsf{H}}_2\right]$, we have

$$\begin{array}{cc}\hfill \left|\mathsf{u}\right(\chi \left)\right|=& \left|\mu \right(\chi ,\mathsf{w}\left(\chi \right),\mathsf{u}\left(\chi \right)\left)\right|\hfill \\ \hfill \le & {\varphi }_1\left(\chi \right)+{\varphi }_2\left(\chi \right)\left|\mathsf{w}\left(\chi \right)\right|+{\varphi }_3\left(\chi \right)\left|\mathsf{u}\left(\chi \right)\right|\hfill \\ \hfill \le & \frac{{\varphi }_1\left(\chi \right)+{\varphi }_2\left(\chi \right)\left|\mathsf{w}\left(\chi \right)\right|}{1-{\varphi }_3\left(\chi \right)}.\hfill \end{array}$$

Thus, from Equation (18), we have

$$\begin{array}{cc}\hfill \parallel {\mathfrak{U}}_{\kappa }{\left(\mathsf{v}\right)\parallel }_{\mathcal{W}}\le & \left[\right|\frac{{\mathsf{a}}_0{\delta }_{31}log\mathrm{T}}{\delta }|+|\frac{(2{\mathsf{a}}_0{\delta }_{21}+{\mathsf{b}}_0{\delta }_{32}){(log\mathrm{T})}^2}{2\delta }|+|\frac{(6{\mathsf{a}}_0{\delta }_{11}+3{\mathsf{b}}_0{\delta }_{22}+{\mathsf{c}}_0{\delta }_{33}){(log\mathrm{T})}^3}{6\delta }|\hfill \\ \hfill & +\left|\frac{(3{\mathsf{b}}_0{\delta }_{12}+{\mathsf{c}}_0{\delta }_{23}){(log\mathrm{T})}^4}{6\delta }\right|+\left|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\mathrm{T})}^5}{6\delta }\right|+\frac{{(log\mathrm{T})}^3}{\mathrm{\Gamma }\left(\kappa \right)}+\left|\frac{{\eta }_1{\delta }_{11}{(log\mathrm{T})}^{2\kappa +1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_1{\delta }_{31}+(2\kappa -1){\eta }_2{\delta }_{22}+(2\kappa -1)(2\kappa -2){\eta }_3{\delta }_{13}){(log\mathrm{T})}^{2\kappa -1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{{\eta }_3{\delta }_{33}{(log\mathrm{T})}^{2\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_1{\delta }_{21}+(2\kappa -1){\eta }_2{\delta }_{12}){(log\mathrm{T})}^{2\kappa }}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{({\eta }_2{\delta }_{32}+(2\kappa -2){\eta }_3{\delta }_{23}){(log\mathrm{T})}^{2\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right|]\frac{2{\varphi }_1^{*}+{\varphi }_2^{*}\mathsf{r}}{2(1-{\varphi }_3^{*})},\hfill \end{array}$$

(19)

which implies that

$$\begin{array}{cc}\hfill \parallel {\mathfrak{U}}_{\kappa }{\left(\mathsf{v}\right)\parallel }_{\mathcal{W}}& \le {\mathfrak{R}}_{\kappa }\frac{2{\varphi }_1^{*}+{\varphi }_2^{*}\mathsf{r}}{2(1-{\varphi }_3^{*})}.\hfill \end{array}$$

(20)

Similarly, we obtain

$$\begin{array}{cc}\hfill \parallel {\mathfrak{U}}_{\sigma }{\left(\mathsf{w}\right)\parallel }_{\mathcal{W}}& \le {\mathfrak{R}}_{\sigma }\frac{2{\phi }_1^{*}+{\phi }_2^{*}\mathsf{r}}{2(1-{\phi }_3^{*})}.\hfill \end{array}$$

(21)

Therefore, Equations (20) and (21) imply that $\mathfrak{U}$ is uniformly bounded.

To prove that $\mathfrak{U}$ is equicontinuous, let $0\le {\chi }_2\le {\chi }_1\le \chi$. Then, we have

$$\begin{array}{cc}\hfill |{(log{\chi }_1)}^{3-\kappa }& {\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left({\chi }_1\right)-{(log{\chi }_2)}^{3-\kappa }{\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left({\chi }_2\right)|\hfill \\ \hfill \le & |\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{{\chi }_1}\left[{(log{\chi }_1)}^{3-\kappa }{(log\frac{{\chi }_1}{\mathtt{s}})}^{\kappa -1}-{(log{\chi }_2)}^{3-\kappa }{(log\frac{{\chi }_2}{\mathtt{s}})}^{\kappa -1}\right]\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_{{\chi }_1}^{{\chi }_2}{(log{\chi }_2)}^{3-\kappa }{(log\frac{{\chi }_2}{\mathtt{s}})}^{\kappa -1}\mathsf{u}\left(\mathtt{s}\right)\frac{\mathtt{ds}}{\mathtt{s}}|\hfill \\ \hfill & +|\frac{{\mathsf{a}}_0{\delta }_{11}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{21}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta }|{\int }_1^{\mathrm{T}}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{b}}_0{\delta }_{12}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{22}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta }|{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{c}}_0{\delta }_{13}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{23}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{2\delta }|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_1{\delta }_{11}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{21}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta \mathrm{\Gamma }(2\kappa -1)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_2{\delta }_{12}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta \mathrm{\Gamma }(2\kappa -2)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_3{\delta }_{13}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{23}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta \mathrm{\Gamma }(2\kappa -3)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}\left|\mathsf{u}\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}.\hfill \end{array}$$

Therefore, we obtain

$$\begin{array}{cc}\hfill |{(log{\chi }_1)}^{3-\kappa }& {\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left({\chi }_1\right)-{(log{\chi }_2)}^{3-\kappa }{\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left({\chi }_2\right)|\hfill \\ \hfill \le & \left[\right|\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{{\chi }_1}\left[{(log{\chi }_1)}^{3-\kappa }{(log\frac{{\chi }_1}{\mathtt{s}})}^{\kappa -1}-{(log{\chi }_2)}^{3-\kappa }{(log\frac{{\chi }_2}{\mathtt{s}})}^{\kappa -1}\right]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_{{\chi }_1}^{{\chi }_2}{(log{\chi }_2)}^{3-\kappa }{(log\frac{{\chi }_2}{\mathtt{s}})}^{\kappa -1}\frac{\mathtt{ds}}{\mathtt{s}}|+|\frac{{\mathsf{a}}_0{\delta }_{11}log\mathrm{T}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta }|\hfill \\ \hfill & +\left|\frac{{\mathsf{a}}_0{\delta }_{21}log\mathrm{T}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta }\right|+\left|\frac{{\mathsf{b}}_0{\delta }_{12}{(log\mathrm{T})}^2[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{2\delta }\right|\hfill \\ \hfill & +\left|\frac{{\mathsf{b}}_0{\delta }_{22}{(log\mathrm{T})}^2[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{2\delta }\right|+\left|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\mathrm{T})}^3[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{6\delta }\right|\hfill \\ \hfill & +\left|\frac{{\mathsf{c}}_0{\delta }_{23}{(log\mathrm{T})}^3[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{6\delta }\right|+\left|\frac{{\eta }_1{\delta }_{11}{(log\mathrm{T})}^{2\kappa -1}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_1{\delta }_{21}{(log\mathrm{T})}^{2\kappa -1}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{{\eta }_2{\delta }_{12}{(log\mathrm{T})}^{2\kappa -2}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta \mathrm{\Gamma }(2\kappa -1)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_2{\delta }_{22}{(log\mathrm{T})}^{2\kappa -2}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta \mathrm{\Gamma }(2\kappa -1)}\right|+\left|\frac{{\eta }_3{\delta }_{13}{(log\mathrm{T})}^{2\kappa -3}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{\delta \mathrm{\Gamma }(2\kappa -2)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_3{\delta }_{23}{(log\mathrm{T})}^{2\kappa -3}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{\delta \mathrm{\Gamma }(2\kappa -2)}\right|]\frac{{\varphi }_1^{*}+{\varphi }_2^{*}\left|\mathsf{w}\right|}{1-{\varphi }_3^{*}}⟶0\mathrm{as}{\chi }_1⟶{\chi }_2.\hfill \end{array}$$

Similarly, we have

$$\begin{array}{cc}\hfill |{(log{\chi }_1)}^{3-\sigma }& {\mathfrak{U}}_{\sigma }\left(\mathsf{w}\right)\left({\chi }_1\right)-{(log{\chi }_2)}^{3-\sigma }{\mathfrak{U}}_{\sigma }\left(\mathsf{w}\right)\left({\chi }_2\right)|\hfill \\ \hfill \le & \left[\right|\frac{1}{\mathrm{\Gamma }\left(\sigma \right)}{\int }_1^{{\chi }_1}\left[{(log{\chi }_1)}^{3-\sigma }{(log\frac{{\chi }_1}{\mathtt{s}})}^{\sigma -1}-{(log{\chi }_2)}^{3-\sigma }{(log\frac{{\chi }_2}{\mathtt{s}})}^{\sigma -1}\right]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\frac{1}{\mathrm{\Gamma }\left(\sigma \right)}{\int }_{{\chi }_1}^{{\chi }_2}{(log{\chi }_2)}^{3-\sigma }{(log\frac{{\chi }_2}{\mathtt{s}})}^{\sigma -1}\frac{\mathtt{ds}}{\mathtt{s}}|+|\frac{{\mathsf{a}}_1{\delta }_{11}^{*}log\mathrm{T}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{{\delta }^{*}}|\hfill \\ \hfill & +\left|\frac{{\mathsf{a}}_1{\delta }_{21}^{*}log\mathrm{T}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{{\delta }^{*}}\right|+\left|\frac{{\mathsf{b}}_1{\delta }_{12}^{*}{(log\mathrm{T})}^2[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{2{\delta }^{*}}\right|\hfill \\ \hfill & +\left|\frac{{\mathsf{b}}_1{\delta }_{22}^{*}{(log\mathrm{T})}^2[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{2{\delta }^{*}}\right|+\left|\frac{{\mathsf{c}}_1{\delta }_{13}^{*}{(log\mathrm{T})}^3[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{6{\delta }^{*}}\right|\hfill \\ \hfill & +\left|\frac{{\mathsf{c}}_1{\delta }_{23}^{*}{(log\mathrm{T})}^3[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{6{\delta }^{*}}\right|+\left|\frac{{\eta }_4{\delta }_{11}^{*}{(log\mathrm{T})}^{2\sigma -1}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{{\delta }^{*}\mathrm{\Gamma }\left(2\sigma \right)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_4{\delta }_{21}^{*}{(log\mathrm{T})}^{2\sigma -1}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{{\delta }^{*}\mathrm{\Gamma }\left(2\sigma \right)}\right|+\left|\frac{{\eta }_5{\delta }_{12}^{*}{(log\mathrm{T})}^{2\sigma -2}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_5{\delta }_{22}^{*}{(log\mathrm{T})}^{2\sigma -2}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}\right|+\left|\frac{{\eta }_6{\delta }_{13}^{*}{(log\mathrm{T})}^{2\sigma -3}[{(log{\chi }_1)}^2-{(log{\chi }_2)}^2]}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_6{\delta }_{23}^{*}{(log\mathrm{T})}^{2\sigma -3}[log\left({\chi }_1\right)-log\left({\chi }_2\right)]}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}\right|]\frac{{\phi }_1^{*}+{\phi }_2^{*}\left|\mathsf{v}\right|}{1-{\phi }_3^{*}}⟶0\mathrm{as}{\chi }_1⟶{\chi }_2.\hfill \end{array}$$

Thus, $\mathfrak{U}(\mathsf{v},\mathsf{w})$ is equicontinuous, and consequently, $\mathfrak{U}(\mathsf{v},\mathsf{w})$ is completely continuous.

Now, we prove that $\mathcal{B}=\left\{(\mathsf{v},\mathsf{w})\in \mathcal{W}\times \mathcal{W}\left|\right(\mathsf{v},\mathsf{w})=\lambda \mathfrak{U}(\mathsf{v},\mathsf{w}),\lambda \in [0,1]\right\}$ is bounded. Let $(\mathsf{v},\mathsf{w})\in \mathcal{B}$. Then, $(\mathsf{v},\mathsf{w})=\lambda \mathfrak{U}(\mathsf{v},\mathsf{w}).$ For $\chi \in \mathcal{M},$ we have

$$\mathsf{v}\left(\chi \right)=\lambda {\mathfrak{U}}_{\kappa }\left(\mathsf{v}\right)\left(\chi \right),\mathsf{w}\left(\chi \right)=\lambda {\mathfrak{U}}_{\sigma }\left(\mathsf{w}\right)\left(\chi \right).$$

Then, we have

$$\begin{array}{cc}\hfill {(log\chi )}^{3-\kappa }\left|\mathsf{v}\left(\chi \right)\right|\le & \left[\right|\frac{{\mathsf{a}}_0{\delta }_{31}log\mathrm{T}}{\delta }|+|\frac{(2{\mathsf{a}}_0{\delta }_{21}+{\mathsf{b}}_0{\delta }_{32}){(log\mathrm{T})}^2}{2\delta }|+\frac{{(log\mathrm{T})}^3}{\mathrm{\Gamma }\left(\kappa \right)}\hfill \\ \hfill & +\left|\frac{(6{\mathsf{a}}_0{\delta }_{11}+3{\mathsf{b}}_0{\delta }_{22}+{\mathsf{c}}_0{\delta }_{33}){(log\mathrm{T})}^3}{6\delta }\right|+\left|\frac{(3{\mathsf{b}}_0{\delta }_{12}+{\mathsf{c}}_0{\delta }_{23}){(log\mathrm{T})}^4}{6\delta }\right|+\left|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\mathrm{T})}^5}{6\delta }\right|\hfill \\ \hfill & +\left|\frac{{\eta }_1{\delta }_{11}{(log\mathrm{T})}^{2\kappa +1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{({\eta }_1{\delta }_{31}+(2\kappa -1){\eta }_2{\delta }_{22}+(2\kappa -1)(2\kappa -2){\eta }_3{\delta }_{13}){(log\mathrm{T})}^{2\kappa -1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_3{\delta }_{33}{(log\mathrm{T})}^{2\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right|+\left|\frac{({\eta }_1{\delta }_{21}+(2\kappa -1){\eta }_2{\delta }_{12}){(log\mathrm{T})}^{2\kappa }}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_2{\delta }_{32}+(2\kappa -2){\eta }_3{\delta }_{23}){(log\mathrm{T})}^{2\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right|]\frac{{\varphi }_1\left(\chi \right)+{\varphi }_2\left(\chi \right)\left|\mathsf{w}\left(\chi \right)\right|}{1-{\varphi }_3\left(\chi \right)},\hfill \end{array}$$

which implies that

$$\begin{array}{c}\hfill {\parallel \mathsf{v}\parallel }_{\mathcal{W}}\le {\mathfrak{R}}_{\kappa }\frac{{\varphi }_1^{*}+{\varphi }_2^{*}{\parallel \mathsf{w}\parallel }_{\mathcal{W}}}{1-{\varphi }_3^{*}}\end{array}$$

(22)

In addition, we have

$$\begin{array}{cc}\hfill {(log\chi )}^{3-\sigma }\left|\mathsf{w}\left(\chi \right)\right|\le & \left[\right|\frac{{\mathsf{a}}_1{\delta }_{31}^{*}log\mathrm{T}}{{\delta }^{*}}|+|\frac{(2{\mathsf{a}}_1{\delta }_{21}^{*}+{\mathsf{b}}_1{\delta }_{32}^{*}){(log\mathrm{T})}^2}{2{\delta }^{*}}|+\frac{{(log\mathrm{T})}^3}{\mathrm{\Gamma }\left(\sigma \right)}\hfill \\ \hfill & +\left|\frac{(6{\mathsf{a}}_1{\delta }_{11}^{*}+3{\mathsf{b}}_1{\delta }_{22}^{*}+{\mathsf{c}}_1{\delta }_{33}^{*}){(log\mathrm{T})}^3}{6{\delta }^{*}}\right|+\left|\frac{(3{\mathsf{b}}_1{\delta }_{12}^{*}+{\mathsf{c}}_1{\delta }_{23}^{*}){(log\mathrm{T})}^4}{6{\delta }^{*}}\right|+\left|\frac{{\mathsf{c}}_1{\delta }_{13}^{*}{(log\mathrm{T})}^5}{6{\delta }^{*}}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_4{\delta }_{11}^{*}{(log\mathrm{T})}^{2\sigma +1}}{{\delta }^{*}\mathrm{\Gamma }\left(2\sigma \right)}\right|+\left|\frac{({\eta }_4{\delta }_{31}^{*}+(2\sigma -1){\eta }_5{\delta }_{22}^{*}+(2\sigma -1)(2\sigma -2){\eta }_6{\delta }_{13}^{*}){(log\mathrm{T})}^{2\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }\left(2\sigma \right)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_6{\delta }_{33}^{*}{(log\mathrm{T})}^{2\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}\right|+\left|\frac{({\eta }_4{\delta }_{21}^{*}+(2\sigma -1){\eta }_5{\delta }_{12}^{*}){(log\mathrm{T})}^{2\sigma }}{{\delta }^{*}\mathrm{\Gamma }\left(2\sigma \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_5{\delta }_{32}^{*}+(2\sigma -2){\eta }_6{\delta }_{23}^{*}){(log\mathrm{T})}^{2\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}\right|]\frac{{\phi }_1\left(\chi \right)+{\phi }_2\left(\chi \right)\left|\mathsf{v}\left(\chi \right)\right|}{1-{\phi }_3\left(\chi \right)},\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill {\parallel \mathsf{w}\parallel }_{\mathcal{W}}\le & {\mathfrak{R}}_{\sigma }\frac{{\phi }_1^{*}+{\phi }_2^{*}{\parallel \mathsf{v}\parallel }_{\mathcal{W}}}{1-{\phi }_3^{*}}.\hfill \end{array}$$

(23)

Equations (22) and (23) imply that

$$\begin{array}{cc}\hfill {\parallel \mathsf{v}\parallel }_{\mathcal{W}}+{\parallel \mathsf{w}\parallel }_{\mathcal{W}}& =\frac{{\mathfrak{R}}_{\kappa }{\varphi }_1^{*}}{1-{\varphi }_3^{*}}+\frac{{\mathfrak{R}}_{\sigma }{\phi }_1^{*}}{1-{\phi }_3^{*}}+\frac{{\mathfrak{R}}_{\sigma }{\phi }_2^{*}{\parallel \mathsf{v}\parallel }_{\mathcal{W}}}{1-{\phi }_3^{*}}+\frac{{\mathfrak{R}}_{\kappa }{\varphi }_2^{*}{\parallel \mathsf{w}\parallel }_{\mathcal{W}}}{1-{\varphi }_3^{*}}.\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}\hfill {\parallel (\mathsf{v},\mathsf{w})\parallel }_{\mathcal{W}\times \mathcal{W}}& \le \frac{{\mathfrak{R}}_{\kappa }{\varphi }_1^{*}+{\mathfrak{R}}_{\sigma }{\phi }_1^{*}}{(1-{\varphi }_3^{*})(1-{\phi }_3^{*})(1-{\mathfrak{R}}_0)},\hfill \end{array}$$

for any $\chi \in \mathcal{M}$, where ${\mathfrak{R}}_0$ is presented in Equation (17), and thus $\mathcal{B}$ is bounded. Consequently, Equation (1) has at least one solution. □

4. Stability

Let us introduce the definitions of the Ulam stabilities for Equation (1).

Let ${\Theta }_{\mu },{\Theta }_{\nu }:\mathcal{M}\to {\mathcal{R}}^{+}$ be nondecreasing functions and ${ϵ}_{\mu },{ϵ}_{\nu }>0$. Additionally, let

$$\left\{\begin{array}{cc}\hfill & |{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)-\mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))|\le {ϵ}_{\mu },\chi \in \mathcal{M},\hfill \\ & |{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)-\nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))|\le {ϵ}_{\nu },\chi \in \mathcal{M},\hfill \end{array}\right.$$

(24)

$$\left\{\begin{array}{cc}\hfill & |{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)-\mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))|\le {\Theta }_{\mu }\left(\chi \right){ϵ}_{\mu },\chi \in \mathcal{M},\hfill \\ & |{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)-\nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))|\le {\Theta }_{\nu }\left(\chi \right){ϵ}_{\nu },\chi \in \mathcal{M},\hfill \end{array}\right.$$

(25)

$$\left\{\begin{array}{cc}\hfill & |{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)-\mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))|\le {\Theta }_{\mu }\left(\chi \right),\chi \in \mathcal{M},\hfill \\ & |{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)-\nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))|\le {\Theta }_{\nu }\left(\chi \right),\chi \in \mathcal{M}.\hfill \end{array}\right.$$

(26)

Definition 3

([37]). Equation (1) has $\mathcal{HUS}$ if ∃ ${\mathbf{C}}_{\mu ,\nu }=({\mathbf{C}}_{\mu },{\mathbf{C}}_{\nu })>0$ such that for some $ϵ=({ϵ}_{\mu },{ϵ}_{\nu })>0$ and for any $(\mathsf{v},\mathsf{w})\in \mathcal{W}\times \mathcal{W}$ satisfying Equation (24), ∃ a solution $(\omega ,\upsilon )\in \mathcal{W}\times \mathcal{W}$ to Equation (1) with

$$|(\mathsf{v},\mathsf{w})\left(\chi \right)-(\omega ,\upsilon )\left(\chi \right)|\le {\mathbf{C}}_{\mu ,\nu }ϵ,\chi \in \mathcal{M}.$$

(27)

Definition 4

([37]). Equation (1) has generalized $\mathcal{HUS}$ if ∃ ${\Phi }_{\mu ,\nu }\in \mathcal{N}({\mathcal{R}}^{+},{\mathcal{R}}^{+})$ with ${\Phi }_{\mu ,\nu }\left(0\right)=0$ such that for any $(\mathsf{v},\mathsf{w})\in \mathcal{W}\times \mathcal{W}$ satisfying Equation (24), ∃ a solution $(\omega ,\upsilon )\in \mathcal{W}\times \mathcal{W}$ to Equation (1) satisfying

$$|(\mathsf{v},\mathsf{w})\left(\chi \right)-(\omega ,\upsilon )\left(\chi \right)|\le {\Phi }_{\mu ,\nu }\left(ϵ\right),\chi \in \mathcal{M}.$$

(28)

Definition 5

([37]). Equation (1) has $\mathcal{HURS}$ corresponding to ${\Theta }_{\mu ,\nu }=({\Theta }_{\mu },{\Theta }_{\nu })\in \mathcal{N}(\mathcal{M},\mathcal{R})$ if ∃ constants ${\mathbf{C}}_{{\Theta }_{\mu },{\Theta }_{\nu }}=({\mathbf{C}}_{{\Theta }_{\mu }},{\mathbf{C}}_{{\Theta }_{\nu }})>0$ such that for some $ϵ=({ϵ}_{\mu },{ϵ}_{\nu })>0$ and for any $(\mathsf{v},\mathsf{w})\in \mathcal{W}\times \mathcal{W}$ satisfying Equation (25), ∃ a solution $(\omega ,\upsilon )\in \mathcal{W}\times \mathcal{W}$ with

$$|(\mathsf{v},\mathsf{w})\left(\chi \right)-(\omega ,\upsilon )\left(\chi \right)|\le {\mathbf{C}}_{{\Theta }_{\mu },{\Theta }_{\nu }}{\Theta }_{\mu ,\nu }\left(\chi \right)ϵ,\chi \in \mathcal{M}.$$

(29)

Definition 6

([37]). Equation (1) has generalized $\mathcal{HURS}$ with respect to ${\Theta }_{\mu ,\nu }=({\Theta }_{\mu },{\Theta }_{\nu })\in \mathcal{N}(\mathcal{M},\mathcal{R})$ if ∃ a constant ${\mathbf{C}}_{{\Theta }_{\mu },{\Theta }_{\nu }}=({\mathbf{C}}_{{\Theta }_{\mu }},{\mathbf{C}}_{{\Theta }_{\nu }})>0$ such that for any $(\mathsf{v},\mathsf{w})\in \mathcal{W}\times \mathcal{W}$ satisfying Equation (26), ∃ a solution $(\omega ,\upsilon )\in \mathcal{W}\times \mathcal{W}$ to Equation (1) satisfying

$$|(\mathsf{v},\mathsf{w})\left(\chi \right)-(\omega ,\upsilon )\left(\chi \right)|\le {\mathbf{C}}_{{\Theta }_{\mu },{\Theta }_{\nu }}{\Theta }_{\mu ,\nu }\left(\chi \right),\chi \in \mathcal{M}.$$

(30)

Remark 3.

Note that $(\mathsf{v},\mathsf{w})\in \mathcal{W}\times \mathcal{W}$ is a solution to Equation (24) if ∃ ${\Psi }_{\mu },{\Psi }_{\nu }\in \mathcal{N}(\mathcal{M},\mathcal{R})$, which depend on $\mathsf{v}$ and $\mathsf{w}$ respectively, in such a way that the following are true:

(A1)

$\left|{\Psi }_{\mu }\left(\chi \right)\right|\le {ϵ}_{\mu },\left|{\Psi }_{\nu }\left(\chi \right)\right|\le {ϵ}_{\nu },\chi \in \mathcal{M}$;

(A2)

$$\left\{\begin{array}{cc}& {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)=\mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))+{\Psi }_{\mu }\left(\chi \right),\chi \in \mathcal{M},\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)=\nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))+{\Psi }_{\nu }\left(\chi \right),\chi \in \mathcal{M}.\hfill \end{array}\right.$$

Lemma 4.

Let $(\mathsf{v},\mathsf{w})\in \mathcal{W}\times \mathcal{W}$ be a solution to Equation (24). Then, we have

$$\left\{\begin{array}{cc}& \parallel \mathsf{v}-{\mathrm{m}}_1{\parallel }_{\mathcal{W}}\le {\mathfrak{R}}_{\kappa }{ϵ}_{\mu },\chi \in \mathcal{M},\hfill \\ & \parallel \mathsf{w}-{\mathrm{m}}_2{\parallel }_{\mathcal{W}}\le {\mathfrak{R}}_{\sigma }{ϵ}_{\nu },\chi \in \mathcal{M}.\hfill \end{array}\right.$$

Proof. 

By applying $\left({\mathrm{A}}_2\right)$ of Remark 3 and letting $\chi \in \mathcal{M}$, then we obtain

$$\left\{\begin{array}{cc}\hfill & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)-\mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))={\Psi }_{\mu }\left(\chi \right);\chi \in \mathcal{M},\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)-\nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))={\Psi }_{\nu }\left(\chi \right);\chi \in \mathcal{M},\hfill \end{array}\right.$$

(31)

with the generalized integro-differential BCs in Equation (2). Thus, utilizing Lemma 1, the solution to Equation (31) is

$$\left\{\begin{array}{cc}\hfill & \mathsf{v}\left(\chi \right)=\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}[\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))+{\Psi }_{\mu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^{\kappa -1}}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{21}{(log\chi )}^{\kappa -2}}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}{(log\chi )}^{\kappa -3}}{\delta }\right]{\int }_1^{\mathrm{T}}[\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))+{\Psi }_{\mu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^{\kappa -1}}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{22}{(log\chi )}^{\kappa -2}}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}{(log\chi )}^{\kappa -3}}{\delta }\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}[\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))+{\Psi }_{\mu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^{\kappa -1}}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{23}{(log\chi )}^{\kappa -2}}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}{(log\chi )}^{\kappa -3}}{2\delta }\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2[\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))+{\Psi }_{\mu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_1{\delta }_{11}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{21}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{31}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}[\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))+{\Psi }_{\mu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_2{\delta }_{12}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{32}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}[\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))+{\Psi }_{\mu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_3{\delta }_{13}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{23}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}[\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))+{\Psi }_{\mu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}},\hfill \\ \hfill & \mathsf{w}\left(\chi \right)=\frac{1}{\mathrm{\Gamma }\left(\sigma \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\sigma -1}[\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))+{\Psi }_{\nu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{a}}_1{\delta }_{11}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}}+\frac{{\mathsf{a}}_1{\delta }_{21}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}}+\frac{{\mathsf{a}}_1{\delta }_{31}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}[\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))+{\Psi }_{\nu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{b}}_1{\delta }_{12}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}}+\frac{{\mathsf{b}}_1{\delta }_{22}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}}+\frac{{\mathsf{b}}_1{\delta }_{32}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}[\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))+{\Psi }_{\nu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{c}}_1{\delta }_{13}^{*}{(log\chi )}^{\sigma -1}}{2{\delta }^{*}}+\frac{{\mathsf{c}}_1{\delta }_{23}^{*}{(log\chi )}^{\sigma -2}}{2{\delta }^{*}}+\frac{{\mathsf{c}}_1{\delta }_{33}^{*}{(log\chi )}^{\sigma -3}}{2{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2[\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))+{\Psi }_{\nu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_4{\delta }_{11}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}+\frac{{\eta }_4{\delta }_{21}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}+\frac{{\eta }_4{\delta }_{31}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -2}[\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))+{\Psi }_{\nu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_5{\delta }_{12}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}+\frac{{\eta }_5{\delta }_{22}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}+\frac{{\eta }_5{\delta }_{32}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -3}[\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))+{\Psi }_{\nu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_6{\delta }_{13}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}+\frac{{\eta }_6{\delta }_{23}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}+\frac{{\eta }_6{\delta }_{33}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -4}[\nu (\mathtt{s},\mathsf{v}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\mathtt{s}\right))+{\Psi }_{\nu }\left(\mathtt{s}\right)]\frac{\mathtt{ds}}{\mathtt{s}}.\hfill \end{array}\right.$$

(32)

By using the first part of Equation (32), we have

$$\begin{array}{cc}\hfill {(log\chi )}^{3-\kappa }|\mathsf{v}\left(\chi \right)-{\mathrm{m}}_1\left(\chi \right)|\le & \frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}\left|{\Psi }_{\mu }\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^2}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{21}log\chi }{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}}{\delta }|{\int }_1^{\mathrm{T}}\left|{\Psi }_{\mu }\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^2}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{22}log\left(\chi \right)}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}}{\delta }|{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\left|{\Psi }_{\mu }\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^2}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{23}log\chi }{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}}{2\delta }|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\left|{\Psi }_{\mu }\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_1{\delta }_{11}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{21}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{31}}{\delta \mathrm{\Gamma }(2\kappa -1)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}\left|{\Psi }_{\mu }\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_2{\delta }_{12}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}log\chi }{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{32}}{\delta \mathrm{\Gamma }(2\kappa -2)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}\left|{\Psi }_{\mu }\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_3{\delta }_{13}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{23}log\chi }{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}}{\delta \mathrm{\Gamma }(2\kappa -3)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}\left|{\Psi }_{\mu }\left(\mathtt{s}\right)\right|\frac{\mathtt{ds}}{\mathtt{s}},\hfill \end{array}$$

(33)

where $m_1\left(\chi \right)$ are those terms which are free of ${\Psi }_{\mathfrak{U}}.$ By using Equation (8) and $\left({\mathrm{A}}_1\right)$ of Remark 3, Equation (33) becomes

$$\begin{array}{cc}\hfill \parallel \mathsf{v}-{\mathrm{m}}_1{\parallel }_{\mathcal{W}}& \le {\mathfrak{R}}_{\kappa }{ϵ}_{\mu }.\hfill \end{array}$$

By following similar steps for Equation (32), we have

$$\begin{array}{cc}\hfill \parallel \mathsf{w}-{\mathrm{m}}_2{\parallel }_{\mathcal{W}}& \le {\mathfrak{R}}_{\sigma }{ϵ}_{\nu }.\hfill \end{array}$$

□

4.1. First Method

Theorem 4.

Let $\left[{\mathsf{H}}_1\right]$ hold, and

$$\begin{array}{c}\hfill \Lambda =1-\frac{{\mathfrak{R}}_{\kappa }{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\mathfrak{U}}{\mathcal{L}}_{\mathsf{g}}}{(1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mathfrak{U}})(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\mathsf{g}})}>0.\end{array}$$

(34)

Then, Equation (1) has $\mathcal{HUS}$.

Proof. 

Let $(\mathsf{v},\mathsf{w})\in \mathcal{W}\times \mathcal{W}$ satisfy Equation (24) and $(\omega ,\upsilon )\in \mathcal{W}\times \mathcal{W}$ satisfy

$$\left\{\begin{array}{cc}\hfill & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\chi \right)-\mathfrak{U}(\chi ,\upsilon \left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\chi \right))=0,\chi \in \mathcal{M},\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\chi \right)-\mathsf{g}(\chi ,\omega \left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\chi \right))=0,\chi \in \mathcal{M},\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\omega \left(1\right)={\mathsf{a}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\omega \left(\mathrm{T}\right)+{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -1}\omega \left(\mathrm{T}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\omega \left(1\right)={\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\omega \left(\mathrm{T}\right)+{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -2}\omega \left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -3}\omega \left(1\right)={\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -3}\omega \left(\mathrm{T}\right)+{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -3}\omega \left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\upsilon \left(1\right)={\mathsf{a}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\upsilon \left(\mathrm{T}\right)+{\eta }_4{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -1}\upsilon \left(\mathrm{T}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\upsilon \left(1\right)={\mathsf{b}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\upsilon \left(\mathrm{T}\right)+{\eta }_5{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -2}\upsilon \left(\mathrm{T}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -3}\upsilon \left(1\right)={\mathsf{c}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -3}\upsilon \left(\mathrm{T}\right)+{\eta }_6{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -3}\upsilon \left(\mathrm{T}\right).\hfill \end{array}\right.$$

(35)

Now, by using Lemma 1, for $\chi \in \mathcal{M}$, we find that Equation (35) has the following solution:

$$\left\{\begin{array}{cc}\hfill & \omega \left(\chi \right)=\frac{1}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^{\kappa -1}}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{21}{(log\chi )}^{\kappa -2}}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}{(log\chi )}^{\kappa -3}}{\delta }\right]{\int }_1^{\mathrm{T}}\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^{\kappa -1}}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{22}{(log\chi )}^{\kappa -2}}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}{(log\chi )}^{\kappa -3}}{\delta }\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^{\kappa -1}}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{23}{(log\chi )}^{\kappa -2}}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}{(log\chi )}^{\kappa -3}}{2\delta }\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_1{\delta }_{11}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{21}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{31}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_2{\delta }_{12}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{32}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_3{\delta }_{13}{(log\chi )}^{\kappa -1}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{23}{(log\chi )}^{\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}{(log\chi )}^{\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}},\hfill \\ \hfill & \upsilon \left(\chi \right)=\frac{1}{\mathrm{\Gamma }\left(\sigma \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\sigma -1}\nu (\mathtt{s},\omega \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{a}}_1{\delta }_{11}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}}+\frac{{\mathsf{a}}_1{\delta }_{21}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}}+\frac{{\mathsf{a}}_1{\delta }_{31}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}\nu (\mathtt{s},\omega \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{b}}_1{\delta }_{12}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}}+\frac{{\mathsf{b}}_1{\delta }_{22}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}}+\frac{{\mathsf{b}}_1{\delta }_{32}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}\nu (\mathtt{s},\omega \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\mathsf{c}}_1{\delta }_{13}^{*}{(log\chi )}^{\sigma -1}}{2{\delta }^{*}}+\frac{{\mathsf{c}}_1{\delta }_{23}^{*}{(log\chi )}^{\sigma -2}}{2{\delta }^{*}}+\frac{{\mathsf{c}}_1{\delta }_{33}^{*}{(log\chi )}^{\sigma -3}}{2{\delta }^{*}}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2\nu (\mathtt{s},\omega \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_4{\delta }_{11}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}+\frac{{\eta }_4{\delta }_{21}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}+\frac{{\eta }_4{\delta }_{31}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -1)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -2}\nu (\mathtt{s},\omega \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_5{\delta }_{12}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}+\frac{{\eta }_5{\delta }_{22}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}+\frac{{\eta }_5{\delta }_{32}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -2)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -3}\nu (\mathtt{s},\omega \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & -\left[\frac{{\eta }_6{\delta }_{13}^{*}{(log\chi )}^{\sigma -1}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}+\frac{{\eta }_6{\delta }_{23}^{*}{(log\chi )}^{\sigma -2}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}+\frac{{\eta }_6{\delta }_{33}^{*}{(log\chi )}^{\sigma -3}}{{\delta }^{*}\mathrm{\Gamma }(2\sigma -3)}\right]{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\sigma -4}\nu (\mathtt{s},\omega \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\upsilon \left(\mathtt{s}\right))\frac{\mathtt{ds}}{\mathtt{s}}.\hfill \end{array}\right.$$

(36)

Consider

$$\begin{array}{cc}\hfill {(log\chi )}^{3-\kappa }|\mathsf{v}\left(\chi \right)-\omega \left(\chi \right)|& \le {(log\chi )}^{3-\kappa }|\mathsf{v}\left(\chi \right)-{\mathrm{m}}_1\left(\chi \right)|+{(log\chi )}^{3-\kappa }|{\mathrm{m}}_1\left(\chi \right)-\omega \left(\chi \right)|.\hfill \end{array}$$

(37)

By applying Lemma 4 in Equation (37), we have

$$\begin{array}{cc}\hfill (log& {\chi )}^{3-\kappa }|\mathsf{v}\left(\chi \right)-\omega \left(\chi \right)|\hfill \\ \hfill \le & {\mathfrak{R}}_{\kappa }{ϵ}_{\mu }+\frac{{(log\chi )}^{3-\kappa }}{\mathrm{\Gamma }\left(\kappa \right)}{\int }_1^{\chi }{(log\frac{\chi }{\mathtt{s}})}^{\kappa -1}|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))-\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\mathsf{a}}_0{\delta }_{11}{(log\chi )}^2}{\delta }\hfill \\ \hfill & +\frac{{\mathsf{a}}_0{\delta }_{21}log\left(\chi \right)}{\delta }+\frac{{\mathsf{a}}_0{\delta }_{31}}{\delta }|{\int }_1^{\mathrm{T}}|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))-\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\mathsf{b}}_0{\delta }_{12}{(log\chi )}^2}{\delta }\hfill \\ \hfill & +\frac{{\mathsf{b}}_0{\delta }_{22}log\left(\chi \right)}{\delta }+\frac{{\mathsf{b}}_0{\delta }_{32}}{\delta }|{\int }_1^{\mathrm{T}}log\frac{\mathrm{T}}{\mathtt{s}}|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))-\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\chi )}^2}{2\delta }\hfill \\ \hfill & +\frac{{\mathsf{c}}_0{\delta }_{23}log\left(\chi \right)}{2\delta }+\frac{{\mathsf{c}}_0{\delta }_{33}}{2\delta }|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^2|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))-\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\eta }_1{\delta }_{31}}{\delta \mathrm{\Gamma }(2\kappa -1)}\hfill \\ \hfill & +\frac{{\eta }_1{\delta }_{21}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -1)}+\frac{{\eta }_1{\delta }_{11}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -1)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -2}|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))-\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill & +|\frac{{\eta }_2{\delta }_{12}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{22}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -2)}+\frac{{\eta }_2{\delta }_{32}}{\delta \mathrm{\Gamma }(2\kappa -2)}|\hfill \\ \hfill & \times {\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -3}|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))-\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}+|\frac{{\eta }_3{\delta }_{13}{(log\chi )}^2}{\delta \mathrm{\Gamma }(2\kappa -3)}\hfill \\ \hfill & +\frac{{\eta }_3{\delta }_{23}log\left(\chi \right)}{\delta \mathrm{\Gamma }(2\kappa -3)}+\frac{{\eta }_3{\delta }_{33}}{\delta \mathrm{\Gamma }(2\kappa -3)}|{\int }_1^{\mathrm{T}}{(log\frac{\mathrm{T}}{\mathtt{s}})}^{2\kappa -4}|\mu (\mathtt{s},\mathsf{w}\left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\mathtt{s}\right))-\mu (\mathtt{s},\upsilon \left(\mathtt{s}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \left(\mathtt{s}\right))|\frac{\mathtt{ds}}{\mathtt{s}}\hfill \\ \hfill \le & {\mathfrak{R}}_{\kappa }{ϵ}_{\mu }+\left[\right|\frac{{\mathsf{a}}_0{\delta }_{31}log\left(\mathrm{T}\right)}{\delta }|+|\frac{(2{\mathsf{a}}_0{\delta }_{21}+{\mathsf{b}}_0{\delta }_{32}){(log\mathrm{T})}^2}{2\delta }|+|\frac{(6{\mathsf{a}}_0{\delta }_{11}+3{\mathsf{b}}_0{\delta }_{22}+{\mathsf{c}}_0{\delta }_{33}){(log\mathrm{T})}^3}{6\delta }|\hfill \\ \hfill & +\left|\frac{(3{\mathsf{b}}_0{\delta }_{12}+{\mathsf{c}}_0{\delta }_{23}){(log\mathrm{T})}^4}{6\delta }\right|+\left|\frac{{\mathsf{c}}_0{\delta }_{13}{(log\mathrm{T})}^5}{6\delta }\right|+\frac{{(log\mathrm{T})}^3}{\mathrm{\Gamma }\left(\kappa \right)}+\left|\frac{({\eta }_1{\delta }_{21}+(2\kappa -1){\eta }_2{\delta }_{12}){(log\mathrm{T})}^{2\kappa }}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|\hfill \\ \hfill & +\left|\frac{({\eta }_1{\delta }_{31}+(2\kappa -1){\eta }_2{\delta }_{22}+(2\kappa -1)(2\kappa -2){\eta }_3{\delta }_{13}){(log\mathrm{T})}^{2\kappa -1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{{\eta }_3{\delta }_{33}{(log\mathrm{T})}^{2\kappa -3}}{\delta \mathrm{\Gamma }(2\kappa -2)}\right|\hfill \\ \hfill & +\left|\frac{{\eta }_1{\delta }_{11}{(log\mathrm{T})}^{2\kappa +1}}{\delta \mathrm{\Gamma }\left(2\kappa \right)}\right|+\left|\frac{({\eta }_2{\delta }_{32}+(2\kappa -2){\eta }_3{\delta }_{23}){(log\mathrm{T})}^{2\kappa -2}}{\delta \mathrm{\Gamma }(2\kappa -1)}\right|]\left({\mathcal{L}}_{\mu }{\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}+{\overline{\mathcal{L}}}_{\mu }{\parallel {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}-{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\omega \parallel }_{\mathcal{W}}\right).\hfill \end{array}$$

(38)

By utilizing $\left[{\mathsf{H}}_1\right]$ of Theorem 1 and Equation (8) in Equation (38), we obtain

$${\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}\le \frac{{\mathfrak{R}}_{\kappa }{ϵ}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }}+\frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }}{\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}.$$

(39)

Equivalently, we have

$${\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}\le \frac{{\mathfrak{R}}_{\sigma }{ϵ}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}+\frac{{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}{\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}.$$

(40)

Equations (39) and (40) can be written as

$$\begin{array}{cc}& {\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}-\frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mathfrak{U}}}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mathfrak{U}}}{\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}\le \frac{{\mathfrak{R}}_{\kappa }{ϵ}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }},\hfill \\ & {\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}-\frac{{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}{\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}\le \frac{{\mathfrak{R}}_{\sigma }{ϵ}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }},\hfill \\ \\ & \Rightarrow \left[\begin{array}{cc}1& -\frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }}\\ \\ -\frac{{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}& 1\end{array}\right]\left[\begin{array}{c}{\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}\\ \\ {\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}\end{array}\right]\le \left[\begin{array}{c}\frac{{\mathfrak{R}}_{\kappa }{ϵ}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }}\\ \\ \frac{{\mathfrak{R}}_{\sigma }{ϵ}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}\end{array}\right].\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}& \left[\begin{array}{c}{\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}\\ \\ {\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}\end{array}\right]\le \left[\begin{array}{cc}\frac{1}{\Lambda }& \frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })}\\ \\ \frac{{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}{\Lambda (1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}& \frac{1}{\Lambda }\end{array}\right]\left[\begin{array}{c}\frac{{\mathfrak{R}}_{\kappa }{ϵ}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }}\\ \\ \frac{{\mathfrak{R}}_{\sigma }{ϵ}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}\end{array}\right],\hfill \end{array}$$

where

$$\Lambda =1-\frac{{\mathfrak{R}}_{\kappa }{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\mu }{\mathcal{L}}_{\nu }}{(1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}>0.$$

Consequently, we have

$$\begin{array}{cc}\hfill {\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}& \le \frac{{\mathfrak{R}}_{\kappa }{ϵ}_{\mu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })}+\frac{{\mathfrak{R}}_{\kappa }{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\mu }{ϵ}_{\nu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })},\hfill \\ \hfill {\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}& \le \frac{{\mathfrak{R}}_{\sigma }{ϵ}_{\nu }}{\Lambda (1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}+\frac{{\mathfrak{R}}_{\kappa }{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }{ϵ}_{\mu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })},\hfill \end{array}$$

from which we have

$$\begin{array}{cc}\hfill {\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}+{\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}\le & \frac{{\mathfrak{R}}_{\kappa }{ϵ}_{\mu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })}+\frac{{\mathfrak{R}}_{\sigma }{ϵ}_{\nu }}{\Lambda (1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}+\frac{{\mathfrak{R}}_{\kappa }{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\mu }{ϵ}_{\nu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}\hfill \\ \hfill & +\frac{{\mathfrak{R}}_{\kappa }{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }{ϵ}_{\mu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}.\hfill \end{array}$$

(41)

By letting $ϵ=max\left\{{ϵ}_{\mu },{ϵ}_{\nu }\right\},$ then from Equation (41), we have

$${\parallel (\mathsf{v},\mathsf{w})-(\omega ,\upsilon )\parallel }_{\mathcal{W}\times \mathcal{W}}\le {\mathbf{C}}_{\mu ,\nu }ϵ,$$

(42)

where

$${\mathbf{C}}_{\mu ,\nu }=\frac{{\mathfrak{R}}_{\kappa }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })}+\frac{{\mathfrak{R}}_{\sigma }}{\Lambda (1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}+\frac{{\mathfrak{R}}_{\kappa }{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\mu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}+\frac{{\mathfrak{R}}_{\kappa }{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}{\Lambda (1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}.$$

□

Remark 4.

By letting ${\Phi }_{\mu ,\nu }\left(ϵ\right)={\mathbf{C}}_{\mu ,\nu }ϵ,{\Phi }_{\mu ,\nu }\left(0\right)=0$ in (42), then by Definition 4, Equation (1) is generalized as $\mathcal{HU}$ stable.

• [$\left({\mathsf{H}}_3\right)$] Let functions ${\Theta }_{\mu },{\Theta }_{\nu }:\mathcal{M}\to {\mathcal{R}}^{+}$ be nondecreasing. Then, there are ${\mathrm{Y}}_{{\Theta }_{\mu }},{\mathrm{Y}}_{{\Theta }_{\nu }}>0$ such that for every $\chi \in \mathcal{M},$ the following inequalities hold:

  $${\mathfrak{I}}^{\kappa }{\Theta }_{\mu }\left(\chi \right)\le {\mathrm{Y}}_{{\Theta }_{\mu }}{\Theta }_{\mu }\left(\chi \right)\mathrm{and}{\mathfrak{I}}^{\sigma }{\Theta }_{\nu }\left(\chi \right)\le {\mathrm{Y}}_{{\Theta }_{\nu }}{\Theta }_{\nu }\left(\chi \right)$$

Remark 5.

Similarly, we obtained the $\mathcal{HURS}$ and $\mathcal{GHURS}$ for Equation (1) by utilizing Lemma 4, Theorem 5 and Definitions 5 and 6 with $\left[{\mathsf{H}}_3\right]$ and ${\Lambda }^{*}>0$.

4.2. Second Method

Theorem 5.

Let $\left[{\mathsf{H}}_1\right]$ hold, and if ${\Lambda }^{*}=1-\left[\frac{{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}+\frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }}\right]>0$, then Equation (1) is $\mathcal{HU}$ stable.

Proof. 

Equations (39) and (40) imply that

$$\begin{array}{cc}\hfill & {\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}+{\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}\hfill \\ \hfill \le & \frac{{\mathfrak{R}}_{\kappa }{ϵ}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }}+\frac{{\mathfrak{R}}_{\sigma }{ϵ}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}+\frac{{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }}{1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu }}{\parallel \mathsf{v}-\omega \parallel }_{\mathcal{W}}+\frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }}{1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu }}{\parallel \mathsf{w}-\upsilon \parallel }_{\mathcal{W}}.\hfill \end{array}$$

(43)

By letting $max\left\{{ϵ}_{\mu },{ϵ}_{\nu }\right\}=ϵ,$ then from Equation (43), we have

$$\begin{array}{cc}\hfill {\parallel (\mathsf{v},\mathsf{w})-(\omega ,\upsilon )\parallel }_{\mathcal{W}\times \mathcal{W}}& \le {\mathbf{C}}_{\mu ,\nu }ϵ,\hfill \end{array}$$

(44)

where

$$\begin{array}{c}\hfill {\mathbf{C}}_{\mu ,\nu }=\left[\frac{{\mathfrak{R}}_{\kappa }}{{\Lambda }^{*}(1-{\mathfrak{R}}_{\kappa }{\overline{\mathcal{L}}}_{\mu })}+\frac{{\mathfrak{R}}_{\sigma }}{{\Lambda }^{*}(1-{\mathfrak{R}}_{\sigma }{\overline{\mathcal{L}}}_{\nu })}\right].\end{array}$$

□

Remark 6.

Using Remark 4, we have $\mathcal{GHUS}$.

Remark 7.

1

The $\mathcal{EU}$ and $\mathcal{HUS}$ results for $\mathbb{CS}$s of third-order nonlinear $\mathcal{DE}\mathrm{s}$ with $\mathcal{AP}$ conditions can be obtained if we set $\kappa =\sigma =3$, ${\mathsf{a}}_{\mathrm{i}}={\mathsf{b}}_{\mathrm{i}}={\mathsf{c}}_{\mathrm{i}}=-1(\mathrm{i}=0,1)$ and ${\eta }_{\mathrm{i}}=0(\mathrm{i}=1,2,\cdots ,6)$ in Equation (1).

2

The $\mathcal{EU}$ and $\mathcal{HUS}$ results for $\mathbb{CS}$s of third-order nonlinear $\mathcal{DE}\mathrm{s}$ with the initial conditions will be obtained if we set $\kappa =\sigma =3$, ${\mathsf{a}}_{\mathrm{i}}={\mathsf{b}}_{\mathrm{i}}={\mathsf{c}}_{\mathrm{i}}=0(\mathrm{i}=0,1)$ and ${\eta }_{\mathrm{i}}=0(\mathrm{i}=1,2,\cdots ,6)$ in Equation (1).

3

The $\mathcal{EU}$ and $\mathcal{HUS}$ results for $\mathbb{CS}$s of third-order nonlinear $\mathcal{DE}\mathrm{s}$ with integro-differential BCs will be obtained if we set $\kappa =\sigma =3$ and ${\mathsf{a}}_{\mathrm{i}}={\mathsf{b}}_{\mathrm{i}}={\mathsf{c}}_{\mathrm{i}}=0(\mathrm{i}=0,1)$ in Equation (1).

5. Example

Example 1.

Let

$$\left\{\begin{array}{cc}\hfill & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)-\frac{2+|{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)|+|\mathsf{w}\left(\chi \right)|}{30{\mathrm{e}}^{\chi +50}(0.5+|{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right)|+|\mathsf{w}\left(\chi \right)\left|\right)}=0,\chi \in [1,\mathrm{e}],\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)-\frac{\chi cos\mathsf{v}\left(\chi \right)-\mathsf{w}\left(\chi \right)sin\chi }{70}-\frac{|{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)|}{50+|{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right)|}=0,\chi \in [1,\mathrm{e}],\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\mathsf{v}\left(1\right)={\mathsf{a}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -1}\mathsf{v}\left(\mathrm{e}\right)+{\eta }_1{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -1}\mathsf{v}\left(\mathrm{e}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\mathsf{v}\left(1\right)={\mathsf{b}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -2}\mathsf{v}\left(\mathrm{e}\right)+{\eta }_2{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -2}\mathsf{v}\left(\mathrm{e}\right)\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -3}\mathsf{v}\left(1\right)={\mathsf{c}}_0{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa -3}\mathsf{v}\left(\mathrm{e}\right)+{\eta }_3{}_{\mathrm{H}}{\mathfrak{I}}^{\kappa -3}\mathsf{v}\left(\mathrm{e}\right),\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\mathsf{w}\left(1\right)={\mathsf{a}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -1}\mathsf{w}\left(\mathrm{e}\right)+{\eta }_4{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -1}\mathsf{w}\left(\mathrm{e}\right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\mathsf{w}\left(1\right)={\mathsf{b}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -2}\mathsf{w}\left(\mathrm{e}\right)+{\eta }_5{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -2}\mathsf{w}\left(\mathrm{e}\right)\hfill \\ & {}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -3}\mathsf{w}\left(1\right)={\mathsf{c}}_1{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma -3}\mathsf{w}\left(\mathrm{e}\right)+{\eta }_6{}_{\mathrm{H}}{\mathfrak{I}}^{\sigma -3}\mathsf{w}\left(\mathrm{e}\right).\hfill \end{array}\right.$$

(45)

Here, we have $\kappa =\sigma =\frac{5}{2},{\mathsf{a}}_0={\mathsf{a}}_1={\eta }_1={\eta }_2=\frac{2}{5},{\mathsf{b}}_0={\mathsf{b}}_1={\eta }_3={\eta }_4=\frac{3}{5}$ and ${\mathsf{c}}_0={\mathsf{c}}_1={\eta }_5={\eta }_6=\frac{1}{5}$. Moreover, we find ${\mathcal{L}}_{\mu }={\overline{\mathcal{L}}}_{\mu }=\frac{1}{30{\mathrm{e}}^{50}}$ and ${\mathcal{L}}_{\nu }={\overline{\mathcal{L}}}_{\nu }=\frac{1}{50}$ from the nonlinear terms of Equation (45). Therefore, we have

$$\begin{array}{c}\hfill \frac{{\mathfrak{R}}_{\kappa }{\mathcal{L}}_{\mu }(1-{\overline{\mathcal{L}}}_{\nu })+{\mathfrak{R}}_{\sigma }{\mathcal{L}}_{\nu }(1-{\overline{\mathcal{L}}}_{\mu })}{(1-{\overline{\mathcal{L}}}_{\nu })(1-{\overline{\mathcal{L}}}_{\mu })}\approx 0.75141<1,\end{array}$$

Thus, Equation (45) has a solution which must be unique.

(i) 

If we take ${\displaystyle \mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))=\frac{{\left(\mathsf{v}\left(\chi \right)\right)}^2+1}{50}+\sqrt{\mathsf{w}\left(\chi \right)},}$${\displaystyle \nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))=}$$\frac{80\mathsf{v}\left(\chi \right)+{\left(\mathsf{w}\left(\chi \right)\right)}^2}{80},$ and $\mathsf{v}\left(\chi \right)=\mathsf{w}\left(\chi \right)=\chi$, then with the values ${\mathsf{a}}_0={\mathsf{a}}_1={\eta }_1={\eta }_2=\frac{2}{5}$, ${\mathsf{b}}_0={\mathsf{b}}_1={\eta }_3={\eta }_4=\frac{3}{5}$ and ${\mathsf{c}}_0={\mathsf{c}}_1={\eta }_5={\eta }_6=\frac{1}{5}$, the graph of the solution is shown in Figure 1.

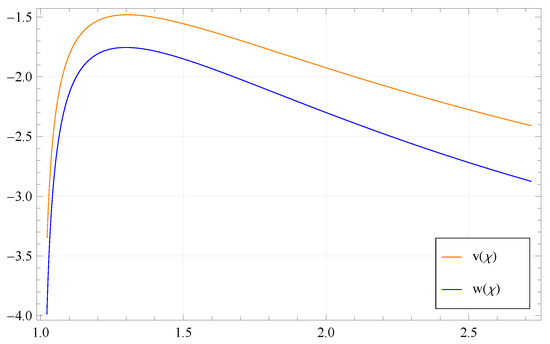Figure 1. Sketch of solution in case (i).

(ii) 

If we take ${\displaystyle \mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))=\frac{{\left(\mathsf{v}\left(\chi \right)\right)}^2+1}{50}+\sqrt{\mathsf{w}\left(\chi \right)},}$${\displaystyle \nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))=}$$\frac{80\mathsf{v}\left(\chi \right)+{\left(\mathsf{w}\left(\chi \right)\right)}^2}{80}$ and $\mathsf{v}\left(\chi \right)=\mathsf{w}\left(\chi \right)=\chi$, then with the values ${\mathsf{a}}_0={\mathsf{a}}_1={\eta }_1={\eta }_2=-\frac{2}{5}$, ${\mathsf{b}}_0={\mathsf{b}}_1={\eta }_3={\eta }_4=-\frac{3}{5}$ and ${\mathsf{c}}_0={\mathsf{c}}_1={\eta }_5={\eta }_6=-\frac{1}{5}$, the graph of the solution is shown in Figure 2.

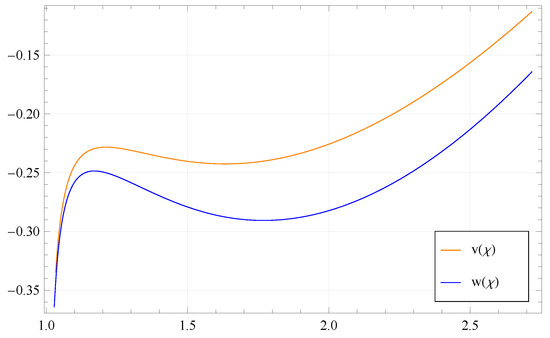Figure 2. Sketch of solution in case (ii).

(iii) 

If we take ${\displaystyle \mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))=\frac{{\left(\mathsf{v}\left(\chi \right)\right)}^2+1}{50}+\sqrt{\mathsf{w}\left(\chi \right)},}$${\displaystyle \nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))=}$$\frac{80\mathsf{v}\left(\chi \right)+{\left(\mathsf{w}\left(\chi \right)\right)}^2}{80}$ and $\mathsf{v}\left(\chi \right)=\mathsf{w}\left(\chi \right)=\chi$, then with the values ${\mathsf{a}}_0={\mathsf{a}}_1=-{\eta }_1=-{\eta }_2=\frac{2}{5}$, ${\mathsf{b}}_0={\mathsf{b}}_1=-{\eta }_3=-{\eta }_4=\frac{3}{5}$ and ${\mathsf{c}}_0={\mathsf{c}}_1=-{\eta }_5=-{\eta }_6=\frac{1}{5}$, the graph of the solution is shown in Figure 3.

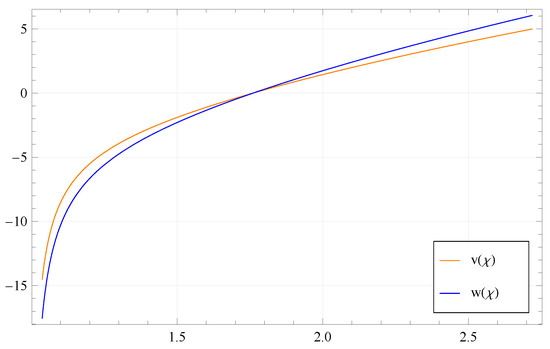Figure 3. Sketch of solution in case (iii).

(iv) 

If we take ${\displaystyle \mu (\chi ,\mathsf{w}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\kappa }\mathsf{v}\left(\chi \right))=\frac{{\left(\mathsf{v}\left(\chi \right)\right)}^2+1}{50}+\sqrt{\mathsf{w}\left(\chi \right)},}$${\displaystyle \nu (\chi ,\mathsf{v}\left(\chi \right),{}_{\mathrm{H}}{\mathfrak{D}}^{\sigma }\mathsf{w}\left(\chi \right))=}$$\frac{80\mathsf{v}\left(\chi \right)+{\left(\mathsf{w}\left(\chi \right)\right)}^2}{80}$ and $\mathsf{v}\left(\chi \right)=\mathsf{w}\left(\chi \right)=\chi$, then with the values $-{\mathsf{a}}_0=-{\mathsf{a}}_1={\eta }_1={\eta }_2=\frac{2}{5}$, $-{\mathsf{b}}_0=-{\mathsf{b}}_1={\eta }_3={\eta }_4=\frac{3}{5}$ and $-{\mathsf{c}}_0=-{\mathsf{c}}_1={\eta }_5={\eta }_6=\frac{1}{5}$, the graph of the solution is shown in Figure 4.

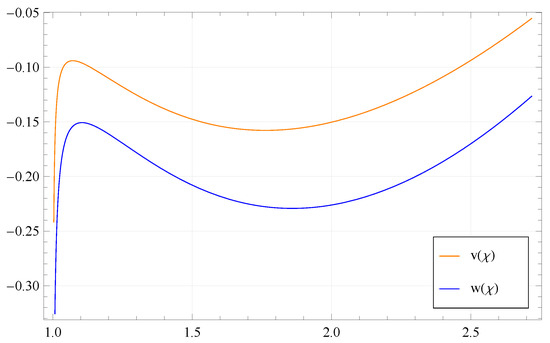Figure 4. Sketch of solution in case (iv).

Furthermore, the conditions $\Lambda >0$ and ${\Lambda }^{*}>0$ of Theorems 4 and 5 are also verified. Therefore, in both approaches, Equation (45) has $\mathcal{HUS}$, $\mathcal{GHUS}$, $\mathcal{HURS}$ and $\mathcal{GHURS}$.

6. Conclusions

We utilized the contraction principle and Leray–Schauder fixed point theorem for the existence theory of $\mathcal{FDE}\mathrm{s}$ (Equation (1)). We concluded that under some specific assumptions, the systems have at least one solution. Furthermore, we presented the $\mathcal{HUS}$, $\mathcal{GHUS}$, $\mathcal{HURS}$ and $\mathcal{GHURS}$ by utilizing the perturbations in Equation (1) and some necessary conditions.

The applicability of the outcomes was checked with an example. The proposed system in Equation (1) is the generalization of third-order $\mathcal{ODE}\mathrm{s}$, particularly for $\kappa =\sigma =3$, which is vastly utilized in applied sciences [2]. See the following for $\kappa =\sigma =3$:

1

${\eta }_{\mathrm{i}}=0(\mathrm{i}=1,2,\cdots ,6)$ and ${\mathsf{a}}_{\mathrm{j}}={\mathsf{b}}_{\mathrm{j}}={\mathsf{c}}_{\mathrm{j}}=0(\mathrm{j}=0,1)$, and then we gain third-order coupled $\mathcal{ODE}\mathrm{s}$ with the initial conditions.

2

${\eta }_{\mathrm{i}}=0(\mathrm{i}=1,2,\cdots ,6)$ and ${\mathsf{a}}_{\mathrm{j}}={\mathsf{b}}_{\mathrm{j}}={\mathsf{c}}_{\mathrm{j}}=-1(\mathrm{j}=0,1)$, and then we gain third-order coupled $\mathcal{ODE}\mathrm{s}$ with BCs in the form of $\mathcal{AP}$.

3

${\mathsf{a}}_{\mathrm{j}}={\mathsf{b}}_{\mathrm{j}}={\mathsf{c}}_{\mathrm{j}}=0(\mathrm{j}=0,1)$, and then we gain third-order coupled $\mathcal{ODE}\mathrm{s}$ with integro-differential BCs. Using MATLAB, we draw graphs for the particular variables and particular functions.