Constructing Analytical Solutions of the Fractional Riccati Differential Equations Using Laplace Residual Power Series Method
Abstract
1. Introduction
2. Basic Concepts and Theorems
- i.
- ii.
- iii.
- iv.
- v.
3. Constructing the Laplace Residual Power Series Solution for the Nonlinear Fractional Riccati Differential Equation
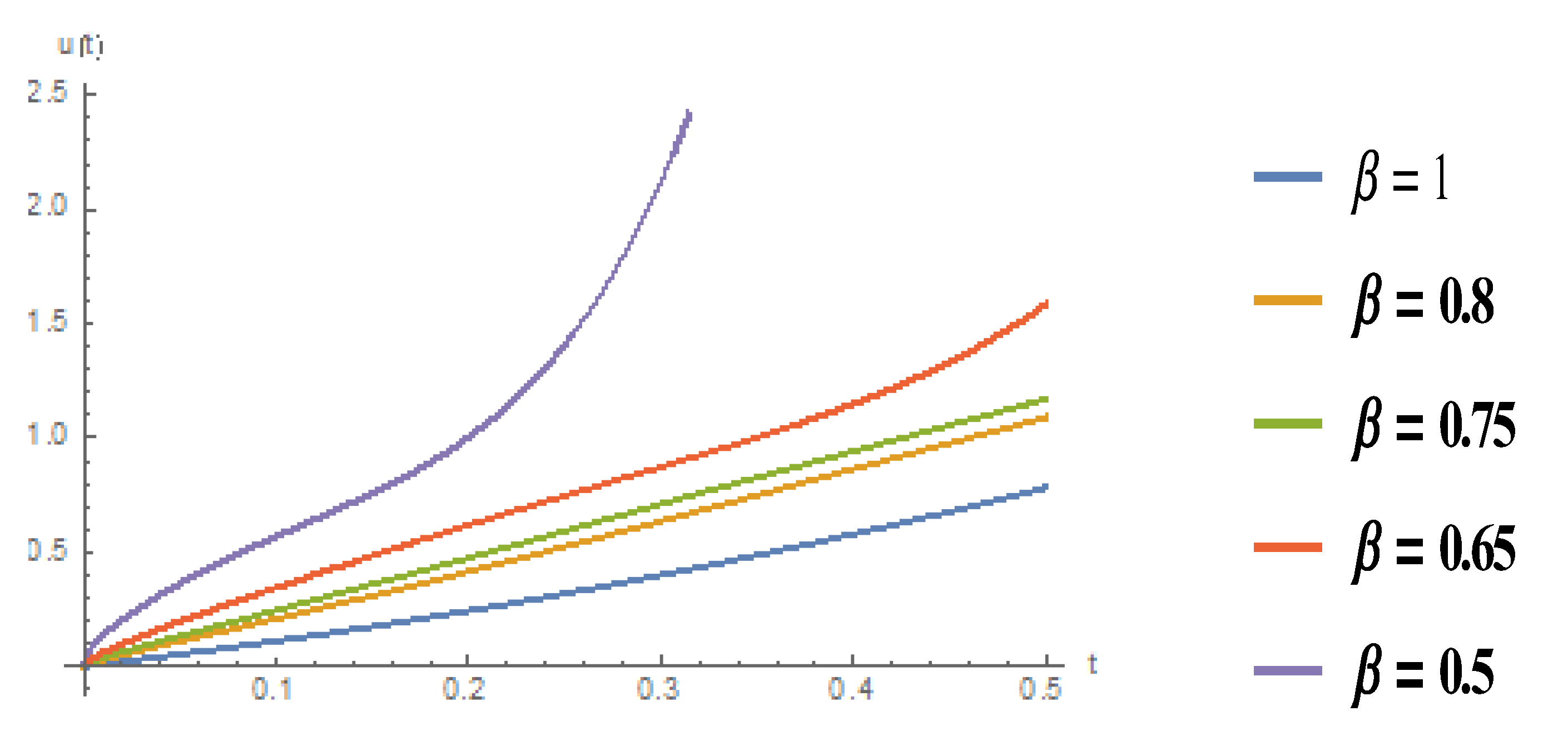
4. Illustrative Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reid, T. Riccati Differential Equations; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Lasiecka, I.; Triggiani, R. (Eds.) Differential and Algebraic Riccati Equations with Application to Boundary Point Control Problems: Continuous Theory and Approximation Theory; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Khalil, I.S.; Doyle, J.C.; Glover, K. Robust and Optimal Control; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Benner, P.; Li, J.-R.; Penzl, T. Numerical solution of large-scale Lyapunov equations, Riccati equations, and linear-quadratic optimal control problems. Numer. Linear Algebra Appl. 2008, 15, 755–777. [Google Scholar] [CrossRef]
- Yong, J. Linear-quadratic optimal control problems for mean-field stochastic differential equations. SIAM J. Control. Optim. 2013, 51, 2809–2838. [Google Scholar] [CrossRef]
- El Karoui, N.; Peng, S.; Quenez, M.C. Backward stochastic differential equations in finance. Math. Financ. 1997, 7, 1–71. [Google Scholar] [CrossRef]
- Bittanti, S.; Laub, A.J.; Willems, J.C. (Eds.) The Riccati Equation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Raja, M.A.Z.; Khan, J.A.; Qureshi, I.M. A new stochastic approach for solution of Riccati differential equation of fractional order. Ann. Math. Artif. Intell. 2010, 60, 229–250. [Google Scholar] [CrossRef]
- Suazo, E.; Sergei, K.S.; José, M.V. The Riccati differential equation and a diffusion-type equation. N. Y. J. Math 2011, 17, 225–244. [Google Scholar]
- Kazem, S. Exact solution of some linear fractional differential equations by Laplace transform. Int. J. Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Yavuz, M.; Ozdemir, N. Numerical inverse Laplace homotopy technique for fractional heat equations. Therm. Sci. 2018, 22, 185–194. [Google Scholar] [CrossRef]
- Jafari, H.; Tajadodi, H. He’s variational iteration method for solving fractional Riccati differential equation. Int. J. Diff. Equ. 2010, 2010, 764738. [Google Scholar] [CrossRef]
- El-Ajou, A.; Odibat, Z.; Momani, S.; Alawneh, A. Construction of analytical solutions to fractional differential equations using homotopy analysis method. Int. J. Appl. Math. 2010, 40, 43–51. [Google Scholar]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial. Differ. Equ. 2009, 26, 448–479. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Khader, M.M.; S Mahdy, A.M. Numerical studies for solving fractional Riccati differential equation. Appl. Appl. Math. Int. J. (AAM) 2012, 7, 8. [Google Scholar]
- Liu, J.; Li, X.; Wu, L. An operational matrix of fractional differentiation of the second kind of Chebyshev polynomial for solving multiterm variable order fractional differential equation. Math. Probl. Eng. 2016, 2016, 7126080. [Google Scholar] [CrossRef]
- Wang, Q. Numerical solutions for fractional KdV–Burgers equation by Adomian decomposition method. Appl. Math. Comput. 2006, 182, 1048–1055. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Burqan, A. A new integral transform: ARA transform and its properties and applications. Symmetry 2020, 12, 925. [Google Scholar] [CrossRef]
- Neamaty, A.; Agheli, B.; Darzi, R. The shifted Jacobi polynomial integral operational matrix for solving Riccati differential equation of fractional order. Appl. Appl. Math. Int. J. (AAM) 2015, 10, 16. [Google Scholar]
- Qazza, A.; Burqan, A.; Saadeh, R. A new attractive method in solving families of fractional differential equations by a new transform. Mathematics 2021, 9, 3039. [Google Scholar] [CrossRef]
- Burqan, A.; Saadeh, R.; Qazza, A. A novel numerical approach in solving fractional neutral pantograph equations via the ara integral transform. Symmetry 2021, 14, 50. [Google Scholar] [CrossRef]
- Burqan, A.; El-Ajou, A.; Saadeh, R.; Al-Smadi, M. A new efficient technique using Laplace transforms and smooth expansions to construct a series solution to the time-fractional Navier-Stokes equations. Alex. Eng. J. 2021, 61, 1069–1077. [Google Scholar] [CrossRef]
- Khandaqji, M.; Burqan, A. Results on sequential conformable fractional derivatives with applications. J. Comput. Anal. Appl. 2021, 29, 1115–1125. [Google Scholar]
- Qiang, X.; Mahboob, A.; Chu, Y.M. Numerical approximation of fractional-order Volterra integrodifferential equation. J. Funct. Spaces 2020, 2020, 8875792. [Google Scholar] [CrossRef]
- Ali, M.; Jaradat, I.; Alquran, M. New computational method for solving fractional Riccati equation. J. Math. Comput. Sci. 2017, 17, 106–114. [Google Scholar] [CrossRef]
- Eriqat, T.; El-Ajou, A.; Oqielat, M.N.; Al-Zhour, Z.; Momani, S. A new attractive analytic approach for solutions of linear and nonlinear neutral fractional pantograph equations. Chaos Solitons Fractals 2020, 138, 109957. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Khan, N.A.; Ara, A.; Khan, N.A. Fractional-order Riccati differential equation: Analytical approximation and numerical results. Adv. Differ. Equ. 2013, 2013, 185. [Google Scholar] [CrossRef][Green Version]
- Odibat, Z.; Momani, S. Modified homotopy perturbation method: Application to quadratic Riccati differential equation of fractional order. Chaos Solitons Fractals 2008, 36, 167–174. [Google Scholar] [CrossRef]

| LRPS | LAPM | HPM | LRPS | LAPM | HPM | ||
|---|---|---|---|---|---|---|---|
| 0.356803 | 0.321730 | 0.193401 | 0.216866 | ||||
| 0.922865 | 0.629666 | 0.454602 | 0.428892 | ||||
| 1.634139 | 0.940941 | 0.784032 | 0.654614 | ||||
| 2.204441 | 1.250737 | 1.161985 | 0.891404 | ||||
| 2.400447 | 1.549439 | 1.543881 | 1.132763 |
| Exact Solution | Approximate Solution | Absolute Error | Relative Error | |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burqan, A.; Sarhan, A.; Saadeh, R. Constructing Analytical Solutions of the Fractional Riccati Differential Equations Using Laplace Residual Power Series Method. Fractal Fract. 2023, 7, 14. https://doi.org/10.3390/fractalfract7010014
Burqan A, Sarhan A, Saadeh R. Constructing Analytical Solutions of the Fractional Riccati Differential Equations Using Laplace Residual Power Series Method. Fractal and Fractional. 2023; 7(1):14. https://doi.org/10.3390/fractalfract7010014
Chicago/Turabian StyleBurqan, Aliaa, Aref Sarhan, and Rania Saadeh. 2023. "Constructing Analytical Solutions of the Fractional Riccati Differential Equations Using Laplace Residual Power Series Method" Fractal and Fractional 7, no. 1: 14. https://doi.org/10.3390/fractalfract7010014
APA StyleBurqan, A., Sarhan, A., & Saadeh, R. (2023). Constructing Analytical Solutions of the Fractional Riccati Differential Equations Using Laplace Residual Power Series Method. Fractal and Fractional, 7(1), 14. https://doi.org/10.3390/fractalfract7010014






