New Adaptive Finite-Time Cluster Synchronization of Neutral-Type Complex-Valued Coupled Neural Networks with Mixed Time Delays

Abstract

The issue of adaptive finite-time cluster synchronization corresponding to neutral-type coupled complex-valued neural networks with mixed delays is examined in this research. A neutral-type coupled complex-valued neural network with mixed delays is more general than that of a traditional neural network, since it considers distributed delays, state delays and coupling delays. In this research, a new adaptive control technique is developed to synchronize neutral-type coupled complex-valued neural networks with mixed delays in finite time. To stabilize the resulting closed-loop system, the Lyapunov stability argument is leveraged to infer the necessary requirements on the control factors. The effectiveness of the proposed method is illustrated through simulation studies.

1. Introduction

Due to sub-network contact and cooperation, coupled neural networks (CNNs) are likelier than conventional neural networks (NNs) [1] to exhibit more complicated dynamical features, as explained in [2,3,4,5]. In view of the potential of CNNs in various fields such as electrical grid, image processing, compression coding, and medical science, there has been an increase in interest in research relating to CNNs over the years [6,7,8,9]. Although complex-valued signals are common in real-world applications, coupled real-valued neural networks (CRVNNs) [2,3] are unable to handle these signals. In order to deal with complex-valued inputs, coupled complex-valued neural networks (CCVNNs) are introduced, leading to a more efficient model by incorporating complex variables as network elements [10,11,12,13]. Compared with CRVNNs, CCVNNs can address important practical problems. As an example, an orthogonal decision boundary and complex signal in a neuron offer effective solutions to tackle the XOR and symmetry detection challenges, as presented in [14,15]. As presented in [16], CCVNNs can accurately represent optical wave fields of phase-conjugate resonators, since their complex-valued signals with respect to the underlying phase and amplitude characteristics can be interpreted conveniently. Additionally, CCVNNs provide a variety of benefits, such as increased learning speed and dependability, as well as efficient computational capabilities. Therefore, CCVNNs have gained importance in real world applications.

In the control field, synchronization has recently attracted a lot of attention, and its application areas, which include biology, medicine, chemistry, electronics, secure communication and information science, have overgrown. Until now, synchronization of dynamical networks has been a significant source of concern, with numerous valuable results reported. For instance, the authors of [5] investigated the global exponential synchronization problem of quaternion-valued coupled neural networks with impulses. An array of memristive neural networks with the inertial term, linear coupling and time-varying delay are considered for the synchronization problem in [9]. The finite-time synchronization problem for delayed neutral-type and uncertain neural networks was investigated in [17] and [18], respectively. A review of the literature reveals a variety of synchronization studies, including lag synchronization, complete synchronization, anti-synchronization, and more; see [17,18,19]. Due to many uses in image encryption, image protection and secure communication, the synchronization issue in CNNs has drawn the most attention. The phenomenon of cluster synchronization (CS) describes how all elements in a network are separated into various clusters. While the elements in the same cluster are completely synchronized, those from separate clusters are desynchronized. Because CS is a widespread phenomenon that can be discovered in a wide range of natural and man-made systems, and it has wide applications in different complex networks, including cellular and metabolic networks, social networks, electrical power grid networks, food webs, biological NNs, telephone cell graphs and the World Wide Web, to name a few, many related research studies have been conducted [20,21,22]. Liu et al. [23] considered a fractional-order linearly coupled system consisting of N NNs. They derived different adequate conditions to determine the synchronization issue of the addressed model. Yang et al. [24] discussed the CS issue of fractional-order networks with complex variables, along with nonlinear coupling in finite time based on the decomposition method. They computed the settling time efficiently using certain important aspects of the Mittag-Leffler functions and fractional Caputo derivatives. Zhang et al. [20] explored the CS issue of delayed CNNs with fixed and switching coupling topology by employing Lyapunov theory and differential inequalities method. While CS of complex networks has been studied widely, the investigation of CS with complex values in complex networks is yet to attract attention, despite its potential use. In [24], CS of complex variable dynamical complex network was examined, but on complex variable networks without time delays. Therefore, CS of complex variables in complex networks in finite time requires further investigation.

Recently the dynamical study of neural networks attracted a lot of attention; see [25,26,27,28,29,30,31]. The work mentioned above [5,9] focuses on the infinite-time synchronization of the drive-response system. Finite-time stability has entered the field of vision of researchers [17,18,23] to make the error between systems tend to zero quickly. Contrarily, from an engineering and application perspective, the convergence rate is critical in determining how well the suggested control algorithm performs and how successful it is. Therefore, the finite-time control approach has received a lot of attention [23,24,32,33]. Practically speaking, the finite-time CS of CCVNNs is trackable. With the aid of suitable controllers, finite-time CS refers to the capability of the controlled systems to establish synchronization in a predetermined amount of time. Compared with asymptotic synchronization, finite time synchronization in some cases not only accelerates synchronization, which happens when time approaches infinity, but also offers the benefit of low interruption and tenacity in the presence of uncertainty. Therefore, it is beneficial to look into CS of CCVNNs in finite time. To this end, Yu et al. [32] studied the finite-time CS problem for a coupled dynamical system without delays. He et al. [34] investigated adaptive CS in finite time for neutral-type CNNs with mixed delays. The finite-time CS problem for a coupled fuzzy cellular NNs was investigated in [35]. To the authors’ knowledge, no many results on CS of CCVNNs in finite time exist, and the conclusions are based on the assumption that the parameters of complex networks are available in the actual world. Furthermore, it is well understood that time delays are unavoidable in NNs, which can cause oscillation or asynchronization. As a result, it is essential to study how time delays affect CNNs. Motivated by the aforementioned aspects, the key objective of this article is to study improved finite-time CS of CCVNNs with mixed time delays. To address adaptive CS of CCVNNs, some useful criteria are derived. Specifically, the the important contributions of this article can be summarized as follows: (1) some adequate conditions are obtained to determining CCVNNs with systems adaptive finite-time CS. The major benefit of the adequate conditions such as linear matrix inequalities (LMIs) is that they are non-singular. (2) Unlike recent CS results work on CVNNs in finite time with nonlinear coupling and no time delay [24], the techniques presented here are applicable to CVNNs with both mixed and time-variable delays.

2. Model Description and Preliminaries

2.1. Preliminaries

Graph Theory: Let $\mathbb{G}=(\mathcal{V},\mathcal{E},G)$ be a graph with a set of nodes $\mathcal{V}=$$\{1,\dots ,V\}(V>2$), $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$, and coupling matrix $\mathbb{J}={\left[{𝚥}_{ij}\right]}_{V\times V}\in {\mathbb{R}}^{V\times V}$ with ${𝚥}_{ii}=-{\sum }_{j=1,j\ne i}^V{𝚥}_{ij}$ for $i=1,\dots ,V$, where ${𝚥}_{ij}>0$ if there is an interaction between nodes i and j, or else ${𝚥}_{ij}=0$. Denote $\left\{{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_M\right\}$ with ${\mathcal{C}}_k=$$\left\{l_{k-1}+1,l_{k-1}+2,\dots ,l_k\right\}$ as a set of partitions of nodes $\mathcal{V}$ with non-empty subset M, such that $(2\le M<V)$. In addition, several notations of graph partition are introduced. $F=\left\{F_1,\dots ,F_m\right\}$ is the partition of the given vertex set $\mathcal{V}$, if the following conditions are satisfied for $p\ne m,p,n=1,2,\dots m$

(i)

$F_{n=1}^m{F}_n=F.$

(ii)

$F_n\ne \varnothing$.

(iii)

$F_p\cup F_m=\varnothing$.

Then, $F_1=\left\{1,2,\dots ,q_1\right\},F_2=\left\{q_1+1,\dots ,q_1+q_2\right\},\dots ,F_n=\{1+{\sum }_{i=1}^n{q}_{i-1},\cdots ,{\sum }_{i=1}^n$

$q_i\},\dots ,F_m=\left\{q_1+\dots +q_{m-1}+1,\dots ,q_1+\dots +q_m\right\},q_1+q_2+\dots +q_m=N,1\le m\le N.$

The following are some useful lemmas:

Lemma 1.

For any two n-dimensional vectors ${\Lambda }_1,{\Lambda }_2$ and any matrix $\mathbb{H}>0\in$${\mathbb{R}}^{n\times n}$, and any scalar $\theta >0$, the following inequality always holds:

$$\begin{array}{c}\hfill 2{\Lambda }_1^T{\Lambda }_2\le \theta {\Lambda }_1^T\mathbb{H}{\Lambda }_1+{\theta }^{-1}{\Lambda }_2^T{\mathbb{H}}^{-1}{\Lambda }_2.\end{array}$$

Lemma 2.

Suppose that a continuous $\mathfrak{V}(t)$ is a positive–definite function, and it satisfies

$$\begin{array}{c}\hfill \dot{\mathfrak{V}}(t)\le -\alpha {\mathfrak{V}}^{\beta }(t),\forall t\ge t_0,\mathfrak{V}\left(t_0\right)\ge 0.\end{array}$$

Here, $\alpha \in {\mathbb{R}}^{+},0<\beta <1$. Then, the following inequality is satisfied for $\mathfrak{V}(t)$:

$$\begin{array}{c}\hfill {\mathfrak{V}}^{1-\beta }(t)\le {\mathfrak{V}}^{1-\beta }\left(t_0\right)-\alpha (1-\beta )\left(t-t_0\right),t_0\le t\le \mathbb{T}.\end{array}$$

where $\mathbb{T}$ denotes the settling time. It follows from $\mathfrak{V}(t)\equiv 0,\forall t\ge \mathbb{T},\mathbb{T}=t_0+\frac{{\mathfrak{V}}^{1-\gamma }\left(t_0\right)}{\beta (1-\gamma )}.$

Lemma 3.

For any chosen matrix $D\in {\mathbb{R}}^{n\times n}>0$ that is positive–definite, scalar $\delta \in {\mathbb{R}}_{+}$, and any function $\phi :[0,\delta ]\to {\mathbb{R}}^n$, the following inequality exists:

$$\begin{array}{c}\hfill {\left({\int }_0^{\delta }\phi (s)ds\right)}^{T}D\left({\int }_0^{\delta }\phi (s)ds\right)\le \delta {\int }_0^{\delta }{\phi }^T(s)D\phi (s)ds.\end{array}$$

(1)

Lemma 4.

For any N-dimensional type vectors $c_1,c_2,\dots ,c_N$ and positive real numbers $x,y$, such that $x>y>0$, then the following condition is true

$$\begin{array}{c}\hfill \sum _{i=1}^N||c_i{||}^y\ge {\left(\sum _{i=1}^N||c_i{||}^x\right)}^{\frac{x}{y}}.\end{array}$$

Remark 1.

Recently, there has been an increase in the number of studies concerning the NN synchronization problem. The analyzed NN models are classified into two types: with time delays [36,37] and without time delays [38,39,40]. Note that the evaluation of model states in delayed NNs is dependent on both the current and prior states, compared with that in NNs without time delays. This makes the investigation on delayed NNs more practical in real-world applications, but with more complex theoretical analyses. One of the most important and complex areas is the analysis of NNs with mixed delays. They include the mixture of state delays, coupling delays and distributed delays [41,42,43]. Furthermore, as a subset of delayed NNs, neutral-type CNNs have been employed in mechatronics and communication areas.

2.2. Model Formulation

Consider the CCVNNs with mixed delays consisting of N nodes, as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \frac{d{\varphi }_i(t)}{dt}=& E{\dot{\varphi }}_i(t-\sigma (t))-D{\xi }_i(t)+A\widehat{f}\left({\varphi }_i(t)\right)+B\widehat{k}({\varphi }_i(t-\tau (t)))+C{\int }_{t-\tau }^t\widehat{h}\left({\varphi }_i(\zeta )\right)d\zeta \hfill \\ & +\sum _{j=1}^N{l}_{ij}\Gamma {\varphi }_j(t-\tau (t))+u_i(t),t>0,\hfill \\ \hfill {\varphi }_i(s)=& {\vartheta }_i(s),s\in [-\tau ,0],i=1,2,\dots ,N,\hfill \end{array}\right.\end{array}$$

(2)

where ${\varphi }_i(t)={({\varphi }_{i1}(t),{\varphi }_{i2}(t),\dots ,{\varphi }_{in}(t))}^T$ and $u_i(t)$ are the state and the controller input of the $i^{th}$ subnetwork with n neurons, respectively; $\widehat{f}({\varphi }_i(t))=({\widehat{f}}_1({\xi }_{i1}(t)),{\widehat{f}}_2({\varphi }_{i2}(t)),\dots ,$

${\widehat{f}}_n({\varphi }_{in}(t)){)}^T,\widehat{k}({\varphi }_i(t-\tau (t)))={({\widehat{k}}_1({\varphi }_{i1}(t-\tau (t))),{\widehat{k}}_2({\varphi }_{i2}(t-\tau (t))),\dots ,{\widehat{k}}_n({\varphi }_{in}(t-\tau (t))))}^T,$

$\widehat{h}({\varphi }_i(\zeta ))={({\widehat{h}}_1({\varphi }_{i1}(\zeta )),{\widehat{h}}_2({\varphi }_{i2}(\zeta )),\dots ,{\widehat{h}}_n({\varphi }_{in}(\zeta )))}^T,$ are the complex-valued neuron activation functions; $D=\mathrm{diag}{(d_1,d_2,\dots ,d_n)}^T\in {\mathbb{R}}^n$ with $d_k>0(k=1,2,\dots ,n)$ is the self-feedback connection between neurons of the $i^{th}$ subnetwork; $A=(a_{pq})\in {\mathbb{C}}^{n\times n},B=(b_{pq})\in {\mathbb{C}}^{n\times n},C=(c_{pq})\in {\mathbb{C}}^{n\times n}$ denote the connection, delayed connection and distributed delayed connection weight matrices, respectively, $p,q=1,2\dots ,n$; $\sigma (t),\tau (t),\tau$ are the neutral-type time delay, coupling delay and distributed delay, respectively, and they satisfy $\tau =\underset{t\ge t_0}{sup}\left\{\sigma (t),\tau (t)\right\},t\ge t_0,\tau \in {\mathbb{R}}^{+}$; $\mathbb{L}={(l_{ij})}_{N\times N}$ denotes the configuration coupling terms of the outer coupling, which satisfies $l_{ij}=-q_{ij},l_{ii}=-{\sum }_{j=1,j\ne i}^N{q}_{ij};\Gamma =\mathrm{diag}\left\{{\delta }_1,{\delta }_2,\dots ,{\delta }_n\right\}$ is the positive diagonal inner coupling matrix; $u_i(t)={(u_{i1},u_{i2},\dots ,u_{in})}^t$ denotes the control input to be designed later, for all $t\ge 0,i,j=1,2,\dots ,N.$

The following assumption is necessary throughout this study:

Assumption 1.

We can decompose the nonlinear continuous activation functions $\widehat{f}(\varphi ),\widehat{h}(\varphi )$ and $\widehat{k}(\varphi (t-\tau (t)))$ into real and imaginary parts, namely:

$$\begin{array}{c}\hfill \widehat{f}(\varphi )={\widehat{f}}^R\left({\varphi }^R,{\varphi }^I\right)+\mathbf{i}{\widehat{f}}^I\left({\varphi }^R,{\varphi }^I\right),\widehat{k}(\varphi )={\widehat{k}}^R\left({\varphi }^R,{\varphi }^I\right)+\mathbf{i}{\widehat{k}}^I\left({\varphi }^R,{\varphi }^I\right)\end{array}$$

where ${\widehat{f}}^R,{\widehat{f}}^I,{\widehat{k}}^R,{\widehat{k}}^I$ and ${\widehat{h}}^R,{\widehat{h}}^I$ are real and imaginary parts of $\widehat{f}(\varphi ),\widehat{h}(\varphi )$ and $\widehat{k}(\varphi (t-\tau (t)))$, and all are real-valued continuous functions.

Assumption 2.

For any vectors ${\varphi }_1(t),{\varphi }_2(t)\in \mathbb{R}$, it is assumed that the real and imaginary parts of the complex-valued activation function ${\widehat{f}}_q(·)$ are able to satisfy

$$\begin{array}{cc}\hfill |{\widehat{f}}_q^R({\varphi }_1(t))|\le & L_q^R,|{\widehat{f}}_q^I({\varphi }_1(t))|\le L_q^I,\hfill \\ \hfill |{\widehat{f}}_q^R({\varphi }_1(t))-{\widehat{f}}_q^R({\varphi }_2(t))|\le & K_q^R|{\varphi }_1(t)-{\varphi }_2(t)|,|{\widehat{f}}_q^I({\varphi }_1(t))-{\widehat{f}}_q^I({\varphi }_2(t))|\le K_q^I|{\varphi }_1(t)-{\varphi }_2(t)|,\hfill \end{array}$$

where ${\widehat{f}}_q^R(·),{\widehat{f}}_q^I(·)$ are the real and imaginary parts of ${\widehat{f}}_q(·)$, and $L_q^R,L_q^I,K_q^R,K_q^I$ are positive constants.

 Remark 2. 

A complex number’s real and imaginary components also exhibit some statistical correlation. It makes more sense to use a complex-valued model rather than a real-valued model when we are aware of how crucial phase and magnitude are to our learning purpose. Complex numbers are used in neural networks for two fundamental reasons.

(a)

In many applications, such as wireless communications or audio processing, where complex numbers occur naturally or intentionally, there is a correlation between the real and imaginary parts of the complex signal. For instance, the Fourier transform is a linear transformation that multiplies the magnitude of the signal in the frequency domain by multiplying the signal’s magnitude by a scalar in the time domain. The circular rotation of a signal in the time domain corresponds to a phase change in the frequency domain. This means a complex number’s real and imaginary parts are statistically correlated during the phase change.

(b)

Suppose the relevance of the magnitude and phase to the learning objective is known a priori. In that case, it makes more sense to use a complex-valued model because it imposes more constraints on the complex-valued model than a real-valued model would.

Assumption 3.

There exists any positive constant δ that satisfies the following condition:

$$\begin{array}{c}\hfill \dot{\tau }(t)\le \delta <1,\forall t\ge 0.\end{array}$$

Assumption 4.

Assume that elements of the outer coupling matrix $\mathbb{L}={(l_{ij})}_{N\times N}$ satisfy $\sum _{j=l_{mi}}^{l_{mx}}{l}_{ij}=0,l_{mi}=1+\sum _{i=1}^h{r}_{i-1},l_{mx}=\sum _{i=1}^h{r}_i,i,j=1,2,\dots ,N.$

By assuming that system (2) is the response system, we can provide the accompanying driving system as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \frac{d{\psi }_h(t)}{dt}=& E{\dot{\psi }}_h(t-\sigma (t))-D{\psi }_h(t)+A\widehat{f}\left({\psi }_h(t)\right)+B\widehat{k}({\psi }_h(t-\tau (t)))\hfill \\ & +C{\int }_{t-\tau }^t\widehat{h}\left({\psi }_h(\zeta )\right)d\zeta ,t>0,\hfill \\ \hfill {\psi }_h(s)=& {\phi }_h(s),s\in [-\tau ,0],h=1,2,\dots ,g,\hfill \end{array}\right.\end{array}$$

(3)

where ${\psi }_g(t)={({\psi }_{g1}(t),{\psi }_{g2}(t),\dots ,{\psi }_{gn}(t))}^T$ denotes the state vector of the drive system (3), and $D,A,B,C$ and E are the feedback, interconnection, delayed interconnection and neutral delayed interconnection matrices, respectively. In addition, $\sigma (t),\tau (t),$ respectively, denote the neutral time delay and time varying delay. There is no consensus in between two clusters of distinct dimensions. Therefore, the delays considered in (2) and (3) are identical.

Definition 1.

The neutral-type CVCNNs with cluster partition Ω can realize finite-time CS, if there exists a settling time $t^s>0$, such that

$$\begin{array}{c}\hfill \underset{t\to t^s}{lim}∥{\varphi }_i(t)-{\psi }_i(t)∥=0,t\ge t^s,i\in {\Omega }_h,h=1,2,\dots ,g.\end{array}$$

Remark 3.

Finite-time control has received a lot of attention from an engineering application perspective. The convergence rate is a crucial variable to consider when evaluating the effectiveness and performance of the proposed control method [33,35]. For instance, the finite-time CS problem in complex dynamical networks’ has been addressed in [33]. However, not many studies focus on adaptive finite-time control methods for tackling the CS problem of neutral type CVCNNs with mixed delays. In the following section, a new finite-time adaptive control scheme is presented to address the this issue.

3. Main Results

The main outcome of this article is discussed in this section. To begin with, the coupling term ${\sum }_{j=1}^N{l}_{ij}\Gamma x_j\left(t-{\tau }_{ij}(t)\right)$ meets Assumption 4 Moreover, the set $\Omega =\left\{{\Omega }_1,{\Omega }_2,\dots ,{\Omega }_g\right\}$ is a partition of the edge set $\Delta =\left\{1,2,\dots ,N\right\},$ if ${\Omega }_{h=1}^g{\Omega }_q=\Omega ,$ ${\Omega }_h\ne \varnothing$, and ${\Omega }_u\cap {\Omega }_v=\varnothing$ for $u\ne v,u,h=1,2,.,g$. Then, ${\Omega }_1=\left\{1,2,\dots ,{\theta }_1\right\},{\Omega }_2=\left\{{\theta }_1+1,\dots ,{\theta }_1+{\theta }_2\right\},\dots$, ${\Omega }_h=\left\{1+{\sum }_{i=1}^h{\theta }_{i-1},\dots ,{\sum }_{i=1}^h{\theta }_i\right\},\dots ,{\Omega }_g=\left\{{\theta }_1+\dots +{\theta }_{g-1}\right.\left.+1,\dots ,{\theta }_1+\dots +{\theta }_g\right\},{\theta }_1+{\theta }_2+\dots +{\theta }_g=N,1\le g\le N$.

$$\begin{array}{cc}\hfill \sum _{j=1}^N{l}_{ij}\Gamma {\varphi }_j\left(t-\tau (t)\right)=& \sum _{h=1}^g\sum _{j\in {\Omega }_h}{l}_{ij}\Gamma {\varphi }_j\left(t-\tau (t)\right)\hfill \\ \hfill & =\sum _{h=1}^g\sum _{j\in {\Omega }_h}{l}_{ij}\Gamma {\xi }_j\left(t-\tau (t)\right)+\sum _{h=1}^g\sum _{j\in {\Omega }_h}{l}_{ij}\Gamma {\psi }_h\left(t-\tau (t)\right)\hfill \\ \hfill & =\sum _{h=1}^g\sum _{j\in {\Omega }_h}{l}_{ij}\Gamma {\xi }_j\left(t-\tau (t)\right)\hfill \end{array}$$

Thus, we consider the following error dynamics for systems (2) and (3)

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\dot{\xi }}_i(t)=& E{\dot{\xi }}_i\left(t-\tau (t)\right)-D{\xi }_i(t)+A\widehat{f}\left({\xi }_i(t)\right)+B\widehat{k}\left({\xi }_i\left(t-\tau (t)\right)\right)+C{\int }_{t-\tau }^t\widehat{h}\left({\xi }_i(\zeta )\right)d\zeta \hfill \\ \hfill & +\sum _{j=1}^N{l}_{ij}\Gamma {\xi }_j\left(t-\tau (t)\right)+u_i(t),\hfill \\ \hfill {\xi }_i(s)=& {\vartheta }_i(s)-{\phi }_h(s),s\in [-\tau ,0],i=1,2,\dots ,N,\hfill \end{array}\right.\end{array}$$

(4)

where $\widehat{f}\left({\xi }_i(t)\right)=f\left({\varphi }_i(t)\right)-f\left({\psi }_h(t)\right),\widehat{k}\left({\xi }_i\left(t-\tau (t)\right)\right)=\widehat{k}\left({\varphi }_i\left(t-\tau (t)\right)\right)-\widehat{k}\left({\psi }_h\left(t-\tau (t)\right)\right),{\int }_{t-\tau }^t\widehat{h}\left({\xi }_i(\zeta )\right)d\zeta ={\int }_{t-\tau }^t\left[\widehat{h}\left({\varphi }_i(\zeta )\right)-\widehat{h}\left({\psi }_h(\zeta )\right)\right]d\zeta ,t\ge 0,i\in \Delta .$ Complex-valued system (4) can be divided into its real and imaginary parts by utilizing Assumption 1, as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\dot{\xi }}_i^R(t)=& E^R{\dot{\xi }}_i^R(t-\tau (t))+E^I{\dot{\xi }}_i^I(t-\tau (t))-D^R{\xi }_i^R(t)+A^R{\widehat{f}}^R({\xi }_i(t))-A^I{\widehat{f}}^I({\xi }_i(t))\hfill \\ & +B^R{\widehat{K}}^R({\xi }_i(t-\tau (t)))-B^I{\widehat{K}}^I({\xi }_i(t-\tau (t)))+C^R{\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta \hfill \\ & -C^I{\int }_{t-\tau }^t{\widehat{h}}^I\left({\xi }_i(\zeta )\right)d\zeta +\sum _{j=1}^N{l}_{ij}\Gamma {\xi }^R(t-\tau (t)+u^R(t),\hfill \\ \hfill {\dot{\xi }}_i^I(t)=& E^I{\dot{\xi }}_i^R(t-\tau (t))+E^R{\dot{\xi }}_i^I(t-\tau (t))-D^R{\xi }_i^I(t)+A^R{\widehat{f}}^I({\xi }_i(t))+A^I{\widehat{f}}^R({\xi }_i(t))\hfill \\ & +B^R{\widehat{K}}^I(\xi (t-\tau (t)))+B^I{\widehat{K}}^R(\xi (t-\tau (t)))+C^R{\int }_{t-\tau }^t{\widehat{h}}^I\left({\xi }_i(\zeta )\right)d\zeta \hfill \\ & +C^I{\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta +\sum _{j=1}^N{l}_{ij}\Gamma {\xi }^I(t-\tau (t)+u^I(t),\hfill \\ \hfill {\xi }_i^R(s)=& {\vartheta }_i^R(s)-{\phi }_h^R(s),{\xi }_i^I(s)={\vartheta }_i^I(s)-{\phi }_h^I(s),s\in [-\tau ,0],i=1,2,\dots ,N,\hfill \end{array}\right.\end{array}$$

(5)

where, ${\xi }_i^R(t)={({\xi }_{i1}^R(t),{\xi }_{i2}^R(t),\dots ,{\xi }_{in}^R(t))}^T,{\xi }_i^I(t)={({\xi }_{i1}^I(t),{\xi }_{i2}^I(t),\dots ,{\xi }_{in}^I(t))}^T,E=E^R+\mathbf{i}{E}^I={(e_{pq}^R)}_{n\times n}+\mathbf{i}{(e_{pq}^I)}_{n\times n},A=A^R+\mathbf{i}{A}^I={(a_{pq}^R)}_{n\times n}+\mathbf{i}{(a_{pq}^I)}_{n\times n},B=B^R+\mathbf{i}{B}^I={(b_{pq}^R)}_{n\times n}+\mathbf{i}{(b_{pq}^I)}_{n\times n},C=C^R+\mathbf{i}{C}^I={(c_{pq}^R)}_{n\times n}+\mathbf{i}{(c_{pq}^I)}_{n\times n},u(t)=u^R(t)+\mathbf{i}{u}^I(t).$ The finite-time CS problem of (2) and (3) is solved when the states of system (5) is finite-time stable.

To design an improved finite-time adaptive controller for CS, the error system (5) can be used, as follows:

$$\begin{array}{cc}\hfill u_i^R(t)=& {\pi }_i^R(t){\xi }_i^R(t),u_i^I(t)={\pi }_i^I(t){\xi }_i^I(t),\hfill \\ \hfill {\dot{\pi }}_i^R(t)=& -{\vartheta }^T(\varsigma ,{\pi }_i^R(t))\left({\xi }_i^{R^T}{E}^R{\dot{\xi }}_i(t-\tau (t))+{\pi }_i^R(t){\xi }^{R^T}(t){\xi }^R(t)+{\xi }^{R^T}(t){\varpi }^R{\xi }_i^R(t)\right.\hfill \\ & \left.+\sum _{j=1}^N{\xi }^{R^T}(t)l_{ij}\Delta {\xi }_j^R(t-\tau (t))\right)-{\tilde{\vartheta }}^R(\tilde{\varsigma },{\vartheta }^R(\varsigma ,{\pi }_i^R(t)))\left(||{\xi }_i^R(t)||-\tilde{\varsigma }\sqrt{\varsigma }sign({\pi }_i^R(t))\right.\hfill \\ & \left.+{\left({\int }_{t-\tau (t)}^t{\xi }^R(\theta )P{\xi }^R(\theta )d\theta \right)}^{0.5}+{\xi }_h^R{\left({\int }_{-\tau }^0{\int }_{t+s}^t{\xi }_i^{R^T}(\zeta ){\xi }_i^R(\zeta )d\zeta ds\right)}^{0.5}\right),\hfill \\ \hfill {\dot{\pi }}_i^I(t)=& -{\vartheta }^I(\varsigma ,{\pi }_i^I(t))\left({\xi }_i^{I^T}{E}^I{\dot{\xi }}_i^I(t-\tau (t))+{\pi }_i^I(t){\xi }^{I^T}(t){\xi }^I(t)+{\xi }^{I^T}(t){\varpi }^I{\xi }_i^I(t)\right.\hfill \\ & \left.+\sum _{j=1}^N{\xi }^{I^T}(t)l_{ij}\Delta {\xi }_j^I(t-\tau (t))\right)-{\tilde{\vartheta }}^I(\tilde{\varsigma },{\vartheta }^I(\varsigma ,{\pi }_i^I(t)))\left(||{\xi }_i^I(t)||-\tilde{\varsigma }\sqrt{\varsigma }sign({\pi }_i^I(t))\right.\hfill \\ & \left.+{\left({\int }_{t-\tau (t)}^t{\xi }^I(\theta )P_1{\xi }^I(\theta )d\theta \right)}^{0.5}+{\xi }_h^I{\left({\int }_{-\tau }^0{\int }_{t+s}^t{\xi }_i^{I^T}(\zeta ){\xi }_i^I(\zeta )d\zeta ds\right)}^{0.5}\right),\hfill \end{array}$$

(6)

where $\varphi ,P$ and $P_1$ are positive–definite matrices, $\varsigma$ and $\tilde{\varsigma }$ are positive constants. ${\vartheta }^R(\tilde{\varsigma },{\pi }_i^R(t))=\frac{\tilde{\varsigma }}{{\pi }_i^R(t)},{\pi }_i^R(t)<0$$\tilde{\vartheta }(\varsigma ,\vartheta (\varsigma ,{\pi }_i^R(t)))=\varsigma {\vartheta }^R(\tilde{\varsigma },{\pi }_i^R(t)),i,j\in \mathcal{V}$${\vartheta }^I(\tilde{\varsigma },{\pi }_i^I(t))=\frac{\tilde{\varsigma }}{{\pi }_i^I(t)},{\pi }_i^I(t)<0$$\tilde{\vartheta }(\varsigma ,\vartheta (\varsigma ,{\pi }_i^I(t)))=\varsigma {\vartheta }^I(\tilde{\varsigma },{\pi }_i^I(t)),i,j\in \mathcal{V}$.

Remark 4.

Complex-valued neural networks have proven useful in domains where the representation of data is complex by nature or design. Most CVNN research has focused on shallow designs and specific signal processing tasks, such as channel equalization. One reason for this is the difficulties associated with training. This is due to the limitation that the complex-valued activation is not complex differentiable and bounded at the same time [44,45]. Several studies have suggested that the condition that a complex-valued activation must be simultaneously bounded and complex differentiable need not be satisfied, and propose activations that are differentiable independently of the real and imaginary components. This remains an open area of research.

Theorem 1.

On the ground that Assumptions 1–4 are true, using adaptive control (6) for system (2), we can prove the existence of positive–diagonal matrix ϕ and symmetric matrices $P,P_1$, such that

$$\begin{gathered} \begin{array}{cc}\hfill -{\lambda }_{min}(D^R)& +\frac{1}{2}{\lambda }_{max}(A^R{A}^{R^T})-\frac{1}{2}{\lambda }_{min}(A^I{A}^{I^T})+\frac{1}{2}{\lambda }_{max}(B^R{B}^{R^T})-\frac{1}{2}{\lambda }_{min}(B^I{B}^{I^T})\hfill \end{array} \\ \begin{array}{c}\hfill +\frac{1}{2}{\lambda }_{max}(C^R{C}^{R^T})-\frac{1}{2}{\lambda }_{min}(C^I{C}^{I^T})+\frac{1}{2}{\lambda }_{max}(P)+\frac{\tau {\xi }_h^{I^2}}{2}<{\lambda }_{min}(\varphi ),\end{array} \end{gathered}$$

(7)

$$\begin{gathered} \begin{array}{cc}\hfill -{\lambda }_{min}(D^I)& +\frac{1}{2}{\lambda }_{max}(A^R{A}^{R^T})+\frac{1}{2}{\lambda }_{max}(A^I{A}^{I^T})+\frac{1}{2}{\lambda }_{max}(B^R{B}^{R^T})+\frac{1}{2}{\lambda }_{max}(B^I{B}^{I^T})\hfill \end{array} \\ \begin{array}{c}\hfill +\frac{1}{2}{\lambda }_{max}(C^R{C}^{R^T})+\frac{1}{2}{\lambda }_{max}(C^I{C}^{I^T})+\frac{1}{2}{\lambda }_{max}(P_1)+\frac{\tau {\xi }_h^{I^2}}{2}<{\lambda }_{min}(\varphi ),\end{array} \end{gathered}$$

(8)

$$\begin{array}{cc}\hfill & \frac{1}{2}{\xi }_k^{R^2}-\frac{1}{2}(1-\overline{\tau }P)<0,\frac{1}{2}{\xi }_k^{I^2}-\frac{1}{2}(1-\overline{\tau }{P}_1)<0\hfill \end{array}$$

(9)

then CS can be obtained in finite time.

Proof. 

A Lyapunov functional candidate is considered, as follows:

$$\begin{array}{c}\hfill V(t)=V_1(t)+V_2(t)+V_3(t)+V_4(t)\end{array}$$

(10)

where,

$$\begin{array}{cc}\hfill V_1(t)=& \frac{1}{2}\sum _{i=1}^N{\xi }_i^{R^T}(t){\xi }_i^R(t)+\frac{1}{2}\sum _{i=1}^N{\xi }_i^{I^T}(t){\xi }_i^I(t),\hfill \\ \hfill V_2(t)=& \frac{1}{2}\sum _{i=1}^N{\int }_{t-\widehat{\tau }(t)}^t{\xi }_i^{R^T}(\theta )P{\xi }_i^R(\theta )d\theta +\frac{1}{2}\sum _{i=1}^N{\int }_{t-\widehat{\tau }(t)}^t{\xi }_i^{I^T}(t)P_1{\xi }_i^I(t)d\theta ,\hfill \\ \hfill V_3(t)=& \frac{1}{2}\sum _{i=1}^N{\int }_{-\tau (t)}^0{\int }_{t+s}^t{\xi }_i^{R^T}(\zeta ){\xi }_h^T{\xi }_h{\xi }_i(\zeta )d\zeta ds+\frac{1}{2}\sum _{i=1}^N{\int }_{-\tau (t)}^0{\int }_{t+s}^t{\xi }_i^{I^T}(\zeta ){\xi }_h^T{\xi }_h{\xi }_i(\zeta )d\zeta ds,\hfill \\ \hfill V_4(t)=& \sum _{i=1}^N\frac{1}{2\omega }{\pi }_i^{R^2}(t)+\sum _{i=1}^N\frac{1}{2\omega }{\pi }_i^{I^2}(t).\hfill \end{array}$$

Differentiating $V_1(t)$ along the state trajectories of model (5) yields:

$$\begin{array}{cc}\hfill {\dot{V}}_1(t)=& \sum _{i=1}^N{\xi }_i^{R^T}(t){\dot{\xi }}_i^R(t)+\sum _{i=1}^N{\xi }_i^{I^T}(t){\dot{\xi }}_i^I(t),\hfill \\ \hfill =& \sum _{i=1}^N{\xi }_i^{R^T}(t)[E^R{\dot{\xi }}_i^R(t-\tau (t))-E^I{\dot{\xi }}_i^I(t-\tau (t))-D^R{\xi }_i^R(t)+A^R{\widehat{f}}^R\left({\xi }_i(t)\right)\hfill \\ & -A^I{\widehat{f}}^I\left({\xi }_i(t)\right)+B^R{\widehat{K}}^R({\xi }_i(t-\tau (t)))-B^I{\widehat{K}}^I({\xi }_i(t-\tau (t)))+C^R{\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta \hfill \\ & -C^I{\int }_{t-\tau }^t{\widehat{h}}^I\left({\xi }_i(\zeta )\right)d\zeta +\sum _{j=1}^N{l}_{ij}\Gamma {\xi }_i^R(t-\tau (t))+u^R(t)]\hfill \\ \hfill & +\sum _{i=1}^N{\xi }_i^{I^T}(t)[E^I{\xi }_i^R(t-\tau (t))+E^R{\xi }_i^I(t-\tau (t))-D^R{\xi }_i^I(t)+A^R{}^r{\widehat{f}}^I\left({\xi }_i(t)\right)\hfill \\ & +A^I{\widehat{f}}^R\left({\xi }_i(t)\right)+B^R{\widehat{k}}^I({\xi }_i(t-\tau (t)))+B^I{\widehat{K}}^R\left({\xi }_i(t-\tau (t))\right)+C^R{\int }_{t-\tau }^t{\widehat{h}}^I\left({\xi }_i(\zeta )\right)d\zeta \hfill \\ & +C^I{\int }_{t-\tau }^t{h}^R\left({\xi }_i(\zeta )\right)d\zeta +\sum _{j=1}^N{l}_{ij}\Gamma {\xi }_i^I(t-\tau (t))+u^I(t)]\hfill \end{array}$$

(11)

The following inequalities can be deduced from Lemma 1 and Assumption 2:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}\hfill \sum _{i=1}^N{\xi }_i^{R^T}(t)A^R{\widehat{f}}^R\left({\xi }_i^R(t)\right)\le & \frac{1}{2}\left\{\sum _{i=1}^N{\xi }_i^{R^T}(t)A^R{A}^{R^T}{\xi }_i^R(t)+\sum _{i=1}^N{\xi }_i^{R^T}(t){\xi }_f^{R^2}{\xi }_i^R(t)\right\},\hfill \\ \hfill \sum _{i=1}^N{\xi }_i^{R^T}(t)A^I{\widehat{f}}^I\left({\xi }_i^I(t)\right)\le & \frac{1}{2}\left\{\sum _{i=1}^N{\xi }_i^{R^T}(t)A^I{A}^{I^T}{\xi }_i^R(t)+\sum _{i=1}^N{\xi }_i^{I^T}{\xi }_f^{I^2}{\xi }_i^2(t)\right\},\hfill \end{array}\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}\hfill \sum _{i=1}^N{\xi }_i^{I^T}(t)A^R{\widehat{f}}^I\left({\xi }_i(t)\right)\le & \frac{1}{2}\left\{\sum _{i=1}^N{\xi }_i^{I^T}(t)A^R{A}^{2R^T}{\xi }_i^I(t)+\sum _{i=1}^N{\xi }_i^{I^T}(t){\xi }_f^{I^2}{\xi }_i^I(t)\right\},\hfill \\ \hfill \sum _{i=1}^N{\xi }_i^{I^T}(t)A^I{\widehat{f}}^R\left({\xi }_i(t)\right)\le & \frac{1}{2}\left\{\sum _{i=1}^N{\xi }_i^{I^T}(t)A^I{A}^{I^T}{\xi }_i^I(t)+\sum _{i=1}^N{\xi }_i^{R^T}(t){\xi }_f^{R^2}{\xi }_i^R(t)\right\},\hfill \end{array}\right.\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}\hfill \sum _{i=1}^N{\xi }_i^{R^T}(t)B^R{\widehat{K}}^R({\xi }_i(t-\tau (t)))\le & \frac{1}{2}\left\{\sum _{i=1}^N{\xi }_i^{R^T}(t)B^R{B}^{R^T}{\xi }_i^R(t)\right.\hfill \\ & \left.+\sum _{i=1}^N{\xi }_i^{R^T}(t-\tau (t)){\xi }_k^{R^2}{\xi }_i^R(t-\tau (t))\right\},\hfill \\ \hfill \sum _{i=1}^N{\xi }_i^R(t)B^I{\widehat{K}}^I(\xi (t-\tau (t)))\le & \frac{1}{2}\left\{\sum _{i=1}^N{\xi }_i^{R^T}(t)B^I{B}^{I^T}{\xi }_i^R(t)\right.\hfill \\ & \left.+\sum _{i=1}^N{\xi }_i^{I^T}(t-\tau (t)){\xi }_K^{I^2}{\xi }_i^I(t-\tau (t))\right\},\hfill \\ \hfill \sum _{i=1}^N{\xi }_i^{I^T}(t)B^R{\widehat{K}}^I{\xi }_i(t-\tau (t))\le & \frac{1}{2}\left\{\sum _{i=1}^N{\xi }_i^T(t)B^R{B}^{R^T}{\xi }_i^I(t)\right.\hfill \\ & \left.+\sum _{i=1}^N{\xi }_i^{I^T}(t-\tau (t)){\xi }_k^{I^2}{\xi }_i^I(t-\tau (t))\right\},\hfill \\ \hfill \sum _{i=1}^N{\xi }_i^{I^T}(t){\overline{B}}^I{\widehat{k}}^R\left({\xi }_i(t-\tau (t))\right)\le & \frac{1}{2}\left\{\sum _{i=1}^N{\xi }_i^{I^T}(t)B^T{B}^{I^T}{\xi }_i^I(t)\right.\hfill \\ & \left.+\sum _{i=1}^N{\xi }_i^{R^T}(t-\tau (t)){\xi }_k^{R^2}{\xi }_i^R(t-\tau (t))\right\},\hfill \end{array}\right.\hfill \end{array}$$

(13)

From Lemma 3, it follows that

$$\begin{array}{cc}\hfill \sum _{i=1}^N{\xi }_i^{R^T}(t)C^R{\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta =& \frac{1}{2}\sum _{i=1}^N\left\{{\xi }_i^{R^T}(t)C^R{\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i^{R^T}(\zeta )\right)d\zeta \right.\hfill \\ & \left.+{\int }_{t-\tau }^t{\widehat{h}}^{R^T}\left({\xi }_i(\zeta )\right)d\zeta C^{R^T}{\xi }_i^{R^T}(t)\right\}\hfill \\ \hfill \le & \frac{1}{2}\sum _{i=1}^N\left\{{\int }_{t-\tau }^t{\widehat{h}}^{R^T}\left({\xi }_i(\zeta )\right)d\zeta {\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta \right.\hfill \\ & \left.+{\xi }_i^{R^T}(t)C^R{C}^{R^T}{\xi }_i^R(t)\right\}\hfill \\ \hfill \le & \frac{1}{2}\sum _{i=1}^N\left\{{\int }_{t-\tau }^t{\widehat{h}}^{R^T}\left({\xi }_i(\zeta )\right){\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta \right.\hfill \\ & \left.+{\xi }_i^{R^T}(t)C^R{C}^{R^T}{\xi }_i^R(t)\right\}\hfill \\ \hfill \le & \frac{1}{2}\sum _{i=1}^N\left\{{\xi }_h^{R^2}{\int }_{t-\tau }^t{\xi }_i^{R^T}(\zeta ){\xi }_i^R(\zeta )d\zeta \right.\hfill \\ & \left.+{\xi }_i^{R^T}(t)C^R{C}^{R^T}{\xi }_i^R(t)\right\}.\hfill \end{array}$$

(14)

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \sum _{i=1}^N{\xi }_i^{R^T}(t)C^I{\int }_{t-\tau }^t{\widehat{h}}^I\left({\xi }_i(\zeta )\right)d\zeta \le & \frac{1}{2}\sum _{i=1}^N\left\{{\xi }_h^{I^2}{\int }_{t-\tau }^t{\xi }_i^{I^T}(\zeta ){\xi }_i^I(\zeta )d\zeta +{\xi }_i^{R^T}(t)C^I{C}^{I^T}{\xi }_i^R(t)\right\},\hfill \\ \hfill \sum _{i=1}^N{\xi }_i^{I^T}(t)C^R{\int }_{t-\tau }^t{\widehat{h}}^I\left({\xi }_i(\zeta )\right)d\zeta \le & \frac{1}{2}\sum _{i=1}^N\left\{{\xi }_h^{I^2}{\int }_{t-\tau }^t{\xi }_i^{I^T}(\zeta ){\xi }_i^I(\zeta )d\zeta +{\xi }_i^{I^T}(t)C^R{C}^{R^T}{\xi }_i^I(t)\right\},\hfill \\ \hfill \sum _{i=1}^N{\xi }_i^{I^T}(t)C^I{\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta \le & \frac{1}{2}\sum _{i=1}^N\left\{{\xi }_h^{R^2}{\int }_{t-\tau }^t{\xi }_i^{R^T}(\zeta ){\xi }_i^R(\zeta )d\zeta +{\xi }_i^{I^T}(t)C^I{C}^{I^T}{\xi }_i^I(t)\right\},\hfill \end{array}\right.\end{array}$$

(15)

Therefore,

$$\begin{gathered} \begin{array}{cc}\hfill {\dot{V}}_1(t)\le & \sum _{i=1}^N\left\{{\xi }_i^{R^T}{E}^R(t){\dot{\xi }}_i^R(t-\tau (t))-{\xi }_i^{R^T}{E}^I(t){\dot{\xi }}_i^I(t-\tau (t))+{\xi }_i^{I^T}{E}^I(t){\dot{\xi }}_i^R(t-\tau (t))\right.\hfill \\ & \left.+{\xi }_i^{I^T}{E}^R(t){\dot{\xi }}_i^I(t-\tau (t))\right\}+\sum _{i=1}^N{\xi }_i^{R^T}(t)\left[-D^R+\frac{1}{2}\left(A^R{A}^{R^T}+{\xi }_f^{R^2}-A^I{A}^{I^T}\right.\right.\hfill \end{array} \\ \begin{array}{cc}& \left.\left.+B^R{B}^{R^T}-B^I{B}^{I^T}+C^R{C}^{R^T}-C^I{C}^{I^T}\right)+{\pi }_i^R(t)\right]{\xi }_i^R(t)\hfill \\ \hfill & +{\xi }_k^{R^2}\sum _{i=1}^N{\xi }_i^{R^T}(t-\tau (t)){\xi }_i^R(t-\tau (t))+{\xi }_k^{I^2}\sum _{i=1}^N{\xi }_i^{I^T}(t-\tau (t)){\xi }_i^I(t-\tau (t))\hfill \end{array} \end{gathered}$$

(16)

Then, the derivative of the Lyapunov term $V_2(t)$ and $V_3(t)$ is described as follows:

$$\begin{array}{cc}\hfill {\dot{V}}_2(t)=& \frac{1}{2}\sum _{i=1}^N{\xi }_i^{R^T}(t)P{\xi }_i^R(t)-\frac{1}{2}\sum _{i=1}^N\left(1-\dot{\widehat{\tau }}(t)\right){\xi }_i^{R^T}\left(t-\widehat{\tau }(t)\right)P{\xi }_i^R\left(t-\widehat{\tau }(t)\right)\hfill \\ & +\frac{1}{2}\sum _{i=1}^N{\xi }_i^{I^T}(t)P_1{\xi }_i^I(t)-\frac{1}{2}\sum _{i=1}^N\left(1-\dot{\widehat{\tau }}(t)\right){\xi }_i^{I^T}\left(t-\widehat{\tau }(t)\right)P_1{\xi }_i^I\left(t-\widehat{\tau }(t)\right),\hfill \\ \hfill \le & \frac{1}{2}\sum _{i=1}^N{\xi }_i^{R^T}(t)P{\xi }_i^R(t)-\frac{1}{2}\sum _{i=1}^N\left(1-\tilde{\tau }\right){\xi }_i^{R^T}\left(t-\widehat{\tau }(t)\right)P{\xi }_i^R\left(t-\widehat{\tau }(t)\right)\hfill \\ & +\frac{1}{2}\sum _{i=1}^N{\xi }_i^{I^T}(t)P_1{\xi }_i^I(t)-\frac{1}{2}\sum _{i=1}^N\left(1-\tilde{\tau }\right){\xi }_i^{I^T}\left(t-\widehat{\tau }(t)\right)P_1{\xi }_i^I\left(t-\widehat{\tau }(t)\right),\hfill \end{array}$$

(17)

$$\begin{gathered} \begin{array}{cc}\hfill {\dot{V}}_3(t)\le & \frac{1}{2}{\xi }_h^{R^2}\sum _{i=1}^N\tau {\xi }_i^{R^T}(t){\xi }_i^R(t)-\frac{{\xi }_h^{R^2}}{2}\sum _{i=1}^N{\int }_{t-\tau }^t{\xi }_i^{R^T}(\zeta ){\xi }_i^R(\zeta )d\zeta \hfill \end{array} \\ \begin{array}{cc}& +\frac{1}{2}{\xi }_h^{I^2}\sum _{i=1}^N\tau {\xi }_i^{I^T}(t){\xi }_i^I(t)-\frac{{\xi }_h^{I^2}}{2}\sum _{i=1}^N{\int }_{t-\tau }^t{\xi }_i^{I^T}(\zeta ){\xi }_i^I(\zeta )d\zeta \hfill \end{array} \end{gathered}$$

(18)

and

$$\begin{array}{cc}\hfill {\dot{V}}_4(t)=& \sum _{i=1}^N\frac{1}{\omega }{\pi }_i^R(t){\dot{\pi }}_i^R(t)+\sum _{i=1}^N\frac{1}{\omega }{\pi }_i^I(t){\dot{\pi }}_i^I(t),\hfill \\ \hfill \le & \sum _{i=1}^N\left[-{\xi }_i^{R^T}(t)E^R{\dot{\xi }}_i^R\left(t-\tau (t)\right)-{\pi }_i^R(t){\xi }_i^{R^T}(t){\xi }_i^R(t)-{\xi }_i^{I^T}(t)E^I{\dot{\xi }}_i^I\left(t-\tau (t)\right)\right.\hfill \\ \hfill & -{\pi }_i^I(t){\xi }_i^{I^T}(t){\xi }_i^I(t)-{\xi }_i^{R^T}(t)\varphi {\xi }_i^R(t)-{\xi }_i^{I^T}(t)\varphi {\xi }_i^I(t)-\sum _{j=1}^N{\xi }_i^{R^T}(t)l_{ij}\Gamma {\xi }_j^R\left(t-\tau (t)\right)\hfill \\ \hfill & -\epsilon ∥{\xi }_i^R(t)∥-\frac{\epsilon }{\sqrt{\epsilon }}\left|{\pi }_i^R(t)\right|-\sum _{j=1}^N{\xi }_i^{I^T}(t)l_{ij}\Gamma {\xi }_j^I\left(t-\tau (t)\right)-\epsilon ∥{\xi }_i^I(t)∥-\frac{\epsilon }{\sqrt{\epsilon }}\left|{\pi }_i^I(t)\right|\hfill \\ \hfill & -\epsilon {\left({\int }_{t-\tau (t)}^t{\xi }_i^{R^T}(s)P{\xi }_i^R(s)ds\right)}^{\frac{1}{2}}-\epsilon {\left({\int }_{t-\tau (t)}^t{\xi }_i^{I^T}(s)P{\xi }_i^I(s)ds\right)}^{\frac{1}{2}}\hfill \\ \hfill & \left.-\epsilon {\xi }_h^{R^2}{\left({\int }_{-\tau }^0{\int }_{t+\theta }^t{\xi }_i^{R^T}(\zeta ){\xi }_i^R(\zeta )d\zeta d\theta \right)}^{\frac{1}{2}}-\epsilon {\xi }_h^{I^2}{\left({\int }_{-\tau }^0{\int }_{t+\theta }^t{\xi }_i^{I^T}(\zeta ){\xi }_i^I(\zeta )d\zeta d\theta \right)}^{\frac{1}{2}}\right]\hfill \end{array}$$

(19)

According to Assumption 3, we have

$$\begin{array}{cc}\hfill \dot{V}(t)\le & {\xi }_i^{R^T}(t)[-D^R+\frac{1}{2}{A}^R{A}^{R^T}-\frac{1}{2}{A}^I{A}^{I^T}+\frac{1}{2}{B}^R{B}^{R^T}-\frac{1}{2}{B}^I{B}^{I^T}+\frac{1}{2}{C}^R{C}^{R^T}\hfill \\ \hfill & -\frac{1}{2}{C}^I{C}^{I^T}+\frac{1}{2}P+\frac{\tau {\xi }_h^{I^2}}{2}-\varphi ]{\xi }^R(t)+{\xi }_i^{I^T}(t)[-D^I+\frac{1}{2}{A}^R{A}^{R^T}+\frac{1}{2}{A}^I{A}^{I^T}\hfill \\ & +\frac{1}{2}{B}^R{B}^{R^T}+\frac{1}{2}{B}^I{B}^{I^T}+\frac{1}{2}{C}^R{C}^{R^T}+\frac{1}{2}{C}^I{C}^{I^T}+\frac{1}{2}{P}_1+\frac{\tau {\xi }_h^{I^2}}{2}-\varphi ]{\xi }^I(t)\hfill \\ & +\sum _{i=1}^N{\xi }_i^{R^T}(t-\tau (t))\left[\frac{1}{2}{\xi }_k^{R^2}-\frac{1}{2}(1-\overline{\tau }P)\right]{\xi }_i^R(t-\tau (t))\hfill \\ & +\sum _{i=1}^N{\xi }_i^{I^T}(t-\tau (t))\left[\frac{1}{2}{\xi }_k^{I^2}-\frac{1}{2}(1-\overline{\tau }{P}_1)\right]{\xi }_i^I(t-\tau (t))\hfill \\ & -\sum _{i=1}^N\epsilon {\left({\int }_{t-\tau (t)}^t{\xi }_i^{R^T}(s)P{\xi }_i^R(s)ds\right)}^{\frac{1}{2}}-\sum _{i=1}^N\epsilon {\left({\int }_{t-\tau (t)}^t{\xi }_i^{I^T}(s)P{\xi }_i^I(s)ds\right)}^{\frac{1}{2}}\hfill \\ & -\sum _{i=1}^N\epsilon {\xi }_h^{R^2}{\left({\int }_{-\tau }^0{\int }_{t+\theta }^t{\xi }_i^{R^T}(\zeta ){\xi }_i^R(\zeta )d\zeta d\theta \right)}^{\frac{1}{2}}-\sum _{i=1}^N\epsilon {\xi }_h^{I^2}{\left({\int }_{-\tau }^0{\int }_{t+\theta }^t{\xi }_i^{I^T}(\zeta ){\xi }_i^I(\zeta )d\zeta d\theta \right)}^{\frac{1}{2}}\hfill \\ & -\sum _{i=1}^N\epsilon ∥{\xi }_i^I(t)∥-\sum _{i=1}^N\frac{\epsilon }{\sqrt{\epsilon }}\left|{\pi }_i^I(t)\right|-\sum _{i=1}^N\epsilon ∥{\xi }_i^I(t)∥-\sum _{i=1}^N\frac{\epsilon }{\sqrt{\epsilon }}\left|{\pi }_i^I(t)\right|.\hfill \end{array}$$

(20)

Then,

$$\begin{array}{cc}\hfill \dot{V}(t)\le & {\xi }_i^{R^T}(t)\left[-{\lambda }_{min}(D^R)+\frac{1}{2}{\lambda }_{max}(A^R{A}^{R^T})-\frac{1}{2}{\lambda }_{min}(A^I{A}^{I^T})+\frac{1}{2}{\lambda }_{max}(B^R{B}^{R^T})\right.\hfill \\ & -\frac{1}{2}{\lambda }_{min}(B^I{B}^{I^T})+\frac{1}{2}{\lambda }_{max}(C^R{C}^{R^T})-\frac{1}{2}{\lambda }_{min}(C^I{C}^{I^T})+\frac{1}{2}{\lambda }_{max}(P)\hfill \\ & \left.+\frac{\tau {\xi }_h^{I^2}}{2}-{\lambda }_{min}(\varphi )\right]{\xi }^R(t)+{\xi }_i^{I^T}(t)\left[-{\lambda }_{min}(D^I)+\frac{1}{2}{\lambda }_{max}(A^R{A}^{R^T})\right.\hfill \\ & +\frac{1}{2}{\lambda }_{max}(A^I{A}^{I^T})+\frac{1}{2}{\lambda }_{max}(B^R{B}^{R^T})+\frac{1}{2}{\lambda }_{max}(B^I{B}^{I^T})\hfill \\ & \left.+\frac{1}{2}{\lambda }_{max}(C^R{C}^{R^T})+\frac{1}{2}{\lambda }_{max}(C^I{C}^{I^T})+\frac{1}{2}{\lambda }_{max}(P_1)+\frac{\tau {\xi }_h^{I^2}}{2}-{\lambda }_{min}(\varphi )\right]{\xi }^I(t)\hfill \\ & +\sum _{i=1}^N{\xi }_i^{R^T}(t-\tau (t))\left[\frac{1}{2}{\xi }_k^{R^2}-\frac{1}{2}(1-\overline{\tau }P)\right]{\xi }_i^R(t-\tau (t))\hfill \\ & +\sum _{i=1}^N{\xi }_i^{I^T}(t-\tau (t))\left[\frac{1}{2}{\xi }_k^{I^2}-\frac{1}{2}(1-\overline{\tau }{P}_1)\right]{\xi }_i^I(t-\tau (t))\hfill \\ & -\sum _{i=1}^N\epsilon {\left({\int }_{t-\tau (t)}^t{\xi }_i^{R^T}(s)P{\xi }_i^R(s)ds\right)}^{\frac{1}{2}}-\sum _{i=1}^N\epsilon {\left({\int }_{t-\tau (t)}^t{\xi }_i^{I^T}(s)P{\xi }_i^I(s)ds\right)}^{\frac{1}{2}}\hfill \\ & -\sum _{i=1}^N\epsilon {\xi }_h^{R^2}{\left({\int }_{-\tau }^0{\int }_{t+\theta }^t{\xi }_i^{R^T}(\zeta ){\xi }_i^R(\zeta )d\zeta d\theta \right)}^{\frac{1}{2}}-\sum _{i=1}^N\epsilon {\xi }_h^{I^2}{\left({\int }_{-\tau }^0{\int }_{t+\theta }^t{\xi }_i^{I^T}(\zeta ){\xi }_i^I(\zeta )d\zeta d\theta \right)}^{\frac{1}{2}}\hfill \\ & -\sum _{i=1}^N\epsilon ∥{\xi }_i^I(t)∥-\sum _{i=1}^N\frac{\epsilon }{\sqrt{\epsilon }}\left|{\pi }_i^I(t)\right|-\sum _{i=1}^N\epsilon ∥{\xi }_i^I(t)∥-\sum _{i=1}^N\frac{\epsilon }{\sqrt{\epsilon }}\left|{\pi }_i^I(t)\right|.\hfill \end{array}$$

(21)

Based on inequality conditions (7)–(9), we have

$$\begin{array}{cc}\hfill \dot{V}(t)\le & \sum _{i=1}^N\left[-\sum _{i=1}^N\epsilon {\left({\int }_{t-\tau (t)}^t{\xi }_i^{R^T}(s)P{\xi }_i^R(s)ds\right)}^{\frac{1}{2}}-\sum _{i=1}^N\epsilon {\left({\int }_{t-\tau (t)}^t{\xi }_i^{I^T}(s)P{\xi }_i^I(s)ds\right)}^{\frac{1}{2}}\right.\hfill \\ & -\sum _{i=1}^N\epsilon {\xi }_h^R{\left({\int }_{-\tau }^0{\int }_{t+\theta }^t{\xi }_i^{R^T}(\zeta ){\xi }_i^R(\zeta )d\zeta d\theta \right)}^{\frac{1}{2}}-\sum _{i=1}^N\epsilon {\xi }_h^I{\left({\int }_{-\tau }^0{\int }_{t+\theta }^t{\xi }_i^{I^T}(\zeta ){\xi }_i^I(\zeta )d\zeta d\theta \right)}^{\frac{1}{2}}\hfill \\ & \left.-\sum _{i=1}^N\epsilon {({∥{\xi }_i^I(t)∥}^2)}^{\frac{1}{2}}-\sum _{i=1}^N\frac{\epsilon }{\sqrt{\epsilon }}{({\left|{\pi }_i^I(t)\right|}^2)}^{\frac{1}{2}}-\sum _{i=1}^N\epsilon {({∥{\xi }_i^I(t)∥}^2)}^{\frac{1}{2}}-\sum _{i=1}^N\frac{\epsilon }{\sqrt{\epsilon }}{({\left|{\pi }_i^I(t)\right|}^2)}^{\frac{1}{2}}\right],\hfill \\ \hfill \le & -\sqrt{2}\epsilon \left[\frac{1}{2}\sum _{i=1}^N{\xi }_i^{R^T}(t){\xi }_i^R(t)+\frac{1}{2}\sum _{i=1}^N{\xi }_i^{I^T}(t){\xi }_i^I(t)+\frac{1}{2}\sum _{i=1}^N{\int }_{t-\widehat{\tau }(t)}^t{\xi }_i^{R^T}(\theta )P{\xi }_i^R(\theta )d\theta \right.\hfill \\ & +\frac{1}{2}\sum _{i=1}^N{\int }_{t-\widehat{\tau }(t)}^t{\xi }_i^{I^T}(t)P_1{\xi }_i^I(t)d\theta +\frac{1}{2}\sum _{i=1}^N{\int }_{-\tau (t)}^0{\int }_{t+s}^t{\xi }_i^{R^T}(\zeta ){\xi }_h^T{\xi }_h{\xi }_i(\zeta )d\zeta ds\hfill \\ & {\left.+\frac{1}{2}\sum _{i=1}^N{\int }_{-\tau (t)}^0{\int }_{t+s}^t{\xi }_i^{I^T}(\zeta ){\xi }_h^T{\xi }_h{\xi }_i(\zeta )d\zeta ds+\sum _{i=1}^N\frac{1}{2\omega }{\pi }_i^{R^2}(t)+\sum _{i=1}^N\frac{1}{2\omega }{\pi }_i^{I^2}(t)\right]}^{\frac{1}{2}},\hfill \\ \hfill =& -\sqrt{2}\epsilon V{(t)}^{\frac{1}{2}}.\hfill \end{array}$$

(22)

□

From Lemma 2 and (22), the error converges to zero in a finite amount of time under $\mathbb{T}=t_0+\frac{{(2V(t_0))}^{\frac{1}{2}}}{\epsilon }$. As such, using the formulated adaptive control scheme, the finite-time CS problem of neutral-type CVCNNs with mixed delays can be solved. This concludes the proof.

4. Numerical Evaluation

To demonstrate the effectiveness of the aforementioned results, we consider the following numerical example

Case (i): A neutral-type CVCNN model with distributed delays is formed, where the $ith$ dynamics of the model is described as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \frac{d{\varphi }_i(t)}{dt}=& E{\dot{\varphi }}_i(t-\sigma (t))-D{\xi }_i(t)+A\widehat{f}\left({\varphi }_i(t)\right)+B\widehat{k}({\varphi }_i(t-\tau (t)))+C{\int }_{t-\tau }^t\widehat{h}\left({\varphi }_i(\zeta )\right)d\zeta \hfill \\ & +\sum _{j=1}^N{l}_{ij}\Gamma {\varphi }_j(t-\tau (t))+u_i(t),t>0,\hfill \\ \hfill {\varphi }_i(s)=& {\vartheta }_i(s),s\in [-\tau ,0],i=1,2,\dots ,N,\hfill \end{array}\right.\end{array}$$

(23)

where ${\varphi }_i(t)={[{\varphi }_{1i}(t),{\varphi }_{2i}(t)]}^T\in {\mathbb{C}}^2$ is the state vector of the model and its parameters are defined as

$$\begin{array}{cc}\hfill E=& \left[\begin{array}{cc}0.5+\mathbf{i}0.5& 0\\ 0& 0.5+\mathbf{i}0.5\end{array}\right],D=\left[\begin{array}{cc}0.1+\mathbf{i}0.6& 0\\ 0& 0.1+\mathbf{i}0.6\end{array}\right],\hfill \\ \hfill A=& \left[\begin{array}{cc}1.2+\mathbf{i}1.0& -0.1+\mathbf{i}3.2\\ -0.5+\mathbf{i}0.1& 0.2+\mathbf{i}0.1\end{array}\right],B=\left[\begin{array}{cc}1+\mathbf{i}0.2& -0.5+\mathbf{i}0.2\\ -1.5+\mathbf{i}1.1& 0.3+\mathbf{i}0.1\end{array}\right],\hfill \\ \hfill C=& \left[\begin{array}{cc}2.2+\mathbf{i}1.4& -0.7+\mathbf{i}3.2\\ -0.6+\mathbf{i}0.1& 0.5+\mathbf{i}0.1\end{array}\right],\hfill \end{array}$$

The time-varying delay is chosen as $\tau (t)=e^t/(1+e^t)$ and $\overline{\tau }=1$, while the activations are considered to be $\widehat{f}({\varphi }_i(t))=tanh({\varphi }_i(t)),\widehat{f}({\varphi }_i(t))=tanh({\varphi }_i(t))$. According to Assumptions 1–4, $\widehat{f}({\varphi }_i(t))=tanh({\varphi }_i^R(t))+\mathbf{i}tanh({\varphi }_i^I(t)),\widehat{f}({\varphi }_i(t))=tanh({\varphi }_i^R(t))+\mathbf{i}tanh({\varphi }_i^I(t))$, let ${\xi }_f^R={\xi }_f^I={\xi }_k^R={\xi }_k^I={\xi }_h^R={\xi }_h^I=1,\varsigma =20,\tilde{\varsigma }=5,{\lambda }_{min}(D^R)=1,{\lambda }_{min}(D^I)=1,{\lambda }_{max}(A^R{A}^{R^T})=1.7190,{\lambda }_{max}(A^I{A}^{I^T})=1.0181,{\lambda }_{max}(B^R{B}^{R^T})=3.5327,$${\lambda }_{max}(B^I{B}^{I^T})=1.2685,{\lambda }_{max}(C^R{C}^{R^T})=5.8611,{\lambda }_{max}(C^I{C}^{I^T})=12.2173,$${\lambda }_{max}(E^R{E}^{R^T})=0.0100,{\lambda }_{max}(E^I{E}^{I^T})=0.3600{\lambda }_{min}(A^R{A}^{R^T})=0.0210,$${\lambda }_{min}(A^I{A}^{I^T})=0.0119,$${\lambda }_{min}(B^R{B}^{R^T})=0.0573,{\lambda }_{min}(B^I{B}^{I^T})=0.0315,{\lambda }_{min}(C^R{C}^{R^T})=0.0789,{\lambda }_{min}(C^I{C}^{I^T})=0.0027,{\lambda }_{min}(E^R{E}^{R^T})=0.0100,{\lambda }_{min}(E^I{E}^{I^T})=0.3600.$ According to Theorem 1, the conditions obtained indicate the feasible solutions are $741.3839<{\lambda }_{min}(\varphi ),755.5942<{\lambda }_{min}({\varphi }_1),$${\lambda }_{max}(P{P}^T)=1.4872\times {10}^3,{\lambda }_{max}(P_1{P}_1^T)=1.4866\times {10}^3.$ The outer coupling term of the given system is given as

$$\begin{array}{c}\hfill {(l_{ij})}_{4\times 4}=\left(\begin{array}{cccc}2& -1& -1& 0\\ 0& 1& 0& 0\\ 0& -1& 1& 0\\ 0& 0& 0& 1\end{array}\right)\end{array}$$

Furthermore, the drive system is described as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \frac{d{\psi }_h(t)}{dt}=& E{\dot{\psi }}_h(t-\sigma (t))-D{\psi }_h(t)+A\widehat{f}\left({\psi }_h(t)\right)+B\widehat{k}({\psi }_h(t-\tau (t)))\hfill \\ & +C{\int }_{t-\tau }^t\widehat{h}\left({\psi }_h(\zeta )\right)d\zeta ,t>0,\hfill \\ \hfill {\psi }_h(s)=& {\phi }_h(s),s\in [-\tau ,0],h=1,2,\dots ,g,\hfill \end{array}\right.\end{array}$$

(24)

where ${\psi }_h(t)={\left[{\psi }_{h1}(t),{\psi }_{h2}(t)\right]}^T$ is the state vector of the drive model, while the parameters of the drive system are considered the same as those of the response system in this example.

Then, by employing Assumption 1, the error model can be obtained as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\dot{\xi }}_i^R(t)=& E^R{\dot{\xi }}_i^R(t-\tau (t))+E^I{\dot{\xi }}_i^I(t-\tau (t))-D^R{\xi }_i^R(t)+A^R{\widehat{f}}^R({\xi }_i(t))-A^I{\widehat{f}}^I({\xi }_i(t))\hfill \\ & +B^R{\widehat{K}}^R({\xi }_i(t-\tau (t)))-B^I{\widehat{K}}^I({\xi }_i(t-\tau (t)))+C^R{\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta \hfill \\ & -C^I{\int }_{t-\tau }^t{\widehat{h}}^I\left({\xi }_i(\zeta )\right)d\zeta +\sum _{j=1}^N{l}_{ij}\Gamma {\xi }^R(t-\tau (t)+u^R(t),\hfill \\ \hfill {\dot{\xi }}_i^I(t)=& E^I{\dot{\xi }}_i^R(t-\tau (t))+E^R{\dot{\xi }}_i^I(t-\tau (t))-D^R{\xi }_i^I(t)+A^R{\widehat{f}}^I({\xi }_i(t))+A^I{\widehat{f}}^R({\xi }_i(t))\hfill \\ & +B^R{\widehat{K}}^I(\xi (t-\tau (t)))+B^I{\widehat{K}}^R(\xi (t-\tau (t)))+C^R{\int }_{t-\tau }^t{\widehat{h}}^I\left({\xi }_i(\zeta )\right)d\zeta \hfill \\ & +C^I{\int }_{t-\tau }^t{\widehat{h}}^R\left({\xi }_i(\zeta )\right)d\zeta +\sum _{j=1}^N{l}_{ij}\Gamma {\xi }^I(t-\tau (t)+u^I(t),\hfill \\ \hfill {\xi }_i^R(s)=& {\vartheta }_i^R(s)-{\phi }_h^R(s),{\xi }_i^I(s)={\vartheta }_i^I(s)-{\phi }_h^I(s),s\in [-\tau ,0],i=1,2,\dots ,N,\hfill \end{array}\right.\end{array}$$

(25)

where ${\xi }_i^R(t)={({\xi }_{i1}^R(t),{\xi }_{i2}^R(t),\dots ,{\xi }_{in}^R(t))}^T,{\xi }_i^I(t)={({\xi }_{i1}^I(t),{\xi }_{i2}^I(t),\dots ,{\xi }_{in}^I(t))}^T,E=E^R+\mathbf{i}{E}^I={(e_{pq}^R)}_{n\times n}+\mathbf{i}{(e_{pq}^I)}_{n\times n},A=A^R+\mathbf{i}{A}^I={(a_{pq}^R)}_{n\times n}+\mathbf{i}{(a_{pq}^I)}_{n\times n},B=B^R+\mathbf{i}{B}^I={(b_{pq}^R)}_{n\times n}+\mathbf{i}{(b_{pq}^I)}_{n\times n},C=C^R+\mathbf{i}{C}^I={(c_{pq}^R)}_{n\times n}+\mathbf{i}{(c_{pq}^I)}_{n\times n},u(t)=u^R(t)+\mathbf{i}{u}^I(t).$

If the state of the above-mentioned system is finite-time stable, then finite-time CS of (23) and (24) is solved.

$$\begin{array}{cc}\hfill E^R=& \left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right],D^R=\left[\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right],A^R=\left[\begin{array}{cc}1.2& -0.1\\ -0.5& 0.2\end{array}\right],B^R=\left[\begin{array}{cc}1& -0.5\\ -1.5& 0.3\end{array}\right],\hfill \\ \hfill E^I=& \left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right],D^I=\left[\begin{array}{cc}0.6& 0\\ 0& 0.6\end{array}\right],A^I=\left[\begin{array}{cc}1.0& 3.2\\ 0.1& 0.1\end{array}\right],B^I=\left[\begin{array}{cc}0.2& 0.2\\ 1.1& 0.1\end{array}\right],\hfill \\ \hfill C^R=& \left[\begin{array}{cc}2.2& -0.7\\ -0.6& 0.5\end{array}\right],C^I=\left[\begin{array}{cc}1.4& 3.2\\ 0.1& 0.1\end{array}\right],\hfill \end{array}$$

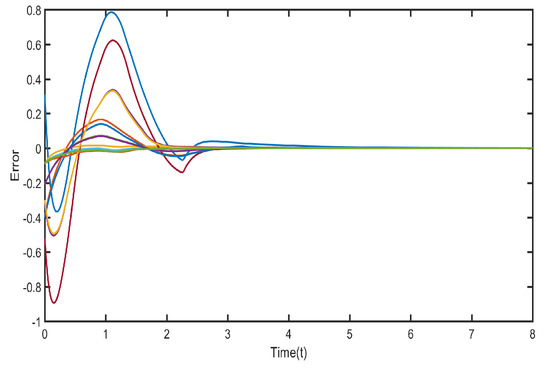
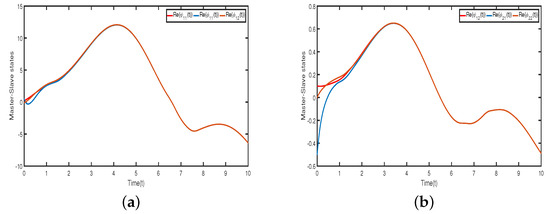
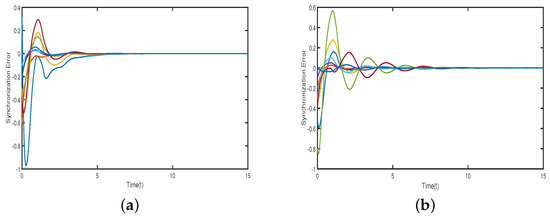
Figure 1, Figure 2, Figure 3 and Figure 4 illustrate that neurons in each cluster can synchronize with their target neurons in a finite amount of time, while under the adaptive controller, synchronization among various clusters is not achievable. Figure 5 displays the trajectories of the CS errors.

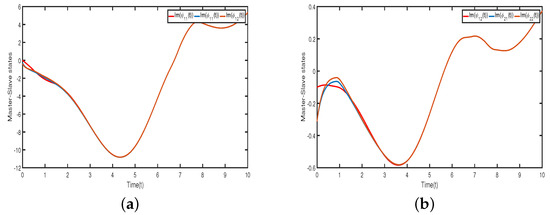
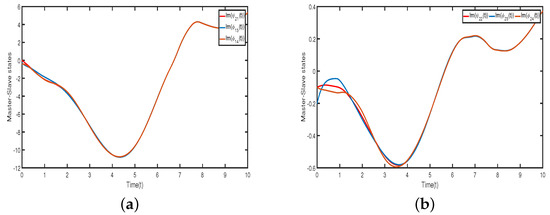
Case (ii): We consider the state of the model (23) as in the three-dimensional complex domain ${\varphi }_i(t)\in {\mathbb{C}}^3$, that is ${\varphi }_i(t)={({\varphi }_{1i}(t),{\varphi }_{2i}(t),{\varphi }_{3i}(t))}^T$. Then, the system parameters are must be three-dimensional and are taken as

$$\begin{array}{cc}\hfill E=& \left[\begin{array}{ccc}0.5+\mathbf{i}0.5& 0& 0\\ 0& 0.5+\mathbf{i}0.5& 0\\ 0& 0& 0.5+\mathbf{i}0.5\end{array}\right],D=\left[\begin{array}{ccc}0.1+\mathbf{i}0.6& 0& 0\\ 0& 0.1+\mathbf{i}0.6& 0\\ 0& 0& 0.1+\mathbf{i}0.6\end{array}\right],\hfill \\ \hfill A=& \left[\begin{array}{ccc}1.78+\mathbf{i}0.1& 21+\mathbf{i}0.02& 0.1+\mathbf{i}0.3\\ 0.1+\mathbf{i}0.0& 1.78+\mathbf{i}0.01& 0.2+\mathbf{i}0.1\\ 0.2+\mathbf{i}0.0& 0+\mathbf{i}0.01& 0.1+\mathbf{i}0.1\end{array}\right],\hfill \\ \hfill B=& \left[\begin{array}{ccc}-1.44-\mathbf{i}0.1& 0.2+\mathbf{i}0.0& 0.1+\mathbf{i}0.2\\ 0.1+\mathbf{i}0.01& -1.44+\mathbf{i}0.0& 0.1+\mathbf{i}0.02\\ 0.2+\mathbf{i}0.07& -0.1-\mathbf{i}0.08& 0.1+\mathbf{i}0.01\end{array}\right],\hfill \\ \hfill C=& \left[\begin{array}{ccc}2.2+\mathbf{i}1.4& -0.7+\mathbf{i}3.2& 0.1+\mathbf{i}0.02\\ -0.6+\mathbf{i}0.1& 0.5+\mathbf{i}0.1& 0+\mathbf{i}0.01\\ 0.01+\mathbf{i}0& 0.02+\mathbf{i}0.1& 0+\mathbf{i}0.02\end{array}\right].\hfill \end{array}$$

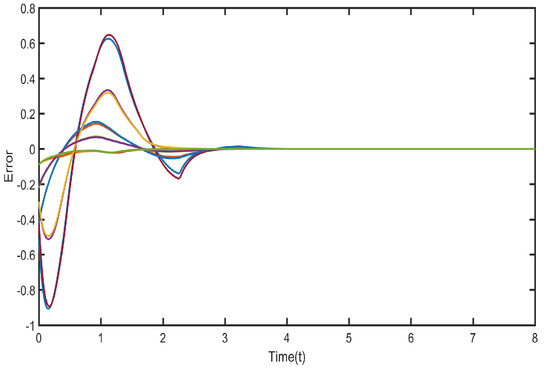
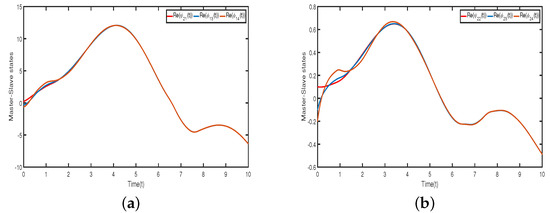
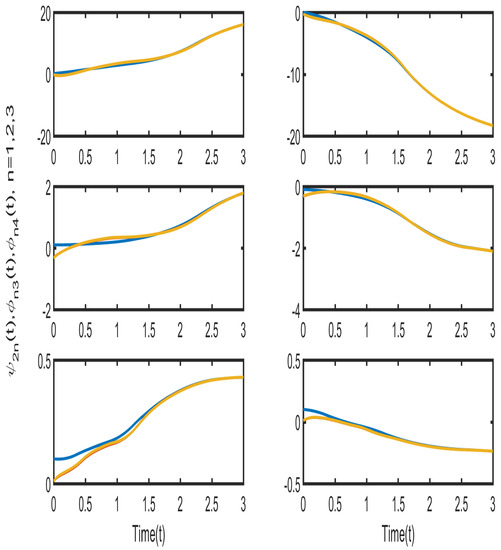
Therefore, according to the Assumptions 1–4 and Theorem 1, the conditions obtained indicate the feasible solutions are $770.7230<{\lambda }_{min}(\varphi ),782.8778<{\lambda }_{min}({\varphi }_1),{\lambda }_{max}(P{P}^T)=1.0990\times {10}^3,{\lambda }_{max}(P_1{P}_1^T)=1.0985\times {10}^3$. Figure 6 and Figure 7 illustrate, that neurons in each cluster can synchronize with their target neurons in a finite amount of time, while under the adaptive controller, synchronization among various clusters is not achievable. Figure 8 and Figure 9 displays the trajectories of the CS errors.

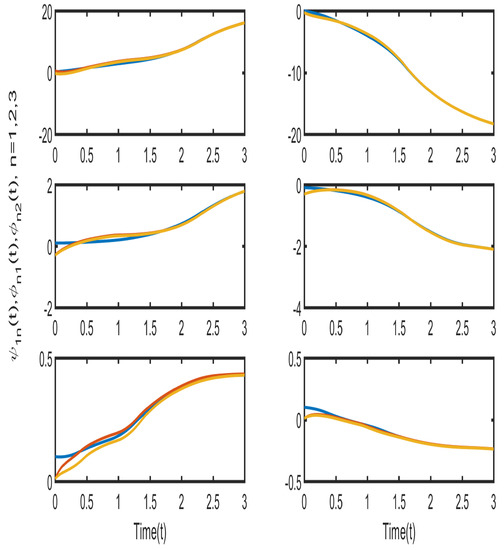
Remark 5.

As a result, many academics have made significant efforts to study delayed neural network systems, and many excellent publications have resulted from their efforts [46,47,48,49]. For instance, the authors of [46] investigated the stability issues of neutral-type Cohen–Grossberg neural networks with multiple time delays. A novel sufficient stability criterion is derived for Cohen–Grossberg neural networks of neutral type with multiple delays by utilizing a modified and enhanced version of a previously introduced Lyapunov functional. The new stability problems for more general models of neutral-type neural network systems were investigated in [47,48]. In this study, new finite-time CS of CCVNN models with single neutral delay were realized under adaptive control. The obtained results can extend further those in the existing literature [46,47,48,49]. For further research, the dynamics of coupled delayed CVNN models with multiple neutral delays and impulsive effects will be investigated.

5. Conclusions

In this study, we examined the issue of adaptive finite-time CS pertaining to neutral-type CVCNNs with mixed time delays. The relevant stability analysis is very challenging, since it takes into account a more general dynamic model of neutral-type CVCNN with mixed time delays. A useful adaptive control scheme has been developed to address this challenging issue. Using the Lyapunov functionals approach and linear matrix inequality, the corresponding adequate conditions have been obtained. The simulation results positively indicate the viability and validity of the proposed method. For further work, finite-time CS of neutral-type delayed CVCNNs with stochastic inputs and disturbances will be studied in detail.