Finite Iterative Forecasting Model Based on Fractional Generalized Pareto Motion
Abstract
:1. Introduction
2. Generalized Pareto Distribution
2.1. Parameter Meaning of Generalized Pareto
2.2. LRD Characteristics of Generalized Pareto Motion
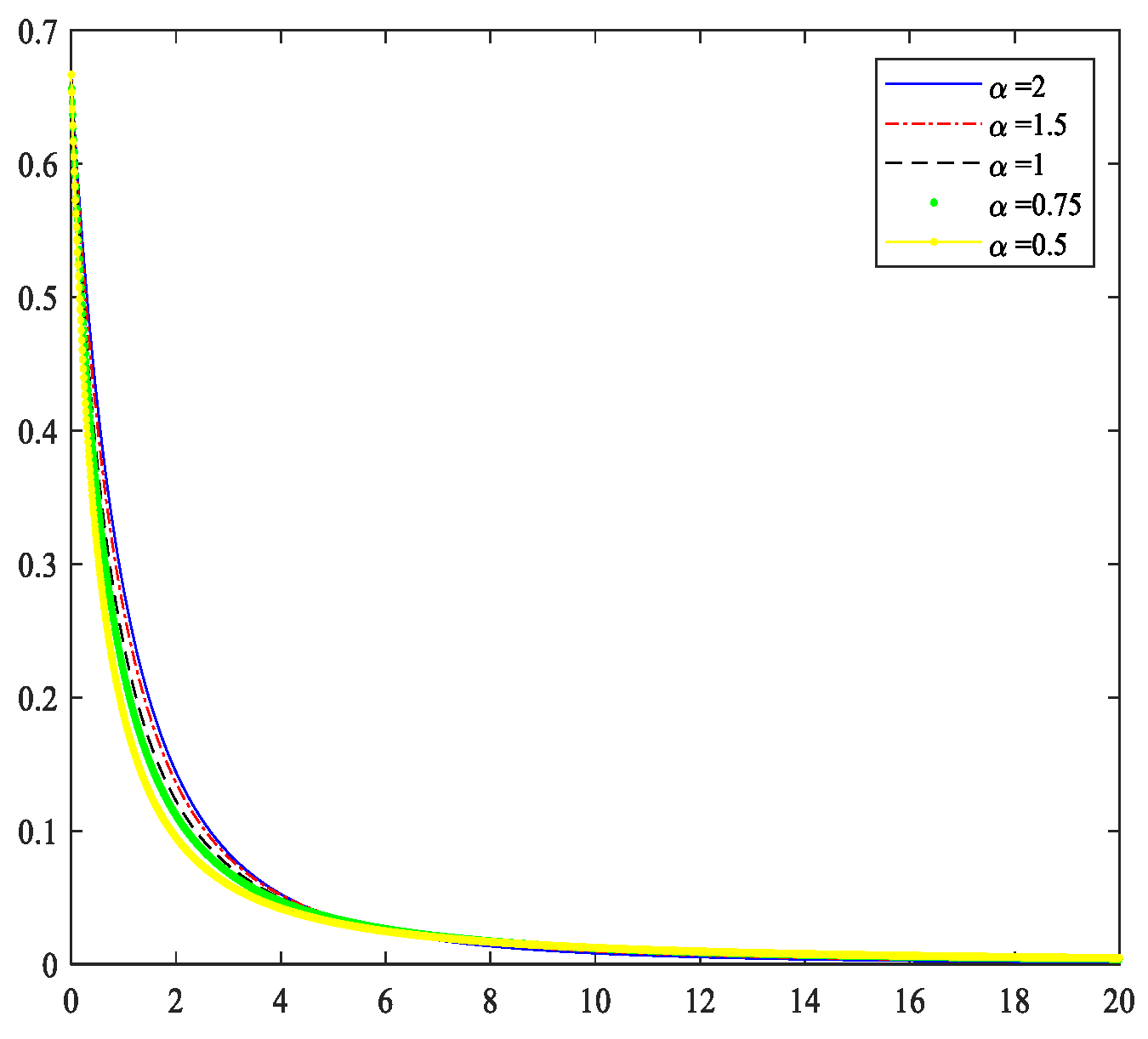
2.3. Incremental Distribution of the Generalized Pareto
- (1).
- Generate GPD-compliant time series.
- (2).
- Determine the time interval , and the two-state quantities separated by in the sequence are differentiated multiple times, i.e., . Repeat the above process to make multiple differences of the generated time series to form an incremental set.
- (3).
- Draw the histogram of the incremental set, in order to obtain the probability density map of the set and select a known distribution to fit it according to the characteristics of the probability distribution.
- (4).
- (1).
- (2).
- Partition the value range of the overall data in Figure 4 into intervals [,], (, can be ), where the size of k is not strictly specified, but if it is too small, it will make the test too rough, and if it is too large, it will increase random errors. Usually, the sample size n is larger, and k can be slightly larger, but generally . In this example, there are four grouping cases k = 10, 12, 14, 16.
- (3).
- Assuming that holds, calculate the theoretical probability and theoretical frequency of each interval:
- (4).
- According to the sample observation values in Figure 4, calculate the actual frequency of falling in the interval [,], and then calculate the observation value of the statistic :
- (5).
- Accordingly, choosing 95% based on confidence, check the distribution Table, and get , where r is the number of unknown parameters in the generalized Pareto distribution PDF, because the generalized Pareto distribution PDF parameters are known, so . The four sets of values found out from the table and the values obtained from the four experiments are compared in Table 1:
3. Fractional Generalized Pareto Motion
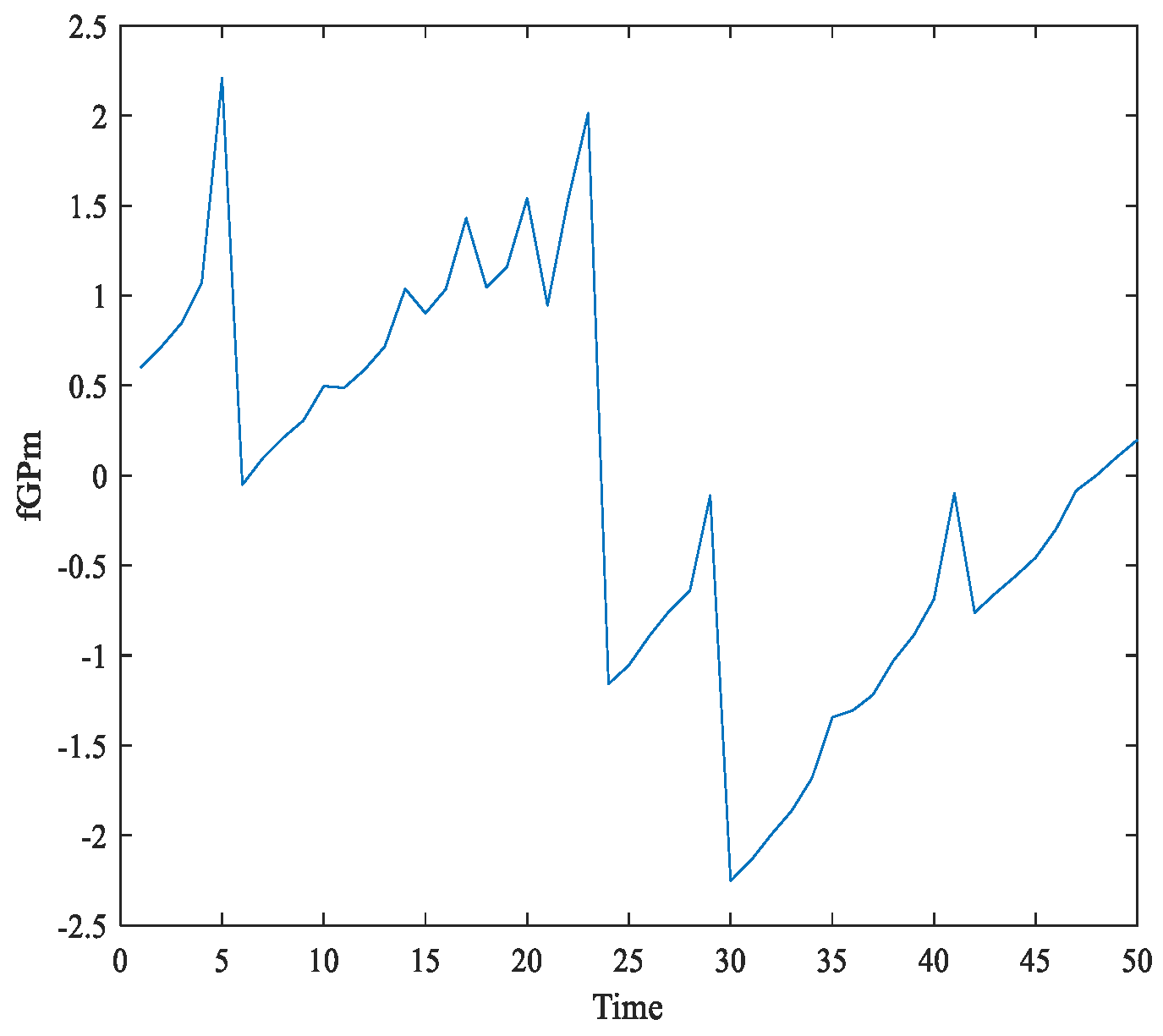
3.1. Fractional Generalized Pareto Motion Model
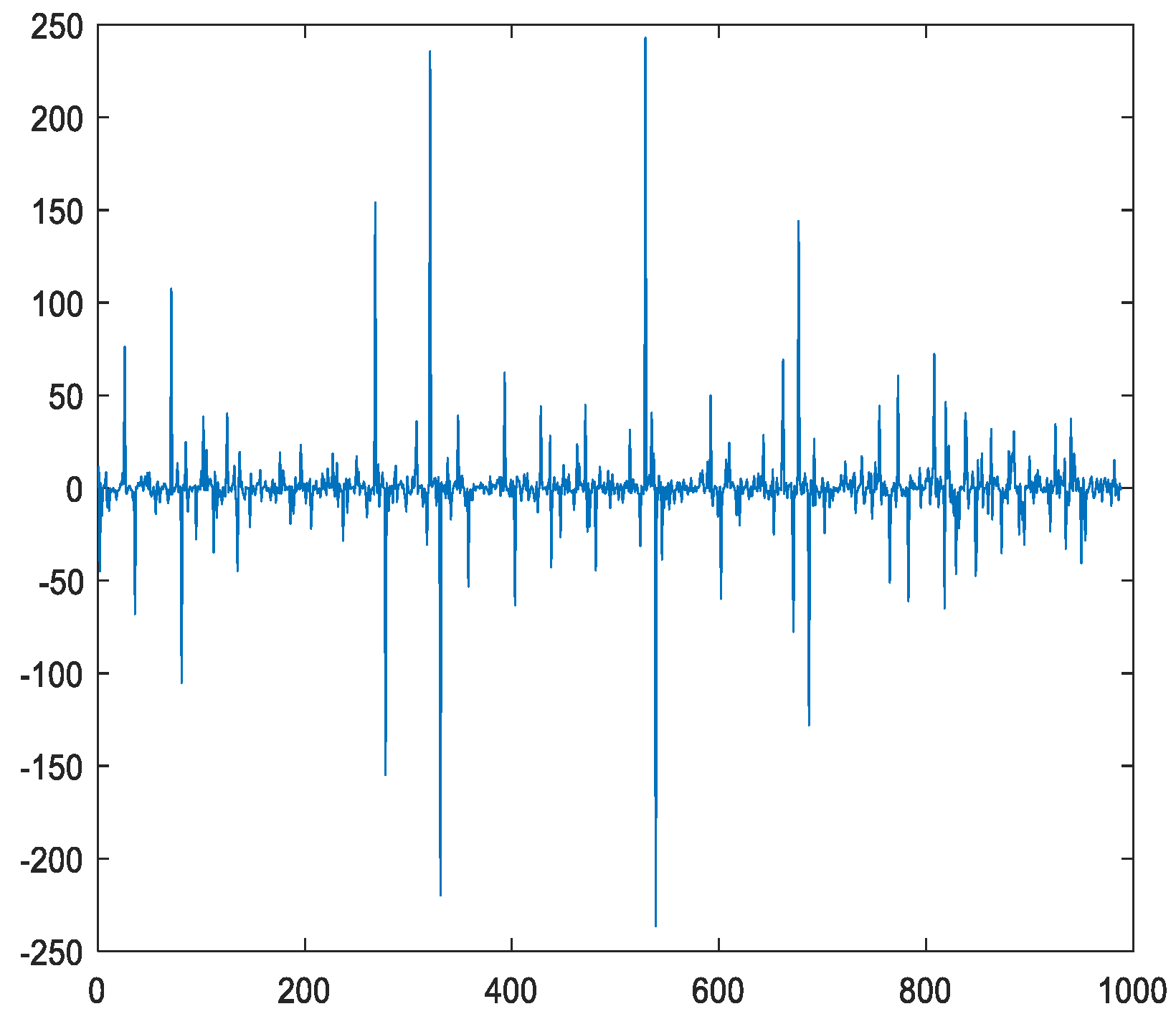
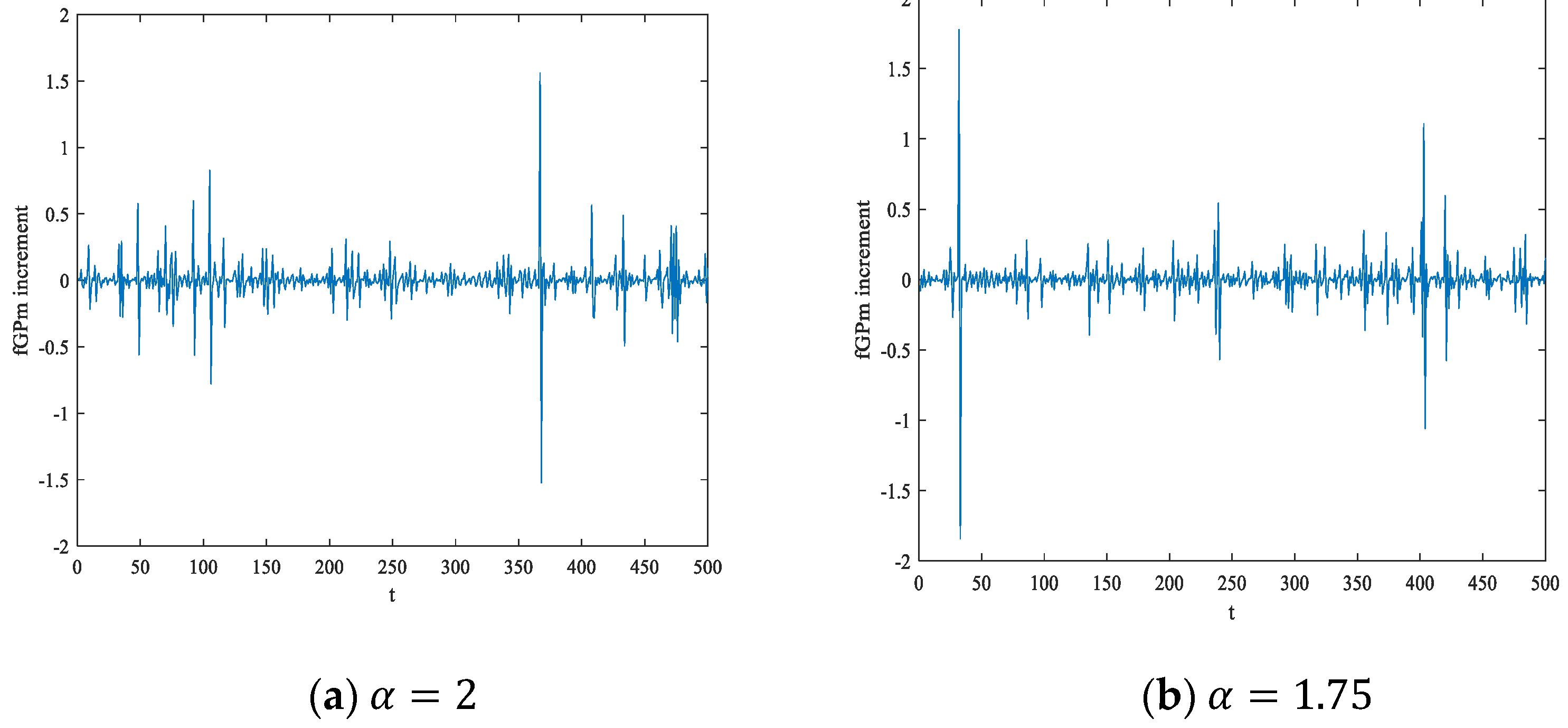
3.2. Fractional Generalized Pareto Motion Incremental Processes Model
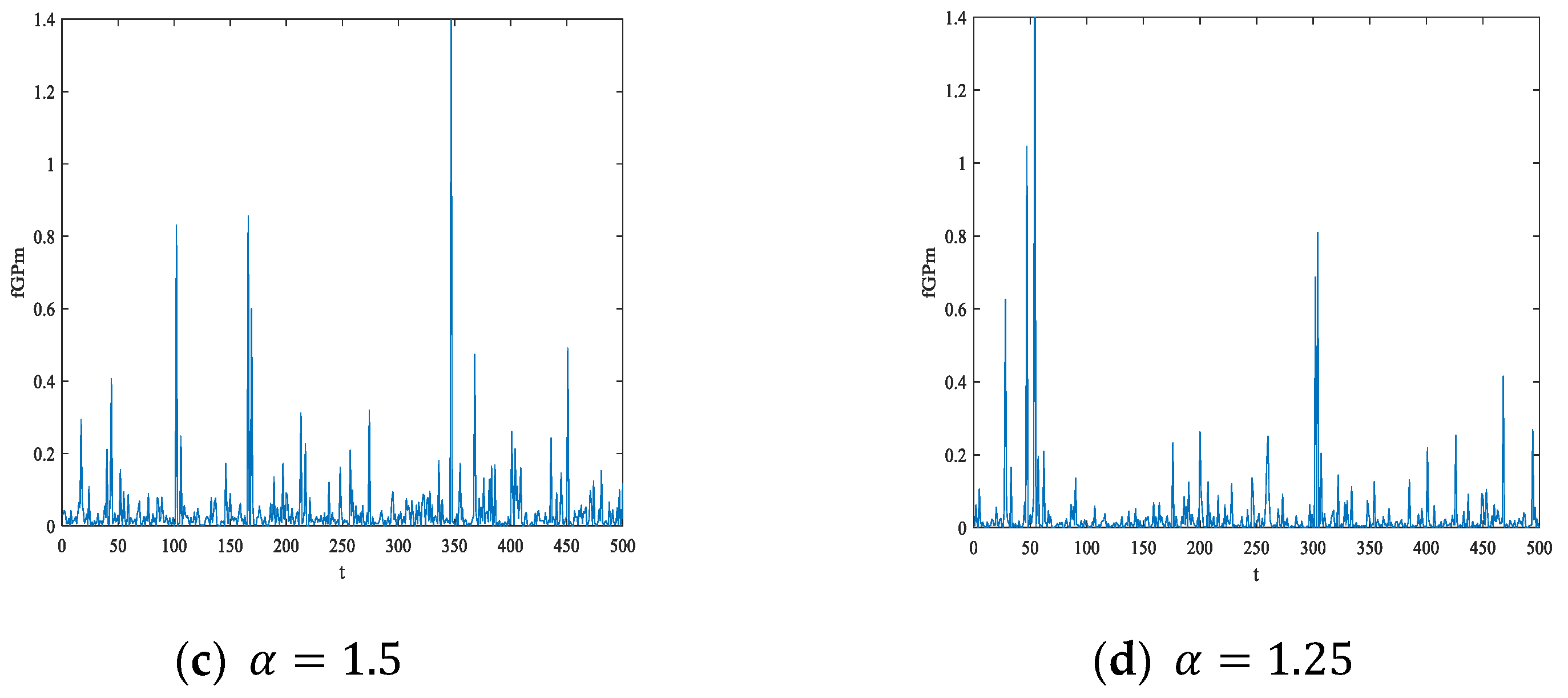
3.3. Long-Range Dependence and Self-Similarity of Fractional Generalized Pareto Motion
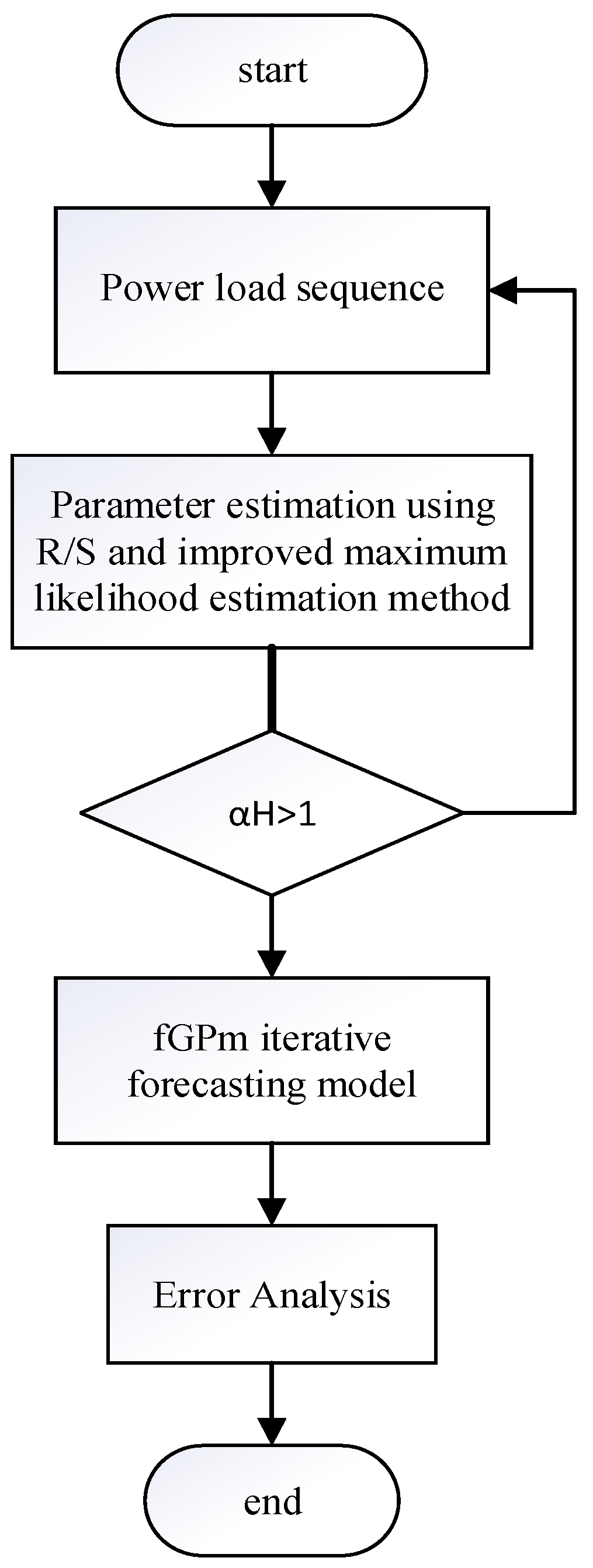
4. Iterative Forecasting Model based on Fractional Generalized Pareto Motion
4.1. Iterative Forecasting Model
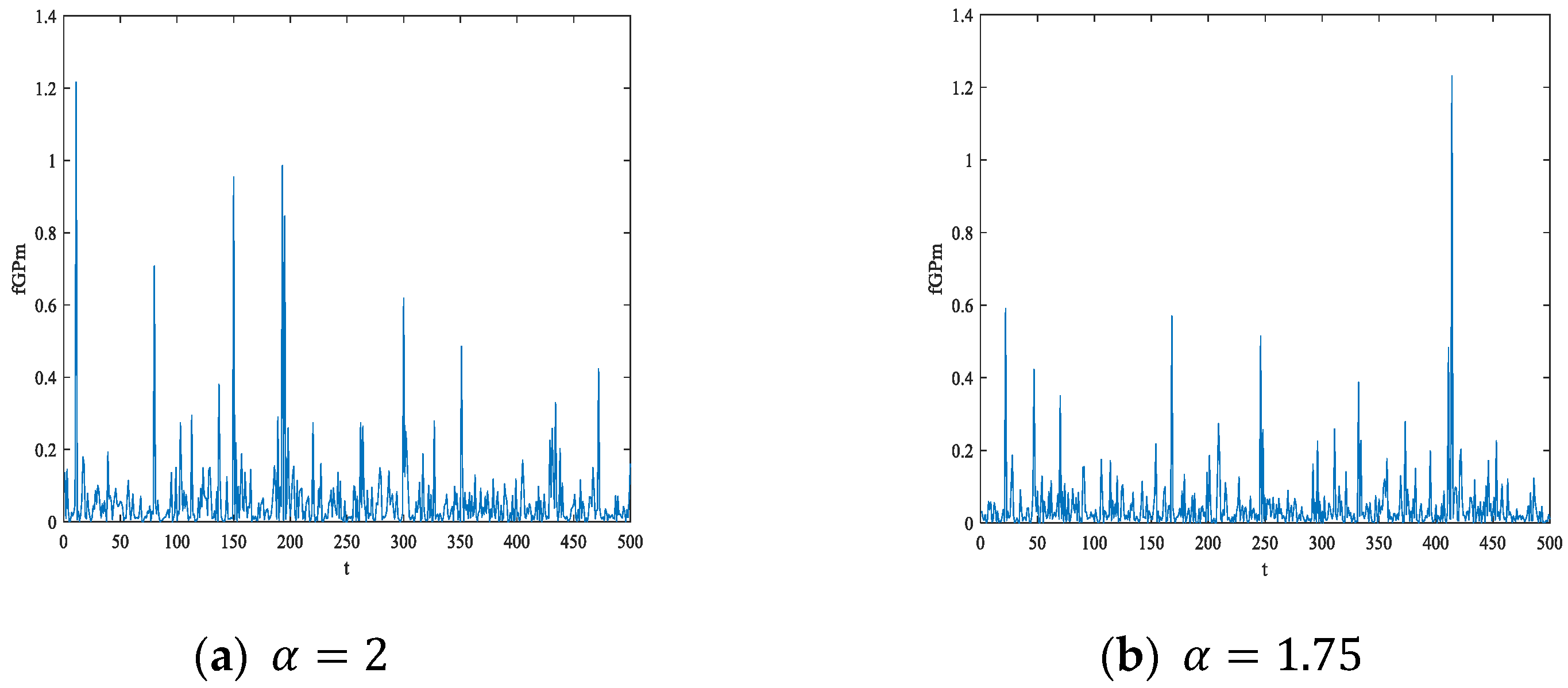
4.2. Parameter Estimation of μ,δ,α
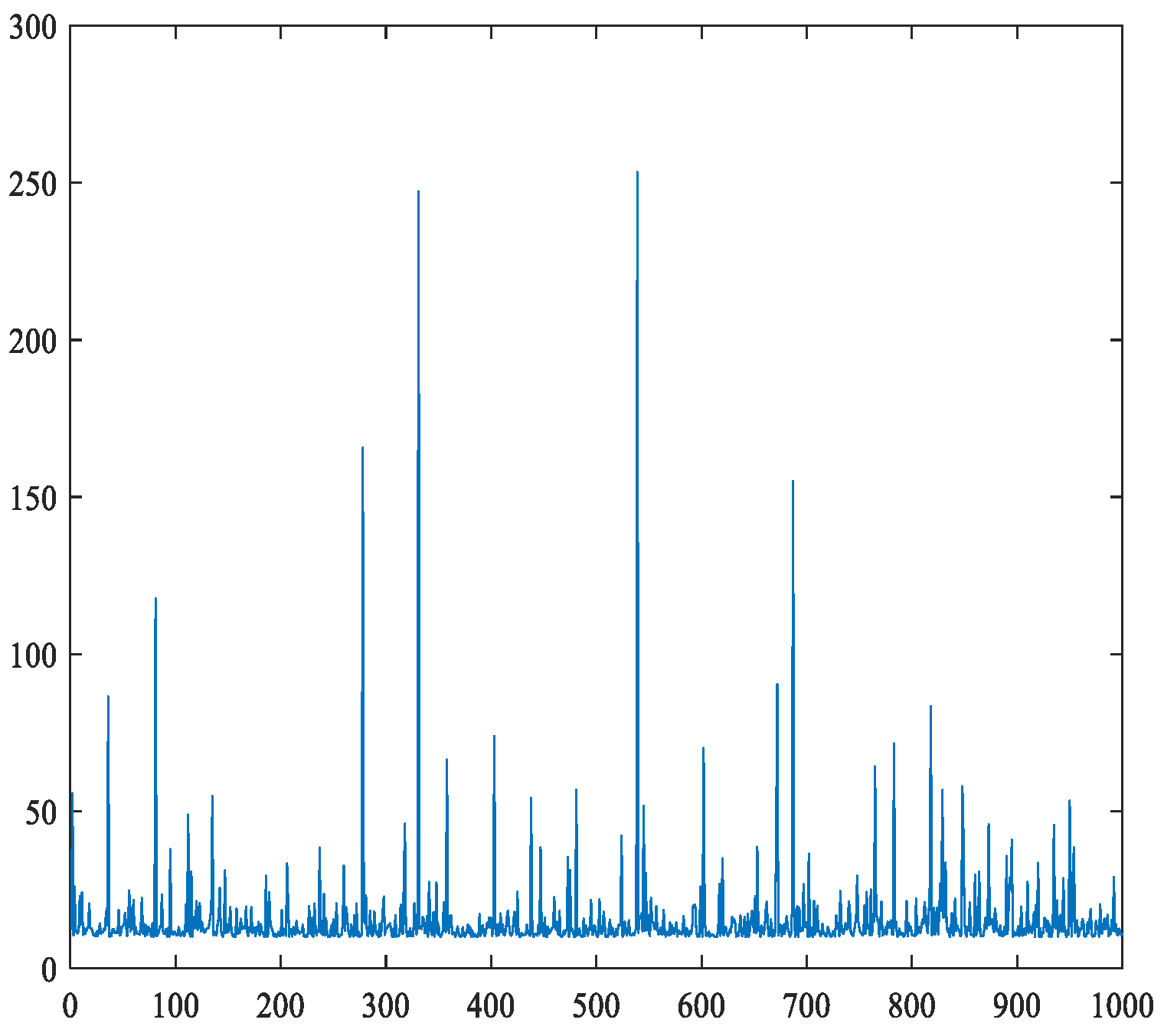
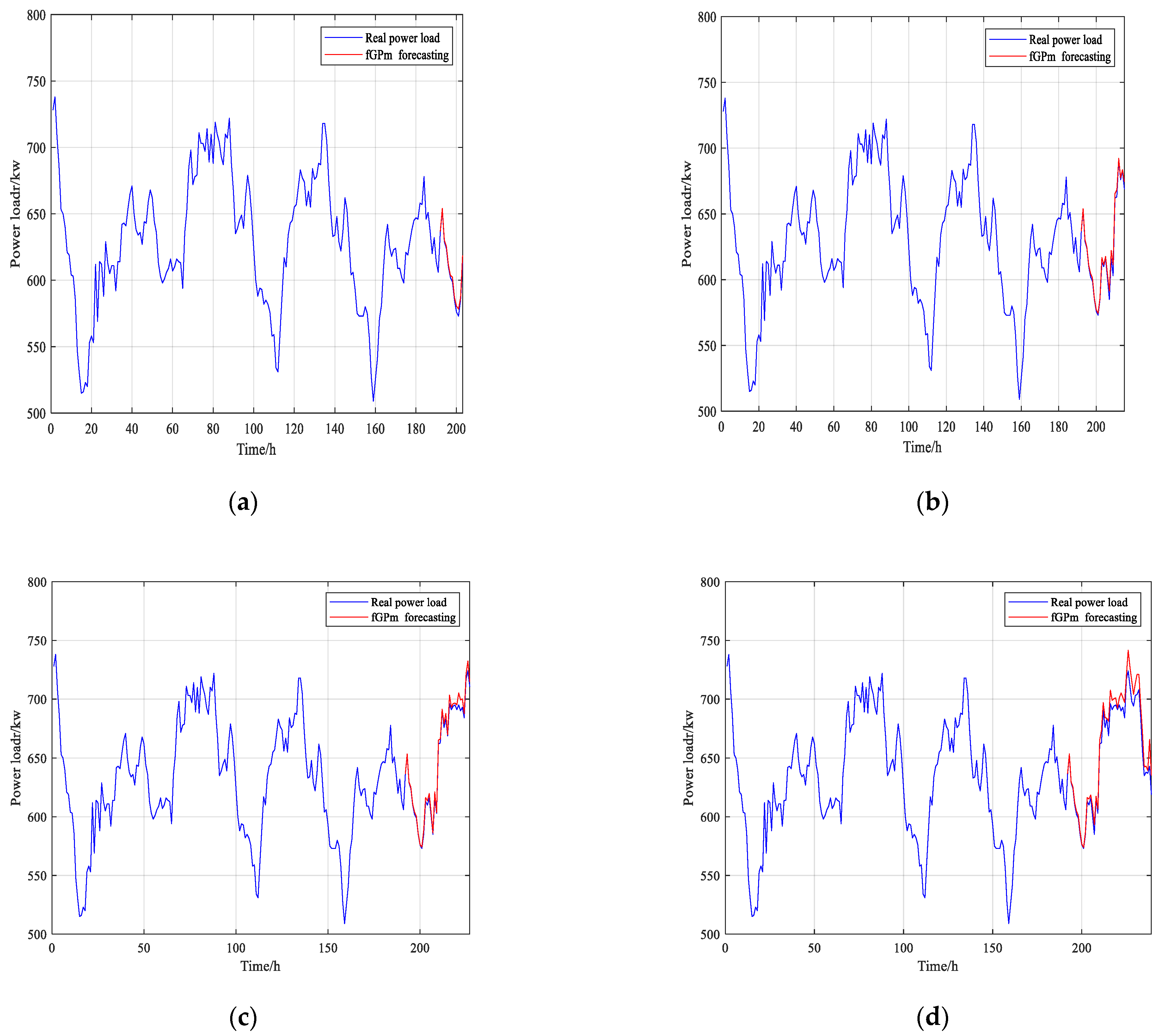
5. Case Study
5.1. Case 1: Weekdays
5.2. Case 2: Weekends
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morf, H. Sunshine and cloud cover prediction based on Markov processes. Sol. Energy 2014, 110, 615–626. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Tseng, S.-T.; Balakrishnan, N. Optimal Design for Degradation Tests Based on Gamma Processes with Random Effects. IEEE Trans. Reliab. 2012, 61, 604–613. [Google Scholar] [CrossRef]
- Ye, Z.-S.; Wang, Y.; Tsui, K.-L.; Pecht, M. Degradation Data Analysis Using Wiener Processes With Measurement Errors. IEEE Trans. Reliab. 2013, 62, 772–780. [Google Scholar] [CrossRef]
- Sottinen, T.; Viitasaari, L. Prediction law of fractional Brownian motion. Stat. Probab. Lett. 2017, 129, 155–166. [Google Scholar] [CrossRef]
- Lahiri, S.N.; Das, U.; Nordman, D.J. Empirical Likelihood for a Long Range Dependent Process Subordinated to a Gaussian Process. J. Time Ser. Anal. 2019, 40, 447–466. [Google Scholar] [CrossRef]
- Li, M. Record length requirement of long-range dependent teletraffic. Phys. A Stat. Mech. Its Appl. 2017, 472, 164–187. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Linear Models with Long-Range Dependence and with Finite or Infinite Variance. In New Directions in Time Series Analysis; Springer: New York, NY, USA, 1993; Volume 46, pp. 325–340. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Routledge: London, UK, 2017. [Google Scholar] [CrossRef]
- Embrechts, P.; Klüppelberg, C.; Mikosch, T. Modelling Extremal Events for Insurance and Finance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Kotz, S.; Nadarajah, S. Extreme Value Distributions: Theory and Applications; World Scientific Publishing Company: Singapore, 2000. [Google Scholar] [CrossRef] [Green Version]
- Ji, J.; Wang, D.; Xu, D.; Xu, C. Combining a self-exciting point process with the truncated generalized Pareto distribution: An extreme risk analysis under price limits. J. Empir. Financ. 2020, 57, 52–70. [Google Scholar] [CrossRef]
- Stanislavsky, A.A.; Burnecki, K.; Magdziarz, M.; Weron, A.; Weron, K. Statistical Modeling of Solar Flare Activity from Empirical Time Series of Soft X-ray Solar Emission. Astrophys. J. Lett. 2009, 693, 1877–1882. [Google Scholar] [CrossRef]
- Beran, J. Statistical Methods for Data with Long-Range Dependence. Stat. Sci. 1992, 7, 404–416. [Google Scholar] [CrossRef]
- Liu, H.; Song, W.; Zio, E. Generalized Cauchy difference iterative forecasting model for wind speed based on fractal time series. Nonlinear Dyn. 2021, 103, 759–773. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Loiseau, P.; Gonçalves, P.; Dewaele, G.; Borgnat, P.; Abry, P.; Primet, P.V.B. Investigating self-similarity and heavy-tailed dis-tributions on a large-scale experimental facility. IEEE/ACM Trans. Netw. 2010, 18, 1261–1274. [Google Scholar] [CrossRef]
- Karasaridis, A.; Hatzinakos, D. Network heavy traffic modeling using α-stable self-similar processes. IEEE Trans. Commun. 2001, 49, 1203–1214. [Google Scholar] [CrossRef]
- Liu, H.; Song, W.Q.; Zio, E. Fractional Lévy stable motion with LRD for RUL and reliability analysis of li-ion battery. ISA Tran. 2022, 125, 360–370. [Google Scholar] [CrossRef] [PubMed]
- Adler, R.; Feldman, R.; Taqqu, M.S. On Estimating the Intensity of Long-Range Dependence in Finite and Infinite Variance Time Series. In A Practical Guide to Heavy Tails: Statistical Techniques and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Janicki, A.; Weron, A. Can One See alpha-stable Variables and Processes? Stat. Sci. 1994, 9, 109–126. [Google Scholar] [CrossRef]
- Benassi, A.; Cohen, S.; Istas, J. On roughness indexes for fractional fields. Bernoalli 2004, 10, 357–373. [Google Scholar]
- Kogon, S.; Manolakis, D. Signal modeling with self-similar α-stable processes: The fractional Levy stable motion model. IEEE Trans. Signal Process. 1996, 44, 1006–1010. [Google Scholar] [CrossRef]
- Liu, H.; Song, W.; Zhang, Y.; Kudreyko, A. Generalized Cauchy Degradation Model With Long-Range Dependence and Maximum Lyapunov Exponent for Remaining Useful Life. IEEE Trans. Instrum. Meas. 2021, 70, 9369345. [Google Scholar] [CrossRef]
- Duan, S.; Song, W.; Zio, E.; Cattani, C.; Li, M. Product technical life prediction based on multi-modes and fractional Lévy stable motion. Mech. Syst. Signal Process. 2021, 161, 107974. [Google Scholar] [CrossRef]
- Magdziarz, M.; Weron, A. Fractional Langevin equation with α-stable noise. A link to fractional ARIMA time series. Stud. Math. 2007, 181, 47–60. [Google Scholar] [CrossRef]
- Weron, A.; Burnecki, K.; Mercik, S.; Weron, K. Complete description of all self-similar models driven by Lévy stable noise. Phys. Rev. E 2005, 71, 016113. [Google Scholar] [CrossRef] [PubMed]
- Lee, P.M.; Janicki, A.; Weron, A. Simulation and Chaotic Behaviour of α-Stable Stochastic Processes; HSC Books: Wroclaw, Poland, 1994. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 2012, 81, 637–654. [Google Scholar] [CrossRef]
- Jumarie, G. Merton’s model of optimal portfolio in a Black-Scholes Market driven by a fractional Brownian motion with short-range dependence. Insur. Math. Econ. 2005, 37, 585–598. [Google Scholar] [CrossRef]
- Grimshaw, S.D. Computing Maximum Likelihood Estimates for the Generalized Pareto Distribution. Technometrics 1993, 35, 185–191. [Google Scholar] [CrossRef]
- Moharram, S.; Gosain, A.; Kapoor, P. A comparative study for the estimators of the Generalized Pareto distribution. J. Hydrol. 1993, 150, 169–185. [Google Scholar] [CrossRef]
- Davison, A.C. Modelling Excesses over High Thresholds, with an Application. In Statistical Extremes and Applications; Springer: Dordrecht, The Netherlands, 1984; pp. 461–482. [Google Scholar] [CrossRef]
- Jumarie, G. On the representation of fractional Brownian motion as an integral with respect to (dt)a. Stat. Extrem. Appl. 2005, 18, 739–748. [Google Scholar] [CrossRef]
- Armagan, A.; Dunson, D.B.; Lee, J. Generalized double Pareto shrinkage. Stat. Sin. 2013, 23, 119–143. [Google Scholar] [CrossRef]
- Lotfi, A. Application of Learning Fuzzy Inference Systems in Electricity Load Forecast; Nottingham Trent University: Nottingham, UK, 2001. [Google Scholar]
- Song, W.; Liu, H.; Zio, E. Long-range dependence and heavy tail characteristics for remaining useful life prediction in rolling bearing degradation. Appl. Math. Model. 2022, 102, 268–284. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar] [CrossRef]
- Best, D.; Rayner, J. Are Two Classes Enough for the X2Goodness of Fit Test? Stat. Neerlandica 1981, 35, 157–163. [Google Scholar] [CrossRef]
- Hsuan, A.; Robson, D.S. The X2-goodness-of-fit tests with moment type estimators. Commun. Stat. Theory Methods 2007. [Google Scholar] [CrossRef]
- Marquardt, T. Fractional Lévy processes with an application to long memory moving average processes. Bernoulli 2006, 12, 1099–1126. [Google Scholar] [CrossRef]
- Laskin, N.; Lambadaris, I.; Harmantzis, F.; Devetsikiotis, M. Fractional Lévy motion and its application to network traffic modeling. Comput. Newt. 2002, 40, 363–375. [Google Scholar] [CrossRef]
- Li, M.; Zhang, P.; Leng, J. Improving autocorrelation regression for the Hurst parameter estimation of long-range dependent time series based on golden section search. Phys. A Stat. Mech. Its Appl. 2016, 445, 189–199. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar] [CrossRef]
- Stoev, S.; Taqqu, M.S.; Park, C.; Marron, J. On the wavelet spectrum diagnostic for Hurst parameter estimation in the analysis of Internet traffic. Comput. Netw. 2005, 48, 423–445. [Google Scholar] [CrossRef]
- Dai, W.; Heyde, C.C. Itô’s formula with respect to fractional Brownian motion and its application. J. Appl. Math. Stoch. Anal. 1996, 9, 439–448. [Google Scholar] [CrossRef]
- Wang, X.-T.; Qiu, W.-Y.; Ren, F.-Y. Option pricing of fractional version of the Black–Scholes model with Hurst exponent H being in (13,12). Chaos Solitons Fractals 2001, 12, 599–608. [Google Scholar] [CrossRef]
- Yan, L.; Shen, G.; He, K. Itô’s formula for a sub-fractional Brownian motion. Commun. Stoch. Anal. 2011, 5, 135–159. [Google Scholar] [CrossRef]
- Lemieux, C. Monte Carlo and Quasi-Monte Carlo Sampling; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef] [Green Version]









| Experimental k Value | k = 10 | k = 12 | k = 14 | k = 16 |
|---|---|---|---|---|
| 16.92 | 19.68 | 22.36 | 25 | |
| 15.42 | 15.83 | 16.15 | 18.21 |
| Case 1 | 0.8242 | 1.7322 | 639.6825 | 3.0220 |
| Case 2 | 0.7883 | 1.7178 | 751.5419 | 2.8802 |
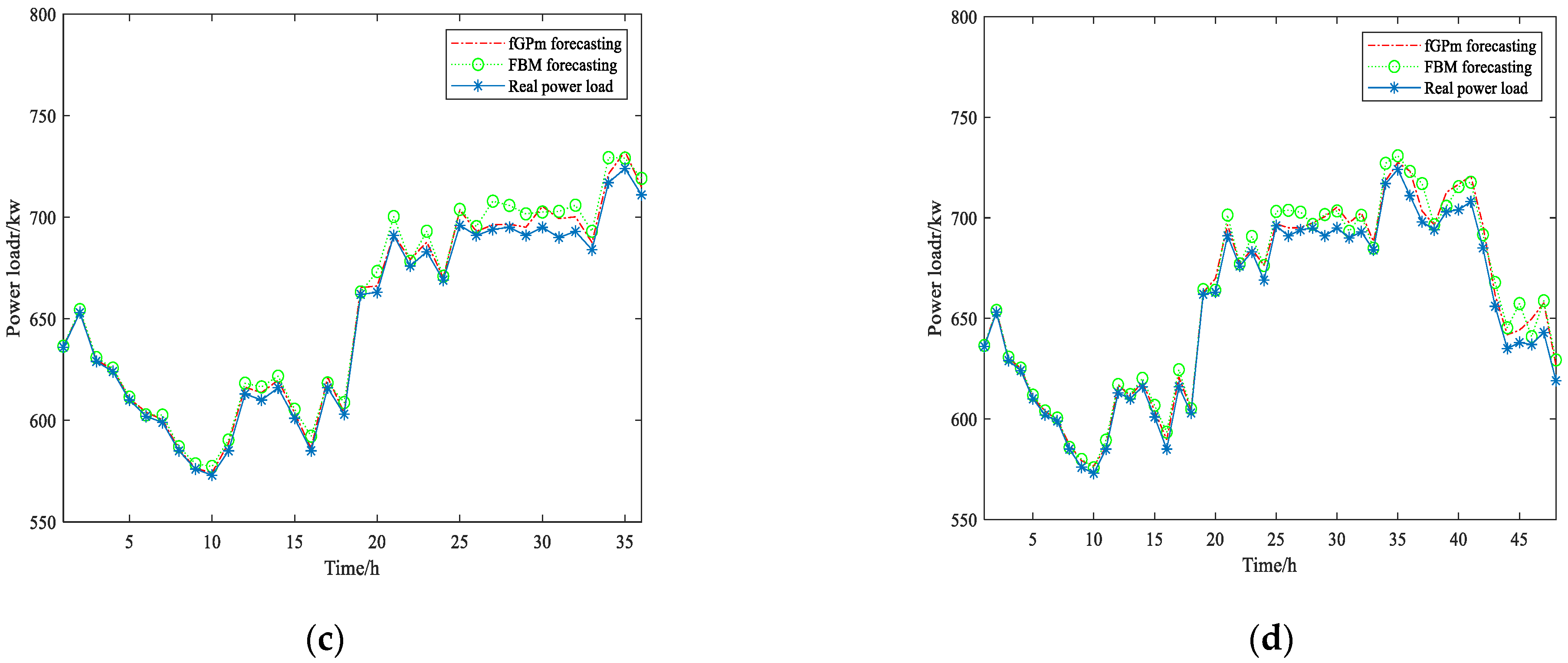
| Forecast Time | Name | fGPm Forecasting | FBM Forecasting |
|---|---|---|---|
| 6 h | Max error percentage | 0.93 | 1.26 |
| 6 h | Mean error percentage | 0.42 | 0.44 |
| 12 h | Max error percentage | 1.40 | 1.95 |
| 12 h | Mean error percentage | 0.46 | 0.60 |
| 18 h | Max error percentage | 1.48 | 2.00 |
| 18 h | Mean error percentage | 0.47 | 0.89 |
| 24 h | Max error percentage | 2.28 | 3.04 |
| 24 h | Mean error percentage | 0.74 | 0.95 |
| Forecast Time | Name | fGPm Forecasting | FBM Forecasting |
|---|---|---|---|
| 6 h | Max error percentage | 0.69 | 1.01 |
| 6 h | Mean error percentage | 0.36 | 0.56 |
| 12 h | Max error percentage | 0.94 | 1.38 |
| 12 h | Mean error percentage | 0.39 | 0.69 |
| 18 h | Max error percentage | 1.32 | 2.66 |
| 18 h | Mean error percentage | 0.45 | 0.72 |
| 24 h | Max error percentage | 1.59 | 3.51 |
| 24 h | Mean error percentage | 0.62 | 1.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Duan, S.; Chen, D.; Zio, E.; Yan, W.; Cai, F. Finite Iterative Forecasting Model Based on Fractional Generalized Pareto Motion. Fractal Fract. 2022, 6, 471. https://doi.org/10.3390/fractalfract6090471
Song W, Duan S, Chen D, Zio E, Yan W, Cai F. Finite Iterative Forecasting Model Based on Fractional Generalized Pareto Motion. Fractal and Fractional. 2022; 6(9):471. https://doi.org/10.3390/fractalfract6090471
Chicago/Turabian StyleSong, Wanqing, Shouwu Duan, Dongdong Chen, Enrico Zio, Wenduan Yan, and Fan Cai. 2022. "Finite Iterative Forecasting Model Based on Fractional Generalized Pareto Motion" Fractal and Fractional 6, no. 9: 471. https://doi.org/10.3390/fractalfract6090471
APA StyleSong, W., Duan, S., Chen, D., Zio, E., Yan, W., & Cai, F. (2022). Finite Iterative Forecasting Model Based on Fractional Generalized Pareto Motion. Fractal and Fractional, 6(9), 471. https://doi.org/10.3390/fractalfract6090471








