Abstract
Alzheimer’s disease (AD) is an age-related degenerative disorder of the cerebral neuro-glial-vascular units. Not only are post-menopausal females, especially those who carry the APOE4 gene, at a higher risk of AD than males, but also AD in females appears to progress faster than in aged-matched male patients. Currently, there is no cure for AD. Mathematical models can help us to understand mechanisms of AD onset, progression, and therapies. However, existing models of AD do not account for sex differences. In this paper a mathematical model of AD is proposed that uses variable-order fractional temporal derivatives to describe the temporal evolutions of some relevant cells’ populations and aggregation-prone amyloid- fibrils. The approach generalizes the model of Puri and Li. The variable fractional order describes variable fading memory due to neuroprotection loss caused by AD progression with age which, in the case of post-menopausal females, is more aggressive because of fast estrogen decrease. Different expressions of the variable fractional order are used for the two sexes and a sharper decreasing function corresponds to the female’s neuroprotection decay. Numerical simulations show that the population of surviving neurons has decreased more in post-menopausal female patients than in males at the same stage of the disease. The results suggest that if a treatment that may include estrogen replacement therapy is applied to female patients, then the loss of neurons slows down at later times. Additionally, the sooner a treatment starts, the better the outcome is.
1. Introduction
Alzheimer’s disease (AD) is a progressive degenerative disorder of the cerebral neuro-glial-vascular units. AD is characterized by an abnormal extracellular accumulation of toxic amyloid- () plaques and formation of tau-containing neurofibrillary tangles inside neurons that cause memory loss, cognitive decline, and behavioral changes [,]. There are approximately 7 million Americans and 38 million people worldwide who have AD presently, and it is estimated that by 2050 these numbers will rise to about 13 million in the United States and 97 million worldwide [,]. Only in the United States, it is projected that the cost of care for AD patients will reach 1 trillion USD by 2050 []. Currently, there is no cure for AD.
Age, sex, and the 4-allele of the apolipoprotein (APOE4) gene are major risk factors for AD [,,,,]. While relevant knowledge about the roles of age and APOE4 in AD has been gained in the last few decades, there is still unclear how sex differences influence the onset and progression of the disease. Not only do more females get AD than males [], with females having the APOE4 gene being at a higher risk for AD than male carriers [,], but also females with AD experience a faster progression of the disease and bigger cognitive decline than age-matched male patients [,,]. In the United States, AD is the fifth and, respectively, eighth, leading cause of death for females and males, respectively [].
Besides the presence of the APOE4 gene, other interconnected factors that may contribute to the sex-biased feature of AD are hormonal state, activation of glial cells (the two types of glial cells considered in this paper are astrocytes and microglia. The resting states of these cells correspond to the healthy brain, while in pathological conditions the cells change to their activated states. In their resting states, astrocytes regulate synaptic plasticity, neurotransmission, cerebral blood flow, and neuronal metabolism [], and microglia monitor the functional status of neuronal synapses []. In their activated states, the astrocytes and microglia participate in phagocytic activities that are responses of the immune system to cerebral pathological conditions. The cells also contribute to phagocytosis in their resting states []), and the neuroinflammatory response to AD progression []. Estrogen, a major group of sex hormones found in much higher amounts in females than males, is a primary regulator of synaptic plasticity which is essential for cognition and memory [,,,]. The neuroprotection provided by estrogen is achieved through direct actions on neurons and indirectly via astrocytes, microglia, and endothelial cells []. Estrogen is involved in the protection of neurons against toxicity, oxidative stress, and the formation of neurofibrillary tangles, and contributes to the activation of neuronal survival factors, deactivation of the so-called death signals in neurons, and the suppression of glia-mediated inflammation that leads to inflammatory damage of neurons and cerebral endothelial cells [,]. As females transition from pre-menopause to post-menopause, the levels of estradiol, the dominant type of estrogen in females, drop dramatically from 30–400 pg/mL to 0–30 pg/mL (for comparison, the normal estradiol levels in males are 10–50b pg/mL) []. This body of evidence suggests that post-menopausal females are at higher risk for AD than males.
Aging produces changes in the resting (inactive) states of astrocytes and microglia conferring them pro-inflammatory-like phenotypes that are dysfunctional, dystrophic, and contribute more to neuroinflammation than neuroprotection [,]. AD pathology benefits from and enhances neuroinflammation leading to chronic inflammation and, thus, activates the proliferative reactive astrocytes, and the classically (pro-inflammatory/neurotoxic phenotype) and alternatively (anti-inflammatory/neuroprotective phenotype) activated microglia. The activations of various glial phenotypes are interlinked [] and some activated phenotypes exhibit AD-induced overlapping (neurotoxic and neuroprotective) profiles []. Additionally, the phenotype, which in females is triggered by estrogen [], experiences an age-associated switch to an -skewed phenotype that intensifies during AD progression []. AD mouse models show that the resting and activated microglia in adult females are more reactive (pro-inflammatory) than in males and could be partially dysfunctional []. Additionally, microglia in male mice are developmentally delayed when compared to female mice. Recently, various linkages between AD and the cerebral small vessel disease that damages the vasculature and the blood-brain barrier and impairs cerebral blood flow have been established [,,,]. Brain damage caused by the cerebral small vessel disease shows as white matter hyperintensities (WMHs) on brain MR images of older people and clinical studies have revealed a causal link between WMHs and AD []. Furthermore, post-menopausal females experience a higher burden and accelerated increase of WMHs than age-matched pre-menopausal females and males []. This body of evidence suggests, yet again, that post-menopausal females have a higher risk of developing AD than males.
Considering the structural and functional complexities of a living human brain, the lack of reliable AD treatments more than a century after a case of a female patient with AD was first reported [] comes as no surprise. Mathematical models can help understand mechanisms of AD onset, progression, and therapies. Existing mathematical models of AD focus on the few known aspects of the disease such as: (1) the formation of fibrils and plaques [,]; (2) interactions among brain cells and the plaques [,,,,,]; (3) temporal evolution of AD biomarkers [,]; (4) the role of the APOE4 gene in the AD onset [,]; (5) the AD-induced dysrhythmic behavior of inhibitory neurons []; and (6) design of potential treatments for AD [,]. However, the existing models of AD do not account for the sex differences mentioned above.
In this paper, a mathematical model of AD that accounts for sex differences is proposed. The model generalizes the work of Puri and Li []. Puri and Li’s model is chosen because it describes multiple crosstalks among relevant cerebral cells’ populations and the aggregation-prone fibrils using a system of coupled first order linear ordinary differential equations with relatively few parameters assumed to be constants. In the present study, the first order temporal derivative is replaced by a variable-order fractional temporal derivative which is an elegant mathematical way of introducing sex dependence into the model without adding new parameters to the model or increasing the complexity of the system of equations. This modeling approach is supported by the successful use of fractional calculus in describing fading memory, non-locality and stochasticity of various complex physical systems [,,,,,,,,,,]. A recent review of the variable-order fractional operators and some of their applications is given in []. Before moving forward, it is important to mention that the proposed system of coupled variable-order fractional differential equations can be seen as a system of Volterra integro-differential equations, and thus belongs to the class of delay differential equations with distributed delay. Delay differential equations with distributed (continuous) delay and/or concentrated (discrete) delay (or lags) are the most used population models [,,].
In this paper, the variable fractional order describes variable fading memory due to neuroprotection loss caused by AD progression with age which, in the case of post-menopausal females, is more aggressive because of the fast estrogen decrease. Different expressions of the variable fractional order are used for the two sexes and a sharper decreasing function models the neuroprotection decay in post-menopausal females with AD. Numerical simulations show that the population of surviving neurons has decreased more in post-menopausal female patients than in males at the same stage of the disease. The results suggest that if a treatment that includes estrogen replacement therapy (ERT) is applied to female patients, then the loss of neurons slows down at later times. Additionally, the sooner a treatment starts the better the outcome is. These results agree with published clinical observations [,,,].
The paper is structured as follows. The Materials and Methods section presents the proposed mathematical model and its numerical discretization. Numerical simulations are shown in the Results section, and the discussion of results is presented in the Discussion section. The paper ends with a Conclusion section.
2. Materials and Methods
2.1. Mathematical Model
As in [], the model describes multiple crosstalks among the following populations: surviving neurons, ; dead neurons, ; activated microglia in pro-inflammatory state, ; activated microglia in anti-inflammatory state, ; quiescent (resting) astrocytes, ; proliferative reactive astrocytes, ; and aggregation-prone amyloid- fibrils, . The model assumes a constant risk for neuronal death and neglects the diffusion of the above-mentioned brain cells and fibrils.
The proposed mathematical model generalizes the model in [] as follows:
where the variable-order fractional Caputo derivative of order is, by definition:
In formula (8), is the gamma function.
The variable-order fractional derivative (8) has the following desirable properties: (1) it models variable fading memory with no memory of its past order [] which gives it the ability to transfer to the output certain features of the variable order function []; and (2) it conserves physical causality [] (the causality-preserving operator of [] coincides with formula (8) for continuous functions which are used as mathematical representations of populations’ dynamics). If is a constant, then the derivative (8) reduces to the left-sided Caputo fractional derivative of order q whose memory gets longer as q gets smaller [].
The right-hand sides of Equations (1)–(7) describe the 16 signalling pathways proposed in []. By using the symbol → for activation and the symbol ⊣ for suppression, the pathways involved in AD inhibition are , and the pathways supporting the AD progression are . The values of the rates in Equations (1)–(7) and corresponding pathways are given in Table 1.

It is further assumed that the initial time corresponds to the AD onset which happens very soon after post-menopause starts in females (around age 55 []). The study is run for a period of years. The initial conditions are []:
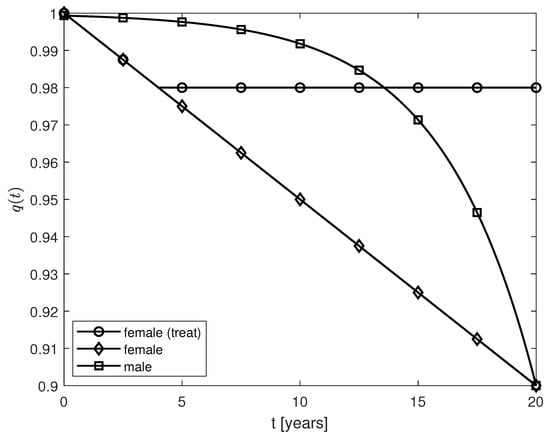
The variable fractional order models neuroprotection loss due to AD progression with age. It is assumed that post-menopausal females with AD experience a sharper decrease in neuroprotection than age-matched males with AD. Given the current lack of knowledge about the temporal decrease of neuroprotection with age, sex, and/or AD, the sex-dependent shapes of are inspired by the fact that post-menopausal females lose sex hormones rapidly, while the age-related decline in the neuroprotective testosterone in males happens gradually []. Thus, the following sex-dependent expressions for are proposed:
for post-menopausal females, and:
for age-matched males.
A treatment for post-menopausal females with AD is also designed by introducing a variable fractional order of the form:
where is the year when the treatment starts (following a diagnosis of AD). As expression (12) suggests, the aim of the treatment is to slow down the progression of the disease by keeping the level of neuroprotection at the same level with the one at . Plots of the functions given by expressions (10)–(12) and years are shown in Figure 1.
2.2. Numerical Scheme
The system of Equations (1)–(7) with initial conditions (9) is solved numerically using a numerical scheme given in [].
Thanks to the linearity of the system of Equations (1)–(7), the system can be written in matrix form:
where , and:
Let be an equally-spaced discretization of the interval of constant step size h. Denote by , for and . The following forward difference approximation scheme of order is used to numerically discretize the variable-order fractional Caputo derivative of order []:
Replacing expression (15) into system (13) and rearranging the terms yield:
where is the identity matrix.
System (16) was solved using the initial conditions (9) and the physical requirement of non-negative solutions (recall that the components of vector represent populations of brain cells and fibrils which must be positive for ). This is a nonnegative least squares problem that was solved using Matlab’s built-in function lsqnonneg which is a numerical implementation of the Kuhn–Tucker conditions []. The code was validated using the case : the solution generated by lsqnonneg coincides with the solution to the system of first order differential Equations (1)–(7) obtained using Matlab’s built-in function ode45 which was constrained to satisfy the NonNegative option selected with the function odeset. Since an analytic solution of the initial value problem (13) and (9) is not known, the convergence of the numerical scheme (15) was observed numerically: the same results were obtained for . Thus, the step size for the numerical simulations presented in the next section was chosen to be . Lastly, the system of Equations (1)–(7) for constant fractional order q was solved numerically using Matlab’s function fde_pi1_ex written by Garrappa []. Details on the convergence and accuracy of the numerical scheme (15) and the one implemented in fde_pi1_ex are given in [] and [] respectively.
Remark: This paper is a proof-of-concept study and thus proving mathematical results on the properties of the solutions to the initial value problem (1)–(7) and (9) is beyond the scope of the work. However, some general ideas on how these results could be obtained are given here. In the case of a constant fractional order q, the results in [] can be applied to show the existence, uniqueness and continuous dependence on initial data of the solution to problem (1)–(7) and (9) (thus, the problem is well-posed in the sense of Hadamard). In the case of a variable fractional order , the variable-order fractional derivative (8) can be approximated by sums containing higher-order integer derivatives [] and thus the system (1)–(7) can be re-written as either a system of Volterra integro-differential equations or a larger system of first order linear differential equations (see [] for details). The existence, uniqueness and continuous dependence on initial conditions of the solution to the system of Volterra integro-differential equations can be derived from the results presented in [], while conditions for positive solutions and stability can be adapted from [,]. Additionally, the Picard–Lindelöf theorem [] may be adapted to show that the initial value problem for the system of first order linear differential equations is well-posed. Lastly, the results obtained for in the manner described above remain valid when is a constant []. This is relevant since only the positive solution to the initial value problem (1)–(7) and (9) is physically correct.
3. Results
Figure 2a and Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 show numerical simulations for variable fractional orders, and Figure 2b, Figure 8 and Figure 9 show results for constant fractional orders.
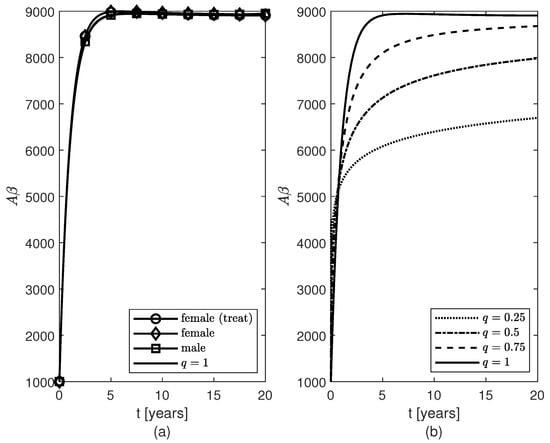
Figure 2.
Temporal variations of populations of fibrils for (a) variable fractional orders and (b) constant fractional orders .
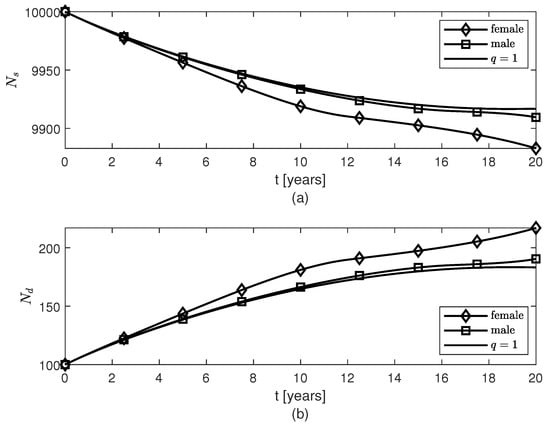
Figure 3.
Temporal variations of populations of (a) surviving neurons , and (b) dead neurons , for variable fractional orders modeling females’ and, respectively, males’ neuroprotection loss due to the AD progression with age.
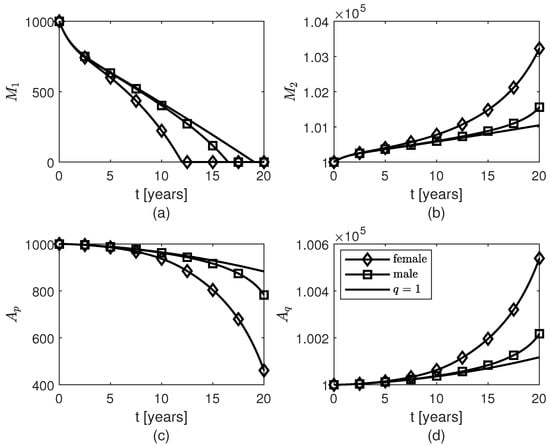
Figure 4.
Temporal variations of populations of glial cells: (a) pro-inflammatory microglia , (b) anti-inflammatory microglia , (c) proliferative reactive astrocytes , and (d) quiescent astrocytes for variable fractional orders modeling female’s and, respectively, male’s neuroprotection loss due to the AD progression with age.
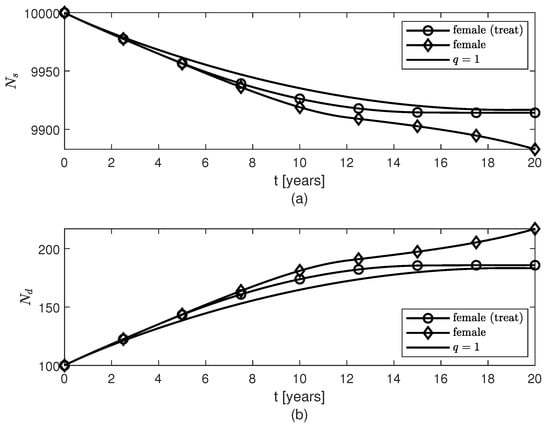
Figure 5.
Temporal variations of populations of (a) surviving neurons , and (b) dead neurons , for variable fractional orders modeling neuroprotection loss in post-menopausal females due to AD progression with age and therapy given to females starting 4 years after the AD onset.
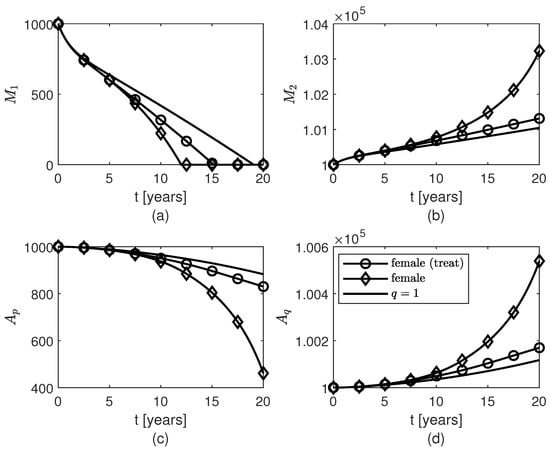
Figure 6.
Temporal variations of populations of glial cells: (a) pro-inflammatory microglia , (b) anti-inflammatory microglia , (c) proliferative reactive astrocytes , and (d) quiescent astrocytes for variable fractional orders modeling neuroprotection loss in post-menopausal females due to AD progression with age and therapy given to females starting 4 years after the AD onset.
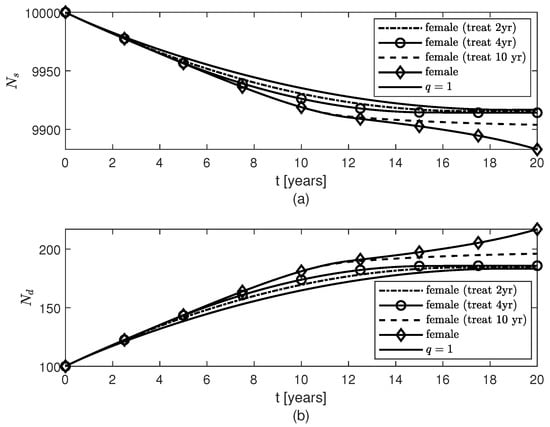
Figure 7.
Temporal variations of populations of (a) surviving neurons , and (b) dead neurons , for variable fractional orders modeling neuroprotection loss in post-menopausal females due to AD progression with age and therapies given to females starting 2 years, 4 years, or 10 years after the AD onset.
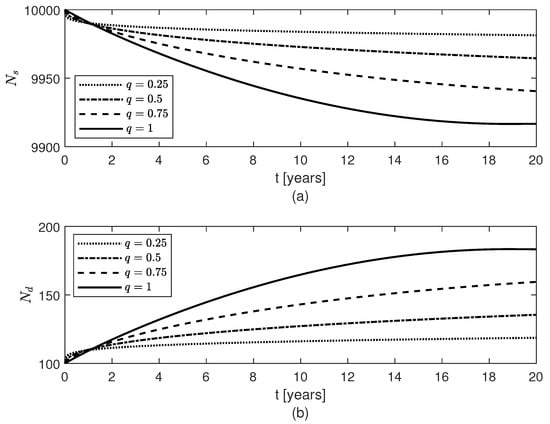
Figure 8.
Temporal variations of populations of (a) surviving neurons , and (b) dead neurons , for constant fractional orders .
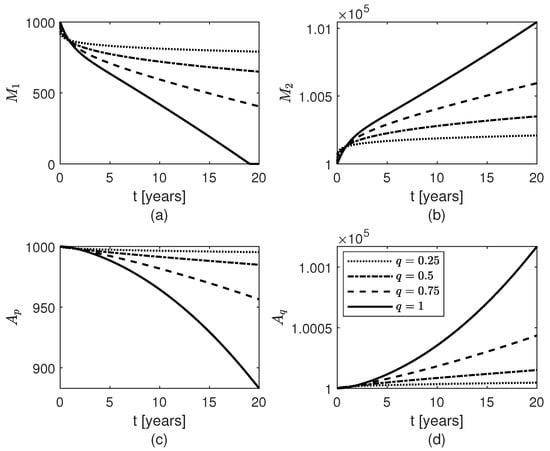
Figure 9.
Temporal variations of populations of glial cells: (a) pro-inflammatory microglia , (b) anti-inflammatory microglia , (c) proliferative reactive astrocytes , and (d) quiescent astrocytes for constant fractional orders .
For the variable fractional order case, the same pattern of accumulation of fibrils is observed for males and post-menopausal females with AD, as well as females whose therapy started or 10 years after the AD onset (Figure 2a, the cases are not shown since they look similar to the case ). As in [], the model makes the population of fibrils reach a plateau around year five (Figure 2a) which slows down the decrease (increase) of the populations of survival (dead) neurons for both sexes (Figure 3). Figure 3 and Figure 4 show that the dynamics of brain cells populations in males are very close to those predicted by the case which corresponds to the original model proposed in []. The decrease in surviving neurons in females resembles the sharper decay in neuroprotection given by in formula (10) (Figure 3a), and thus more neuronal death is observed in post-menopausal females than in aged-matched males with AD (Figure 3b). Figure 4 shows sex differences in the temporal evolutions of the two microglia phenotypes, and , and the two populations of astrocytes, and . The fact that the population of cells is zero at later times (due to the constraint of non-negative solutions for system (16)) is probably unphysical and may create numerical artifacts in the dynamics of the other brain cells. This issue will be studied in a future work.
Figure 5, Figure 6 and Figure 7 show temporal variations of the populations of brain cells of post-menopausal females with AD for the case when the variable fractional order is given by formula (12). A treatment for AD is designed such that the level of neuroprotection is kept constant for , where is the year when the treatment starts. Not only does this treatment slow down the loss of surviving neurons after approximately 2 years of keeping the level of neuroprotection constant, but also the populations of and cells increase slower after although the amount of present is unchanged by the treatment (Figure 2a). As expected, the sooner the treatment starts the more neurons are saved and thus the better the outcome will be (Figure 7). Again, the shape of the variable fractional order (12) is transferred to the dynamics of the population of surviving neurons (Figure 5a and Figure 7a).
Lastly, Figure 2b, Figure 8, and Figure 9 show results for the constant fractional order case. As the fractional order decreases from 1 to 0, the population of fibrils gets smaller (Figure 2b) and, consequently, the least decrease in the population of surviving neurons (Figure 8a) and the least increases in the populations of and cells (Figure 9b,d) are observed. For the differential operator (8), a smaller value of the constant fractional order q confers a longer memory which translates into a longer protection against AD. Thus, the longer the memory of neuroprotection is due to treatment the better the outcome will be.
4. Discussion
In this paper, a mathematical model of AD progression is proposed. The clinically observed bias of AD toward post-menopausal females is modeled as variable fading memory dynamics of the fibrils and populations of surviving and dead neurons, activated microglia, and resting and reactive astrocytes. The fading memory is due to neuroprotection decay which is assumed to mimic decreasing patterns of the sex hormones with age: a rapid loss of estrogen in post-menopausal females and a gradual yet relevant decline in testosterone in males []. The variable-order fractional Caputo derivative of order is the mathematical tool chosen to model fading memory in this application because of the following desirable features: (1) certain properties (such as monotonic or oscillatory behavior) of the function are transferred to the outcome [], and (2) when is a constant, the memory gets longer as q gets closer to 0 []. Two cases are investigated via numerical simulations: (1) sex differences in the amount of dead neurons due to AD progression with age; and (2) outcomes of a potential treatment that aims to keep the level of neuroprotection constant. Not only is the model able to predict a greater amount of dead neurons in post-menopausal females with AD than in age-matched male patients for the same temporal evolution of the population, but also the results suggest that the treatment for AD should be aimed at preserving the level of neuroprotection either preventively or as soon as an AD diagnosis is established, rather than at removing the plaques. Additionally, the earlier the treatment starts the better the outcome is.
The transfer of the monotonic behavior of the variable fractional orders for post-menopausal females () and males () to the temporal variations of the corresponding populations of surviving neurons is apparent when comparing Figure 1 and Figure 3a. For the same pattern of AD progression (Figure 2), the post-menopausal females with AD experience a greater loss (increase) of surviving (dead) neurons than age-matched male patients (Figure 3). As in [], the population of fibrils is modeled so that it reaches a plateau after about five years (Figure 2) which slows down the decrease (increase) of the populations of survival (dead) neurons for both sexes at later times (Figure 3). The temporal variations of the populations of survival neurons for the two sexes resemble somewhat the profiles of the results to the mini-mental state examination (MMSE) administered to males and females suffering from late mild cognitive impairment, a cerebral degenerative disorder that, in some cases, is a precursor to AD, for a period of 10 years (Figure 3c in []). MMSE is a well-known and easy to administer test of cognitive function that checks the orientation, concentration, attention, verbal memory, naming, and visuospatial skills []. In addition, the increase in the amounts of the and cells (and, consequently, decrease of the populations of and cells) observed in both sexes may prevent a further increase in the population of fibrils for times greater than 5 years (Figure 4). The fact that these larger populations of and cells cannot decrease the amount of fibrils and stop the increase or even decrease the population of dead neurons, hint at the possibility that the interlinked dynamics among the brain cells and the fibrils make these cells behave in a dysfunctional manner specific to their corresponding pro-inflammatory mutations caused by the age- and AD-related chronic inflammation [,]. The sex differences shown in Figure 4 may be because the fading memory due to the neuroprotection loss controlled by a sharper estrogen decrease in post-menopausal females is able to capture the more reactive (pro-inflammatory) behavior of the activated microglia observed in females []. Clinical studies have shown that microglial activation and neuronal death correlate with the severity of AD symptoms []. Thus, the excessive activation of microglia and larger number of dead neurons predicted by the model for post-menopausal females with AD suggest that post-menopausal females undergo a faster AD progression and suffer a greater cognitive decline than age-matched males with AD which agree with clinical observations [,,].
Numerical simulations of a treatment that aims to keep the level of neuroprotection constant either after the onset of AD or preventively are shown in Figure 2 and Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. If the treatment starts two, four, or ten years after AD onset, then the death of the neurons and the excessive activation of and cells are slowed down at later times (Figure 5, Figure 6 and Figure 7), and the sooner the treatment starts the more neurons survive (Figure 7a). Although the treatment does not change the amount of fibrils present (Figure 2a), the results suggest that the treatment may be able to lessen the symptoms of the disease and slow down the AD progression. This observation is supported by recent studies which have shown that people with high levels of plaques (brain amyloidosis) similar to those seen in patients with AD do not suffer from and most likely will never develop the disease, having normal cognitive functions and memory for their age [,]. The results also suggest that the neuroprotection offered by surviving neurons and normal amounts of and cells can be preserved in post-menopausal females with AD by other means than the removal of the fibrils, and this agrees with clinical trials which found various drugs that target failed at reducing AD symptoms []. Lastly, Figure 2b, Figure 8 and Figure 9 show that for a constant fractional order , less amounts of and cells, and , and a higher level of surviving neurons are obtained for values of q close to 0. Since long fading memory is obtained for values of q close to 0 (Figure 8a), the results suggest that a treatment that keeps the neuroprotection level constant the longest has the best outcome. These results agree with the study in [] which showed that lower amounts of reactive astrocytes and activated microglia are linked to reduced levels of and improved cognitive functions in an AD mouse model. This suggests that a preventive therapy designed for people at risk of AD, such as the APOE4 carriers, that preserves the level of neuroprotection could slow the progression of AD or potentially prevent the onset of AD.
Until a cure for AD is found, anti-inflammatory therapies combined with a healthy lifestyle may provide the optimal level of neuroprotection to prevent or delay the onset of AD or slow down the progression of disease. For instance, the use of common non-steroidal anti-inflammatory drugs (NSAID) for ten years were associated with reduced AD prevalence with diclofenac, showing reduced incidence and slower cognitive decline []. An anti-TNF- inhibitor therapy used in patients with rheumatoid arthritis to lower insulin resistance was found to also reduce the risk for AD []. Since insulin resistance is a characteristic of type 2 diabetes and chronic inflammation is a common feature of rheumatoid arthritis, diabetes, and AD [], it is not surprising that antidiabetic drugs, some which have anti-inflammatory properties [], were tested and showed some promising potential in treating patients with AD who do not have diabetes []. However, in females, estrogen has powerful anti-inflammatory properties and numerous studies have shown that estrogen replacement therapy (ERT) in post-menopausal women can decrease the risk for AD and delay AD onset [,,,,,,,]. Athough some studies suggest that if ERT starts late after the AD onset or at an advanced age the treatment is unsuccessful [], very recent studies indicate that the age when the treatment starts and the long-term use of estrogen do not increase the risk for AD [,]. Females who had ERT for less than one year showed an increased risk for AD, while a decreased risk of developing the disease was found among females younger than 80 years who had been exposed to ERT for at least 10 years []. These clinical observations agree with the predictions made by the proposed model.
Some of the limitations of the model are as follows. A sensitivity analysis is needed to better understand how the values of the model’s parameters and initial conditions affect the results and to prevent the population of cells from becoming zero at later times which may be an unphysical behavior. Preliminary results show that small perturbations of the initial conditions do not affect the solution. When the initial condition of only one population was doubled and the initial conditions of the other populations were kept fixed, changes in the solution were observed only when the initial conditions of and were modified. The solution was also sensitive when only the initial condition of was halved. However, when the initial conditions of both and were changed by the same amount (either doubled or halved), the solution looked the same as that presented in the paper. A similar behavior was observed when the initial conditions of and were both doubled. Given the biological linkages existing between the populations and , and respectively the populations and , changing their initial conditions by the same amount may be physically justified. A proper link between experimentally or clinically measured estrogen loss in females and the variable fractional order of the model should be established. In future work, contributions from the tau pathology, APOE4 gene, and endothelial cells will be incorporated in the model and the properties of the brain cells and crosstalks among them and fibrils will be updated using the latest discoveries [,,,].
5. Conclusions
In this paper, a mathematical model of AD is proposed that accounts for sex differences. The model uses variable-order fractional temporal derivatives to describe the temporal evolutions of some relevant cells’ populations and the aggregation-prone amyloid- fibrils. The variable fractional order describes variable fading memory due to neuroprotection loss caused by AD progression with age which, in the case of post-menopausal females, is more aggressive because of fast estrogen decrease. Different expressions of the variable fractional order are used for the two sexes and a sharper decreasing function corresponds to the females’ neuroprotection decay. Numerical simulations show that: (1) the population of surviving neurons has decreased more in post-menopausal female patients than in age-matched males at the same stage of the disease; and (2) if a treatment that may include ERT is administered to female patients, then the loss of neurons slows down at later times. The results suggest that: (1) the focus of a treatment for AD should be the preservation of neuroprotection levels rather than the removal of the plaques which agrees with clinical observations of older people with large plaques who do not have AD [,]; and (2) ERT administered to post-menopausal females with AD at any age and for a long period of time may slow the progression of AD. The model also predicts that ERT can either delay the onset of AD or protect against the disease in post-menopausal females which agrees with clinical evidence [,]. Quantifying neuroprotection levels in both sexes through clinical/experimental observations will not only help calibrate the model (and, thus, improve its predictive abilities) but also provide a potentially powerful biomarker for AD prevention and treatment.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used:
| AD | Alzheimer’s disease |
| Proliferative reactive astrocytes (in activated state) | |
| Quiescent astrocytes (in resting state) | |
| Amyloid- | |
| Activated microglia in pro-inflammatory state | |
| Activated microglia in anti-inflammatory state | |
| Surviving neurons | |
| Dead neurons |
References
- Pospich, S.; Raunser, S. The molecular basis of Alzheimer’s plaques. Science 2017, 358, 45–46. [Google Scholar] [CrossRef] [PubMed]
- Nebel, R.A.; Aggarwal, N.T.; Barnes, L.L.; Gallagher, A.; Goldstein, J.M.; Kantarci, K.; Mallampalli, M.P.; Mormino, E.C.; Scott, L.; Yu, W.H.; et al. Understanding the impact of sex and gender in Alzheimer’s disease: A call to action. Alzheimers Dement. 2018, 14, 1171–1183. [Google Scholar] [CrossRef] [PubMed]
- Alzheimer’s Disease Facts and Figures. Available online: https://www.alz.org/alzheimers-dementia/facts-figures (accessed on 28 June 2022).
- Dementia. Available online: https://www.who.int/news-room/fact-sheets/detail/dementia (accessed on 28 June 2022).
- Wang, Y.; Mishra, A.; Brinton, R.D. Transitions in metabolic and immune systems from pre-menopause to post-menopause: Implications for age-associated neurodegenerative diseases. F1000Research 2020, 9, 68. [Google Scholar] [CrossRef] [PubMed]
- Zarate, S.; Stevnsner, T.; Gredilla, R. Role of estrogen and other sex hormones in brain aging. Neuroprotection and DNA repair. Front Aging Neurosci. 2017, 9, 430. [Google Scholar] [CrossRef]
- Mishra, A.; Brinton, R.D. Inflammation: Bridging age, menopause and APOEϵ4 genotype to Alzheimer’s disease. Front. Aging Neurosci. 2018, 10, 312. [Google Scholar] [CrossRef]
- Liu, C.C.; Liu, C.C.; Kanekiyo, T.; Xu, H.; Bu, G. Apolipoprotein E and Alzheimer disease: Risk, mechanisms and therapy. Nat. Rev. Neurol. 2013, 9, 106–118. [Google Scholar] [CrossRef]
- Dubal, D.B. Sex difference in Alzheimer’s disease: An updated, balanced and emerging perspective on differing vulnerabilities. Handb. Clin. Neurol. 2020, 175, 261–273. [Google Scholar] [CrossRef]
- Pontifex, M.G.; Martinsen, A.; Saleh, R.N.M.; Harden, G.; Tejera, N.; Muller, M.; Fox, C.; Vauzour, D.; Minihane, A.-M. APOE4 genotype exacerbates the impact of menopause on cognition and synaptic plasticity in APOE-TR mice. FASEB J. 2021, 35, e21583. [Google Scholar] [CrossRef]
- Corder, E.H.; Ghebremedhin, E.; Taylor, M.G.; Thal, D.R.; Ohm, T.G.; Braak, H. The biphasic relationship between regional brain senile plaque and neurofibrillary tangle distributions: Modification by age, sex, and APOE polymorphism. Ann. N. Y. Acad. Sci. 2004, 1019, 24–28. [Google Scholar] [CrossRef]
- Delage, C.I.; Simoncicova, E.; Tremblay, M.E. Microglial heterogeneity in aging and Alzheimer’s disease: Is sex relevant? J. Pharmacol. Sci. 2021, 146, 169–181. [Google Scholar] [CrossRef]
- Navakkode, S.; Gaunt, J.R.; Pavon, M.V.; Bansal, V.A.; Abraham, R.P.; Chong, Y.S.; Ch’ng, T.H.; Sajikumar, S. Sex-specific accelerated decay in time/activity-dependent plasticity and associative memory in an animal model of Alzheimer’s disease. Aging Cell. 2021, 20, e13502. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Park, J.; Choi, Y.K. The role of astrocytes in the central nervous system focused on BK channel and heme oxygenase metabolites: A review. Antioxidants 2019, 8, 121. [Google Scholar] [CrossRef]
- Wake, H.; Moorhouse, A.J.; Jinno, S.; Kohsaka, S.; Nabekura, J. Resting microglia directly monitor the functional state of synapses in vivo and determine the fate of ischemic terminals. J. Neurosci. 2009, 29, 3974–3980. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.-J.; Chung, W.-S. Phagocytic roles of glial cells in healthy and diseased brains. Biomol. Ther. 2018, 26, 350–357. [Google Scholar] [CrossRef] [PubMed]
- Dubal, D.B.; Wise, P.M. Estrogen and neuroprotection: From clinical observations to molecular mechanisms. Dialogues Clin. Neurosci. 2002, 4, 149–161. [Google Scholar] [CrossRef]
- Brann, D.W.; Dhandapani, K.; Wakade, C.; Mahesh, V.B.; Khan, M.M. Neurotrophic and neuroprotective actions of estrogen: Basic mechanisms and clinical implications. Steroids 2007, 72, 381–405. [Google Scholar] [CrossRef]
- What Are the Symptoms of High Estrogen? Available online: https://www.medicalnewstoday.com/articles/323280#treatment (accessed on 30 June 2022).
- Lynch, A.M.; Murphy, K.J.; Deighan, B.F.; O’Reilly, J.A.; Gun’ko, Y.K.; Cowley, T.R.; Gonzalez-Reyes, R.E.; Lynch, M.A. The impact of glial activation in the aging brain. Aging Dis. 2010, 1, 262–278. [Google Scholar]
- Chun, H.; Marriott, I.; Lee, C.J.; Cho, H. Elucidating the interactive roles of glia in Alzheimer’s disease using established and newly developed experimental models. Front. Neurol. 2018, 9, 797. [Google Scholar] [CrossRef]
- Jiwaji, Z.; Tiwari, S.S.; Aviles-Reyes, R.X.; Hooley, M.; Hampton, D.; Torvell, M.; Johnson, D.A.; McQueen, J.; Baxter, P.; Sabari-Sankar, K.; et al. Reactive astrocytes acquire neuroprotective as well as deleterious signatures in response to Tau and Aβ pathology. Nat Commun. 2022, 13, 135. [Google Scholar] [CrossRef]
- Varnum, M.M.; Ikezu, T. The classification of microglial activation phenotypes on neurodegeneration and regeneration in Alzheimer’s disease brain. Arch. Immunol. Ther. Exp. 2012, 60, 251–266. [Google Scholar] [CrossRef]
- Klohs, J. An integrated view on vascular dysfunction in Alzheimer’s disease. Neurodegener. Dis. 2019, 19, 109–127. [Google Scholar] [CrossRef] [PubMed]
- Korte, N.; Nortley, R.; Attwell, D. Cerebral blood flow decrease as an early pathological mechanism in Alzheimer’s disease. Acta Neuropathol. 2020, 140, 793–810. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J.L.; Pritchard, H.A.T.; Walsh, K.R.; Strangward, P.; White, C.; Hill-Eubanks, D.; Alakrawi, M.; Hennig, G.W.; Allan, S.M.; Nelson, M.T.; et al. Functionally linked potassium channel activity in cerebral endothelial and smooth muscle cells is compromised in Alzheimer’s disease. Pharmacology 2022, 119, e2204581119. [Google Scholar] [CrossRef]
- Wang, D.; Chen, F.; Han, Z.; Yin, Z.; Ge, X.; Lei, P. Relationship between amyloid-β deposition and blood-brain barrier dysfunction in Alzheimer’s disease. Front Cell Neurosci. 2021, 15, 695479. [Google Scholar] [CrossRef]
- Prins, N.; Scheltens, P. White matter hyperintensities, cognitive impairment and dementia: An update. Nat. Rev. Neurol. 2015, 11, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Lohner, V.; Pehlivan, G.; Sanroma, G.; Miloschewski, A.; Schirmer, M.D.; Stocker, T.; Reuter, M.; Breteler, M.M.B. The relation between sex, menopause, and white matter hyperintensities: The Rhineland study. Neurology 2022. [Google Scholar] [CrossRef]
- Alzheimer, A. Über einen eigenartigen schweren Erkrankungsprozeß der Hirnrincle. Neurol. Central. 1906, 25, 1134. [Google Scholar]
- Pallitto, M.M.; Murphy, R.M. A mathematical model of the kinetics of beta-amyloid fibril growth from the denatured state. Biophys J. 2001, 81, 1805–1822. [Google Scholar] [CrossRef]
- Helal, M.; Hingant, E.; Pujo-Menjouet, L.; Webb, G.F. Alzheimer’s disease: Analysis of a mathematical model incorporating the role of prions. J. Math. Biol. 2014, 69, 1207–1235. [Google Scholar] [CrossRef]
- Craft, D.L.; Wein, L.M.; Selkoe, D.J. A mathematical model of the impact of novel treatments on the A beta burden in the Alzheimer’s brain, CSF and plasma. Bull. Math. Biol. 2002, 64, 1011–1031. [Google Scholar] [CrossRef] [PubMed]
- Puri, I.K.; Li, L. Mathematical modeling for the pathogenesis of Alzheimer’s disease. PLoS ONE 2010, 5, e15176. [Google Scholar] [CrossRef] [PubMed]
- Hao, W.; Friedman, A. Mathematical model on Alzheimer’s disease. BMC Syst. Biol. 2016, 10, 108. [Google Scholar] [CrossRef] [PubMed]
- Bertsch, M.; Franchi, B.; Marcello, N.; Tesi, M.C.; Tosin, A. Alzheimer’s disease: A mathematical model for onset and progression. Math. Med. Biol. 2017, 34, 193–214. [Google Scholar] [CrossRef] [PubMed]
- Pal, S.; Melnik, R. Nonlocal models in the analysis of brain neurodegenerative protein dynamics with application to Alzheimer’s disease. Sci. Rep. 2022, 12, 7328. [Google Scholar] [CrossRef]
- Vosoughi, A.; Sadigh-Eteghad, S.; Ghorbani, M.; Shahmorad, S.; Farhoudi, M.; Rafi, M.A.; Omidi, Y. Mathematical models to shed light on amyloid-beta and tau protein dependent pathologies in Alzheimer’s disease. Neuroscience 2020, 424, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Jack, C.R., Jr.; Holtzman, D.M. Biomarker modeling of Alzheimer’s disease. Neuron 2013, 80, 1347–1358. [Google Scholar] [CrossRef]
- Young, A.L.; Oxtoby, N.P.; Daga, P.; Cash, D.M.; Fox, N.C.; Ourselin, S.; Schott, J.M.; Alexander, D.C. A data-driven model of biomarker changes in sporadic Alzheimer’s disease. Brain J. Neurol. 2014, 137, 2564–2577. [Google Scholar] [CrossRef]
- Macdonald, A.; Pritchard, D. A mathematical model of Alzheimer’s disease and the Apoe gene. ASTIN Bull. 2000, 30, 69–110. [Google Scholar] [CrossRef]
- Hane, F.; Augusta, C.; Bai, O. A hierarchical Bayesian model to predict APOE4 genotype and the age of Alzheimer’s disease onset. PLoS ONE 2018, 13, e0200263. [Google Scholar] [CrossRef]
- Perez, C.; Ziburkus, J.; Ullah, G. Analyzing and modeling the dysfunction of inhibitory neurons in Alzheimer’s disease. PLoS ONE 2016, 11, e0168800. [Google Scholar] [CrossRef]
- Proctor, C.J.; Boche, D.; Gray, D.A.; Nicoll, J.A.R. Investigating interventions in Alzheimer’s disease with computer simulation models. PLoS ONE 2013, 8, e73631. [Google Scholar] [CrossRef]
- Hadjichrysanthou, C.; Ower, A.K.; de Wolf, F.; Anderson, R.M. Alzheimer’s disease neuroimaging initiative. The development of a stochastic mathematical model of Alzheimer’s disease to help improve the design of clinical trials of potential treatments. PLoS ONE 2018, 13, e0190615. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Mathematics in Science and Engineering 198; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: River Edge, NJ, USA, 2000. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Dover: Mineola, NY, USA, 2006. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; Series on Complexity, Nonlinearity and Chaos 3; World Scientific: Hackensack, NJ, USA, 2012. [Google Scholar]
- West, B.J. Fractional Calculus View of Complexity Tomorrow’S Science; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- West, B.J. Nature’s Patterns and the Fractional Calculus; Series Fractional Calculus in Applied Sciences and Engineering 2; De Gruyter: Berlin, Germany, 2017. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Yang, X.-Y.; Yang, G.J. General Fractional Derivatives with Applications in Viscoelasticity; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef] [PubMed]
- Wangersky, P.J. Lotka-Volterra population models. Ann. Rev. Ecol. Syst. 1978, 9, 189–218. [Google Scholar] [CrossRef]
- Cushing, J.M. Volterra integrodifferential equations in population dynamics. In Mathematics of Biology; Iannelli, M., Ed.; CIME Summer Schools 80; Springer: Berlin/Heidelberg, Germany, 2010; pp. 81–148. [Google Scholar]
- Ruan, S. Delay differential equations in single species dynamics. In Delay Differential Equations and Applications; Arino, O., Hbid, M.L., Ait Dads, E., Eds.; NATO science series. Series II, Mathematics, physics, and chemistry 205; Springer: Dordrecht, The Netherlands, 2006; pp. 477–517. [Google Scholar]
- Roberts, R.O.; Aakre, J.A.; Kremers, W.K.; Vassilaki, M.; Knopman, D.S.; Mielke, M.M.; Alhurani, R.; Geda, Y.E.; Machulda, M.M.; Coloma, P.; et al. Prevalence and outcomes of amyloid positivity among persons without dementia in a longitudinal, population-based detting. JAMA Neurol. 2018, 75, 970–979. [Google Scholar] [CrossRef]
- Sturchioa, A.; Dwivedic, A.K.; Youngd, C.B.; Malme, T.; Marsilia, L.; Sharmaa, J.S.; Mahajana, A.; Hilla, E.J.; Andaloussif, S.E.L.; Postond, K.L.; et al. High cerebrospinal amyloid-β 42 is associated with normal cognition in individuals with brain amyloidosis. E. Clin. Med. 2021, 38, 100988. [Google Scholar] [CrossRef]
- Song, Y.; Li, S.; Li, X.; Chen, X.; Wei, Z.; Liu, Q.; Cheng, Y. The effect of estrogen replacement therapy on Alzheimer’s disease and Parkinson’s disease in post-menopausal women: A meta-analysis. Front. Neurosci. 2020, 14, 157. [Google Scholar] [CrossRef]
- Vinogradova, Y.; Dening, T.; Hippisley-Cox, J.; Taylor, L.; Moore, M.; Coupland, C. Use of menopausal hormone therapy and risk of dementia: Nested case-control studies using QResearch and CPRD databases. BMJ 2021, 374, n2182. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Wei, H.; Chen, Y. A comparative study of constant-order and variable- order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. Top. 2011, 193, 185–192. [Google Scholar] [CrossRef]
- Ramirez, L.; Coimbra, C. On the selection and meaning of variable order operators for dynamic modeling. Int. J. Diff. Equ. 2010, 2010, 846107. [Google Scholar] [CrossRef]
- De Barros, L.C.; Lopes, M.M.; Pedro, F.S.; Esmi, E.; dos Santos, J.P.C.; Sanchez, D.E. The memory effect on fractional calculus: An application in the spread of COVID-19. Comput. Appl. Math. 2021, 40, 72. [Google Scholar] [CrossRef]
- When Does Menopause Start? Understanding the Symptoms by Age. Available online: https://www.healthpartners.com/blog/menopause-symptoms-by-age/ (accessed on 26 June 2022).
- Moghaddam, B.P.; Machado, J.A.T. Extended algorithms for approximating variable order fractional derivatives with applications. J. Sci. Comput. 2017, 71, 1351–1374. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1995; p. 161. [Google Scholar]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Almeida, R.; Malinowska, A.B.; Odzijewicz, T. On systems of fractional differential equations with the ψ-Caputo derivative and their applications. Math. Meth. Appl. Sci. 2021, 44, 8026–8041. [Google Scholar] [CrossRef]
- Almeida, R.; Torres, D.F.M. An expansion formula with higher-order derivatives for fractional operators of variable order. Sci. World J. 2013, 2013, 915437. [Google Scholar] [CrossRef]
- Hale, J. Functional Differential Equations; Applied Mathematical Sciences 3; Springer: New York, NY, USA, 1971. [Google Scholar]
- Berezansky, L.; Braverman, E. On the existence of positive solutions for systems of differential equations with a distributed delay. Comput. Math. Appl. 2012, 63, 1256–1265. [Google Scholar] [CrossRef][Green Version]
- Berezansky, L.; Braverman, E. On nonoscillation and stability for systems of differential equations with a distributed delay. Automatica 2012, 48, 612–618. [Google Scholar] [CrossRef]
- Teschl, G. Ordinary Differential Equations and Dynamical Systems; Graduate Studies in Mathematics 140; American Mathematical Society: Providence, RI, USA, 2012. [Google Scholar]
- Pooseh, S.; Almeida, R.; Torres, D.F.M. A numerical scheme to solve fractional optimal control problems. Conf. Pap. Sci. 2013, 2013, 165298. [Google Scholar] [CrossRef]
- Rivers-Auty, J.; Mather, A.E.; Peters, R.; Lawrence, C.B.; Brough, D. Anti-inflammatories in Alzheimer’s disease-potential therapy or spurious correlate? Brain Commun. 2020, 2, fcaa109. [Google Scholar] [CrossRef]
- Arevalo-Rodriguez, I.; Smailagic, N.; Roqué-Figuls, M.; Ciapponi, A.; Sanchez-Perez, E.; Giannakou, A.; Pedraza, O.L.; Bonfill Cosp, X.; Cullum, S. Mini-Mental State Examination (MMSE) for the early detection of dementia in people with mild cognitive impairment (MCI). Cochrane Database Syst Rev. 2021, 7, CD010783. [Google Scholar] [CrossRef] [PubMed]
- Jack, C.R., Jr.; Knopman, D.S.; Jagust, W.J.; Shaw, L.M.; Aisen, P.S.; Weiner, M.W.; Petersen, R.C.; Trojanowski, J.Q. Hypothetical model of dynamic biomarkers of the Alzheimer’s pathological cascade. Lancet Neurol. 2010, 9, 119–128. [Google Scholar] [CrossRef]
- Makin, S. The amyloid hypothesis on trial. Nature 2018, 559, S4–S7. [Google Scholar] [CrossRef] [PubMed]
- Furman, J.L.; Sama, D.M.; Gant, J.C.; Beckett, T.L.; Murphy, M.P.; Bachstetter, A.D.; Van Eldik, L.J.; Norris, C.M. Targeting astrocytes ameliorates neurologic changes in amouse model of Alzheimer’s disease. J Neurosci. 2012, 32, 16129–16140. [Google Scholar] [CrossRef]
- Chou, R.C.; Kane, M.; Ghimire, S.; Gautam, S.; Gui, J. Treatment for rheumatoid arthritis and risk of Alzheimer’s disease: A nested case-control analysis. CNS Drugs 2016, 30, 1111–1120. [Google Scholar] [CrossRef]
- Furman, D.; Campisi, J.; Verdin, E.; Carrera-Bastos, P.; Targ, S.; Franceschi, C.; Ferrucci, L.; Gilroy, D.W.; Fasano, A.; Miller, G.W.; et al. Chronic inflammation in the etiology of disease across the life span. Nat. Med. 2019, 25, 1822–1832. [Google Scholar] [CrossRef]
- Yaribeygi, H.; Atkin, S.L.; Pirro, M.; Sahebkar, A. A review of the anti-inflammatory properties of antidiabetic agents providing protective effects against vascular complications in diabetes. J. Cell Physiol. 2019, 234, 8286–8294. [Google Scholar] [CrossRef]
- Munoz-Jimenez, M.; Zaarkti, A.; Garcia-Arnes, J.A.; Garcia-Casares, N. Antidiabetic drugs in Alzheimer’s disease and mild cognitive impairment: A systematic review. Dement. Geriatr. Cogn. Disord. 2020, 49, 423–434. [Google Scholar] [CrossRef]
- Chowen, J.A.; Garcia-Segura, L.M. Role of glial cells in the generation of sex differences in neurodegenerative diseases and brain aging. Mech. Ageing Dev. 2021, 196, 111473. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).