Abstract
Fractional-order systems have proved to be accurate in describing the spread of the COVID-19 pandemic by virtue of their capability to include the memory effects into the system dynamics. This manuscript presents a novel fractional discrete-time COVID-19 model that includes the number of vaccinated individuals as an additional state variable in the system equations. The paper shows that the proposed compartment model, described by difference equations, has two fixed points, i.e., a disease-free fixed point and an epidemic fixed point. A new theorem is proven which highlights that the pandemic disappears when an inequality involving the percentage of the population in quarantine is satisfied. Finally, numerical simulations are carried out to show that the proposed incommensurate fractional-order model is effective in describing the spread of the COVID-19 pandemic.
1. Introduction
Epidemic models have received considerable attention over the last years [1]. They can be represented by either dynamic continuous-time or discrete-time systems, i.e., they are described by either differential or difference equations [1]. Recently, several continuous and discrete dynamic models have been proposed involving both integer-order equations and fractional equations [2,3,4,5,6,7,8]. These dynamic models divide communities into classes (for example, susceptible (S), infected (I), and recovered (R)) and describe the evolution of a disease over time [9]. For example, in [2], an SIR model is utilized for estimating infectivity and recovery rates from real COVID-19 data. Then, the estimated rates are exploited to analyse the evolution of the pandemic over time. In [10], another SIR model is presented with the aim of describing the spread of the COVID-19 epidemic in Wuhan. The model is updated with real-time input data in order to derive clinical parameters that can support public officials in decision-making. In [11], two new fractional-order versions for the SEIR model were proposed in view of two fractional-order differential operators, namely, the Caputo and the Caputo–Fabrizio operators. In [12], a novel fractional-order discrete model was proposed to adapt the periodic change in the number of infections. In [13], the role of fractional calculus in describing the growth of COVID-19 dynamics implemented in Saudi society over a specific period was explored. In [14], the authors investigated the nonlinear dynamic behavior of a novel COVID-19 pandemic model described by commensurate and incommensurate fractional-order derivatives. In [15], a novel fractional-order version of the SEIR model was established by proposing different physical conditions of its growth.
Approaches to modelling the spread of the COVID-19 pandemic have becgun to change at this point at the beginning of the year 2021 by virtue of the introduction of vaccines. A number of papers have been published taking into account the role of vaccination in controlling the pandemic [16,17] in different ways. Most of these models are described by differential equations, whereas very few models involve difference equations [18,19].
Referring to fractional-order models, i.e., systems described by non-integer order differential or difference equations, they have proven to be accurate in describing the spread of the COVID-19 pandemic by virtue of their capability to include memory effects in the system dynamics [3,20]. The use of fractional operators enables them take into account the fact that the spread of infectious diseases depends on both the current state and the past states [20]. For example, in [20] a fractional model with seven compartments was proposed for analysing the spread of the COVID-19 pandemic. In [21], the Caputo derivative was exploited to study the transmission of COVID-19. The existence and uniqueness of the solutions available with the proposed fractional model was discussed as well. In [22], the dynamics of the COVID-19 pandemic were described using both the Caputo–Fabrizio derivative and the Atangana–Baleanu–Caputo derivative, and, stability analyses for the two modelling approaches were conducted. In [23], a fractional SEIR model was introduced in which the fractional derivatives presented different orders for each of the different populations being studied.
Starting from the beginning of the year 2021, in several countries a vaccine against the COVID-19 virus became available. Consequently, new research could be conducted with the introduction of epidemic models able to take into account the role of vaccination in controlling the COVID-19 pandemic [16,18]. Referring to integer-order models, a number of different papers have been published [18,24]. However, all these papers consider vaccination as a control law or a preventive action, rather than as an additional state variable to be added to the compartment model. For example, in [18], an integer-order discrete SEIR epidemic model was developed in which a feedback vaccination control law was included to stabilize the system dynamics. In [25], an integer-order SEIR epidemic model was presented that incorporated both a feedback vaccination control law and an antiviral treatment control law. In [26], an integer-order COVID-19 model was developed in which vaccination was considered a preventive action. Only two papers have been published thus far with fractional-order models that incorporate the role of vaccination [16,27].
This manuscript is organized as follows. In Section 2, basic notions of fractional difference are provided, and in Section 3 a new fractional-order discrete compartment model for describing the spread of the COVID-19 pandemic is presented. The non-integer order dynamics are described via the Caputo difference using five state variables, i.e., the Susceptible class (S), the Recovered class (R), the Infection class (I), the Infection dangerous class (Id), and the Vaccinated class (V). Section 4 first shows that the model possesses a disease-free fixed point and an epidemic fixed point. Then, the asymptotic stability of the disease-free fixed point is proven in Section 5. In Section 6, a new theorem is illustrated which highlights that the pandemic disappears when an inequality involving the percentage of the population in quarantine is satisfied. Finally, in Section 7, numerical simulations are described, showing that the proposed incommensurate fractional-order model is effective in describing the spread of the COVID-19 pandemic.
2. Basic Tools about Discrete Fractional Calculus
Recently, discrete fractional calculus has shown great efficacy in modeling natural phenomena because it is more compatible with realistic results, which are discontinuous in nature, and is compatible with computer algorithms. In this section, we present definitions and results about discrete fractional calculus which are used later in our study. In all of the definitions below, the functions we consider are defined on a set with the form where .
Definition 1
([28]). Let . Then, the fractional sum of is defined by
where is Euler’s gamma function and
Based on the previous definition, we can define the fractional difference of Riemann–Liouville as follows:
Definition 2
([28]). Let . Then, the -order Riemann–Liouville fractional difference of a function f is defined by:
This definition is very good from a mathematical point of view. However, there is great difficulty in its application; as studying the systems defined by it is not possible using the classical initial conditions, we use the following definition:
Definition 3
([28]). Let . Then, the α-order Caputo fractional difference of a function f defined on is defined by
For this operator, we have the following result:
Proposition 1
([28]). Let and let f be defined on Then,
In the same way and for the same goals as above, we mention the following definitions:
Definition 4
([28]). For a function , the nabla fractional sum of order is defined by
where is Euler’s gamma function and
Definition 5
([28]). The nabla Riemann–Liouville fractional difference of order (starting from a) is defined by
where
Definition 6
([28]). Assume that , and f is defined on . Then, the left Caputo fractional difference of order α starting at a is defined by
for
The Mittag–Leffler of fractional nabla calculus is the solution of the linear system defined by the Caputo nabla operator, and is defined as follows:
Definition 7
([29]). For and define the one parameter Mittag–Leffler function of fractional nabla calculus by
This function satisfies the following properties:
Proposition 2
([29]). If then , as
Proposition 3
([29]).
The comparison theory, which is needed later, is as follows:
Theorem 1
([30]). Assume , , and . Then, we have for
3. A New Discrete Fractional Model including the Vaccinated Class
To understand the behavior of the spread of the epidemic, we divide the studied population into five classes: people who are exposed to infection and were not previously infected and did not receive vaccination, people who were previously infected and recovered from the disease and are at risk of being infected again, and people vaccinated against the epidemic. As for the class of infected persons, it is divided into two secondary classes: people with good immunity and for whom infection does not pose a great risk (for whom we suppose the ratio in society to be (), and those infected persons for whom the infection is dangerous, consisting of the elderly, pregnant women, and people with chronic diseases (whose ratio in society is .
Below, we explain the migration from each class to the other:
Susceptible class: This class acquires a number of people, which is the number of people entering the studied area, and in the event that the studied area is isolated, then represents the birth rate in this area. This class loses people who are exposed to infection, people who have been vaccinated against the disease, and natural deaths.
Recovered class: This class is acquired at the rate of new recovered persons and loses people who are exposed to infection, as well as losing people who have been vaccinated against the disease and natural deaths.
Vaccinated class: This class is acquired at the rate of new vaccinated persons, and class loses people who are infected and natural deaths.
Infection class: This class consists of acquired new infection. This class loses people who are recovered and natural deaths (we assume that in this class there are no deaths due to the epidemic).
Infection dangerous class: This class consists of acquired new infected persons. This class loses people who recover, natural deaths, and deaths due to infection.
The classes described above are summarized in Figure 1.
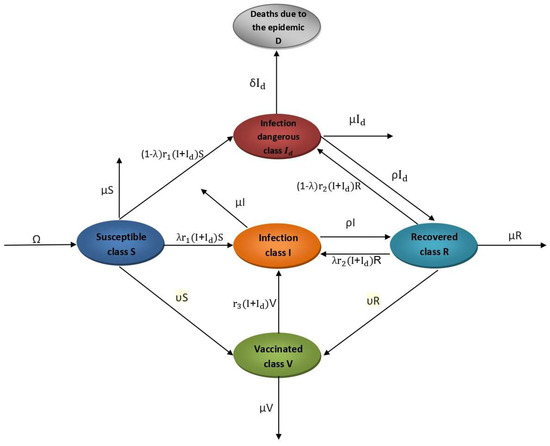
Figure 1.
Diagram showing the transitions between categories.
The proposed model’s flowchart and parameters description are explained in Table 1.

Table 1.
Parameters description.
The mathematical translation of the above in the system of differential equations is as follows [31]:
The total population is as follows:
In addition, the following initial conditions are taken into consideration:
In this paper, we study the general case of the discrete system provided by the Caputo incommensurate fractional differences; we choose the order for the healthy class and the order for the infected class. The incommensurate order allows for greater flexibility in modeling, resulting in a more realistic model.
When converting System (9) to a fractional difference system, there are two types of systems, the forward difference system and the backward difference system.
The fractional incommensurate order forward difference system is provided by
where . Using Proposition 1, System (11) can be written as follows:
where and
Thus, it is defined by a regression relationship. Note that existence and uniqueness are trivial in this case. It cannot be shown that the solution is positive for System (11). In fact, the solution to System (11) is not always positive even when the initial conditions are positive.
In the rest of the paper, we study the fractional incommensurate order backward difference system, written as follows:
where . By adding the equations from System (14), we obtain
Consequently, we have
and thus
Let and suppose that for t; then, we have
and by induction, for all t when the solution exists
Therefore, the solution belongs to the invariant region
where for as the invariant region.
4. Fixed Points and Basic Reproduction Number
To study the dynamics of (14), it is necessary to first find the fixed points; to find the fixed points, the following equation must be solved:
The equation has the point as a solution. It can be seen that at this point the disease is non-existent, and this is therefore called the disease-free fixed point, which we are interested in studying for its stability and discuss later.
If we suppose that we have
which is a complex and difficult system to solve in the abstract case. Even if we were able to solve it, studying the stability of this fixed point contains many obstacles. Overall, this point is called the epidemic equilibrium point,
The basic reproduction number is very important in the study of stability for the disease-free fixed point, which represents the rate of new people being infected by one sick person until their recovery. Following the steps described in [32], we find that
5. Stability Analysis of the Disease-Free Fixed Point
One of the most important dynamic behaviors in the system is the stability of fixed points. Therefore, we always resort to studying it, as for the purpose of knowing whether the disease disappears or not, it is important to study the asymptotic stability of the disease-free fixed point of the system.
The stability of the system from System (14) was studied in [33], in which the authors mention the following theorem:
Theorem 2
([33]). Let M be the lowest common multiple (LCM) of the denominators of ’s, where for Then, (14) has a unique solution for all initial vectors close enough to ; moreover, is asymptotically stable if any zero solution of the polynomial equation
lies inside the set
where J is the Jacobian matrix of F at
Based on this theorem, we can find the following result:
Theorem 3.
Suppose that ; then, the disease-free fixed point of System (14) is locally asymptotically stable.
Proof.
To apply Theorem 2, we must first calculate the Jacobian matrix for the right-hand side of system (14) at fixed point ; by simple calculation we obtain
The characteristic Equation (18) is provided by
where
Thus, to solve this equation we have
and thus
which means that
and therefore
Alternatively, we have
if then . Thus, according to the Routh–Hurwitz criterion [34], both roots of
are in the open left half plane, and thus
from which the condition of Theorem 2 fulfilled. Accordingly, the disease-free fixed point of System (14) is locally asymptotically stable. □
Remark 1.
We note that this result is very logical and compatible with the definition of the number . As it is clear that if every infected person leaves less than one infection, the disease will disappear.
6. A Condition for the Disappearance of the Pandemic
The primary objective of the study of the mathematical model of the epidemic is to study the possibility of finding solutions to get rid of the epidemic. By adding the last two equations into System (14), we find that the infection is described by the next equation:
because I is positive and ,
Applying the comparison from Theorem 1, we have
where is the solution of
According to Proposition 2,
then we have
Note that if then according to Proposition 3, when . Thus, we obtain the following result:
Theorem 4.
If
then the disease will disappear.
Remark 2.
While the condition of Theorem 4 is considered to be higher than the condition of Theorem 3, it guarantees global stability.
In real applications, it is always the case that , and the condition (21) becomes .
The authorities in all countries of the world have imposed preventive measures such as protective masks and the use of sterilizer in public places, which affects the probabilities of contagion (). The authorities can impose quarantine, which affects the friction as in all cases (, where the only possible control is to reduce infection rates ().
Let be the control function, which represents the percentage of quarantine (quarantine cannot be 100%, as this is considered impossible). The controlled system is written as follows:
When the initial condition is close enough to the disease-free fixed point, it suffices to choose a controller to ensure the asymptotic stability of the disease-free fixed point, which is what we do in the following theorem:
Theorem 5.
Suppose that
Then, the disease-free fixed point is locally asymptotically stable.
Proof.
The characteristic equation becomes
where
If then . Thus, according to the Routh–Hurwitz criterion, both roots of
are in the open left half plane, and thus
This fulfills the condition of Theorem 2. Accordingly, the disease-free fixed point is locally asymptotically stable. □
When the initial condition is far from the disease-free fixed point, it is not possible to guarantee stability. To reduce the spread of the epidemic in this case, we present the following result:
Theorem 6.
Suppose that
then, the disease will disappear.then, the disease will disappear.
Proof.
Let Adding the last two equations to System (22), we find that infection is described by the following equation:
because I is positive
Because ,
Applying the comparison in Theorem 4, we have
where is the solution of
According to Proposition 3,
then
We note that if then when □
Remark 3.
We note that the control provided in Theorem 6 is more expensive than the control given in Theorem 5. Therefore, it is better to impose quarantine and other procedures before the spread of the disease, that is, when the initial condition is very close to the disease-free fixed point.
7. Numerical Simulations and Application
To review the effectiveness of the studied system, in this section we apply it to the state of Germany and compare the results of the integer order system with the fractional incommensurate system to determine their compatibility with realistic results. All statistics are taken as N(0) = 1,000,000. According to [35], the initial population can be divided as follows:
On the other hand, according to the same source [35] and according to [36], we can calculate the values of the system parameters and find
We take real data on active cases in Germany during the period from 26 April to 30 May 2022, represented in Figure 2.
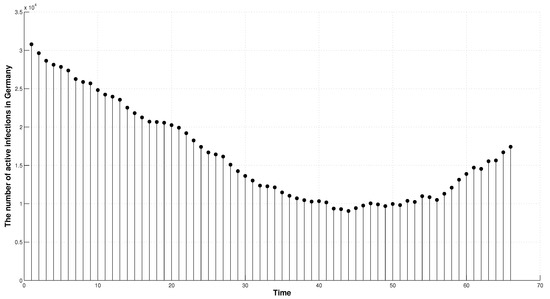
Figure 2.
The number of active infections in Germany in the period 26 April to 30 May 2022 [35].
To apply Theorem 3, we must first calculate :
We note that as , according to Theorem 3 the disease-free fixed point is locally asymptotically stable. While we thus know that the number of active cases is decreasing with time, we do not know what the nature of this decrease is. First, when applying the integer order system () it can be seen from the simulations in Figure 3 that the model provides a good result at first, then completes an exponential decrease in contrast to the real results, which increase after a period of time.
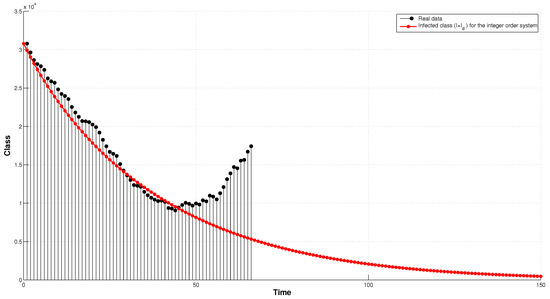
Figure 3.
Numerical simulation of infected class with integer order and comparison with the real data.
We now apply the fractional incommensurate model by taking and . Note from Figure 4 that the results are very compatible and realistic, and in the end the number of active cases is decreasing, although is should be noted that there is an epidemic wave before this decrease as well. In particular, Figure 3 and Figure 4 show numerical comparisons between real data which represents the number of active infections in Germany for the period 26 April to 30 May 2022 along with the results obtained from the integer-order system and fractional-order systems. Based on these two figures, we can clearly conclude that the fractional-order system is closer than the integer-order system to the real data, enabling us to rely on the construction of the fractional-order system to set a more suitable effective prediction than the integer-order system.
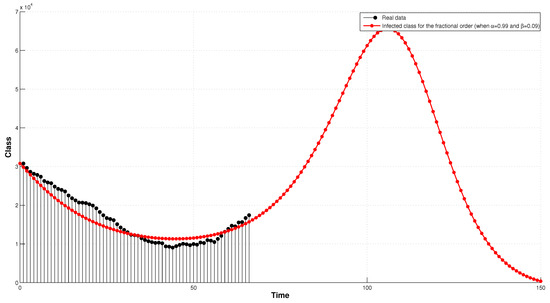
Figure 4.
Numerical simulation of infected class with fractional-order system and comparison with real data.
8. Conclusions and Future Perspectives
In the context of the spread of the COVID-19 pandemic, this paper has presented a new discrete fractional-order compartment model incorporating the number of vaccinated individuals as an additional state variable describing the system dynamics. In this manuscript, we have shown that the proposed fractional-order model described by fractional difference equations possesses an asymptotically stable disease-free fixed point. In particular, we have proven a novel theorem which provides a condition for the disappearance of the pandemic when an inequality involving some epidemic parameters is satisfied. This result represents a remarkable finding of the proposed approach, and may help decision-makers to better understand the epidemiological behaviour of the COVID-19 pandemic over time. Finally, several numerical simulations were performed with the aim of showing the role of discrete fractional calculus in describing the dynamics of the COVID-19 pandemic more effectively. This can be considered one of the main contributions of this work, coupled with the use of fractional-order difference operators, which except for a very few works have not previously been used in the context of COVID-19 modeling. Our future goal is to summarize this model and try to formulate it with as few equations as possible while maintaining the same accuracy.
Author Contributions
Conceptualization, N.D.; Formal analysis, A.D. and I.H.J.; Funding acquisition, G.G.; Investigation, N.D. and G.G.; Methodology, A.D., A.O. and I.M.B.; Resources, A.D.; Software, N.D.; Supervision, A.O. and I.H.J.; Validation, G.G. and I.M.B.; Visualization, A.O.; Writing—original draft, I.H.J.; Writing—review & editing, I.M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef] [Green Version]
- Tchavdar, T.; Marinov, R.; Marinova, S. Dynamics of COVID-19 using inverse problem for coefficient identification in SIR epidemic models. Chaos Solitons Fractals X 2020, 5, 100041. [Google Scholar]
- Lu, Z.; Yu, Y.; Chen, Y.; Ren, G.; Xu, C.; Wang, S.; Yin, Z. A fractional-order SEIHDR model for COVID-19 with inter-city networked coupling effects. Nonlinear Dyn. 2020, 101, 1717–1730. [Google Scholar] [CrossRef] [PubMed]
- Batiha, I.M.; Albadarneh, R.B.; Momani, S.; Jebril, I.H. Dynamics analysis of fractional-order Hopfield neural networks. Int. J. Biomath. 2020, 13, 2050083. [Google Scholar] [CrossRef]
- Batiha, I.M.; Oudetallah, J.; Ouannas, A.; Al-Nana, A.A.; Jebril, I.H. Tuning the Fractional-order PID-Controller for Blood Glucose Level of Diabetic Patients. Int. J. Adv. Soft Comput. Its Appl. 2021, 13, 1–10. [Google Scholar]
- Jebril, I.H.; Batiha, I.M. On the Stability of Commensurate Fractional-Order Lorenz System. Prog. Fract. Differ. Appl. 2022, 8, 401–407. [Google Scholar]
- Batiha, I.M.; Njadat, S.A.; Batyha, R.M.; Zraiqat, A.; Dababneh, A.; Momani, S. Design Fractional-order PID Controllers for Single-Joint Robot Arm Model. Int. J. Adv. Soft Comput. Its Appl. 2022, 14, 96–114. [Google Scholar] [CrossRef]
- Hammad, M.A.; Jebril, I.H.; Batiha, I.M.; Dababneh, A.M. Fractional Frobenius Series Solutions of Confluent α-Hypergeometric Differential Equation. Prog. Fract. Differ. Appl. 2022, 8, 297–304. [Google Scholar]
- Anderson, B.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Wu, J.T.; Leung, K.; Bushman, M.; Kishore, N.; Niehus, R.; de Salazar, P.M.; Cowling, B.J.; Lipsitch, M.; Leung, G.M. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat. Med. 2020, 26, 506–510. [Google Scholar] [CrossRef] [Green Version]
- Batiha, I.M.; Momani, S.; Ouannas, A.; Momani, Z.; Hadid, S.B. Fractional-order COVID-19 pandemic outbreak: Modeling and stability analysis. Int. J. Biomath. 2022, 15, 2150090. [Google Scholar] [CrossRef]
- Djenina, N.; Ouannas, A.; Batiha, I.M.; Grassi, G.; Oussaeif, T.-E.; Momani, S. A Novel Fractional-Order Discrete SIR Model for Predicting COVID-19 Behavior. Mathematics 2022, 10, 2224. [Google Scholar] [CrossRef]
- Batiha, I.M.; Al-Nana, A.A.; Albadarneh, R.B.; Ouannas, A.; Al-Khasawneh, A.; Momani, S. Fractional-order coronavirus models with vaccination strategies impacted on Saudi Arabia’s infections. AIMS Math. 2022, 7, 12842–12858. [Google Scholar] [CrossRef]
- Debbouche, N.; Ouannas, A.; Batiha, I.M.; Grassi, G. Chaotic dynamics in a novel COVID-19 pandemic model described by commensurate and incommensurate fractional-order derivatives. Nonlinear Dyn. 2022, 109, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Albadarneh, R.B.; Batiha, I.M.; Ouannas, A.; Momani, S. Modeling COVID-19 Pandemic Outbreak using Fractional-Order Systems. Int. J. Math. Comput. Sci. 2021, 16, 1405–1421. [Google Scholar]
- Kumara, P.; Erturk, V.S.; Murillo-Arcila, M. A new fractional mathematical modelling of COVID-19 with the availability of vaccine. Results Phys. 2021, 24, 104213. [Google Scholar] [CrossRef]
- Hwang, E. Prediction intervals of the COVID-19 cases by HAR models with growth rates and vaccination rates in top eight affected countries: Bootstrap improvement. Chaos Solitons Fractals 2022, 155, 111789. [Google Scholar] [CrossRef] [PubMed]
- De la Sen, M.; Alonso-Quesada, S.; Ibeas, A. On a discrete SEIR epidemic model with exposed infectivity, feedback vaccination and partial delayed re-susceptibility. Mathematics 2021, 9, 520. [Google Scholar] [CrossRef]
- Judeh, D.A.; Hammad, M.A. Applications of conformable fractional pareto probability distribution. Int. J. Advance Soft Compu. Appl. 2022, 14, 115–124. [Google Scholar]
- Biala, T.A.; Khaliq, A.Q.M. A fractional-order compartmental model for the spread of the COVID-19 pandemic. Commun. Nonlinear Sci. Numer. Simul. 2021, 98, 105764. [Google Scholar] [CrossRef]
- Tuan, N.H.; Mohammadi, H.; Rezapour, S. A mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Chaos Solitons Fractals 2020, 140, 110107. [Google Scholar] [CrossRef]
- Panwar, V.S.; Uduman, P.S.S.; Gómez-Aguilar, J.F. Mathematical modeling of coronavirus disease COVID-19 dynamics using CF and ABC non-singular fractional derivatives. Chaos Solitons Fractals 2021, 145, 110757. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yu, X.; Sun, H.; Tick, G.R.; Wei, W.; Jin, B. Applicability of time fractional derivative models for simulating the dynamics and mitigation scenarios of COVID-19. Chaos Solitons Fractals 2020, 138, 109959. [Google Scholar] [CrossRef] [PubMed]
- Badfar, E.; Zaferani, E.J.; Nikoofard, A. Design a robust sliding mode controller based on the state and parameter estimation for the nonlinear epidemiological model of Covid-19. Nonlinear Dyn. 2021, 109, 5–18. [Google Scholar] [CrossRef] [PubMed]
- De la Sen, M.; Ibeas, A. On an SE(Is)(Ih)AR epidemic model with combined vaccination and antiviral controls for COVID-19 pandemic. Adv. Differ. Equ. 2021, 2021, 92. [Google Scholar] [CrossRef]
- Gozalpour, N.; Badfar, E.; Nikoofard, A. Transmission dynamics of novel coronavirus sars-cov-2 among healthcare workers, a case study in Iran. Nonlinear Dyn. 2021, 105, 3749–3761. [Google Scholar] [CrossRef]
- Omame, A.; Okuonghae, D.; Nwajeri, U.K.; Onyenegecha, C.P. A fractional-order multi-vaccination model for COVID-19 with non-singular kernel. Alex. Eng. J. 2022, 61, 6089–6104. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional diferences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar]
- Eloe, P.; Jonnalagadda, J. Mittag-Leffler Stability of Systems of Fractional Nabla Difference Equations. Bull. Korean Math. Soc. 2019, 56, 977–992. [Google Scholar]
- Christopher, G.; Allan, C.P. Discrete Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-319-25560-6. [Google Scholar]
- Almatroud, A.O.; Djenina, N.; Ouannas, A.; Grassi, G.; Al-sawalha, M.M. A novel discrete-time COVID-19 epidemic model including the compartment of vaccinated individuals. Math. Biosci. Eng. 2022, preprint. [Google Scholar]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Djenina, N.; Ouannas, A.; Oussaeif, T.-E.; Grassi, G.; Batiha, I.M.; Momani, S.; Albadarneh, R.B. On the Stability of Incommensurate h-Nabla Fractional-OrderDifference Systems. Fractal Fract. 2022, 6, 158. [Google Scholar] [CrossRef]
- Mahardika, R.; Widowati; Sumanto, Y.D. Routh-hurwitz criterion and bifurcation method for stability analysis of tuberculosis transmission model. J. Phys. Conf. Ser. 2019, 1217, 012056. [Google Scholar] [CrossRef]
- Available online: https://www.worldometers.info (accessed on 8 August 2022).
- Staudinger, U.; Schneider, N.F. Demographic facts and Trends in Germany 2010–2020; Federal Institute for Population Research: Wiesbaden, Germany, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).