The Fractal Characteristics of Soft Soil under Cyclic Loading Based on SEM
Abstract
:1. Introduction
2. Materials and Methods
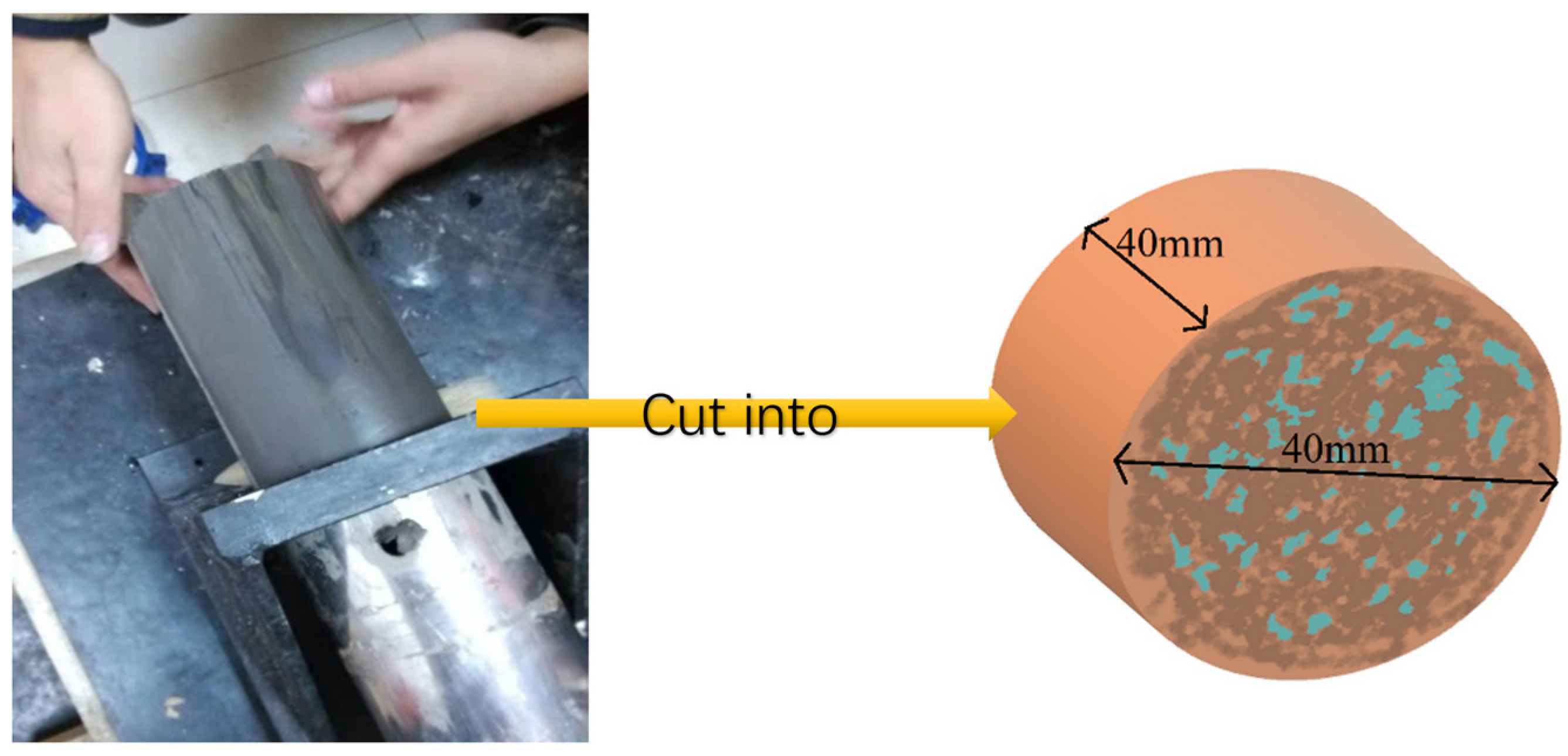
2.1. Materials
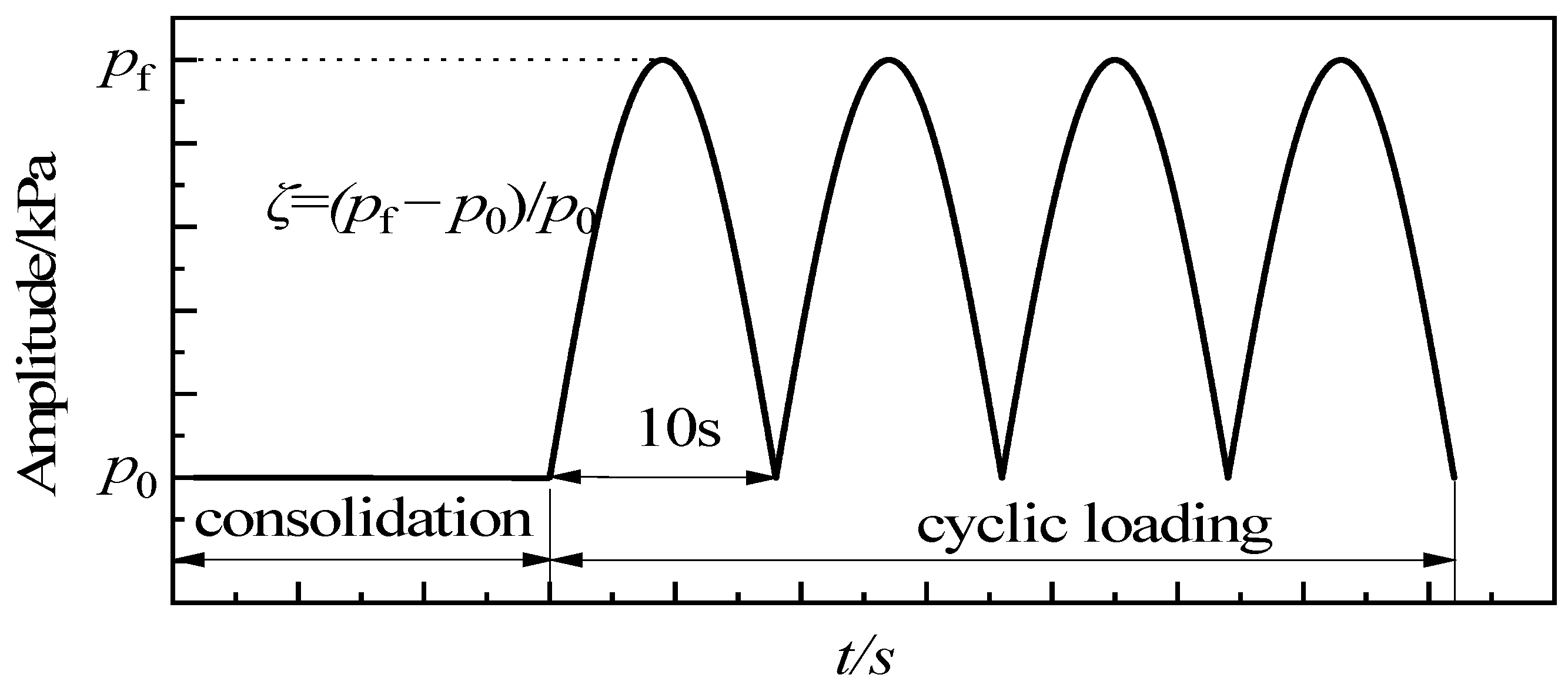
2.2. Methods
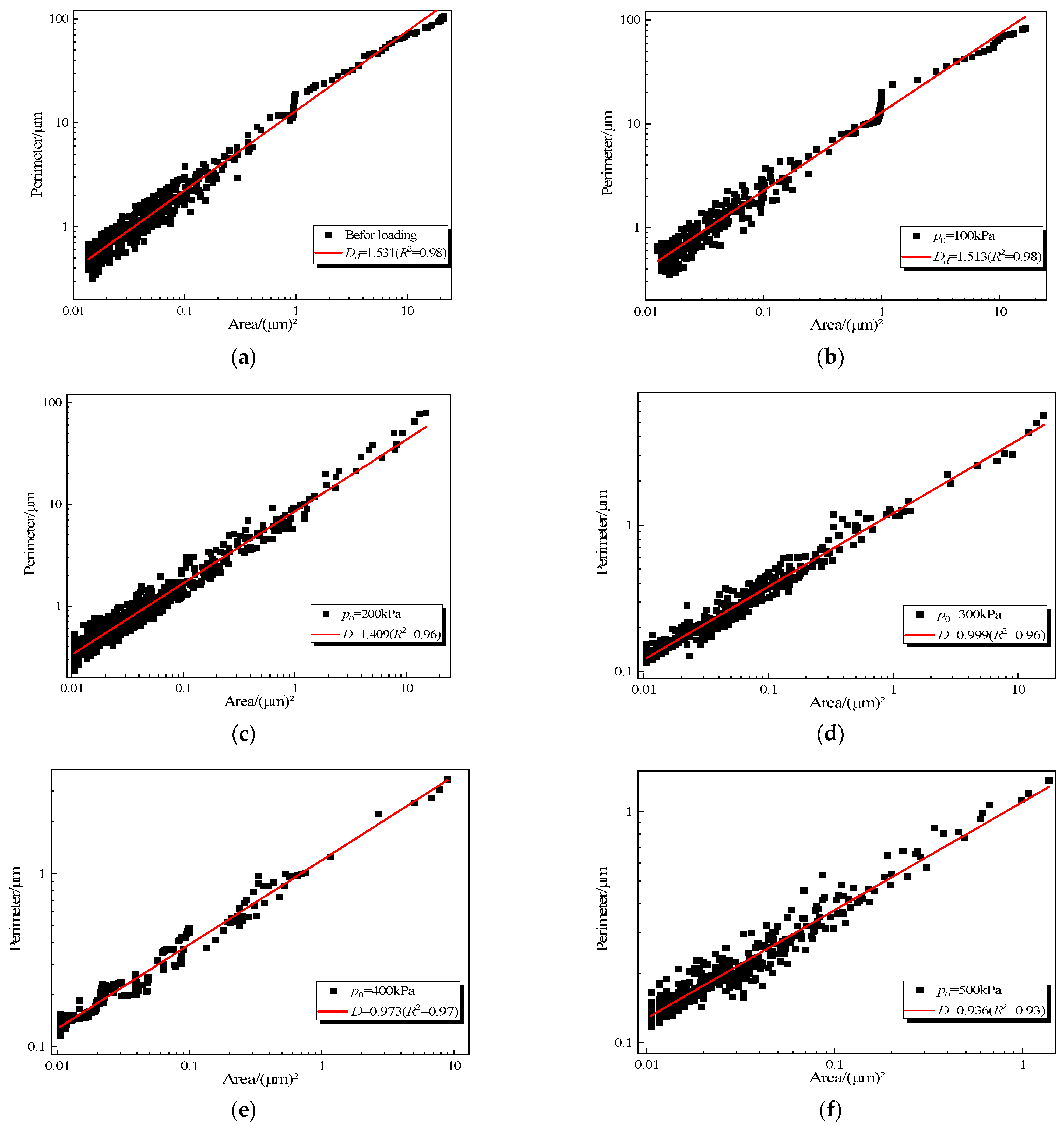
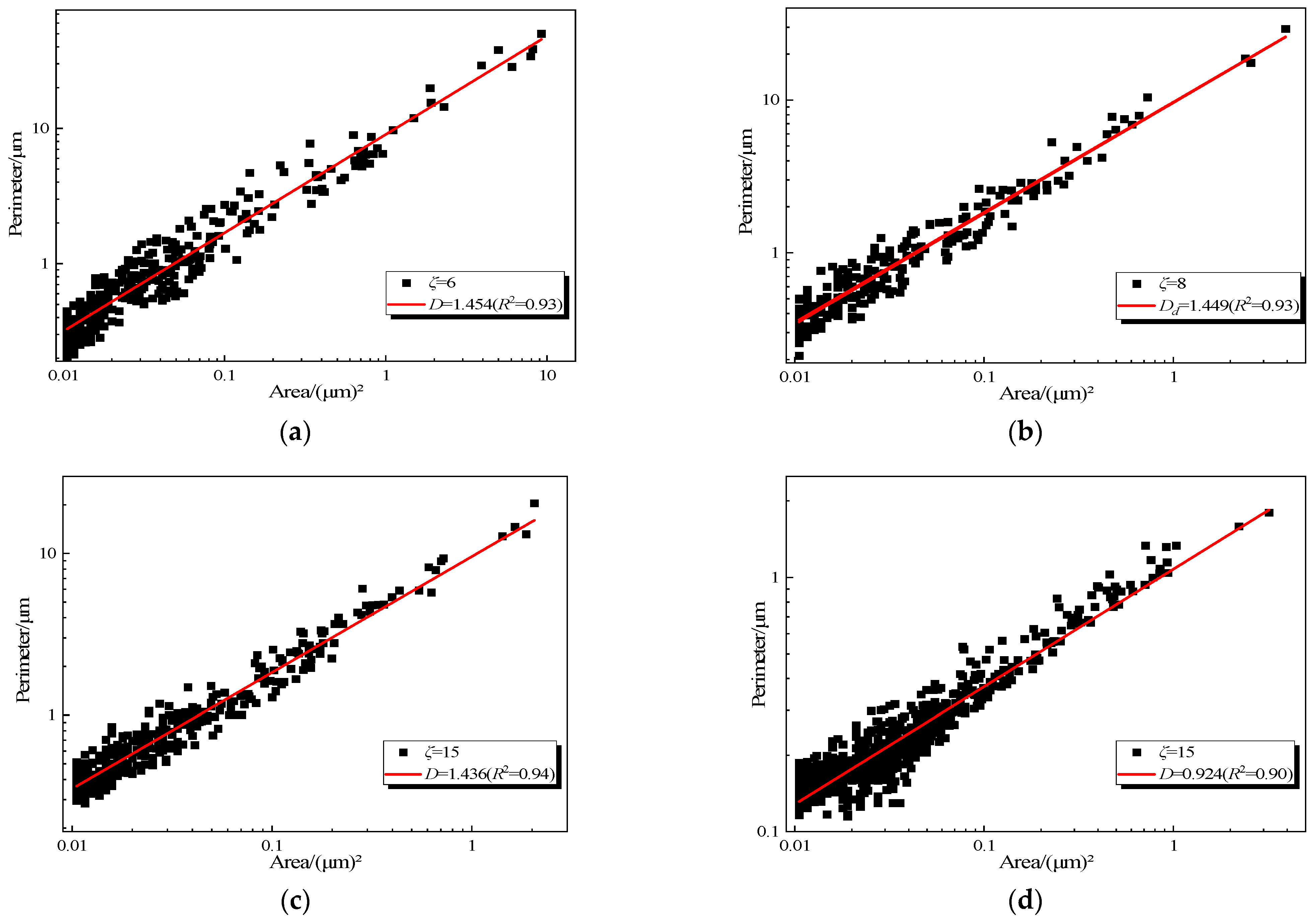
3. Results
4. Discussion
5. Conclusions
- (1)
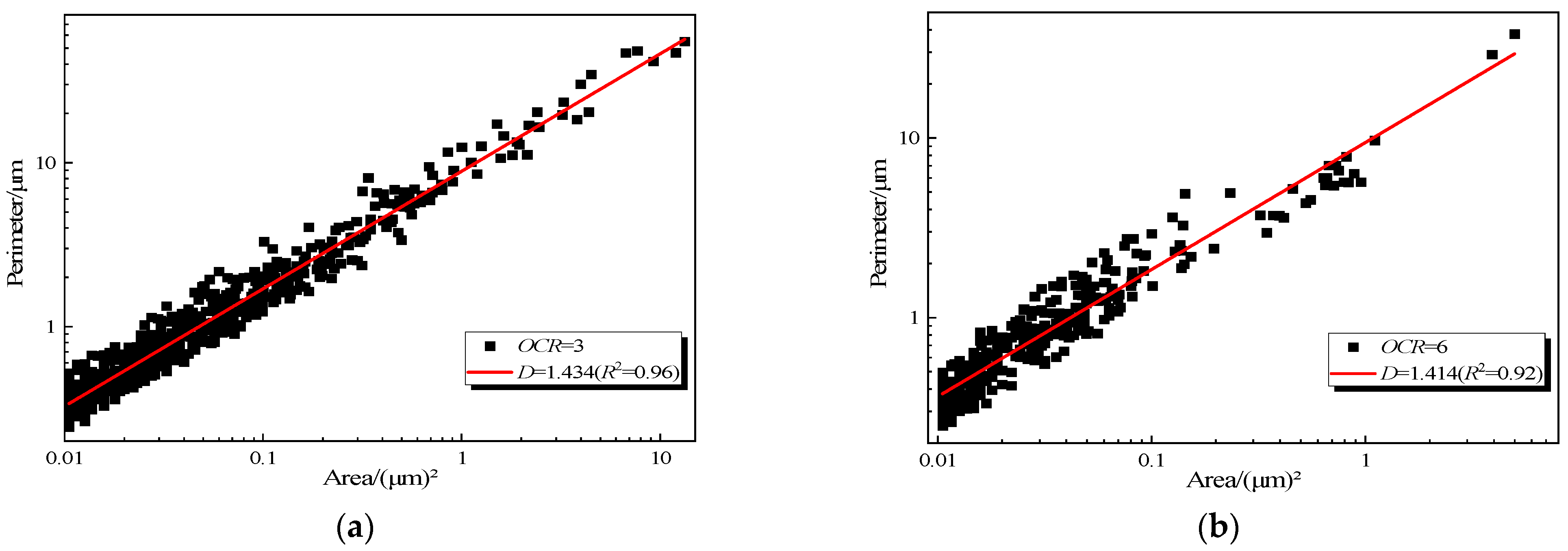
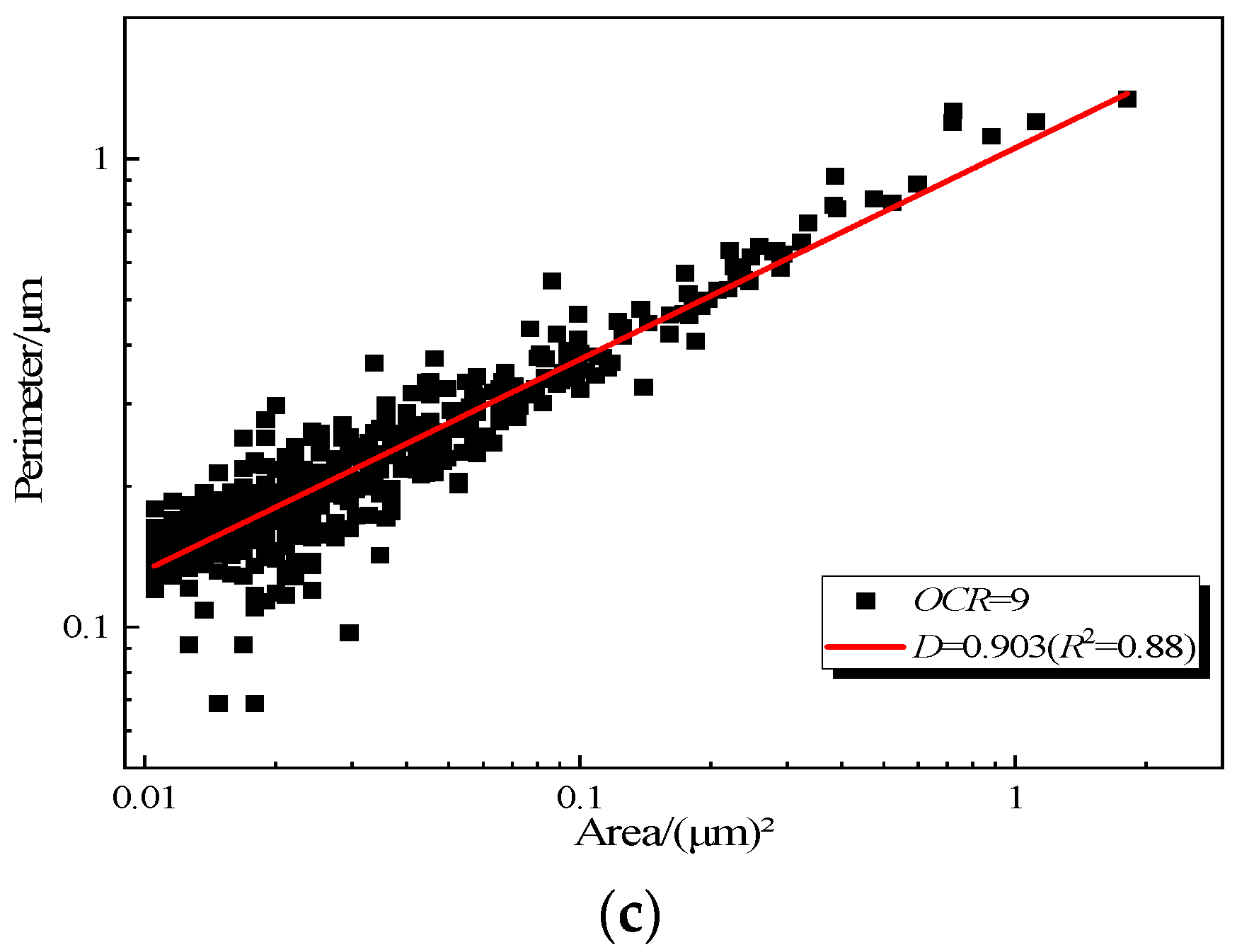
- The soft soil of Hangzhou marine has a flocculation structure. The distribution of soil particles in the microstructure of soft clay conforms to the fractal characteristics, and the fractal dimension number is between 1 and 2.
- (2)
- After loading, the pores become more orderly. The larger the consolidation confining pressure, the greater the cyclic dynamic stress ratio and the greater the overconsolidation ratio, the smaller the fractal dimension number of soil samples.
- (3)
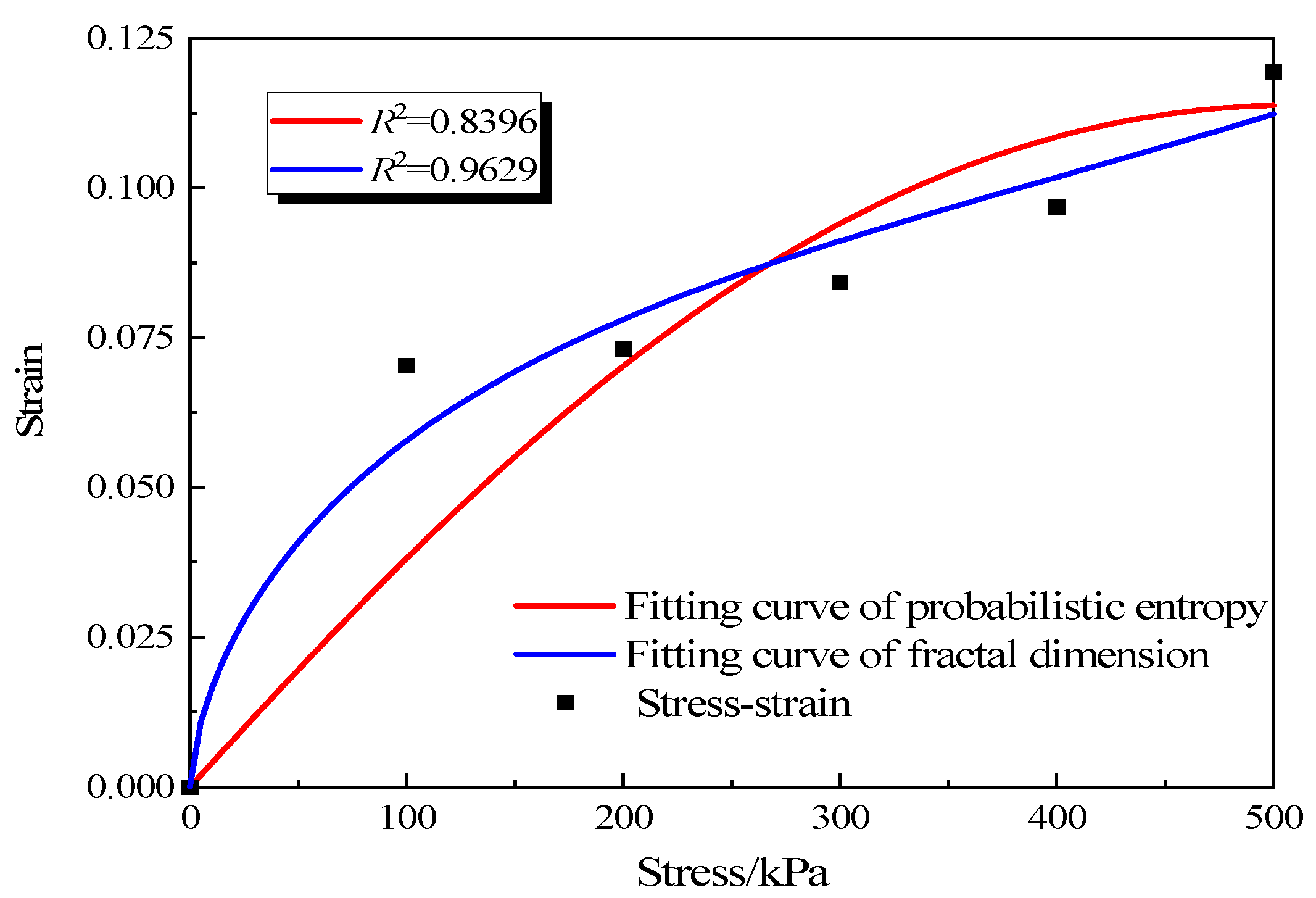
- Fractal dimension and probabilistic entropy are closely related to cumulative strain. Based on the empirical fitting formula of strain index, an empirical fitting formula for cumulative strain considering microstructure parameters was established.
- (4)
- The trends from the fractal dimension and probabilistic entropy are consistent with each other. The accuracy of the predicted probabilistic entropy strain is 0.83, whereas this value is 0.96 for the fractal dimension. Then, a new way to predict subsidence based on fractal dimension information was obtained for soft soil.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, Y.F.; Sumelka, W. Bounding surface model refined with fractional dilatancy relation for sand. Soils Found. 2022, 62, 101149. [Google Scholar] [CrossRef]
- Sumelka, W.; Blaszczyk, T. Fractional continua for linear elasticity. Arch. Mech. 2014, 66, 147–172. [Google Scholar]
- Li, Y.; Zhang, H.; Huang, M.; Yin, H.; Jiang, K.; Xiao, K.; Tang, S. Influence of Different Alkali Sulfates on the Shrinkage, Hydration, Pore Structure, Fractal Dimension and Microstructure of Low-Heat Portland Cement, Medium-Heat Portland Cement and Ordinary Portland Cement. Fractal Fract. 2021, 5, 79. [Google Scholar] [CrossRef]
- Pfeifer, P.; Avnir, D. Chemistry in noninteger dimensions between two and three. I. Fractal theory of heterogeneous surfaces. J. Chem. Phys. 1983, 79, 7. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, B.; Yuan, S.; Shen, Z.; Feng, D. Seepage–Fractal Model of Embankment Soil and Its Application. Fractal Fract. 2022, 6, 277. [Google Scholar] [CrossRef]
- Fu, X.; Ding, H.; Sheng, Q.; Zhang, Z.; Yin, D.; Chen, F. Fractal Analysis of Particle Distribution and Scale Effect in a Soil–Rock Mixture. Fractal Fract. 2022, 6, 120. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, D.; Cai, Y.; Yao, Y. Fractal characterization of pore–fracture in low-rank coals using a low-field NMR relaxation method. Fuel 2016, 181, 218–226. [Google Scholar] [CrossRef]
- Sun, W.; Zuo, Y.; Wu, Z.; Liu, H.; Xi, S.; Shui, Y.; Wang, J.; Liu, R.; Lin, J. Fractal analysis of pores and the pore structure of the Lower Cambrian Niutitang shale in northern Guizhou province: Investigations using NMR, SEM and image analyses. Mar. Pet. Geol. 2018, 99, 416–428. [Google Scholar] [CrossRef]
- Delage, P.; Lefebvre, G. Study of the structure of a sensitive Champlain clay and of its evolution during consolidation. Can. Geotech. J. 1984, 21, 21–35. [Google Scholar] [CrossRef]
- Peyton, R.L.; Gantzer, C.J.; Anderson, S.H.; Haeffner, B.A.; Pfeifer, P. Fractal dimension to describe soil macropore structure using X ray computed tomography. Water Resour. Res. 1994, 30, 691–700. [Google Scholar] [CrossRef]
- Zeng, Y.; Payton, R.L.; Gantzer, C.J.; Anderson, S.H. Fractal Dimension and Lacunarity of Bulk Density Determined with X-ray Computed Tomography. Soil Sci. Soc. Am. J. 1996, 60, 1718–1724. [Google Scholar] [CrossRef]
- He, S.-H.; Ding, Z.; Hu, H.-B.; Gao, M. Effect of Grain Size on Microscopic Pore Structure and Fractal Characteristics of Carbonate-Based Sand and Silicate-Based Sand. Fractal Fract. 2021, 5, 152. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, Z.; Ji, W.; Zhang, C.; Yuan, Y.; Chen, L. Heterogeneity of intergranular, intraparticle and organic pores in long- maxi shale in Sichuan basin, south China: Evidence from SEM digital images and fractal and multifractal geometries. Mar. Pet. Geol. 2016, 72, 122–138. [Google Scholar] [CrossRef]
- Kong, B.; He, S.-H.; Tao, Y.; Xia, J. Pore Structure and Fractal Characteristics of Frozen–Thawed Soft Soil. Fractal Fract. 2022, 6, 183. [Google Scholar] [CrossRef]
- Yang, R.; He, S.; Yi, J.; Hu, Q. Nano-scale pore structure and fractal dimension of organic-rich Wufeng-Longmaxi shale from Jiaoshiba area, Sichuan Basin: Investigations using FE-SEM, gas adsorption and helium pycnometry. Mar. Pet. Geol. 2015, 7, 27–45. [Google Scholar] [CrossRef]
- Dai, C.-X.; Zhang, Q.-F.; He, S.-H.; Zhang, A.; Shan, H.-F.; Xia, T.-D. Variation in micro-pores during dynamic consolidation and compression of soft marine soil. J. Mar. Sci. Eng. 2021, 9, 750. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Hao, B.B.; Gu, C.; Wang, J.; Pan, L.Y. Effect of anisotropic consolidation stress paths on the undrained shear behavior of reconstituted Wenzhou clay. Eng. Geol. 2018, 242, 23–33. [Google Scholar] [CrossRef]
- Yuan, B.; Li, Z.; Chen, W.; Zhao, J.; Lv, J.; Song, J.; Cao, X. Influence of Groundwater Depth on Pile–Soil Mechanical Properties and Fractal Characteristics under Cyclic Loading. Fractal Fract. 2022, 6, 198. [Google Scholar] [CrossRef]
- Bohaienko, V.; Bulavatsky, V. Fractional-Fractal Modeling of Filtration-Consolidation Processes in Saline Saturated Soils. Fractal Fract. 2020, 4, 59. [Google Scholar] [CrossRef]
- Voss, R.F.; Laibowitz, R.B.; Alessandrini, E.I. Fractal Geometry of Percolation in Thin Gold Films; Springer: New York, NY, USA, 1991. [Google Scholar]
- Moore, C.A.; Donaldson, C.F. Quantifying soil microstructure using fractals. Geotechnique 1995, 45, 105–116. [Google Scholar] [CrossRef]
- Sumelka, W.; Nowak, M. Non-normality and induced plastic anisotropy under fractional plastic flow rule: A numerical study. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 651–675. [Google Scholar] [CrossRef]
- Zhang, M.J.; Zhang, L.P. The study on the licrostructure parameters and rheological constitutive relations of structural soft soils. J. Shenyang Jianzhu Univ. Nat. Sci. Ed. 2006, 22, 177–180. [Google Scholar]



| Soil Type | Unit Weight/kN/m3 | Water Content/% | Specific Gravity | Plastic Limit/% | Liquid Limit/% | Plasticity Index | Liquid Index |
|---|---|---|---|---|---|---|---|
| Soft soil | 15.7 | 62.47 | 2.74 | 27 | 44.6 | 17.6 | 2.01 |
| Group | Number | p0/(kPa) | ζ | Nmax | OCR |
|---|---|---|---|---|---|
| A | A0 | not loaded | |||
| A1 | 100 | 3 | 20,000 | 1 | |
| A2 | 200 | 3 | 20,000 | 1 | |
| A3 | 300 | 3 | 20,000 | 1 | |
| A4 | 400 | 3 | 20,000 | 1 | |
| A5 | 500 | 3 | 20,000 | 1 | |
| B | B0 | not loaded | |||
| B1 | 100 | 3 | 20,000 | 1 | |
| B2 | 100 | 6 | 20,000 | 1 | |
| B3 | 100 | 8 | 20,000 | 1 | |
| B4 | 100 | 10 | 20,000 | 1 | |
| B5 | 100 | 15 | 20,000 | 1 | |
| C | C0 | not loaded | |||
| C1 | 100 | 3 | 20,000 | 1 | |
| C2 | 300 | 3 | 20,000 | 3 | |
| C3 | 600 | 3 | 20,000 | 6 | |
| C4 | 900 | 3 | 20,000 | 9 | |
| Parameter | am | bm | cm | ad | bd | cd | ||
| numeric value | −1.279 × 10−7 | −4267 × 10−5 | 0.9834 | 3831 × 10−7 | −0.0016 | 1.597 | ||
| Parameter | Am0 | Am | βm | R2 | Ad0 | Ad | βd | R2 |
| numeric value | 9.451 × 105 | 1.871 × 107 | 10.98 | 0.8396 | 7.106 × 104 | 981.5 | −1.76 | 0.9629 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, B.; Dai, C.-X.; Hu, H.; Xia, J.; He, S.-H. The Fractal Characteristics of Soft Soil under Cyclic Loading Based on SEM. Fractal Fract. 2022, 6, 423. https://doi.org/10.3390/fractalfract6080423
Kong B, Dai C-X, Hu H, Xia J, He S-H. The Fractal Characteristics of Soft Soil under Cyclic Loading Based on SEM. Fractal and Fractional. 2022; 6(8):423. https://doi.org/10.3390/fractalfract6080423
Chicago/Turabian StyleKong, Bowen, Chen-Xiang Dai, Haibo Hu, Jianzhong Xia, and Shao-Heng He. 2022. "The Fractal Characteristics of Soft Soil under Cyclic Loading Based on SEM" Fractal and Fractional 6, no. 8: 423. https://doi.org/10.3390/fractalfract6080423
APA StyleKong, B., Dai, C.-X., Hu, H., Xia, J., & He, S.-H. (2022). The Fractal Characteristics of Soft Soil under Cyclic Loading Based on SEM. Fractal and Fractional, 6(8), 423. https://doi.org/10.3390/fractalfract6080423






