Discrete Element Modelling of Fractal Behavior of Particle Size Distribution and Breakage of Ballast under Monotonic Loading
Abstract
:1. Introduction
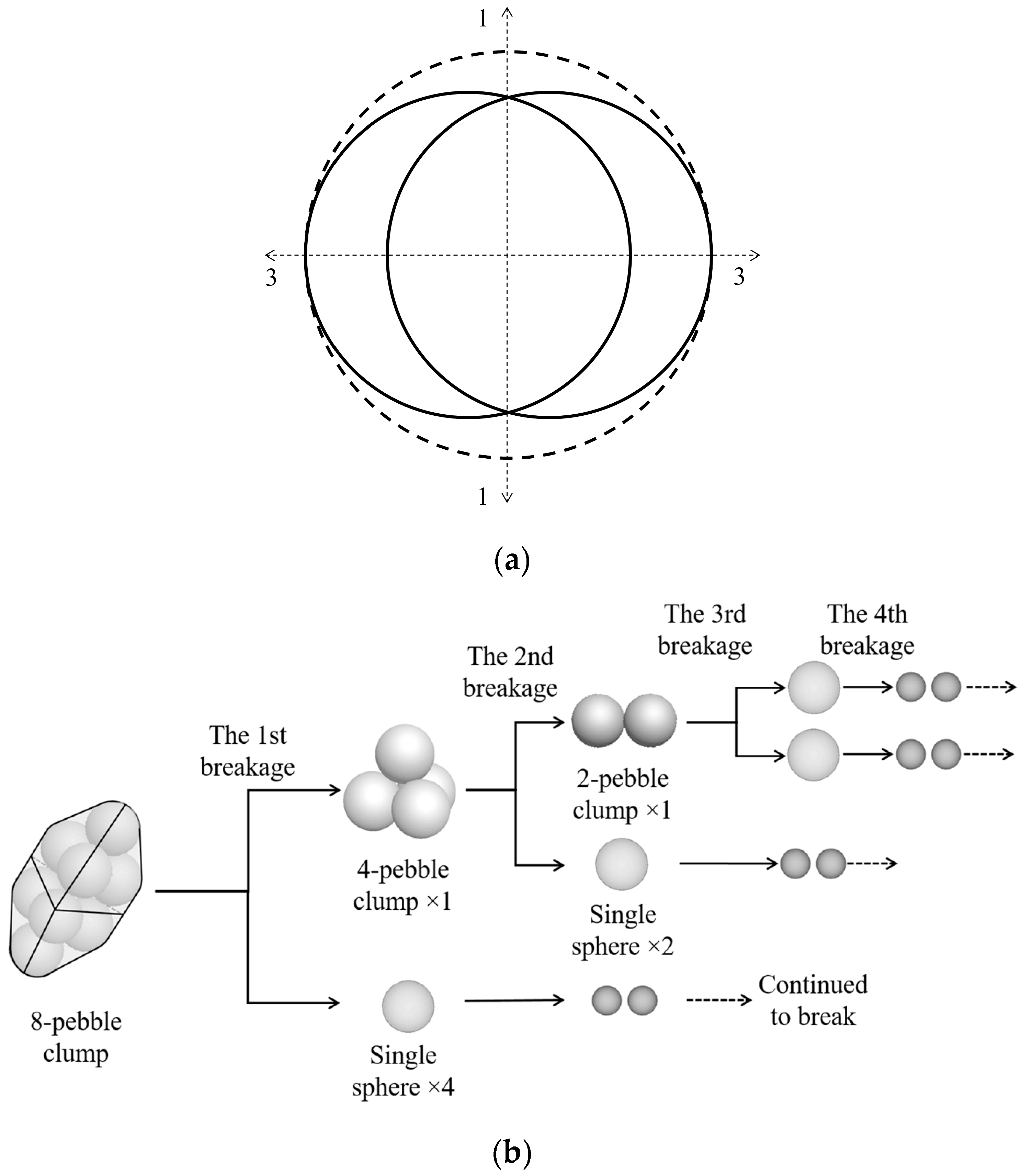
2. Ballast Breakage Model Using FRM
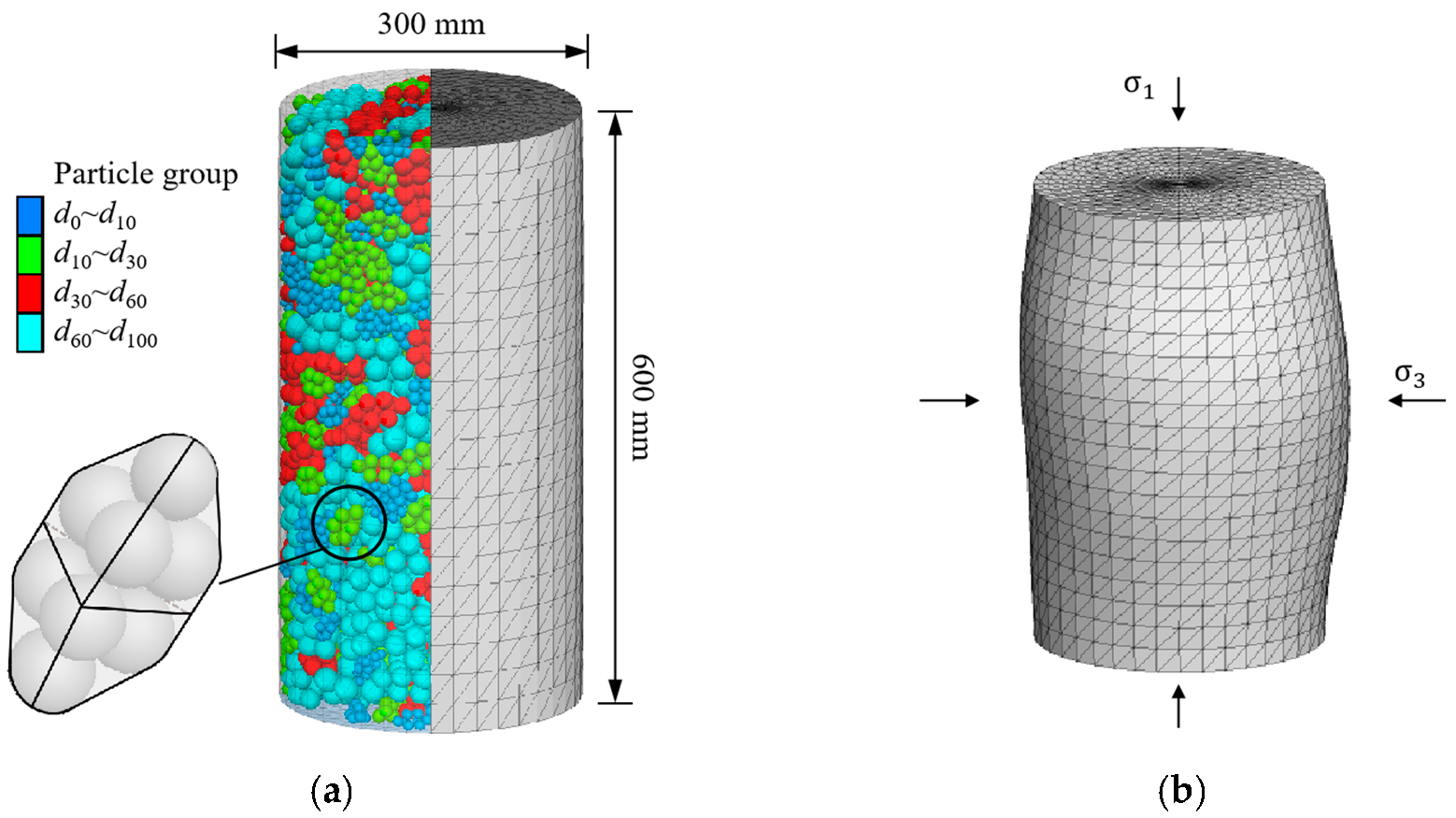
3. Simulations of Monotonic Triaxial Test
4. Results and Discussion
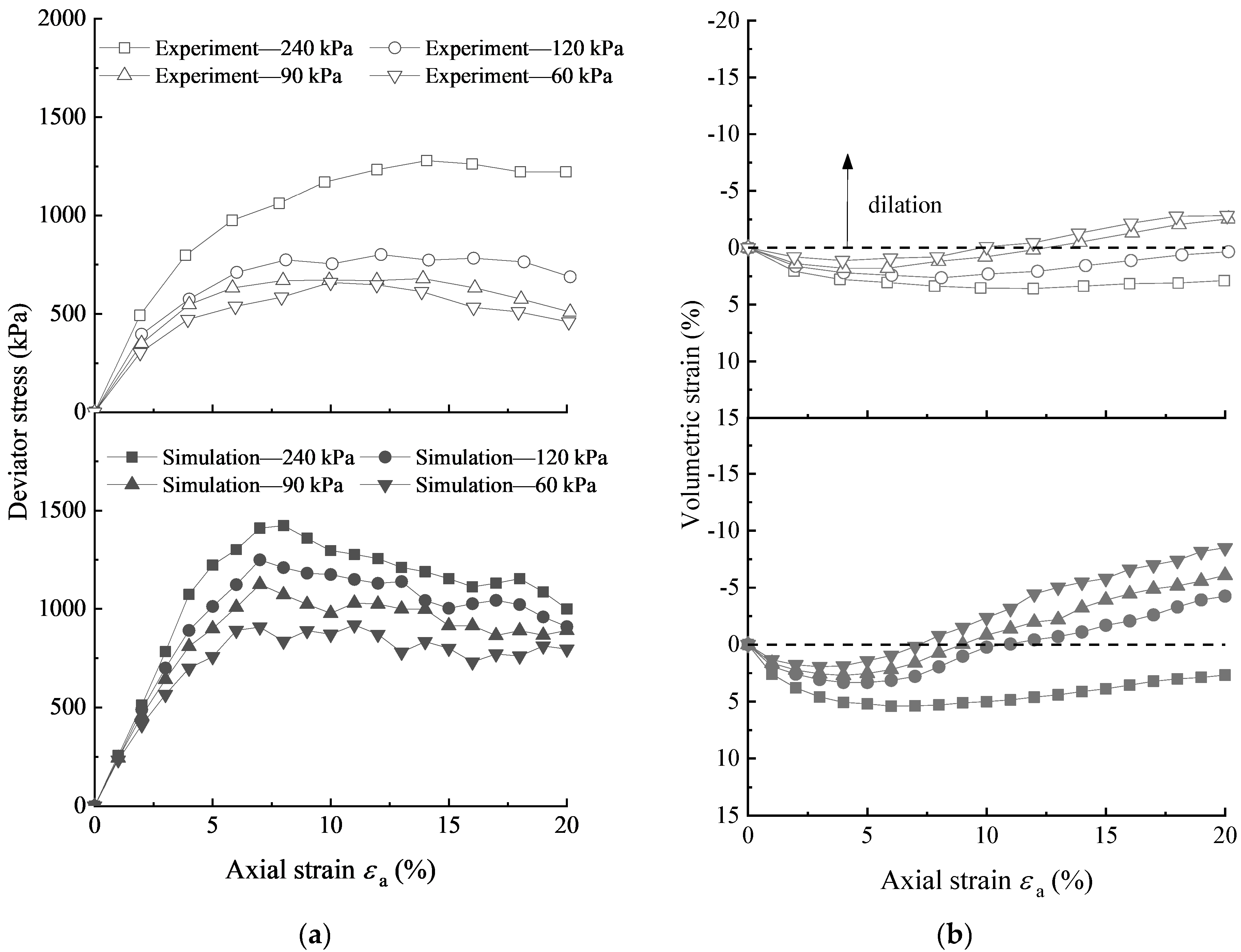
4.1. Stress–Strain Response
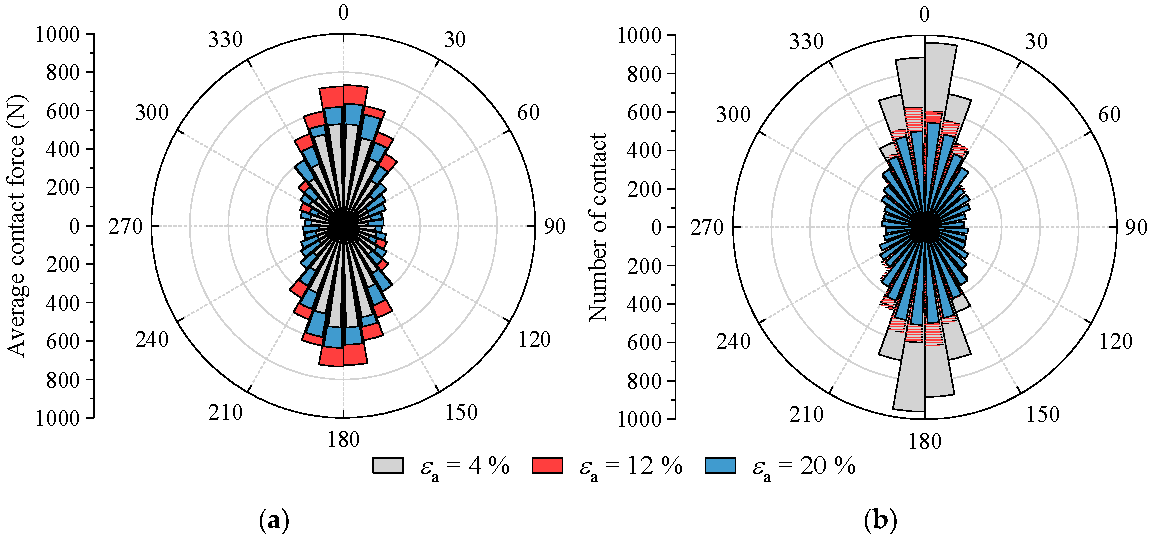
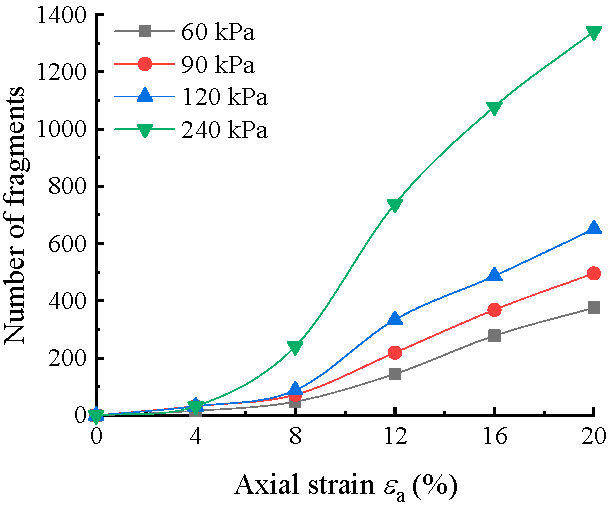
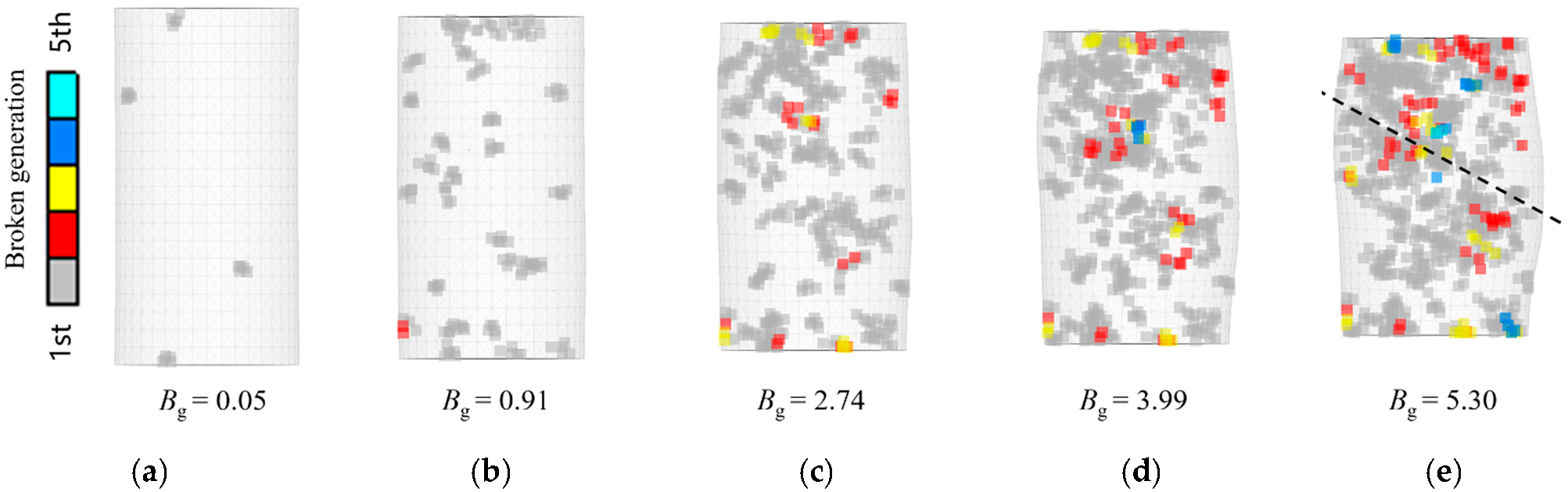
4.2. Particle Breakage
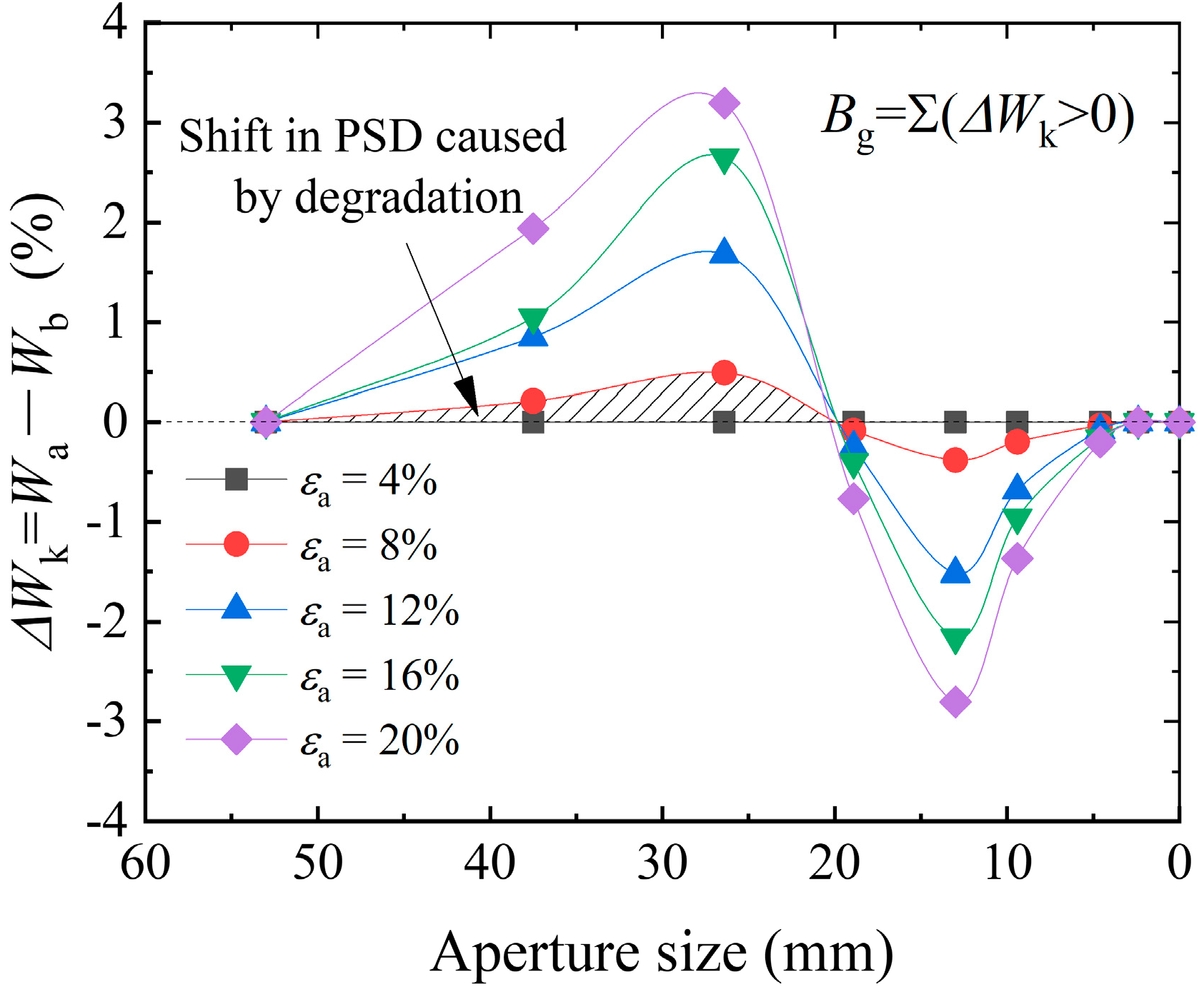
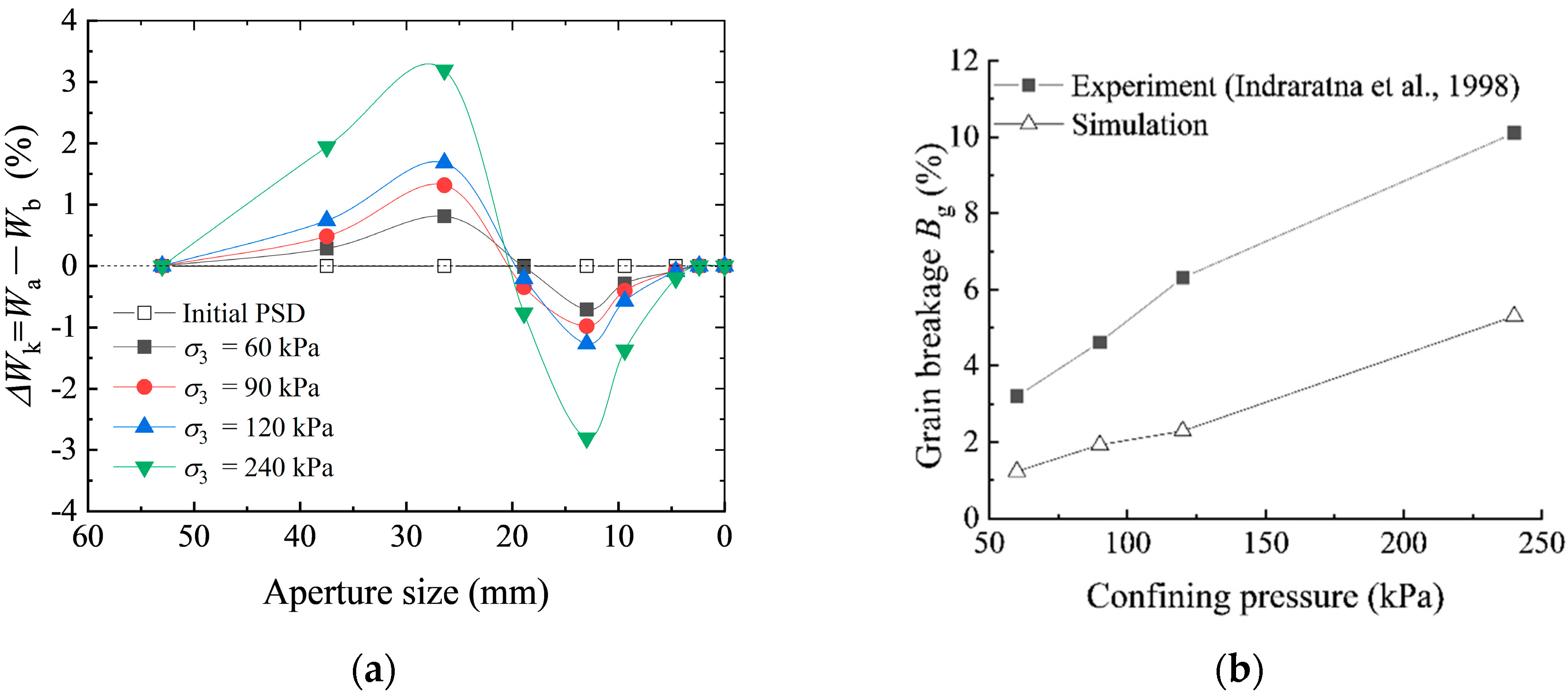
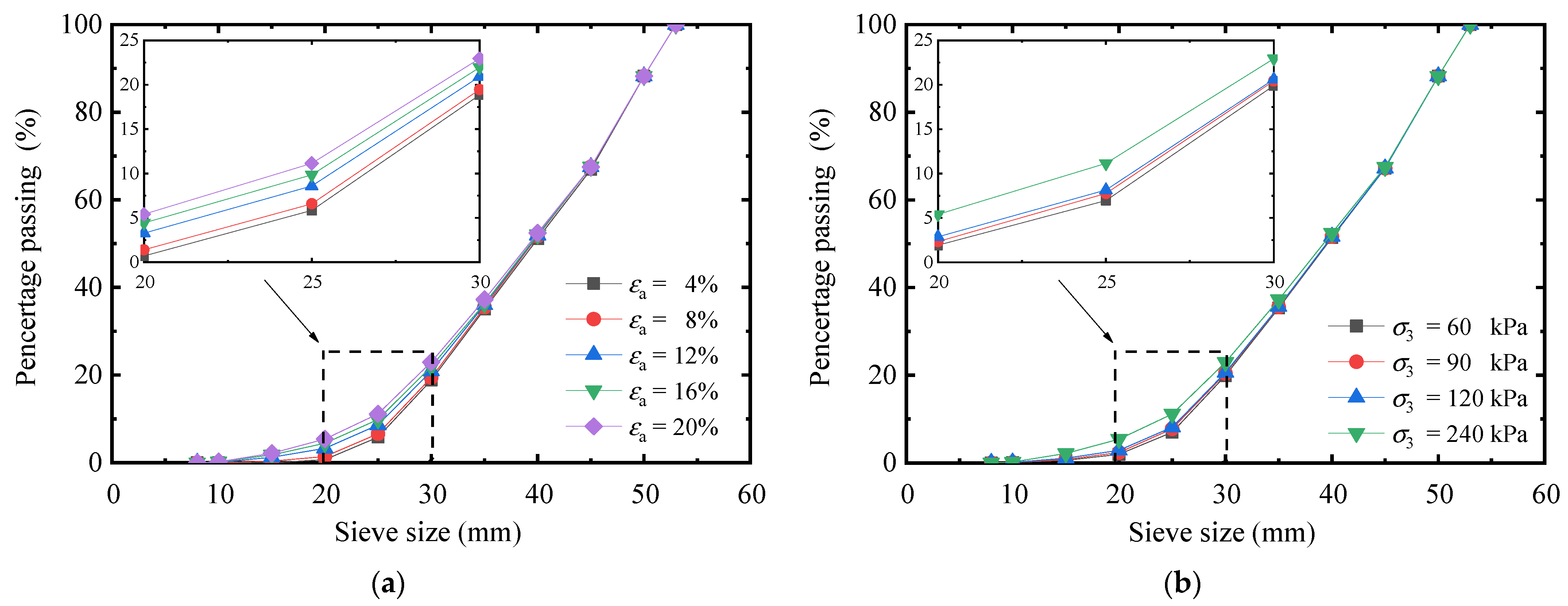
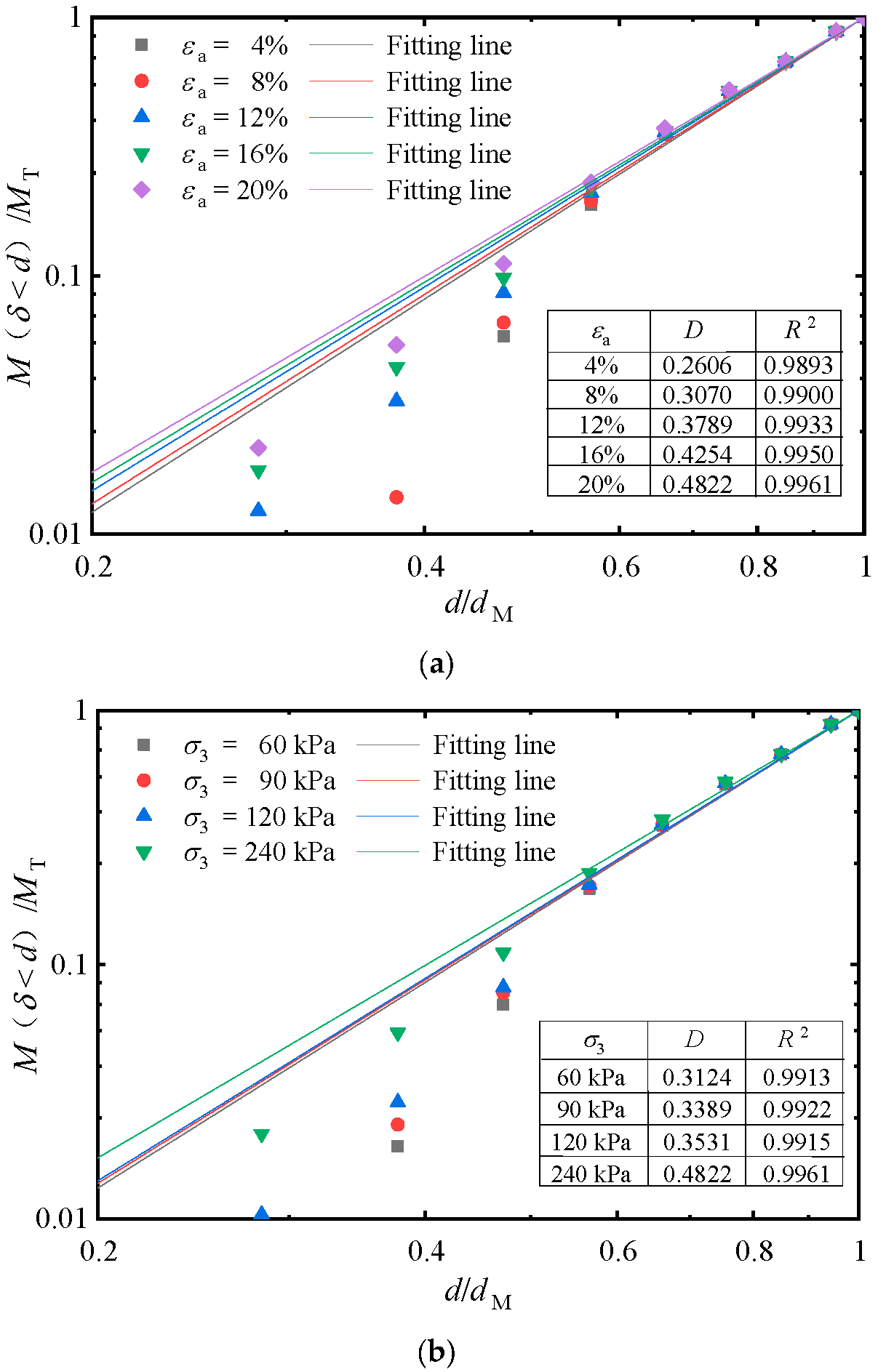
4.3. Gradation Evolution and Fractal Distribution
5. Conclusions
- (1)
- The proposed FRM model can simulate the ballast breakage and capture the essential features of the stress-dilatancy in the monotonic triaxial test. During the loading process, the particles within the top and bottom half moved toward the horizontal plane in the middle. With axial strains above 4%, due to mutual resistance, the intermediate particles started to move outward to produce a shear sliding surface, where the angle between the sliding surface and the horizontal direction gradually increased.
- (2)
- More particle breakage occurred under higher confining pressure or larger axial strain and most such breakage was in the second generation or earlier. The number of fragments could be ignored at the initial compaction stage and the majority of particle breakage occurred with axial strain of 8% or above. Compared with the experimental results, the simulation underestimated the degree of particle breakage. This could be explained by that the simple splitting model of FRM did not take particle abrasion and small corner breakage into consideration.
- (3)
- With increasing axial strain or confining pressure, the percentage of small particle fragments increased in correspondence with the PSD curves which remained concave upwards, leading to an increasing fractal dimension. However, a different situation applies to granular materials in natural state because the grading ballast used in railway is usually qualified by the ballast specification, leading to much smaller values of D.
- (4)
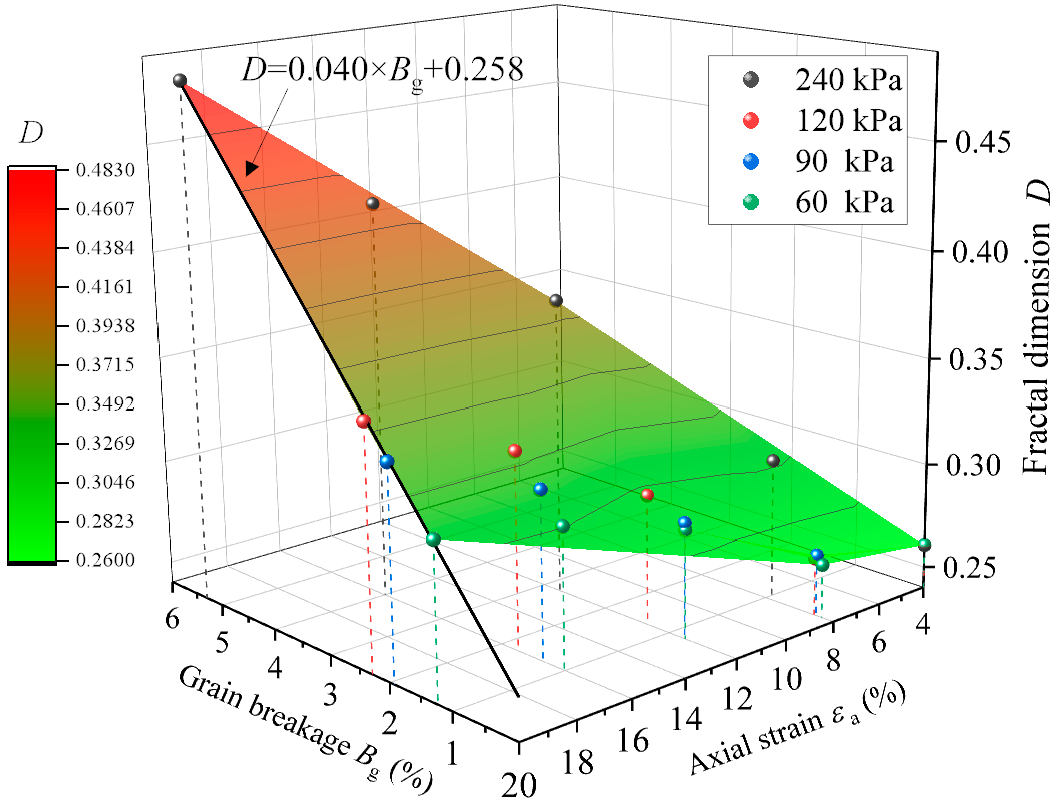
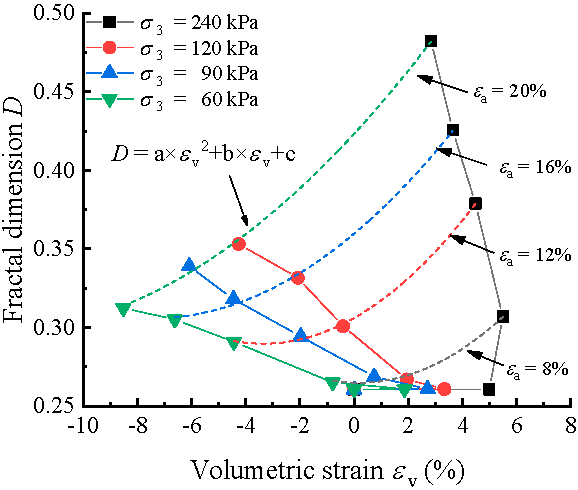
- The evolution of fractal dimension against grain breakage showed a linear relation, Conversely, a quadratic curve relation was obtained between the fractal dimension and volumetric strain under different axial strain stages. Therefore, D has the potential to be a key indicator to evaluate the degree of ballast crushing and PSD degradation, which can contribute to better decision making concerning railway track bed maintenance in practice.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raymond, G.P.; Diyaljee, V.A. Railroad ballast load ranking classification. J. Geotech. Eng. Div. 1979, 105, 1133–1153. [Google Scholar] [CrossRef]
- Selig, E.T.; Waters, J.M. Track Geotechnology and Substructure Management; Thomas Telford: London, UK, 1994; pp. 16–26. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and fragmentation. J. Geophys. Res. 1986, 91, 1921–1926. [Google Scholar] [CrossRef]
- Zhao, W.J.; Cui, Z.; Ma, H. Fractal features of soil particle-size distributions and their relationships with soil properties in gravel mulched fields. Arab. J. Geosci. 2017, 10, 211–218. [Google Scholar] [CrossRef]
- Tao, G.; Wang, Q.; Chen, Q.; Nimbalkar, S.; Peng, Y.; Dong, H. Simple graphical prediction of relative permeability of unsaturated soils under deformations. Fractal Fract. 2021, 5, 153. [Google Scholar] [CrossRef]
- Bai, Y.; Qin, Y.; Lu, X.; Zhang, J.; Chen, G.; Li, X. Fractal dimension of particle-size distribution and their relationships with alkalinity properties of soils in the western Songnen Plain, China. Sci. Rep.-UK 2020, 10, 20603. [Google Scholar] [CrossRef]
- He, S.H.; Ding, Z.; Hu, H.B.; Gao, M. Effect of grain size on microscopic pore structure and fractal characteristics of carbonate-based sand and silicate-based sand. Fractal Fract. 2021, 5, 152. [Google Scholar] [CrossRef]
- Sui, L.; Yu, J.; Cang, D.; Miao, W.; Wang, H.; Zhang, J.; Yin, S.; Chang, K. The fractal description model of rock fracture networks characterization. Chaos Soliton Fract. 2019, 129, 71–76. [Google Scholar] [CrossRef]
- Xiao, Y.; Meng, M.; Daouadji, A.; Chen, Q.; Wu, Z.; Jiang, X. Effects of particle size on crushing and deformation behaviors of rockfill materials. Geosci. Front. 2020, 11, 375–388. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, X.; Liu, W.; Zhang, S. Influence of weak inclusions on the fracturing and fractal behavior of a jointed rock mass containing an opening: Experimental and numerical studies. Comput. Geotech. 2021, 132, 104011. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle-size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Tang, l.; Song, Y.; Jiang, Z.; Jiang, S.; Li, Q. Pore structure and fractal characteristics of distinct thermally mature shales. Energy Fuels 2019, 33, 5116–5128. [Google Scholar] [CrossRef]
- Railway Ballast: TB/T2140-2018; China Railway Specifications. China Railway Administration: Beijing, China, 2018.
- Tavarez, F.A.; Plesha, M.E. Discrete element method for modelling solid and particulate materials. Int. J. Numer Meth. Eng. 2007, 70, 379–404. [Google Scholar] [CrossRef]
- Adhikari, S.; You, Z. 3D discrete element models of the hollow cylindrical asphalt concrete specimens subject to the internal pressure. Int. J. Pavement Eng. 2010, 11, 429–439. [Google Scholar] [CrossRef]
- McDowell, G.R.; De Bono, J.P. On the micro mechanics of one-dimensional normal compression. Géotechnique 2013, 63, 895–908. [Google Scholar] [CrossRef] [Green Version]
- Ciantia, M.O.; Arroyo, M.; Calvetti, F.; Gens, A. An approach to enhance efficiency of DEM modelling of soils with crushable grains. Géotechnique 2015, 65, 91–110. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Wang, D.; Ma, G. Discrete element modeling of particle breakage considering different fragment replacement modes. Powder Technol. 2020, 360, 312–323. [Google Scholar] [CrossRef]
- Vallejo, L.E.; Lobo-Guerrero, S. Fractal fragmentation of granular materials under compression. AIP Conf. Proc. 2009, 1145, 847–850. [Google Scholar] [CrossRef]
- De Bono, J.P.; McDowell, G.R. Particle breakage criteria in discrete-element modelling. Géotechnique 2016, 66, 1014–1027. [Google Scholar] [CrossRef] [Green Version]
- Li, H.Y.; Chai, H.W.; Xiao, X.H.; Huang, J.Y.; Luo, S.N. Fractal breakage of porous carbonate sand particles: Microstructures and mechanisms. Powder Technol. 2020, 363, 112–121. [Google Scholar] [CrossRef]
- Lu, M.; McDowell, G.R. The importance of modelling ballast particle shape in the discrete element method. Granul. Matter 2007, 9, 69–80. [Google Scholar] [CrossRef]
- Sun, Y.; Indraratna, B.; Nimbalkar, S. Three-dimensional characterization of particle size and shape for ballast. Géotechnique Lett. 2014, 4, 197–202. [Google Scholar] [CrossRef] [Green Version]
- Jaeger, J.C. Failure of rocks under tensile conditions. Int. J. Rock Mech. Min. Sci. 1967, 4, 219–227. [Google Scholar] [CrossRef]
- Lim, W.L.; McDowell, G.R. Discrete element modelling of railway ballast. Granul. Matter 2003, 7, 19–29. [Google Scholar] [CrossRef]
- Indraratna, B.; Ionescu, D.; Christie, H.D. Shear behaviour of railway ballast based on large scale triaxial testing. J. Geotech. Geoenviron. 1998, 5, 439–449. [Google Scholar] [CrossRef]
- Roner, C.J. Some Effect of Shape, Gradation and Size on the Performance of Railroad Ballast. Master’s Thesis, Report No. AAR85-324P. Department of Civil Engineering, University of Massachusetts, Amherst, MA, USA, 1985. [Google Scholar]
- Marsal, R.J. Mechanical properties of rockfill: In embankment-dam engineering. Int. J. Rock Mech. Min. Sci. 1975, 12, 67. [Google Scholar] [CrossRef]



| Parameters | d10/mm | d30/mm | d50/mm | d60/mm | dmax/mm | Cu | Cc | Size Ratio |
|---|---|---|---|---|---|---|---|---|
| Value | 27.1 | 32.6 | 38.9 | 41.3 | 53 | 1.5 | 0.9 | 5.7 |
| Input Parameters | Value |
|---|---|
| Normal and shear stiffness of particles: N/m | 2 × 106 |
| Friction coefficient of clumps | 0.5 |
| Density: kg/m3 | 2650 |
| Friction coefficient of walls and membrane | 0.1 |
| Normal stiffness of walls: N/m | 2 × 107 |
| Shear stiffness of walls: N/m | 0 |
| Normal stiffness of membrane: N/m | 2 × 105 |
| Shear stiffness of membrane: N/m | 0 |
| Young’s modulus of membrane: kPa | 400 |
| Sample porosity | 0.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Zhang, X.; Sun, Y.; Zhang, L.; Rui, R.; Wang, Z. Discrete Element Modelling of Fractal Behavior of Particle Size Distribution and Breakage of Ballast under Monotonic Loading. Fractal Fract. 2022, 6, 382. https://doi.org/10.3390/fractalfract6070382
Chen C, Zhang X, Sun Y, Zhang L, Rui R, Wang Z. Discrete Element Modelling of Fractal Behavior of Particle Size Distribution and Breakage of Ballast under Monotonic Loading. Fractal and Fractional. 2022; 6(7):382. https://doi.org/10.3390/fractalfract6070382
Chicago/Turabian StyleChen, Cheng, Xin Zhang, Yifei Sun, Lei Zhang, Rui Rui, and Zhide Wang. 2022. "Discrete Element Modelling of Fractal Behavior of Particle Size Distribution and Breakage of Ballast under Monotonic Loading" Fractal and Fractional 6, no. 7: 382. https://doi.org/10.3390/fractalfract6070382
APA StyleChen, C., Zhang, X., Sun, Y., Zhang, L., Rui, R., & Wang, Z. (2022). Discrete Element Modelling of Fractal Behavior of Particle Size Distribution and Breakage of Ballast under Monotonic Loading. Fractal and Fractional, 6(7), 382. https://doi.org/10.3390/fractalfract6070382







