Sensitivity of Uniformly Convergent Mapping Sequences in Non-Autonomous Discrete Dynamical Systems

Abstract

Let H be a compact metric space. The metric of H is denoted by d. And let $(H,f_{1,\infty })$ be a non-autonomous discrete system where $f_{1,\infty }={\left\{f_n\right\}}_{n=1}^{\infty }$ is a mapping sequence. This paper discusses infinite sensitivity, m-sensitivity, and m-cofinitely sensitivity of $f_{1,\infty }$. It is proved that, if $f_n(n\in \mathbb{N})$ are feebly open and uniformly converge to $f:H\to H$, $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$, and ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, then $(H,f)$ has the above sensitive property if and only if $(H,f_{1,\infty })$ has the same property where $D(·,·)$ is the supremum metric.

1. Introduction

Chaos, as a universal motion form of topological dynamical systems, is one of the core contents of the research for dynamical systems. At present, fruitful results of chaos theory have been obtained in autonomous discrete dynamical systems. However, many complex systems in real life, such as medicine, biology, and physics, are difficult to describe by autonomous systems. Therefore, it is necessary to use other models (for example, non-autonomous discrete systems). Since 1996, chaos of non-autonomous discrete dynamical systems (for convenience, we abbreviate it to NDDS) has began to be studied [1]. In recent years, the discussion about the chaotic properties in NDDS has been active. Si [2] gives some sufficient conditions for NDDS to have asymptotically stable sets. Lan and Peris [3] showed the relation between the weak stability of an NDDS and its induced set-valued system. Li, Zhao, and Wang [4] studied stronger forms of sensitivity and transitivity for NDDS by using the Furstenberg family. Meanwhile, under the condition $\underset{n\to \infty }{lim}{d}_{\infty }(g_m^m,g^m)=0$, a necessary and sufficient condition for g to be $\mathcal{F}$-mixing is established in [5]. Vasisht and Das [6] discussed the difference between $\mathcal{F}$-sensitivity and some other stronger forms of sensitivity by some examples. Salman and Das [7] proved that on a compact metric space, every finitely generated NDDS which is topologically transitive and has a dense set of periodic points is thickly syndetically sensitive. Vasisht and Das [8] proved that if the rate of convergence at which $\left(f_n\right)$ converges to f is “sufficiently fast”, then various forms of sensitivity for the autonomous system $(X,f)$ and the NDDS $(X,f_{1,\infty })$ coincide. For the chaoticity of other maps in NDDS, see [9,10,11,12] and other literature.

This paper further studies the chaotic properties in the sense of sensitivity. The basic definitions of chaos are given in Section 2. In Section 3, under the conditions of that, $f_n:H\to H(n\in \mathbb{N})$ are feebly open and uniformly converge to $f:H\to H$, $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$, and ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$. This paper proves that $(H,f)$ is $\mathcal{Q}$-sensitive if and only if $(H,f_{1,\infty })$ is $\mathcal{Q}$-sensitive where, $D(·,·)$ is the supremum metric (see Section 3), $\mathcal{Q}$-sensitive denotes one of the four properties: accessible, infinitely sensitive, m-sensitive, and m-cofinitely sensitive.

2. Preliminaries

For any initial value $x_0\in H$, the orbit of x under $f_{1,\infty }$ is denoted by $\{f_n\circ f_{n-1}\circ \cdots \circ f_1\left(x_0\right):n\in \mathbb{N}\}$.

A subset K of $\mathbb{N}$ is cofinite [4,5] if there exists a $N\in \mathbb{N}$ such that $[N,+\infty ]\subset K$.

A system $(H,f_{1,\infty })$ (or maps sequence ${\left\{f_n\right\}}_{n\in \mathbb{N}}$) is called “feebly open” [4,5] if for any nonempty open subset V of H, int$\left(f_n\left(V\right)\right)\ne \varphi$ for any $n\in \mathbb{N}$. Where intA denotes the interior of set A.

A pair $(x,y)$ is proximal [13] for $(H,f_{1,\infty })$ if for any $x\in H$, $\underset{n\mapsto \infty }{lim\; inf}d(f_1^n\left(x\right),f_1^n\left(y\right))=0$.

Definition 1

([14]). A system $(H,f_{1,\infty })$ is "spatio-temporal chaotic" if for any $x\in H$ and each neighborhood V of x, there is a $y\in V$ such that $\underset{n\mapsto \infty }{lim\; sup}d(f_1^n\left(a\right),f_1^n\left(b\right))>0$ but $\underset{n\mapsto \infty }{lim\; inf}d(f_1^n\left(a\right)$, $f_1^n\left(b\right))=0$.

Definition 2

([4,5]). A system $(H,f_{1,\infty })$ is called "sensitive dependent on initial condition" if there exists an $\eta >0$ such that for any $x\in H$ and $\epsilon >0$, there exists a $y\in B(x,\epsilon )$ and an $n\in \mathbb{N}$ such that $d(f_1^n\left(x\right),f_1^n\left(y\right))>\eta$.

Definition 3

([7,8]). A system $(H,f_{1,\infty })$ is called "infinitely sensitive" if there exists an $\eta >0$ such that, for any $x\in H$ and $\epsilon >0$, one can find a $y\in B(x,\epsilon )$ and an $n\in \mathbb{N}$ such that $\underset{n\to \infty }{lim\; sup}d(f_1^n\left(x\right),f_1^n\left(y\right))\ge \eta$.

Definition 4

([15]). A system $(H,f_{1,\infty })$ is called "accessible" if for any $\epsilon >0$ and any two nonempty open subsets $U_1,U_2\subset H$, there are two points $x\in U_1$ and $y\in U_2$ such that $d(f_1^n\left(x\right),f_1^n\left(y\right)))<\epsilon$ for some integer $n>0$.

For convenience, write

$$A(U,m,n)=min\{d(f_1^n\left(x_i\right),f_1^n\left(y_j\right)):x_i,y_j\in U,i,j\in \{1,2,\dots ,m\},i\ne j\}$$

and

$S_{f_{1,\infty },m}(U,\lambda )=\{n\in \mathbb{N}$: there is $x_i,y_j\in U$ ($i,j\in \{1,2,\dots ,m\},i\ne j$) such that $A(U,m,n)\ge \lambda \},$

where $m,n\in \mathbb{N}$, U is an arbitrary nonempty open subset in X.

Definition 5

([16]). Given an integer m with $m\ge 2$. The system $(H,f_{1,\infty })$ is called "m-sensitive", if there is a real number $\lambda >0$ such that for any nonempty open subset U of H, there are $2m$ points $x_1,x_2,\dots ,x_m;y_1,y_2,\dots ,y_m\in U$ such that $S_{f_{1,\infty },m}(U,\lambda )$ is nonempty.

Definition 6

([16]). Given an integer m with $m\ge 2$. The system $(H,f_{1,\infty })$ is called "m-cofinitely sensitive", if there is a real number $\lambda >0$ such that for any nonempty open subset U of H, there are $2m$ points $x_1,x_2,\dots ,x_m;y_1,y_2,\dots ,y_m\in U$ such that $S_{f_{1,\infty },m}(U,\lambda )$ is a cofinite set.

3. The Relation of Chaoticity between ${\mathit{f}}_{\mathbf{1},\infty }$ and Its Limit Map $\mathit{f}$

Let $\mathcal{C}\left(H\right)$ be the set of all continuous self-maps on $(H,d)$. For any $f,g\in \mathcal{C}\left(H\right)$, the supremum metric (see [4]) is defined by $D(f,g)=\underset{x\in H}{sup}d(f\left(x\right),g\left(x\right)).$ This section will give equivalence of chaotic properties between $(H,f_{1,\infty })$ and $(H,f)$.

Lemma 1

([5]). Let $(H,f_{1,\infty })$ be an NDDS on a nontrivial compact metric space $(H,d)$ and $f\in \mathcal{C}\left(H\right)$. If $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$, then for any $x\in H$, any integer $q\ge 1$ and any integer $p\ge 1$ one has

$$d(f_1^{q+p}\left(x\right),f^q\left(f_1^p\left(x\right)\right))\le \sum _{j=p+1}^{q+p}D(f_j,f).$$

Theorem 1.

If $f_n(n\in \mathbb{N})$ are a feebly open mapping sequence which uniformly converges to f, $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$, and ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, then $(H,f)$ is accessible if and only if $(H,f_{1,\infty })$ is accessible.

Proof. 

Suppose that $(H,f)$ is accessible. Given $\epsilon >0$, let $U,V$ are two nonempty open subsets in H. Because $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$, by Lemma 1, for the above $\epsilon >0$, $d(f_1^{p^0+q}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))<{\sum }_{j=p_0+1}^{q+p_0}D(f_j,f)$ for any $x\in H$ and any integer $p^0,q\ge 1$. Moreover, because ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, then there is an integer $S_0\ge 1$ such that ${\sum }_{j=s}^{\infty }D(f_j,f)<\frac{1}{3}\epsilon$ for any $s\ge s_0$. Combine with the arbitrariness of $p_0,q$, one can get that $d(f_1^{p^0+q}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))$$<\frac{\epsilon }{3}$. Because $f_i(i\in \{1,2,\dots \})$ are feebly open, the interiors of $f_1^{p^0}\left(U\right)$ and $f_1^{p^0}\left(V\right)$ are nonempty sets. Let $U^{\prime }$, $V^{\prime }$ be the interiors of $f_1^{p^0}\left(U\right)$ and $f_1^{p^0}\left(V\right)$, respectively.

Because $(H,f)$ is accessible, for the above $\epsilon >0$, there are $x\in U^{\prime }$ and $y\in V^{\prime }$ such that $d(f^q\left(x\right),f^q\left(y\right))<\frac{\epsilon }{3}$ for some $q>0$. Then, there exist $x^{\prime }\in U$, $y^{\prime }\in V$ satisfying $x=f_1^{p^0}\left(x^{\prime }\right)$, $y=f_1^{p^0}\left(y^{\prime }\right)$. Thus, $d(f^q\left(f_1^{p^0}\left(x^{\prime }\right)\right),f^q\left(f_1^{p^0}\left(y^{\prime }\right)\right))<\frac{\epsilon }{3}$. Noting that $d(f_1^{q+p^0}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))<\frac{\epsilon }{3}$ for $x\in H$, by triangle inequality, one has that

$$\begin{array}{ccc}\hfill d(f_1^{p^0+q}\left(x^{\prime }\right),f_1^{p^0+q}\left(y^{\prime }\right))& \le & d(f_1^{p^0+q}\left(x^{\prime }\right),f^q\left(f_1^{p^0}\right)\left(x^{\prime }\right))+d(f^q\left(f_1^{p^0}\right)\left(x^{\prime }\right),f^q\left(f_1^{p^0}\right)\left(y^{\prime }\right))\hfill \\ & & +d(f_1^{p^0+q}\left(y^{\prime }\right),f^q\left(f_1^{p^0}\right)\left(y^{\prime }\right))\hfill \\ & \le & \frac{\epsilon }{3}+\frac{\epsilon }{3}+\frac{\epsilon }{3}\hfill \\ & =& \epsilon .\hfill \end{array}$$

Hence, $(H,f_{1,\infty })$ is accessible.

Now, suppose that $(H,f_{1,\infty })$ is accessible. For a given $\epsilon >0$, let $U,V\subset H$ be nonempty and open. Because ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, by Lemma 1, there is an integer $p^0\ge 1$ such that for the above $\epsilon >0$, $x\in H$, $d(f_1^{p^0+q}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))<\frac{\epsilon }{3}$ for any integer $q\ge 1$. Because $f_i(i\in \{1,2,\dots \})$ are feebly open, then the interiors of $f_1^{p^0}\left(U\right)$ and $f_1^{p^0}\left(V\right)$ are nonempty sets. Let $U^{\prime }$, $V^{\prime }$ be the interiors of $f_1^{p^0}\left(U\right)$ and $f_1^{p^0}\left(V\right)$, respectively.

Because $(H,f_{1,\infty })$ is accessible for the above $\epsilon >0$, there are $x\in U$ and $y\in V$ such that $d(f_1^{q+p^0}\left(x\right),f_1^{q+p^0}\left(y\right))<\frac{\epsilon }{3}$ for some $q>0$. Then, there exist $x^{\prime }\in U^{\prime }$, $y^{\prime }\in V^{\prime }$ satisfying $x^{\prime }=f_1^{p^0}\left(x\right)$, $y^{\prime }=f_1^{p^0}\left(y\right)$. Noted that $d(f_1^{q+p^0}\left(x\right),f^q\left(x^{\prime }\right)<\frac{\epsilon }{3}$, by triangle inequality,

$$\begin{array}{c}\hfill \begin{array}{cc}& d(f^q\left(x^{\prime }\right),f^q\left(y^{\prime }\right))\hfill \\ & \le d(f^q\left(x^{\prime }\right),f^{q+p^0}\left(x\right))+d(f^{q+p^0}\left(x\right),f^{q+p^0}\left(y\right))+d(f^q\left(y^{\prime }\right),f^{q+p^0}\left(y\right))<\epsilon .\hfill \end{array}\end{array}$$

Hence, $(H,f)$ is accessible. □

Theorem 2.

If $f_n(n\in \mathbb{N})$ is a feebly open mapping sequence which uniformly converges to f, $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$, and ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, then $(H,f)$ is infinitely sensitive if and only if $(H,f_{1,\infty })$ is infinitely sensitive.

Proof. 

Suppose that $(H,f)$ is infinitely sensitive with $\lambda >0$ as an infinitely sensitive constant. Let $\epsilon >0$, $U\subset H$ is a nonempty open set. Because ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, by Lemma 1, there is an integer $p\ge 1$ such that $d(f_1^{p+q}\left(x\right),f^q\left(f_1^p\left(x\right)\right))<\epsilon$ for any integer $q\ge 1$, $x\in H$ and the above $\epsilon >0$. Taking an integer $k\in \{1,2,\dots \}$ satisfying $k>\frac{4}{\lambda }$. Then, there is an integer $p^0\ge 1$ such that $d(f_1^{p^0+q}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))<\frac{1}{k}$ for any integer $q\ge 1$ and $x\in H$. Because $f_i$ is feebly open ($i\in \{1,2,\dots \}$), then the interior of $f_1^{p^0}\left(U\right)$ is nonempty. Let $U^{\prime }$ be the interior of $f_1^{p^0}\left(U\right)$. Because $(H,f)$ is infinitely sensitive with infinitely sensitive constant $\lambda >0$, then there is a $y\in U^{\prime }$ such that $\underset{q\to \infty }{lim\; sup}d(f^q\left(x\right),f^q\left(y\right))>\lambda$. Because

$$x=f_1^{p^0}\left(x^{\prime }\right),y=f_1^{p^0}\left(y^{\prime }\right),\underset{q\to \infty }{lim\; sup}d(f^q\left(f_1^{p^0}\left(x^{\prime }\right)\right),f^q\left(f_1^{p^0}\left(y^{\prime }\right)\right))>\lambda ,$$

and because

$$d(f_1^{p^0+q}\left(x^{\prime }\right),f^q\left(f_1^{p^0}\left(x^{\prime }\right)\right))<\frac{1}{k} \mathrm{and} d(f_1^{p^0+q}\left(y^{\prime }\right),f^q\left(f_1^{p^0}\left(y^{\prime }\right)\right))<\frac{1}{k}$$

for any integer $q\ge 1$. By triangle inequality,

$$d(f_1^{p^0+q}\left(x^{\prime }\right),f_1^{p^0+q}\left(y^{\prime }\right))>\lambda -\frac{2}{k}>\frac{1}{2}\lambda .$$

Taking the upper limit of both sides of the inequality, one has that

$$\underset{q\to \infty }{lim\; sup}d(f^{q+p^0}\left(x^{\prime }\right),f^{q+p^0}\left(y^{\prime }\right))>\frac{1}{2}\lambda .$$

Therefore, $(H,f_{1,\infty })$ is infinitely sensitive.

Conversely, let $(H,f_{1,\infty })$ be infinitely sensitive with $\lambda >0$ as an infinitely sensitive constant. Let $\epsilon >0$, $U\subset H$ be a nonempty open set. Because ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, by Lemma 1, there is an integer $p\ge 1$ such that $d(f_1^{p+q}\left(x\right),f^q\left(f_1^p\left(x\right)\right))<\epsilon$ for any integer $q\ge 1$, $x\in H$, and the above $\epsilon >0$. Taking an integer $k\in \{1,2,\dots \}$ satisfying $k>\frac{4}{\lambda }$. Then, there is an integer $p^0\ge 1$ such that $d(f_1^{p^0+q}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))<\frac{1}{k}$ for any integer $q\ge 1$ and $x\in H$. Because $f_i$ is feebly open ($i\in \{1,2,\dots \}$), the interior of $f_1^{p^0}\left(U\right)$ is nonempty. Let $U^{\prime }$ be the interior of $f_1^{p^0}\left(U\right)$. Because $(H,f_{1,\infty })$ is infinitely sensitive with $\lambda >0$ as a sensitive constant, then there is a $y\in U^{\prime }$ such that $\underset{q\to \infty }{lim\; sup}d\left(f_1^{q+p^0}\left(x\right)\right),f_1^{q+p^0}\left(y\right)\left)\right)>\lambda$. So, there exist $x^{\prime },y^{\prime }\in U$ such that $x^{\prime }=f_1^{p^0}\left(x\right),y^{\prime }=f_1^{p^0}\left(y\right)$. Noted that

$$d(f_1^{p^0+q}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))<\frac{1}{k}$$

for any integer $q\ge 1$, then

$$d(f_1^{p^0+q}\left(x\right),f^q\left(x^{\prime }\right))<\frac{1}{k}$$

for any integer $q\ge 1$. By triangle inequality, one has that

$$d(f^q\left(x^{\prime }\right),f^q\left(y^{\prime }\right))>\lambda -\frac{2}{k}>\frac{1}{2}\lambda .$$

Taking the upper limit of both sides of the inequality, one has that $\underset{q\to \infty }{lim\; sup}d\left(f^q\left(x^{\prime }\right)\right)$, $f^q\left(y^{\prime }\right)\left)\right)>\frac{1}{2}\lambda$. Consequently, $(H,f)$ is infinitely sensitive. □

Theorem 3.

If $f_n(n\in \mathbb{N})$ is a feebly open mapping sequence which uniformly converges to f, $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$, and ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, then $(H,f)$ is m-sensitive if and only if $(H,f_{1,\infty })$ is m-sensitive.

Proof. 

Suppose that $(H,f)$ is m-sensitive with m-sensitive constant $\lambda >0$. Let $\epsilon >0$ and a open set $U\subset H:U\ne \varphi$. Because ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, by Lemma 1, there is an integer $p\ge 1$ such that $d(f_1^{p+q}\left(x\right),f^q\left(f_1^p\left(x\right)\right))<\epsilon$ for any integer $q\ge 1$, $x\in H$, and the above $\epsilon >0$. Taking $m\in \{1,2,\dots \}$ with $m>\frac{4}{\lambda }$. Then, there is an integer $p^0\ge 1$ such that $d(f_1^{p^0+q}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))<\frac{1}{m}$ for any integer $q\ge 1$ and $x\in H$. Because $f_i$ is feebly open for all $i\in \{1,2,\dots \}$, the interior of $f_1^{p^0}\left(U\right)$ is nonempty. Let $U^{\prime }$ be the interior of $f_1^{p^0}\left(U\right)$. Because $(H,f)$ is m-sensitive with m-sensitive constant $\lambda >0$, there are m points $x_1,x_2,\dots ,x_m\in U^{\prime }$ and a $q\in \mathbb{N}$such that

$$min\{d(f^q\left(x_i\right),f^q\left(x_j\right)):i,j\in \{1,2,\dots ,m\}i\ne j\}\ge \lambda .$$

Because $x_1,x_2,\dots ,x_m\in f_1^{p^0}\left(U\right)$, there are $x_1^{\prime },x_2^{\prime },\dots ,x_m^{\prime }\in U$ satisfying $x_1=f_1^{p^0}\left(x_1^{\prime }\right),$$x_2=f_1^{p^0}\left(x_2^{\prime }\right),\dots ,x_m=f_1^{p^0}\left(x_m^{\prime }\right)$ and

$$min\{d(f^q\left(f_1^{p^0}\left(x_i^{\prime }\right)\right),f^q\left(f_1^{p^0}\left(x_j^{\prime }\right)\right)):i,j\in \{1,2,\dots ,m\}i\ne j\}\ge \lambda .$$

And because $d(f_1^{p^0+q}\left(x_i^{\prime }\right),f^q\left(f_1^{p^0}\left(x_i^{\prime }\right)\right))<\frac{1}{m}$ for any $i=1,2,\dots ,m$. By triangle inequality,

$$min\{d(f_1^{p^0+q}\left(x_i^{\prime }\right),f_1^{p^0+q}\left(x_j^{\prime }\right)):i,j\in \{1,2,\dots ,m\}i\ne j\}\ge \lambda -\frac{2}{m}>\frac{1}{2}\lambda .$$

This implies $(H,f_{1,\infty })$ is m-sensitive.

Conversely, let $\epsilon >0$ and $U\subset H:U\ne \varphi$ be an open set. Because ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, by Lemma 1, there is an integer $p\ge 1$ such that $d(f_1^{p+q}\left(x\right),f^q\left(f_1^p\left(x\right)\right))<\epsilon$ for any integer $q\ge 1$$x\in H$, and the above $\epsilon >0$. Taking $m\in \{1,2,\dots \}$ with $m>\frac{4}{\lambda }$. Then, there is an integer $p^0\ge 1$ such that $d(f_1^{p^0+q}\left(x\right),f^q\left(f_1^{p^0}\left(x\right)\right))<\frac{1}{m}$ for any integer $q\ge 1$ and $x\in H$. Because $f_i$ is feebly open for all $i\in \{1,2,\dots \}$, the interior of $f_1^{p^0}\left(U\right)$ is nonempty. Let $U^{\prime }$ be the interior of $f_1^{p^0}\left(U\right)$. Because $(H,f_{1,\infty })$ is m-sensitive with $\lambda >0$ as a sensitive constant, there are m points $x_1,x_2,\dots ,x_m\in U^{\prime }$ and $p^0>0$ such that $min\{d(f_1^q\left(x_i\right),f_1^q\left(x_j\right)):i\ne j\in \{1,2,\dots ,m\}\}>\lambda$ for any integer $q>0$. Because $x_1,x_2,\dots ,x_m\in U^{\prime }$, then there are $x_1^{\prime },x_2^{\prime },\dots ,x_m^{\prime }\in U$ satisfying $x_1=f_1^{p^0}\left(x_1^{\prime }\right),x_2=f_1^{p^0}\left(x_2^{\prime }\right),\dots ,x_m=f_1^{p^0}\left(x_m^{\prime }\right)$. And because $d(f_1^{p^0+q}\left(x_i^{\prime }\right),f^q\left(f_1^{p^0}\left(x_i^{\prime }\right)\right))<\frac{1}{m}$ for any $i\in \{1,2,\dots ,m\}$, then $d(f_1^{p^0+q}\left(x_i^{\prime }\right),f^q\left(x_i\right))<\frac{1}{m}$ for any $i\in \{1,2,\dots ,m\}$. By triangle inequality, one has that

$$min\{d(f^q\left(x_i^{\prime }\right),f^q\left(x_j^{\prime }\right)):i\ne j\in \{1,2,\dots ,m\}\}>\lambda -\frac{2}{m}>\frac{1}{2}\lambda .$$

Hence, $(H,f)$ is m-sensitive with $\frac{1}{2}\lambda$ as an m-sensitive constant. □

Theorem 4.

If $f_n(n\in \mathbb{N})$ is a feebly open mapping sequence which uniformly converge to f, $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$, and ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$, then $(H,f)$ is m-cofinitely sensitive if and only if $(H,f_{1,\infty })$ is m-cofinitely sensitive.

Proof. 

This proof is similar to that of Theorem 1, and hence is omitted. □

Example 1.

Let H be the compact interval [0,1] and $g,h$ be defined by $g\left(x\right)=x$ for any $x\in [0,1]$ and

$$h\left(x\right)=\left\{\begin{array}{c}\hfill 2x+\frac{1}{3}forx\in [0,\frac{1}{3}]\\ \hfill -3x+2forx\in [\frac{1}{3},\frac{2}{3}]\\ \hfill x-\frac{2}{3}forx\in [\frac{2}{3},1]\end{array}.\right.$$

In fact, for any nonempty open subset V of H, int $\left(h\right(V\left)\right)\ne \varphi$. Then $h\left(x\right)$ is feeble open. It is easy to know that, for any $x_1,x_2\in [0,1]:x_1\ne x_2$ (without loss of generality, $x_1<x_2$), the following conclusions are held.

If $x_1,x_2\in [0,\frac{1}{3}]$ or $x_1,x_2\in [\frac{1}{3},\frac{2}{3}]$ or $x_1,x_2\in [\frac{2}{3},1]$, one can get that

$$\begin{array}{c}\hfill \mid h\left(x_1\right)-h\left(x_2\right)\mid \ge \mid x_1-x_2\mid .\end{array}$$

If $x_1\in [0,\frac{1}{3}],x_2\in [\frac{1}{3},\frac{2}{3}]$, one has

$$\begin{array}{c}\hfill \mid h\left(x_1\right)-h\left(x_2\right)\mid =\mid 2x_1+\frac{1}{3}-(-3x_2+2)\mid =\mid 2x_1+3x_2-\frac{5}{3}\mid >\mid x_1+\frac{3}{2}{x}_2-\frac{5}{6}\mid .\end{array}$$

If $x_1\in [\frac{1}{3},\frac{2}{3}],x_2\in [\frac{2}{3},1]$, one has

$$\begin{array}{c}\hfill \mid h\left(x_1\right)-h\left(x_2\right)\mid =\mid -3x_1+2-(x_2-\frac{2}{3})\mid =\mid 3x_1+x_2-\frac{8}{3}\mid >\mid x_1+\frac{1}{3}{x}_2-\frac{8}{9}\mid .\end{array}$$

If $x_1\in [0,\frac{1}{3}],x_2\in [\frac{2}{3},1]$, one has

$$\begin{array}{c}\hfill \mid h\left(x_1\right)-h\left(x_2\right)\mid =\mid 2x_1+\frac{1}{3}-(x_2-\frac{2}{3})\mid =\mid 2x_1-x_2+1\mid >\mid x_1-\frac{1}{2}{x}_2+\frac{1}{2}\mid .\end{array}$$

Write

$$\begin{array}{c}\hfill {\mathsf{\Delta }}_1=\{\mid x_1-x_2\mid :x_1,x_2\in [0,\frac{1}{3}]\};{\mathsf{\Delta }}_2=\{\mid x_1-x_2\mid :x_1,x_2\in [\frac{1}{3},\frac{2}{3}]\};\end{array}$$

$$\begin{array}{c}\hfill {\mathsf{\Delta }}_3=\{\mid x_1-x_2\mid :x_1,x_2\in [\frac{2}{3},1]\};{\mathsf{\Delta }}_4=\{\mid x_1+\frac{3}{2}{x}_2-\frac{5}{6}\mid :x_1\in [0,\frac{1}{3}],x_2\in [\frac{1}{3},\frac{2}{3}]\}\end{array}$$

$$\begin{array}{c}\hfill {\mathsf{\Delta }}_5=\{\mid x_1+\frac{1}{3}{x}_2-\frac{8}{9}\mid :x_1\in [\frac{1}{3},\frac{2}{3}],x_2\in [\frac{2}{3},1]\};\\ \hfill {\mathsf{\Delta }}_6=\{\mid x_1-\frac{1}{2}{x}_2+\frac{1}{2}\mid :x_1\in [0,\frac{1}{3}],x_2\in [\frac{2}{3},1]\}.\end{array}$$

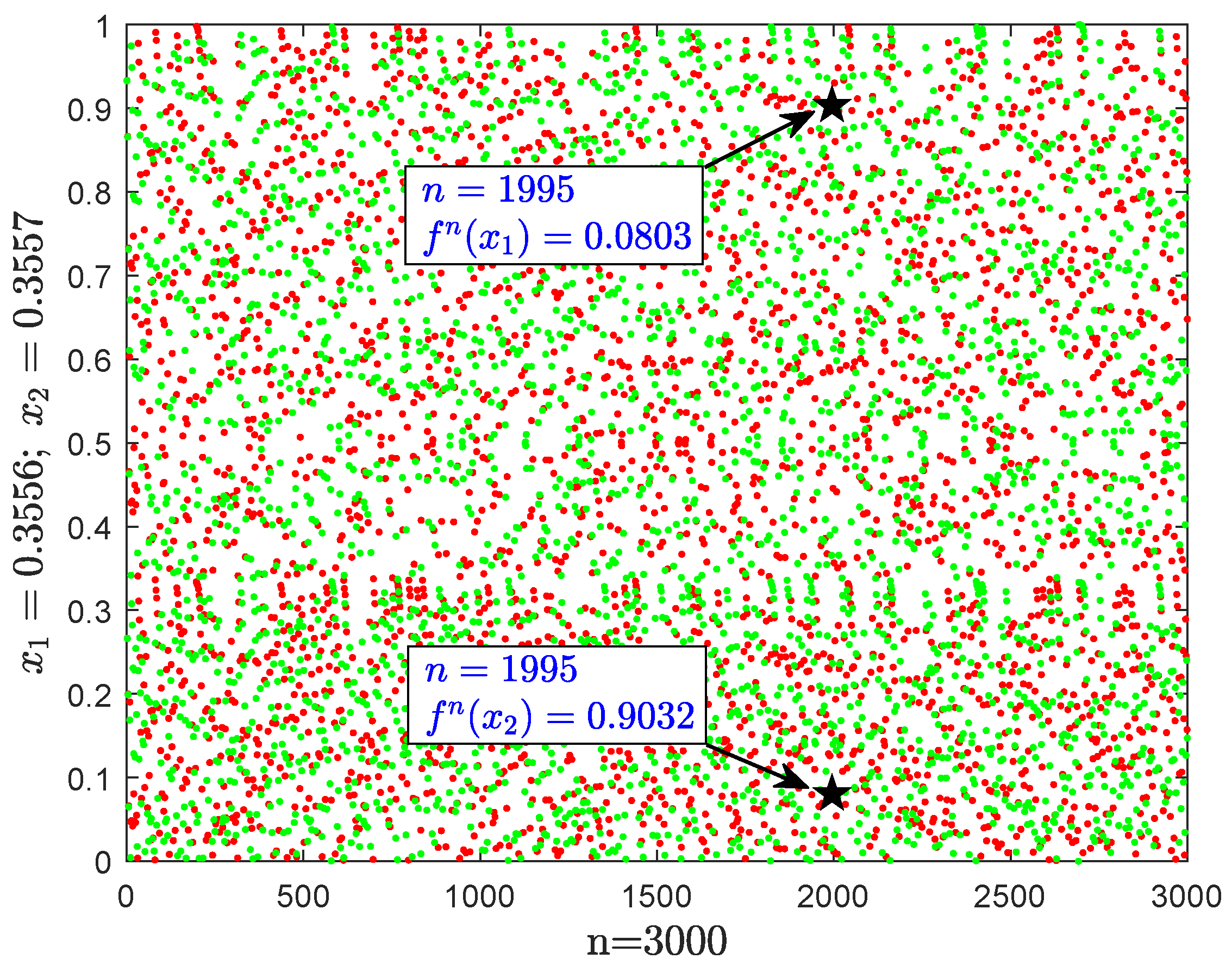
Taking $\delta =inf({\bigcup }_{i=1}^6{\mathsf{\Delta }}_i$). Then, for any $n\in \mathbb{N}$, $\mid h^n\left(x_1\right)-h^n\left(x_2\right)\mid \ge \delta$. This implies that the map $h:[0,1]\to [0,1]$ is sensitive-dependent on initial condition. The computer simulation with explanation of chaotic behavior is provided in Figure 1. The red dots and the green dots represent the trajectories of initial value $x_1=0.3556$ and $x_2=0.3557$ iterate for 3000 times, respectively. It can be seen that, after iteration, the orbit of $x_1$ (or $x_2$) is ergodic and disorder (see red dots or green dots). And with little difference between initial values $x_1$ and $x_2$, there is a big gap between the iterative values after 1995 times (see $h^{1995}\left(x_1\right)=0.0803$, $h^{1995}\left(x_2\right)=0.9032$). This means that h is sensitive-dependent on initial condition.

Then, it can be proved that the system $(H,h)$ is infinitely sensitive, m-sensitive, and m-cofinitely sensitive.

Now, let $f_n\left(x\right)=g\left(x\right)(n=2k+1,k\in \mathbb{N})$ and $f_n\left(x\right)=h\left(x\right)(n=2k,k\in \mathbb{N})$. Then the family $\left(f_n\right)$ consists of feebly open mappings converging uniformly to h. Obviously, $(H,f_{1,\infty })$ is also infinitely sensitive, m-sensitive, and m-cofinitely sensitive. Thus, the system $(H,f_{1,\infty })$ is conform to the assumption of Theorems 1–4.

Example 2.

Defining

$$p\left(x\right)=25saw\left(x\right)+cos\left(x^2(1-x)\right),x\in H=\mathbb{R},$$

where, $saw\left(x\right)$ is the sawtooth function defined by

$$saw\left(x\right)={(-1)}^m(x-2m),2m-1\le x\le 2m+1,m\in \mathbb{Z}.$$

One can prove that the map $p\left(x\right)$ satisfies the definitions of chaos in Section 2. The computer simulation with explanation of chaotic behavior is provided in Figure 2. The red dots and the green dots represent the trajectories of initial value $x_1=0.3556$ and $x_2=0.3557$ iterate for 6000 times, respectively. And with little difference between initial values $x_1$ and $x_2$, there is a big gap between the iterative values after 4123 times (see $p^n\left(x_1\right)=18.3449$, $p^n\left(x_2\right)=-24.1185$).

Now, let $f_n\left(x\right)=p\left(x\right)(n\in \mathbb{N})$. Then $f_n(n\in \mathbb{N})$ are feebly open mappings which uniformly converge to p. Similar to Example 1, $(H,f_{1,\infty })$ is infinitely sensitive, m-sensitive, and m-cofinitely sensitive.

Remark 1.

The above discussion tells us that under some conditions, studying the effect of a series of disturbances on the system can be simplified to studying the effect of a single map (i.e., the limit map) on the system.

4. Some Supplements

In NDDS, is there any connection between the chaos in the sense of proximity and sensitivity? The following theorem answers this question in part.

Theorem 5.

Let H be a compact metric space and $(H,f_{1,\infty })$ be a proximal non-autonomous system, then $(H,f_{1,\infty })$ is spatio-temporal chaotic if and only if $(H,f_{1,\infty })$ is sensitive.

Proof. 

(Sufficiency) $(H,f_{1,\infty })$ be a proximal system, i.e., for any $x,y\in H$, $\underset{n\to \infty }{lim\; inf}d(f_1^n\left(x\right)$, $f_1^n\left(y\right))=0$. Because $(H,f_{1,\infty })$ is sensitive with sensitive constant $\delta >0$, then for any $x\in H$ and any neighborhood U of x, there exist a $y\in U$ and an $n\in \mathbb{N}$ such that $d(f_1^n\left(x\right),f_1^n\left(y\right))>\delta$.

First, we prove that $(H,f_{1,\infty })$ is infinitely sensitive. This is similar to the proof of Theorem 2.1 in Ref. [17].

Given any $N\in \mathbb{N}$, set ${\mathcal{D}}_N=\{(x,y):\rho (f_1^n\left(x\right),f_1^n\left(y\right))\le \frac{\eta }{4}\}$ for an $\eta >0$. It is clear that ${\mathcal{D}}_N$ is a closed set. And we can claim that int${\mathcal{D}}_N=\varphi$ for any $N\in \mathbb{N}$. In fact, if there are some $N\in \mathbb{N}$ such that int ${\mathcal{D}}_N\ne \varphi$, then there exist nonempty open sets $U,V\in H$ such that $U\times V\subset {\mathcal{D}}_N$. Thus, for any pair $(x,y)\in U\times V$, $\rho (f_1^n\left(x\right),f_1^n\left(y\right))\le \frac{\eta }{4}$ holds for any $n>\mathbb{N}$. So for arbitrary two points $x_1,x_2\in U$ and any $n>\mathbb{N}$,

$$\rho (f_1^n\left(x_1\right),f_1^n\left(x_2\right))\le \rho (f_1^n\left(x_1\right),f_1^n\left(y\right))+\rho (f_1^n\left(y\right),f_1^n\left(x_2\right))\le \frac{\eta }{2}.$$

It is easy to prove that, there exists a nonempty open set $U^{*}\subset U$ such that for any points pair $x_1,x_2\in U^{*}$ and any $0\le m\le N$, $\rho (f_1^m\left(x_1\right),f_1^m\left(x_2\right))\le \frac{\eta }{2}$. Hence, for any points pair $x_1,x_2\in U^{*}$ and any $n\in \mathbb{N}$, $\rho (f_1^m\left(x_1\right),f_1^m\left(x_2\right))\le \frac{\eta }{2}$, which contradicts the sensitivity of $(H,f_{1,\infty })$. So int ${\mathcal{D}}_N=\varphi$ for any $N\in \mathbb{N}$. It follows that set $\mathcal{D}={\cup }_{N\in \mathbb{N}}{\mathcal{D}}_N$ is a first category set in $H\times H$. Then, the set

$$(H\times H)\setminus \mathcal{D}=\{(x,y):\forall N\in \mathbb{N},\exists n>Nsuchthat\rho (f_1^n\left(x\right),f_1^n\left(y\right))>\frac{\eta }{4}\}$$

is residual in $X\times X$.

Assume that $(H,f_{1,\infty })$ is not infinitely sensitive, then there exist an $x_0\in H$ and a $\xi >0$ such that $\underset{n\to \infty }{lim\; sup}\rho (f_1^n\left(x_0\right),f_1^n\left(y\right))\le \frac{\eta }{16}$ for any $y\in B(x_0,\xi )$. Noting the fact that $(H\times H)\setminus \mathcal{D}$ is residual in $H\times H$, it follows that there exists a pair $(y_1,y_2)\in [B(x_0,\xi )\times B(x_0,\xi )]\cap [(H\times H)\setminus \mathcal{D}]$. Then for any $n\in \mathbb{N}$,

$$\rho (f_1^n\left(y_1\right),f_1^n\left(y_2\right))\le \rho (f_1^n\left(y_1\right),f_1^n\left(x_0\right))+\rho (f_1^n\left(x_0\right),f_1^n\left(y_2\right))\le \frac{\eta }{8}.$$

So,

$$\underset{n\to \infty }{lim\; sup}\rho (f_1^n\left(y_1\right),f_1^n\left(y_2\right))\le \frac{\eta }{8},$$

which contradicts to $(y_1,y_2)\in H\times H\setminus \mathcal{D}$.

Hence, $(H,f_{1,\infty })$ is infinitely sensitive. That is to say, there exists an ${\eta }^{*}>0$ such that $\underset{n\to \infty }{lim\; sup}\rho (f_1^n\left(x\right),f_1^n\left(y\right))\ge {\eta }^{*}$. Then, it is easy to get that $(H,f)$ is spatio-temporal chaotic.

(Necessity) It is clearly held, and hence is omitted.

The proof is completed. □

Corollary 1.

Let H be a compact metric space and $(H,f)$ be a proximal system, then $(H,f)$ is spatio-temporal chaotic if and only if $(H,f)$ is sensitive.

Remark 2.

In fact, there are some other relationships among chaotic properties in non-autonomous discrete systems. For example, topologically weak mixing implies sensitive, dense δ-chaos implies sensitive, generic δ-chaos implies sensitive, and Li-Yorke sensitive is equivalent to sensitive under the condition that $\overline{{\bigcap }_{k=1}^{\infty }{\bigcup }_{n=1}^{\infty }{f}_1^{-n}\left(\{y\in H:d(f_1^n\left(x\right),y)<\frac{1}{k}\}\right)}=H$. These results are in [18,19,20,21].

5. Conclusions

For a mapping sequence $f_{1,\infty }={\left(f_n\right)}_{n=1}^{\infty }$, this paper gives four hypotheses. That is, (1) $f_n(n\in \mathbb{N})$ are feebly open; (2) $f_n(n\in \mathbb{N})$ uniformly converge to f; (3) $f_i\circ f=f\circ f_i$ for any $i\in \{1,2,\dots \}$; and (4) ${\sum }_{i=1}^{\infty }D(f_i,f)<\infty$. It is proved that, under the conditions of (1)–(4), accessible or sensitivity between $f_{1,\infty }$ and its limit map f is coincide. Then, the natural problems rise. Can the above (1)–(4) be reduced? Do other chaotic properties, such as transitive, mixing, or distributional chaos, have similar conclusions? These are topics worth studying in the future.