Hidden and Coexisting Attractors in a Novel 4D Hyperchaotic System with No Equilibrium Point
Abstract
:1. Introduction
2. The Novel 4D Hyperchaotic System
3. Complex Dynamical Structure of the Proposed Hyperchaotic System
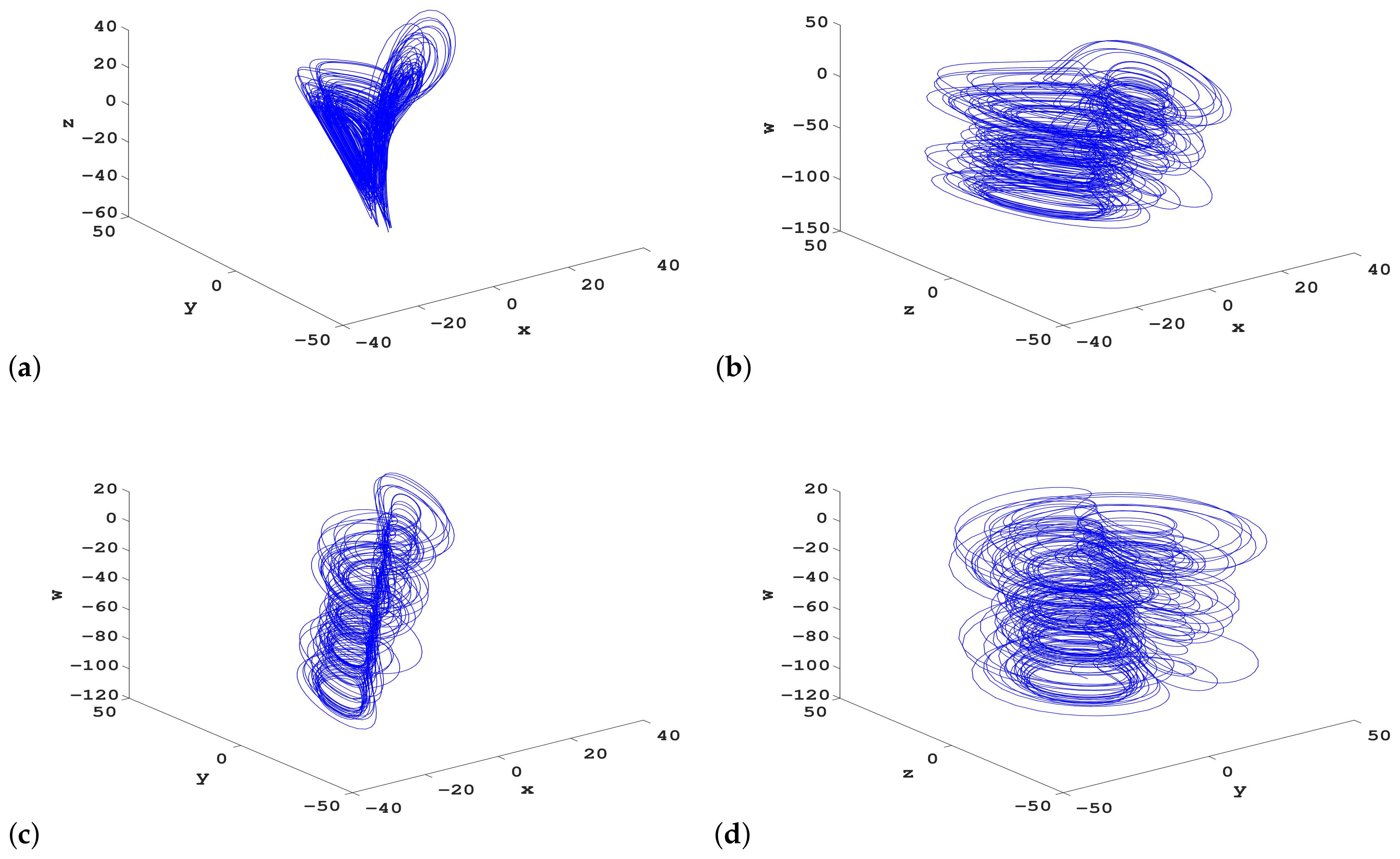
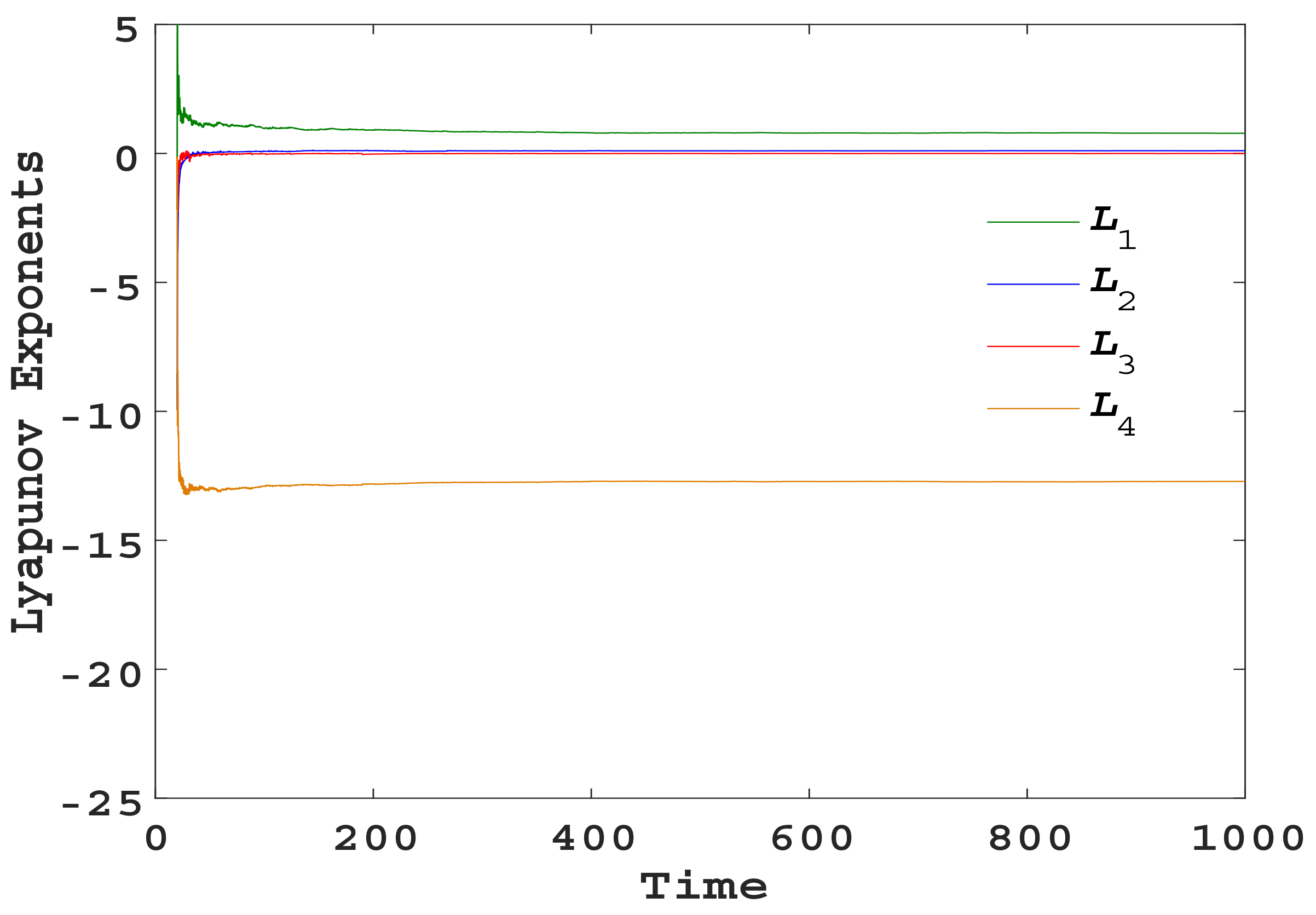
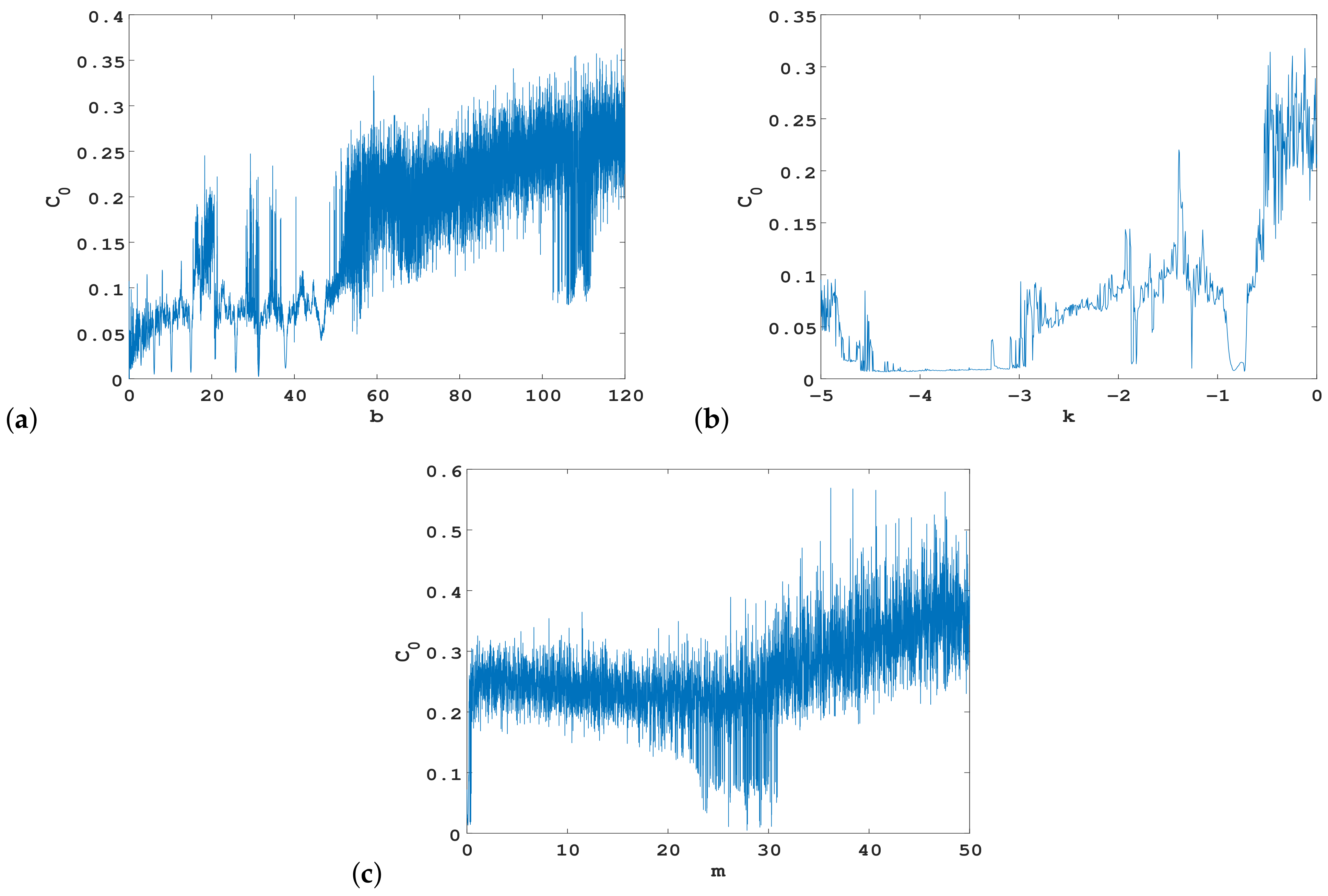
3.1. Lyapunov Exponents, Bifurcation Diagram, and Complexity Analysis
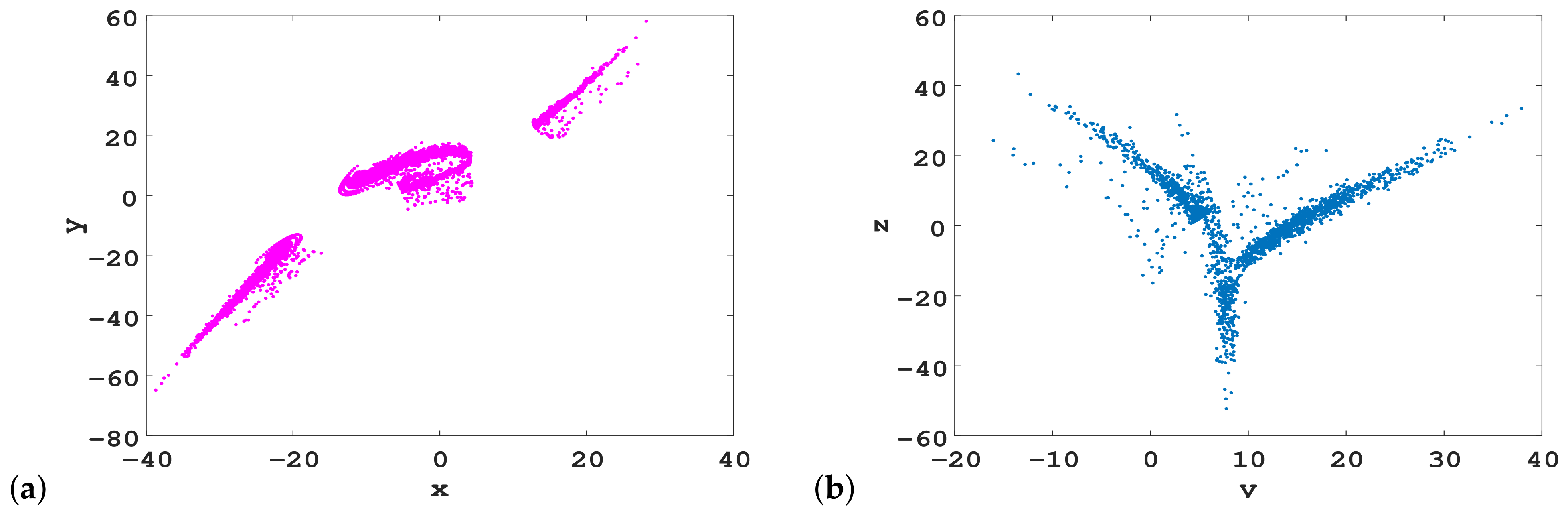
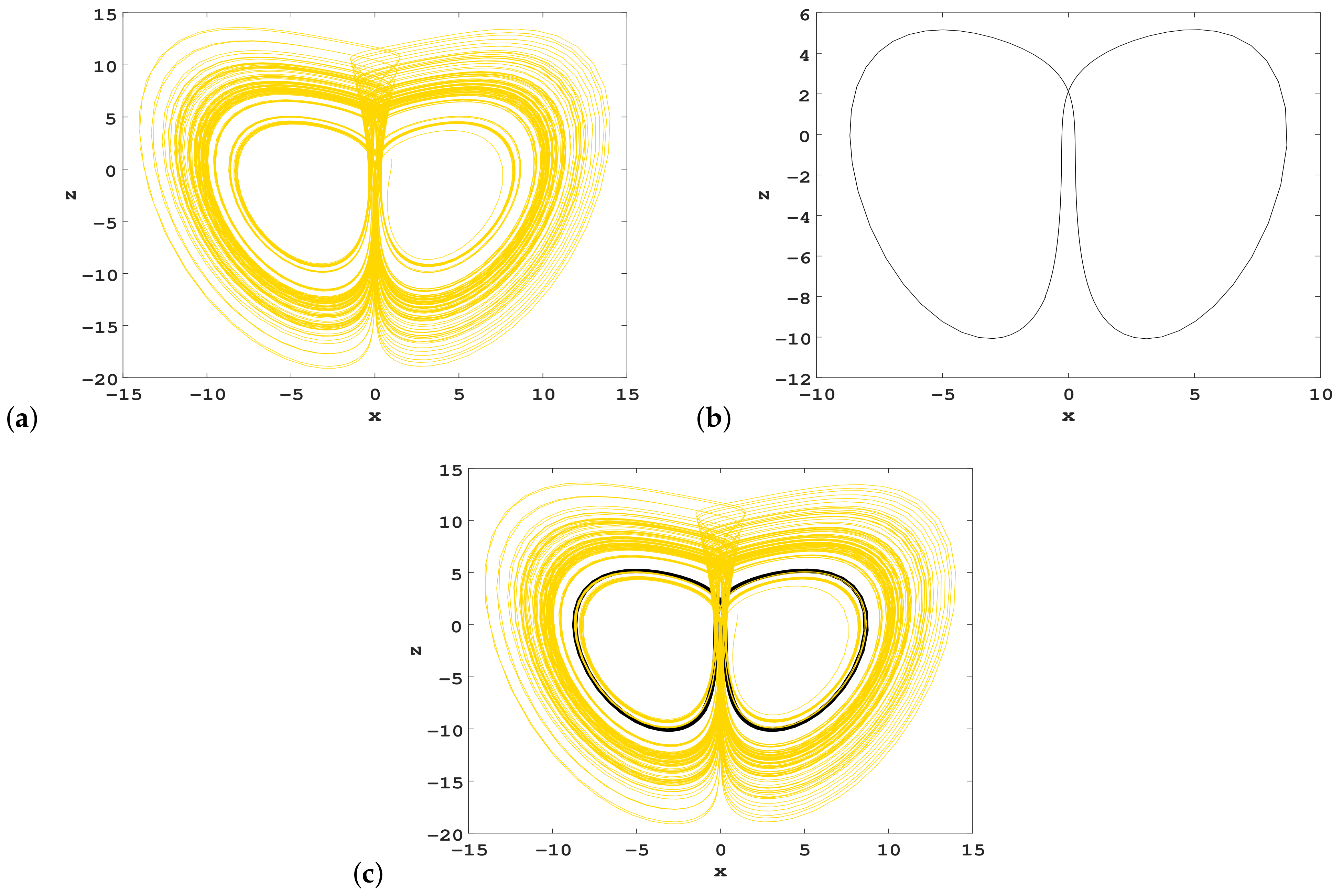
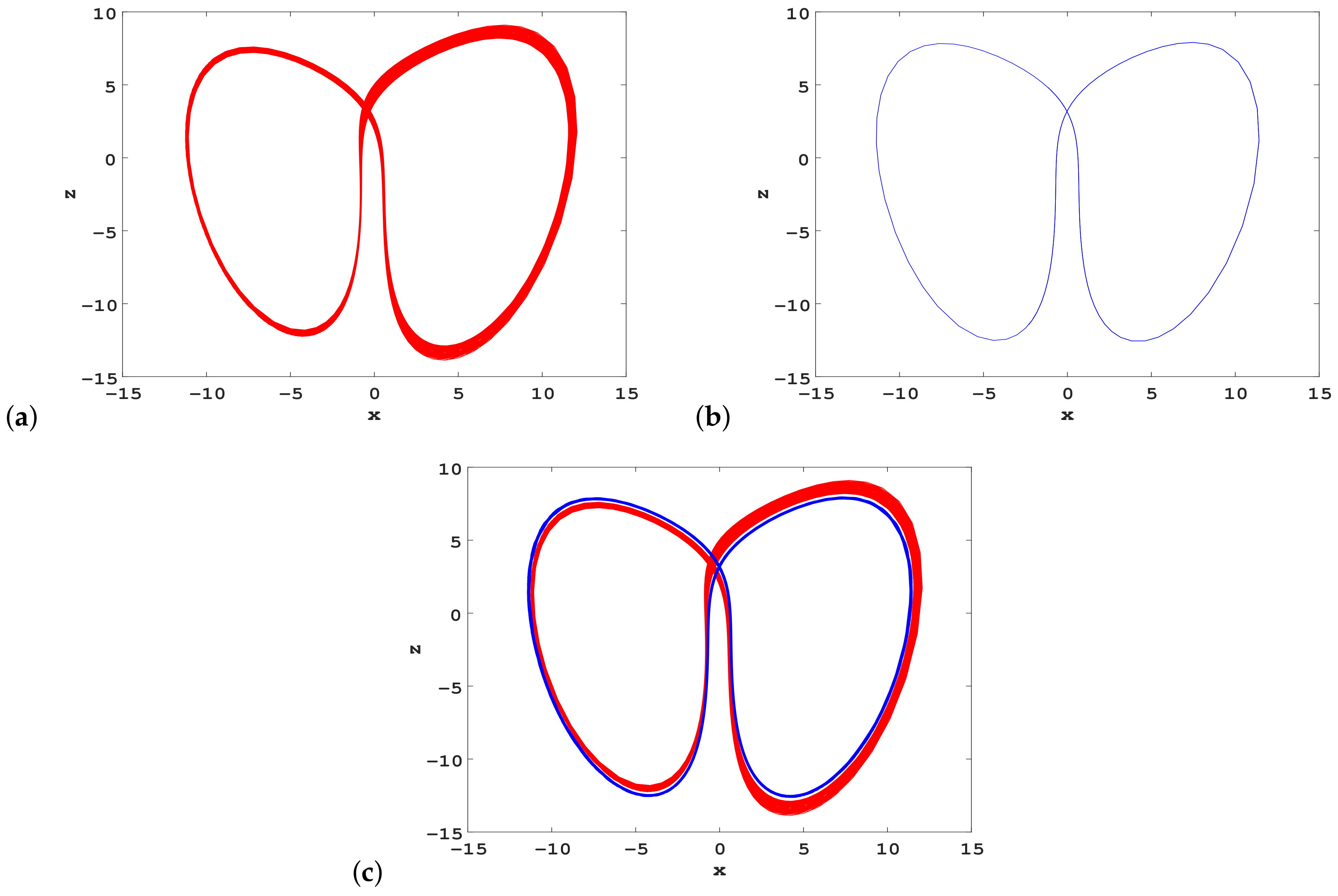
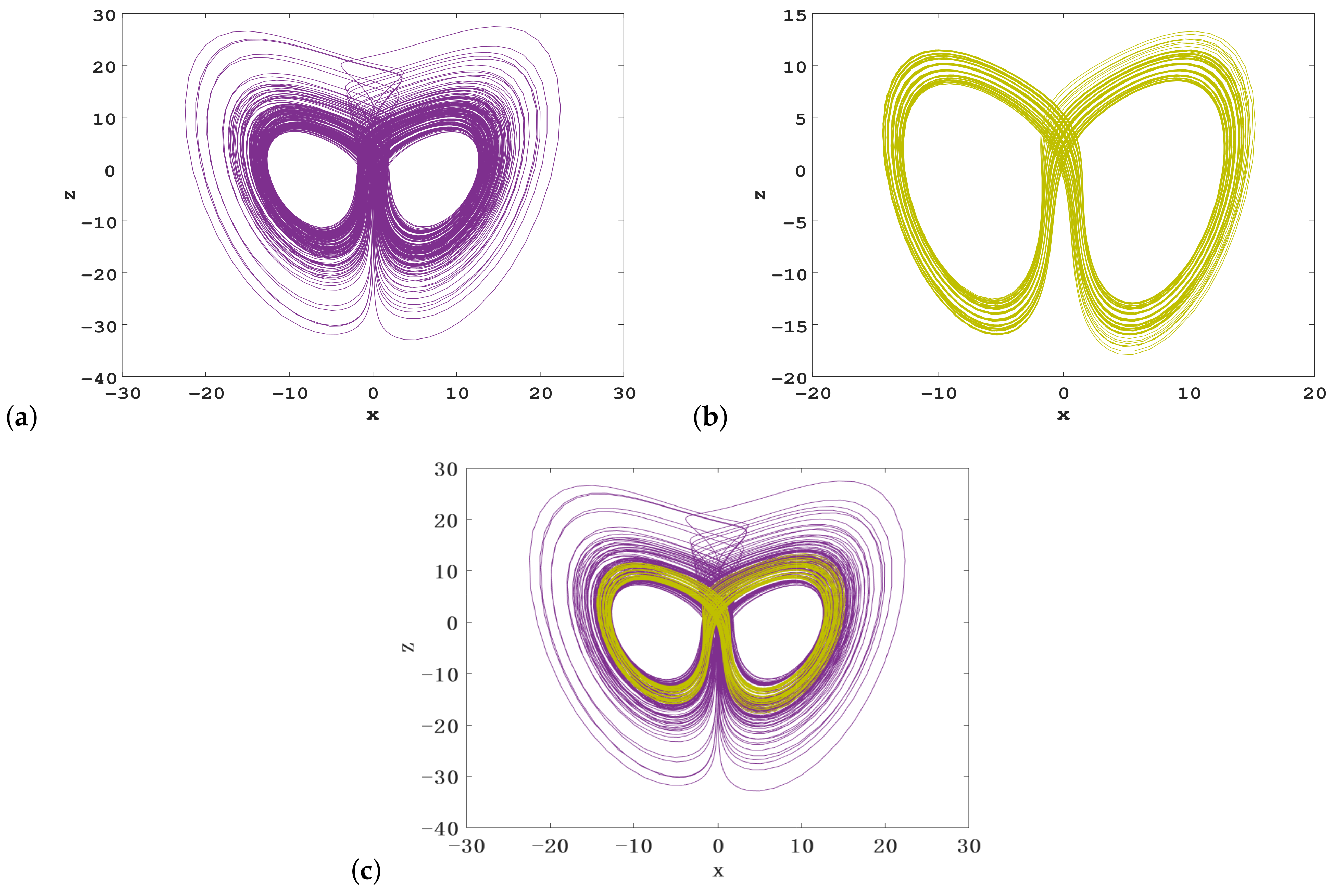
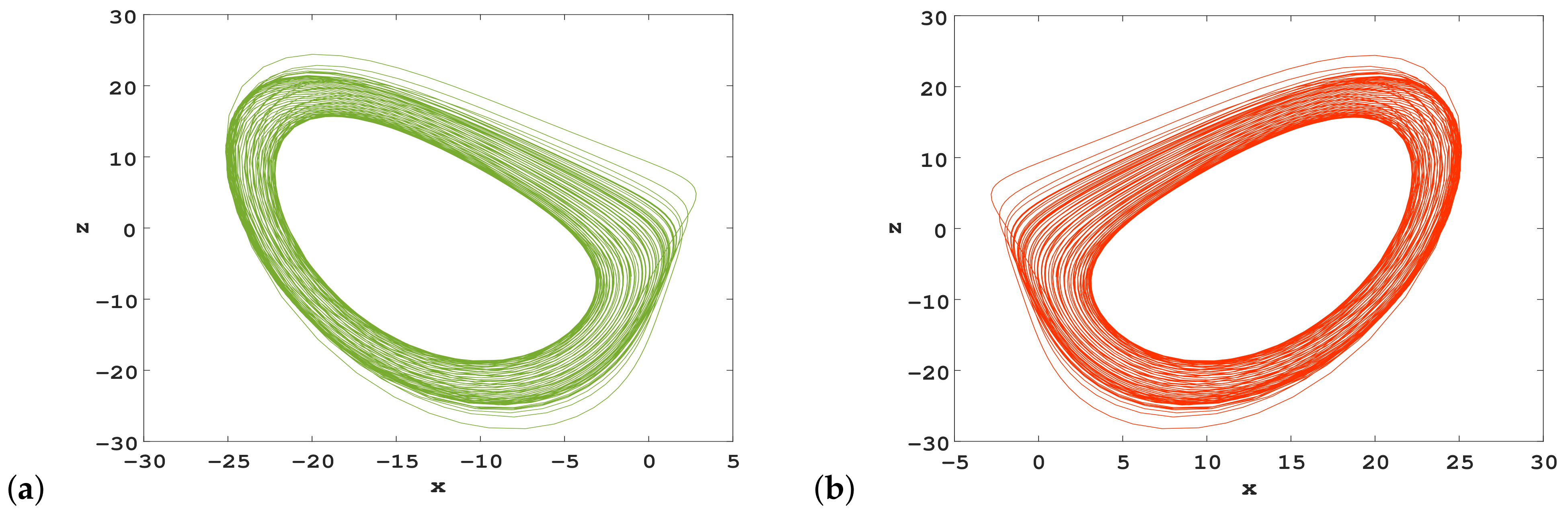
3.2. Coexisting Attractors
3.2.1. Coexistence of Chaotic and Periodic Attractors
3.2.2. Coexistence of Quasi-Periodic and Periodic Attractors
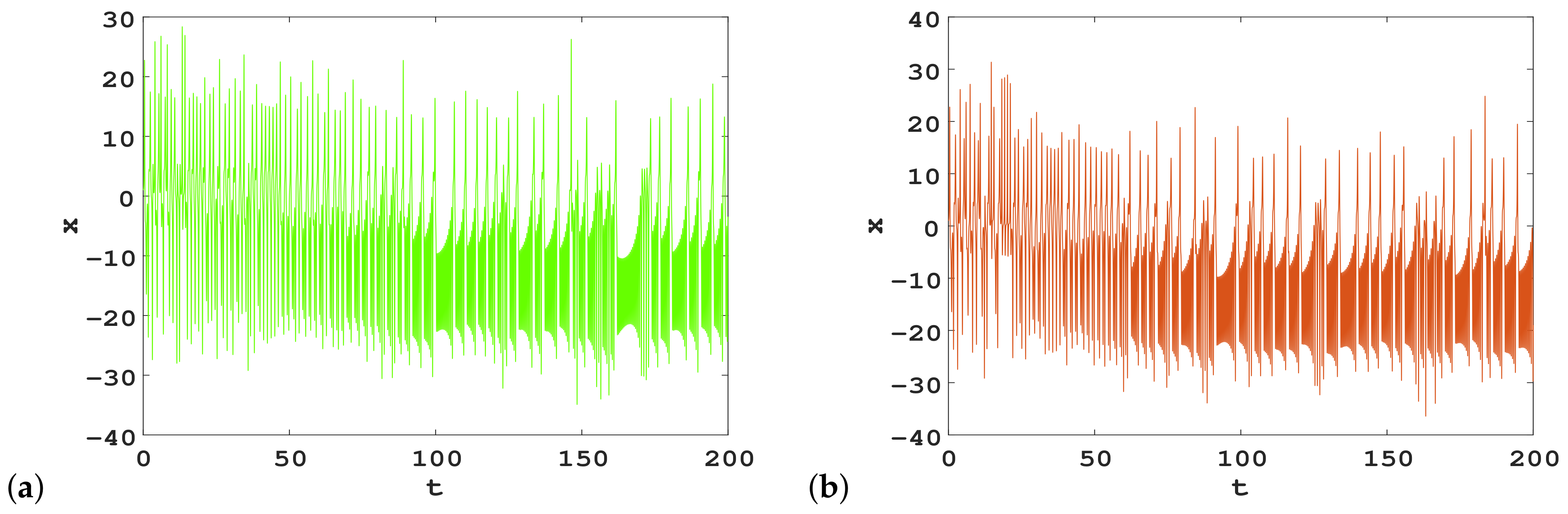
3.2.3. Coexistence of Chaotic and Quasi-Periodic Attractors
3.2.4. Coexistence of Hidden Periodic Attractors
3.2.5. Coexistence of Hidden Hyperchaotic Attractors
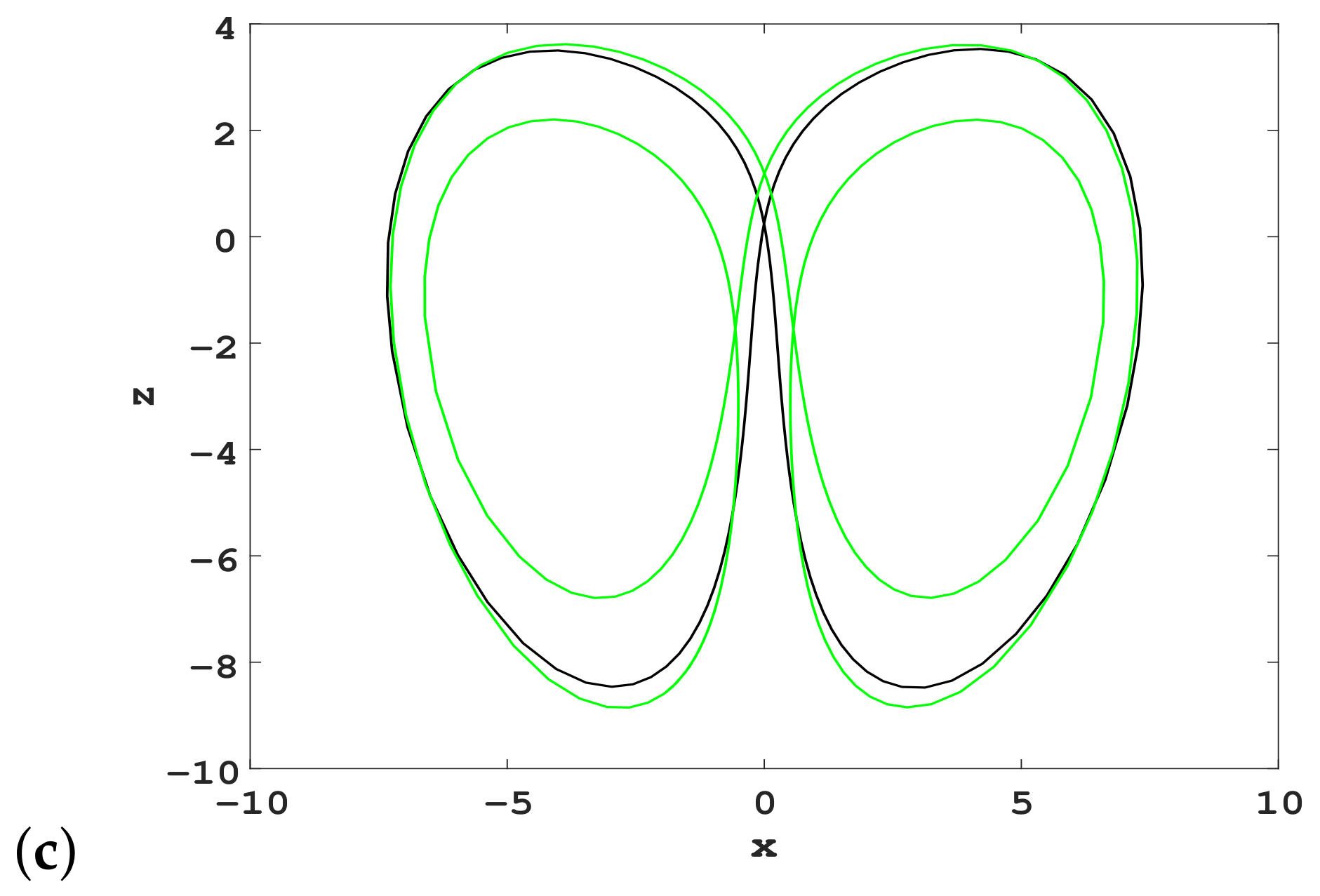
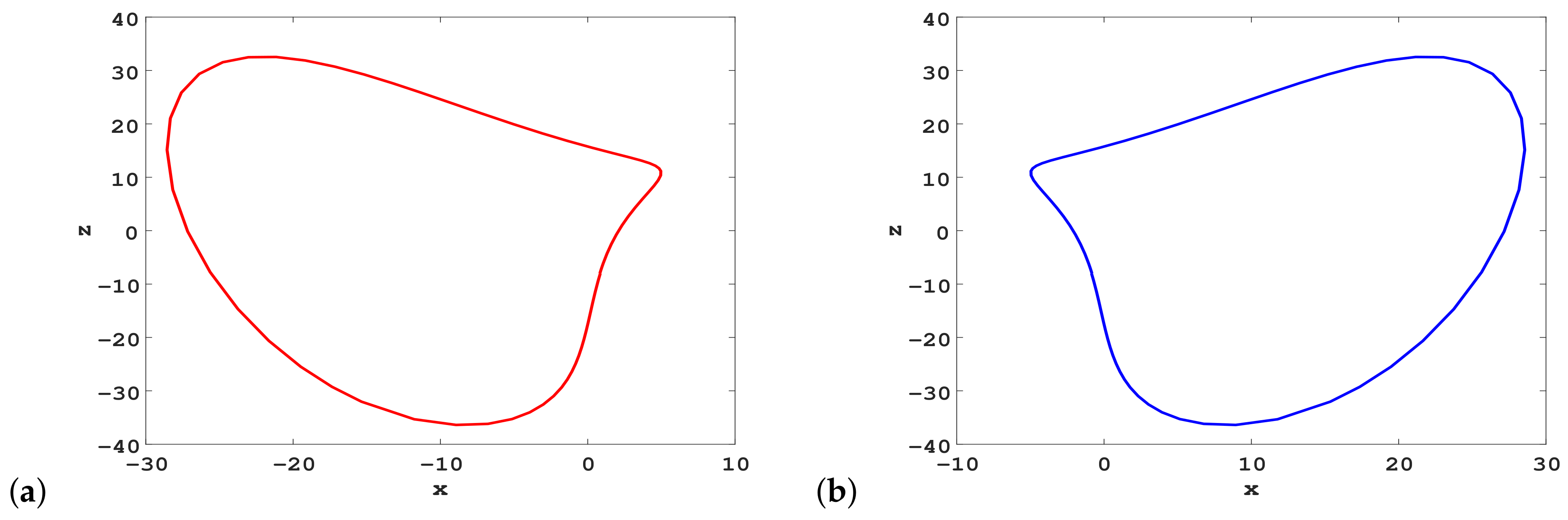
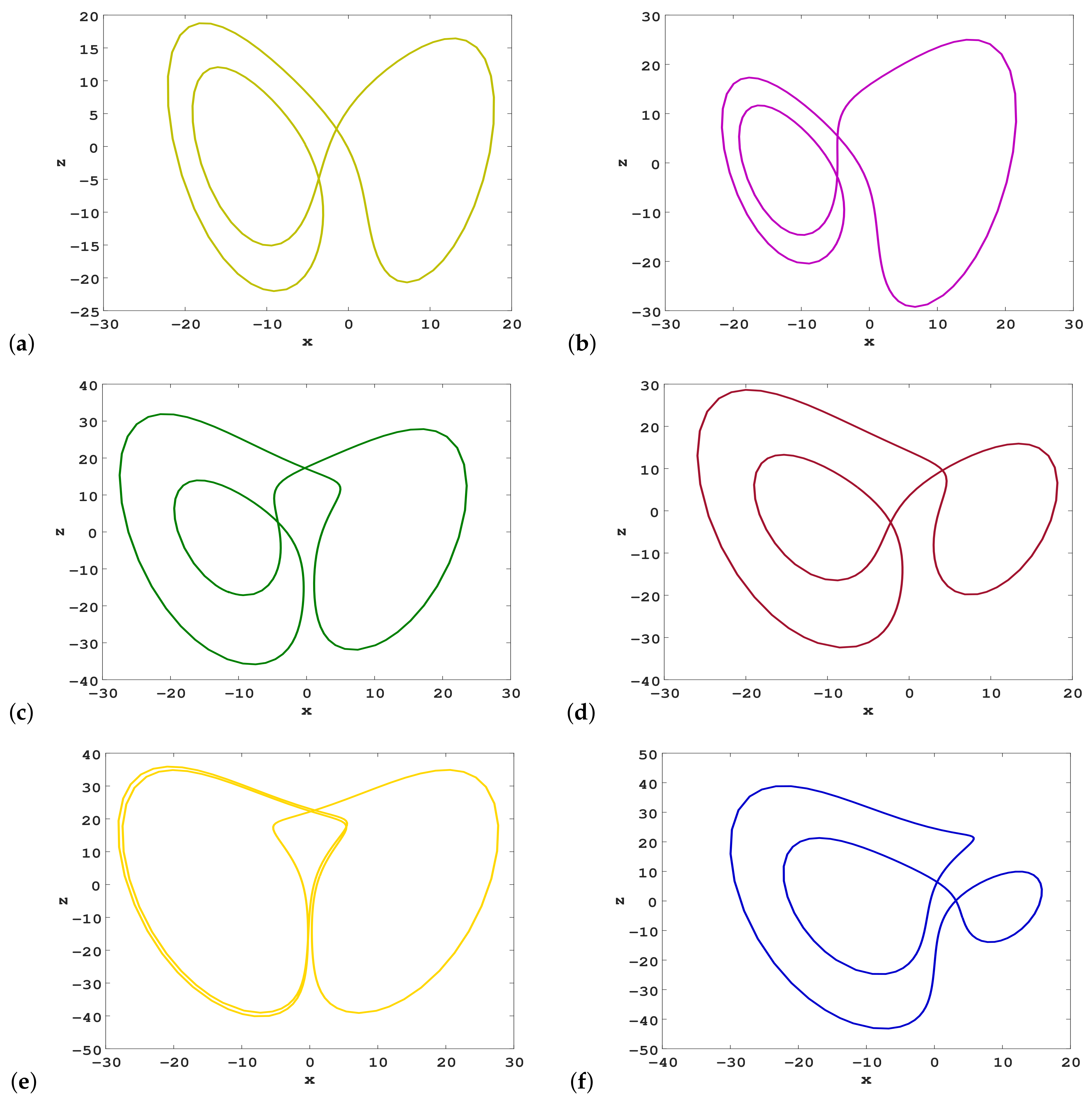
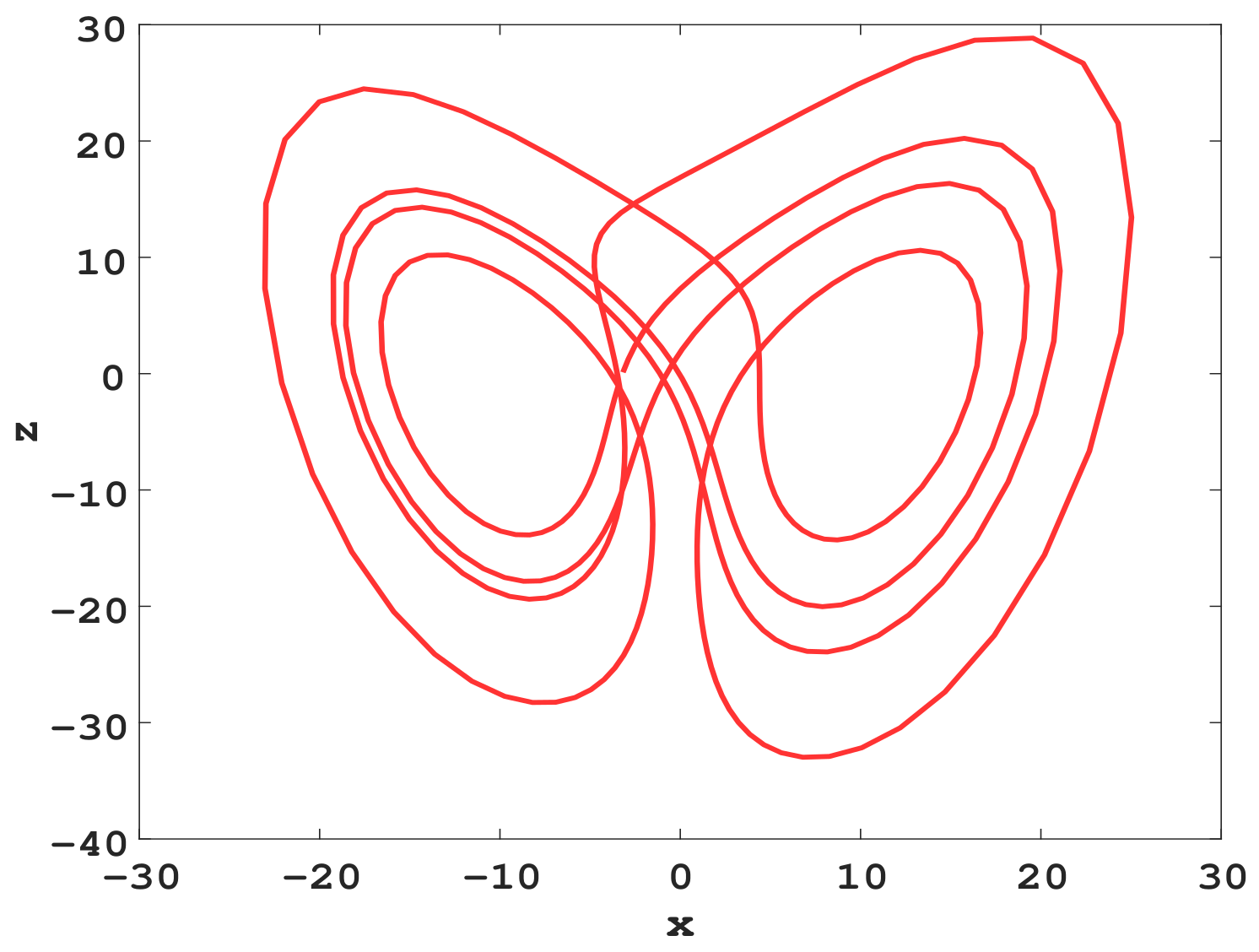
4. Analysis of Unstable Cycles for New 4D Hyperchaotic System via Variational Approach
4.1. Variational Method for Calculations
4.2. Extracting Unstable Cycles in a Hidden Hyperchaotic Attractor
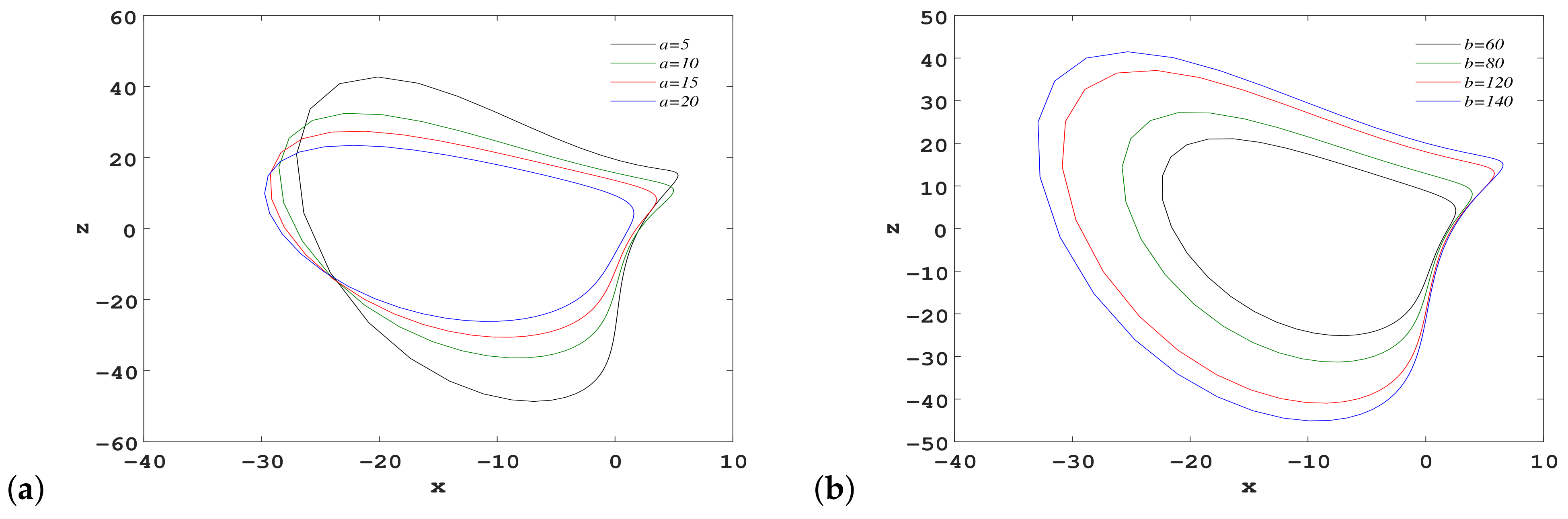
4.3. Homotopy Evolution of Cycle Variation with Different Parameters
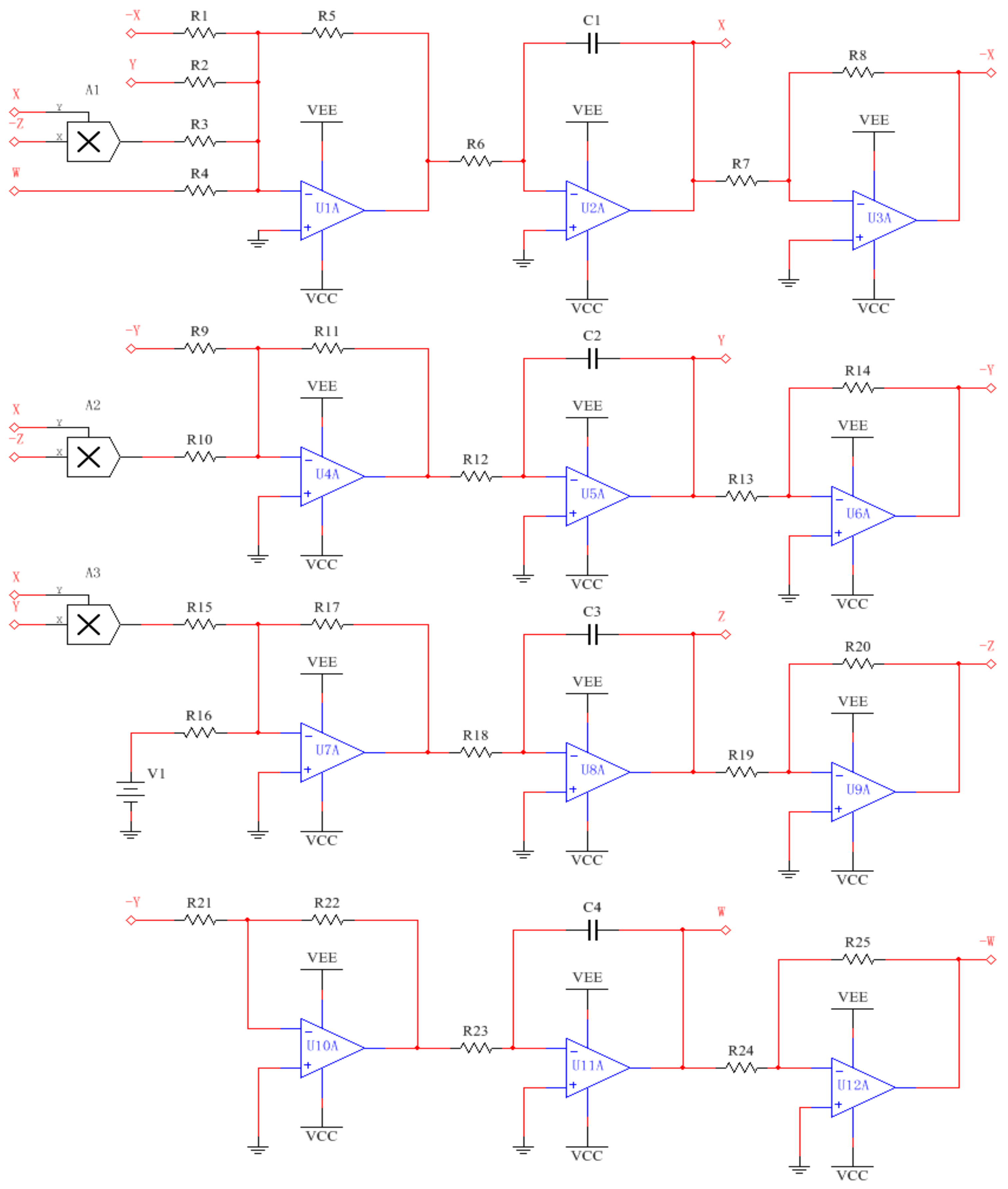
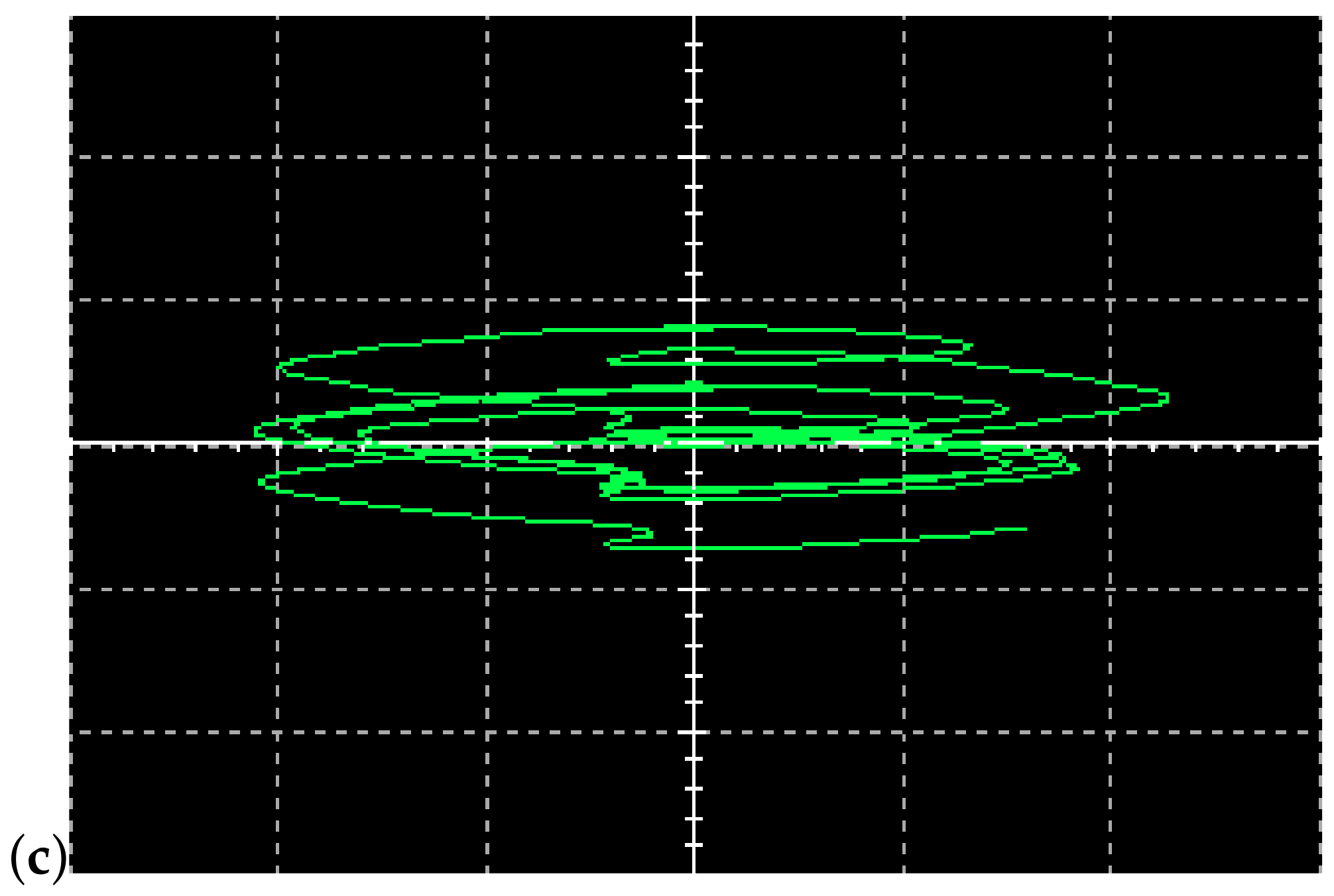
5. Circuit Design and Realization of New System
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Perseus Books: Reading, MA, USA, 1994. [Google Scholar]
- Cvitanović, P. Universality in Chaos, 2nd ed.; Adam Hilger: Bristol, UK, 1989. [Google Scholar]
- Rössler, O.E. An equation for hyperchaos. Phy. Lett. A 1979, 71, 155–156. [Google Scholar] [CrossRef]
- Wang, X.; Kuznetsov, N.V.; Chen, G. (Eds.) Chaotic Systems with Multistability and Hidden Attractors; Emergence, Complexity and Computation; Springer: Cham, Switzerland, 2021; Volume 40, pp. 149–150. [Google Scholar]
- Gao, T.; Chen, Z.; Yuan, Z.; Chen, G. A hyperchaos generated from Chen’s system. Int. J. Mod. Phys. C 2011, 17, 471–478. [Google Scholar] [CrossRef]
- Wang, F.Q.; Liu, C.X. Hyperchaos evolved from the Liu chaotic system. Chin. Phys. 2006, 15, 963–968. [Google Scholar]
- Wang, X.; Wang, M. A hyperchaos generated from Lorenz system. Phys. A Stat. Mech. Appl. 2008, 387, 3751–3758. [Google Scholar] [CrossRef]
- Li, Y.; Tang, W.; Chen, G. Hyperchaos evolved from the generalized Lorenz equation. Int. J. Circ. Theor. Appl. 2005, 33, 235–251. [Google Scholar] [CrossRef]
- Bao, B.; Xu, J.; Liu, Z.; Ma, Z. Hyperchaos from an augmented Lü system. Int. J. Bifurcat. Chaos 2010, 20, 3689–3698. [Google Scholar] [CrossRef]
- Yang, Q.; Bai, M. A new 5D hyperchaotic system based on modified generalized Lorenz system. Nonlinear Dyn. 2017, 88, 189–221. [Google Scholar] [CrossRef]
- Shen, C.; Yu, S.; Lü, J.; Chen, G. Generating hyperchaotic systems with multiple positive Lyapunov exponents. In Proceedings of the 9th Asian Control Conference (ASCC), Istanbul, Turkey, 23–26 June 2013; pp. 1–5. [Google Scholar]
- Yang, Q.; Zhu, D.; Yang, L. A New 7D hyperchaotic system with five positive Lyapunov exponents coined. Int. J. Bifurcat. Chaos 2018, 28, 1850057. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurcat. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.R.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurcat. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurcat. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, 647–650. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, R.; Liu, A. A new finding of the existence of hidden hyperchaotic attractors with no equilibria. Math. Comput. Simulat. 2014, 100, 13–23. [Google Scholar] [CrossRef]
- Cao, H.Y.; Zhao, L. A new chaotic system with different equilibria and attractors. Eur. Phys. J. Spec. Top. 2021, 230, 1905–1914. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P. Modelling and circuit realisation of a new no-equilibrium chaotic system with hidden attractor and coexisting attractors. Electron. Lett. 2020, 56, 1044–1046. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Jafari, S.; Wei, Z.; Wang, X. Constructing a novel no-equilibrium chaotic system. Int. J. Bifurcat. Chaos 2014, 24, 1450073. [Google Scholar] [CrossRef]
- Azar, A.T.; Volos, C.; Gerodimos, N.A.; Tombras, G.S.; Pham, V.T.; Radwan, A.G.; Vaidyanathan, S.; Ouannas, A.; Munoz-Pacheco, J.M. A novel chaotic system without equilibrium: Dynamics, synchronization, and circuit realization. Complexity 2017, 2017, 7871467. [Google Scholar] [CrossRef]
- Yang, Q.; Wei, Z.; Chen, G. An unusual 3d autonomous quadratic chaotic system with two stable node-foci. Int. J. Bifurcat. Chaos 2010, 20, 1061–1083. [Google Scholar] [CrossRef]
- Dong, C. Dynamics, periodic orbit analysis, and circuit implementation of a new chaotic system with hidden attractor. Fractal Fract. 2022, 6, 190. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Kapitaniak, T. Constructing a chaotic system with an infinite number of equilibrium points. Int. J. Bifurcat. Chaos 2016, 26, 1650225. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. Constructing a chaotic system with any number of equilibria. Nonlinear Dyn. 2013, 71, 429–436. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Qiao, X. Constructing a new 3D chaotic system with any number of equilibria. Int. J. Bifurcat. Chaos 2019, 29, 1950060. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Leonov, G.A.; Vagaitsev, V.I. Analytical-numerical method for attractor localization of generalized Chua’s system. In Proceedings of the IFAC Proceedings Volumes (IFAC-Papers Online), Antalya, Turkey, 26–28 August 2010. [Google Scholar]
- Ren, S.; Panahi, S.; Rajagopal, K.; Akgul, A.; Pham, V.T. A new chaotic flow with hidden attractor: The first hyperjerk system with no equilibrium. Z. Nat. A 2018, 73, 239–249. [Google Scholar] [CrossRef]
- Wei, Z.; Rajagopal, K.; Zhang, W.; Kingni, S.T.; Akgül, A. Synchronisation, electronic circuit implementation, and fractional-order analysis of 5D ordinary differential equations with hidden hyperchaotic attractors. Pramana–J. Phys. 2018, 90, 50. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, L.; Ou, B. Hidden hyperchaotic attractors in a new 5D system based on chaotic system with two stable node-foci. Int. J. Bifurcat. Chaos 2019, 29, 1950092. [Google Scholar] [CrossRef]
- Cui, L.; Luo, W.; Ou, Q. Analysis of basins of attraction of new coupled hidden attractor system. Chaos Soliton. Fract. 2021, 146, 110913. [Google Scholar] [CrossRef]
- Lai, Q.; Akgul, A.; Li, C.; Xu, G.; Cavusoglu, U. A new chaotic system with multiple attractors: Dynamic analysis, circuit realization and S-Box design. Entropy 2017, 20, 12. [Google Scholar] [CrossRef] [Green Version]
- Bayani, A.; Rajagopal, K.; Khalaf, A.J.M.; Jafari, S.; Leutcho, G.D.; Kengne, J. Dynamical analysis of a new multistable chaotic system with hidden attractor: Antimonotonicity, coexisting multiple attractors, and offset boosting. Phys. Lett. A 2019, 383, 1450–1456. [Google Scholar] [CrossRef]
- Nazarimehr, F.; Rajagopal, K.; Kengne, J.; Jafari, S.; Pham, V.T. A new four-dimensional system containing chaotic or hyper-chaotic attractors with no equilibrium, a line of equilibria and unstable equilibria. Chaos Soliton. Fract. 2018, 111, 108–118. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, C.; Zhao, X.W.; Kengne, J.; Volos, C. Constructing chaotic system with multiple coexisting attractors. IEEE Access 2019, 7, 24051–24056. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Xiong, L.; Banerjee, S.; Liu, T.; Han, X. Dynamical analysis of a new chaotic system: Asymmetric multistability, offset boosting control and circuit realization. Nonlinear Dyn. 2021, 103, 2867–2880. [Google Scholar] [CrossRef]
- Lai, Q.; Norouzi, B.; Liu, F. Dynamic analysis, circuit realization, control design and image encryption application of an extended Lü system with coexisting attractors. Chaos Soliton. Fract. 2018, 114, 230–245. [Google Scholar] [CrossRef]
- Natiq, H.; Said, M.; Al-Saidi, N.; Kilicman, A. Dynamics and complexity of a new 4D chaotic laser system. Entropy 2019, 21, 34. [Google Scholar] [CrossRef] [Green Version]
- Rajagopal, K.; Akgul, A.; Pham, V.T.; Alsaadi, F.E.; Nazarimehr, F.; Alsaadi, F.E.; Jafari, S. Multistability and coexisting attractors in a new circulant chaotic system. Int. J. Bifurcat. Chaos 2019, 29, 1950174. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.; Fotsin, H. Coexisting attractors, circuit implementation and synchronization control of a new chaotic system evolved from the simplest memristor chaotic circuit. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105341. [Google Scholar] [CrossRef]
- Sprott, J.C. A proposed standard for the publication of new chaotic systems. Int. J. Bifurcat. Chaos 2011, 21, 2391–2394. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Tang, W.K. S; Chen, G.R. Generating hyperchaos via state feedback control. Int. J. Bifurcat. Chaos 2005, 15, 3367–3375. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Sriram, M.S. A comparative study of computation of Lyapunov spectra with different algorithms. Phys. D Nonlinear Phenom. 2000, 139, 72–86. [Google Scholar] [CrossRef] [Green Version]
- Cvitanović, P.; Artuso, R.; Mainieri, R.; Tanner, G.; Vattay, G. Chaos: Classical and Quantum; Niels Bohr Institute: Copenhagen, Denmark, 2012; pp. 131–133. [Google Scholar]
- Lan, Y.; Cvitanović, P. Variational method for finding periodic orbits in a general flow. Phys. Rev. E 2004, 69, 016217. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Jia, L.; Jie, Q.; Li, H. Symbolic encoding of periodic orbits and chaos in the Rucklidge system. Complexity 2021, 2021, 4465151. [Google Scholar] [CrossRef]
- Dong, C.; Liu, H.; Li, H. Unstable periodic orbits analysis in the generalized Lorenz–type system. J. Stat. Mech. 2020, 2020, 073211. [Google Scholar] [CrossRef]
- Dong, C.; Lan, Y. Organization of spatially periodic solutions of the steady Kuramoto–Sivashinsky equation. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2140–2153. [Google Scholar] [CrossRef]
- Dong, C.; Liu, H.; Jie, Q.; Li, H. Topological classification of periodic orbits in the generalized Lorenz-type system with diverse symbolic dynamics. Chaos Soliton. Fract. 2022, 154, 111686. [Google Scholar] [CrossRef]
- Hao, B.L.; Zheng, W.M. Applied Symbolic Dynamics and Chaos; World Scientic: Singapore, 1998; pp. 11–13. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Dong, C. Topological classification of periodic orbits in the Yang-Chen system. EPL Europhys. Lett. 2018, 123, 20005. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Anzo-Hernández, A. A novel antimonotic hyperjerk system: Analysis, synchronization and circuit design. Physica D Nonlinear Phenom. 2021, 424, 132927. [Google Scholar] [CrossRef]
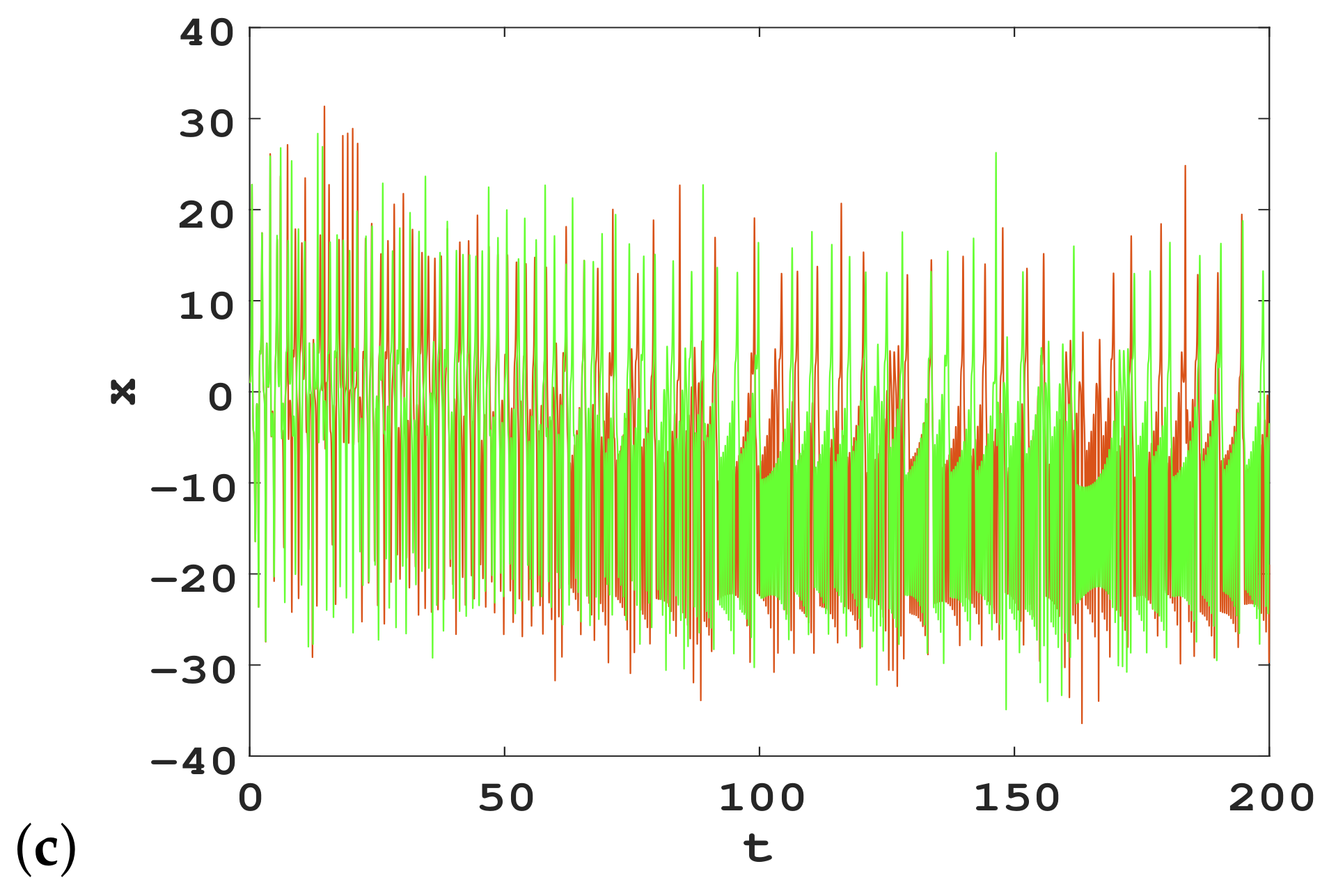

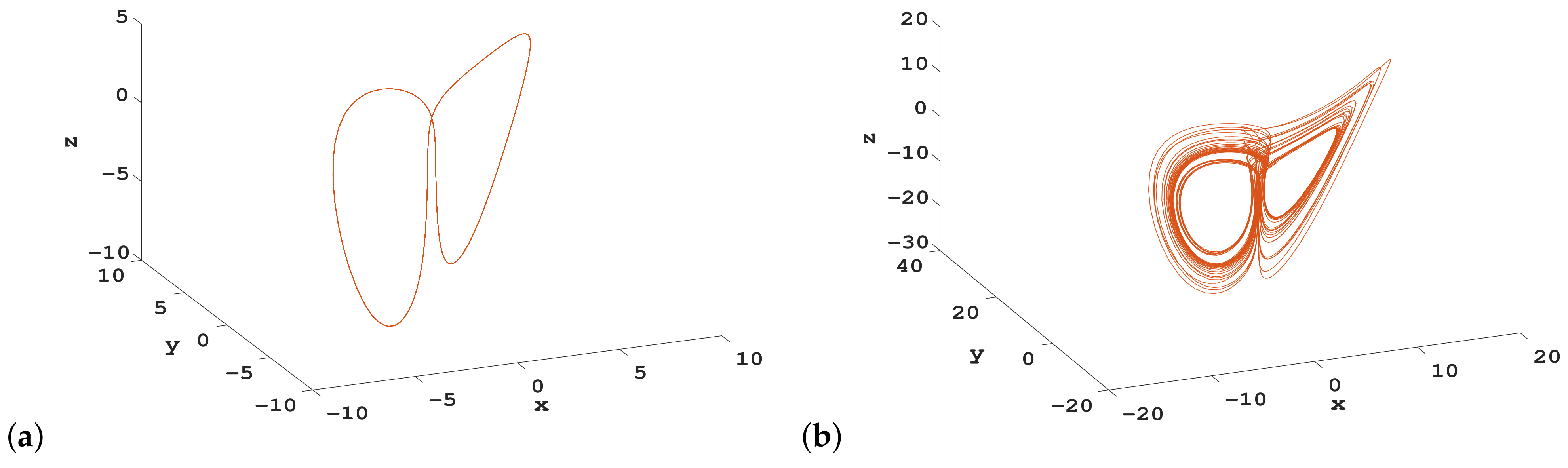
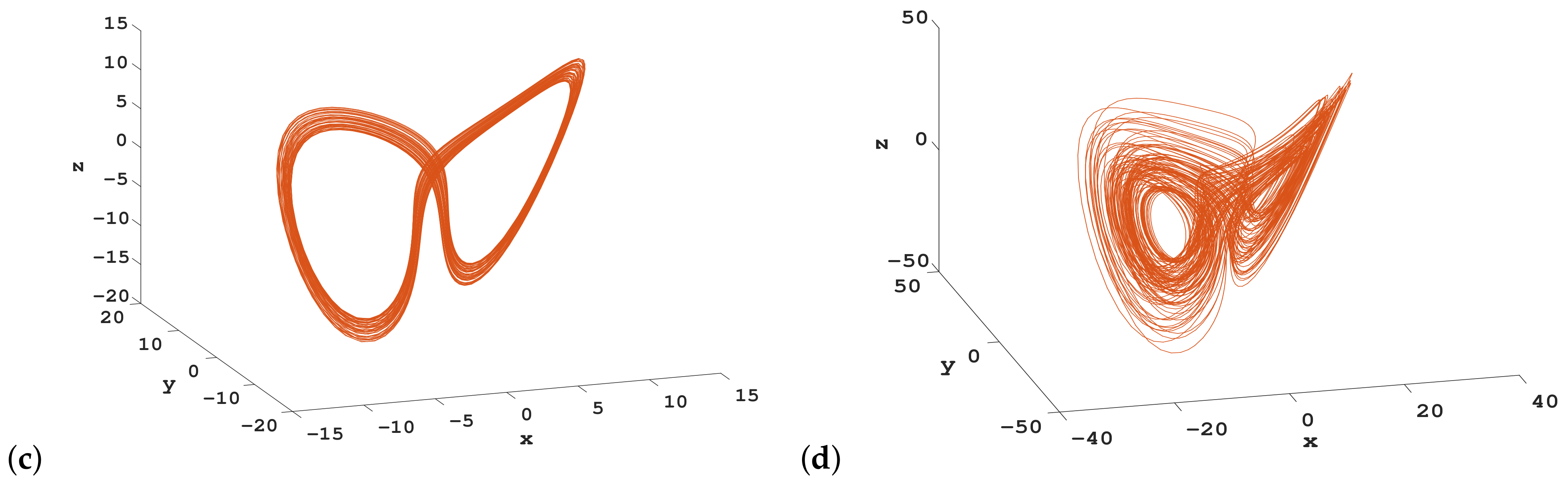







| b | Dynamics | |||||
|---|---|---|---|---|---|---|
| 10 | 0 | −0.0377 | −0.4173 | −11.6842 | 1.0 | Periodic |
| 20 | 0.0483 | 0 | −0.2258 | −11.9110 | 2.24 | Chaos |
| 38 | 0 | −0.0227 | −0.0243 | −12.0242 | 1.0 | Periodic |
| 42 | 0 | 0 | −0.1340 | −11.9278 | 2.0 | Quasi-periodic |
| 50 | 0.0182 | 0 | −0.2922 | −11.7656 | 2.06 | Chaos |
| 120 | 0.9302 | 0.0850 | 0 | −12.8638 | 3.08 | Hyperchaos |
| Length | p | x | y | z | w | |
|---|---|---|---|---|---|---|
| 1 | 2 | 0.858233 | 0.851259 | 3.599482 | −8.032931 | −39.656931 |
| 3 | 0.858233 | −0.851259 | −3.599482 | −8.032931 | 39.656931 | |
| 2 | 03 | 1.362034 | −4.076805 | −1.813737 | 1.109695 | −14.135359 |
| 12 | 1.362034 | 4.076805 | 1.813737 | 1.109695 | 14.135359 | |
| 01 | 1.194275 | 5.206540 | 7.525051 | −17.639962 | 1.385740 | |
| 23 | 1.830597 | 0.626331 | −0.321247 | −4.302274 | 1.490707 | |
| 3 | 001 | 1.732553 | −5.282481 | 3.245260 | 0.268165 | −34.418329 |
| 011 | 1.732553 | 5.282481 | −3.245260 | 0.268165 | 34.418329 | |
| 003 | 1.821191 | −4.653735 | 2.777113 | −2.962048 | −38.837657 | |
| 112 | 1.821191 | 4.653735 | −2.777113 | −2.962048 | 38.837657 | |
| 132 | 2.211630 | 11.320228 | 14.639216 | −16.413004 | 25.186818 | |
| 023 | 2.211630 | −11.320228 | −14.639216 | −16.413004 | −25.186818 | |
| 021 | 1.968277 | −6.298304 | 3.295041 | 5.572765 | −20.401797 | |
| 013 | 1.968277 | 6.298304 | −3.295041 | 5.572765 | 20.401797 | |
| 223 | 2.766255 | 1.453074 | −0.422130 | 2.547336 | 1.463103 | |
| 233 | 2.766255 | −1.453074 | 0.422130 | 2.547336 | −1.463103 | |
| 012 | 2.207939 | 4.137109 | 5.676602 | −5.643553 | −9.306008 | |
| 031 | 2.207939 | −4.137109 | −5.676602 | −5.643553 | 9.306008 |
| a | b | c | k | m | |||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.082797 | 60 | 0.953492 | −2 | 0.880703 | −0.5 | 0.705715 | −40 | 0.996271 |
| 10 | 0.858233 | 80 | 0.911549 | 0 | 0.873372 | −0.3 | 0.821457 | −20 | 0.968155 |
| 15 | 0.729400 | 120 | 0.811395 | 2 | 0.864607 | 0.1 | 0.964986 | 10 | 0.799075 |
| 20 | 0.610639 | 140 | 0.771540 | 4 | 0.833397 | 0.5 | 1.140899 | 30 | 0.611363 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, C.; Wang, J. Hidden and Coexisting Attractors in a Novel 4D Hyperchaotic System with No Equilibrium Point. Fractal Fract. 2022, 6, 306. https://doi.org/10.3390/fractalfract6060306
Dong C, Wang J. Hidden and Coexisting Attractors in a Novel 4D Hyperchaotic System with No Equilibrium Point. Fractal and Fractional. 2022; 6(6):306. https://doi.org/10.3390/fractalfract6060306
Chicago/Turabian StyleDong, Chengwei, and Jiahui Wang. 2022. "Hidden and Coexisting Attractors in a Novel 4D Hyperchaotic System with No Equilibrium Point" Fractal and Fractional 6, no. 6: 306. https://doi.org/10.3390/fractalfract6060306
APA StyleDong, C., & Wang, J. (2022). Hidden and Coexisting Attractors in a Novel 4D Hyperchaotic System with No Equilibrium Point. Fractal and Fractional, 6(6), 306. https://doi.org/10.3390/fractalfract6060306







