Fractional View Analysis of Cahn–Allen Equations by New Iterative Transform Method
Abstract
:1. Introduction
2. Basic Concepts
3. The General Discussion of the Technique
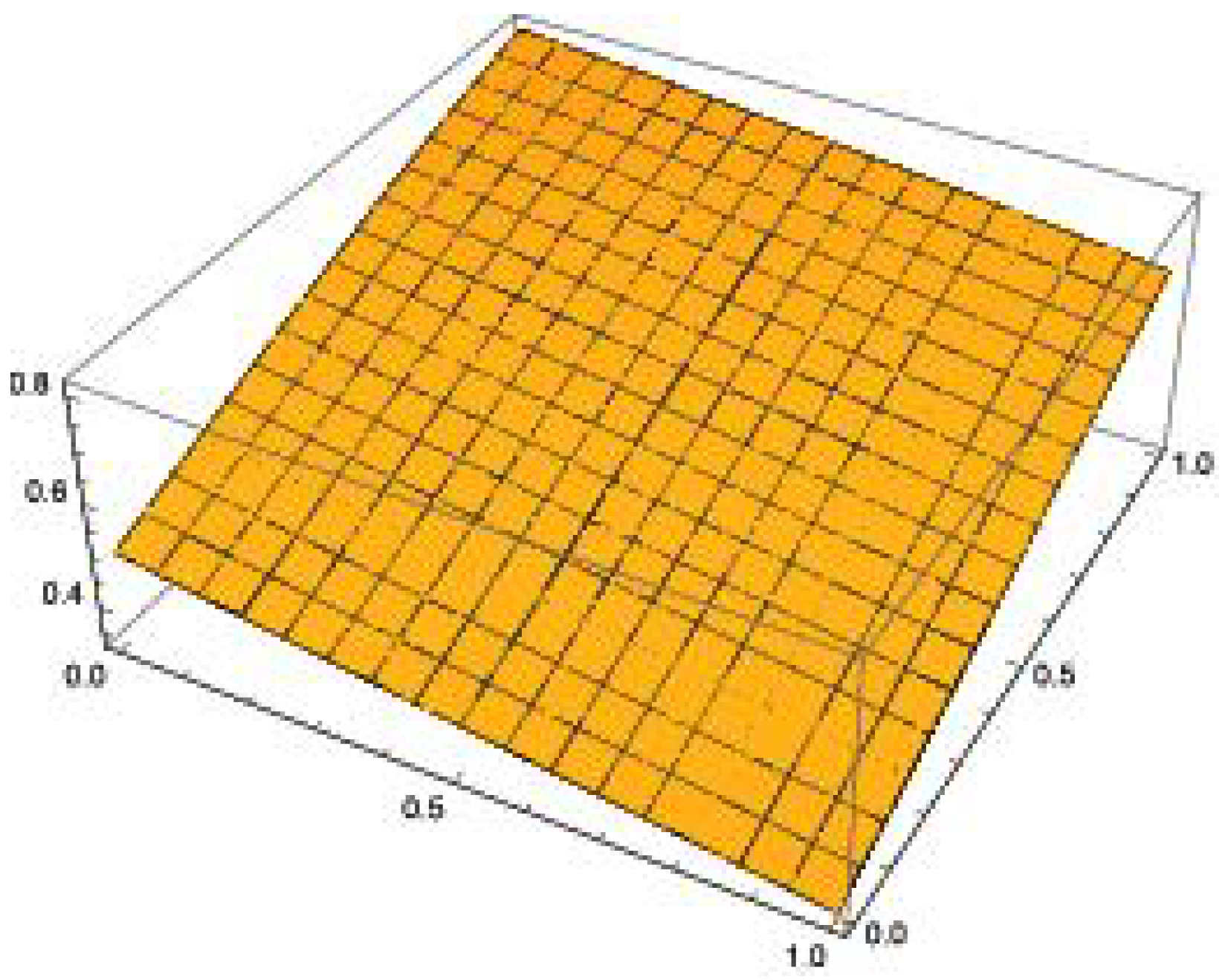
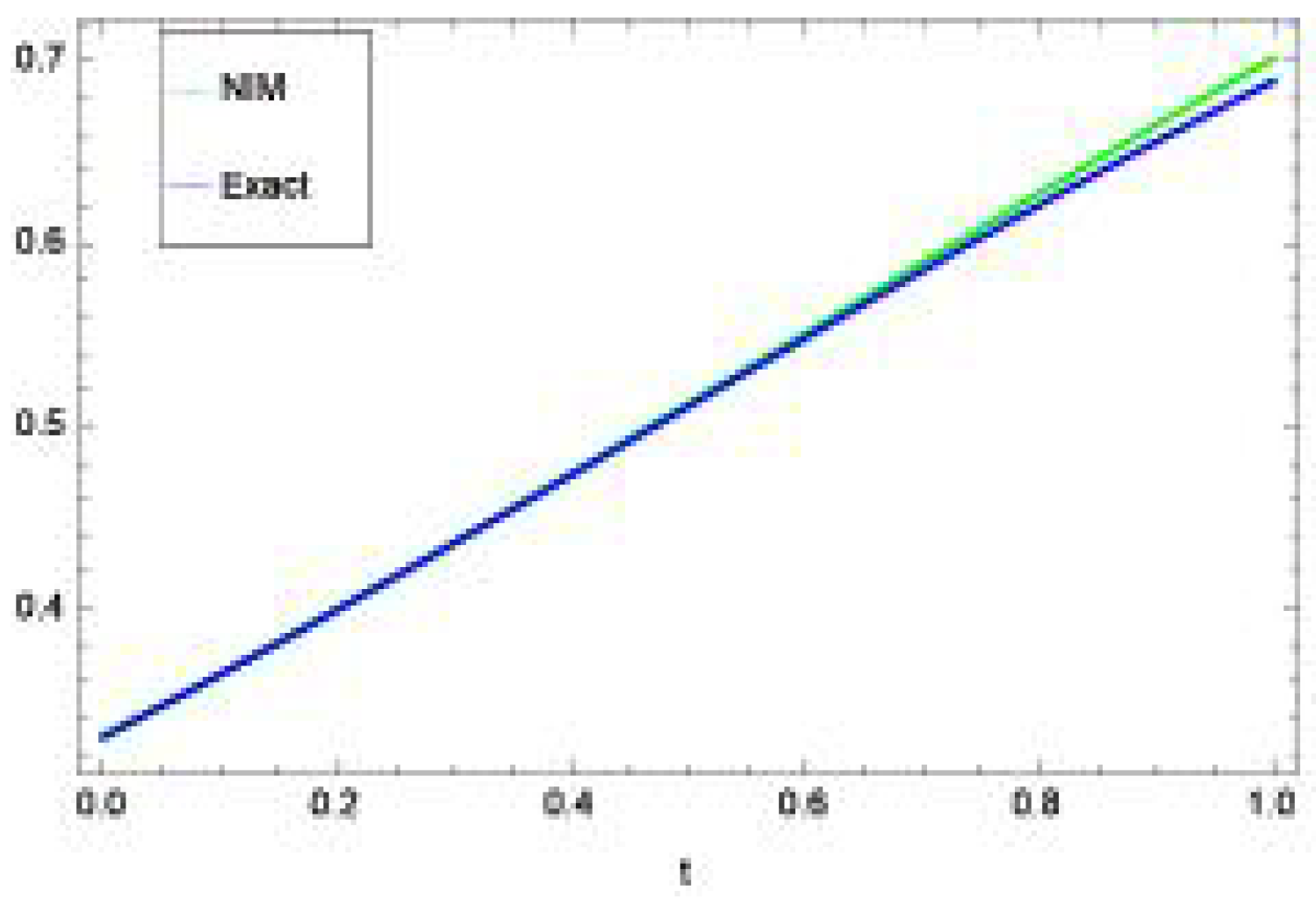
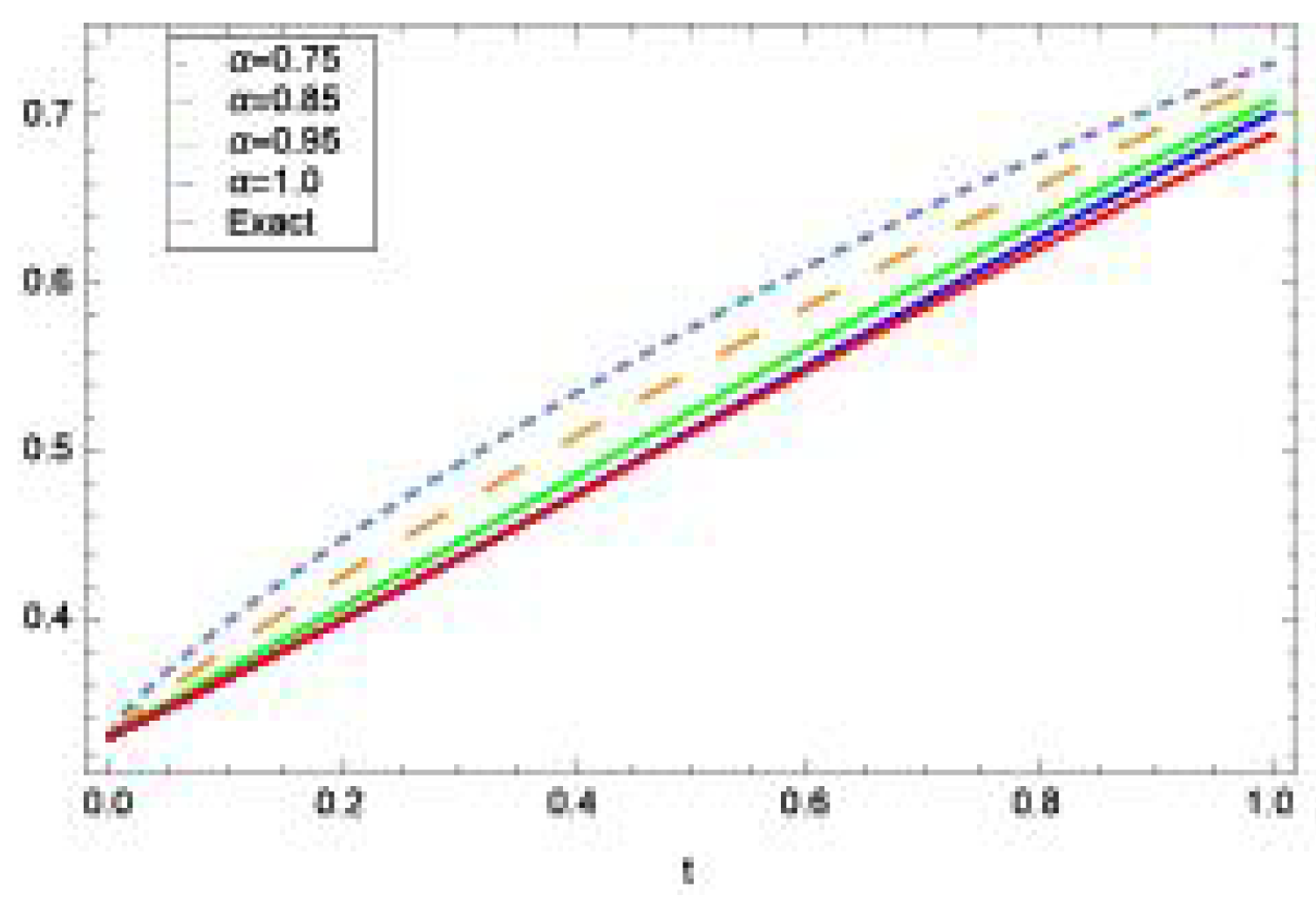
4. Numerical Implementation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baleanu, D.; Guvenc, Z.B.; Machado, J.T. (Eds.) New Trends in Nanotechnology and Fractional Calculus Applications; Springer: New York, NY, USA, 2010; p. C397. [Google Scholar]
- Caponetto, R. Fractional Order Systems: Modeling and Control Applications; World Scientific: Singapore, 2010; Volume 72. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Wazwaz, A.M. First Course In Integral Equations, A; World Scientific Publishing Company: Singapore, 2015. [Google Scholar]
- Shah, R.; Khan, H.; Baleanu, D.; Kumam, P.; Arif, M. A novel method for the analytical solution of fractional Zakharov-Kuznetsov equations. Adv. Differ. Equ. 2019, 2019, 517. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Helal, M.A.; Mehanna, M.S. A comparative study between two different methods for solving the general Korteweg-de Vries equation (GKdV). Chaos Solitons Fractals 2007, 33, 725–739. [Google Scholar] [CrossRef]
- Jibran, M.; Nawaz, R.; Khan, A.; Afzal, S. Iterative solutions of Hirota Satsuma coupled KDV and modified coupled KDV systems. Math. Probl. Eng. 2018, 2018, 9042039. [Google Scholar] [CrossRef]
- Yasar, E.; Giresunlu, I.B. The (G′/G,1/G)-expansion method for solving nonlinear space-time fractional differential equations. Pramana 2016, 87, 17. [Google Scholar] [CrossRef]
- Esen, A.L.A.A.T.T.I.N.; Yagmurlu, N.M.; Tasbozan, O. Approximate analytical solution to time-fractional damped Burger and Cahn-Allen equations. Appl. Math. Inf. Sci. 2013, 7, 1951. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H.; Tajadodi, H.; Baleanu, D. Application of a homogeneous balance method to exact solutions of nonlinear fractional evolution equations. J. Comput. Nonlinear Dyn. 2014, 9, 021019-1. [Google Scholar] [CrossRef]
- Hariharan, G.; Kannan, K. Haar wavelet method for solving Cahn-Allen equation. Appl. Math. Sci. 2009, 3, 2523–2533. [Google Scholar]
- Tascan, F.; Bekir, A. Travelling wave solutions of the Cahn-Allen equation by using first integral method. Appl. Math. Comput. 2009, 207, 279–282. [Google Scholar]
- Tariq, H.; Akram, G. New traveling wave exact and approximate solutions for the nonlinear Cahn-Allen equation: Evolution of a nonconserved quantity. Nonlinear Dyn. 2017, 88, 581–594. [Google Scholar] [CrossRef]
- Bekir, A. Multisoliton solutions to Cahn-Allen equation using double exp-function method. Phys. Wave Phenom. 2012, 20, 118–121. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A.; Cevikel, A.C. A variety of exact solutions for the time fractional Cahn-Allen equation. Eur. Phys. J. Plus 2015, 130, 1–13. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H. Iterative Methods for Solving System of Fractional Differential Equations. Ph.D. Thesis, Pune University, Pune, India, 2006. [Google Scholar]
- Jafari, H.; Nazari, M.; Baleanu, D.; Khalique, C.M. A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 2013, 66, 838–843. [Google Scholar] [CrossRef]
- Ramadan, M.A.; Al-luhaibi, M.S. New iterative method for solving the fornberg-whitham equation and comparison with homotopy perturbation transform method. J. Adv. Math. Comput. Sci. 2014, 4, 1213–1227. [Google Scholar] [CrossRef]
- Prakash, A.; Kumar, M.; Baleanu, D. A new iterative technique for a fractional model of nonlinear Zakharov-Kuznetsov equations via Sumudu transform. Appl. Math. Comput. 2018, 334, 30–40. [Google Scholar] [CrossRef]
- Yan, L. Numerical solutions of fractional Fokker-Planck equations using iterative Laplace transform method. In Abstract and Applied Analysis; Hindawi: London, UK, 2013; Volume 2013. [Google Scholar]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Alshikh, A.A.; Mahgob, M.M.A. A comparative study between Laplace transform and two new integrals “Elzaki” transform and “Aboodh” transform. Pure Appl. Math. J. 2016, 5, 145–150. [Google Scholar] [CrossRef] [Green Version]
- Elzaki, T.M.; Alkhateeb, S.A. Modification of Sumudu transform “Elzaki transform” and Adomian decomposition method. Appl. Math. Sci. 2015, 9, 603–611. [Google Scholar] [CrossRef]
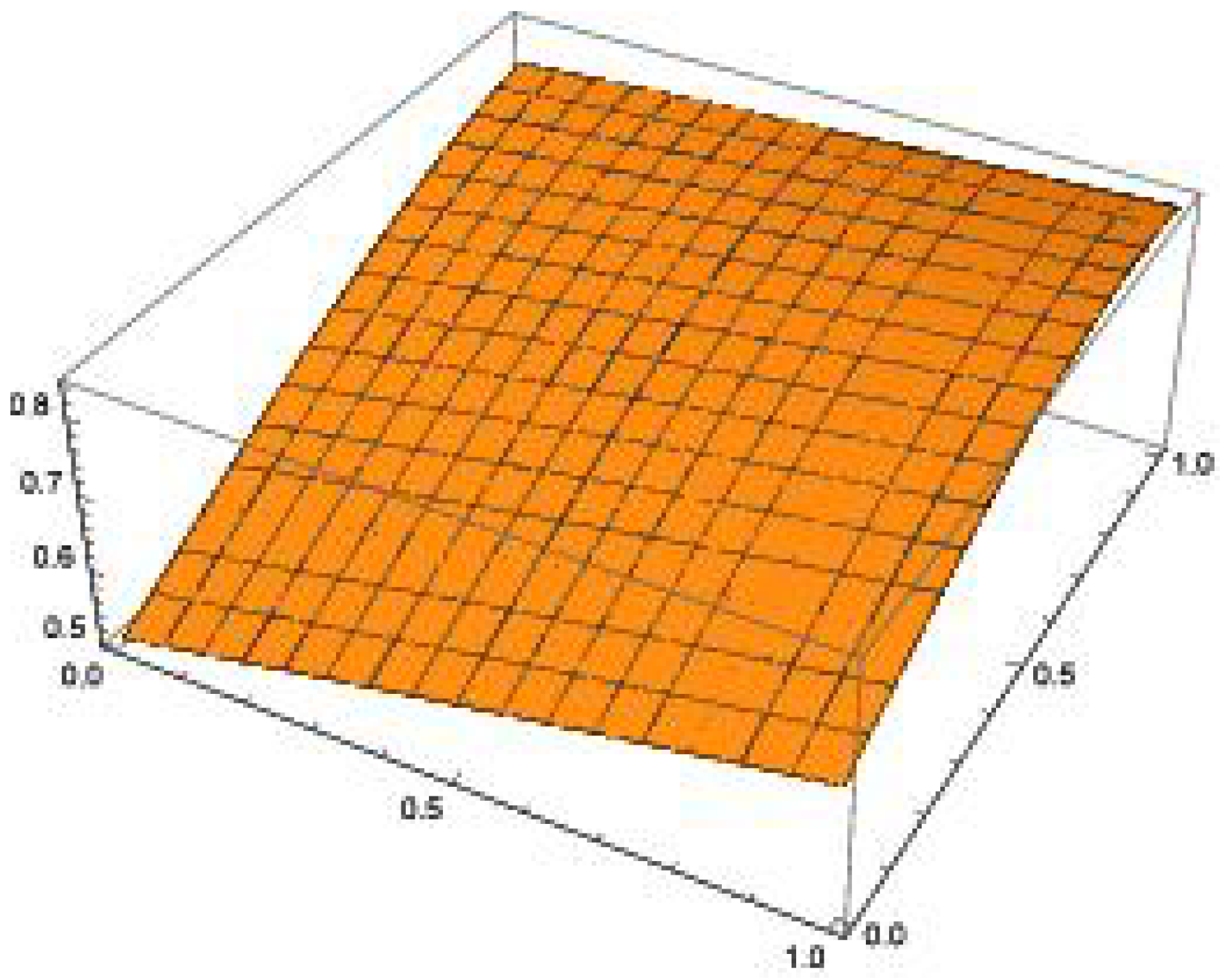
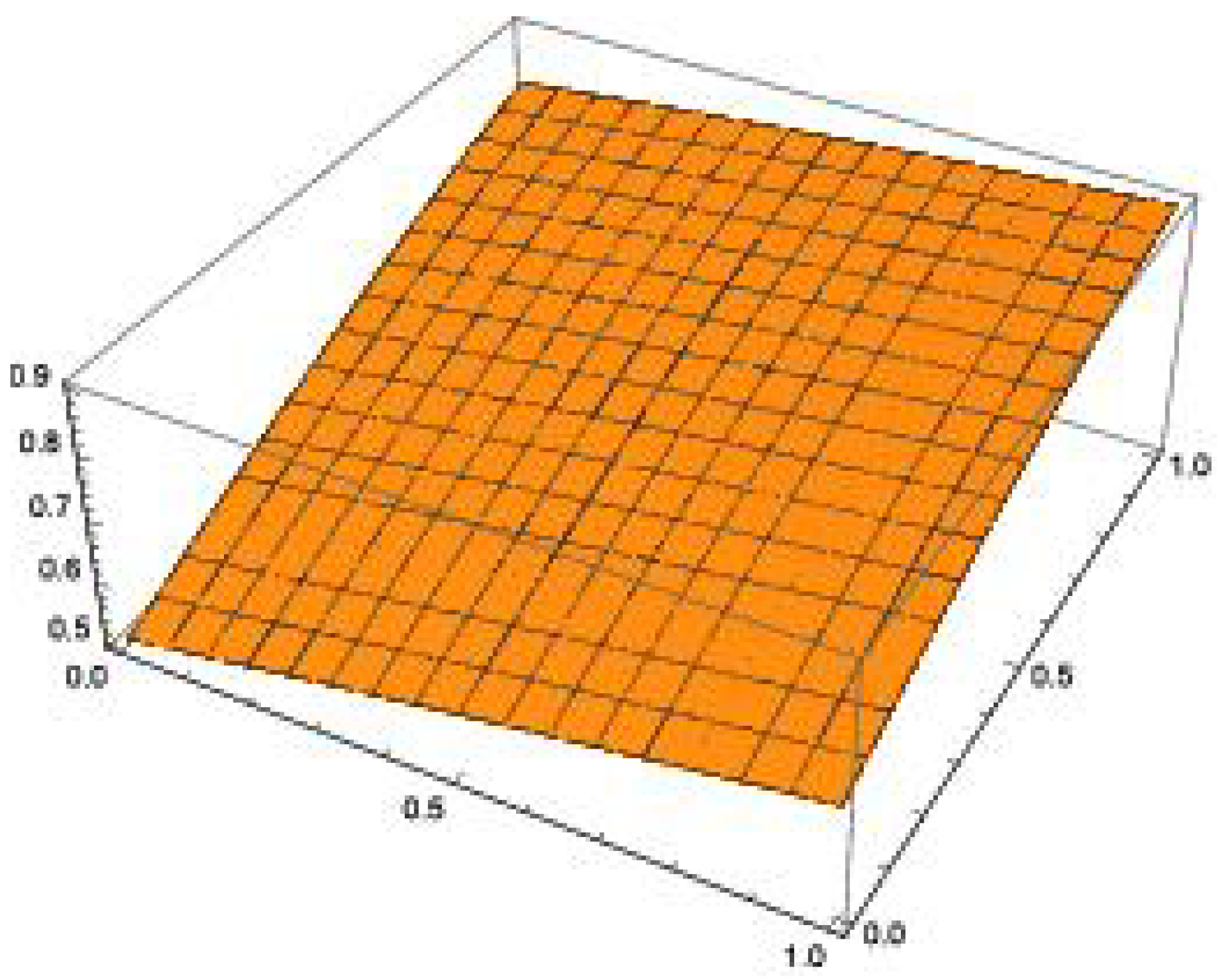
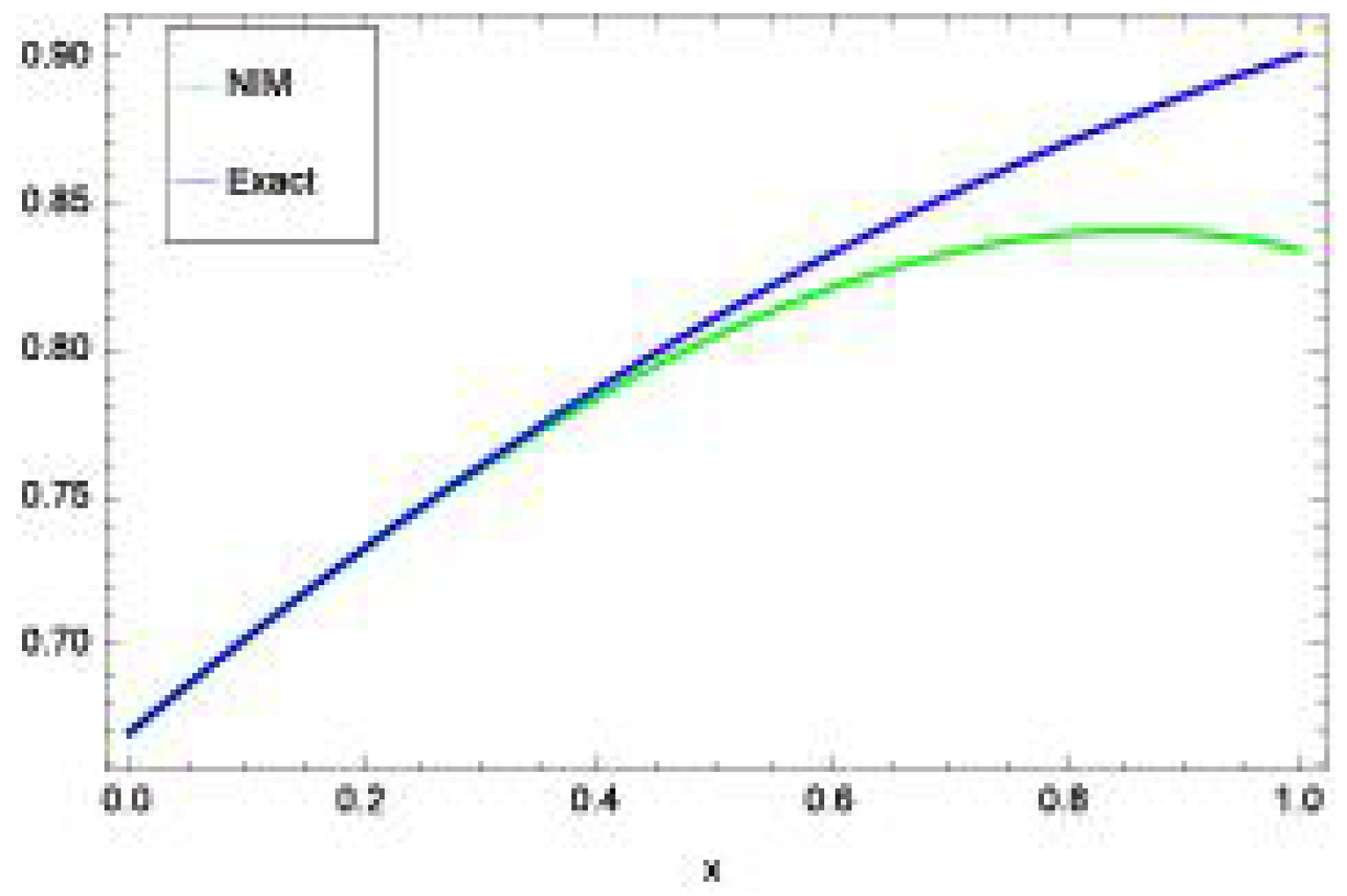

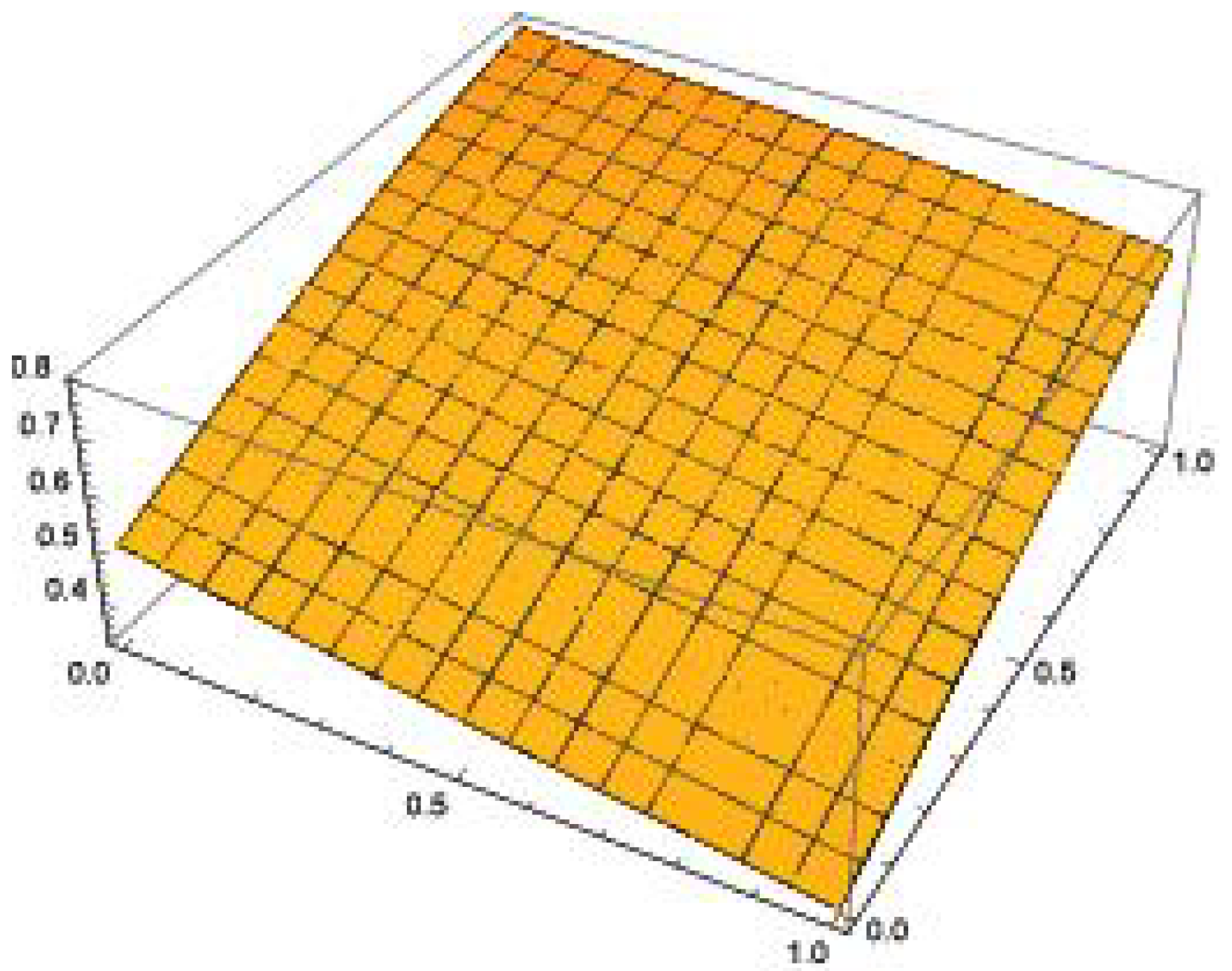
| Exact | HPM | NITM | |||
|---|---|---|---|---|---|
| 0.001 | 1 | 0.670093 | 0.670093 | 1.0 × | 3.3 × |
| 0.002 | 1 | 0.670425 | 0.670425 | 1.0 × | 2.6 × |
| 0.003 | 1 | 0.670756 | 0.670756 | 9.0 × | 8.9 × |
| 0.004 | 1 | 0.671087 | 0.671087 | 2.5 × | 2.1 × |
| 0.005 | 1 | 0.671418 | 0.671418 | 4.7 × | 4.1 × |
| 0.006 | 1 | 0.671749 | 0.671749 | 8.6 × | 7.1 × |
| 0.007 | 1 | 0.67208 | 0.67208 | 1.3 × | 1.1 × |
| 0.008 | 1 | 0.67241 | 0.67241 | 2.0 × | 1.7 × |
| 0.009 | 1 | 0.672741 | 0.672741 | 2.9 × | 2.4 × |
| 0.01 | 1 | 0.673071 | 0.673071 | 4.0 × | 3.3 × |
| Exact | HPM | NITM | |||
|---|---|---|---|---|---|
| 0.001 | 1 | 0.33057 | 0.33057 | 7.6 × | 4.3 × |
| 0.002 | 1 | 0.330902 | 0.330902 | 3.8 × | 3.5 × |
| 0.003 | 1 | 0.331235 | 0.331235 | 1.1 × | 1.1 × |
| 0.004 | 1 | 0.331567 | 0.331567 | 2.6 × | 2.8 × |
| 0.005 | 1 | 0.331899 | 0.331899 | 5.0 × | 5.5 × |
| 0.006 | 1 | 0.332232 | 0.332232 | 9.7 × | 9.6 × |
| 0.007 | 1 | 0.332565 | 0.332565 | 1.5 × | 1.5 × |
| 0.008 | 1 | 0.332898 | 0.332898 | 2.0 × | 2.2 × |
| 0.009 | 1 | 0.333231 | 0.333231 | 2.9 × | 2.3 × |
| 0.01 | 1 | 0.333565 | 0.333565 | 4.0 × | 4.5 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, L.; Shah, R.; Weera, W. Fractional View Analysis of Cahn–Allen Equations by New Iterative Transform Method. Fractal Fract. 2022, 6, 293. https://doi.org/10.3390/fractalfract6060293
Ali L, Shah R, Weera W. Fractional View Analysis of Cahn–Allen Equations by New Iterative Transform Method. Fractal and Fractional. 2022; 6(6):293. https://doi.org/10.3390/fractalfract6060293
Chicago/Turabian StyleAli, Liaqat, Rasool Shah, and Wajaree Weera. 2022. "Fractional View Analysis of Cahn–Allen Equations by New Iterative Transform Method" Fractal and Fractional 6, no. 6: 293. https://doi.org/10.3390/fractalfract6060293
APA StyleAli, L., Shah, R., & Weera, W. (2022). Fractional View Analysis of Cahn–Allen Equations by New Iterative Transform Method. Fractal and Fractional, 6(6), 293. https://doi.org/10.3390/fractalfract6060293







