Linearly Implicit High-Order Exponential Integrators Conservative Runge–Kutta Schemes for the Fractional Schrödinger Equation
Abstract
:1. Introduction
2. The GSAV Approach for the NLS Equation
3. Construction of the Energy-Preserving Schemes
3.1. Fourier Pseudo-Spectral Approximation of Spatial Derivatives
3.2. Fully Discrete Energy-Preserving Schemes
- The tanh SAV scheme: In this scheme, we select , where is a positive constant to make not too close to numerically since . Thus, we setand prove that the corresponding scheme can preserve the following discrete energy
- The exponential SAV scheme: The exponential function is a special function that can keep the range constant positive. Thus, we define an exponential scalar auxiliary variableThen, we derive the following discrete energy conservation law
3.3. Fast Solvers for the Proposed Schemes
4. Numerical Experiments
- LI-EI-i (i = 3 or 4): The paper constructs third and fourth order energy-preserving schemes by using the Runge-Kutta methods shown in Table 1.
- LI-4: A fourth order linearly implicit conservative RK method is based on the GSAV approach [40].
- LI-EI-2: A second order linearly-implicit exponential time differencing conservative scheme is developed in Ref. [33].
- FI-EI-4: A fourth order fully-implicit conservative exponential time differencing method is presented in Ref. [32].
4.1. Two Dimension Case
4.2. Three Dimension Case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Laskin, N. Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 2000, 268, 298–305. [Google Scholar] [CrossRef] [Green Version]
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.L.; Huo, Z.H. Global well-posedness for the fractional nonlinear Schrödinger equation. Commun. Partial Differ. Equ. 2010, 36, 247–255. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Xu, Z.Z.; Cai, W.J.; Wang, Y.S. An efficient energy-preserving method for the two-dimensional fractional Schrödinger equation. Appl. Numer. Math. 2021, 165, 232–247. [Google Scholar] [CrossRef]
- Ionescu, A.D.; Pusateri, F. Nonlinear fractional Schrödinger equations in one dimension. J. Funct. Anal. 2014, 266, 139–176. [Google Scholar] [CrossRef]
- Lieb, E.H.; Seiringer, R.; Yngvason, J. A rigorous derivation of the Grossc-Pitaevskii energy functional for a two-dimensional bose gas. Comm. Math. Phys. 2001, 224, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Pitaevskii, V. Vortex lines in an imperfect bose gas. Sov. Phys. J. Exp. Theor. Phys. 1961, 13, 451–454. [Google Scholar]
- Hu, D.D.; Gong, Y.Z.; Wang, Y.S. On convergence of a structure preserving difference scheme for two–dimensional space–fractional nonlinear Schrödinger equation and its fast implementation. Comput. Math. Appl. 2021, 98, 10–23. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. Numerical study of the nonlinear anomalous reaction-subdiffusion process arising in the electroanalytical chemistry. J. Comput. Sci. 2021, 53, 101394. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Z.Z.; Hao, Z.P. A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrödinger equation. SIAM J. Comput. 2014, 36, A2865–A2886. [Google Scholar] [CrossRef]
- Wang, P.D.; Huang, C.M. Structure-preserving numerical methods for the fractional Schrödinger equation. Appl. Numer. Math. 2018, 129, 137–158. [Google Scholar] [CrossRef]
- Wang, Y.; Mei, L.Q.; Li, Q.; Bu, L.L. Split-step spectral Galerkin method for the two-dimensional nonlinear space-fractional Schrödinger equation. Appl. Numer. Math. 2019, 136, 257–278. [Google Scholar] [CrossRef]
- Lim, F.Y.; Bao, W.Z. Numerical methods for computing the ground state of spin-1 Bose-Einstein condensates in a uniform magnetic field. Phys. Rev. E 2008, 78, 066704. [Google Scholar] [CrossRef]
- Wang, Z. Numerical analysis of local discontinuous Galerkin method for the time-fractional fourth-order equation with initial singularity. Fractal. Fract. 2022, 6, 206. [Google Scholar] [CrossRef]
- Ran, M.; Zhang, C. A conservative difference scheme for solving the strongly coupled nonlinear fractional Schrödinger equations. Commun. Nonlinear. Sci. Numer. Simul. 2016, 41, 64–83. [Google Scholar] [CrossRef]
- Wang, P.D.; Huang, C.M. A conservative linearized difference scheme for the nonlinear fractional Schrödinger equation. Numer. Algorithms 2015, 69, 625–641. [Google Scholar] [CrossRef]
- Li, M.; Gu, X.M.; Huang, C.M.; Fei, M.F.; Zhang, G.Y. A fast linearized conservative finite element method for the strongly coupled nonlinear fractional Schrödinger equations. J. Comput. Phys. 2018, 358, 256–282. [Google Scholar] [CrossRef]
- Wang, D.L.; Xiao, A.G.; Yang, W. A linearly implicit conservative difference scheme for the space fractional coupled nonlinear Schrödinger equations. J. Comput. Phys. 2014, 272, 644–655. [Google Scholar] [CrossRef]
- Duo, S.W.; Zhang, Y.Z. Mass-conservative Fourier spectral methods for solving the fractional nonlinear Schrödinger equation. Comput. Math. Appl. 2016, 71, 2257–2271. [Google Scholar]
- Fu, Y.Y.; Hu, D.D.; Wang, Y.S. High-order structure-preserving algorithms for the multi-dimensional fractional nonlinear Schrödinger equation based on the SAV approach. Math. Comput. Simul. 2021, 185, 238–255. [Google Scholar]
- Li, M.; Huang, C.M.; Wang, P.D. Galerkin finite element method for nonlinear fractional Schrödinger equations. Numer. Algorithms 2017, 74, 499–525. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Hamiltonian boundary value methods (energy preserving discrete line integral methods). J. Numer. Anal. Ind. Appl. Math. 2010, 5, 17–37. [Google Scholar]
- Brugnano, L.; Zhang, C.J.; Li, D.F. A class of energy-conserving Hamiltonian boundary value methods for nonlinear Schrödinger equation with wave operator. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 33–49. [Google Scholar] [CrossRef]
- Li, H.C.; Wang, Y.S.; Qin, M.Z. A sixth order averaged vector field method. J. Comput. Math. 2016, 34, 479–498. [Google Scholar] [CrossRef] [Green Version]
- Quispel, G.; McLaren, D. A new class of energy-preserving numerical integration methods. J. Phys. A Math. Theor. 2008, 41, 045206. [Google Scholar] [CrossRef]
- Cui, J.; Wang, Y.S.; Jiang, C.L. Arbitrarily high-order structure-preserving schemes for the Gross-Pitaevskii equation with angular momentum rotation in three dimensions. Comput. Phys. Commun. 2021, 261, 107767. [Google Scholar] [CrossRef]
- Jiang, C.L.; Wang, Y.S.; Gong, Y.Z. Explicit high-order energy-preserving methods for general Hamiltonian partial differential equations. J. Comput. Appl. Math. 2020, 388, 113298. [Google Scholar] [CrossRef]
- Zhang, H.; Qian, X.; Yan, J.; Song, S.H. Highly efficient invariant-conserving explicit Runge-Kutta schemes for nonlinear Hamiltonian differential equations. J. Comput. Phys. 2020, 418, 109598. [Google Scholar] [CrossRef]
- Celledoni, E.; Cohen, D.; Owren, B. Symmetric exponential integrators with an application to the cubic Schrödinger equation. Found. Comput. Math. 2008, 8, 303–317. [Google Scholar] [CrossRef]
- Du, Q.; Ju, L.L.; Li, X.L.; Qiao, Z.H. Maximum principle preserving exponential time differencing schemes for the nonlocal Allen–Cahn equation. SIAM J. Numer. Anal. 2019, 57, 875–898. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.W.; Wu, X.Y. Exponential integrators preserving first integrals or Lyapunov functions for conservative or dissipative systems. SIAM J. Sci. Comput. 2016, 38, A1876–A1895. [Google Scholar] [CrossRef]
- Cui, J.; Xu, Z.Z.; Wang, Y.S.; Jiang, C.L. Mass- and energy-preserving exponential Runge–Kutta methods for the nonlinear Schrödinger equation. Appl. Math. Lett. 2021, 112, 106770. [Google Scholar] [CrossRef]
- Jiang, C.L.; Wang, Y.S.; Cai, W.J. A linearly implicit energy-preserving exponential integrator for the nonlinear Klein-Gordon equation. J. Comput. Phys. 2020, 419, 109690. [Google Scholar] [CrossRef]
- Cai, J.X.; Shen, J. Two classes of linearly implicit local energy-preserving approach for general multi-symplectic Hamiltonian PDEs. J. Comput. Phys. 2019, 401, 108975. [Google Scholar] [CrossRef]
- Cai, W.J.; Jiang, C.L.; Wang, Y.S.; Song, Y.Z. Structure-preserving algorithms for the two-dimensional sine-Gordon equation with Neumann boundary conditions. J. Comput. Phys. 2019, 395, 166–185. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; Xu, J. Convergence and error analysis for the scalar auxiliary variable (SAV) schemes to gradient flows. SIAM J. Numer. Anal. 2018, 56, 2895–2912. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; Xu, J.; Yang, J. The scalar auxiliary variable (SAV) approach for gradient flows. J. Comput. Phys. 2018, 353, 407–416. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, C.; Shen, J. Generalized SAV approaches for gradient systems. J. Comput. Appl. Math. 2021, 394, 113532. [Google Scholar] [CrossRef]
- Liu, Z.G.; Li, X.L. The exponential scalar auxiliary variable (E-SAV) approach for phase field models and its explicit computing. SIAM J. Sci. Comput. 2019, 42, B630–B655. [Google Scholar] [CrossRef]
- Bo, Y.H.; Wang, Y.S.; Cai, W.J. Arbitrary high–order linearly implicit energy–preserving algorithms for hamiltonian PDEs. Numer. Algorithms 2022. [Google Scholar] [CrossRef]
- Lawson, D. Generalized Runge–Kutta processes for stable systems with large Lipschitz constants. SIAM J. Numer. Anal. 1967, 4, 372–380. [Google Scholar] [CrossRef]
- Shen, J.; Xu, J.; Yang, J. A new class of efficient and robust energy stable schemes for gradient flows. SIAM Rev. 2019, 61, 474–506. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.Z.; Zhao, J.; Wang, Q. Arbitrarily high–order linear energy stable schemes for gradient flow models. J. Comput. Phys. 2020, 419, 109610. [Google Scholar] [CrossRef]
- Li, D.F.; Sun, W.W. Linearly implicit and high-order energy-conserving schemes for nonlinear wave equations. J. Sci. Comput. 2020, 83, A3703–A3727. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer Science: London, UK, 2006. [Google Scholar]
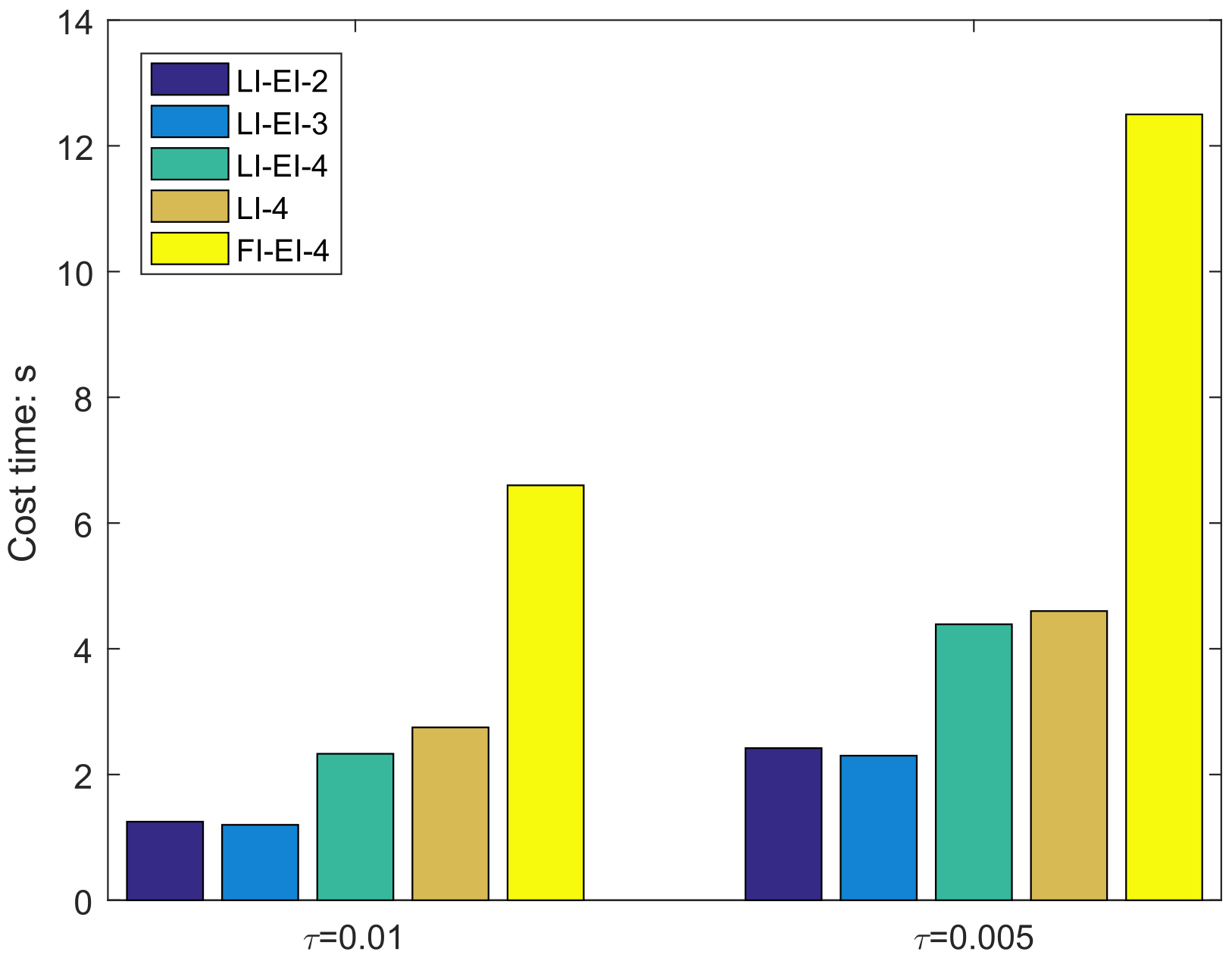
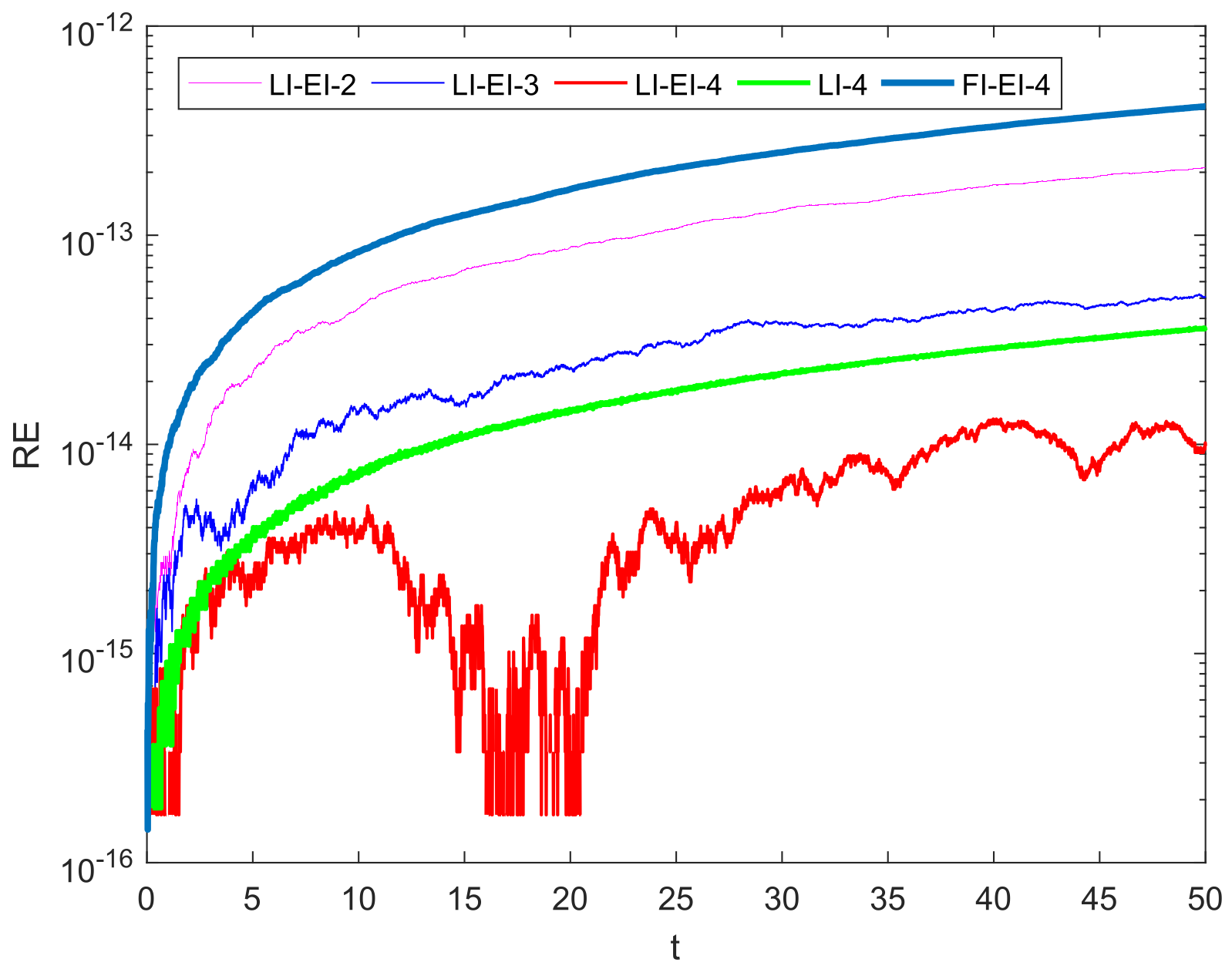
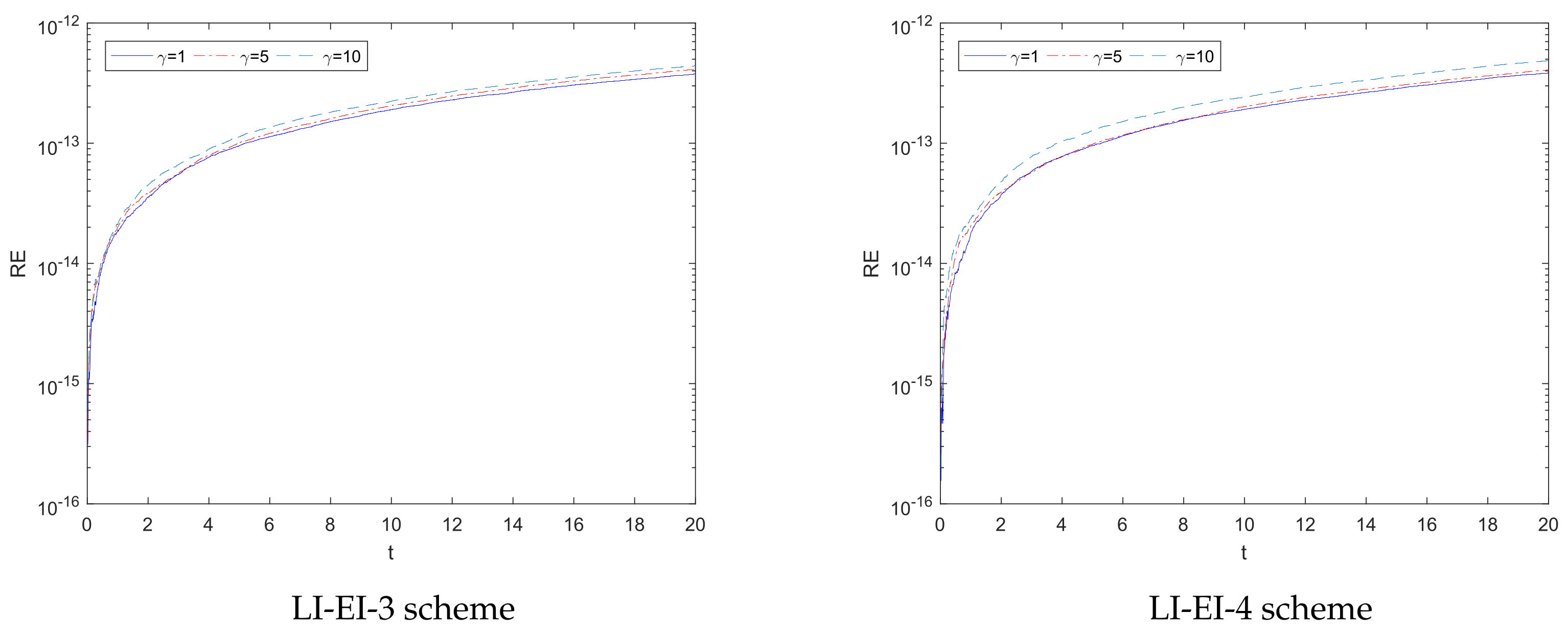
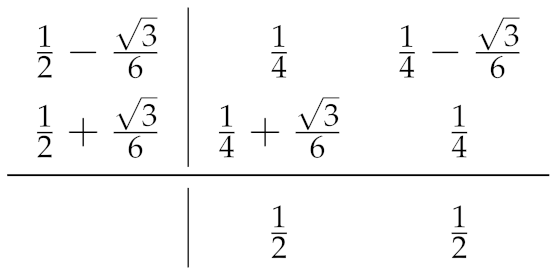 |  |
| Scheme | |||||
|---|---|---|---|---|---|
| LI-EI-2 [33] | 5.7897 × 10 | 1.4276 × 10 | 3.5439 × 10 | 8.8282 × 10 | |
| Rate | * | 2.0198 | 2.0101 | 2.0051 | |
| LI-EI-3 | 1.1578 × 10 | 1.3051 × 10 | 1.6205 × 10 | 2.04488 × 10 | |
| Rate | * | 3.1492 | 3.0096 | 2.9863 | |
| LI-EI-4 | 9.0072 × 10 | 7.1453 × 10 | 4.9858 × 10 | 3.2867 × 10 | |
| Rate | * | 3.6560 | 3.8411 | 3.9231 | |
| LI-4 [40] | NaN | 3.2550 × 10 | 2.0345 × 10 | 1.2529 × 10 | |
| Rate | * | * | 3.9999 | 4.0213 | |
| FI-EI-4 [32] | 8.2450 × 10 | 5.1562 × 10 | 3.2231 × 10 | 2.0145 × 10 | |
| Rate | * | 3.9991 | 3.9997 | 3.9999 |
| Scheme | ||||||
|---|---|---|---|---|---|---|
| LI-EI-3 | 5.2663 × 10 | 6.5894 × 10 | 8.2372 × 10 | 1.0295 × 10 | ||
| Rate | * | 2.9985 | 2.9999 | 3.0001 | ||
| LI-EI-4 | 1.0439 × 10 | 7.1192 × 10 | 4.6417 × 10 | 2.9909 × 10 | ||
| Rate | * | 3.8742 | 3.9389 | 3.9559 | ||
| LI-EI-3 | 3.26618 × 10 | 4.0989 × 10 | 5.1349 × 10 | 6.4260 × 10 | ||
| Rate | * | 2.9942 | 2.9968 | 2.9983 | ||
| LI-EI-4 | 6.5017 × 10 | 4.6648 × 10 | 3.1119 × 10 | 2.0090 × 10 | ||
| Rate | * | 3.8009 | 3.9059 | 3.9532 | ||
| 2 | LI-EI-3 | 5.2780 × 10−3 | 6.5852 × 10 | 8.2299 × 10 | 1.0289 × 10 | |
| Rate | * | 3.0027 | 3.0002 | 2.9997 | ||
| LI-EI-4 | 1.1272 × 10 | 6.6838 × 10 | 4.0734 × 10 | 2.5485 × 10 | ||
| Rate | * | 4.0759 | 4.0363 | 3.9985 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Zheng, Q.; Zhao, Y.; Xu, Z. Linearly Implicit High-Order Exponential Integrators Conservative Runge–Kutta Schemes for the Fractional Schrödinger Equation. Fractal Fract. 2022, 6, 243. https://doi.org/10.3390/fractalfract6050243
Fu Y, Zheng Q, Zhao Y, Xu Z. Linearly Implicit High-Order Exponential Integrators Conservative Runge–Kutta Schemes for the Fractional Schrödinger Equation. Fractal and Fractional. 2022; 6(5):243. https://doi.org/10.3390/fractalfract6050243
Chicago/Turabian StyleFu, Yayun, Qianqian Zheng, Yanmin Zhao, and Zhuangzhi Xu. 2022. "Linearly Implicit High-Order Exponential Integrators Conservative Runge–Kutta Schemes for the Fractional Schrödinger Equation" Fractal and Fractional 6, no. 5: 243. https://doi.org/10.3390/fractalfract6050243
APA StyleFu, Y., Zheng, Q., Zhao, Y., & Xu, Z. (2022). Linearly Implicit High-Order Exponential Integrators Conservative Runge–Kutta Schemes for the Fractional Schrödinger Equation. Fractal and Fractional, 6(5), 243. https://doi.org/10.3390/fractalfract6050243





