On the Equivalence between Integer- and Fractional Order-Models of Continuous-Time and Discrete-Time ARMA Systems

Abstract

The equivalence of continuous-/discrete-time autoregressive-moving average (ARMA) systems is considered in this paper. For the integer-order cases, the interrelations between systems defined by continuous-time (CT) differential and discrete-time (DT) difference equations are found, leading to formulae relating partial fractions of the continuous and discrete transfer functions. Simple transformations are presented to allow interconversions between both systems, recovering formulae obtained with the impulse invariant method. These transformations are also used to formulate a covariance equivalence. The spectral correspondence implied by the bilinear (Tustin) transformation is used to study the equivalence between the two types of systems. The general fractional CT/DT ARMA systems are also studied by considering two DT differential fractional autoregressive-moving average (FARMA) systems based on the nabla/delta and bilinear derivatives. The interrelations CT/DT are also considered, paying special attention to the systems defined by the bilinear derivatives.

1. Introduction

A system is a combination of components acting together to fulfill a certain objective. During many years, such components were physical objects that could have a mathematical representation called a (mathematical) model. For example, the differential equation

$${\displaystyle \frac{y(t)}{dt}}+ay(t)=x(t),t\in \mathbb{R},$$

is the model for an RC lowpass circuit or for the speed of a falling body. In our daily lives and in nature, we find many examples of such kinds of systems. However, since the 1980s, in the last century, things changed with the development introduced by signal processing and the dissemination of the micro-processor use that allowed the implementation, in real time, of mathematical algorithms, leading to the substitution of hardware-based systems by software-based equivalents. The most common example is represented by the mobile phone. Therefore, the model became itself a system, and currently, we use interchangeably the designations “model” and “system”, when referring to a mathematical representation or its computational implementation. In the following, we use “system” with this enlarged meaning and, sometimes, substitute it by “model”.

Mathematically, a system is defined as an application in the set of signals, that is a transformation of a signal, $x(t)$, into another one, $y(t)$. Let $T[.]$ be an operator that symbolically represents such a transformation,

$$y(t)=T[x(t)]$$

(1)

$x(t)$ is the input or excitation, and $y(t)$ is the output or response.

A system is linear if it is formally represented by a linear operator [1,2,3]. This means that it satisfies the properties of additivity and homogeneity (superposition principle).

$$\begin{array}{cc}\hfill y(t)& =T[a_1{x}_1(t)+a_2{x}_2(t)]\hfill \\ \hfill & =a_{1}T[x_1(t)]+a_{2}T[x_2(t)]\hfill \\ \hfill & =a_1{y}_1(t)+a_2{y}_2(t).\hfill \end{array}$$

(2)

Although linear systems are mere approximations to the real systems, they are very useful and deserve a deep study. Hence, while linear systems may assume different forms, the most interesting are the ones represented by pole-zero or autoregressive-moving average models. The designation system will be attached to this particular class.

In this paper, we discuss the equivalence between continuous- and discrete-time invariant linear systems. It is a long-standing subject, since in engineering applications, we interchange continuous and discrete domains very frequently. We designed discrete-time systems by applying well-known continuous-time procedures and used s to z conversions. Similarly, we need to find continuous-time models from discrete-time measurements. Therefore, it is important to state the equivalence of both types of systems. We present first a new formulation based on the equality of input and output signals taken at the instants $t_n=nT,n\in \mathbf{Z}$. Based on this formulation, we deduced a set of formulae allowing the s to z and reverse conversions. It is shown that there is a one-to-one correspondence between the original and image poles, but not of zeroes. This methodology was applied to the covariance-based equivalence. Both equivalences were compared. We studied also an approximate correspondence stated by the bilinear transformation.

In addition, while not dismissing the estimation aspects and corresponding methodologies, we are mainly interested in finding deterministic relationships between the structures of both systems. We propose a new methodology similar to the well-known invariant response methods [4], but with wider generality. The most common are the impulse invariant, the step invariant, and the ramp invariant, although the first has greater use. We must note, however, that they give different transformation rules. In [5], a methodology based on the autocorrelation of the impulse response was proposed, leading to formulae similar to those we will deduce here.

Essentially, we formulated an equivalence principle between continuous- and discrete-time systems based on the equality of input and output signals taken at the instants $t_n=nT,n\in \mathbf{Z}$. It is important to mention that we did not fix any particular input signal; we can use any signal in agreement with the statements in Section 2.3. On the other hand, the algorithm is valid even if the system at hand is not minimum phase. Based on the proposed formulation, we obtained a set of formulae allowing the s to z conversion of partial fractions. Another set was obtained for the reverse conversion. It is shown that there is a one-to-one correspondence between the original and converted poles, but not necessarily of the zeroes. However, we can go in a one-to-one way from the original continuous transfer function (TF) to the discrete and back, allowing us to compute the parameters of the continuous-time system from the discrete-time TF. This is possible because the identification of discrete-time systems is a well-established theme with many algorithms [6,7,8,9].

The above-described framework is mainly interesting in integer-order cases. When we move into the fractional-order (FARMA) cases, the situation is slightly different: the equivalence between continuous- and discrete-time systems based on the equality of input and output signals is not easy to handle. We adopted the spectral correspondence that states an approximation of the frequency responses in the interval $[-\frac{\pi }{T},\frac{\pi }{T}].$ This was achieved through two fractional discrete-time FARMA models [10,11,12]. One is based on the classic Euler s to z conversion, while the second uses the bilinear (Tustin) transformation. Our interest is mainly directed to the latter, since it is more general and allows a one-to-one correspondence between the s and z planes.

The paper is organized as follows. In Section 2, we introduce the integer-order ARMA models by their differential and difference equations, which are used to define the problem we want to solve together with the signal framework. The notion of equivalence continuous/discrete is also introduced. In Section 3, we perform a study of the integer-order continuous-time ARMA models by performing a revision of the main concepts and the sampling problem and obtain a continuous-time difference equation, which leads to the classic discrete-time analogue, which states the equivalence between the CT and DT systems. The results we obtained were applied to the conversion of a partial fraction. This leads to two sets of rules for transforming partial fractions for s to z and z to s. In Section 4, we describe the covariance equivalence. The bilinear-transformation-based correspondence is studied in Section 5. Section 6 is reserved for the study of the conversion between the CT and DT fractional systems. The Euler- and Tustin-type systems are considered. Since the Tustin one is more general, we dedicate more attention to it. Finally, we state some conclusions. In the Appendix, we describe some of the conventions we assumed.

Remark 1.

The paper is developed having as a base the following assumptions:

• We work always on the sets of reals, $\mathbb{R}$, and integers, $\mathbb{Z}$.
• All the ARMA systems, continuous-time or discrete-time, are considered as time-invariant, meaning that the corresponding equations are defined by constant parameters.
• We used the bilateral Laplace transform (LT) [13]:

  $$\mathcal{L}[f(t)]=F(s)=\underset{\mathbb{R}}{\int }f(t)e^{-st}\mathrm{d}t,$$

  (3)
  where $f(t)$ is any real or complex function/distribution defined on $\mathbb{R}$ and $F(s)$ is its transform, provided it has a non-void region of convergence (ROC)
• The Fourier transform (FT) is obtained from the LT through the substitution $s=i\omega$ with $\omega \in \mathbb{R}$.
• The standard convolution is given by

  $$f(t)\ast g(t)=\underset{\mathbb{R}}{\int }f(\tau )g(t-\tau )\mathrm{d}\tau .$$

  (4)
• The Z transform (ZT) is defined by

  $$\mathcal{Z}[f(n)]=F(z)=\sum _{n=-\infty }^{\infty }f(n)z^{-n},$$

  (5)
  where $f(n)$ is any discrete-time signal and $z\in \mathbb{C}$.
• With the substitution, $z=e^{i\omega },\left|\omega \right|\le \pi ,$ we obtain the discrete-time Fourier transform.

2. Background

2.1. Classic ARMA Models

The autoregressive-moving average models were introduced in the context of time series analysis and modeling and described by Peter Whittle in 1951 in his PhD thesis. However, after the publication of the book by George E. P. Box and Gwilym Jenkins [6], they became very popular. In the 1970s of the 20th Century, they were adopted as the base for the development of pole-zero models in digital signal processing [2,4,14,15]. Let $x(n)$ and $y(n)$ be two discrete-time signals (time series). The ARMA systems are described by difference equations with the general format

$$\sum _{k=0}^{n_0}{a}_{k}y(n-k)=\sum _{k=0}^{m_0}{b}_{k}x(n-k) n\in \mathbb{Z}$$

(6)

where $n_0$ and $m_0$ are any positive integer numbers that are the system orders and $a_k,b_k,k=0,1,\cdots$ are real parameters. Without loss of generality, $a_0=1$. Currently, we write ARMA ($n_0,m_0$). Meanwhile, similar, but continuous-time, systems were already used in circuit theory, after the works of O. Heaviside, leading to continuous-time signal processing [16,17,18]. These systems are described by differential equations:

$$\sum _{k=0}^{N_0}{A}_k{D}^{k}y(t)=\sum _{k=0}^{M_0}{B}_k{D}^{k}x(t) t\in \mathbb{R}$$

(7)

where $D^k$ means the classic integer k-order derivative and $N_0,M_0$ the orders. The parameters, $A_k,B_k,k=0,1,\cdots$, are considered real numbers. Without loss of generality, we set $A_{N_0}=1$. By an abuse of language, the designation continuous-time (CT) ARMA systems has been also attached to this kind of system [19]. They have had a large number of applications in engineering since a long time ago [17,18,20,21] and have been increasing in their importance in economics and finance [22,23]. Very early in the development of applications, the need for relations between the two types of systems was felt. Many papers dealing with the identification of continuous-time systems from sampled data were published—see, for example, [22,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38], and the references therein. However, almost all deal preferably with estimation problems, discarding mathematical relations between both classes of systems, and did not lead to a general, definite, and clear methodology. There are several interesting schemes allowing us to go from continuous-time to discrete-time systems or reverse, as the well-known “impulse invariance” [4] or the spline sampling/interpolation [39]. However, we want to go further and look for an embedding of a given DT-ARMA system into a continuous-time model [37,40,41]. We present relations that allow the interconversion of CT/DT of systems described by integer-order ARMA models. The introduction of fractional (F) ARMA systems brought new different questions and solutions for the problem, since the fractionalization of DT-ARMA systems of the type (6) is not immediate and leads to systems with fractional delays, but that are not “fractional” in the correct assertion of the word [42]. However, we can introduce DT-ARMA versions of differential systems [3,12] that approximate CT-ARMA systems. We leave the study of these systems for a later section. For now, we will consider integer-order systems only.

Remark 2.

We will assume that the independent variable in (6) and (7) is time, although this is not mandatory, and the systems may not be causal.

2.2. The Problem

There are at least four different approaches that can be applied to the discretization of an integer-order CT-ARMA time-invariant system and that consist of approximating:

• The differential equation by a difference equation;
• The TF by pole-zero mapping techniques;
• The TF by the zero-order hold-equivalence technique;
• The system response by a covariance equivalence technique.

The first approach approximates the CT differential equation describing the system by a difference equation, using one of the three approximation schemes: the forward rectangular rule, the backward rectangular rule, or the trapezoidal rule. The first rule is also known as Euler’s rule, whereas the last sometimes is referred to as Tustin’s rule [18,43]. The second approach finds an equivalent discrete-time system by matching the poles and zeroes of the transfer functions of the two systems [4,25]. In the third approach, the continuous-time excitation of the system is held constant between each pair of sampling instants by assuming a zero-order hold [13]. The continuous-time system is then excited by this input, and the result is a discrete-time output. The discrete-time TF can then be obtained as the ratio between the transforms of the discrete-time input and output. In the last approach, the equivalent discrete-time system is approximated by requiring that the covariance function of the system response for a Gaussian white noise input coincides at all discrete time lags with that of the continuous-time system [44]. The reason why this approach is adopted is that the excitation is unknown, which makes the system response the only information available about the system. Assuming that this response is Gaussian distributed, a covariance equivalent model will thus be exact at all discrete time steps and, as such, be the most accurate approximation approach. It is shown how to convert a covariance equivalent discrete-time stochastic model into a multivariate continuous-system of arbitrary order. This covariance correspondence will be established for a noise-free system.

2.3. Signal Framework

The signals we will use to deal with systems must be chosen with care, so that the results reach the maximum possible generality. We will consider three classes of signals:

• Deterministic signals that we will assume are bounded piecewise continuous or tempered distributions [45]. Besides, they are:

  (a)

  Exponential-order signals that have Laplace or Z transforms.

  In the CT case, these signals are assumed to be synthesized through the Bromwich integral (inverse Laplace transform):

  $$f(t)={\mathcal{L}}^{-1}[F(s)]=\frac{1}{2\pi i}\underset{a-i\infty }{\overset{a+i\infty }{\int }}F(s)e^{st}\mathrm{d}s, t\in \mathbb{R},$$

  (8)

  where $F(s)$ is the LT of $f(t)$, $a\in \mathbb{R}$ is the abscissa of a vertical straight line inside the corresponding region of convergence, and $i=\sqrt{-1}$.

  In the DT case, the signals are obtained with the Cauchy integral, inverse Z transform:

  $$f(n)={\mathcal{Z}}^{-1}[F(z)]=\frac{1}{2\pi i}{\oint }_{c}F(z)z^{n-1}\mathrm{d}z, n\in \mathbb{Z},$$

  (9)

  where $F(z)$ is the ZT and $c\in \mathbb{R}$ is a circle inside the corresponding region of convergence.

  With this class of signals, we can define the TF of a given system.

  (b)

  Signals absolutely or square integrable (summable) that have a Fourier transform. We may include periodic signals.

  These signals are synthesized by the CT and DT inverse Fourier transforms given by:

  $$f(t)={\mathcal{F}}^{-1}[F(i\omega )]=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}F(i\omega )e^{i\omega t}\mathrm{d}\omega , t\in \mathbb{R},$$

  (10)

  where $F(i\omega )$ is the CT Fourier transform of $f(t)$, and

  $$f(n)={\mathcal{F}}^{-1}[F(z)]=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }F(e^{i\omega })e^{i\omega n}\mathrm{d}\omega , n\in \mathbb{Z},$$

  (11)

  where $F(e^{i\omega })$ is the DT Fourier transform.

  With this class of signals, we can obtain the frequency response of any linear system.

• Stochastic processes
  Let $x(t)$, $\left(x(n)\right),$ be a zero-mean, second-order stationary process with the power spectral density function (PSD) $S_x(\omega )$. For each realization of the process, we can introduce a Crámer spectral representation [46] that assumes the form

  $$x(t)={\int }_{-\infty }^{\infty }{e}^{i\omega t}\mathrm{d}X(\omega ), t\in \mathbb{R},$$

  (12)

  in the CT case. Similarly, for the DT case, we have [35,46]

  $$x(n)={\int }_{-\infty }^{\infty }{e}^{i\omega n}\mathrm{d}X(\omega ) n\in \mathbb{Z}.$$

  (13)
  In each case, $X(\omega )$ is an orthogonal stochastic process with $E[\mathrm{d}X(\omega )]=0$ and $E[{\left|\mathrm{d}X(\omega )\right|}^2]=S_x(\omega ).$ The operator $E[(·)]$ stands for the expected value. As in the deterministic case, with this class of signals, we can obtain the frequency response of any linear system. To show it, we insert (12) into (14) and define the frequency response as the FT of the impulse response.

Attending to the fact that a bounded-input–bounded-output (BIBO)-stable system has a frequency response and this one is obtained as a particular limit case of the TF [2,3,18], the results we obtain using deterministic exponential-type signals have a wider validity. These considerations can be extended to the wide-sense-stable systems [47]. Therefore, we will use exponential-type signals in the following.

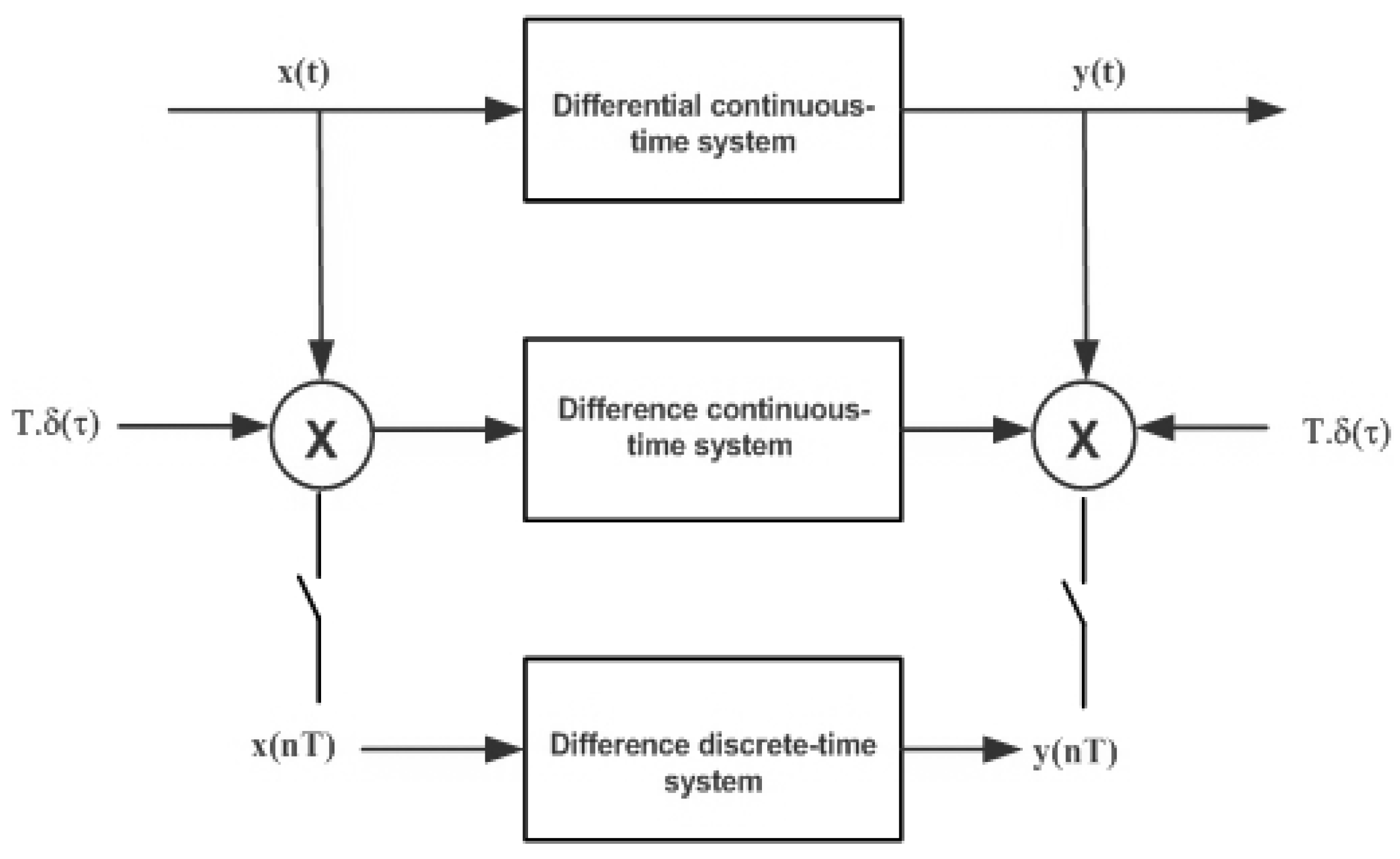
2.4. Equivalent Systems

In Figure 1, we give an illustration of our definition of equivalent systems. Assume that we have a continuous-time system characterized by a given TF, $H_c(s)$. Its input and output are the signals $x(t)$ and $y(t)$, respectively. Sample these signals to obtain the discrete-time signals $x(nT)$ and $y(nT)$. Some questions we can draw are:

• Is there any discrete-time linear system that gives $y(nT)$ as the output when the input is $x(nT)$?
• If it exists, which is its TF, $H_d(z)$?
• Is there any relation between the transfer functions of the continuous- and discrete-time systems?
• Can we use the parameters of the discrete-time system to identify the continuous-time system?

If the answers to these questions are affirmative, we say that both systems are equivalent. Of course, we can invert the sequence of operations: start from discrete-time signals and ask for a continuous-time system relating the corresponding interpolated continuous-time signals. We can formulate the problem as follows. Assume that we have a discrete-time system with TF $H_d(z)$ with input and output signals $x(nT)$ and $y(nT)$, respectively. Let $x_i(t)$ and $y_i(t)$ be continuous-time signals such that $x_i(nT)=x(nT)$ and $y_i(nT)=y(nT)$. As we will see next, we say that they are interpolated functions of $x(nT)$ and $y(nT),$ respectively. We put the questions:

• Is there any continuous-time linear system that relates the interpolated signals $x_i(t)$ and $y_i(t)$?
• If it exists, which is its TF, $H_c(s)$?
• Is there any relation between the transfer functions of the continuous- and discrete-time systems?
• How can we compute the TF $H_c(s)$ from $H_d(z)$?

Again, in the affirmative answers case, we say that the systems are equivalent. More formally, we can introduce the following definition.

Definition 1.

Let $x(t)$ and $y(t)$ be two CT signals and $T>0$ be a sampling interval, and consider the two systems defined by (6) and (7). If

$$\sum _{k=0}^{n_0}{a}_{k}y\left((n-k)T\right)=\sum _{k=0}^{m_0}{b}_{k}x\left((n-k)T\right), n\in \mathbb{Z},$$

and

$$\sum _{k=0}^{N_0}{A}_k{D}^{k}y(t)=\sum _{k=0}^{M_0}{B}_k{D}^{k}x(t), t\in \mathbb{R},$$

we say that the systems are equivalent.

Therefore, the equivalence will imply the existence of relations between the two sets of parameters $\left\{a_k,b_k,k=0,1,\cdots \right\}$ and $\left\{A_k,B_k,k=0,1,\cdots \right\}$. This is the problem that we will solve in several steps in Section 3. In applications, we know one of the sets and intend to compute the other. In this case, the AR and MA orders of the system are known. The transformation rules we will find guarantee that the order of the autoregressive part does not change. The order of the moving average part may change. This is related to the pole preservation of the transformations, which is not extended to the zeroes.

3. From Continuous-Time to Discrete-Time in Integer-Order Systems

3.1. Generalities

Let the CT-ARMA models be defined by the integer-order differential Equation (7). In current applications, we assume that $M\le N$ for stability reasons. Equation (7) defines a shift-invariant system, and so convolutional, implying the input–output relation

$$y(t)=x(t)\ast h(t)={\int }_{-\infty }^{\infty }x(\tau )h(t-\tau )\mathrm{d}\tau ,$$

(14)

where $x(t)$ is the input signal, $y(t)$ the output, and $h(t)$ the impulse response (Green’s function) of the system. From this relation, we can deduce immediately the following result.

Theorem 1.

Eigenfunctions

The particular solution of the differential Equation (7) when $x(t)=e^{st}t\in \mathbf{R},s\in \mathbf{C}$ is given by

$$y(t)=H(s)e^{st}$$

(15)

provided that $H(s)$ exists.

The proof is very simple from (14) [3]. In [47], the singular cases ($H(s)=0$ for some values of s) were treated.

This theorem shows that the exponential is the eigenfunction of any constant coefficient ordinary differential Equation (7). The corresponding eigenvalue, $H(s)$, is the TF of the system defined by the differential equation and is the Laplace transform (LT) of the impulse response.

Inserting (15) into (7), we conclude immediately that

$$H(s)=\frac{B(s)}{A(s)}=\frac{{\displaystyle \sum _{k=0}^{M_0}}{B}_k{s}^k}{{\displaystyle \sum _{k=0}^{N_0}}{A}_k{s}^k},$$

(16)

which can be rewritten as

$$H(s)=\sum _{k=1}^{N_p}{\displaystyle \frac{R_k}{{(s-p_k)}^{n_k}}},$$

(17)

where $N_p$ is the number of distinct poles and the pairs $R_k,n_k,k=1,2,\cdots$ are the residues and pole multiplicities.

Remark 3.

If $N_0=M_0$, $H(s)$ can be decomposed into a sum of a constant and a proper fraction. Therefore, we will consider $N_0>M_0$ in the following.

3.2. Sampling

The comb signal is an important entity in signals and systems theory, because of its connections with Fourier series and ideal sampling. The usual comb is a periodic repetition of the Dirac delta function [17,18,42,43]. Here, we state it in the following format, which will be understood later.

$$c(t)=\sum _{n=-\infty }^{+\infty }\delta (\frac{t}{T}-n),$$

(18)

where T is the sampling interval. As a periodic generalized function, it has an associated Fourier series, as shown in [42,48]:

$$c(t)=\sum _{m=-\infty }^{+\infty }{e}^{im\frac{2\pi }{T}t}.$$

(19)

Its generalized convergence was studied in [42]. Computing the Fourier transform (FT) of this function, we obtain also a periodic comb.

$$FT[\sum _{n=-\infty }^{+\infty }\delta (t-nT)]=\frac{2\pi }{T}\sum _{m=-\infty }^{+\infty }\delta (\omega -m\frac{2\pi }{T}).$$

(20)

The comb is called the ideal sampler because, when multiplying a given function, $x(t)$, by a comb, $c(t)$, it retains the samples of the original function, giving rise to a modulated comb:

$$x_s(t)=x(t)·c(t)=\sum _{n=-\infty }^{+\infty }x(t)\delta (\frac{t}{T}-n)=T\sum _{n=-\infty }^{+\infty }x(nT)\delta (t-nT).$$

(21)

In the third relation, we use two properties of the impulse: $\delta (t/a)=a\delta (t),a>0$ and $f(t)\delta (t-a)=f(a)\delta (t-a)$. If $x(t)$ has a jump at $t=n_{0}T$, we use the half sum of the lateral limits $x(n_{0}T)=\frac{x(n_0{T}^{+})+x(n_0{T}^{-})}{2}$, in agreement with the inverse Laplace and Fourier integrals.

Let $X(s)$ be the LT of $x(t)$. Then, the LT of $x_s(t)$ is, using (19), given by

$$X_s(s)=FT[x(t)·c(t)]=\sum _{m=-\infty }^{+\infty }X(s-im\frac{2\pi }{T}),$$

(22)

stating the well-known phenomenon: sampling in a given domain implies a repetition in the transform domain, meaning that the sampling operation produces a repetition of the transform in parallel with the real axis in strips of width $\frac{2\pi }{T}$. We observe here the reason for including T in (22): the term corresponding to $m=0$ is $X(s)$. The study we performed was based on the Laplace transform, but it can be performed also with the Fourier transform. The former is better, since it allows us to make $X(s)$ equal to the TF or one of its partial fractions.

From Equation (21), we pick the relation

$$x_s(t)=T\sum _{n=-\infty }^{+\infty }x(nT)\delta (t-nT).$$

Using the Laplace transform, we obtain:

$$X_s(s)=T\sum _{n=-\infty }^{+\infty }x(nT)e^{-snT},$$

(23)

that is the discrete-time Laplace transform. With the $z=e^{sT}$ variable change, we obtain the Z-transform. Equating the right-hand side in (23) to the corresponding one in (22), we obtain:

$$T\sum _{n=-\infty }^{+\infty }x(nT)e^{-snT}=\sum _{m=-\infty }^{+\infty }X(s-im\frac{2\pi }{T}),$$

(24)

that is a generalized version of Polya’s formula [49,50] and a consequence of the Poisson summation formula.

Now, we are going to say something about the choice of T. We must have in mind that we may be interested in allowing the recovery of $X(s)$ from $X_s(s)$. We have to impose that $X(s)$ and $X_s(s)$ have the same poles in the strip defined by $\left|Im(s)\right|<\frac{\pi }{T}$. Assume that $X(s)$ has N poles ${\lambda }_i,i=1,2,\cdots ,N$. Then, we must choose T such that $\frac{\pi }{T}>max\left\{|Im({\lambda }_i)|\right\}$. This criterion is based on the poles of the system and does not depend on the input and output bandwidths.

3.3. The “Sampled” System

Returning now back to Equation (7), assume that we sample simultaneously both the input and output to obtain two signals:

$$x_s(t)=x(t)·c(t)=T\sum _{n=-\infty }^{+\infty }x(nT)\delta (t-nT)$$

and

$$y_s(t)=y(t)·c(t)=T\sum _{n=-\infty }^{+\infty }y(nT)\delta (t-nT).$$

We are looking for a new system having an impulse response $h_s(t),$ such that

$$y_s(t)=x_s(t)\ast h_s(t).$$

(25)

Attending to the above reasoning, we can conclude that:

• Using (14),

  $$y(nT)\delta (t-nT)=T{\int }_{-\infty }^{\infty }\sum _{k=-\infty }^{+\infty }x(kT)\delta (\tau -kT)h_s(nT-\tau )\mathrm{d}\tau \delta (t-nT),$$

  and so, there is a relation between $y(nT)$ and $x(nT)$:

  $$y(nT)=T\sum _{k=-\infty }^{+\infty }x(kT)h_s(nT-kT),$$

  (26)

  that is the discrete-time convolution (The factor T may seem useless in several expressions. It serves to give coherence to the formulae and to allow the recovery of the continuous formulation when T goes to zero.).
• Again, from (14), we can write:

  $$y(nT)\delta (t-nT)={\int }_{-\infty }^{\infty }h(nT-\tau )x(\tau )\mathrm{d}\tau \delta (t-nT)$$

  and from the above relation,

  $${\int }_{-\infty }^{\infty }h(nT-\tau )x(\tau )\mathrm{d}\tau =T\sum _{k=-\infty }^{+\infty }x(kT)h_s(nT-kT)$$

  that can be verified if $h_s(t)=h(t)·c(t)$.
• The function $h_s(nT)$ is a discrete-time signal resulting from the sampling of the impulse response of the system (7). Therefore, there is a TF, $H_s(s)$, of the “sampled system” such that $Y_s(s)=H_s(s)X_s(s)$ and given by

  $$H_s(s)=\sum _{m=-\infty }^{+\infty }{H}_c(s-im\frac{2\pi }{T}).$$

  (27)
• The eigenvalue corresponding to the eigenfunction $H_s(s)$ is

  $$\sum _{n=-\infty }^{+\infty }{e}^{nT}\delta (\frac{t}{T}-n).$$

3.4. A Continuous-Time Difference Equation

We are going to look for the time equation corresponding to $H_s(s)$. To do this, return to (17), and note that we can solve our problem by treating each type of partial fraction separately. Therefore, let us begin by considering that our original system is a first-order continuous-time autoregressive (AR) system defined by the TF $H(s)=\frac{1}{s-p}$.

The corresponding $H_s(s)$ function is

$$H_s(s)=\sum _{m=-\infty }^{+\infty }\frac{1}{s-p-im\frac{2\pi }{T}}.$$

The series on the right-hand side can be brought to a closed form. Knowing that $sin(\pi z)$ has zeroes at $z=n\in \mathbb{Z}$ and using the residue theorem, it is not hard to see that [50]

$$\pi {\displaystyle \frac{cos(\pi z)}{sin(\pi z)}}=\sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{z-n}},$$

(28)

and then,

$$\pi {\displaystyle \frac{cosh(\pi z)}{sinh(\pi z)}}=i\sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{iz-n}}=\sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{z+in}}=\sum _{n=-\infty }^{\infty }{\displaystyle \frac{1}{z-in}}.$$

(29)

As

$$\sum _{m=-\infty }^{+\infty }\frac{1}{s-p-im\frac{2\pi }{T}}=\frac{T}{2\pi }\sum _{m=-\infty }^{+\infty }\frac{1}{T\frac{s-p}{2\pi }-im},$$

putting $w=T\frac{s-p}{2\pi }$ and using Formula (29), we can write

$$\sum _{m=-\infty }^{+\infty }\frac{1}{s-p-im\frac{2\pi }{T}}=\frac{T}{2}\frac{1+e^{-(s-p)T}}{1-e^{-(s-p)T}}.$$

(30)

We can generalize this result for high-order partial fractions, by repeated derivative computation, so that we obtain successively

$$\sum _{m=-\infty }^{+\infty }\frac{1}{{(s-p-im\frac{2\pi }{T})}^2}=T^2\frac{e^{-(s-p)T}}{{(1-e^{-(s-p)T})}^2},$$

(31)

$$\sum _{m=-\infty }^{+\infty }\frac{2}{{(s-p-im\frac{2\pi }{T})}^3}=T^3\frac{e^{-(s-p)T}\left(1+e^{-(s-p)T}\right)}{{(1-e^{-(s-p)T})}^3}.$$

(32)

These relations show how the partial fractions of orders $1,2$, and 3 are converted and are exactly the ones obtained with the impulse invariant method. We do not continue here, but we will return to the subject to obtain a general formula by induction. With the above relations, we can obtain the sampled version of a given TF. We only have to obtain its partial fraction decomposition and convert each fraction. For now, and only by simplification, we will assume frequently transfer functions that are proper fractions with only order-one poles. We do not need to say anything about the orders of the zeros. Therefore, we assume that $N_0>M_0$ in (7), leading to

$$H(s)=\sum _{j=1}^{N_0}\frac{R_j}{s-{\lambda }_j}$$

(33)

As $N_0>M_0$, ${\sum }_{j=1}^{N_0}{R}_j=0$ and, from (30)

$$H_s(s)=T\sum _{j=1}^{N_0}\frac{R_j}{1-e^{{\lambda }_{j}T}{e}^{-sT}}$$

(34)

Example 1.

Consider the TF:

$$H_c(s)=\frac{1}{(s+1)(s+2)}=\frac{1}{s+1}-\frac{1}{s+2}.$$

It is transformed into

$$H_s(s)=T\frac{(e^{-T}-e^{-2T})e^{-sT}}{(1-e^{-T}{e}^{-sT})(1-e^{-2T}{e}^{-sT})}.$$

Example 2.

Similarly, the TF

$$H_c(s)=\frac{s-3}{(s+1)(s+2)}=\frac{-4}{s+1}+\frac{5}{s+2}$$

is transformed into

$$H_s(s)=T\frac{1+(4e^{-2T}-5e^{-T})e^{-sT}}{(1-e^{-T}{e}^{-sT})(1-e^{-2T}{e}^{-sT})}.$$

Example 3.

Consider the TF that has a pole in the right-hand half plane.

$$H_c(s)=\frac{1}{(s+1)(s-1)(s+2)}=\frac{-\frac{1}{2}}{s+1}+\frac{\frac{1}{6}}{s-1}+\frac{\frac{1}{3}}{s+2}.$$

It is transformed into

$$H_s(s)=T\frac{(\frac{1}{6}{e}^T-\frac{1}{2}{e}^{-T}+\frac{1}{3}{e}^{-2T})e^{-sT}+(\frac{1}{3}-\frac{1}{2}{e}^{-T}+\frac{1}{6}{e}^{-3T})e^{-2sT}}{(1-e^{-T}{e}^{-sT})(1-e^T{e}^{-sT})(1-e^{-2T}{e}^{-sT})}.$$

If any multiple pole is involved, the transformation is similar provided that we use the relations (31) or (32).

Example 4.

Consider the TF:

$$H_c(s)=\frac{1}{{(s+1)}^2(s+2)}=\frac{1}{{(s+1)}^2}-\frac{1}{s+1}+\frac{1}{s+2}.$$

The summation of the residues corresponding to the order-one fractions is zero. We have then

$$H_s(s)=\frac{-T^2{e}^{-T}{e}^{-sT}}{{(1-e^{-T}{e}^{-sT})}^2}-\frac{T}{1-e^{-T}{e}^{-sT}}+\frac{T}{1-e^{-2T}{e}^{-sT}},$$

$$H_s(s)=T\frac{(-T-1+e^{-T})e^{-T}{e}^{-sT}+(1+T{e}^{-T}+e^{-T})e^{-2T}{e}^{-2sT}}{{(1-e^{-T}{e}^{-sT})}^2(1-e^{-2T}{e}^{-sT})}.$$

The above results show that:

Theorem 2.

Given a TF with the format

$$H_c(s)=H_0\frac{{\displaystyle \prod _{k=1}^{M_0}}(s-{\vartheta }_k)}{{\displaystyle \prod _{k=1}^{N_0}}(s-{\lambda }_k)},$$

(35)

it is transformed into

$$H_s(s)=H_0\frac{{\displaystyle \prod _{k=1}^{K_0}}(1-e^{{\zeta }_k}{e}^{-sT})}{{\displaystyle \prod _{k=1}^{N_0}}(1-e^{{\lambda }_k}{e}^{-sT})}$$

(36)

where $M_0\le K_0<N_0$. This is achieved through the relations (30) to (32) and their obvious generalizations.

It must be emphasized that, while there is a one-to-one correspondence between the set of the original, ${\lambda }_k,$ and transformed, $e^{{\lambda }_k},$ poles, there is no simple relation between ${\vartheta }_k$ and ${\zeta }_k$.

Corollary 1.

The CT difference equation:

$$\sum _{k=0}^{N_0}{a}_{k}y(t-kT)=\sum _{k=0}^{K_0}{b}_{k}x(t-kT),t \in \mathbb{R}$$

(37)

is equivalent to (7).

To show it, we use (36) to obtain

$$H_s(s)=\frac{{\displaystyle \sum _{k=0}^{K_0}}{b}_k{e}^{-ksT}}{{\displaystyle \sum _{k=0}^{N_0}}{a}_k{e}^{-ksT}}$$

(38)

with $a_0=1$. Using the properties of the Laplace transform, we obtain the corresponding time equation, which allows us to conclude that the sampling operation leads naturally to a difference equation. It is important to remark also that the above equation is defined over the real domain.

3.5. Non-Ideal Sampling and Interpolation

We may wonder about the possibility of using other than the ideal sampling. Consider, for example, the sample, and hold

$${\overline{x}}_s(t)=T\sum _{n=-\infty }^{+\infty }x(nT)p_{\tau }(\frac{t}{T}-n),$$

(39)

where $p_{\tau }(t)$ is a rectangular pulse with amplitude 1 and width $\tau$ and Laplace transform $P_{\tau }(s)$. It is not difficult to conclude that

$${\overline{x}}_s(t)=x_s(t)\ast p_{\tau }(t)$$

and so, the corresponding LT relation gives

$${\overline{X}}_s(s)=X_s(s)P_{\tau }(s).$$

As it is easy to see, the term $P_{\tau }(s)$ will cancel out, since it affects simultaneously the input and output transforms. Therefore, the formula for $H_s(s)$ (27) remains valid.

The inverse of the sampling operation is the reconstruction. The perfect reconstruction only can be achieved in particular situations as it is the band-limited case. In a general framework, we can speak of interpolation instead, in the sense that it is a procedure consisting of obtaining a continuous-time signal that sampled gives the discrete-time signal at hand. The expression in (39) is an interpolation formula provided that $p_{\tau }(t)$ is a continuous-time pulse with support interval, S, having a width inferior to T or satisfying [43]:

$$p(t)=\left\{\begin{array}{cc}1\hfill & t=0\hfill \\ 0\hfill & t=kT,k\in \mathbf{Z}\hfill \end{array}\right.$$

In this case, ${\overline{x}}_s(nT)=x(nT)$.

3.6. Discrete-Time Difference Equations

The time discretization operation leads to the discrete-time counterpart of the original CT-ARMA system. The obtained discrete-time ARMA model is defined by the discrete constant coefficient ordinary difference equations written in the general format stated in (6):

$$\sum _{k=0}^{n_0}{a}_{k}y(n-k)=\sum _{k=0}^{m_0}{b}_{k}x(n-k),$$

where $n\in \mathbf{Z}$. We assume always that behind this equation, there is a real time scale, $t_n=nT$. The sampling interval, $T,$ was omitted because, in general, it is not needed, except in frequency representations.

The relations stated in Formulae (35) to (38) suggest the substitution z for $e^{sT}$ to give the TF, $H_d(z),$ of the discrete-time system:

$$H_d(z)=H_0\frac{{\displaystyle \prod _{k=1}^{K_0}}(1-e^{{\zeta }_k}{z}^{-1})}{{\displaystyle \prod _{k=1}^{N_0}}(1-e^{{\lambda }_k}{z}^{-1})},$$

(40)

where $K_0<N_0$. With a similar substitution for the poles (${\theta }_k=e^{{\zeta }_k}$) and (${\varsigma }_k=e^{{\lambda }_k}$) zeroes, we obtain

$$H_d(z)=H_0\frac{{\displaystyle \prod _{k=1}^{K_0}}(1-{\varsigma }_k{z}^{-1})}{{\displaystyle \prod _{k=1}^{N_0}}(1-{\theta }_k{z}^{-1})}.$$

(41)

From (38), we obtain easily

$$H_d(z)=\frac{{\displaystyle \sum _{k=0}^K}{b}_k{z}^{-k}}{{\displaystyle \sum _{k=0}^N}{a}_k{z}^{-k}}$$

(42)

with $a_0=1$. The referenced substitution transforms the segment $s=i\omega ,\left|\omega \right|<\frac{\pi }{T}$ of the imaginary axis into the unit circle $\left|z\right|=1$. The criterion for choosing T implies that there is no possibility of having a pole at $z=-1$. The left part of strip defined by $Re(s)<0$ and $\left|Im(s)\right|<\frac{\pi }{T}$ is transformed into the unit disk $\left|z\right|<1$.

In summary:

• The pole transformation is one-to-one $p⟶e^{pT}$;
• The stability is preserved;
• The zeros are not preserved, because the new ones depend also on the poles;
• If $N>1$, the sampled ARMA model we obtain has in general $N-1$ zeroes. Attending to (30), the system with only one pole is transformed into a system with also a zero.

As above, the eigenfunctions of difference equations are the discrete exponentials as stated in the following. Starting from the discrete convolution as defined above:

$$x(n)\ast y(n)=T\sum _{k=-\infty }^{\infty }x(k)y(n-k),$$

it is easy to verify that the neutral element of the convolution is the discrete impulse defined by

$$\delta (n)=\left\{\begin{array}{cc}\frac{1}{T}\hfill & n=0\hfill \\ 0\hfill & n\ne 0\hfill \end{array}\right.$$

(43)

The discrete impulse response $h(n)$ is the solution of

$$\sum _{k=0}^N{a}_{k}h(n-k)=\sum _{k=0}^M{b}_k\delta (n-k)$$

and of course, the solution of (6) is the convolution of $x(n)$ with the impulse response

$$y(n)=h(n)\ast x(n).$$

Theorem 3.

The particular solution of the difference Equation (6) when $x(n)=z^n,z\in \mathbf{C}$ is given by

$$y(n)=H(z)z^n$$

(44)

provided that $H(z)$ exists.

This theorem shows that the exponentials are the eigenfunctions of the constant coefficient ordinary difference equations and is a direct result of (15).

From (25), we obtain

$$H_d(z)=\sum _{k=-\infty }^{\infty }h(k)z^{-k}$$

(45)

also called the TF of the system defined by the difference Equation (6) and is the Z transform of the impulse response.

3.7. Conversion Rules For Equivalence

3.7.1. Continuous To Discrete

The results we deduced in Section 3.4 can be recast to formally present conversion rules for obtaining the discrete equivalent for a given continuous-time system. We assume that the starting system has a TF as in (16), but decomposed into partial fractions, eventually with higher orders (17), which we reproduce here:

$$H_c(s)=\sum _{k=1}^{N_0}\frac{R_k}{{(s-p_k)}^{n_k}}$$

Let p be a generic pole, and put $\theta =e^{pT}.$ To obtain the discrete-time TF, we use the results deduced in the previous section to state several substitutions. We start from a system defined as in (7). The sampling procedure led us to a continuous-time system defined by (37). This new system has infinite poles resulting from the periodic repetition implied by the Polya Formula (24). Consider the set of all the horizontal strips in the complex plane:

$$S_j=\left\{s\in \mathbf{C}:\frac{\pi (2j-1)}{T}<Im(s)<\frac{\pi (2j+1)}{T}j\in \mathbf{Z}\right\}.$$

With the variable change $z=e^{sT},$ all the left-hand side parts of the horizontal strips are transformed into the unit disk in the plane of the variable z. If we restrict s to be in the main strip $S_0=\left\{s\in \mathbf{C}:-\frac{\pi }{T}<Im(s)<\frac{\pi }{T}\right\}$, there is a one-to-one relationship between the set $s\in S_0:Re(s)<0$ in the plane of the variable s and the unit circle in the plane of the variable z (see Figure 2). In the following, we will assume that $s\in S_0$ and $z=e^{sT}$.

This allows us to write the following transformations:

• Simple poles:

  $$\frac{1}{s-p}=\frac{T}{2}\frac{1+\theta z^{-1}}{1-\theta z^{-1}}=T[-\frac{1}{2}+\frac{1}{1-\theta z^{-1}}];$$

  (46)
• Double poles:

  $$\frac{1}{{(s-p)}^2}=T^2\frac{\theta z^{-1}}{{(1-\theta z^{-1})}^2}=T^2[-\frac{1}{1-\theta z^{-1}}+\frac{1}{{(1-\theta z^{-1})}^2}];$$

  (47)
• Triple poles:

  $$\begin{array}{cc}\hfill \frac{2}{{(s-p)}^3}=& T^3\frac{\theta z^{-1}(1+\theta z^{-1})}{{(1-\theta z^{-1})}^3}\hfill \\ \hfill =& T^3[\frac{1}{1-\theta z^{-1}}-\frac{3}{{(1-\theta z^{-1})}^2}+\frac{2}{{(1-\theta z^{-1})}^3}];\hfill \end{array}$$

  (48)
• For higher-order poles, we can obtain similar formulae by successive derivation. However, the above expressions suggest a general formulation:

  $$\frac{n!}{{(s-p)}^{n+1}}=T^n\sum _{k=0}^n{(-1)}^k{\gamma }_{(n,k)}\frac{1}{{(1-\theta z^{-1})}^{k+1}}-\frac{T}{2}{\delta }_n,$$

  (49)

  where ${\gamma }_{(n,k)},k=1,2,\cdots ,n$ numbers (see the “On-Line Encyclopedia of Integer Sequences ”: https://oeis.org/, accessed on 28 January 2022) are given by

  $${\gamma }_{(n,k)}=\frac{1}{k}\sum _{l=1}^k{(-1)}^{k-l}\left(kl\right)l^{n}k=1,2,\cdots ,n.$$

  (50)

We can give the above formula a matrix format:

$$\left[\begin{array}{c}1\\ \frac{1/T}{s-p}\\ \frac{1/T^2}{{(s-p)}^2}\\ \frac{2/T^3}{{(s-p)}^3}\\ \frac{6/T^4}{{(s-p)}^4}\\ \frac{24/T^5}{{(s-p)}^5}\\ ⋮\\ \end{array}\right]=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ -\frac{1}{2}& 1& 0& 0& 0& 0\\ 0& -1& 1& 0& 0& 0& \cdots \\ 0& 1& -3& 2& 0& 0& \cdots \\ 0& -1& 7& -12& 6& 0& \cdots \\ 0& 1& -15& 50& -60& 24& \cdots \\ \cdots & & \cdots & & \cdots & \cdots \end{array}\right]\left[\begin{array}{c}1\\ \frac{1}{(1-\theta z^{-1})}\\ \frac{1}{{(1-\theta z^{-1})}^2}\\ \frac{1}{{(1-\theta z^{-1})}^3}\\ \frac{1}{{(1-\theta z^{-1})}^4}\\ \frac{1}{{(1-\theta z^{-1})}^5}\\ ⋮\end{array}\right]$$

(51)

For illustration, we recover the above examples and give the final discrete-time transfer functions

Example 5.

With ${\theta }_1=e^{-T}$ and ${\theta }_2=e^{-2T},$ the TF

$$H_c(s)=\frac{1}{(s+1)(s+2)}=\frac{1}{s+1}-\frac{1}{s+2}$$

is transformed into

$$H_d(z)=T\frac{({\theta }_1-{\theta }_2)z^{-1}}{(1-{\theta }_1{z}^{-1})(1-{\theta }_2{z}^{-1})}.$$

Example 6.

Again, with ${\theta }_1=e^{-T}$ and ${\theta }_2=e^{-2T},$ the TF

$$H_c(s)=\frac{s-3}{(s+1)(s+2)}=\frac{-4}{s+1}+\frac{5}{s+2}$$

is transformed into

$$H_d(z)=T\frac{1+(4{\theta }_2-5{\theta }_1)z^{-1}}{(1-{\theta }_1{z}^{-1})(1-{\theta }_2{z}^{-1})}.$$

Example 7.

Similarly, put ${\theta }_0=e^T$, and use the above variables, so that the TF:

$$H_c(s)=\frac{1}{(s+1)(s-1)(s+2)}=\frac{-\frac{1}{2}}{s+1}+\frac{\frac{1}{6}}{s-1}+\frac{\frac{1}{3}}{s+2}$$

is transformed into

$$H_d(z)=T\frac{(\frac{1}{6}{\theta }_0-\frac{1}{2}{\theta }_1+\frac{1}{3}{\theta }_2)z^{-1}+(\frac{1}{3}-\frac{1}{2}{\theta }_1+\frac{1}{6}{\theta }_1{\theta }_2)z^{-2}}{(1-{\theta }_1{z}^{-1})(1-{\theta }_0{z}^{-1})(1-{\theta }_2{z}^{-1})}.$$

Example 8.

Consider the TF:

$$H_c(s)=\frac{1}{{(s+1)}^2(s+2)}=\frac{1}{{(s+1)}^2}-\frac{1}{s+1}+\frac{1}{s+2}.$$

The summation of the residues corresponding to the order-one fractions is again zero. We have then

$$H_d(z)=\frac{-T^2{\theta }_1{z}^{-1}}{{(1-{\theta }_1{z}^{-1})}^2}-\frac{T}{1-{\theta }_1{z}^{-1}}+\frac{T}{1-{\theta }_2{z}^{-1}}.$$

As it is easy to observe and according to what we said above:

• There is a one-to-one correspondence between the original poles and the poles of the discrete system;
• The stability is preserved, since $Re(p)<0$ gives $\left|\theta \right|<1$;
• The zeros are not preserved. The new zeros depend on the original, but also on the poles. To see this, consider a simple example $H(s)=\frac{s-q}{s-p}=1+\frac{p-q}{s-p}$. The corresponding discrete system is:

  $$H_d(z)=1+(p-q)\frac{T}{2}\frac{1+\theta z^{-1}}{1-\theta z^{-1}}=\frac{2}{(p-q)T+2}\frac{1+\theta \frac{(p-q)T-2}{(p-q)T+2}{z}^{-1}}{1-\theta z^{-1}}.$$

3.7.2. Discrete to Continuous

The above transformations can be inverted to allow the discrete to continuous transformation. Assume a discrete-time ARMA model:

$$H_d(z)=\frac{{\displaystyle \sum _{k=0}^{m_0}}{b}_k{z}^{-k}}{{\displaystyle {\displaystyle \sum _{k=0}^{n_0}}}{a}_k{z}^{-k}}=\sum _{k=1}^{N_p}\frac{R_k}{{(1-{\theta }_k{z}^{-1})}^{n_k}}$$

(52)

with $m_0<n_0$. The $N_p$ poles, ${\theta }_k,k=1,2,\dots ,$ have multiplicities $n_k,k=1,2,\dots ,$ and the parameters $R_k,k=1,2,\dots$ are the corresponding residues. Therefore, we want to convert this system into a continuous-time ARMA system.

As above, we transform each partial fraction according to the rules we will present next. These were obtained from Section 3.7.1 by inversion of the s to z rules:

• Simple poles:

  $$\frac{1}{1-\theta z^{-1}}=\frac{\frac{1}{T}}{s-p}+\frac{1}{2}.$$

  (53)

  If all the poles in (35) have order one, the sum of the residues is null and we can forget the constant term ($\frac{1}{2}$).
• Second order poles

  $$\frac{1}{{(1-\theta z^{-1})}^2}=\frac{1}{2}+\frac{\frac{1}{T}}{s-p}+\frac{\frac{1}{T^2}}{{(s-p)}^2};$$

  (54)
• Third-order poles:

  $$\frac{1}{{(1-\theta z^{-1})}^3}=\frac{1}{2}+\frac{\frac{1}{T}}{s-p}+\frac{\frac{\frac{3}{2}}{T^2}}{{(s-p)}^2}+\frac{\frac{1}{T^3}}{{(s-p)}^3};$$

  (55)
• In the fourth order, we have

  $$\frac{1}{{(1-\theta z^{-1})}^4}=\frac{1}{2}+\frac{\frac{1}{T}}{s-p}+\frac{\frac{11}{6T^2}}{{(s-p)}^2}+\frac{\frac{2}{T^3}}{{(s-p)}^3}+\frac{\frac{1}{T^4}}{{(s-p)}^4};$$

  (56)
• The fifth order is

  $$\frac{1}{{(1-\theta z^{-1})}^5}=\frac{1}{2}+\frac{\frac{1}{T}}{s-p}+\frac{\frac{25}{T^2}}{{(s-p)}^2}+\frac{\frac{25}{12T^3}}{{(s-p)}^3}+\frac{\frac{3}{2T^4}}{{(s-p)}^4}+\frac{\frac{1}{T^5}}{{(s-p)}^5};$$

  (57)
• In a matrix formulation, we can write

  $$\left[\begin{array}{c}1\\ \frac{1}{(1-\theta z^{-1})}\\ \frac{1}{{(1-\theta z^{-1})}^2}\\ \frac{1}{{(1-\theta z^{-1})}^3}\\ \frac{1}{{(1-\theta z^{-1})}^4}\\ \frac{1}{{(1-\theta z^{-1})}^5}\\ ⋮\end{array}\right]=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ \frac{1}{2}& 1& 0& 0& 0& 0& \cdots \\ \frac{1}{2}& 1& 1& 0& 0& 0& \cdots \\ \frac{1}{2}& 1& \frac{3}{2}& 1& 0& 0& \cdots \\ \frac{1}{2}& 1& \frac{11}{6}& 2& 1& 0& \cdots \\ \frac{1}{2}& 1& \frac{25}{12}& \frac{35}{12}& \frac{5}{2}& 1& \cdots \\ \cdots & & \cdots & & \cdots & & \ddots \end{array}\right]\left[\begin{array}{c}1\\ \frac{1/T}{s-p}\\ \frac{1/T^2}{{(s-p)}^2}\\ \frac{2/T^3}{{(s-p)}^3}\\ \frac{6/T^4}{{(s-p)}^4}\\ \frac{24/T^5}{{(s-p)}^5}\\ ⋮\end{array}\right].$$

  (58)
  A general formula remains to be found.

The above relations show that we can imbed a given discrete-time system into a continuous-time one by verifying the equivalence statement we formulated above. As shown in Section 3.5, this is independent of the interpolation method we used.

3.8. Consequences

The above relations have important consequences:

• Identifiability of continuous-time systems:
  We can identify a continuous-time system using the following procedure:

  (a)

  Sample input and output signals;

  (b)

  Compute the impulse response or directly the TF of the equivalent discrete system;

  (c)

  Obtain the partial fraction decomposition of the TF;

  (d)

  Using the conversion formulae, compute the TF of the continuous system;

  (e)

  From the TF, obtain the differential equation.

• Design of discrete-time systems from continuous-time templates:
  The design of continuous-time systems is a very well-studied and established theme with many methods existing, which have led to several templates. With these templates and using the above conversion formulae, we can obtain discrete-time equivalent systems. This procedure is exact and does not require a very small sampling interval.
• Embedding
  We can find always a continuous-time system equivalent to a given discrete-time one.

4. Covariance Equivalence

We return back to Section 3.1 and, in particular, to Equation (14), which we reproduce here:

$$y(t)=h(t)\ast x(t).$$

It is a simple task to write

$$y(t)\ast y(-t)=[h(t)\ast x(t)]\ast [h(-t)\ast x(-t)]=[h(t)\ast h(-t)]\ast [x(t)\ast x(-t)].$$

In engineering applications, the convolution $x(t)\ast x(-t)$ is called autocorrelation, but this may create confusion; we will avoid its use. We are going to consider four special situations:

• Energy signals:
  A signal $x(t)$ is an energy signal or type energy [17] if $E_x=\underset{-\infty }{\overset{+\infty }{\int }}{x}^2(t)\mathrm{d}t<\infty$. In this case, we define the function:

  $$R_x(t)=\underset{-\infty }{\overset{+\infty }{\int }}x(\tau +t)x(\tau )\mathrm{d}\tau ,$$

  such that $E_x=R_x(0)$. We conclude that

  $$R_y(t)=[h(t)\ast h(-t)]\ast R_x(t).$$

  (59)
• Power signals:
  There are signals with infinite energy, but that have finite mean power defined by $P_x=\underset{T⟶\infty }{lim}\frac{1}{2T}\underset{-T}{\overset{+T}{\int }}{x}^2(t)\mathrm{d}t<\infty$. We call them power signals or signals-type power. In this case, we define the function:

  $$R_x(t)=\underset{T⟶\infty }{lim}\frac{1}{2T}\underset{-T}{\overset{+T}{\int }}x(\tau +t)x(\tau )\mathrm{d}\tau$$

  such that $P_x=R_x(0)$. With this function, we reobtain (59).
• Stationary stochastic processes:
  For this case, we could also use the last result, since stationary stochastic processes are power signals. However, we would need to assume that the process was ergodic. Either way, we introduce the autocovariance:

  $$R_x(t)=E[x(\tau +t)x(\tau )]$$

  and obtain (59) again. Here, we can have a problem: the process may have a non-zero average. This is equivalent to including an intercept term [37], $x_0$. According to the results in Section 3.1, when the input is a constant, the corresponding output is given by $H(0)x_0$. For now, we assume that the system does not have a pole at the origin (singular case).
• Non-stationary stochastic processes:
  Consider the more involved situation in which the autocovariance is defined by

  $$R_x(t,\tau )=E[x(\tau +t)x(\tau )].$$
  However, it is not difficult to obtain

  $$R_y(t,\tau )=[h(t)\ast h(-t)]\ast R_x(t,\tau ),$$

  which is similar to (59) and has the same interpretation: there is a new (non-causal) linear system having the TF $G_c(s)=H_c(s)·H_c(-s)$ with input $R_x(t)$ and output $R_y(t),$ verifying the differential equation:

  $$\sum _{k=}^{2N}{\overline{A}}_k{D}^k{R}_y(t)=\sum _{k=0}^{2M}{\overline{B}}_k{D}^k{R}_x(t),$$

  (60)

  where ${\overline{A}}_k={\sum }_{j=0}^N{(-1)}^j{A}_j{A}_{j+k},$ with $k=0,\cdots ,2N$ and ${\overline{B}}_k={\sum }_{j=0}^N{(-1)}^j{B}_j{B}_{j+k}$ with $k=0,\cdots ,2M$.

The impulse response of this system is the two-sided function $g_c(t)=h_c(t)\ast h_c(-t)$.

Starting from the partial fraction decomposition of the TF, we can obtain the corresponding decomposition of the covariance transform. The expression is somewhat involved in the multiple pole case. Therefore, we will present the order-one pole case. From (17),

$$H_c(s)=\sum _{k=1}^N\frac{R_k}{s-{\lambda }_k},$$

we obtain

$$G_c(s)=\sum _{k=1}^N\frac{R_k}{s-{\lambda }_k}·\sum _{m=1}^N\frac{R_m}{-s-{\lambda }_m}={(-1)}^N\sum _{k=1}^N\sum _{m=1}^N\frac{R_k{R}_m}{(s-{\lambda }_k)(s+{\lambda }_m)}$$

If ${\lambda }_k\ne {\lambda }_m\forall k\ne m$, meaning that there are no poles on the imaginary axis, it is a simple task to show that

$$\frac{R_k{R}_m}{(s-{\lambda }_k)(s+{\lambda }_m)}=\frac{\frac{R_k{R}_m}{{\lambda }_m-{\lambda }_k}}{s-{\lambda }_k}+\frac{\frac{R_k{R}_m}{{\lambda }_k-{\lambda }_m}}{s+{\lambda }_m}.$$

Therefore,

$$G_c(s)=\sum _{k=1}^{2N}\frac{{\overline{R}}_k}{s-{\lambda }_k},$$

(61)

with ${\overline{R}}_k={\sum }_{m=1}^N\frac{R_k{R}_m}{{\lambda }_m-{\lambda }_k}$ and ${\lambda }_{N+k}={\lambda }_k,k=1,2,\cdots N$. For the multiple pole case, a similar formula can be obtained, but it seems not to be very interesting for applications. The conversion Formula (51) can now be used to obtain the discrete-time representation of the covariance function. Of course, the discrete to continuous conversion formula is similar.

We are now at the stage of going ahead with the covariance equivalence of ARMA models.

We have to consider two situations:

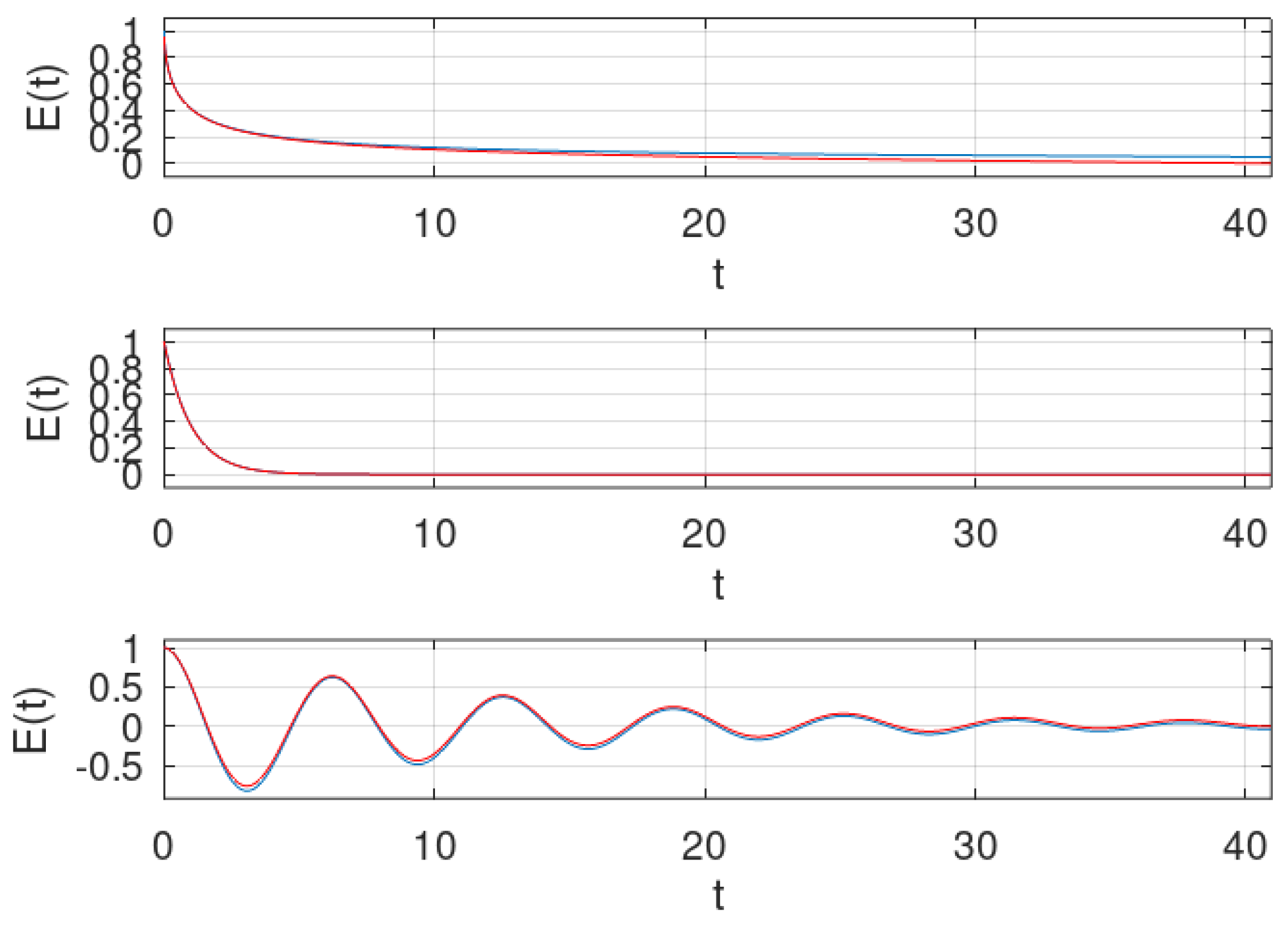
• No poles on the imaginary axis:
  If the TF of the original system, $H_c(s)$, has no poles on the imaginary axis, $G_c(s)$ is analytical on a vertical strip that includes such an axis. This means that the system described by (61) is a stable system and all the considerations made in Section 3.1 and Section 3.7 remain valid, in particular all the conversion rules are applied also.
  The stability is assured by the absolute integrability of the impulse response, $h(t)\ast h(-t)$.
• Poles on the imaginary axis:
  If $H_c(s)$ has poles on the imaginary axis, then $G_c(s)$ doubles the poles there. This is a singular case that was treated in [47]. The corresponding time response increases without bound. The system is unstable.

From the above considerations we conclude that:

• The covariance equivalence implies the input–output equivalence;
• The input–output equivalence may not imply the covariance equivalence (we can have poles on the imaginary axis);
• The input–output equivalence and the covariance equivalence are the same if:
  • There are no poles on the imaginary axis of the continuous-time system (on the unit circle in the discrete case);
  • All the zeroes are in the left half plane (in the unit disk).
  The covariance “loses the phase” of the system.

5. The Bilinear Transformation: A Spectral Equivalence

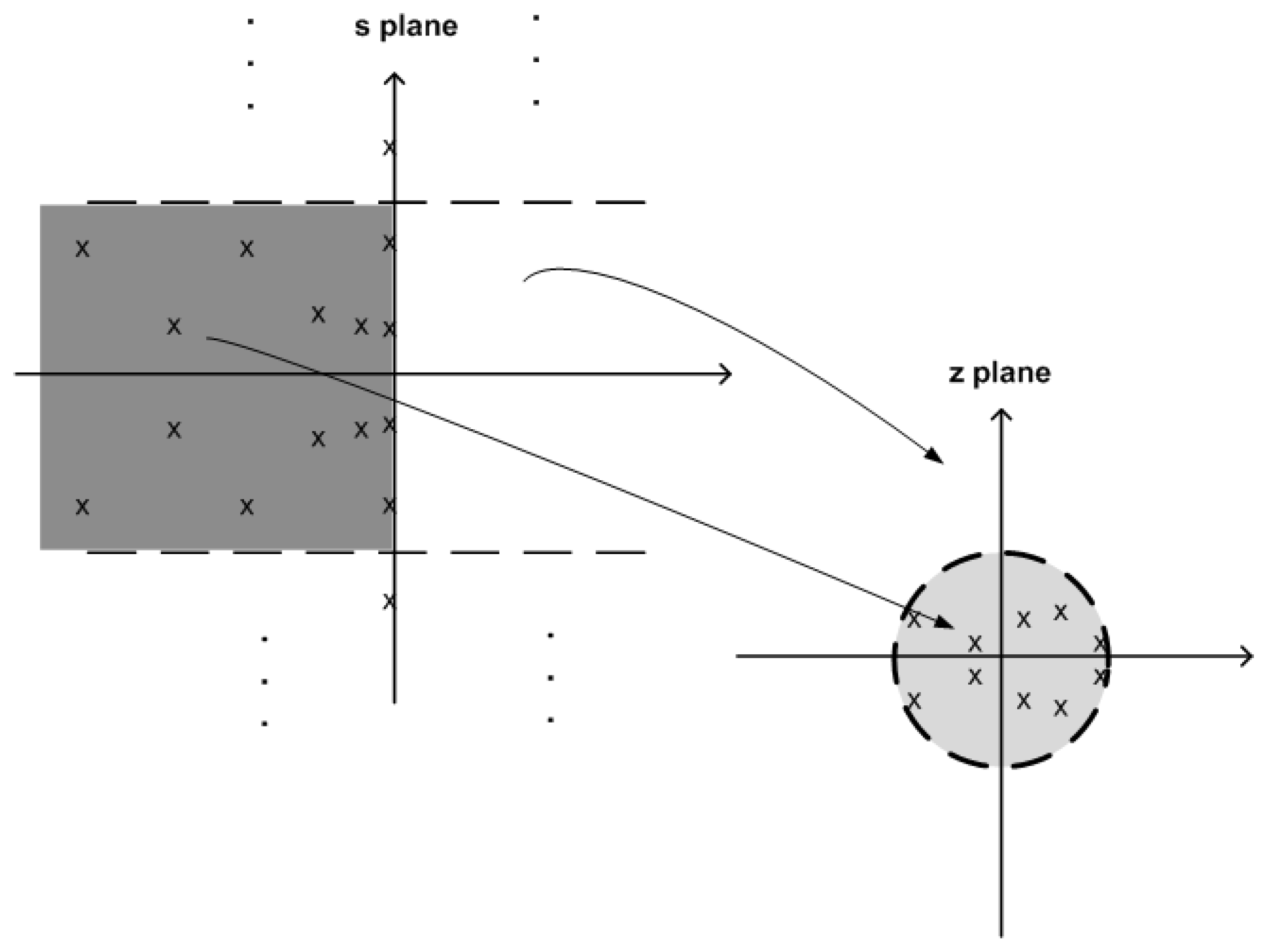
5.1. The s to z Conversion

There are several transformations that allow us to go from the plane s of the Laplace transform to the plane z of the Z transform [4]. The most important is the bilinear transformation. This can be obtained from (31) with $p=0$ and $z=e^{sT}$:

$$\frac{1}{s}=\frac{T}{2}\frac{1+z^{-1}}{1-z^{-1}},$$

(62)

or

$$z^{-1}=\frac{2-sT}{2+sT}.$$

(63)

The bilinear transformation is a conformal mapping used in filter design. Essentially, it allows the use of continuous domain information to design discrete systems. It is very interesting and useful because:

• It transforms the whole left complex plane into the unit disk;
• It maps the imaginary axis on the unit circle;
• It allows a one-to-one transformation from pole to pole and from zero to zero;
• It has an interpretation in terms of the trapezoidal integration.

The main drawbacks of the transformation are:

• The frequency warping that happens in going from the imaginary axis to the unit circle [4];
• The zero at $z=-1$.

Remark 4.

The CT systems with poles on the imaginary axis are considered as singular, since they are not stable in the BIBO sense, but if the poles are not multiple, they are wide-sense-stable [2,18,47]. The equivalent DT systems have poles on the unit circle. One of these systems is very important: it is the autoregressive-integrated moving average (ARIMA) system, which has a pole at $z=1$ ($s=0$) [51,52].

To understand the action of the bilinear transformation, consider two cases corresponding to simple transfer functions:

• $H_{1c}(s)=\frac{1}{s-p}$:
  The discrete TF we obtain with the bilinear transformation is

  $$H_{1d}(z)=\frac{T}{2-pT}\frac{1+z^{-1}}{1-\theta z^{-1}},$$

  with the new pole located at

  $$\theta =\frac{2+pT}{2-pT}.$$

  (64)
  We conclude that the new pole is at $\zeta =\frac{2+pT}{2-pT}$, but it should be at $\theta =e^{pT}$. We will study this change below for several values of p. Meanwhile, we must realize that the static gain does not change: $H_{1c}(0)=-\frac{1}{p}=H_{1d}(1)$. As above, a zero at $z=-1$ appears.
• $H_{2c}(s)={\displaystyle \frac{s-q}{s-p}};$
  Now, we obtain

  $$H_{2d}(z)=\frac{2-qT}{2-pT}\frac{1-\zeta z^{-1}}{1-\theta z^{-1}}$$

  with $\zeta ={\displaystyle \frac{2+qT}{2-qT}}$.
  On the other hand, we have again $H_{2c}(0)=\frac{q}{p}=H_{2d}(1).$

With these results, we confirm our above affirmations. Moreover, we can state:

• If the continuous-time system is stable, the corresponding discrete-time one is also stable;
• If the continuous-time system is minimum phase, so is the corresponding discrete-time one—if zeros on the left half complex plane are transformed into zeros inside the unit circle, as is easy to see;
• The static gain is invariant;
• If the original system is an ARMA(N,M), the TF of the discrete-time system is an ARMA(N,N). This is clear from the above examples. We can see that the simple fractions without zero originate a zero at $z=-1$. Therefore, the corresponding spectrum is zero at $\omega =\pi$. The zero at $-1$ has order $N-M$.

To test the magnitude of the error we make when using $\zeta =\frac{2+pT}{2-pT}$ instead of $\theta =e^{pT},$ we generated randomly 100 poles on the left half plane and computed the two sets of transformed poles using the above transformations for three values of T: $0.1,0.01,0.001$. Then, we computed the quotient $e^{pT}/\frac{2+pT}{2-pT}$. The maximum and minimum absolute values were recorded together with the maximum phase deviation. In

Table 1. Approximations of $\theta =e^{pT},$ by $\zeta =\frac{2+pT}{2-pT}$.

T	$0.1$	$0.05$	$0.01$
Max-abs	$1.0026$	$1.0003$	$1.000$
Min-abs	$0.9981$	$0.9998$	$1.000$
Max-angle	$0.029$	$3.5\times {10}^{-4}$	$2.8\times {10}^{-6}$

, we present the results.

5.2. Spectral Equivalence

The bilinear transformation does not guarantee an input–output correspondence, but it can ensure a spectral equivalence in the sense that the discrete-time system has a frequency response that equals the continuous-time system frequency response for frequencies below $\frac{1}{T}$ where T is the sampling interval. To do this, we consider again (25) and the transformation suffered by the imaginary axis to give the unit circle. Denote by $s=i\mathsf{\Omega },\mathsf{\Omega }\in \mathbf{R}$ the representation of the imaginary axis and by $x=e^{i\omega },\omega \in (-\pi ,\pi ).$ We can write

$$\mathsf{\Omega }=\frac{2}{T}tan\left(\frac{\omega }{2}\right)$$

(65)

stating a nonlinear relation between the “continuous” frequency $\mathsf{\Omega }$ and the “discrete” $\omega$, which is called “frequency warping” [4]. This means that there is always a spectral distortion. Anyway, it can be reduced to a negligible effect. We have two different situations:

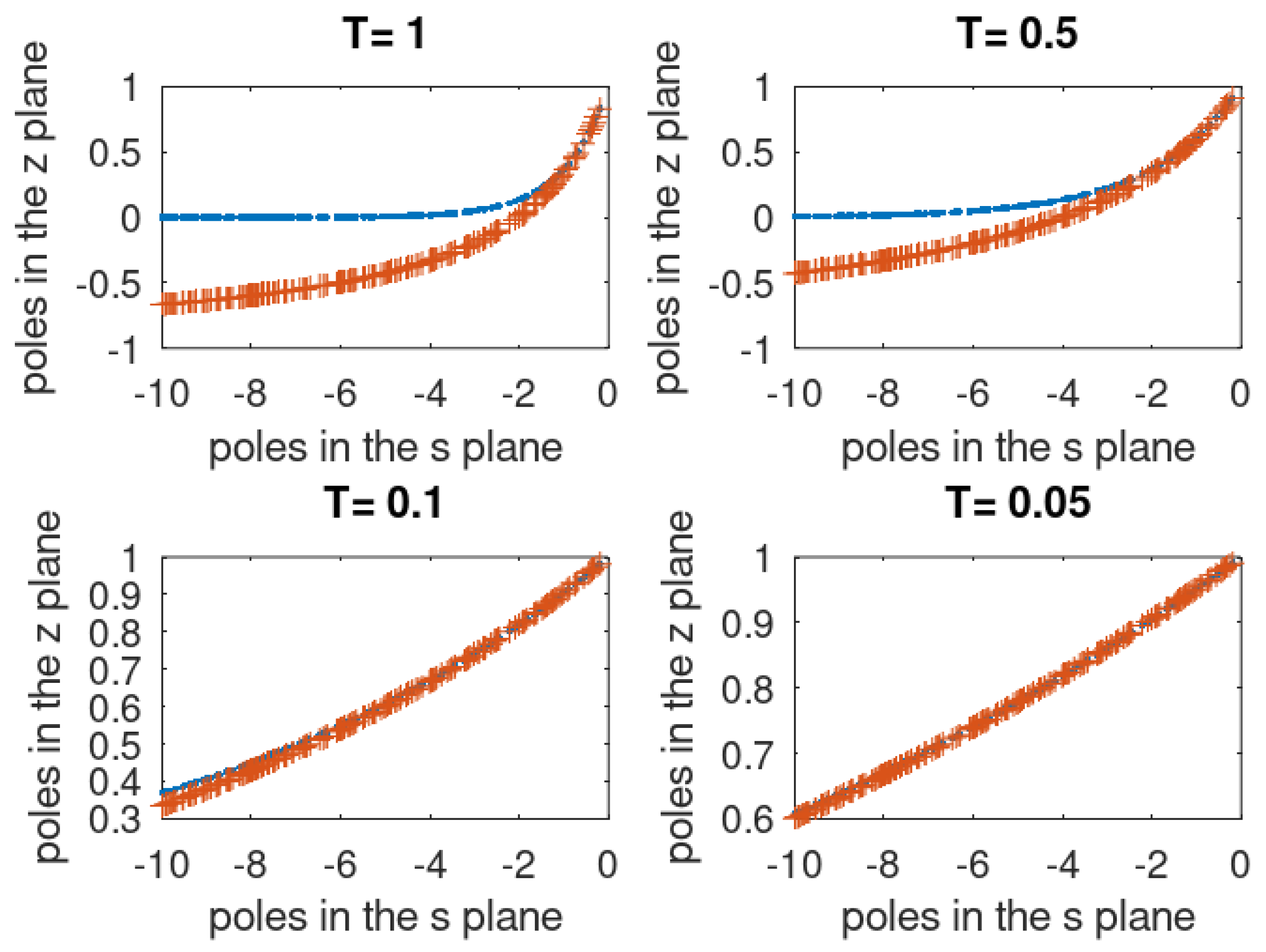
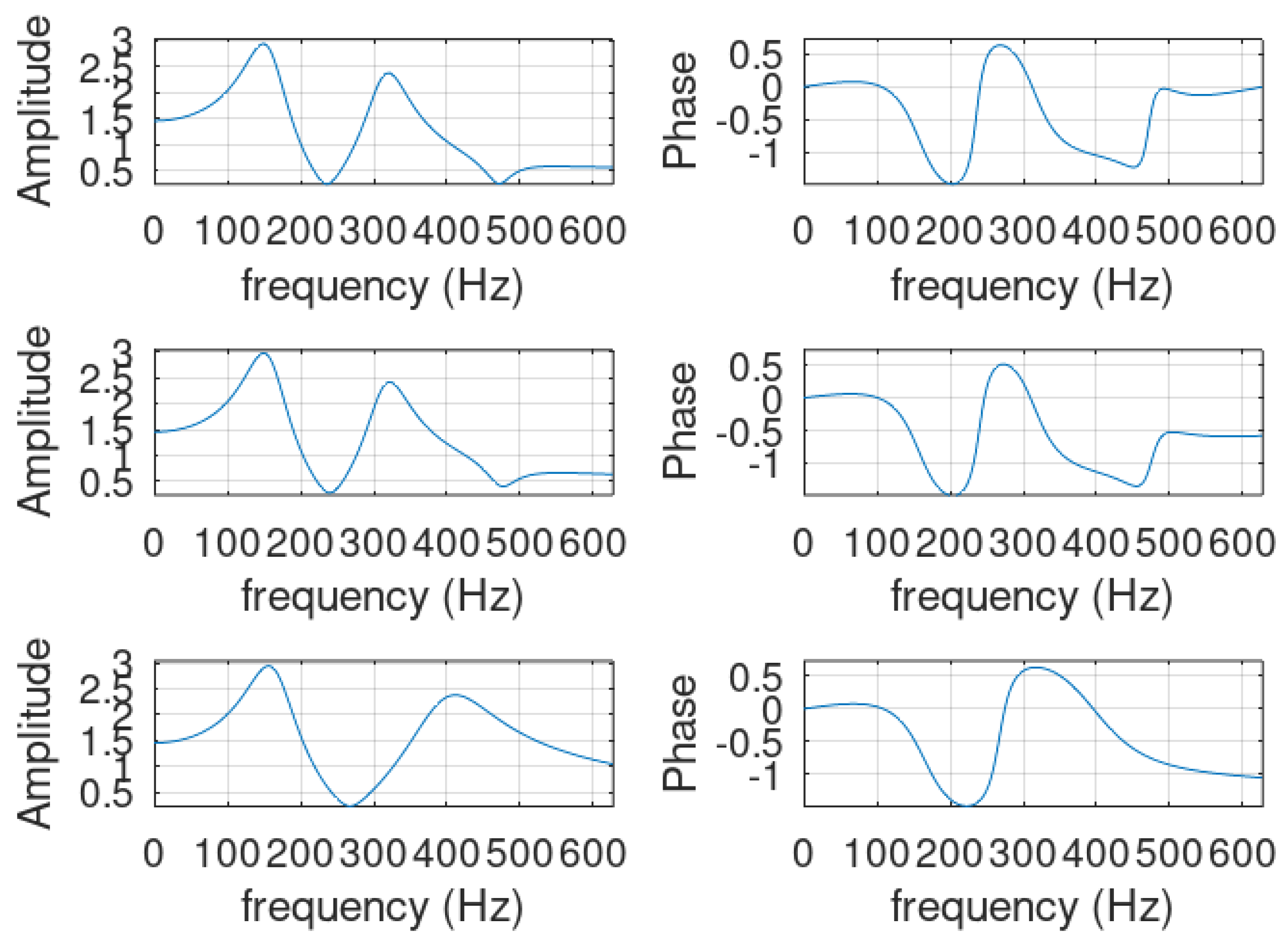
• Continuous to discrete:
  In this case, we can write from above

  $$\omega =2arctan\left(\frac{\mathsf{\Omega }T}{2}\right)$$

  (66)

  We can choose T as small as we can to obtain

  $$\omega \approx \mathsf{\Omega }T$$

  (67)
  This means that the bilinear equivalence can be assured, as we will see later, in the continuous to discrete conversion.
  In Figure 3, we illustrate the evolution of the transformed poles. We generated 200 negative real poles and applied the exponential $\theta =e^{pT}$ and the binomial transformation $\zeta =\frac{2+pT}{2-pT}$ for $T=1,0.5,0.1,0.05$.
  As seen in the lower pictures, there are almost no visible differences between the correct, $\theta ,$ and the approximated, $\zeta$. To give a better idea, we performed spectral computations, which we present in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.
• Discrete to continuous:
  This situation is different from the above since the approximation does not depend on T. In fact, from (65), $\tan (\frac{\omega }{2})\approx \frac{\omega }{2}$ only if $\omega$ is small and which is independent of the sampling interval. This leads us to conclude that only the spectral components with a low frequency can remain undistorted when going from discrete to continuous. We will illustrate this situation later.

5.3. The FIR Systems

The finite impulse systems (FIR) are exactly the MA systems and do not fall inside the computational framework we just presented. Anyway, we can obtain continuous-time equivalents. The more suitable way to do this is with the bilinear transformation, since, from (62), each power of $z^{-1}$ is transformed into an “all-pass” filter.

5.4. The Pole at $z=-1$

According to the procedure we used to go from the continuous-time to discrete-time in Section 3, there is no possibility of having a pole at $z=-1$ because it would correspond to one pole at $s=i\frac{\pi }{T}$, but not at $s=-i\frac{\pi }{T}$. This cannot happen if the original continuous-time one is real. This means that a discrete-time system with a pole at $z=-1$ does not have a real continuous-time equivalent. However, zero at $z=-1$ can result from the use of the bilinear transformation.

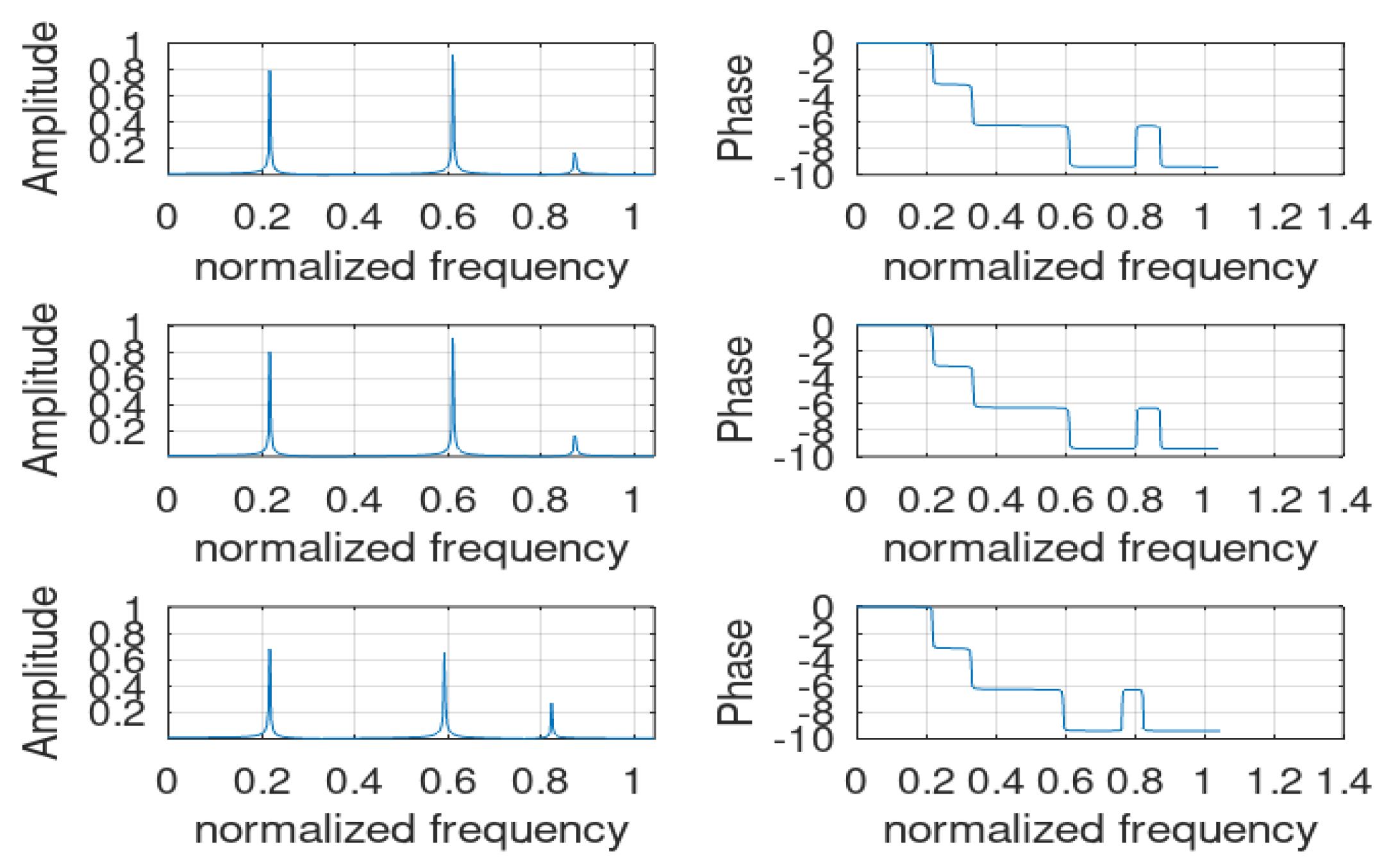
5.5. Simulation Results

To test the performance of the above transformations in frequency, we considered an ARMA(6,4) with poles at $-0.08\pm 70i,-0.07\pm 25i,-0.05\pm 100i$ and zeroes at $0.09\pm 38i$, $-0.04\pm 92i$; the gain was set to $K=20$. In Figure 4, Figure 5 and Figure 6, we present illustrations of the behavior of the algorithms for $T=0.0262,0.0087,0.0033$ by plotting the frequency responses of the original system and two discrete-time equivalents. The left sides represent the amplitude spectra, while the right represent the phase spectra. As seen, the bilinear transformation performs worst at higher frequencies, although it becomes better as T decreases.

As is clear, there is a small difference between both transformations. This does not happen for $T=0.0033$, where they are very similar. Another conclusion we can extract is that, although the transformations do not guarantee the preservation of the zeroes, the figure shows that it seems to preserve.

In Figure 7, we depict the plots corresponding to the conversion of a CARMA(6,6) having the same poles and zeroes of the CARMA(6,4) considered above, but with two zeroes at $s=-10;+1$. It is interesting to note that the influence of the zero at $z=-1$ visible in Figure 5 and Figure 6 disappears.

Similarly, we proceed to perform the conversion from discrete-time to continuous-time. We used an ARMA(6,4) model with poles at $0.85e^{\pm i\pi /4},0.85e^{\pm i\pi /2},0.85e^{\pm i3\pi /4}$ and zeroes at $0.95e^{\pm i0.375\pi }0.95e^{\pm i0.75\pi }.$ Figure 8 and Figure 9 illustrate the conversions for two sampling intervals: $0.01,0.005$. In the third strip of the two pictures, we see the result of the above-mentioned spectral distortion, which is independent of the sampling interval (Figure 9).

6. From Continuous-Time to Discrete-Time in Fractional Systems

6.1. The Fractional Linear Systems

Let us return to (7) and “fractionalize” it to the so-called commensurate form [3]:

$$\sum _{k=0}^{N_0}{A}_k{D}^{k\alpha }y(t)=\sum _{k=0}^{M_0}{B}_k{D}^{k\alpha }x(t) t\in \mathbb{R}$$

(68)

where $\alpha$ is any positive number. While in the integer-order case, we could write a difference equation with the same format and establish a correspondence relation between both, the fractional delay equations [53], although assuming some similarities with the CT-FARMA, are not really fractional systems. Traditionally, discrete approximations to the fractional derivatives have been used. The most utilized are the Grünwald–Letnikov approximations generalizing Euler’s procedure. However, this is done frequently without the formal introduction of any fractional DT systems. This was done in [11], where DT differential systems were introduced in a way that mimics the CT system study. Recently, the same was done with the bilinear transformation, leading to the corresponding DT systems. We are going to describe them briefly.

6.2. On the Fractional Discrete-Time Models

6.2.1. Euler Type Systems

The Euler-type systems [3,11,12] are based on the generalization of Euler’s approximations for the derivatives. Consider that the time scale:

$$\mathbb{T}=(T\mathbb{Z})=\left\{\cdots ,-3T,-2T,-T,0,T,2T,3T,\cdots \right\},$$

with $T\in {\mathbb{R}}^{+}$ the working domain. Set $t=nT$. We define the nabla derivative by

$$f_{\nabla }^{\prime }(t)=\frac{f(t)-f(t-T)}{T},$$

(69)

and the delta derivative by

$$f_{\Delta }^{\prime }(t)=\frac{f(t+T)-f(t)}{T}.$$

(70)

As can be seen, the first derivative is causal, while the second is anti-causal. The application of the LT to (69) leads to

$$s={\displaystyle \frac{(1-e^{-sT})}{T}}$$

and, with $z=e^{-sT},$ to the transformation

$$s={\displaystyle \frac{(1-z^{-1})}{T}}.$$

(71)

Although (69) approximates the CT derivative for small T, the transformation $s\to z$ stated by (71) is not very interesting, since the image of the imaginary axis in the s plane is a circle with the center at $1/T$ passing at $z=0$, contrary to the useful unit circle. This has several consequences including:

• Many stable DT systems are outside the stability region implied by this derivative;
• We have to define a new DT Laplace transform [11], preventing the direct use of the Z transform and, consequently, the FFT.

However, this procedure leads to difference equations, although with large orders that approximate CT FARMA systems. To do this, generalizations for the non-integer order are introduced [11]:

$$f_{\nabla }^{(\alpha )}(t)=\frac{{\displaystyle \sum _{n=0}^{\infty }}\frac{{(-\alpha )}_n}{n!}f(t-nT)}{T^{\alpha }}$$

(72)

and

$$f_{\Delta }^{(\alpha )}(t)=e^{-i\alpha \pi }\frac{{\displaystyle \sum _{n=0}^{\infty }}\frac{{(-\alpha )}_n}{n!}f(t+nT)}{T^{\alpha }},$$

(73)

obtained from the generalized Grünwald–Letnikov (GL) derivative (see [54]). The symbol ${\left(-\alpha \right)}_n$ stands for the Pochhammer representation of the rising factorial: ${\left(-\alpha \right)}_0=1,$ ${\left(-\alpha \right)}_n={\prod }_{k=0}^{n-1}\left(-\alpha +k\right).$

For the stated reasons, we will not consider this method as suitable for establishing CT/DT equivalence relations.

Remark 5.

The fractional counterpart of the ARIMA model is the ARFIMA system, which is a particular case of fractional DT systems resulting from the transformation of a CT system with a pseudo-pole at the origin $H_c(s)=\frac{1}{s^{\alpha }}$, leading to $H_d(z)=\frac{1}{{(1-z^{-1})}^{\alpha }}$ [55].

6.2.2. Bilinear-Type Systems

In Section 5, the DT approximation of CT systems by the Tustin (bilinear) transformation [56] was studied and its main features introduced. The objective was the conversion from a CT ARMA system to a DT (ARMA) one defined by a difference equation. However, instead of moving on to a difference equation, we can move on to a differential equation that we can solve with appropriate methods. This is particularly useful, since the Tustin transformation establishes a bijection between the left (right) half complex plane and the interior (exterior) of the unit disk. This property permitted the use of such a transformation for defining alternative DT derivatives and corresponding FARMA systems that mimic the analogous CT versions. Such a strategy allows the adoption of the tools and the results available for the CT fractional systems. Moreover, the proposed framework has the important feature of being suitable to be implemented through the FFT with the corresponding advantages, from the numerical and calculation time perspectives. Although both forward (causal) and backward (anti-causal) formulations can be introduced, we will consider the first only.

Let $x(nT)$ be a discrete-time function; we define the order-one forward bilinear derivative $Dx(nT)$ of $x(nT)$ as the solution of the difference equation:

$$Dx(nT)+Dx(nT-T)=\frac{2}{T}[x(nT)-x(nT-T)].$$

(74)

We define the bilinear exponential $e_s(nT)$ as the eigenfunction of the Equation (74). Setting $x(nT)=e_s(nT),$ $y(nT)=s{e}_s(nT),s\in \mathbb{C},$ with $e_s(0)=1,$ then

$$e_s(nT)={\left(\frac{2+Ts}{2-Ts}\right)}^n, n\in \mathbb{Z},s\in \mathbb{C}.$$

(75)

Consequently, letting $z=\frac{2+Ts}{2-Ts}$, we obtain a transformation that sets the unit circle $\left|z\right|=1$ as the image of the imaginary axis in s, independently of the value of T. Consider the DT exponential function, $e_s(nT)=z^n,n\in \mathbb{Z}$. We define the forward bilinear derivative ($D_f$) as an elementary DT system such that

$$D_f{z}^n=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}{z}^n.$$

(76)

The TF of a such derivative, $H_f(z)$, is defined by

$$H_f(z)=\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}, \left|z\right|>1.$$

(77)

In general, we can introduce the $\alpha$-order forward bilinear FD as a DT LS with TF:

$$H_f(z)={\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right)}^{\alpha }, \left|z\right|>1,$$

(78)

such that

$$D_f^{\alpha }{z}^n={\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right)}^{\alpha }{z}^n, \left|z\right|>1.$$

(79)

Remark 6.

It is important to note that we have two branch cut points $z=\pm 1$, and there is a corresponding branch cut line that is any simple line joining the two points and lying inside the unit disk. We can extend the domain of validity to include the unit circumference, $z=e^{i\omega n},\left|\omega \right|\in (0,\pi ),$ with the exception of the points $z=\pm 1.$ In these cases, the integration path in (81) must be deformed around such points. For applying the FFT, a small numerical trick can be used if needed: push the branch-cut points slightly inside the unit circle, that is to $z=-1+ϵ$ and $z=1-ϵ$$(-1-ϵ,1+ϵ)$, with ϵ being a small positive real number.

Having defined the derivative of an exponential, we are in the conditions of obtaining the derivative of any signal having ZT by using the inversion integral of the ZT

$$x(n)=\frac{1}{2\pi i}{\oint }_{\gamma }X(z)z^{n-1}\mathrm{d}z.$$

(80)

Therefore, we conclude, from (80) and (79) that, if $x(n)$ is a function with ZT $X(z),$ analytic in the ROC defined by $z\in \mathbb{C}:\left|z\right|>a,a\le 1,$ then

$$D_f^{\alpha }x(n)=\frac{1}{2\pi i}{\oint }_{\gamma }{\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right)}^{\alpha }X(z)z^{n-1}\mathrm{d}z,$$

(81)

where the integration path lies outside the unit disk. This implies that

$$\mathcal{Z}[D_f^{\alpha }x(n)]={\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right)}^{\alpha }X(z), \left|z\right|>1.$$

(82)

According to what we just wrote, we can extend the above definitions to include sinusoids.

We define the derivative of $x(n)=e^{j\omega n},n\in \mathbb{Z},$ through

$$D_{f,b}{e}^{j\omega n}={[\frac{2}{T}tan(\frac{\omega }{2})]}^{\alpha }{e}^{j\omega n}, \left|\omega \right|<\pi ,$$

(83)

independently of considering the forward or backward derivatives. With this result, we can obtain the derivative of any function having discrete-time FT, which is expressed as:

$$D_{f,b}x(n)=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}X(e^{i\omega }){\left[\frac{2}{T}tan\left(\frac{\omega }{2}\right)\right]}^{\alpha }{e}^{i\omega n}\mathrm{d}\omega .$$

(84)

6.3. The Bilinear Discrete-Time Linear Systems

The above derivatives led us to consider systems defined by constant coefficient differential equations with the general form (68), where the operator D is substituted by the forward (or backward) derivative previously defined.

Let $g(n)$ be its IR. The output is $y(n)=g(n)\ast v(n).$ With the definition of the forward derivative and mainly Formula (82), we write the TF

$$G(z)=\frac{{\displaystyle \sum _{k=0}^M}{b}_k{\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right)}^{{\beta }_k}}{{\displaystyle \sum _{k=0}^N}{a}_k{\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right)}^{{\alpha }_k}}, \left|z\right|>1,$$

(85)

for the causal case, and

$$G(z)=\frac{{\displaystyle \sum _{k=0}^M}{b}_k{\left(\frac{2}{T}\frac{z-1}{z+1}\right)}^{{\beta }_k}}{{\displaystyle \sum _{k=0}^N}{a}_k{\left(\frac{2}{T}\frac{z-1}{z+1}\right)}^{{\alpha }_k}}, \left|z\right|<1,$$

(86)

for the anti-causal case. We can give to Expressions (85) and (86) a form that states their similarity with the classic fractional LS [57,58]. For example, for the first, let $v=\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right)$. We have

$$G(v)=\frac{{\displaystyle \sum _{k=0}^M}{b}_k{v}^{{\beta }_k}}{{\displaystyle \sum _{k=0}^N}{a}_k{v}^{{\alpha }_k}}.$$

(87)

Remark 7.

It is important to note that the factors ${\left(\frac{2}{T}\right)}^{{\alpha }_k},k=1,2,\dots ,$ do not have any important role in the computations. Therefore, they can be merged with the coefficients $a_k$ and $b_k$.

The procedure to invert (87) is identical to the one we followed in the CT system [12,54]. For simplicity, we assume the commensurate case:

$$G(v)=\frac{{\displaystyle \sum _{k=0}^M}{b}_k{v}^{k\alpha }}{{\displaystyle \sum _{k=0}^N}{a}_k{v}^{k\alpha }}.$$

(88)

with $M<N$, and all the roots, $p_k,k=1,2,\cdots ,$ of ${\displaystyle \sum _{k=0}^N}{a}_k{w}^k$ are simple, which allows us to write

$$G(v)={\displaystyle \sum _{k=1}^N}\frac{A_k}{v^{\alpha }-p_k},$$

(89)

where the $A_k$ are the residues obtained by substituting w for $v^{\alpha }$ in (88). The IR results from the inversion of a combination of partial fractions such as:

$$F(v)=\frac{A}{v^{\alpha }-p}.$$

(90)

6.4. Equivalence

Usually, DT systems are considered as mere approximations of their CT counterparts. Nevertheless, and as shown above, the DT systems exist by themselves and have properties that, although similar to, are independent of the CT analogues. However, this observation does not prevent us from establishing a continuous path from one to the other. In fact, we can go from the discrete into the continuous domain by reducing the graininess. To see this, let us return to (81) and rewrite it as

$$D_f^{\alpha }x(nT)={\left(\frac{2}{T}\right)}^{\alpha }\sum _{k=0}^{\infty }{\psi }_k^{\alpha }x(nh-kT),$$

where ${\psi }_k^{\alpha }$ in the impulse response inverse of (77). Assume that $x(nT)$ resulted from a CT function $x(t)$, and define a new function, $y(t),$ by

$$y(t)={\left(\frac{2}{T}\right)}^{\alpha }\sum _{k=0}^{\infty }{\psi }_k^{\alpha }x(t-kT).$$

(91)

The LT of Expression (91) is

$$Y(s)={\left(\frac{2}{T}\right)}^{\alpha }\sum _{k=0}^{\infty }{\psi }_k^{\alpha }{e}^{-kTs}X(s)={\left(\frac{2}{T}\frac{1-e^{-Ts}}{1+e^{-Ts}}\right)}^{\alpha }X(s),$$

(92)

where $Y(s)=\mathcal{L}[y(t)]$ and $X(s)=\mathcal{L}[x(t)].$ Knowing that $\underset{T\to 0}{lim}\frac{1-e^{-Ts}}{T}=s$, we can write

$$Y(s)=s^{\alpha }X(s), Re(s)>0,$$

meaning that $Y(s)$ is the LT of the (continuous-time) derivative of $x(t).$ This relation expresses the compatibility between the new formulation described above and the well-known results from the continuous-time derivative formulation [54,57]. In the backward cases, we would obtain the same result, but with an ROC valid for $Re(s)<0$. The above equations lead to the conclusion that, for $t\in \mathbb{R},$ we can write:

$$D_f^{\alpha }x(t)=\underset{T\to 0}{lim}{\left(\frac{2}{T}\right)}^{\alpha }\sum _{k=0}^{\infty }{\psi }_k^{\alpha }x(t-kT).$$

(93)

Similarly, from the backward formulation, mainly (82), we obtain

$$D_b^{\alpha }x(t)=e^{i\alpha \pi }\underset{T\to 0}{lim}{\left(\frac{2}{T}\right)}^{\alpha }\sum _{k=0}^{\infty }{\psi }_k^{\alpha }x(t+kT).$$

(94)

Relations (93) and (94) state two new ways of computing the continuous-time FD that are similar to the Grünwald–Letnikov derivatives. However, it may be interesting to remark that we can compute derivatives with (91) instead of (93).

Example 9.

As a simple exercise, compare two CT and DT fractional systems, defined by:

$$D_f^{\alpha }y(t)+y(t)=D_f^{\alpha }x(t),$$

having TF:

$$G(s)={\displaystyle \frac{s^{\alpha }}{s^{\alpha }+1}}, Re(s)>0.$$

It is easy to verify that its step response is the well-known Mittag–Leffler function, $E_{\alpha }(p{t}^{\alpha })u(t),$ which is defined by [59]

$$E_{\alpha }(z)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\alpha k+1)}, z\in \mathbb{C}.$$

(95)

In the CT case, we used the algorithm introduced in [60]. It is important to remark that for $\alpha <1$, there is no integer-order part, since there is no pole [3]. However, for $\alpha >1,$ it is convenient to decompose $G(s)$ into the form:

$$G(s)=\frac{1}{2}{\displaystyle \frac{s^{\frac{\alpha }{2}}}{s^{\frac{\alpha }{2}}+i}}+\frac{1}{2}{\displaystyle \frac{s^{\frac{\alpha }{2}}}{s^{\frac{\alpha }{2}}-i}} Re(s)>0,$$

(96)

which leads to

$$E_{\alpha }(-t^{\alpha })u(t)=Re\left(E_{\frac{\alpha }{2}}(i{t}^{\frac{\alpha }{2}})u(t)\right).$$

Note that $\frac{\alpha }{2}<1$, and each term in (96) has a pole (at ${(\pm i)}^{\frac{2}{\alpha }}$). In the DT case, the implementation of $G(s)$ on the unit circle is immediate using the FFT,

$$G(e^{i\omega })={\displaystyle \frac{{\left(\frac{2}{T}\frac{1-e^{-i\omega }}{1+e^{-i\omega }}\right)}^{\alpha }}{{\left(\frac{2}{T}\frac{1-e^{-i\omega }}{1+e^{-i\omega }}\right)}^{\alpha }+1}} \omega \in [0,2\pi ).$$

The inverse FFT gives the impulse response (the value at the origin must be corrected, since the transform gives $\frac{1}{2}$ instead of 1). As $\frac{1}{s}$ is the TF of an accumulator, we compute easily the DT Mittag–Leffler function. In Figure 10, we illustrate the computations of the functions. To make a comparison, we computed both Mittag–Leffler functions for $\alpha =0.6,1,1.9$, with $T=0.01.$ For other values, the results are similar. It is important to call attention to the good approximation supplied by the discrete function (we represented it in a continuous line for easier comparison). This is very interesting, since it is easier to implement than the continuous version.

7. Conclusions

The equivalence between continuous-time and discrete-time ARMA models was treated in this paper. The input–output equivalence of continuous- and discrete-time ARMA systems can be achieved through suitable transformations. We showed how to obtain the covariance equivalence and the inter-relations between them. We studied also the spectral equivalence based on the bilinear transformation. The general fractional CT/DT ARMA systems were also studied by considering two DT FARMA systems: the nabla/delta and bilinear-based derivatives. The CT/DT interrelations were also considered, paying special attention to the systems defined by the bilinear derivatives.

The proposed framework solves most of application problems in the frequency domain. Therefore, it would be important to make an evaluation of the quality of the interconversions. As a continuation, it would be interesting to study the interconversions of causal tempered systems [61], as well as the ones based on two-sided derivatives [38,44,62,63].