High-Order Dissipation-Preserving Methods for Nonlinear Fractional Generalized Wave Equations
Abstract
:1. Introduction
2. Preliminaries
3. Numerical Approximations of Nonlinear Fractional Generalized Wave Equations
3.1. Equivalent System via the SAV Approach
3.2. Structure-Preserving Spatial Discretization
3.3. Collocation Method in Temporal Direction
| Algorithm 1 The SAV-WSLD-Gauss method procedure |
|
4. The Properties of the Numerical Methods
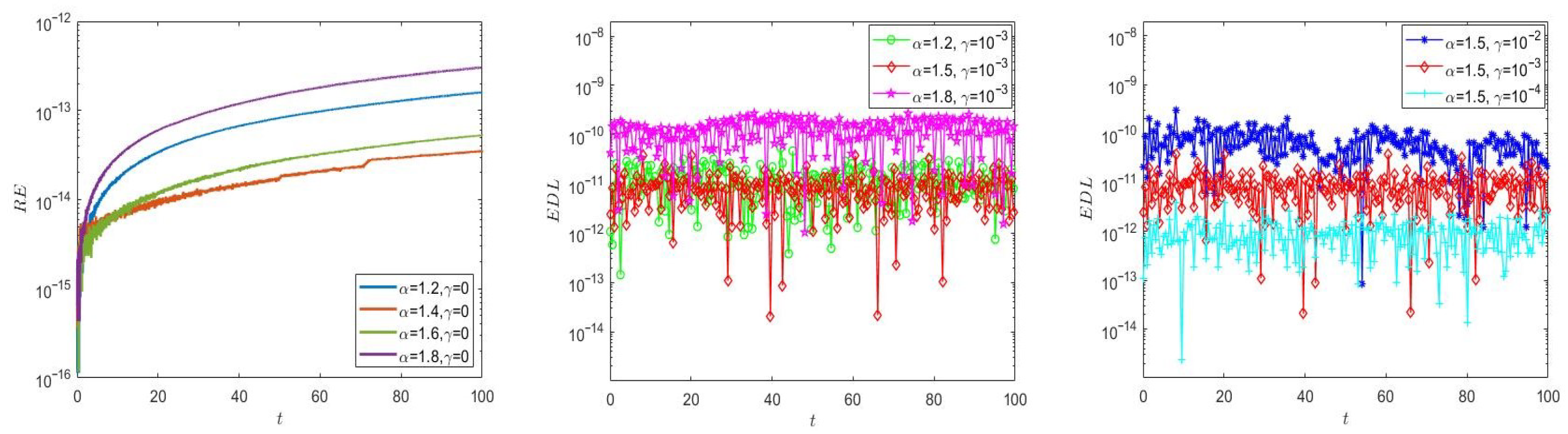
4.1. Convergence, Stability, and Dissipation Property of Energy
4.2. Extend to Two-Dimensional Problems
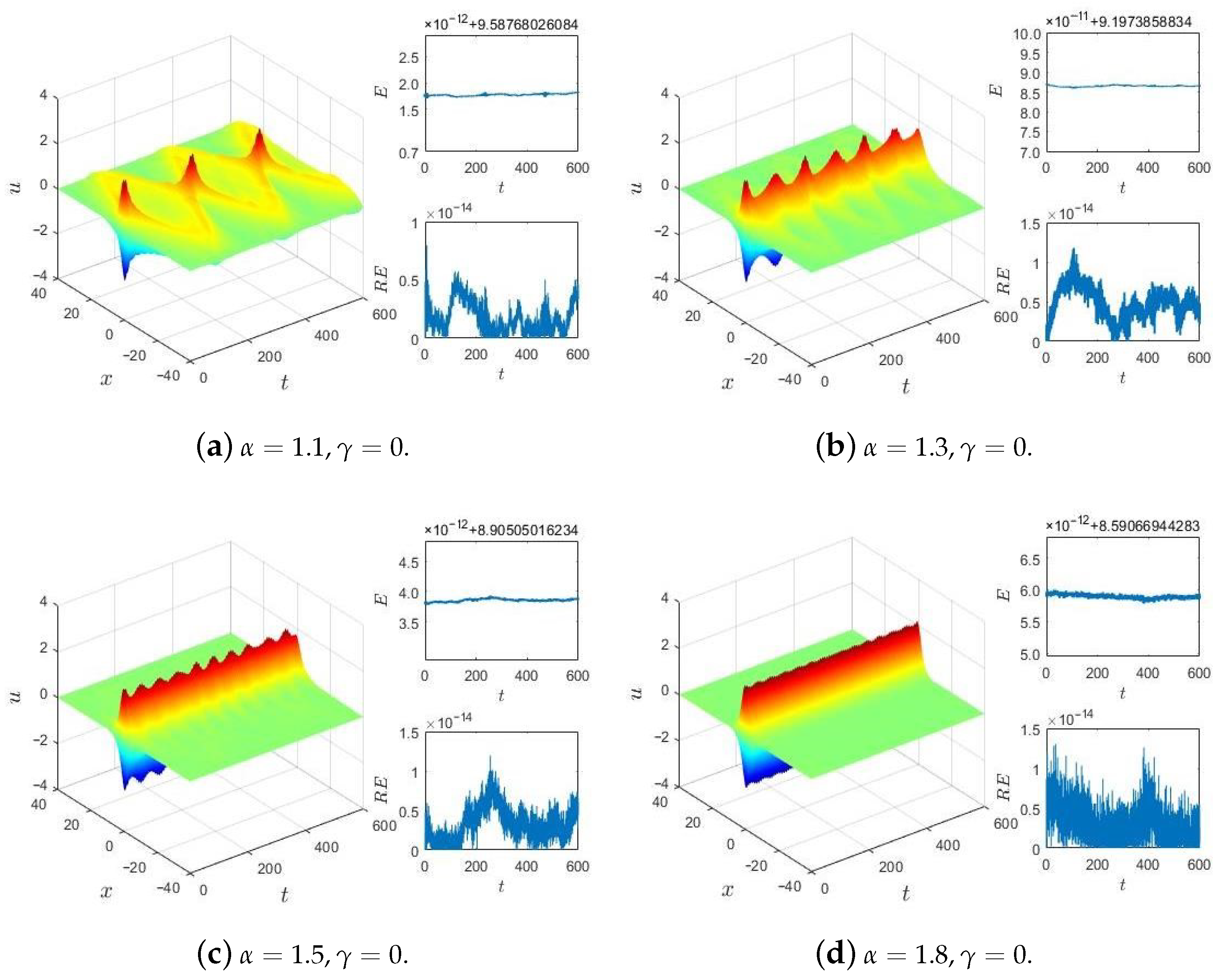
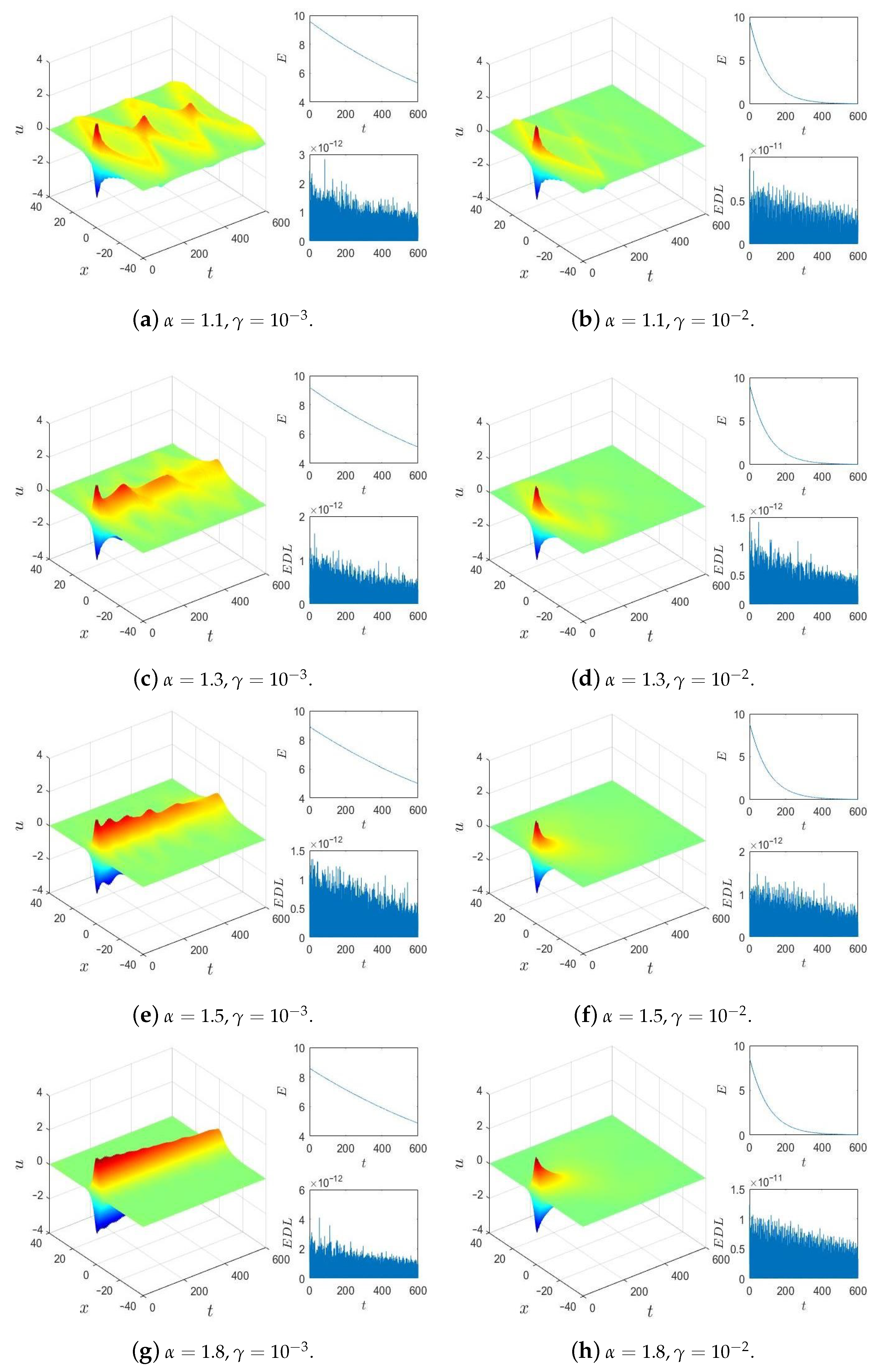
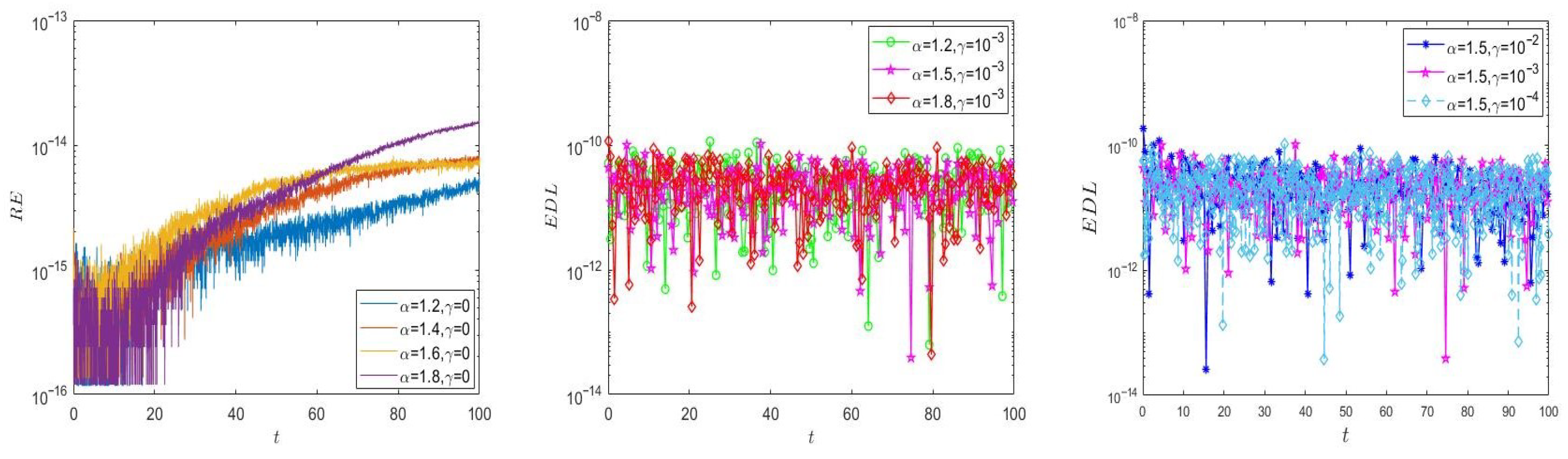
5. Numerical Experiments and Discussions
5.1. One-Dimensional Problem
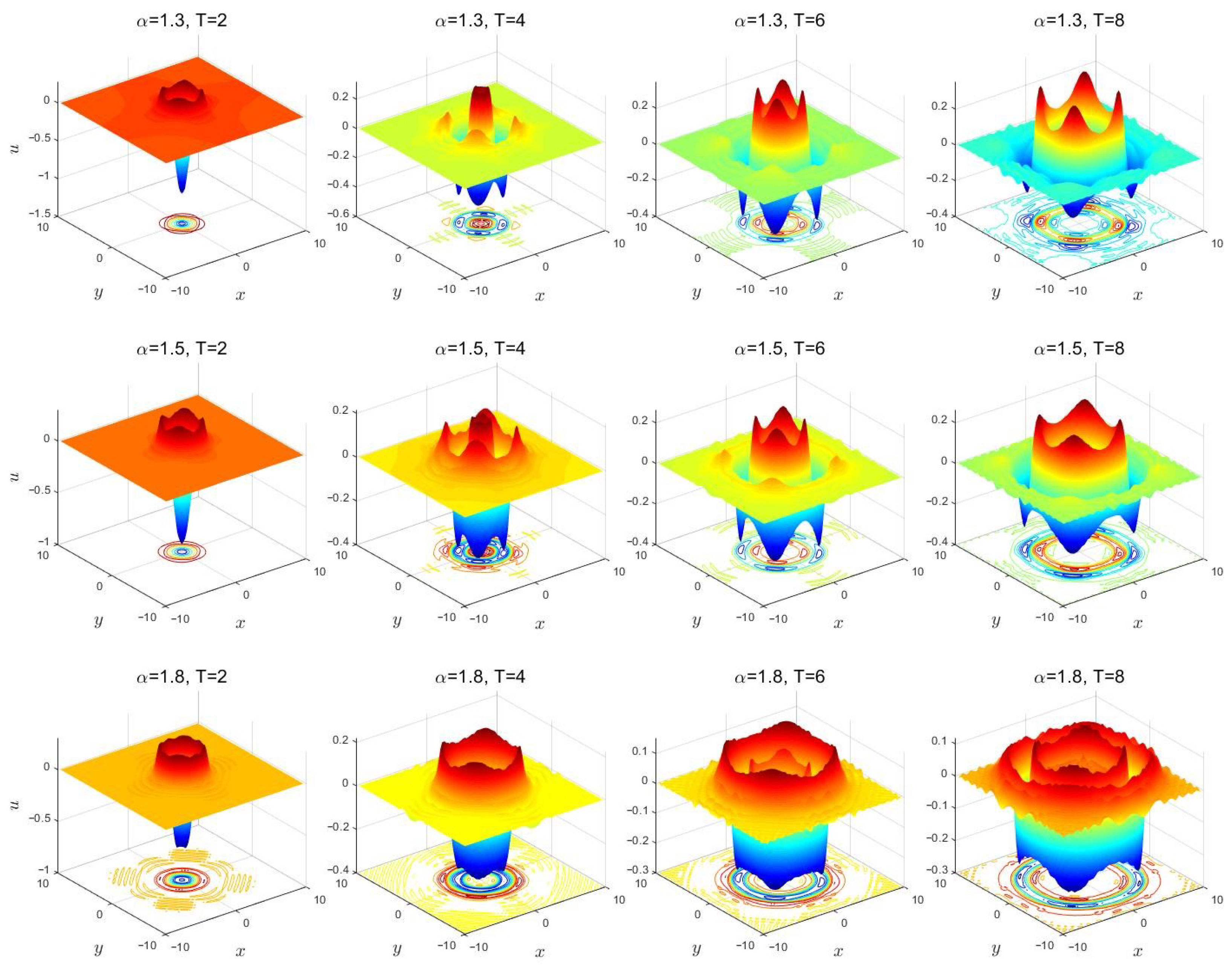
5.2. Two-Dimensional Problem
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAV | Scalar auxiliary variable |
| FGWE | Fractional generalized wave equation |
| WSLD | Weighted and shifted Lubich difference |
| EOC | Experimentally determined orders of convergence |
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Gu, X.M.; Zhao, Y.L.; Zhao, X.L.; Carpentieri, B.; Huang, Y.Y. A note on parallel preconditioning for the all-at-once solution of Riesz fractional diffusion equations. Numer. Math. Theor. Meth. Appl. 2021, 14, 893–919. [Google Scholar]
- Zhao, J.; Jiang, X.; Xu, Y. A kind of generalized backward differentiation formulae for solving fractional differential equations. Appl. Math. Comput. 2022, 419, 126872. [Google Scholar] [CrossRef]
- Tarasov, V.E. Continuous limit of discrete systems with long-range interaction. J. Phys. A Math. Gen. 2006, 39, 14895. [Google Scholar] [CrossRef] [Green Version]
- Campa, A.; Dauxois, T.; Ruffo, S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 2009, 480, 57–159. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Li, M.; Huang, C. Unconditional energy dissipation and error estimates of the SAV Fourier spectral method for nonlinear fractional generalized wave equation. J. Sci. Comput. 2021, 88, 1–32. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Gu, X.M.; Gong, Y.; Li, H.; Zhao, Y.L.; Carpentieri, B. A fast preconditioned semi-implicit difference scheme for strongly nonlinear space-fractional diffusion equations. Fractal Fract. 2021, 5, 230. [Google Scholar] [CrossRef]
- Macías-Díaz, J. A numerically efficient dissipation-preserving implicit method for a nonlinear multidimensional fractional wave equation. J. Sci. Comput. 2018, 77, 1–26. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y. The Grünwald-Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Sun, Z.; Cao, W. A fourth-order approximation of fractional derivatives with its applications. J. Comput. Phys. 2015, 281, 787–805. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Deng, W. Fourth order accurate scheme for the space fractional diffusion equations. SIAM J. Numer. Anal. 2014, 52, 1418–1438. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Cai, W.; Wang, Y. A linearly implicit structure-preserving scheme for the fractional sine-Gordon equation based on the IEQ approach. Appl. Numer. Math. 2021, 160, 368–385. [Google Scholar] [CrossRef]
- Macías-Díaz, J. An explicit dissipation-preserving method for Riesz space-fractional nonlinear wave equations in multiple dimensions. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 67–87. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Xu, Y. An explicit fourth-order energy-preserving scheme for Riesz space fractional nonlinear wave equations. Appl. Math. Comput. 2019, 351, 124–138. [Google Scholar] [CrossRef]
- Serna-Reyes, A.J.; Macías-Díaz, J.E. A mass-and energy-conserving numerical model for a fractional Gross–Pitaevskii system in multiple dimensions. Mathematics 2021, 9, 1765. [Google Scholar] [CrossRef]
- Fu, Y.; Cai, W.; Wang, Y. An explicit structure-preserving algorithm for the nonlinear fractional Hamiltonian wave equation. Appl. Math. Lett. 2020, 102, 106123. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, Z. An effective dissipation-preserving fourth-order difference solver for fractional in space nonlinear wave equations. J. Sci. Comput. 2019, 79, 1753–1776. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, Z.; Liang, D. A new fourth-order energy dissipative difference method for high-dimensional nonlinear fractional generalized wave equations. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104850. [Google Scholar] [CrossRef]
- Li, M.; Fei, M.; Wang, N.; Huang, C. A dissipation-preserving finite element method for nonlinear fractional wave equations on irregular convex domains. Math. Comput. Simul. 2020, 177, 404–419. [Google Scholar] [CrossRef]
- Kang, M.; You, D. A low dissipative and stable cell-centered finite volume method with the simultaneous approximation term for compressible turbulent flows. Mathematics 2021, 9, 1206. [Google Scholar] [CrossRef]
- Wang, N.; Shi, D. Two efficient spectral methods for the nonlinear fractional wave equation in unbounded domain. Math. Comput. Simul. 2021, 185, 696–718. [Google Scholar] [CrossRef]
- Shen, J.; Xu, J.; Yang, J. The scalar auxiliary variable (SAV) approach for gradient flows. J. Comput. Phys. 2018, 353, 407–416. [Google Scholar] [CrossRef]
- Huang, F.; Shen, J.; Yang, Z. A highly efficient and accurate new scalar auxiliary variable approach for gradient flows. SIAM J. Sci. Comput. 2020, 42, A2514–A2536. [Google Scholar] [CrossRef]
- Fu, Y.; Hu, D.; Wang, Y. High-order structure-preserving algorithms for the multi-dimensional fractional nonlinear Schrödinger equation based on the SAV approach. Math. Comput. Simul. 2021, 185, 238–255. [Google Scholar] [CrossRef]
- Cui, J.; Xu, Z.; Wang, Y.; Jiang, C. Mass and energy-preserving exponential Runge-Kutta methods for the nonlinear Schrödinger equation. Appl. Math. Lett. 2021, 112, 106770. [Google Scholar] [CrossRef]
- Li, X.; Gong, Y.; Zhang, L. Linear high-Order energy-preserving schemes for the nonlinear schrödinger equation with wave operator using the scalar auxiliary variable approach. J. Sci. Comput. 2021, 88, 1–25. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, G.; Wu, B. Fully-discrete energy-preserving scheme for the space-fractional Klein-Gordon equation via Lagrange multiplier type scalar auxiliary variable approach. Math. Comput. Simul. 2022, 192, 265–277. [Google Scholar] [CrossRef]
- Hendy, A.S.; Macías-Díaz, J. On a nonlinear energy-conserving scalar auxiliary variable (SAV) model for Riesz space-fractional hyperbolic equations. Appl. Numer. Math. 2021, 165, 339–347. [Google Scholar] [CrossRef]
- Lischke, A.; Pang, G.; Gulian, M. What is the fractional Laplacian? A comparative review with new results. J. Comput. Phys. 2020, 404, 109009. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, F.; Turner, I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Mathe. Model. 2010, 34, 200–218. [Google Scholar] [CrossRef] [Green Version]
- Vong, S.; Wang, Z. A compact difference scheme for a two dimensional fractional Klein-Gordon equation with Neumann boundary conditions. J. Comput. Phys. 2014, 274, 268–282. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, X.; Liu, F.; Turner, I. High order unconditionally stable difference schemes for the Riesz space-fractional telegraph equation. J. Comput. Appl. Math. 2015, 278, 119–129. [Google Scholar] [CrossRef] [Green Version]
- Leimkuhler, B.; Reich, S. Simulating Hamiltonian Dynamics; Number 14; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 31. [Google Scholar]
- Wang, P.; Huang, C. An implicit midpoint difference scheme for the fractional Ginzburg-Landau equation. J. Comput. Phys. 2016, 312, 31–49. [Google Scholar] [CrossRef] [Green Version]
- Hu, D.; Cai, W.; Song, Y.; Wang, Y. A fourth-order dissipation-preserving algorithm with fast implementation for space fractional nonlinear damped wave equations. Commun. Nonlinear Sci. Numer. Simul. 2020, 91, 105432. [Google Scholar] [CrossRef]
- Xing, Z.; Wen, L.; Wang, W. An explicit fourth-order energy-preserving difference scheme for the Riesz space-fractional sine-Gordon equations. Math. Comput. Simul. 2021, 181, 624–641. [Google Scholar] [CrossRef]
- Jiang, C.; Cai, W.; Wang, Y. A linearly implicit and local energy-preserving scheme for the sine-Gordon equation based on the invariant energy quadratization approach. J. Sci. Comput. 2019, 80, 1629–1655. [Google Scholar] [CrossRef] [Green Version]
| EOC | EOC | EOC | |||||
|---|---|---|---|---|---|---|---|
| 0 | 1/32 | – | – | – | |||
| 1/64 | 3.3440 | 3.2321 | 3.4569 | ||||
| 1/128 | 3.2372 | 3.7035 | 3.5815 | ||||
| 1/256 | 3.5794 | 3.9308 | 3.8328 | ||||
| 1/512 | 3.7820 | 4.0795 | 3.9063 | ||||
| 1/32 | – | – | – | ||||
| 1/64 | 3.3999 | 3.1503 | 3.5561 | ||||
| 1/128 | 3.2497 | 3.6848 | 3.6252 | ||||
| 1/256 | 3.5911 | 3.9302 | 3.8324 | ||||
| 1/512 | 3.8009 | 3.9659 | 3.9118 | ||||
| EOC | EOC | EOC | ||||
|---|---|---|---|---|---|---|
| 1/4 | – | – | – | |||
| 1/8 | 5.1271 | 2.1051 | 2.9932 | |||
| 1/16 | 1.5745 | 3.5800 | 3.7804 | |||
| 1/32 | 2.2323 | 3.8479 | 3.9265 | |||
| 1/64 | 1.7511 | 1.0540 | 3.6865 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Shan, W.; Zhang, Y. High-Order Dissipation-Preserving Methods for Nonlinear Fractional Generalized Wave Equations. Fractal Fract. 2022, 6, 264. https://doi.org/10.3390/fractalfract6050264
Li Y, Shan W, Zhang Y. High-Order Dissipation-Preserving Methods for Nonlinear Fractional Generalized Wave Equations. Fractal and Fractional. 2022; 6(5):264. https://doi.org/10.3390/fractalfract6050264
Chicago/Turabian StyleLi, Yu, Wei Shan, and Yanming Zhang. 2022. "High-Order Dissipation-Preserving Methods for Nonlinear Fractional Generalized Wave Equations" Fractal and Fractional 6, no. 5: 264. https://doi.org/10.3390/fractalfract6050264
APA StyleLi, Y., Shan, W., & Zhang, Y. (2022). High-Order Dissipation-Preserving Methods for Nonlinear Fractional Generalized Wave Equations. Fractal and Fractional, 6(5), 264. https://doi.org/10.3390/fractalfract6050264







