Second-Order Time Stepping Scheme Combined with a Mixed Element Method for a 2D Nonlinear Fourth-Order Fractional Integro-Differential Equations
Abstract
:1. Introduction
2. Fully Discrete Scheme
3. Stability Analysis
4. Error Analysis
5. Numerical Tests
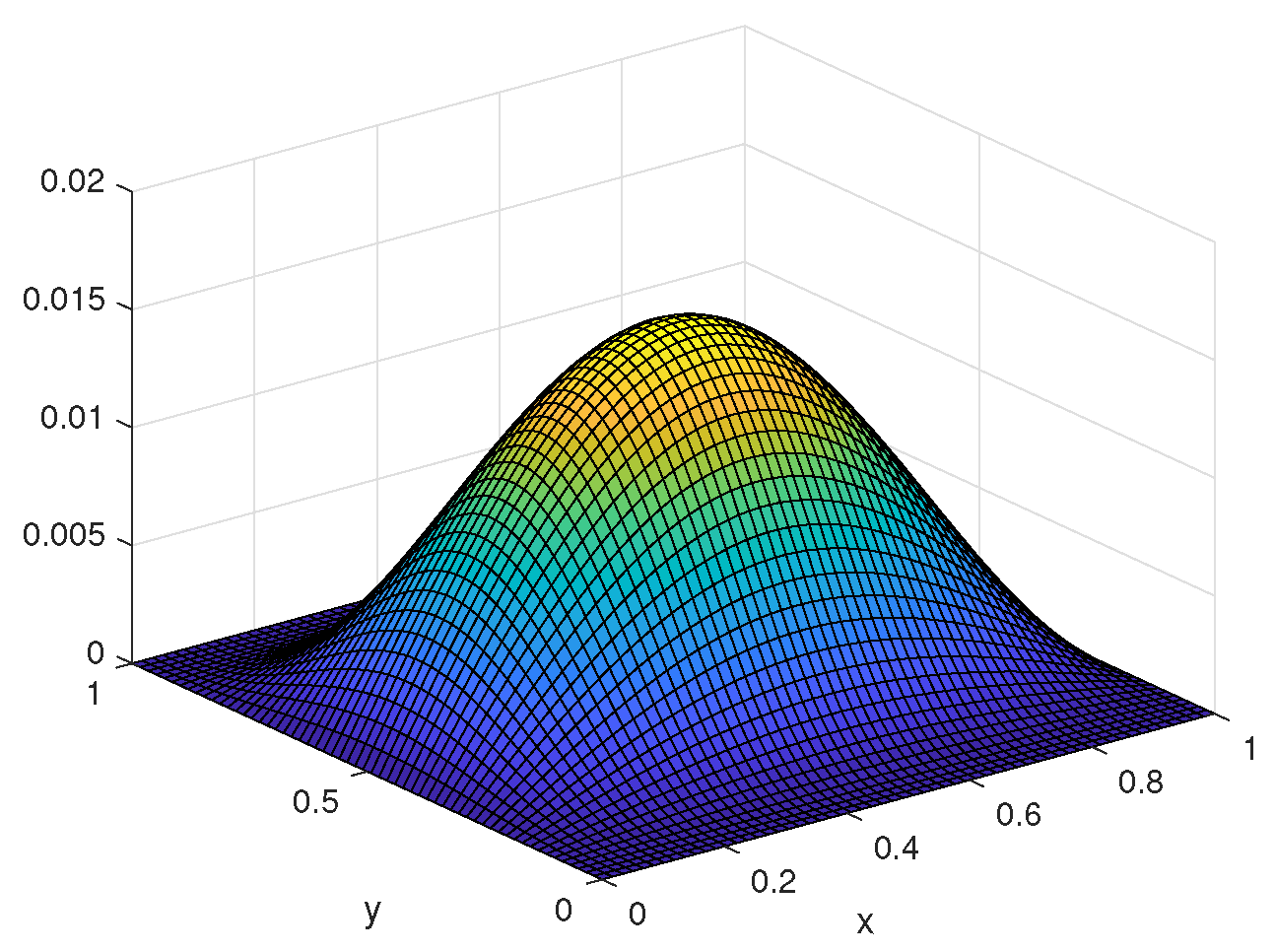
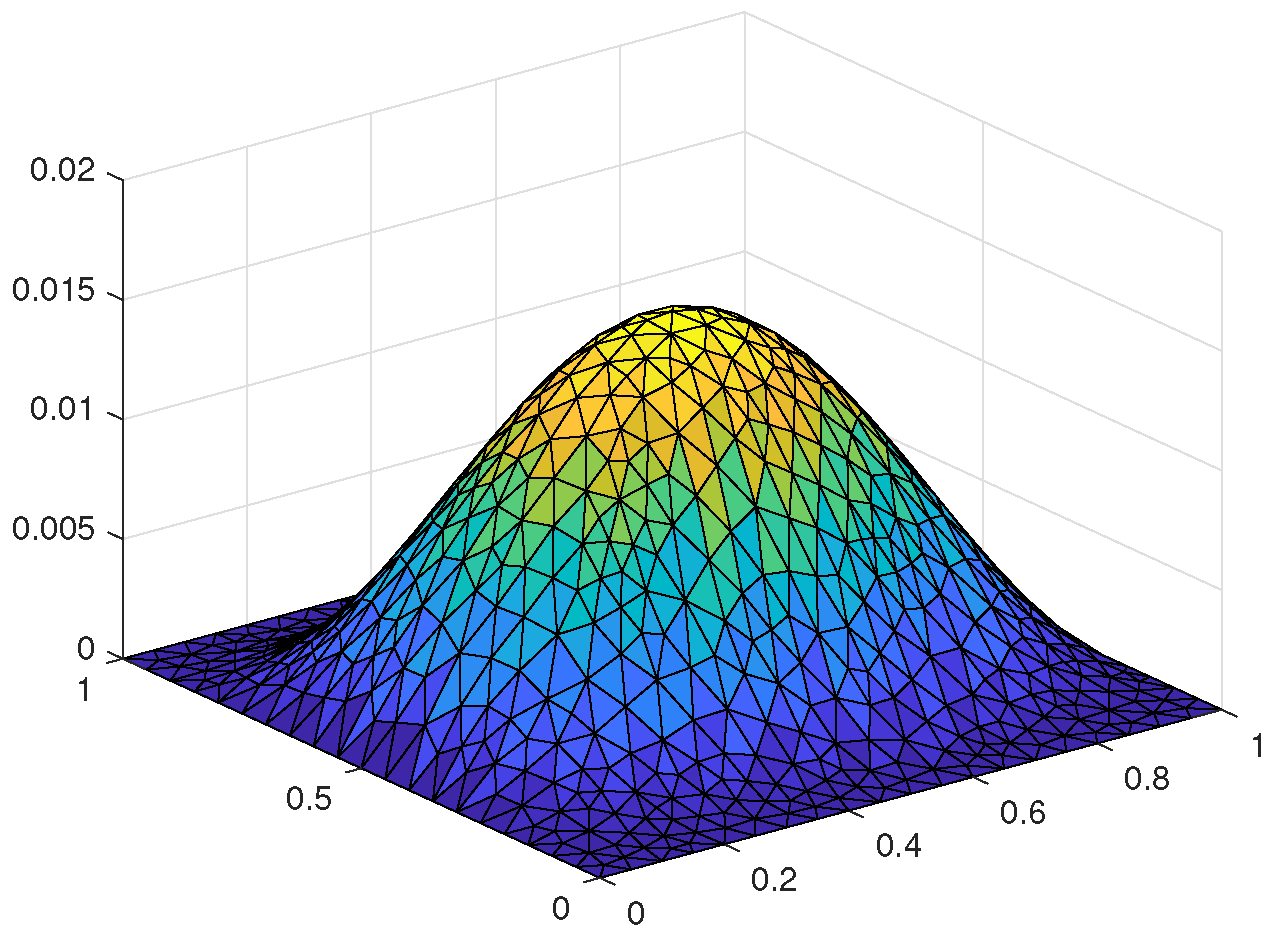
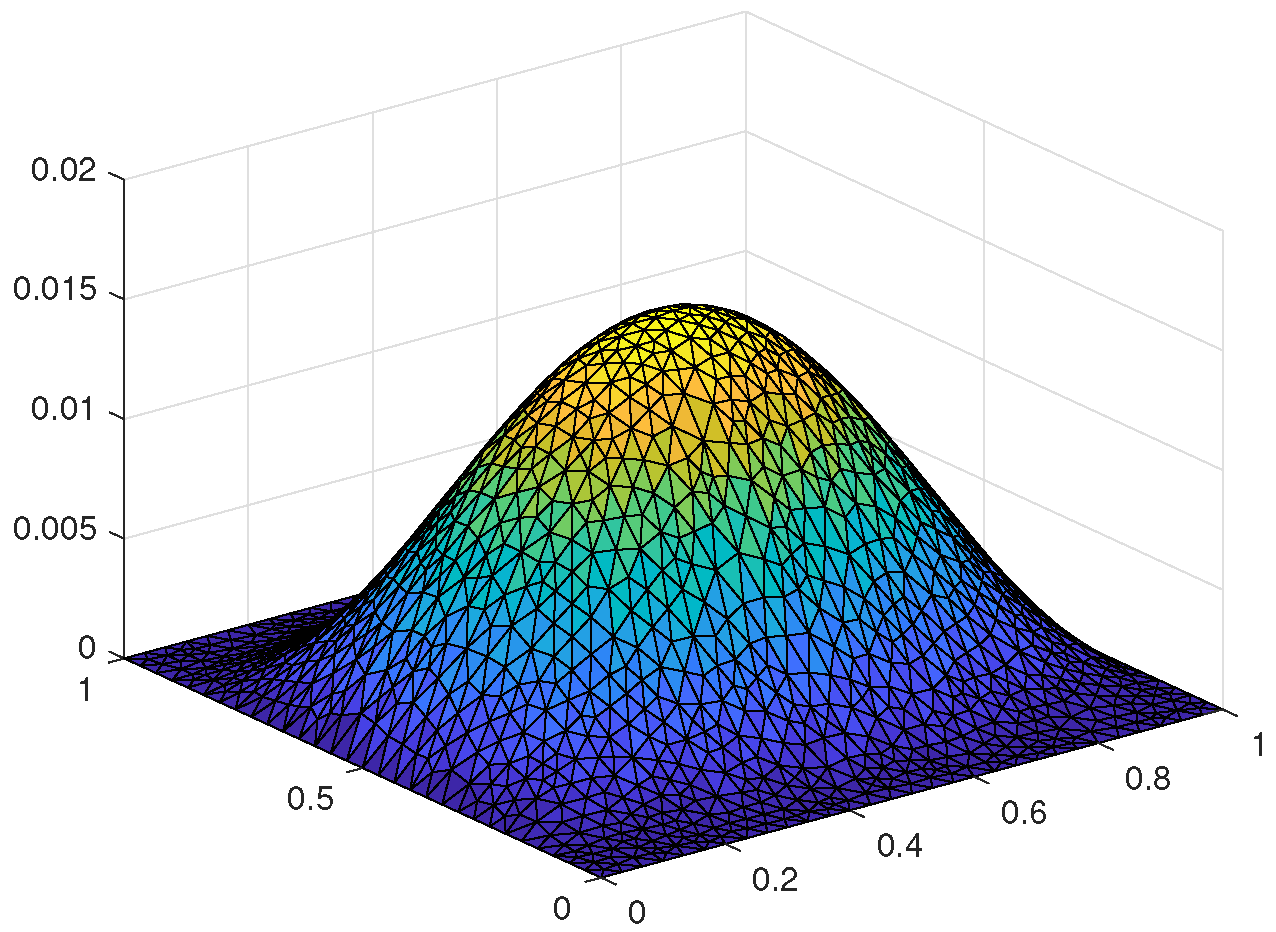
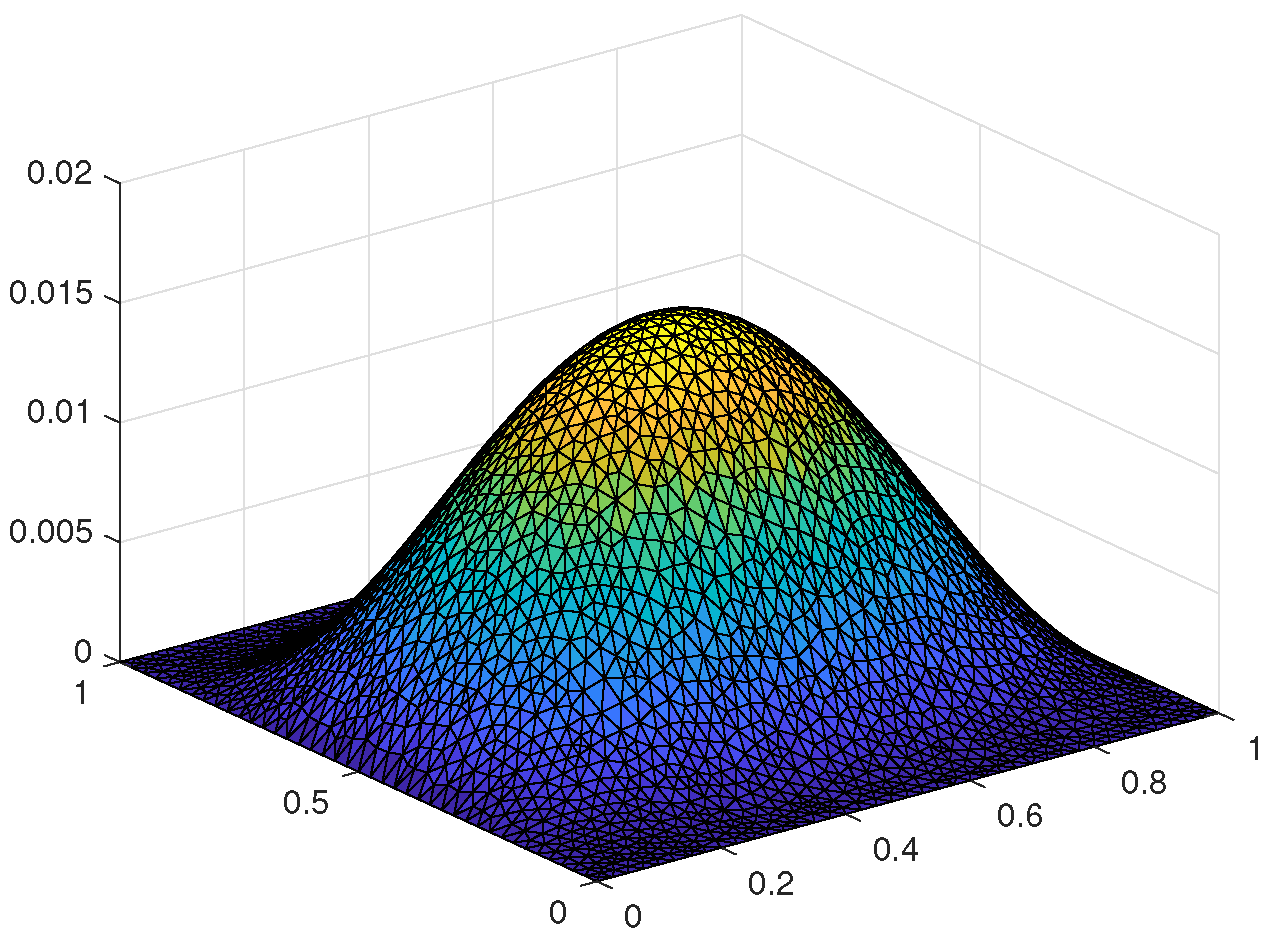
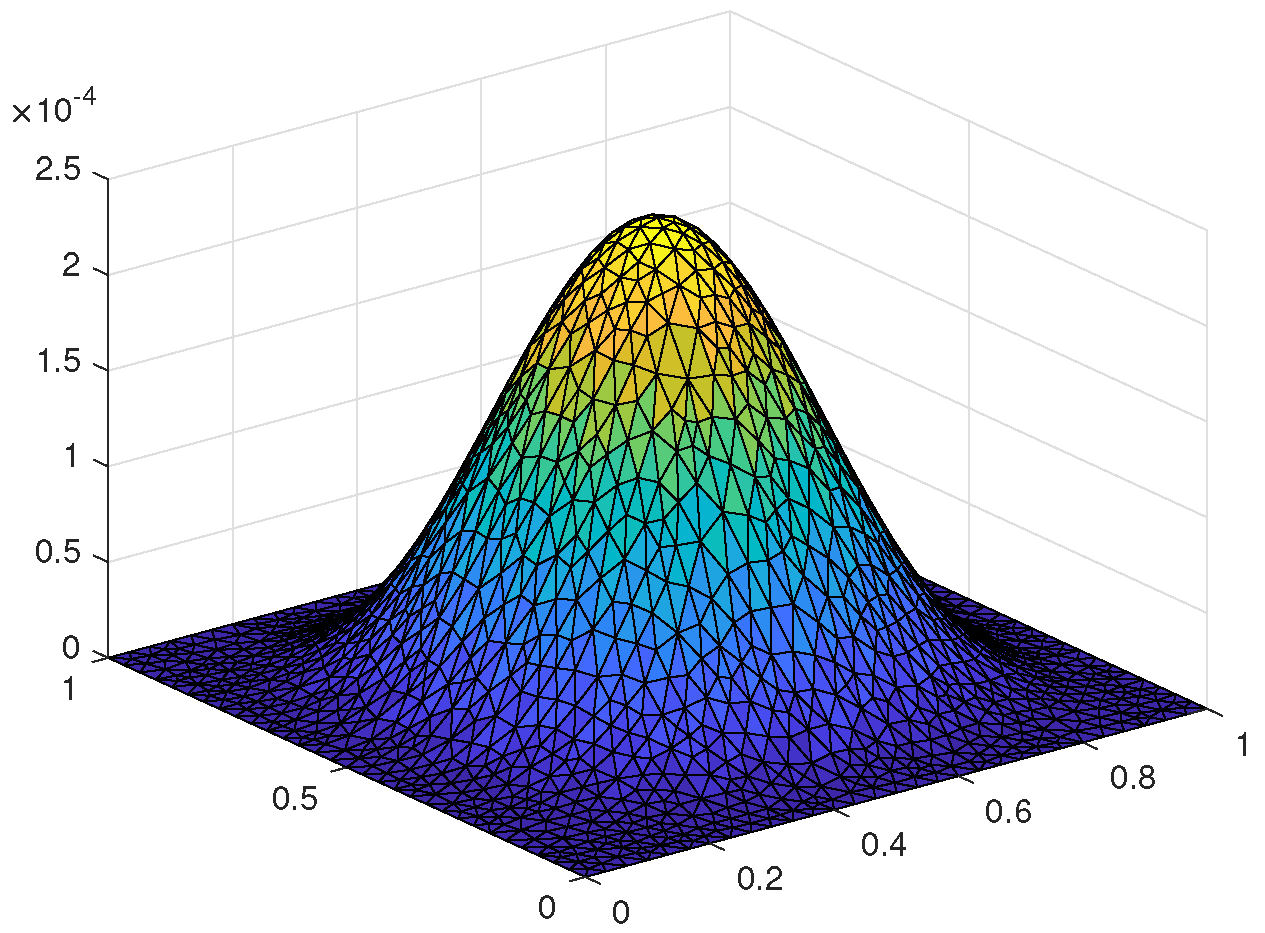
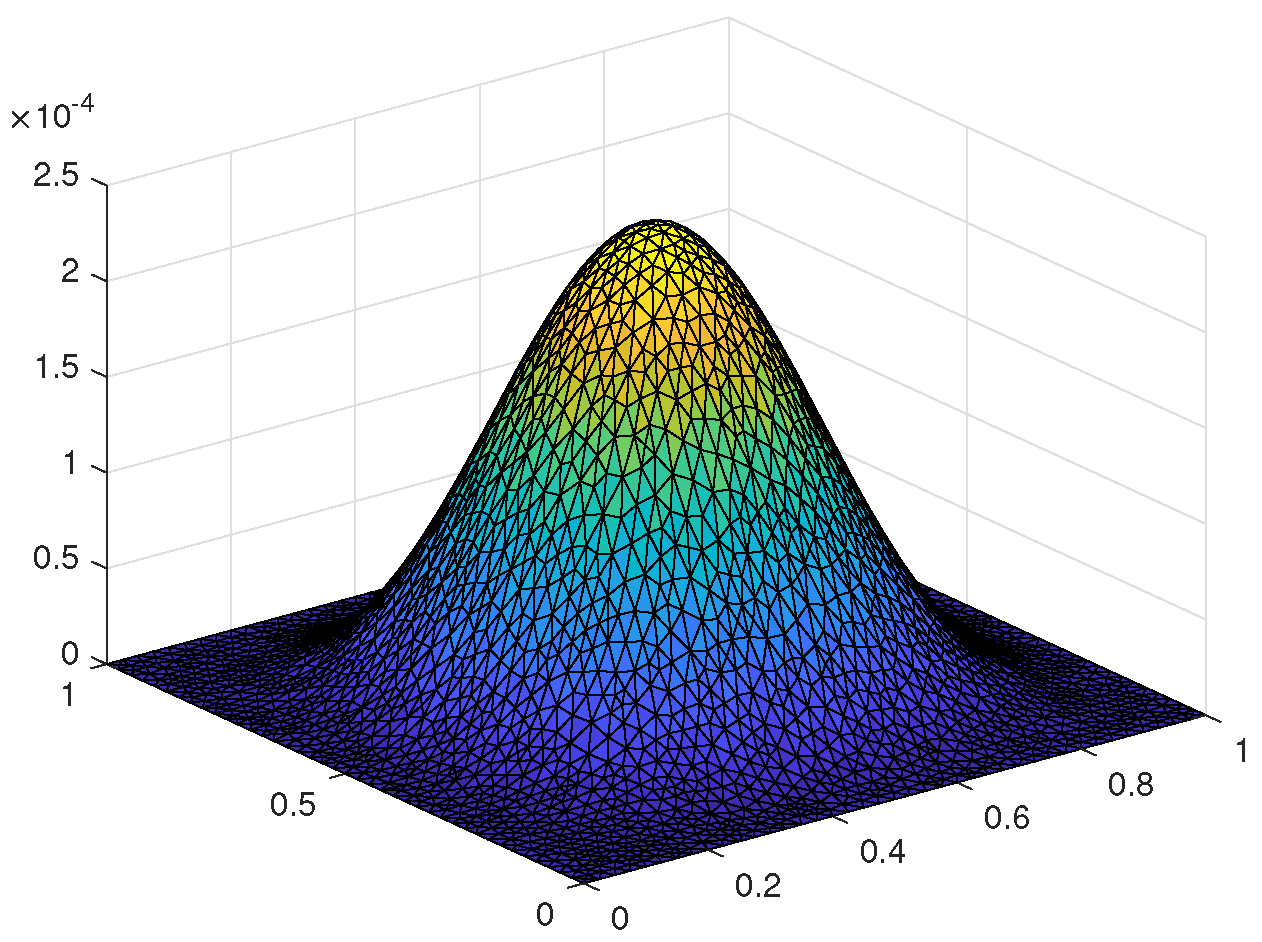
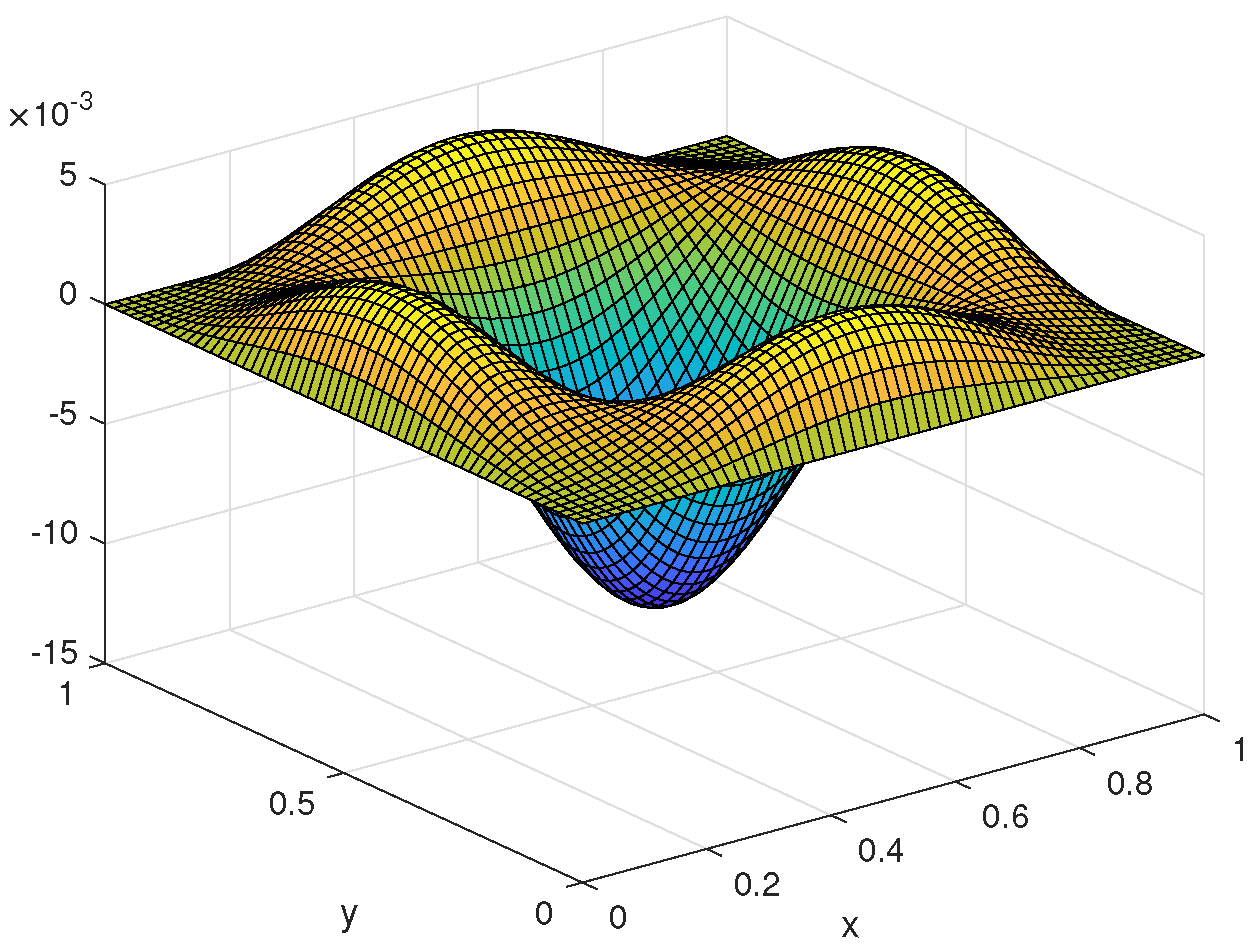
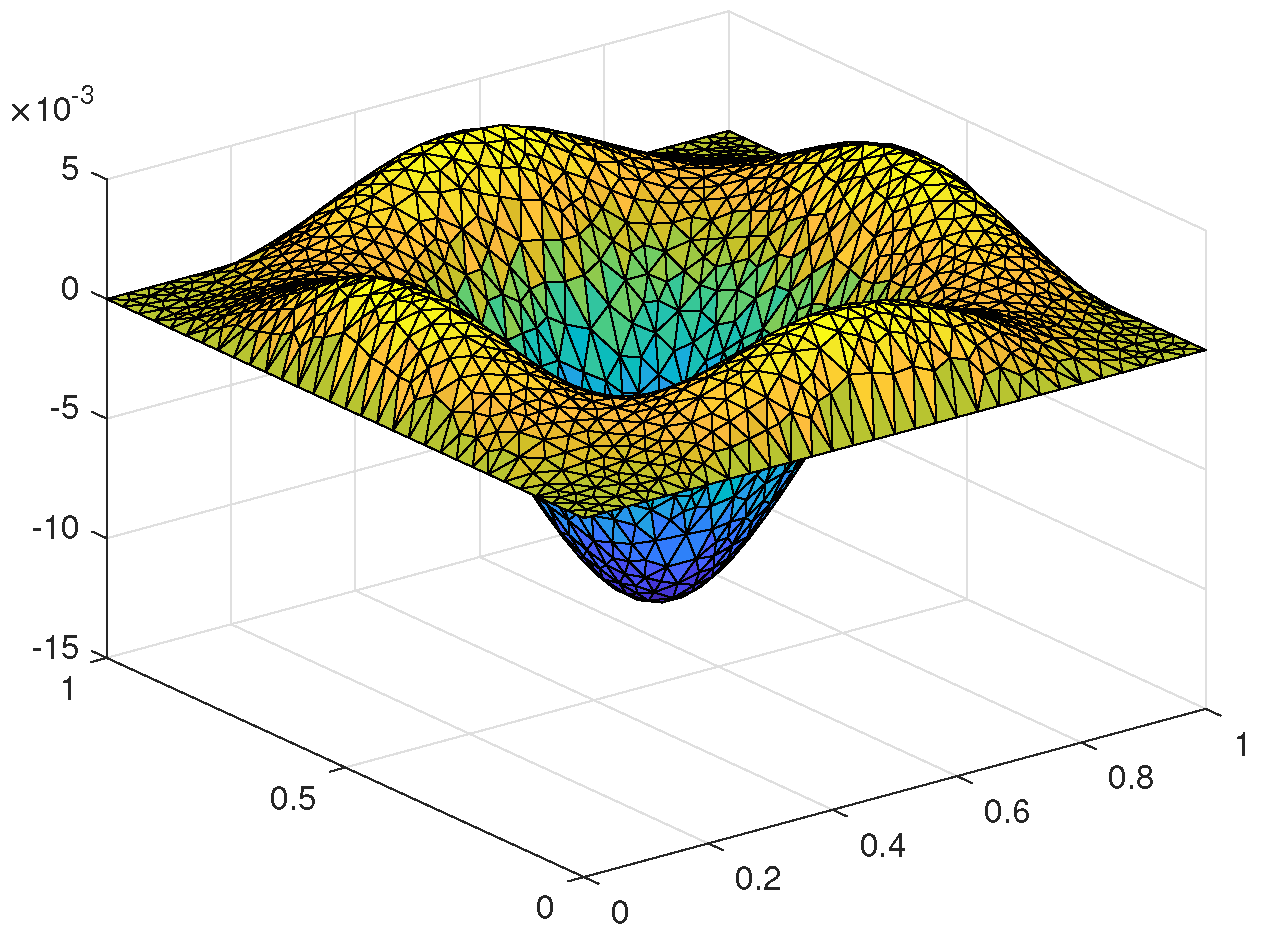
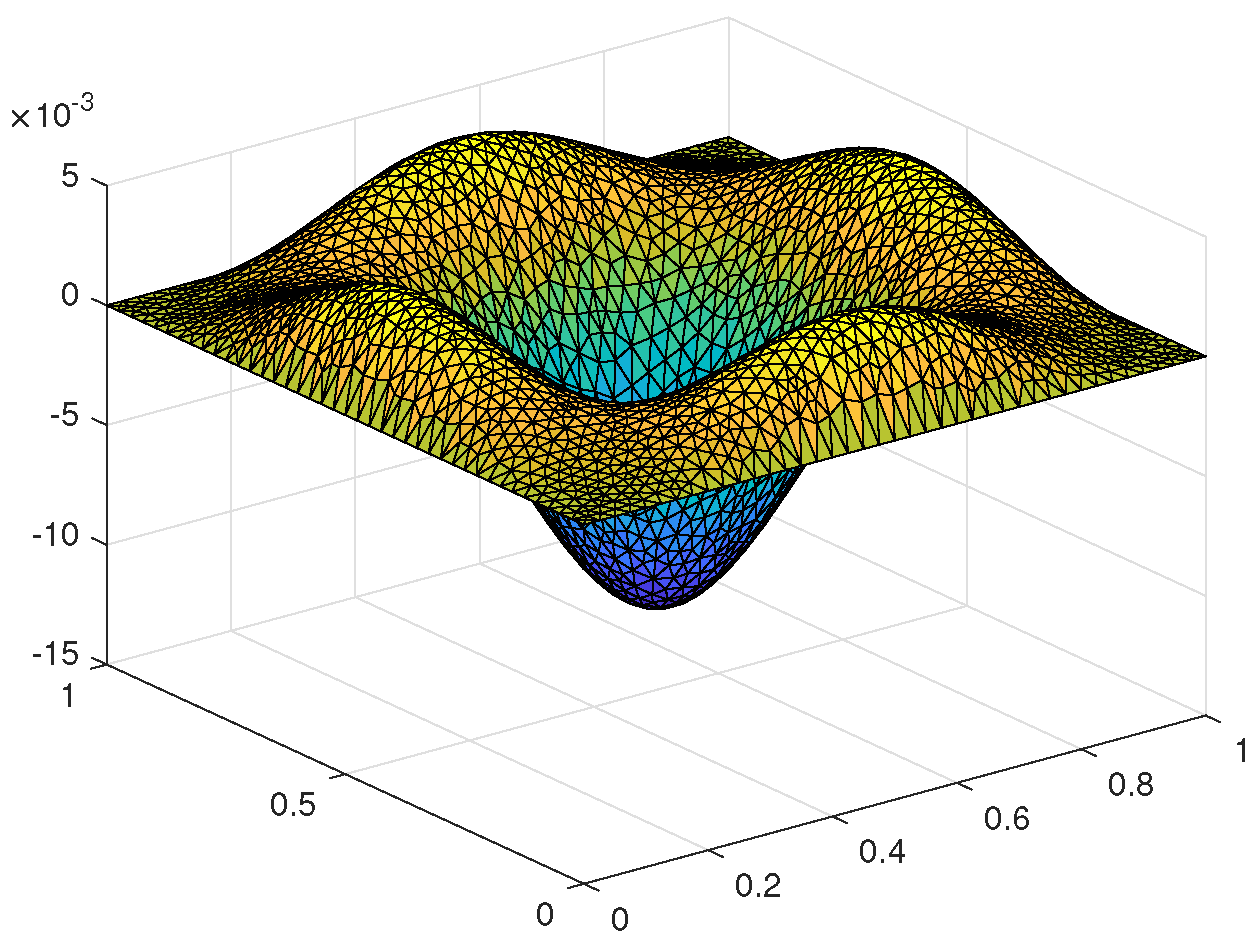
5.1. Two-Dimensional Example Based on the Triangular Meshes
5.1.1. Numerical Algorithm
5.1.2. Numerical Calculations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abbaszadeh, M.; Dehghan, M. Direct meshless local Petrov-Galerkin (DMLPG) method for time-fractional fourth-order reaction-diffusion problem on complex domains. Comput. Math. Appl. 2020, 79, 876–888. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.W.; Li, H.; Li, J.C.; He, S. A two-grid mixed finite element method for a nonlinear fourth-order reaction-diffusion problem with time-fractional derivative. Comput. Math. Appl. 2015, 70, 2474–2492. [Google Scholar] [CrossRef]
- Nikan, O.; Machado, J.A.T.; Golbabai, A. Numerical solution of time-fractional fourth-order reaction-diffusion model arising in composite environments. Appl. Math. Model. 2021, 89, 819–836. [Google Scholar] [CrossRef]
- Ji, C.C.; Sun, Z.Z.; Hao, Z.P. Numerical algorithms with high spatial accuracy for the fourth-order fractional sub-diffusion equations with the first Dirichlet boundary conditions. J. Sci. Comput. 2016, 66, 1148–1174. [Google Scholar] [CrossRef]
- Haghi, M.; Ilati, M.; Dehghan, M. A fourth-order compact difference method for the nonlinear time-fractional fourth-order reaction-diffusion equation. Eng. Comput. 2021, 1–12. [Google Scholar] [CrossRef]
- Wang, J.R.; Liu, Y.; Wen, C.; Li, H. Efficient numerical algorithm with the second-order time accuracy for a two-dimensional nonlinear fourth-order fractional wave equation. Results Appl. Math. 2022. [Google Scholar]
- Li, X.H.; Wong, P.J.Y. A non-polynomial numerical scheme for fourth-order fractional diffusion-wave model. Appl. Math. Comput. 2018, 331, 80–95. [Google Scholar] [CrossRef]
- Akram, G.; Abbas, M.; Tariq, H.; Sadaf, M.; Abdeljawad, T.; Alqudah, M.A. Numerical approximations for the solutions of fourth order time fractional evolution problems using a novel spline technique. Fractal Fract. 2022, 6, 170. [Google Scholar] [CrossRef]
- Fakhar-Izadi, F.; Shabgard, N. Time-space spectral Galerkin method for time-fractional fourth-order partial differential equations. J. Appl. Math. Comput. 2022, 1–20. [Google Scholar] [CrossRef]
- Arshad, S.; Wali, M.; Huang, J.F.; Khalid, S.; Akbar, N. Numerical framework for the Caputo time-fractional diffusion equation with fourth order derivative in space. J. Appl. Math. Comput. 2021, 1–22. [Google Scholar] [CrossRef]
- Nandal, S.; Pandey, D.N. Numerical technique for fractional variable-order differential equation of fourth-order with delay. Appl. Numer. Math. 2021, 161, 391–407. [Google Scholar] [CrossRef]
- Ran, M.H.; Zhang, C.J. New compact difference scheme for solving the fourth-order time fractional sub-diffusion equation of the distributed order. Appl. Numer. Math. 2018, 129, 58–70. [Google Scholar] [CrossRef]
- Nawaz, Y. Variational iteration method and homotopy perturbation method for fourth-order fractional integro-differential equations. Comput. Math. Appl. 2011, 61, 2330–2341. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.H.; Xu, D.; Zhang, H.X. Crank-Nicolson/quasi-wavelets method for solving fourth order partial integro-differential equation with a weakly singular kernel. J. Comput. Phys. 2013, 234, 317–329. [Google Scholar] [CrossRef]
- Liu, Y.L.; Yang, X.H.; Zhang, H.X.; Liu, Y. Analysis of BDF2 finite difference method for fourth-order integro-differential equation. Comput. Appl. Math. 2021, 40, 57. [Google Scholar] [CrossRef]
- Qiu, W.L.; Xu, D.; Guo, J. Numerical solution of the fourth-order partial integro-differential equation with multi-term kernels by the Sinc-collocation method based on the double exponential transformation. Appl. Math. Comput. 2021, 392, 125693. [Google Scholar] [CrossRef]
- Wang, Z.B.; Vong, S. Compact difference schemes for the modified anomalous fractional sub-diffusion equation and the fractional diffusion-wave equation. J. Comput. Phys. 2014, 277, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Tian, W.Y.; Zhou, H.; Deng, W.H. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef] [Green Version]
- Feng, R.H.; Liu, Y.; Hou, Y.X.; Li, H.; Fang, Z.C. Mixed element algorithm based on a second-order time approximation scheme for a two-dimensional nonlinear time fractional coupled sub-diffusion model. Eng. Comput. 2022, 38, 51–68. [Google Scholar] [CrossRef]
- Cao, Y.; Yin, B.L.; Liu, Y.; Li, H. Crank-Nicolson WSGI difference scheme with finite element method for multi-dimensional time-fractional wave problem. Comput. Appl. Math. 2018, 37, 5126–5145. [Google Scholar] [CrossRef]
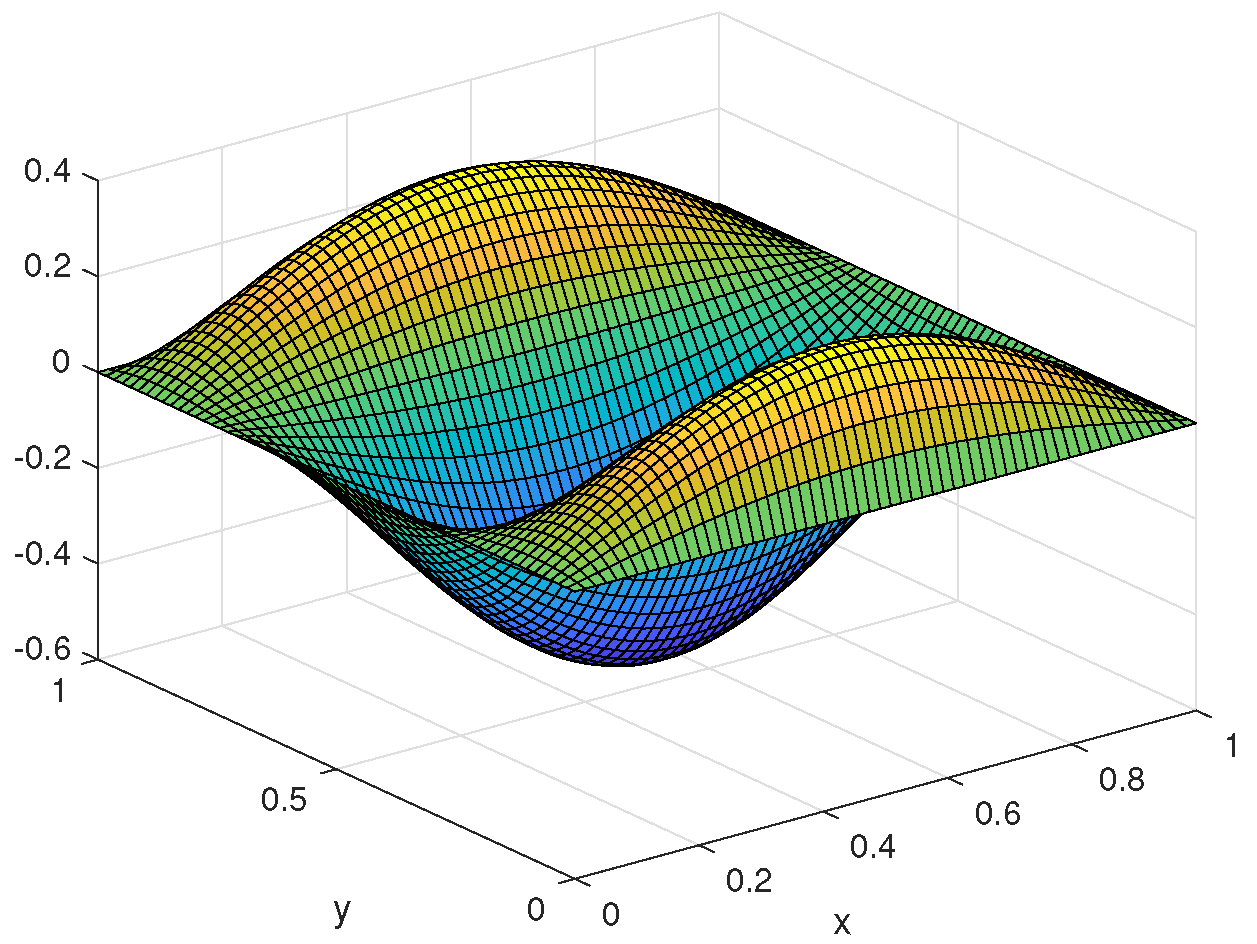
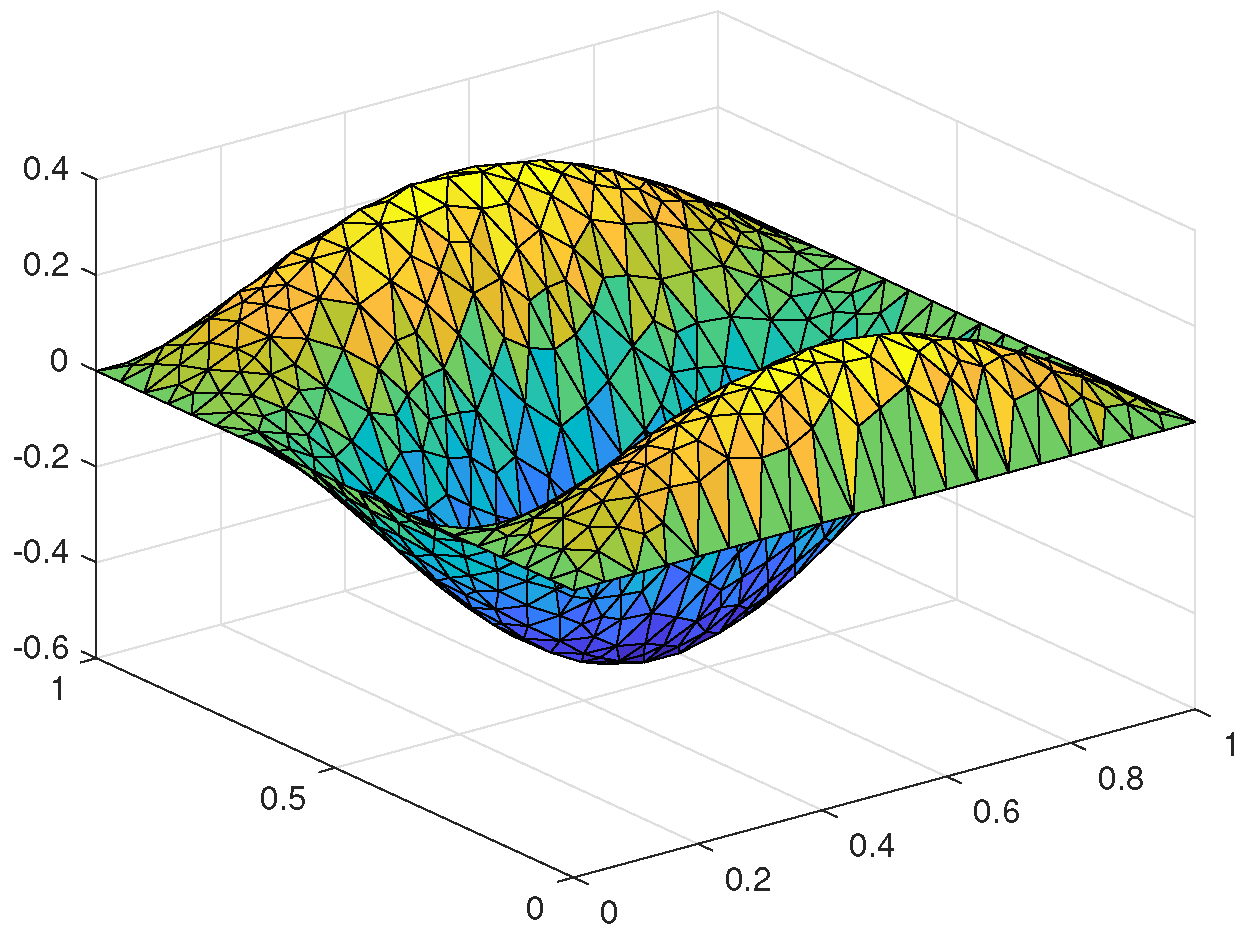

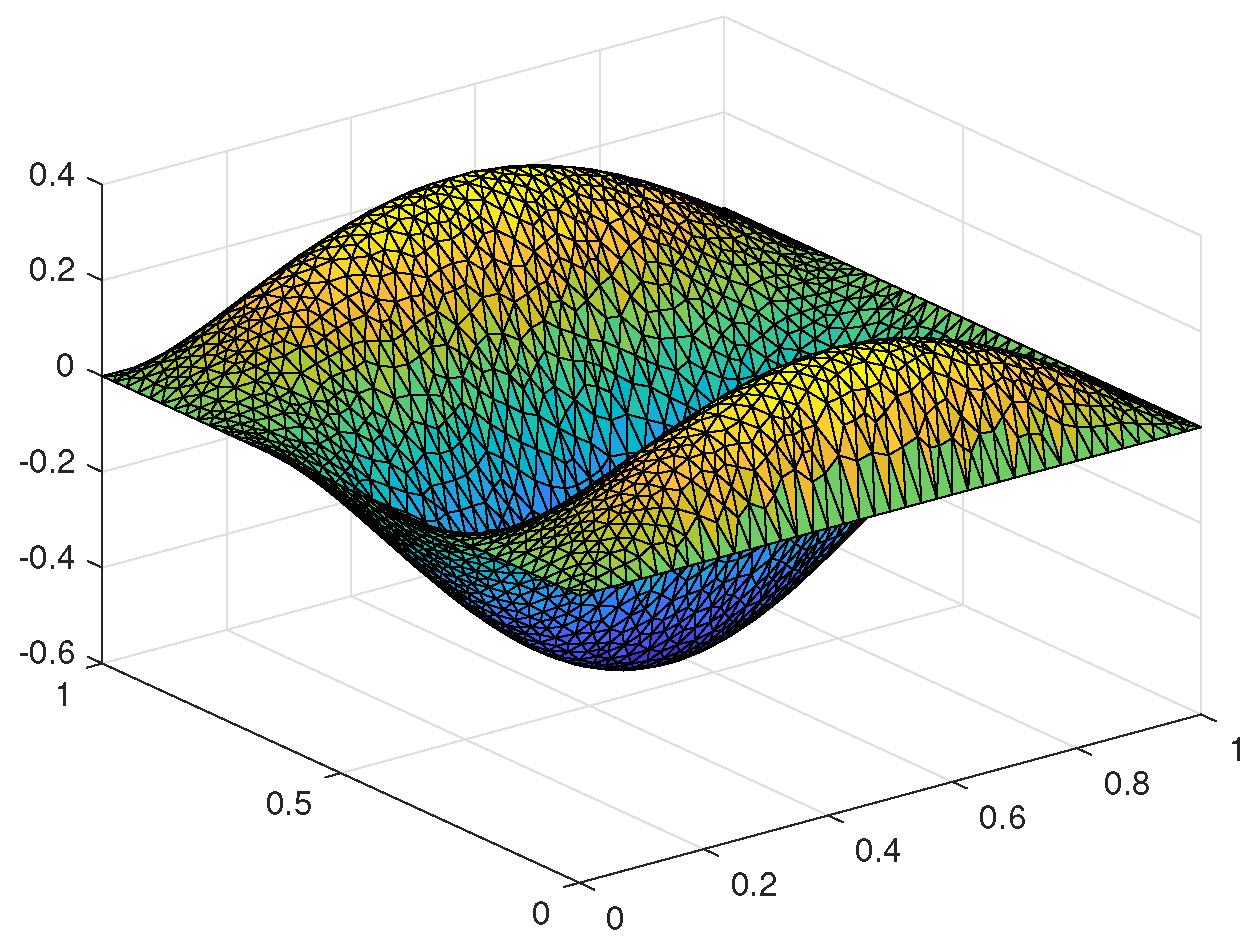

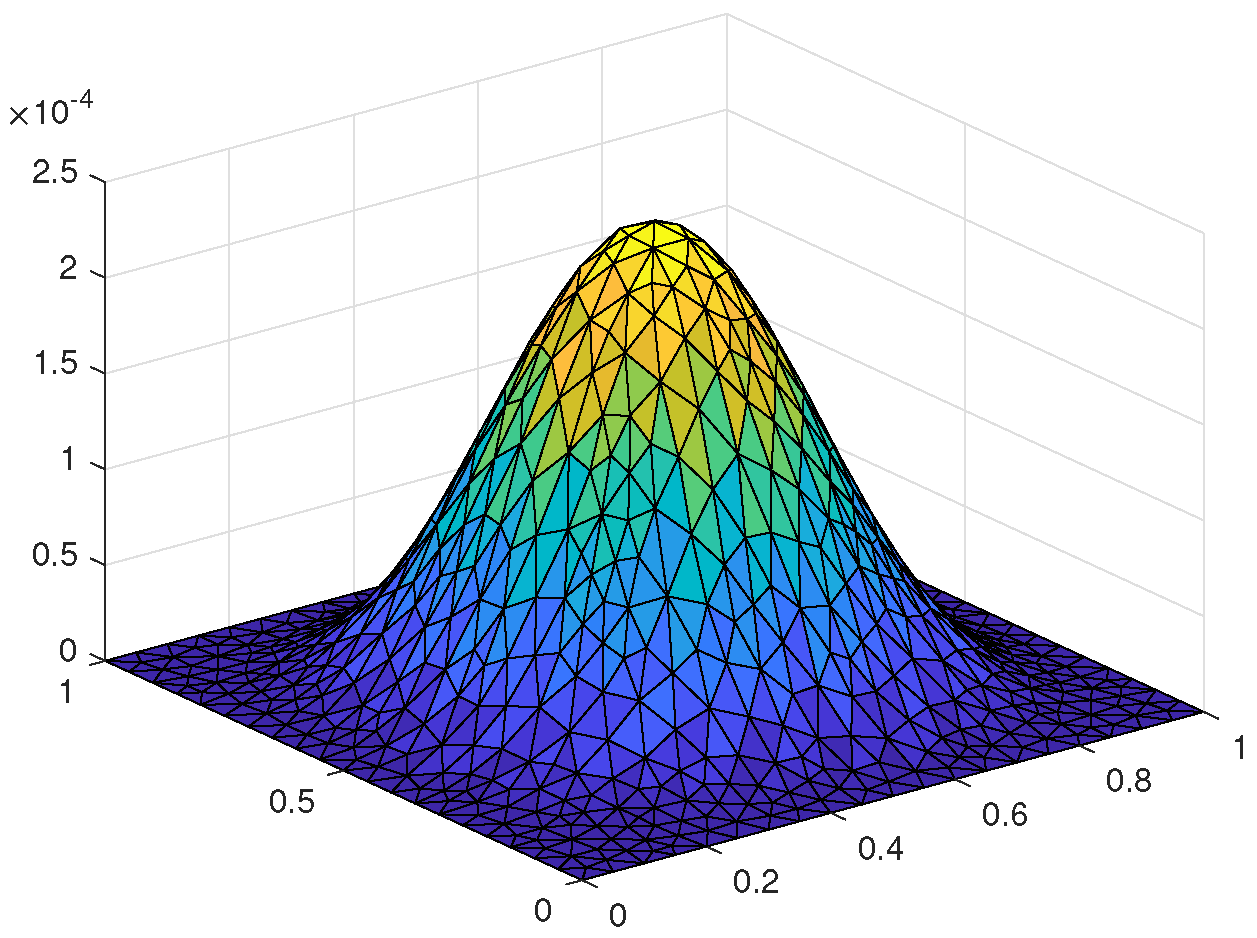

| h | Rate | Rate | |||
|---|---|---|---|---|---|
| 0.1 | 1/4 | 1.2160 × 10 | — | 7.3073 × 10 | — |
| 1/8 | 3.0300 × 10 | 2.0047 | 1.8151 × 10 | 2.0093 | |
| 1/16 | 7.5223 × 10 | 2.0101 | 4.7932 × 10 | 1.9210 | |
| 1/32 | 1.8735 × 10 | 2.0054 | 1.1330 × 10 | 2.0809 | |
| 0.3 | 1/4 | 1.2189 × 10 | — | 7.3130 × 10 | — |
| 1/8 | 3.0367 × 10 | 2.0050 | 1.8170 × 10 | 2.0089 | |
| 1/16 | 7.5369 × 10 | 2.0104 | 4.7981 × 10 | 1.9210 | |
| 1/32 | 1.8771 × 10 | 2.0055 | 1.1342 × 10 | 2.0807 | |
| 0.5 | 1/4 | 1.2212 × 10 | — | 7.3175 × 10 | — |
| 1/8 | 3.0420 × 10 | 2.0052 | 1.8185 × 10 | 2.0086 | |
| 1/16 | 7.5486 × 10 | 2.0107 | 4.8020 × 10 | 1.9210 | |
| 1/32 | 1.8799 × 10 | 2.0055 | 1.1353 × 10 | 2.0806 | |
| 0.7 | 1/4 | 1.2230 × 10 | — | 7.3210 × 10 | — |
| 1/8 | 3.0463 × 10 | 2.0054 | 1.8197 × 10 | 2.0084 | |
| 1/16 | 7.5579 × 10 | 2.0110 | 4.8052 × 10 | 1.9210 | |
| 1/32 | 1.8821 × 10 | 2.0056 | 1.1361 × 10 | 2.0806 | |
| 0.9 | 1/4 | 1.2245 × 10 | — | 7.3238 × 10 | — |
| 1/8 | 3.0496 × 10 | 2.0055 | 1.8206 × 10 | 2.0082 | |
| 1/16 | 7.5651 × 10 | 2.0112 | 4.8076 × 10 | 1.9210 | |
| 1/32 | 1.8839 × 10 | 2.0057 | 1.1367 × 10 | 2.0805 |
| Rate | Rate | ||||
|---|---|---|---|---|---|
| 0.1 | (1/10,1/10) | 2.0896 × 10 | — | 1.3569 × 10 | — |
| (1/20,1/20) | 4.6046 × 10 | 2.1821 | 3.0399 × 10 | 2.1582 | |
| (1/30,1/30) | 2.0672 × 10 | 1.9751 | 1.3515 × 10 | 1.9993 | |
| (1/40,1/40) | 1.1502 × 10 | 2.0381 | 7.4700 × 10 | 2.0609 | |
| 0.3 | (1/10,1/10) | 2.0955 × 10 | — | 1.3585 × 10 | — |
| (1/20,1/20) | 4.6178 × 10 | 2.1820 | 3.0437 × 10 | 2.1582 | |
| (1/30,1/30) | 2.0731 × 10 | 1.9753 | 1.3532 × 10 | 1.9992 | |
| (1/40,1/40) | 1.1535 × 10 | 2.0377 | 7.4796 × 10 | 2.0609 | |
| 0.5 | (1/10,1/10) | 2.0995 × 10 | — | 1.3597 × 10 | — |
| (1/20,1/20) | 4.6263 × 10 | 2.1821 | 3.0465 × 10 | 2.1581 | |
| (1/30,1/30) | 2.0768 × 10 | 1.9754 | 1.3545 × 10 | 1.9991 | |
| (1/40,1/40) | 1.1557 × 10 | 2.0374 | 7.4866 × 10 | 2.0609 | |
| 0.7 | (1/10,1/10) | 2.1018 × 10 | — | 1.3606 × 10 | — |
| (1/20,1/20) | 4.6309 × 10 | 2.1822 | 3.0484 × 10 | 2.1581 | |
| (1/30,1/30) | 2.0788 × 10 | 1.9754 | 1.3554 × 10 | 1.9990 | |
| (1/40,1/40) | 1.1568 × 10 | 2.0373 | 7.4916 × 10 | 2.0609 | |
| 0.9 | (1/10,1/10) | 2.1028 × 10 | — | 1.3612 × 10 | — |
| (1/20,1/20) | 4.6327 × 10 | 2.1824 | 3.0498 × 10 | 2.1581 | |
| (1/30,1/30) | 2.0795 × 10 | 1.9755 | 1.3560 × 10 | 1.9990 | |
| (1/40,1/40) | 1.1573 × 10 | 2.0373 | 7.4950 × 10 | 2.0609 |
| h | Rate | Rate | |||
|---|---|---|---|---|---|
| 0.1 | 1/4 | 1.9466 × 10 | — | 1.4787 × 10 | — |
| 1/8 | 4.8028 × 10 | 2.0190 | 3.2835 × 10 | 2.1711 | |
| 1/16 | 1.2213 × 10 | 1.9755 | 8.8243 × 10 | 1.8957 | |
| 1/32 | 3.1213 × 10 | 1.9682 | 2.1371 × 10 | 2.0458 | |
| 0.3 | 1/4 | 1.9495 × 10 | — | 1.4795 × 10 | — |
| 1/8 | 4.8101 × 10 | 2.0190 | 3.2864 × 10 | 2.1705 | |
| 1/16 | 1.2229 × 10 | 1.9758 | 8.8322 × 10 | 1.8957 | |
| 1/32 | 3.1254 × 10 | 1.9682 | 2.1392 × 10 | 2.0457 | |
| 0.5 | 1/4 | 1.9520 × 10 | — | 1.4801 × 10 | — |
| 1/8 | 4.8163 × 10 | 2.0190 | 3.2889 × 10 | 2.1701 | |
| 1/16 | 1.2242 × 10 | 1.9760 | 8.8388 × 10 | 1.8957 | |
| 1/32 | 3.1289 × 10 | 1.9681 | 2.1409 × 10 | 2.0456 | |
| 0.7 | 1/4 | 1.9541 × 10 | — | 1.4806 × 10 | — |
| 1/8 | 4.8213 × 10 | 2.0190 | 3.2909 × 10 | 2.1697 | |
| 1/16 | 1.2253 × 10 | 1.9763 | 8.8442 × 10 | 1.8957 | |
| 1/32 | 3.1317 × 10 | 1.9681 | 2.1423 × 10 | 2.0456 | |
| 0.9 | 1/4 | 1.9557 × 10 | — | 1.4811 × 10 | — |
| 1/8 | 4.8254 × 10 | 2.0190 | 3.2925 × 10 | 2.1694 | |
| 1/16 | 1.2262 × 10 | 1.9764 | 8.8485 × 10 | 1.8957 | |
| 1/32 | 3.1340 × 10 | 1.9681 | 2.1434 × 10 | 2.0455 |
| Rate | Rate | ||||
|---|---|---|---|---|---|
| 0.1 | (1/10,1/10) | 3.6207 × 10 | — | 2.5835 × 10 | — |
| (1/20,1/20) | 8.4923 × 10 | 2.0920 | 5.9985 × 10 | 2.1066 | |
| (1/30,1/30) | 3.7741 × 10 | 2.0002 | 2.6440 × 10 | 2.0204 | |
| (1/40,1/40) | 2.0890 × 10 | 2.0561 | 1.4528 × 10 | 2.0816 | |
| 0.3 | (1/10,1/10) | 3.6281 × 10 | — | 2.5859 × 10 | — |
| (1/20,1/20) | 8.5093 × 10 | 2.0921 | 6.0046 × 10 | 2.1065 | |
| (1/30,1/30) | 3.7812 × 10 | 2.0005 | 2.6468 × 10 | 2.0203 | |
| (1/40,1/40) | 2.0931 × 10 | 2.0556 | 1.4543 × 10 | 2.0816 | |
| 0.5 | (1/10,1/10) | 3.6338 × 10 | — | 2.5879 × 10 | — |
| (1/20,1/20) | 8.5222 × 10 | 2.0922 | 6.0095 × 10 | 2.1065 | |
| (1/30,1/30) | 3.7865 × 10 | 2.0008 | 2.6490 × 10 | 2.0203 | |
| (1/40,1/40) | 2.0963 × 10 | 2.0553 | 1.4555 × 10 | 2.0816 | |
| 0.7 | (1/10,1/10) | 3.6379 × 10 | — | 2.5894 × 10 | — |
| (1/20,1/20) | 8.5315 × 10 | 2.0923 | 6.0133 × 10 | 2.1064 | |
| (1/30,1/30) | 3.7903 × 10 | 2.0010 | 2.6508 × 10 | 2.0202 | |
| (1/40,1/40) | 2.0986 × 10 | 2.0550 | 1.4565 × 10 | 2.0816 | |
| 0.9 | (1/10,1/10) | 3.6407 × 10 | — | 2.5905 × 10 | — |
| (1/20,1/20) | 8.5375 × 10 | 2.0923 | 6.0162 × 10 | 2.1063 | |
| (1/30,1/30) | 3.7927 × 10 | 2.0011 | 2.6521 × 10 | 2.0202 | |
| (1/40,1/40) | 2.1000 × 10 | 2.0549 | 1.4572 × 10 | 2.0816 |
| h | Rate | Rate | |||
|---|---|---|---|---|---|
| 0.1 | 1/4 | 2.5596 × 10 | — | 1.8764 × 10 | — |
| 1/8 | 5.6306 × 10 | 2.1845 | 4.2919 × 10 | 2.1283 | |
| 1/16 | 1.4004 × 10 | 2.0075 | 1.0788 × 10 | 1.9922 | |
| 1/32 | 3.5652 × 10 | 1.9738 | 2.7133 × 10 | 1.9913 | |
| 0.3 | 1/4 | 2.5633 × 10 | — | 1.8737 × 10 | — |
| 1/8 | 5.6380 × 10 | 2.1847 | 4.2868 × 10 | 2.1279 | |
| 1/16 | 1.4020 × 10 | 2.0077 | 1.0776 × 10 | 1.9921 | |
| 1/32 | 3.5693 × 10 | 1.9738 | 2.7104 × 10 | 1.9913 | |
| 0.5 | 1/4 | 2.5664 × 10 | — | 1.8714 × 10 | — |
| 1/8 | 5.6443 × 10 | 2.1849 | 4.2826 × 10 | 2.1275 | |
| 1/16 | 1.4033 × 10 | 2.0079 | 1.0766 × 10 | 1.9920 | |
| 1/32 | 3.5727 × 10 | 1.9738 | 2.7079 × 10 | 1.9913 | |
| 0.7 | 1/4 | 2.5689 × 10 | — | 1.8695 × 10 | — |
| 1/8 | 5.6494 × 10 | 2.1850 | 4.2792 × 10 | 2.1272 | |
| 1/16 | 1.4044 × 10 | 2.0081 | 1.0758 × 10 | 1.9919 | |
| 1/32 | 3.5755 × 10 | 1.9738 | 2.7059 × 10 | 1.9912 | |
| 0.9 | 1/4 | 2.5710 × 10 | — | 1.8680 × 10 | — |
| 1/8 | 5.6535 × 10 | 2.1851 | 4.2765 × 10 | 2.1270 | |
| 1/16 | 1.4053 × 10 | 2.0083 | 1.0752 × 10 | 1.9919 | |
| 1/32 | 3.5777 × 10 | 1.9738 | 2.7043 × 10 | 1.9912 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Liu, Y.; Li, H.; Fang, Z. Second-Order Time Stepping Scheme Combined with a Mixed Element Method for a 2D Nonlinear Fourth-Order Fractional Integro-Differential Equations. Fractal Fract. 2022, 6, 201. https://doi.org/10.3390/fractalfract6040201
Wang D, Liu Y, Li H, Fang Z. Second-Order Time Stepping Scheme Combined with a Mixed Element Method for a 2D Nonlinear Fourth-Order Fractional Integro-Differential Equations. Fractal and Fractional. 2022; 6(4):201. https://doi.org/10.3390/fractalfract6040201
Chicago/Turabian StyleWang, Deng, Yang Liu, Hong Li, and Zhichao Fang. 2022. "Second-Order Time Stepping Scheme Combined with a Mixed Element Method for a 2D Nonlinear Fourth-Order Fractional Integro-Differential Equations" Fractal and Fractional 6, no. 4: 201. https://doi.org/10.3390/fractalfract6040201
APA StyleWang, D., Liu, Y., Li, H., & Fang, Z. (2022). Second-Order Time Stepping Scheme Combined with a Mixed Element Method for a 2D Nonlinear Fourth-Order Fractional Integro-Differential Equations. Fractal and Fractional, 6(4), 201. https://doi.org/10.3390/fractalfract6040201







