Abstract
We look at the stochastic fractional-space Bogoyavlenskii equation in the Stratonovich sense, which is driven by multiplicative noise. Our aim is to acquire analytical fractional stochastic solutions to this stochastic fractional-space Bogoyavlenskii equation via two different methods such as the -expansion method and sine–cosine method. Since this equation is used to explain the hydrodynamic model of shallow-water waves, the wave of leading fluid flow, and plasma physics, scientists will be able to characterize a wide variety of fascinating physical phenomena with these solutions. Furthermore, we evaluate the influence of noise on the behavior of the acquired solutions using 2D and 3D graphical representations.
1. Introduction
Fractional partial differential equations (FPDEs) have received much interest due to their application in several fields of science including biochemistry and chemistry [1,2], hydrology [3], biology [4,5], physics [6,7], finance [8], etc.
As a result, many researchers have recently focused their efforts on discovering new and improved general closed form exact wave solutions of FPDEs such as (-expansion [9,10], Fan sub-equation [11], improved extended Fan subequation [12], tanh-sech [13,14], sine–cosine [15], perturbation [16,17], Jacobi elliptic function [18,19], F-expansion [20], -expansion [21,22,23] methods, and the references therein.
On the other hand, stochastic partial differential equations (SPDEs) have been extensively studied as mathematical models for spatial–temporal physical, biological, and chemical systems subject to random perturbations during the last few years. The importance of including stochastic effects in complicated system modeling has been highlighted. For instance, there is a significant focus on using SPDEs to mathematically model complex phenomena in finance, materials sciences, electrical and mechanical engineering, information systems, condensed matter physics, biology, and climate systems [24,25,26,27].
It seems that studying FPDE models with stochastic influences is more important. To the best of knowledge, little research has been conducted in order to obtain exact solutions to fractional SPDEs, for instance [28,29,30,31]. As a result, the purpose of this paper is to find the exact solution to the following space-fractional stochastic Bogoyavlenskii equation (SFSBE) [32] in the Stratonovich sense:
where and are real functions, is the conformable derivative (CD) [33], is the noise strength, and is the standard Brownian motion.
Many authors have reviewed the deterministic Bogoyavlenskii Equation (1) with integer-order derivatives (i.e., and ) to achieve analytical solutions using different techniques for example exp -expansion [34], Khater [35], multiple (-expansion [36], singular manifold [37], modified simple equation [38,39], modified extended tanh-function [40], generalized Riccati equation mapping [41], and sine–cosine [42]. Furthermore, the deterministic fractional Bogoyavlenskii Equation (1) has been solved by utilizing multiple techniques including -expansion [43], exp -expansion and rational -expansion [44], first integral [45], (-expansion [46], improved fractional sub-equation [47], Bäcklund transformation [48], Jacobi elliptic equation [49], (, -expansion and ()-expansion [50], and numerical multistep approach [51]. On the other hand, the stochastic Bogoyavlenskii equation has not yet been investigated.
Our contribution of this work is to consider the stochastic fractional-space Bogoyavlenskii equation in the Stratonovich sense, which is driven by multiplicative noise. This equation has never been discussed before via a combination of fractional space and multiplicative noise. Specifically, the exact solutions for the stochastic Bogoyavlenskii equation have never been obtained before. In addition, after we get the solutions by two various methods including the exp -expansion and sine–cosine, we address the impact of noise on these solutions. As we know, the stochastic solutions are more accurate than deterministic solutions. Therefore, the acquired solutions are very useful for scientists to describe a wide variety of complicated physical phenomena because Equation (1) is used to explain the wave of leading fluid flow, plasma physics, and the hydrodynamic model of shallow-water waves. We also show how the stochastic term affects the behavior of SFSBE analytical solutions by using graphical representations for various noise intensity values. Moreover, some previously obtained solutions, for instance the one stated in [34,42], were expanded.
The following is a summary of this paper: In Section 2, we give a definition and features of the CD and Brownian motion. In Section 3, we utilize a convenient wave transformation to attain the wave equation of the SFSBE (1). In Section 4, the analytical space-fractional stochastic solution of the SFSBE (1) is obtained. While in Section 5, we investigate how the Brownian motion influences the SFSBE (1) solution’s behavior. Finally, we present the paper’s conclusions.
2. Preliminaries
Here, we state some definitions and features of the CD [33] and Brownian motion. First, we define the CD as follows:
Definition 1.
Define the CD of of order as
Theorem 1.
Suppose are differentiable, and α is a differentiable function too, then, the next rule satisfies:
The following include some features of the CD:
- is a constant,
In the next, we define the Brownian motion:
Definition 2
(cf. [52]). For , is called Brownian motion if it satisfies: (1) is continuous, (2) , (3) has independent increments, (4) has normal distribution with variance and mean
It is worth noting that there are two types of stochastic integrals that are widely used: Stratonovich and Itô [53]. Modeling considerations usually decide the type is appropriate, but once one is selected, a similar equation of the other type can be established with the same solutions. Hence, the following is a possible switch between Stratonovich (written as ) and Itô (written as ):
where is a stochastic process and is considered to be sufficiently regular.
3. The Wave Equation
Here, we implement the following wave transformation
to get wave equation for SFSBE (1). and defined in (3) are real deterministic functions, k are constants. We see that
and
using Equation (2) in differential form and multiplying it by , we get
Considering expectation on both sides, where and are deterministic functions, we get
In fact, for every standard normal process is distributed similarly to . Therefore . Now, Equation (7) takes the form
We have by integrating the second equation in (8) once and setting the integration constant to zero
Integrating (10) once and putting the constant of integration equal zero, we obtain
4. Analytical Solutions of SFSBE
To get different analytical solutions of the SFSBE, we can apply many methods such as Lie symmetry methods, Painlevé expansion, sine–cosine, generalized Riccati equation, tanh–coth, -expansion, auxiliary equation, variational iteration, Backlund transformation, first integral, etc. However, in this section, we use two distinct methods such as -expansion and sine–cosine methods.
4.1. The -Expansion Method
Let us employ here the -expansion method [21,22,23,34] to find the traveling wave solutions of (11) and then the exact solutions shown in Equation (1). First, we assume the solutions of (11) are
where are constants to be calculated later. fulfills the next ODE:
where are arbitrary constants. By balancing and in (11), yields .
Hence, the solution of Equation (11) becomes
By plugging Equation (14) into Equation (11), and utilizing Equation (13), we obtain a polynomial of After that, we set the coefficients of to zero, which gives
Solving the above equations, we have
where are arbitrary constants.
Putting the values of into Equation (14), we get
Case I: When , then the solution of Equation (13) is
where is an arbitrary constant. Plugging Equation (18) into (17), we attain
Therefore, the solutions of SFSBE (1), by substituting Equation (19) into Equation (3) and using Equation (9), are
where .
Case II: When , then the solution of Equation (13) is
Thus, the solutions of SFSBE (1), by substituting Equation (23) into Equation (3) and using Equation (9), are
where .
Case III: When and , then the solutions of Equation (13) is
Therefore, the solutions of SFSBE (1), by substituting Equation (27) into Equations (3) and using Equation (9), are
where .
Case IV: When and , then the solutions of Equation (13) is
Thus, the solutions of SFSBE (1), by substituting Equation (31) into Equation (3) and using Equation (9), are
where .
Case V: When and , then the solution of Equation (13) is
4.2. Sine–Cosine Method
We implement here the sine–cosine method. We assume the solution of Equation (11) depend on [15] are
where
where A and B are undefined constants. Putting Equation (38) into Equation (11), we have
rewriting the equation above
Now, Equation (14) becomes
Inserting each coefficient of and equal zero, we obtain
and
By solving these equation we get
There are two cases:
First case: If hence the solutions of Equation (11) take the form:
Second case: If then the solutions of Equation (11) are
5. Impact of Multiplicative Brownian Motion
We address in this section the influence of the multiplicative Brownian motion on the solutions of the SFSBE (1). We employ MATLAB tools [54] to display some graphical representations for distinct values of the noise strength and explore the influence of multiplicative Brownian motion on these solutions. We fixed the parameters In the following, we plot the solution (48) for , and :
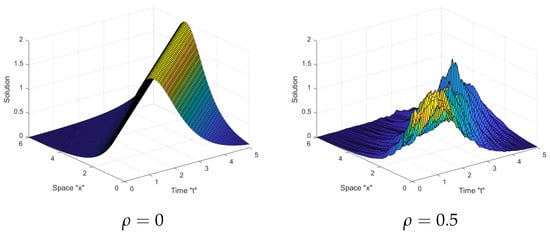
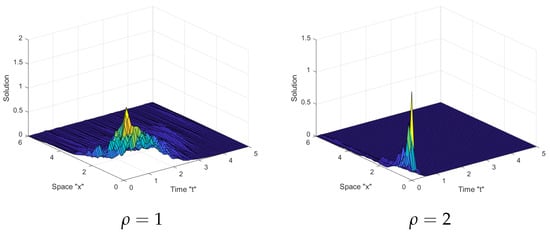
Figure 1.
Three-dimensional (3D) plots of the solution (48) with .
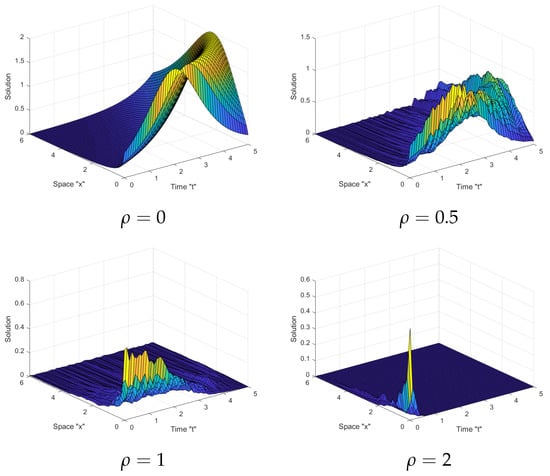
Figure 2.
Three-dimensional (3D) plots of the solution (48) with .
- The surface shrank as the order of the fractional operator decreases,
- At the surface is not completely flat and has some fluctuation,
- After minor transit patterns, the surface becomes considerably flatter when noise is included and its strength is increased .
Thus, we can deduce from Figure 1, Figure 2 and Figure 3 that the multiplicative Brownian motion influences the solutions of SFSBE and it stabilizes the solutions around zero.
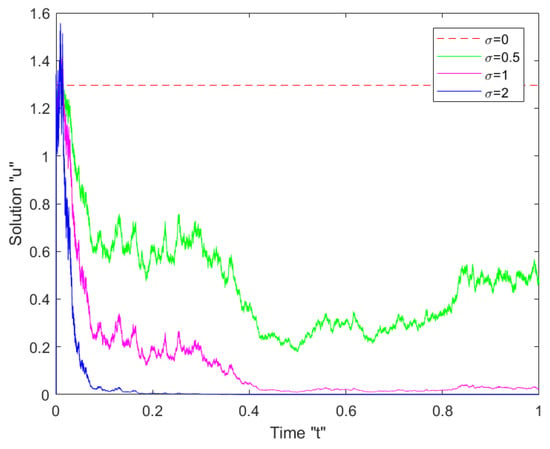
Figure 3.
Two-dimensional (2D) plots of the solution (48) with .
6. Conclusions
In this study, we considered the stochastic fractional-space Bogoyavlenskii equation with multiplicative Brownian motion in the Stratonovich sense. We attained the exact fractional stochastic solutions of the SFSBE via two distinct methods: for instance, the -expansion method and sine–cosine method. We extended some previously acquired results, including the results sated in [34,42]. These forms of solutions can be applied to a wide range of complex physical phenomena because Equation (1) is used to explain the wave of leading fluid-flow, plasma physics, and the hydrodynamic model of shallow-water waves. Finally, we demonstrated how Brownian motion affects solution behavior and indicated that Brownian motion stabilizes the solutions of SFSBE around zero. We can consider multi-dimensional multiplicative noise and additive noise in future work.
Author Contributions
Conceptualization, F.M.A.-A., W.W.M., A.M.A., M.E.-M.; methodology, F.M.A.-A., W.W.M.; software, W.W.M., M.E.-M.; formal analysis, F.M.A.-A., W.W.M., A.M.A., M.E.-M.; investigation, F.M.A.-A., W.W.M.; resources, F.M.A.-A., W.W.M., A.M.A., M.E.-M.; data curation, F.M.A.-A., W.W.M.; writing—original draft preparation, F.M.A.-A., W.W.M., A.M.A., M.E.-M.; writing—review and editing, F.M.A.-A., W.W.M.; visualization, F.M.A.-A., W.W.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R273), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yuste, S.B.; Acedo, L.; Lindenberg, K. Reaction front in an A + B → C reaction–subdiffusion process. Phys. Rev. E 2004, 69, 036126. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, W.W.; Iqbal, N. Impact of the same degenerate additive noise on a coupled system of fractional space diffusion equations. Fractals 2022, 30, 2240033. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional-order governing equation of Lévy motion. Water Resour. Res. 2000, 36, 1413–1423. [Google Scholar] [CrossRef]
- Yuste, S.B.; Lindenberg, K. Subdiffusion-limited A + A reactions. Phys. Rev. Lett. 2001, 87, 118301. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, N.; Wu, R.; Mohammed, W.W. Pattern formation induced by fractional cross-diffusion in a 3-species food chain model with harvesting. Math. Comput. Simul. 2021, 188, 102–119. [Google Scholar] [CrossRef]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker–Planck equation. Phys. Rev. 2000, 61, 132–138. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Random walk models for space–fractional diffusion processes. Fract. Calc. Appl. Anal. 1998, 1, 167–191. [Google Scholar]
- Shakeel, M.; Ul-Hassan, Q.M.; Ahmad, J. Applications of the novel (G′/G)-expansion method to the time fractional simplified modified Camassa–Holm (MCH) equation. Abstr. Appl. Anal. 2014, 2014, 601961. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Yomba, E. The modified extended Fan sub-equation method and its application to the (2+1)-dimensional Broer-Kaup-Kupershmidt equation. Chaos Soliton Fractal 2006, 27, 187–196. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, T.C. Further improved extended Fan sub-equation method and new exact solutions of the (2+1)-dimensional Broer–Kaup–Kupershmidt equations. Appl. Math. Comput. 2006, 182, 1651–1660. [Google Scholar] [CrossRef]
- Malfliet, W.; Hereman, W. The tanh method. I. Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 1996, 54, 563–568. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The tanh method for traveling wave solutions of nonlinear equations. Appl. Math. Comput. 2004, 154, 713–723. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Mohammed, W.W. Approximate solution of the Kuramoto-Shivashinsky equation on an unbounded domain. Chin. Ann. Math. Ser. 2018, 39, 145–162. [Google Scholar] [CrossRef]
- Mohammed, W.W. Modulation Equation for the Stochastic Swift–Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line. Mathematics 2019, 7, 1217. [Google Scholar] [CrossRef] [Green Version]
- Fan, E.; Zhang, J. Applications of the Jacobi elliptic function method to special-type nonlinear equations. Phys. Lett. A 2002, 305, 383–392. [Google Scholar] [CrossRef]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Zhang, J.L.; Wang, M.L.; Wang, Y.M.; Fang, Z.D. The improved F-expansion method and its applications. Phys. Lett. A 2006, 350, 103–109. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. Application of exp(-φ(η))-expansion Method to find the Exact Solutions of Modified Benjamin-Bona-Mahony Equation. World Appl. Sci. J. 2013, 24, 1373–1377. [Google Scholar]
- Khan, K.; Akbar, M.A. The exp(-φ(η))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar] [CrossRef]
- Hafez, M.G.; Ali, M.Y.; Chowdury, M.K.H.; Kauser, M.A. Application of the exp(-φ(η)) expansion method for solving nonlinear TRLW and Gardner equations. Int. J. Math. Comput. 2016, 27, 44–56. [Google Scholar]
- Capasso, V.; Morale, D. Stochastic modelling of tumour-induced angiogenesis. J. Math. Biol. 2009, 58, 219–233. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, W.W.; Blomker, D. Fast diffusion limit for reaction-diffusion systems with stochastic Neumann boundary conditions. SIAM J. Math. Anal. 2016, 48, 3547–3578. [Google Scholar] [CrossRef] [Green Version]
- Hu, G.; Lou, Y.; des Christo, P.D. Dynamic output feedback covariance control of stochastic dissipative partial differential equations. Chem. Eng. Sci. 2008, 63, 4531–4542. [Google Scholar] [CrossRef]
- Prevôt, C.; Rockner, M. A Concise Course on Stochastic Partial Di Erential Equations; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Mohammed, W.W.; Alesemi, M.; Albosaily, S.; Iqbal, N.; El-Morshedy, M. The Exact Solutions of Stochastic Fractional-Space Kuramoto-Sivashinsky Equation by using (G′/G)-expansion method. Mathematics 2021, 9, 2712. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Albalahi, A.M.; El-Morshedy, M. The Impact of the Wiener process on the analytical solutions of the stochastic (2+1)-dimensional breaking soliton equation by using tanh–coth method. Mathematics 2022, 10, 817. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Bazighifan, O.; Al-Sawalha, M.M.; Almatroud, A.O.; Aly, E.S. The Influence of Noise on the Exact Solutions of the Stochastic Fractional-Space Chiral Nonlinear Schrodinger equation. Fractal Fract. 2021, 5, 262. [Google Scholar] [CrossRef]
- Albosaily, S.; Mohammed, W.W.; Hamza, A.E.; El-Morshedy, M.; Ahmad, H. The exact solutions of the stochastic fractional space Allen–Cahn equation. Open Phys. 2022, 20, 23–29. [Google Scholar] [CrossRef]
- Bogoyavlenskii, O.I. Overturning solitons in two-dimensional integrable equations, (Russian) Usp. Mat. Nauk 1990, 45, 17–77. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Alam, M.d.N.; Tunc, C. An analytical method for solving exact solutions of the nonlinear Bogoyavlenskii equation and the nonlinear diffusive predator-prey system. Alex. Eng. J. 2016, 55, 1855–1865. [Google Scholar] [CrossRef] [Green Version]
- Khater, M.M.A.; Seadawy, A.R.; Lu, D. Elliptic and solitary wave solutions for Bogoyavlenskii equations system, couple Boiti-Leon-Pempinelli equations system and Time-fractional Cahn-Allen equation. Results Phys. 2017, 7, 2325–2333. [Google Scholar] [CrossRef]
- Malik, A.; Ch, F.; Kumar, H.; Mishra, S.C. Exact solutions of the Bogoyavlenskii equation using the multiple (G′/G)-expansion method. Comput. Math. Appl. 2012, 64, 2850–2859. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Shen, M. On exact solutions of the Bogoyavlenskii equation. Pramana 2006, 67, 449–456. [Google Scholar] [CrossRef]
- Yu, J.; Sun, Y. Modified method of simplest equation and its applications to the Bogoyavlenskii equation. Comput. Math. Appl. 2016, 72, 1943–1955. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Amer, Y.A. The modified simple equation method for solving nonlinear diffusive predator–prey system and Bogoyavlenskii equations. Int. J. Phys. Sci. 2015, 10, 133–141. [Google Scholar]
- Zahran, E.H.M.; Khater, M.M.A. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl. Math. Model. 2016, 40, 1769–1775. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Nowehy, A. Solitons and other solutions to the nonlinear Bogoyavlenskii equations using the generalized Riccati equation mapping method. Opt. Quantum Electron. 2017, 49, 1–23. [Google Scholar] [CrossRef]
- Najafi, M.; Arbabi, S.; Najafi, M. New Exact Solutions of (2 + 1)-Dimensional Bogoyavlenskii Equation by the sine-cosine Method. Int. J. Basic Appl. Sci. 2012, 1, 490–497. [Google Scholar]
- Hammouch, Z.; Mekkaoui, T.; Agarwal, P. Optical solitons for the Calogero-Bogoyavlenskii-Schiff equation in (2+1) dimensions with time-fractional conformable derivative. Eur. Phys. J. Plus 2018, 133, 248. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ilhan, O.A.; Manafian, J.; Shahriari, M.; Soybas, D. Analytical behavior of the fractional Bogoyavlenskii equations with conformable derivative using two distinct reliable methods. Results Phys. 2021, 22, 103975. [Google Scholar] [CrossRef]
- Eslami, M.; Khodadad, F.S.; Nazari, F.; Rezazadeh, H. The first integral method applied to the Bogoyavlenskii equations by means of conformable fractional derivative. Opt. Quantum Electron. 2017, 49, 1–18. [Google Scholar] [CrossRef]
- Alam, M.d.N.; Tunc, C. The new solitary wave structures for the (2 + 1)-dimensional time-fractional Schrodinger equation and the space-time nonlinear conformable fractional Bogoyavlenskii equations. Alex. Eng. J. 2020, 59, 2221–2232. [Google Scholar] [CrossRef]
- Li, C.; Zhao, M. Analytical solutions of the (2 + 1)-dimensional space–time fractional Bogoyavlenskii’s breaking soliton equation. Appl. Math. Lett. 2018, 84, 13–18. [Google Scholar] [CrossRef]
- Liu, X.Z.; Yu, J.; Lou, Z.M. New Backlund transformations of the (2 + 1)-dimensional Bogoyavlenskii equation via localization of residual symmetries. Comput. Math. Appl. 2018, 76, 1669–1679. [Google Scholar] [CrossRef]
- Feng, Q. A new approach for seeking coeficient function solutions of conformable fractional partial differential equations based on the Jacobi elliptic equation. Chin. J. Phys. 2018, 56, 2817–2828. [Google Scholar] [CrossRef]
- Yokus, A.; Durur, H.; Ahmad, H.; Thounthong, P.; Zhang, Y.F. Construction of exact traveling wave solutions of the Bogoyavlenskii equation by (G′/G, 1/G)-expansion and (1/G′)-expansion techniques. Results Phys. 2020, 19, 103409. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Freihat, A.; Khalil, H.; Momani, S.; Khan, R.A. Numerical multistep approach for solving fractional partial differential equations. Int. J. Comput. Meth. 2017, 14, 1750029. [Google Scholar] [CrossRef]
- Calin, O. An Informal Introduction to Stochastic Calculus with Applications; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2015. [Google Scholar]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: New York, NY, USA, 1995. [Google Scholar]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).