Exact Controllability Results for Sobolev-Type Hilfer Fractional Neutral Delay Volterra-Fredholm Integro-Differential Systems

Abstract

This manuscript mainly focuses on the exact controllability of Sobolev-type Hilfer fractional neutral delay Volterra-Fredholm integro-differential systems. The principal findings of this discussion are established by using the theories on fractional calculus, the measure of noncompactness and Mönch fixed point technique. Initially, the exact controllability of the system is presented and then we improve the discussion to the system with nonlocal conditions. Finally, abstract and filter systems are provided for the illustration.

1. Introduction

In many physical processes, fractional differential equations incorporating not only one fractional derivative but also several fractional derivatives are heavily concentrated. The meaning of fractional systems has recently attracted a lot of attention due to its astonishing applications in showcasing the wonders of science and engineering. The use of fractional order differential equations allows for the management of a wide range of issues in a variety of fields, including fluid flow, electrical systems, visco-elasticity, electro-chemistry, and so on. The monographs [1,2,3,4,5,6,7,8,9] and the research articles [8,9,10,11,12,13] show the interlinking in the same way that the separation between classical and fractional differential representations seems to. Applications of the differential systems can be found in [14,15,16]. Neutral structures with delays or without delays, in particular, serve as a summary association of a large number of partial neutral structures that appear in problems involving heat flow in substances, visco-elasticity, and a variety of natural processes. Neutral systems appear in many areas of applied mathematics; as a result, the most successful neutral structures have gotten a lot of attention in the current generation; readers can look at [12,13,17,18,19,20,21].

Recently, in [22,23], the author initiated another kind of derivative of fractional order, that including Riemann-Liouville and Caputo fractional derivative. In [24], the authors proved the existence of mild solution for evolution equation with Hilfer fractional derivative which generalized the famous Riemann-Liouville fractional derivative by using the semigroup theory, measure of noncompactness and fixed point approach. In [25], the authors proved the approximate controllability of Hilfer fractional neutral stochastic integro-differential systems by using fractional calculus and Bohenblust-Karlin’s theorem. In [18,26,27], the authors proved the existence and controallbility of various extensions related with Hilfer fractional derivative by using semigroup theory, measure of noncompactness and various fixed point theorems.

In [28], the authors discussed the approximate controllability of non-densely defined Sobolev-type Hilfer fractional neutral delay differential system by using Bohenblust-Karlin’s fixed point theorem. In [29], the authors proved the existence of nonlocal functional integro-differential equations via Hilfer fractional derivative by using Mönch fixed point theorem. In [13], the authors discusssed the existence of Sobolev-type Hilfer fractional neutral integro-differential equations with infinite delay by uisng Mönch fixed point theorem. In [30], the authors proved the approximate controllability of Hilfer fractional differential inclusions with nonlocal conditions by using Bohenblust-Karlin’s fixed point theorem. The existence and exact controllability described in our paper have still to be investigated, and it is the motivation of this article.

Motivated by the monograph, nowadays, several authors focus on this Hilfer fractional derivative, and we refer to [13,18,22,24,25,26,27,29,30,31,32]. The potential of controllability is an important part of engineering and mathematical control theory. Finding a suitable control function to the point where one may guide the considered dynamic system to a final state is the controllability problem. As a result, many researchers have investigated the controllability of a variety of nonlinear systems in recent years, and the articles are available for viewing. For instance, refs. [12,13,18,19,30,32,33,34,35,36,37,38,39,40,41,42,43,44,45] and references therein.

Assume that the Hilfer fractional neutral delay Volterra-Fredholm integro-differential system of Sobolev-type has the following form

$$\begin{array}{cc}\hfill D_{0^{+}}^{\nu ,\zeta }[Ju\left(t\right)-& F_1(t,u_t)]=Au\left(t\right)+Bx\left(t\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill +F_2\left(t,u_t,{\int }_0^{t}e(t,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(t,\tau ,u_{\tau })d\tau \right),t\in I=(0,c],\end{array}$$

(1)

$$\begin{array}{cc}\hfill I_{0^{+}}^{(1-\nu )(1-\zeta )}u\left(0\right)& =\varphi \in {\mathcal{R}}_l,\hfill \end{array}$$

(2)

where $D_{0^{+}}^{\nu ,\zeta }$ stands for the Hilfer fractional derivative, $0\le \nu \le 1;\frac{1}{2}<\zeta <1;$ and $x(·)$ takes value in Banach Space X with $\parallel ·\parallel$. The histories $u_{\varrho }:(-\infty ,0]\to {\mathcal{R}}_l$, $u_{\varrho }\left(s\right)=u(\varrho +s)$, $s\le 0$ with phase space ${\mathcal{R}}_l$. $F_1:I\times {\mathcal{R}}_l\to X$, $F_2:I\times {\mathcal{R}}_l\times X\times X\to X$, $e:I\times I\times {\mathcal{R}}_l\to X$ and $f:I\times I\times {\mathcal{R}}_l\to X$ are appropriate functions. $u(·)$ is a control function and B is a bounded linear operator from $\mathcal{V}$→X.

The rest of the paper is organized as follows:

• Section 2: Theoretical notions linked to fractional calculus and the measure of noncompactness are presented.
• Section 3: This section is focused on exact controllability results of the fractional system (1) and (2).
• Section 4: Our findings are expanded to include the concept of nonlocal situations.
• Section 5: Finally, abstract and filter systems are provided for the illustration of the obtained theory.

2. Preliminaries

We now provide some fundamental theories, lemmas, and facts to discuss our main results. $C(I,X)$- the spaces of all continuous functions. Let us take $\eta =\nu +\zeta -\nu \zeta$, then $(1-\eta )=(1-\nu )(1-\zeta )$. Assume $C_{1-\eta }(I,X)=\{u:t^{1-\eta }u\left(t\right)\in C(I,X)\}$ with ${\parallel ·\parallel }_{\eta }$ by ${\parallel u\parallel }_c=sup\{t^{1-\eta }\parallel u\left(t\right)\parallel ,t\in I,\eta =(\nu +\zeta -\nu \zeta )\}$. Clearly, $C_{1-\eta }(I,X)$ is a Banach space. Define H with ${\parallel H\parallel }_{L^{\rho }(I,{\mathbb{R}}^{+})}$ if $H\in L^{\rho }(I,{\mathbb{R}}^{+})$ for any $\rho$ with $1\le \rho \le \infty$. $A^{\alpha }$, $0<\alpha \le 1$, a closed linear operator on $D\left(A^{\alpha }\right)$ with inverse $A^{-\alpha }$, see [46].

Definition 1

([46]).

(i) 

$D\left(A^{\alpha }\right)$, a Banach space with ${\parallel u\parallel }_{\alpha }=\parallel A^{\alpha }u\parallel$ for $u\in D\left(A^{\alpha }\right).$

(ii) 

$T\left(t\right):X\to X_{\alpha }$, for $t\ge 0.$

(iii) 

$A^{\alpha }T\left(t\right)u=T\left(t\right)A^{\alpha }u$, for $u\in D\left(A^{\alpha }\right)$ and $t\ge 0.$

(iv) 

$A^{\alpha }T\left(t\right)$ is bounded on X and there exists $M_{\alpha }>0$ such that

$$\parallel A^{\alpha }T\left(t\right)\parallel \le \frac{M_{\alpha }}{t^{\alpha }}.$$

Definition 2

([47]). The operators define $A:D\left(A\right)\subset X\to X$ and $J:D\left(A\right)\subset X\to X$ satisfy the following:

(J1)

A and J are closed linear operators.

(J2)

$D\left(J\right)\subset D\left(A\right)$ and J is bijective.

(J3)

$J^{-1}:X\to D\left(J\right)$ is continuous.

Additionally, because of $\left({\mathbf{J}}_{\mathbf{1}}\right)$ and $\left({\mathbf{J}}_{\mathbf{2}}\right)$$J^{-1}$ is closed, by $\left({\mathbf{J}}_{\mathbf{3}}\right)$ and by referring closed graph theorem, we obtain the boundedness of $A{J}^{-1}:X\to X$. Define $\parallel J^{-1}\parallel ={\tilde{J}}_m$ and $\parallel J\parallel =J_m$.

Definition 3

([4]). The left sided Riemann-Liouville fractional integral of order ζ having lower limit c for $F:[c,+\infty )\to \mathbb{R}$ is presented as

$$I_{c^{+}}^{\zeta }F\left(\varrho \right)=\frac{1}{\mathsf{\Gamma }\left(\zeta \right)}{\int }_c^{\varrho }\frac{F\left(\tau \right)}{{(\varrho -\tau )}^{1-\zeta }}d\tau ,\varrho >c;\zeta >0,$$

if the right side is pointwise determined on $[c,+\infty )$, where $\mathsf{\Gamma }(·)$ denotes gamma function.

Definition 4

([4]). The left-sided Riemann-Liouville fractional derivative of order $\zeta \in [k-1,k)$, $k\in X$ for $F:[c,+\infty )\to \mathbb{R}$ is given by

$$\begin{array}{c}{{}^L{D}^{\zeta }}_{c^{+}}F\left(\varrho \right)=\frac{1}{\mathsf{\Gamma }(k-\zeta )}\frac{d^k}{d{\varrho }^k}{\int }_c^{\varrho }\frac{F\left(\tau \right)}{{(\varrho -\tau )}^{\zeta +1-k}}d\tau ,\varrho >c,k-1<\zeta <k.\end{array}$$

Definition 5

([4]). The left-sided Hilfer fractional derivative of order $0\le \nu \le 1$ and $0<\zeta <1$ function of $F\left(\varrho \right)$ is given by

$$D_{c^{+}}^{\nu ,\zeta }F\left(\varrho \right)=\left(I_{c^{+}}^{\nu (1-\zeta )}D\left(I_{d^{+}}^{(1-\nu )(1-\zeta )}F\right)\right)\left(\varrho \right).$$

Remark 1

([23]).

(i)

Given $\zeta =0$, $0<\nu <1$ also $c=0$, the Hilfer fractional derivative identical with standard Riemann-Liouville fractional derivative:

$$\begin{array}{cc}\hfill D_{0^{+}}^{0,\zeta }F\left(\varrho \right)& =\frac{d}{d\varrho }{I}_{0^{+}}^{1-\zeta }F\left(\varrho \right)={{}^L{D}^{\zeta }}_{0^{+}}F\left(\varrho \right).\hfill \end{array}$$

(ii)

Given $\zeta =1$, $0<\nu <1$ also $c=0$, the Hilfer fractional derivative identical with standard Caputo derivative:

$$\begin{array}{cc}\hfill D_{0^{+}}^{1,\zeta }F\left(\varrho \right)& =I_{0^{+}}^{1-\zeta }\frac{d}{d\varrho }F\left(\varrho \right)={{}^C{D}^{\zeta }}_{0^{+}}F\left(\varrho \right).\hfill \end{array}$$

We define the abstract phase space ${\mathcal{R}}_l$ by referring [33]. Consider $l:(-\infty ,0]\to (0,+\infty )$ is continuous along with $j={\int }_{-\infty }^{0}l\left(\gamma \right)d\gamma <+\infty$. Now for every $a>0$,we define

$$\begin{array}{c}\hfill {\mathcal{R}}_l=\left\{\eta :[-a,0]\to X\mathrm{such}\mathrm{that}\eta \left(\gamma \right)\mathrm{is}\mathrm{bounded}\mathrm{and}\mathrm{measurable}\right\},\end{array}$$

and

$$\begin{array}{c}\hfill {\parallel \eta \parallel }_{[-a,0]}=\underset{\zeta \in [-a,0]}{sup}\parallel \eta \left(\zeta \right)\parallel ,\mathrm{for}\mathrm{all}\eta \in \mathcal{R}.\end{array}$$

Now, we define

$$\begin{array}{cc}\hfill {\mathcal{R}}_l=\{\eta :(-\infty ,0]& {\to X\mathrm{such}\mathrm{that}\mathrm{for}\mathrm{some}c>0,\eta |}_{[-c,0]}\in \mathcal{R}\hfill \\ & \mathrm{and}{\int }_{-\infty }^{0}l\left(\zeta \right){\parallel \eta \parallel }_{[\zeta ,0]}d\zeta <+\infty \},\hfill \end{array}$$

and

$$\begin{array}{c}{\parallel \eta \parallel }_{{\mathcal{R}}_l}={\int }_{-\infty }^{0}j\left(\zeta \right){\parallel \eta \parallel }_{[\zeta ,0]}d\zeta ,\forall \eta \in {\mathcal{R}}_l,\end{array}$$

therefore $({\mathcal{R}}_l,\parallel ·{\parallel }_{{\mathcal{R}}_l})$ is a Banach space.

Consider

$$\begin{array}{cc}\hfill {\mathcal{R}}_l^{\prime }=& {\{u:(-\infty ,c]\to X\mathrm{such}\mathrm{that}u|}_V\in C(I,X),u\left(0\right)=\varphi \left(0\right)\in {\mathcal{R}}_l\}.\hfill \end{array}$$

Set ${\parallel ·\parallel }_c$ be a seminorm in ${\mathcal{R}}_l^{\prime }$ which is defined by

$$\begin{array}{c}{\parallel u\parallel }_c={\parallel \varphi \left(0\right)\parallel }_{{\mathcal{B}}_h}+sup\left\{\right|y\left(\zeta \right)|:\zeta \in [0,c]\},u\in {\mathcal{R}}_l^{\prime }.\end{array}$$

Lemma 1

([48]). If $u\in {\mathcal{R}}_l^{\prime }$, then for $\gamma \in I,u_{\gamma }\in {\mathcal{R}}_l$. Furthermore,

$$\begin{array}{c}\hfill j\parallel u\left(\gamma \right)\parallel \le \parallel u_{\gamma }{\parallel }_{{\mathcal{R}}_l}\le {\parallel \varphi \left(0\right)\parallel }_{{\mathcal{R}}_l}+l\underset{\zeta \in [0,\gamma ]}{sup}\left|u\left(\zeta \right)\right|,\end{array}$$

where $j={\int }_{-\infty }^{0}l\left(\gamma \right)d\gamma <+\infty$.

Lemma 2.

The function $u:[0,c]\to X$ is said to be an integral solution of the fractional system (1) and (2) if it satisfies the following:

• $u:[0,c]\to X$ is continuous.
• $I_{0^{+}}^{1-\zeta }u\left(t\right)\in D\left(A\right)$, for $t\in I$.
• The fractional system (1) and (2) is similar with

  $$\begin{array}{cc}\hfill u\left(t\right)& =\frac{J^{-1}[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]}{\mathsf{\Gamma }\left(\nu \right(1-\zeta )+\zeta )}J{t}^{(\nu -1)(1-\zeta )}+J^{-1}{F}_1(t,u_t)\hfill \\ & +\frac{1}{\mathsf{\Gamma }\left(\zeta \right)}{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}[Au\left(s\right)+Bx\left(s\right)\hfill \\ & +F_2\left(s,u_s,{\int }_0^{s}e(s,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,u_{\tau })d\tau \right)]ds,t\in I.\hfill \end{array}$$

Remark 2.

By referring Wright function $M_{\zeta }\left(s\right)$, we present the mild solution of the fractional system (1) and (2) is as follows:

$$\begin{array}{c}{M}_{\zeta }\left(s\right)=\sum _{k=1}^{\infty }\frac{{(-s)}^{k-1}}{(k-1)!\mathsf{\Gamma }(1-k\zeta )},0<\zeta <1,s\in \mathbb{C},\end{array}$$

and satisfies

$$\begin{array}{c}{\int }_0^{\infty }{s}^s{M}_{\zeta }\left(s\right)ds=\frac{\mathsf{\Gamma }(1+s)}{\mathsf{\Gamma }(1+\zeta s)},fors\ge 0.\end{array}$$

Lemma 3.

If the fractional system (1) and (2) are satisfied, then there exists $F_1:I\times {\mathcal{R}}_l\to X$ and $F_2:I\times {\mathcal{R}}_l\times X\times X\to X$ such that

$$\begin{array}{cc}\hfill u\left(t\right)=& J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t\right)J(\varphi \left(0\right)-F_1(0,\varphi \left(0\right))+J^{-1}{F}_1(t,u_t)+{\int }_0^t{J}^{-1}{\mathcal{R}}_{\zeta }\left(t\right)A{F}_1\left(s,u_s\right)ds\hfill \\ & +{\int }_0^t{J}^{-1}{\mathcal{R}}_{\zeta }\left(t\right)F_2\left(s,u_s,{\int }_0^{s}e(s,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,u_{\tau })d\tau \right)ds\hfill \\ & +{\int }_0^t{J}^{-1}{\mathcal{R}}_{\zeta }\left(t\right)Bx\left(s\right)ds,t\in I,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\mathcal{P}}_{\nu ,\zeta }\left(t\right)=I_{0^{+}}^{v(1-\zeta )}{\left(t\right)}^{\zeta -1}{\mathcal{S}}_{\zeta }\left(t\right);{\mathcal{R}}_{\zeta }\left(t\right)=t^{\zeta -1}{\mathcal{S}}_{\zeta }\left(t\right);{\mathcal{S}}_{\zeta }\left(t\right)={\int }_0^{\infty }\zeta \omega M_{\zeta }\left(\omega \right)S\left(t^{\zeta }\omega \right)d\omega .\end{array}$$

Definition 6

([20]). A function $u:(-\infty ,c]\to X$ is said to be a mild solution of the fractional system (1) and (2) provided that $u_0=\varphi \left(0\right)\in {\mathcal{R}}_l$ on $(-\infty ,0]$ and satisfies the following integral equation

$$\begin{array}{cc}\hfill u\left(t\right)& =J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t\right)J[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]+J^{-1}{F}_1\left(t,u_t\right)\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)A{J}^{-1}{F}_1\left(s,u_s\right)ds\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)F_2\left(s,u_s,{\int }_0^{s}e(s,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,u_{\tau })d\tau \right)ds\hfill \end{array}$$

$$\begin{array}{c}\hfill +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)Bx\left(s\right)ds,t\in I,\end{array}$$

(3)

where

$$\begin{array}{cc}\hfill {\mathcal{P}}_{\nu ,\zeta }\left(t\right)& ={\int }_0^{\infty }{\xi }_{\zeta }\left(\omega \right)M\left(t^{\zeta }\omega \right)d\omega ,{\mathcal{S}}_{\zeta }=\zeta {\int }_0^{\infty }\omega {\xi }_{\zeta }\left(\omega \right)M\left(t^{\zeta }\omega \right)d\omega ,\hfill \end{array}$$

and for $\omega \in (0,\infty )$

$${\xi }_{\zeta }\left(\omega \right)=\frac{1}{\zeta }{\omega }^{-1-\frac{1}{\zeta }}{\overline{w}}_{\zeta }({\omega }^{-\frac{1}{\zeta }})\ge 0,$$

$$\begin{array}{cc}\hfill {\overline{w}}_{\zeta }\left(\omega \right)& =\frac{1}{\pi }\sum _{n=1}^{\infty }{(-1)}^{n-1}{t}^{-n\zeta -1}\frac{\mathsf{\Gamma }(n\zeta +1)}{n!}sin\left(n\pi \zeta \right),\hfill \end{array}$$

where ${\xi }_{\zeta }$ is a probability density function defined on $(0,\infty )$, that is,

$${\xi }_{\zeta }\left(\omega \right)\ge 0,\omega \in (0,\infty )\mathrm{and}{\int }_0^{\infty }{\xi }_{\zeta }\left(\omega \right)d\omega =1.$$

Lemma 4

([20]). The operators ${\mathcal{P}}_{\nu ,\zeta }$ and ${\mathcal{S}}_{\zeta }$ satisfies the following:

(i)

For $t\ge 0$, ${\mathcal{P}}_{\nu ,\zeta }$ and ${\mathcal{S}}_{\zeta }$ are linear and bounded, that is, for every $u\in X$,

$$\parallel {\mathcal{P}}_{\nu ,\zeta }\left(t\right)u\parallel \le \frac{M{t}^{\eta -1}}{\mathsf{\Gamma }\left(\nu \right(1-\zeta )+\zeta )}\parallel u\parallel \mathrm{and}\parallel {\mathcal{S}}_{\zeta }\left(t\right)u\parallel \le \frac{M}{\mathsf{\Gamma }\left(\zeta \right)}\parallel u\parallel ,$$

where ${\mathcal{P}}_{\nu ,\zeta }\left(t\right)=I_{0^{+}}^{\nu (1-\zeta )}{\mathcal{R}}_{\zeta }\left(t\right)$, ${\mathcal{R}}_{\zeta }\left(t\right)=t^{\zeta -1}{\mathcal{S}}_{\zeta }\left(t\right).$

(ii)

The operators ${\left\{{\mathcal{P}}_{\nu ,\zeta }\left(t\right)\right\}}_{t\ge 0}$ and ${\left\{{\mathcal{S}}_{\zeta }\left(t\right)\right\}}_{\ge 0}$ are strongly continuous.

(iii)

For every $u\in X$, $\mu ,\zeta \in (0,1]$, we have

$$\begin{array}{c}A{\mathcal{S}}_{\zeta }\left(t\right)u=A^{1-\mu }{\mathcal{S}}_{\zeta }\left(t\right)A^{\mu }u,0\le t\le c;\\ \parallel A^{\mu }{\mathcal{S}}_{\zeta }\left(t\right)\parallel \le \frac{\zeta C_{\mu }\mathsf{\Gamma }(2-\mu )}{t^{\zeta \mu }\mathsf{\Gamma }(1+\zeta (1-\mu ))},0<t\le c.\end{array}$$

Lemma 5.

The operators ${\left\{{\mathcal{S}}_{\zeta }\left(t\right)\right\}}_{t>0}$ and ${\left\{{\mathcal{P}}_{\nu ,\zeta }\left(t\right)\right\}}_{t>0}$ are strongly continuous, that is, $0<t^{\prime }<t^{″}\le c$,

$$\parallel {\left(t^{\prime }\right)}^{\zeta -1}{\mathcal{S}}_{\zeta }\left(t^{\prime }\right)u-{\left(t^{\prime \prime }\right)}^{\zeta -1}{\mathcal{S}}_{\zeta }\left(t^{″}\right)u\parallel \to 0\mathrm{and}\parallel {\mathcal{P}}_{\nu ,\zeta }\left(t^{\prime }\right)u-{\mathcal{P}}_{\nu ,\zeta }\left(t^{″}\right)u\parallel \to 0\mathrm{as}{t}^{″}\to t^{\prime }.$$

Definition 7

([49,50]). The Measure of noncompactness of Hausdorff $\mathcal{T}(·)$ determined on every bounded subset ϱ of X by $\mathcal{T}\left(\varrho \right)=inf\{ϵ>0:\varrho$ can be covered by a finite number of balls of radii lesser than ϵ}.

Definition 8

([35]). Let $F^{+}$ be the positive cone of an order Banach space $(F,\le )$. The value E of $F^{+}$ is said to be measure of noncompactness on X of $\mathcal{D}$ determined on the set of all bounded subsets of X if and only if $E\left(\overline{co}\varrho \right)=E\left(\varrho \right)$ for all bounded subsets $\varrho \subseteq X$, where $\overline{co}\varrho$ is a closed convex hull of ϱ.

Definition 9

([49,51]). For every bounded subsets $\varrho ,{\varrho }_1,{\varrho }_2$ of X.

(i)

Monotone if and only if for all bounded subsets ϱ, ${\varrho }_1$, ${\varrho }_2$ of X we get: $({\varrho }_1\subseteq {\varrho }_2)\Rightarrow (\mathcal{D}\left({\varrho }_1\right)\le \mathcal{D}\left({\varrho }_2\right))$;

(ii)

Non singular if and only if $\mathcal{D}\left(\right\{a\}\cup \varrho )=\mathcal{D}\left(\varrho \right)$ for each $a\in X$, $\varrho \subset U$;

(iii)

Regular if and only if $\mathcal{D}\left(\varrho \right)=0$ if and only if ϱ is relatively compact in X;

(iv)

$\mathcal{T}({\varrho }_1+{\varrho }_2)\le \mathcal{T}\left({\varrho }_1\right)+\mathcal{T}\left({\varrho }_2\right)$, where ${\varrho }_1+{\varrho }_2=\{x_1+x_2:x_1\in {\varrho }_1,x_2\in {\varrho }_2\}$;

(v)

$\mathcal{T}({\varrho }_1\cup {\varrho }_2)\le max\{\mathcal{T}\left({\varrho }_1\right),\mathcal{T}\left({\varrho }_2\right)\}$;

(vi)

$\mathcal{T}\left(\gamma \varrho \right)\le \left|\gamma \right|\mathcal{T}\left(\varrho \right)$, for all $\gamma \in \mathbb{R}$;

(vii)

If $Q:D\left(Q\right)\subseteq X\to Y$ is a Lipschitz continuous function with $k>0$, then ${\mathcal{T}}_Y\left(Q\varrho \right)\le k\mathcal{T}\left(\varrho \right)$, for $\varrho \subseteq D\left(Q\right)$ and Y is a Banach space.

Lemma 6

([49]). Assume that $\mathcal{X}\subset C\left(\right[a,b],X)$ is bounded and equicontinuous, then $\mathcal{T}\left(\mathcal{X}\right(t\left)\right)$ is continuous for any $t\in [a,b],$

$$\begin{array}{c}\mathcal{T}\left(\mathcal{X}\right)=\underset{t\in N}{sup}\{\mathcal{T}\left(\mathcal{X}\left(t\right)\right),t\in [a,b]\},whereby\mathcal{X}\left(t\right)=\{u\left(t\right):u\in \mathcal{X}\}\subseteq X.\end{array}$$

Theorem 1

([45,52]). Assume ${\left\{u_n\right\}}_{n=1}^{\infty }$ is a sequence of Bochner integrable functions from $I\to X$ with $\parallel u_n\left(t\right)\parallel \le \epsilon \left(t\right)$, for all $t\in I$ and every $n\ge 1$, where $\epsilon \in L^1(I,\mathbb{R})$, then $\varrho \left(t\right)=\mathcal{T}\left(\{u_n\left(t\right):n\ge 1\}\right)\in L^1(I,\mathbb{R})$ and satisfies $\mathcal{T}\{{\int }_0^t\varrho \left(\tau \right)d\tau :n\ge 1\}\le 2{\int }_0^t\varrho \left(\tau \right)d\tau$.

Lemma 7

([53]). Assume F be closed convex subset of X and $0\in F$, $K:F\to X$ is continuous and that satisfies Mönch’s condition, that is, $(P\subseteq F$ is countable, $P\subseteq \overline{co}(\left\{0\right\}\cup K\left(P\right))\Rightarrow \overline{P}$ is compact). Then K has a fixed point in F.

3. Existence

The reason for this part is to examine the existence of the fractional system (1) and (2).

(H0)

If $F\subset X$ and $w\in F$, then

$$\parallel T\left(t_2^v\varrho \right)w-T\left(t_1^v\varrho \right)w\parallel \to 0,\mathrm{when}{t}_2\to t_1,$$

for each fixed $\varrho \in (0,\infty )$.

(H1)

The function $F_1:I\times {\mathcal{R}}_l\to X$ is continuous and there exists $\mu \in (0,1)$ such that $F_1\in D\left(A^{\mu }\right)$, for every $w\in X$, $t\in I$, $A^{\mu }{J}^{-1}{F}_1(·,w)$ is strongly measurable, there exists $M_g>0$, $M_g^{\prime }>0$ such that $r,s\in X$, $A^{\mu }{F}_1(t,·)$ satisfies the following

$$\parallel A^{\mu }{J}^{-1}{F}_1(t,r\left(t\right))-A^{\mu }{J}^{-1}{F}_1(t,s\left(t\right))\le M_g{t}^{1-\eta }{\parallel r\left(t\right)-s\left(t\right)\parallel }_{{\mathcal{R}}_l},$$

$$\parallel A^{\mu }{J}^{-1}{F}_1(t,w\left(t\right))\parallel \le M_g^{\prime }(1+t^{1-\eta }{\parallel w\parallel }_{{\mathcal{R}}_l}).$$

(H2)

The function $F_2:I\times {\mathcal{R}}_l\times X\times X\to X$ satisfies the following:

$\left(\mathbf{i}\right)$

The function $F_2(·,\varphi ,y,z)$ is measurable for all $(\varphi ,y,z)\in {\mathcal{R}}_l\times X$ and $F_2(t,·,·,·)$ is continuous for a.e. $t\in I$, $u\in {\mathcal{R}}_l$, $F_2(·,\varphi ,y,z):I\to X$ is strongly measurable.

$\left(\mathbf{ii}\right)$

There exists $q_1\in (0,q)$ and ${ϵ}_1\in L^{\frac{1}{q_1}}(I,{\mathbb{R}}^{+})$ and the integrable function $\kappa :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ such that $\parallel E(t,\varphi ,y,z)\parallel$$\le {ϵ}_1\left(t\right)\kappa (t^{1-\eta }{\parallel \varphi \parallel }_{{\mathcal{R}}_l}+t^{1-\eta }\parallel y\parallel +t^{1-\eta }\parallel z\parallel )$, for all $(t,\varphi ,y,z)\in N\times {\mathcal{R}}_l\times X\times X$, where $\kappa$ satisfies ${\displaystyle \underset{n\to \infty }{lim}inf\frac{\kappa \left(n\right)}{n}=0}$.

$\left(\mathbf{iii}\right)$

There exists $q_2\in (0,q)$ and ${ϵ}_2\in L^{\frac{1}{q_2}}(I,{\mathbb{R}}^{+})$ such that for any bounded subset $D_1\subset X$ and $G_1\subset {\mathcal{R}}_l$,

$${\displaystyle \mathcal{T}\left(F_2(t,G_1,D_1,D_2)\right)\le {ϵ}_2\left(t\right)\left[\underset{-\infty <\phi \le 0}{sup}\mathcal{T}\left(G_1\left(\phi \right)\right)+\mathcal{T}\left(D_1\right)+\mathcal{T}\left(D_2\right)\right],}$$

for a.e. $t\in I$, $G_1\left(\varrho \right)=\{v\left(\varrho \right):v\in G_1\}$ and $\mathcal{T}$ is the Hausdorff MNC.

(H3)

The function $e:I\times I\times {\mathcal{R}}_l\to X$ satisfies the following:

$\left(\mathbf{i}\right)$

$e(·,\varphi ,z)$ is measurable for all $(\varphi ,z)\in {\mathcal{R}}_l\times X$, $f(t,·,·)$ is continuous for a.e. $t\in I$.

$\left(\mathbf{ii}\right)$

There exists $E_0>0\mathrm{such}\mathrm{that}\parallel e(t,\tau ,\varphi )\parallel \le E_0{(1+\parallel \varphi \parallel }_{{\mathcal{R}}_l})$, for all $t\in I$, $\tau \in X$, $\varphi \in {\mathcal{R}}_l$.

$\left(\mathbf{iii}\right)$

There exists $q_3\in (0,q)$ and ${ϵ}_3\in L^{\frac{1}{q_3}}(I,{\mathbb{R}}^{+})$ such that for any bounded subset $D_3\subset X$,

$${\displaystyle \mathcal{T}\left(F_2(t,\tau ,D_3)\right)\le {ϵ}_3(t,\tau )\left[\underset{-\infty <t\le 0}{sup}\mathcal{T}\left(D_3\left(\phi \right)\right)\right]\mathrm{for}\mathrm{a}.\mathrm{e}.t\in I,}$$

with ${ϵ}_3^{*}={sup}_{\tau \in N}{\int }_0^{\tau }{ϵ}_3(t,\epsilon )d\epsilon <\infty$.

(H4)

The function $f:I\times I\times {\mathcal{R}}_l\to X$ satisfies the following:

$\left(\mathbf{i}\right)$

$f(·,\varphi ,z)$ is measurable for all $(\varphi ,z)\in {\mathcal{R}}_l\times X$, $f(t,·,·)$ is continuous for a.e. $t\in I$.

$\left(\mathbf{ii}\right)$

There exists $E_1>0$ such that $\parallel f(t,\tau ,\varphi )\parallel \le E_1{(1+\parallel \varphi \parallel }_{{\mathcal{R}}_l})$, for all $t\in I$, $\tau \in X$, $\varphi \in {\mathcal{R}}_l$.

$\left(\mathbf{iii}\right)$

There exists $q_4\in (0,q)$ and ${ϵ}_4\in L^{\frac{1}{q_4}}(I,{\mathbb{R}}^{+})$ such that for any bounded subset $D_4\subset X$,

$${\displaystyle \mathcal{T}\left(F_2(t,\tau ,D_4)\right)\le {ϵ}_4(t,\tau )\left[\underset{-\infty <t\le 0}{sup}\mathcal{T}\left(D_4\left(\phi \right)\right)\right]\mathrm{for}\mathrm{a}.\mathrm{e}.t\in I,}$$

with ${ϵ}_4^{*}={sup}_{\tau \in N}{\int }_0^{\tau }{ϵ}_4(t,\epsilon )d\epsilon <\infty$.

(H5)

The operator $B:L^2(I,\mathcal{V})\to L^1(I,\mathcal{V})$ is bounded and $W:L^2(I,\mathcal{V})\to L^1(I,\mathcal{V})$ is defined by

$$\begin{array}{c}\hfill Wx={\int }_0^c{(c-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)Bx\left(s\right)ds,\end{array}$$

which satisfies the following:

(i)

W have an inverse $W^{-1}$ acquires the value in $L^2(I,\mathcal{V})/KerW$, there exists ${ϵ}_b>0,{ϵ}_w>0$ such that $\parallel B\parallel \le {ϵ}_b$ and $\parallel W^{-1}\parallel \le {ϵ}_w$.

(ii)

For $q_5\in (0,q)$ and for every bounded subset $D\in X$, there exists ${ϵ}_4\in L^{\frac{1}{q_5}}(I,{\mathbb{R}}^{+})$ such that $\mathcal{R}\left(W^{-1}\left(D\right)\left(t\right)\right)\le {ϵ}_5\left(t\right)\mathcal{R}\left(D\right)$. Here ${ϵ}_n\in L^{\frac{1}{q_n}}(I,{\mathbb{R}}^{+})$.

(iii)

For $q_0\in (0,q)$ and $M_{\mathcal{W}}\in L^{\frac{1}{q_0}(I,{\mathbb{R}}^{+})}$ such that for any $S\subset X$, $\mathcal{T}\left(\left(W^{-1}S\right)\left(t\right)\right)\le M_{\mathcal{W}}\left(t\right)\mathcal{T}\left(S\right),q_n\in (0,q),n=0,1,2,3$.

We present the following for our convenience:

$$\begin{array}{cc}\hfill & K_1=k_1\parallel {ϵ}_1{\parallel }_{L^{\frac{1}{q_1}(I,{\mathbb{R}}^{+})}},K_2=k_2\parallel {ϵ}_2{\parallel }_{L^{\frac{1}{q_2}(I,{\mathbb{R}}^{+})}},K_3=k_3\parallel {ϵ}_3{\parallel }_{L^{\frac{1}{q_3}(I,{\mathbb{R}}^{+})}},\parallel A^{-\mu }\parallel =M_0,\hfill \\ & K_4=k_4\parallel {ϵ}_4{\parallel }_{L^{\frac{1}{q_4}(I,{\mathbb{R}}^{+})}},K_5=k_5\parallel {ϵ}_5{\parallel }_{L^{\frac{1}{q_5}(I,{\mathbb{R}}^{+})}},K_0=k_0{\parallel M_{\mathcal{W}}\parallel }_{L^{\frac{1}{q_0}(I,{\mathbb{R}}^{+})}},\hfill \\ & k_n={\left[\left(\frac{1-q_n}{\zeta -q_n}\right)c^{\left(\frac{\zeta -q_n}{1-q_n}\right)}\right]}^{1-q_n},n=0,1,2,3,4,K=\frac{\zeta -1}{1-\rho },K^{*}=\frac{c^{(1+K)(1-\rho )}}{{(1+K)}^{1-\rho }}.\hfill \end{array}$$

Theorem 2.

Suppose that the hypotheses $\left({\mathbf{H}}_{\mathbf{0}}\right)$–$\left({\mathbf{H}}_{\mathbf{5}}\right)$ are satisfied, then the fractional system (1) and (2) is controllable if

$$\begin{array}{c}{L}^{*}=\frac{2M{\tilde{J}}_m{K}_2(1+2{ϵ}_3^{*}+2{ϵ}_4^{*})c^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}\left[1+\frac{2M{\tilde{J}}_m{K}_0{ϵ}_c}{\mathsf{\Gamma }\left(\zeta \right)}\right],\mathit{for}\mathit{some}\frac{1}{2}<\zeta <1.\end{array}$$

(4)

Proof. 

We now define the operator $\Phi :{\mathcal{R}}_l^{\prime }\to {\mathcal{R}}_l^{\prime }$ by

$$\begin{array}{c}\hfill \Phi u\left(t\right)=\left\{\begin{array}{c}\varphi \left(t\right),t\in (-\infty ,0],\hfill \\ J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t\right)J[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]+J^{-1}{F}_1(t,u_t)\hfill \\ +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}A{\mathcal{S}}_{\zeta }(t-s)J^{-1}{F}_1(s,u_s)ds\hfill \\ +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)F_2\left(s,u_s,{\int }_0^{s}e(s,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,u_{\tau })d\tau \right)ds\hfill \\ +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)Bx\left(s\right)ds,t\in I.\hfill \end{array}\right.\end{array}$$

For $\varphi \in {\mathcal{R}}_l$, we present $\widehat{\beta }$ as follows:

$$\begin{array}{c}\hfill \widehat{\beta }\left(t\right)=\left\{\begin{array}{c}\varphi \left(t\right),t\in (-\infty ,0],\hfill \\ {\mathcal{P}}_{\nu ,\zeta }\left(t\right)\varphi \left(0\right),t\in I,\hfill \end{array}\right.\end{array}$$

then $\widehat{\beta }\in {\mathcal{R}}_l^{\prime }$. Let $u\left(t\right)=p\left(t\right)+\widehat{\beta }\left(t\right),-\infty <t\le d$. Clearly u satisfies (3), if and only if p satisfies $p_0=0$ and

$$\begin{array}{cc}\hfill p\left(t\right)=& -J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t\right)J{F}_1(0,\varphi \left(0\right))+J^{-1}{F}_1(t,p_t+{\widehat{\beta }}_t)\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}A{\mathcal{S}}_{\zeta }(t-s)J^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)B{x}_p\left(s\right)ds\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds.\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill x_p& \left(t\right)=W^{-1}[u^1-J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(c\right)J[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]-J^{-1}{F}_1(c,u_c)\hfill \\ & -{\int }_0^c{(c-s)}^{\zeta -1}{J}^{-1}A{\mathcal{S}}_{\zeta }(c-s)J^{-1}{F}_1(s,u_s)ds\hfill \\ & +{\int }_0^c{(c-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(c-s)F_2\left(s,u_s,{\int }_0^{s}e(s,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,u_{\tau })d\tau \right)ds]\left(t\right).\hfill \end{array}$$

Take ${\mathcal{R}}_l^{″}=\{p\in {\mathcal{R}}_l^{\prime }:p_0=0\in {\mathcal{R}}_l\}$. For every $p\in {\mathcal{R}}_l^{″}$,

$$\begin{array}{cc}\hfill {\parallel p\parallel }_c& =\parallel p_0{\parallel }_{{\mathcal{R}}_l}+sup\{\parallel p\left(s\right)\parallel :0\le s\le c\},\hfill \\ \hfill & =sup\{\parallel p(s)\parallel :0\le s\le c\}.\hfill \end{array}$$

Hence $({\mathcal{R}}_l^{″},\parallel ·{\parallel }_c)$ is a Banach space. For $r>0$, fix $F_r=\{p\in {\mathcal{R}}_l^{″}{:\parallel w\parallel }_c\le r\}$, thus $F_r\subseteq {\mathcal{R}}_l^{″}$ is uniformly bounded, and for $p\in F_r$, by referring Lemma 1, we have

$$\begin{array}{cc}\hfill \parallel p_t+{\widehat{\beta }}_t{\parallel }_{{\mathcal{R}}_l}& \le \parallel p_t{\parallel }_{{\mathcal{R}}_l}+{\parallel {\widehat{\beta }}_t\parallel }_{{\mathcal{R}}_l}\hfill \\ \hfill & \le j\left(r+\frac{M}{\mathsf{\Gamma }\left(\nu \right(1-\zeta )+\zeta )}\left|\varphi \left(0\right)\right|\right)+{\parallel \varphi \parallel }_{{\mathcal{R}}_l}=r^{\prime }.\hfill \end{array}$$

(5)

Introduce $\widetilde{\mathsf{{\rm Y}}}:{\mathcal{R}}_l^{″}\to {\mathcal{R}}_l^{″}$ by

$$\widetilde{\mathsf{{\rm Y}}}p\left(t\right)=\left\{\begin{array}{c}0,t\in (-\infty ,0],\hfill \\ -{\mathcal{P}}_{\nu ,\zeta }\left(t\right)F_1(0,\varphi )+J^{-1}{F}_1(t,p_t+{\widehat{\beta }}_t)\hfill \\ +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}A{\mathcal{S}}_{\zeta }(t-s)J^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\hfill \\ +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)B{x}_p\left(s\right)ds\hfill \\ +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)\hfill \\ (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds.\hfill \end{array}\right.$$

Clearly, $\mathsf{{\rm Y}}$ having a fixed point and which is similar to $\widetilde{\mathsf{{\rm Y}}}$. To prove $\widetilde{\mathsf{{\rm Y}}}$ having a fixed point, we subdivide the whole proof as follows:

Step 1:

We state that there exists $r>0$ such that $\widetilde{\mathsf{{\rm Y}}}\left(F_r\right)\subseteq F_r$.

If it is not correct, then there exists $p^r(·)\in F_r$ and $t\in I$ such that $\parallel \widetilde{\mathsf{{\rm Y}}}\left(p^r\right)\left(t\right)\parallel >r,$ i.e., $\widetilde{\mathsf{{\rm Y}}}\left(p^r\right)\notin F_r$.

Fix $r>0$, and assume $\{F_r=u\in C:\parallel u{\parallel }_c\le r\}.$ Clearly, $F_r$ is a closed, bounded and convex set of C.

Now, we need to check there exists $r>0$ such that $\varphi \left(F_r\right)\subseteq F_r$. If it fails, then $p^r\in F_r$. However, $\varphi \left(u^r\right)\notin F_r$. Hence,

$$\parallel \widetilde{\mathsf{{\rm Y}}}\left(u^r\right){\parallel }_c\equiv sup\{t^{1-\eta }\parallel s^r{\parallel }_c:s^r\in \varphi \left(u^r\right)>r\}.$$

Using assumptions $\left({\mathbf{H}}_{\mathbf{2}}\right)$ and $\left({\mathbf{H}}_{\mathbf{3}}\right)$ and Lemma 4, we have

$$\begin{array}{cc}\hfill r& <\underset{t\in I}{sup}{t}^{1-\eta }\parallel (\widetilde{\mathsf{{\rm Y}}}{p}^r)\left(t\right)\parallel \hfill \\ & \le c^{1-\eta }(\parallel -J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t\right)J{F}_1(0,\varphi \left(0\right))\parallel +\parallel J^{-1}{F}_1(t,p_t+{\widehat{\beta }}_t)\parallel \hfill \\ & +\parallel {\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}A{\mathcal{S}}_{\zeta }(t-s)J^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\parallel \hfill \\ & +\parallel {\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)B{x}_p\left(s\right)ds\parallel \hfill \\ & +\parallel {\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\parallel )\hfill \\ & =\sum _{i=1}^5{V}_i,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill V_1& =c^{1-\eta }\parallel J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t\right)J{F}_1(0,\varphi \left(0\right))\parallel \hfill \\ & \le \frac{M_{0}M{\tilde{J}}_m{J}_m}{\mathsf{\Gamma }\left(\nu \right(1-\zeta )+\zeta )}{M}_g^{\prime },\hfill \\ \hfill V_2& =c^{1-\eta }\parallel J^{-1}{F}_1(t,p_t+{\widehat{\beta }}_t)\parallel \hfill \\ & \le c^{1-\eta }{M}_0{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime }).\hfill \end{array}$$

By referring the Hölder’s inequality and Lemma 4, we have

$$\begin{array}{cc}\hfill V_3& =c^{1-\eta }{\int }_0^t\parallel {(t-s)}^{\zeta -1}{J}^{-1}{A}^{1-\zeta }{\mathcal{S}}_{\zeta }(t-s)A^{\zeta }{J}^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)\parallel ds\hfill \\ & \le c^{1-\eta +\mu \zeta }\frac{C_{1-\mu }\mathsf{\Gamma }(1+\mu )}{\mu \mathsf{\Gamma }(1+\mu \zeta )}{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime }).\hfill \end{array}$$

By referring the Hypotheses $\left({\mathbf{H}}_{\mathbf{1}}\right)$–$\left({\mathbf{H}}_{\mathbf{5}}\right)$, we get

$$\begin{array}{cc}\hfill V_4& =c^{1-\eta }\parallel {\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\parallel ,\hfill \\ \hfill & \le c^{1-\eta }{\tilde{J}}_m\parallel {\int }_0^t{(t-s)}^{\zeta -1}{\mathcal{S}}_{\zeta }(t-s){ϵ}_1\left(s\right)\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime }))ds\parallel \hfill \\ \hfill & \le c^{1-\eta }\frac{M{\tilde{J}}_m}{\mathsf{\Gamma }\left(\zeta \right)}{K}_1\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime })),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill V_5& =c^{1-\eta }\parallel {\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)B{x}_p\left(s\right)ds\parallel ,\hfill \\ \hfill \le & c^{1-\eta }\parallel {\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)B{W}^{-1}[u^1-J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(c\right)J[\varphi \left(0\right)-F_1(0,\varphi )]\hfill \\ & +J^{-1}{F}_1(c,p_c+{\widehat{\beta }}_c)+{\int }_0^c{(c-s)}^{\zeta -1}{J}^{-1}A{\mathcal{S}}_{\zeta }(c-s)J^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\hfill \\ & +{\int }_0^c{(c-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(c-s)\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds]ds\parallel \hfill \\ \hfill \le & c^{1-\eta +\zeta }\frac{M{\tilde{J}}_m{ϵ}_b{ϵ}_w}{\mathsf{\Gamma }\left(\eta \right)}[u^1+\frac{M{\tilde{J}}_m{J}_m{c}^{\eta -1}}{\mathsf{\Gamma }\left(s\right(1-\eta )+\eta )}{M}_0(\parallel \varphi \left(0\right)\parallel +K_h^{\prime })\hfill \\ & +M_0{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime })+c^{\mu \zeta }\frac{C_{1-\mu }\mathsf{\Gamma }(1+\mu )}{\mu \mathsf{\Gamma }(1+\mu \zeta )}{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime })\hfill \\ & +\frac{M{\tilde{J}}_m}{\mathsf{\Gamma }\left(\zeta \right)}{K}_1\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime }))].\hfill \end{array}$$

Combining all the above results $V_1$–$V_5,$ we get

$$\begin{array}{cc}\hfill r& \le \frac{M_{0}M{\tilde{J}}_m{J}_m}{\mathsf{\Gamma }\left(\nu \right(1-\zeta )+\zeta )}{M}_g^{\prime }+c^{1-\eta }{M}_0{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime })+c^{1-\eta +\mu \zeta }\frac{C_{1-\mu }\mathsf{\Gamma }(1+\mu )}{\mu \mathsf{\Gamma }(1+\mu \zeta )}{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime })\hfill \\ & +c^{1-\eta }\frac{M{\tilde{J}}_m}{\mathsf{\Gamma }\left(\zeta \right)}{K}_1\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime }))\hfill \\ & +c^{1-\eta +\zeta }\frac{M{\tilde{J}}_m{ϵ}_b{ϵ}_w}{\mathsf{\Gamma }\left(\eta \right)}[u^1+\frac{M_{0}M{\tilde{J}}_m{J}_m{c}^{\eta -1}}{\mathsf{\Gamma }\left(\nu \right(1-\zeta )+\zeta )}{M}_0\parallel \varphi \left(0\right)\parallel \hfill \\ & +\frac{M_{0}M{\tilde{J}}_m{J}_m{c}^{\eta -1}}{\mathsf{\Gamma }\left(\nu \right(1-\zeta )+\zeta )}{M}_0{K}_h^{\prime }+M_0{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime })+c^{\mu \zeta }\frac{C_{1-\mu }\mathsf{\Gamma }(1+\mu )}{\mu \mathsf{\Gamma }(1+\mu \zeta )}{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime })\hfill \\ & +\frac{M{\tilde{J}}_m}{\mathsf{\Gamma }\left(\zeta \right)}{K}_1\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime }))]\hfill \\ & \le c^{1-\eta +\zeta }\frac{M{\tilde{J}}_m{ϵ}_b{ϵ}_w}{\mathsf{\Gamma }\left(\eta \right)}\left[u^1+\frac{M{\tilde{J}}_m{J}_m{c}^{\eta -1}}{\mathsf{\Gamma }\left(s\right(1-\eta )+\eta )}{M}_0\parallel \varphi \left(0\right)\parallel \right]\hfill \\ & +\left[1+c^{\zeta }\frac{M{\tilde{J}}_m{ϵ}_b{ϵ}_w}{\mathsf{\Gamma }\left(\zeta \right)}\right][\frac{M_{0}M{\tilde{J}}_m{J}_m}{\mathsf{\Gamma }\left(\nu \right(1-\zeta )+\zeta )}{M}_g^{\prime }+c^{1-\eta }{M}_0{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime })\hfill \\ & +c^{1-\eta +\mu \zeta }\frac{C_{1-\mu }\mathsf{\Gamma }(1+\zeta )}{\zeta \mathsf{\Gamma }(1+\mu \zeta )}{\tilde{J}}_m{M}_g^{\prime }(1+r^{\prime })\hfill \\ & +c^{1-\eta }\frac{M{\tilde{J}}_m}{\mathsf{\Gamma }\left(\zeta \right)}{K}_1\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime }))].\hfill \end{array}$$

(6)

If we divide (6) by r, and assuming $r\to \infty$, we have $1\le 0$, and this contradicts with (4), then, $\tilde{\varphi }\left(F_r\right)\subseteq F_r.$

Step 2:

$\widetilde{\mathsf{{\rm Y}}}$ is continuous on $F_r$.

For $\tilde{\varphi }$ maps $F_r\left(I\right)$ into itself. For any $(p^n+\widehat{\beta }),p,\widehat{\beta }\in F_r(I),n=0,1,2,\cdots$, with ${lim}_{n\to \infty }{p}^n+\widehat{\beta }=(p+\widehat{\beta })$, we have ${lim}_{n\to \infty }(p^n+\widehat{\beta })\left(t\right)=(p+\widehat{\beta })\left(t\right)$ and

$$\underset{n\to \infty }{lim}{t}^{1-\eta }(p^n+\widehat{\beta })=t^{1-\eta }(p+\widehat{\beta }).$$

Assume $u\left(t\right)=t^{1-\eta }(p+\widehat{\beta })$, then ${\{(p^n+\widehat{\beta })\}}_{n\in N}\subset F_r$ with $(p^n+\widehat{\beta })\to (p+\widehat{\beta })$ in $F_r$ when $n\to \infty$. Define

$$\begin{array}{cc}\hfill & F_2\left(t,u_n\left(t\right),{\int }_0^{t}e\left(t,\tau ,{\tau }^{1-\eta }{u}^n\left(\tau \right)\right)d\tau ,{\int }_0^{c}f\left(t,\tau ,{\tau }^{1-\eta }{u}^n\left(\tau \right)\right)d\tau \right)\hfill \\ & =F_2(t,t^{1-\eta }(p^n+\widehat{\beta })\left(t\right),{\int }_0^{t}e\left(t,\tau ,{\tau }^{1-\eta }(p^n+\widehat{\beta })\left(\tau \right)\right)d\tau ,\hfill \\ & {\int }_0^{c}f\left(t,\tau ,{\tau }^{1-\eta }(p^n+\widehat{\beta })\left(\tau \right)\right)d\tau )\hfill \\ & \to F_2(t,t^{1-\eta }(p+\widehat{\beta })\left(t\right),{\int }_0^{t}e\left(t,\tau ,{\tau }^{1-\eta }(p+\widehat{\beta })\left(\tau \right)\right)d\tau ,\hfill \\ & {\int }_0^{c}f\left(t,\tau ,{\tau }^{1-\eta }(p+\widehat{\beta })\left(\tau \right)\right)d\tau )\hfill \\ & =F_2\left(t,u\left(t\right),{\int }_0^{t}e\left(t,\tau ,{\tau }^{1-\eta }u\left(\tau \right)\right)d\tau ,{\int }_0^{c}f\left(t,\tau ,{\tau }^{1-\eta }u\left(\tau \right)\right)d\tau \right),\mathrm{as}n\to \infty ,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill & {\mathcal{F}}_n\left(s\right)=F_2(s,s^{1-\eta }{(p^n+\widehat{\beta })}_s,{\int }_0^{s}e\left(s,\tau ,{\tau }^{1-\eta }{(p^n+\widehat{\beta })}_{\tau }\right)d\tau ,\hfill \\ & {\int }_0^{c}f\left(s,\tau ,{\tau }^{1-\eta }{(p^n+\widehat{\beta })}_{\tau }\right)d\tau )\mathrm{and}\hfill \\ & \mathcal{F}\left(s\right)=F_2(s,s^{1-\eta }{(p+\widehat{\beta })}_s,{\int }_0^{s}e\left(s,\tau ,{\tau }^{1-\eta }{(p+\widehat{\beta })}_{\tau }\right)d\tau ,\hfill \\ & {\int }_0^{c}f\left(s,\tau ,{\tau }^{1-\eta }{(p+\widehat{\beta })}_{\tau }\right)d\tau ).\hfill \end{array}$$

By referring $\left({\mathbf{H}}_{\mathbf{1}}\right)$ and Lebesgue’s dominated convergence theorem, we have

$$\begin{array}{c}\hfill {\int }_0^t{(t-s)}^{\zeta -1}\parallel J^{-1}{\mathcal{F}}_n\left(s\right)-J^{-1}\mathcal{F}\left(s\right)\parallel ds\to 0\mathrm{as}n\to \infty ,t\in I.\end{array}$$

(7)

In view of $\left({\mathbf{H}}_{\mathbf{1}}\right)$,

$$\begin{array}{c}\hfill \parallel \widetilde{\mathsf{{\rm Y}}}{p}^n-\widetilde{\mathsf{{\rm Y}}}{p\parallel }_{L^{\rho }}\le \frac{M{\tilde{J}}_m}{\mathsf{\Gamma }\left(\zeta \right)}{\int }_0^t{(t-s)}^{\zeta -1}\parallel {\mathcal{F}}_n\left(s\right)-\mathcal{F}\left(s\right)\parallel ds+\frac{M{\tilde{J}}_m{ϵ}_c{L}^{*}}{\mathsf{\Gamma }\left(\zeta \right)}{\parallel x_{p^n}-x_p\parallel }_{L^{\rho }},\end{array}$$

where

$$\begin{array}{cc}\hfill \parallel x_{p^n}-x_p{\parallel }_{L^{\rho }}=& W^{-1}\left[{\int }_0^c{(c-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(c-s)[{\mathcal{F}}_n\left(s\right)-\mathcal{F}\left(s\right)]ds\right]\left(t\right)\hfill \\ & \hfill \le \frac{M{\tilde{J}}_m{ϵ}_w}{\mathsf{\Gamma }\left(\zeta \right)}{\int }_0^c{(c-s)}^{\zeta -1}[{\mathcal{F}}_n\left(s\right)-\mathcal{F}\left(s\right)]ds.\end{array}$$

(8)

By using (7) and (8), we have

$$\parallel \widetilde{\mathsf{{\rm Y}}}{p}^n-\widetilde{\mathsf{{\rm Y}}}{p\parallel }_{L^{\rho }}\to 0\mathrm{when}n\to \infty .$$

Therefore $\widetilde{\mathsf{{\rm Y}}}$ is continuous on $F_r$.

Step 3:

For $p\in F_r$, assume $p\left(t\right)=t^{\eta -1}u\left(t\right)$, $\widetilde{\mathsf{{\rm Y}}}$ sends bounded sets into equicontinuous sets of C, for all $z\in F_r$, there exists $z\in \widetilde{\mathsf{{\rm Y}}}\left(z\right)$ such that $\parallel z\left(t_2\right)-z\left(t_1\right)\parallel \to 0$ when $t_2\to t_1$.

$$\begin{array}{cc}\hfill z\left(t\right)=& J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t\right)J[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]+J^{-1}{F}_1(t,p_t+{\widehat{\beta }}_t)\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)A{J}^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)B{x}_p\left(s\right)ds.\hfill \end{array}$$

Assume $0<\delta <t$ and $0<t_1<t_2<c$. Then $\widetilde{\mathsf{{\rm Y}}}\left(F_r\right)$ is equicontinuous on I.

$$\begin{array}{cc}\hfill \parallel & z\left(t_2\right)-z\left(t_1\right)\parallel \hfill \\ & =\parallel t_2^{1-\eta }{J}^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t_2\right)J^{-1}[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]\hfill \\ & -t_1^{1-\eta }{J}^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t_1\right)J^{-1}[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]\parallel \hfill \\ & +\parallel A^{-\mu }{J}^{-1}[t_2^{1-\eta }{A}^{\mu }{F}_1(t_2,w_{t_2}+{\widehat{\beta }}_{t_2})-t_1^{1-\eta }{A}^{\mu }{F}_1(t_1,w_{t_1}+{\widehat{\beta }}_{t_1})]\parallel \hfill \\ & +\parallel t_2^{1-\eta }{\int }_0^{t_2}{(t_2-s)}^{\zeta -1}{J}^{-1}{A}^{1-\mu }{\mathcal{S}}_{\zeta }(t_2-s)A^{\mu }{J}^{-1}{F}_1(s,w_s+{\widehat{\beta }}_s)ds\hfill \\ & -t_1^{1-\eta }{\int }_0^{t_1}{(t_1-s)}^{\zeta -1}{J}^{-1}{A}^{1-\mu }{\mathcal{S}}_{\zeta }(t_1-s)A^{\mu }{J}^{-1}{F}_1(s,w_s+{\widehat{\beta }}_s)ds\parallel \hfill \\ & +\parallel t_2^{1-\eta }{\int }_0^{t_2}{(t_2-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t_2-s)\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\hfill \\ & -t_1^{1-\eta }{\int }_0^{t_1}{(t_1-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t_1-s)\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\parallel \hfill \\ & +\parallel t_2^{1-\eta }{\int }_0^{t_2}{(t_2-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t_2-s)B{x}_p\left(s\right)ds\hfill \\ & -t_1^{1-\eta }{\int }_0^{t_1}{(t_1-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t_1-s)B{x}_p\left(s\right)ds\parallel \hfill \\ \hfill \le & \frac{{\tilde{J}}_m{J}_m}{\mathsf{\Gamma }\left(\nu \right(1-\zeta \left)\right)}\parallel {\int }_0^{t_2}{t}_2^{1-\eta }{(t_2-s)}^{\nu (1-\zeta )-1}{s}^{\zeta -1}{Q}_{\zeta }\left(s\right)[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]ds\hfill \\ & -{\int }_0^{t_1}{t}_1^{1-\eta }{(t_1-s)}^{v(1-\zeta )-1}{s}^{\zeta -1}[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]ds\parallel \hfill \\ & +M_0{\tilde{J}}_m\parallel t_2^{1-\eta }{A}^{\mu }{F}_1(t_2,p_{t_2}+{\widehat{\beta }}_{t_2})-t_1^{1-\eta }{A}^{\mu }{F}_1(t_1,p_{t_1}+{\widehat{\beta }}_{t_1})\parallel \hfill \\ & +t_2^{1-\eta }{\tilde{J}}_m\parallel {\int }_{t_1}^{t_2}{(t_2-s)}^{\zeta -1}{A}^{1-\mu }{\mathcal{S}}_{\zeta }(t_2-s)A^{\mu }{J}^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\parallel \hfill \\ & +{\tilde{J}}_m\parallel {\int }_0^{t_1}[t_2^{1-\eta }{(t_2-s)}^{\zeta -1}-t_1^{1-\eta }{(t_1-s)}^{\zeta -1}]A^{1-\mu }{\mathcal{S}}_{\zeta }(t_2-s)\hfill \\ & (\times )A^{\mu }{J}^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\parallel \hfill \\ & +t_1^{1-\eta }{\tilde{J}}_m\parallel {\int }_0^{t_1-\delta }{(t_1-s)}^{\zeta -1}\hfill \\ & (\times )[A^{1-\mu }{\mathcal{S}}_{\zeta }(t_2-s)-A^{1-\mu }{\mathcal{S}}_{\zeta }(t_1-s)]A^{\mu }{J}^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\parallel \hfill \\ & +t_1^{1-\eta }{\tilde{J}}_m\parallel {\int }_{t_1-\delta }^{t_1}{(t_1-s)}^{\zeta -1}[A^{1-\mu }{\mathcal{S}}_{\zeta }(t_2-s)-A^{1-\mu }{\mathcal{S}}_{\zeta }(t_1-s)]\hfill \\ & (\times )A^{\mu }{J}^{-1}{F}_1(s,p_s+{\widehat{\beta }}_s)ds\parallel \hfill \\ & +t_2^{1-\eta }{\tilde{J}}_m\parallel {\int }_{t_1}^{t_2}{(t_2-s)}^{\zeta -1}{\mathcal{S}}_{\zeta }(t_2-s)F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\parallel \hfill \\ & +{\tilde{J}}_m{\int }_0^{t_1}\parallel [t_2^{1-\eta }{(t_2-s)}^{\zeta -1}-t_1^{1-\eta }{(t_1-s)}^{\zeta -1}]{\mathcal{S}}_{\zeta }(t_2-s)\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\parallel \hfill \\ & +t_1^{1-\eta }{\tilde{J}}_m\parallel {\int }_0^{t_1-\delta }{(t_1-s)}^{\zeta -1}[{\mathcal{S}}_{\zeta }(t_2-s)-{\mathcal{S}}_{\zeta }(t_1-s)]\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\parallel \hfill \\ & +t_1^{1-\eta }{\tilde{J}}_m\parallel {\int }_{t_1-\delta }^{t_1}{(t_1-s)}^{\zeta -1}[{\mathcal{S}}_{\zeta }(t_2-s)-{\mathcal{S}}_{\zeta }(t_1-s)]\hfill \\ & (\times )F_2\left(s,p_s+{\widehat{\beta }}_s,{\int }_0^{s}e(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,p_{\tau }+{\widehat{\beta }}_{\tau })d\tau \right)ds\parallel \hfill \\ & +t_2^{1-\eta }{\tilde{J}}_m\parallel {\int }_{t_1}^{t_2}{(t_2-s)}^{\zeta -1}{\mathcal{S}}_{\zeta }(t_2-s)B{x}_p\left(s\right)ds\parallel \hfill \\ & +{\tilde{J}}_m{\int }_0^{t_1}\parallel [t_2^{1-\eta }{(t_2-s)}^{\zeta -1}-t_1^{1-\eta }{(t_1-s)}^{\zeta -1}]{\mathcal{S}}_{\zeta }(t_2-s)B{x}_p\left(s\right)ds\parallel \hfill \\ & +t_1^{1-\eta }{\tilde{J}}_m\parallel {\int }_0^{t_1-\delta }{(t_1-s)}^{\zeta -1}[{\mathcal{S}}_{\zeta }(t_2-s)-{\mathcal{S}}_{\zeta }(t_1-s)]B{x}_p\left(s\right)ds\parallel \hfill \\ & +t_1^{1-\eta }{\tilde{J}}_m\parallel {\int }_{t_1-\delta }^{t_1}{(t_1-s)}^{\zeta -1}[{\mathcal{S}}_{\zeta }(t_2-s)-{\mathcal{S}}_{\zeta }(t_1-s)]B{x}_p\left(s\right)ds\parallel \hfill \\ \hfill \le & \sum _{i=1}^{16}{T}_i,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill T_1=& \frac{M{\tilde{J}}_m{J}_m}{\mathsf{\Gamma }\left(\nu \right(1-\zeta \left)\right)\mathsf{\Gamma }\left(\zeta \right)}\parallel {\int }_{t_1}^{t_2}{t}_2^{1-\eta }{(t_2-s)}^{\nu (1-\zeta )-1}{s}^{\zeta -1}[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]ds\parallel ,\hfill \\ \hfill T_2=& t_2^{1-\eta }\frac{M{\tilde{J}}_m{J}_m}{\mathsf{\Gamma }\left(\zeta \right)}\parallel {\int }_0^{t_1}[{(t_2-s)}^{\zeta -1}-{(t_1-s)}^{\zeta -1}]s^{\zeta -1}[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]ds\parallel ,\hfill \\ \hfill T_3=& (t_2^{1-\eta }-t_1^{1-\eta })\frac{M{\tilde{J}}_m{J}_m}{\mathsf{\Gamma }\left(\zeta \right)}\parallel {\int }_0^{t_1}{(t_1-s)}^{\zeta -1}{s}^{\zeta -1}[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]ds\parallel ,\hfill \\ \hfill T_4=& M_0{\tilde{J}}_m[t_2^{1-\eta }-t_1^{1-\eta }]M_g^{{}^{\prime }}(1+r^{\prime }),\hfill \\ \hfill T_5=& t_2^{1-\eta }\frac{K_{1-\mu }\mathsf{\Gamma }(1+\mu )}{\mathsf{\Gamma }(1+\zeta \mu )}[{(t_2-t_1)}^{\zeta \mu }]{\tilde{J}}_m{M}_g^{{}^{\prime }}(1+r^{\prime }),\hfill \\ \hfill T_6=& \frac{\zeta K_{1-\mu }\mathsf{\Gamma }(1+\mu )}{\mathsf{\Gamma }(1+\zeta \mu )}{\tilde{J}}_m{M}_g^{{}^{\prime }}(1+r^{\prime })\parallel \hfill \\ & (\times ){\int }_0^{t_1}\frac{1}{{(t_2-s)}^{\zeta (1-\mu )}}[t_2^{1-\eta }{(t_2-s)}^{\zeta -1}-t_1^{1-\eta }{(t_1-s)}^{\zeta -1}]ds\parallel ,\hfill \\ \hfill T_7=& t_1^{1-\eta }\frac{{\left(t_1\right)}^{\zeta }-{\left(\delta \right)}^{\zeta }}{\zeta }\underset{[0,t_1-\delta ]}{sup}[A^{1-\mu }{\mathcal{S}}_{\zeta }(t_2-s)-A^{1-\mu }{\mathcal{S}}_{\zeta }(t_1-s)]{\tilde{J}}_m{M}_g^{{}^{\prime }}(1+r^{\prime }),\hfill \\ \hfill T_8=& t_1^{1-\eta }\frac{{\delta }^{\zeta }}{\zeta }\underset{[0,t_1-\delta ]}{sup}[A^{1-\mu }{\mathcal{S}}_{\zeta }(t_2-s)-A^{1-\mu }{\mathcal{S}}_{\zeta }(t_1-s)]{\tilde{J}}_m{M}_g^{{}^{\prime }}(1+r^{\prime }),\hfill \\ \hfill T_9=& \frac{M{\tilde{J}}_m{c}^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}\frac{{(t_2-t_1)}^{(1+K)(1-\rho )}}{{(1+K)}^{(1-\rho )}}{\parallel {ϵ}_1\parallel }_{L^{\frac{1}{\rho }}}\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime })),\hfill \\ \hfill T_{10}=& \frac{M{\tilde{J}}_m\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime }))}{\mathsf{\Gamma }\left(\zeta \right)}\parallel {\int }_0^{t_1}[t_2^{1-\eta }{(t_2-s)}^{\zeta -1}-t_1^{1-\eta }{(t_1-s)}^{\zeta -1}]{ϵ}_1\left(s\right)ds\parallel ,\hfill \\ \hfill T_{11}=& c^{1-\eta }{\tilde{J}}_m\frac{{(t_1^{(1+K)}-{\delta }^{(1+K)})}^{1-\rho }}{{(1+K)}^{1-\rho }}\underset{[0,t_1-\delta ]}{sup}\parallel {\mathcal{S}}_{\zeta }(t_2-s)-{\mathcal{S}}_{\zeta }(t_1-s)\parallel \parallel {ϵ}_1{\parallel }_{L^{\frac{1}{\rho }}}\hfill \\ & (\times )\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime })),\hfill \\ \hfill T_{12}=& t_1^{1-\eta }\frac{{\delta }^{(1+K)(1-\rho )}}{{(1+K)}^{1-\rho }}\frac{2M{\tilde{J}}_m}{\mathsf{\Gamma }\left(\zeta \right)}{\parallel {ϵ}_1\parallel }_{L^{\frac{1}{\rho }}}\mathsf{{\rm Y}}(r^{\prime }+c{E}_0(1+r^{\prime })+c{E}_1(1+r^{\prime })),\hfill \\ \hfill T_{13}=& t_1^{1-\eta }\frac{M{\tilde{J}}_m{ϵ}_b}{\mathsf{\Gamma }\left(\zeta \right)}\parallel {\int }_{t_1}^{t_2}{(t_2-s)}^{\zeta -1}w\left(s\right)ds\parallel ,\hfill \\ \hfill T_{14}=& \frac{M{\tilde{J}}_m{ϵ}_b}{\mathsf{\Gamma }\left(\zeta \right)}\parallel {\int }_0^{t_1}[t_2^{1-\eta }{(t_2-s)}^{\zeta -1}-t_1^{1-\eta }{(t_1-s)}^{\zeta -1}]w\left(s\right)ds\parallel ,\hfill \\ \hfill T_{15}=& d^{1-\eta }\frac{M{\tilde{J}}_m{ϵ}_b}{\mathsf{\Gamma }\left(\zeta \right)}\parallel {\int }_0^{t_1-\delta }{(t_1-s)}^{\zeta -1}w\left(s\right)ds\parallel \underset{[0,t_1-\delta ]}{sup}\parallel Q_{\zeta }(t_2-s)-Q_{\zeta }(t_1-s)\parallel ,\hfill \\ \hfill T_{16}=& d^{1-\eta }\frac{M{\tilde{J}}_m{ϵ}_b}{\mathsf{\Gamma }\left(\zeta \right)}\parallel {\int }_{t_1-\delta }^{t_1}{(t_1-s)}^{\zeta -1}w\left(s\right)ds\parallel .\hfill \end{array}$$

The right-hand side of $T_1$ to $T_{12}$ tends to ’0’ as $\delta \to 0$. On implementing the absolute continuity of the Lebesgue integral dominance convergence theorem for inequality, we conclude that $T_1$ to $T_{12}$ gives ’0’ when $t_2-t_1\to 0.$ Therefore, $\widetilde{\mathsf{{\rm Y}}}\left(F_r\right)$ is equicontinuous on $I.$

Step 4:

Now, we need to prove that the Mönch’s condition holds.

Consider $(p^0+\widehat{\beta })\left(t\right)=t^{1-\eta }{\mathcal{P}}_{\nu ,\zeta }\left(t\right)\varphi \left(0\right)$, for all $t\in I$ and $(p^{m+1}+\widehat{\beta })=\widetilde{\mathsf{{\rm Y}}}(p^m+\widehat{\beta }),m=0,1,2,3,\cdots$ and $\widetilde{\mathsf{{\rm Y}}}$ is relatively compact.

Consider $\mathcal{H}\subseteq F_r$ is countable and $\mathcal{H}\subseteq conv(\{0\}\cup \widetilde{\mathsf{{\rm Y}}}\left(\mathcal{H}\right))$. We need to verify that $\mathcal{T}\left(\mathcal{H}\right)=0$, where $\mathcal{T}$ is the Hausdorff measure of noncompactness. Consider $\mathcal{H}={\{(p^m+\widehat{\beta })\}}_{m=1}^{\infty }$. Presently we have to verify that $\widetilde{\mathsf{{\rm Y}}}\left(\mathcal{H}\right)\left(t\right)$ is relatively compact in X, for all $t\in I$. By referring Theorem 1,

$$\begin{array}{cc}\hfill \mathcal{T}(\mathcal{H}(t))& =\mathcal{T}({\{(p^m+\widehat{\beta })(t)\}}_{m=0}^{\infty })=\mathcal{T}(\{(p^0+\widehat{\beta })(t)\}\cup {\{(p^m+\widehat{\beta })(t)\}}_{m=1}^{\infty })\hfill \\ & =\mathcal{T}({\{(p^m+\widehat{\beta })(t)\}}_{m=1}^{\infty }),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \mathcal{T}\left({\{\left(\widetilde{\mathsf{{\rm Y}}}{p}^m\right)(t)\}}_{m=1}^{\infty }\right)& =\mathcal{T}\left({\left\{t^{1-\eta }{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)[{\mathcal{E}}_m(s)+B{x}_{p^m}(s)]\right\}}_{m=1}^{\infty }\right)\hfill \\ \hfill & \le \frac{2M{\tilde{J}}_m{c}^{1-\eta }}{\mathsf{\Gamma }(\zeta )}{\int }_0^t{(t-s)}^{\zeta -1}\mathcal{T}\left({\left\{{\mathcal{E}}_m(s)\right\}}_{m=1}^{\infty }\right)ds\hfill \\ & +\frac{2M{\tilde{J}}_m{c}^{1-\eta }}{\mathsf{\Gamma }(\zeta )}{\int }_0^t{(t-s)}^{\zeta -1}\mathcal{T}\left({\left\{B{x}_{p^m}(s)\right\}}_{m=1}^{\infty }\right)ds\hfill \\ & =U_1+U_2.\hfill \end{array}$$

Now,

$$\begin{array}{cc}\hfill U_1& \le \frac{2M{\tilde{J}}_m{c}^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}{\int }_0^t{(t-s)}^{\zeta -1}\mathcal{T}\left({\left\{{\mathcal{E}}_m(p_s^m+{\widehat{\beta }}_s)\right\}}_{m=1}^{\infty }\right)ds\hfill \\ \hfill & \le \frac{2M{\tilde{J}}_m{c}^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}{\int }_0^t{(t-s)}^{\zeta -1}[\mathcal{T}\left({\left\{p^m(\tau +\phi )+\widehat{\beta }(\tau +\phi )\right\}}_{m=1}^{\infty }\right)\hfill \\ & +\mathcal{T}\left({\left\{{\int }_0^{\tau }e(\tau ,\epsilon ,p_{\epsilon }^m+{\widehat{\beta }}_{\epsilon })d\epsilon ,{\int }_0^{b}f(\tau ,\epsilon ,p_{\epsilon }^m+{\widehat{\beta }}_{\epsilon })d\epsilon \right\}}_{m=1}^{\infty }\right)]ds\hfill \\ \hfill & {\displaystyle \le \frac{2M{\tilde{J}}_m{c}^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}{K}_2(1+2{ϵ}_3^{*}+2{ϵ}_4^{*})\underset{-\infty <\phi \le 0}{sup}\mathcal{T}\left(\mathcal{X}\left(\phi \right)\right),}\hfill \\ \hfill U_2& =\mathcal{T}\left({\left\{c^{1-\eta }{\int }_0^t{(t-s)}^{\eta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(c-s)B{w}_{p^m}\left(s\right)ds\right\}}_{m=1}^{\infty }\right)\hfill \\ & \le \frac{2M{\tilde{J}}_m{ϵ}_b{c}^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}{\int }_0^t{(t-s)}^{\eta -1}\mathcal{T}\left({\left\{w_{p^m}\left(s\right)\right\}}_{m=1}^{\infty }\right)ds\hfill \\ & \le \frac{2M{\tilde{J}}_m{ϵ}_b{c}^{1-\eta }}{\mathsf{\Gamma }{\left(\zeta \right)}^2}{\int }_0^t{(t-s)}^{\eta -1}\hfill \\ & (\times )\mathcal{T}\left[W^{-1}\left({\int }_0^c{(c-s)}^{\eta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(c-s)\mathcal{T}({E_m(p_s^m+{\widehat{\varphi }}_s)}_{m=1}^{\infty })ds\right)\right]ds\hfill \\ \hfill & {\displaystyle \le \frac{2M{\tilde{J}}_m{ϵ}_b{c}^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}{\int }_0^t{(t-s)}^{\eta -1}{M}_{\mathcal{W}}\left(s\right)ds\frac{2M}{\mathsf{\Gamma }\left(\zeta \right)}{K}_2{\tilde{J}}_m(1+2{ϵ}_3^{*}+2{ϵ}_4^{*})\underset{-\infty <\phi \le 0}{sup}\mathcal{T}\left(\mathcal{X}\left(\phi \right)\right)}\hfill \\ \hfill & {\displaystyle \le \frac{4M^2{\tilde{J}}_m{ϵ}_b{c}^{1-\eta }}{\mathsf{\Gamma }{\left(\zeta \right)}^2}{K}_0{K}_2{\tilde{J}}_m(1+2{ϵ}_3^{*}+2{ϵ}_4^{*})\underset{-\infty <\phi \le 0}{sup}\mathcal{T}\left(\mathcal{X}\left(\phi \right)\right).}\hfill \end{array}$$

Now

$$\begin{array}{cc}\hfill U_1+U_2& {\displaystyle \le \frac{2M{\tilde{J}}_m{K}_2(1+2{ϵ}_3^{*}+2{ϵ}_4^{*})c^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}\left[1+\frac{2M{\tilde{J}}_m{K}_0{ϵ}_b}{\mathsf{\Gamma }\left(\zeta \right)}\right]\underset{-\infty <\phi \le 0}{sup}\mathcal{R}\left(\mathcal{X}\left(\phi \right)\right).}\hfill \end{array}$$

By referring Lemma 5,

$$\mathcal{T}\left(\widetilde{\mathsf{{\rm Y}}}\left(H\right)\right)\le L^{*}\mathcal{T}\left(H\right).$$

Hence by using Mönch’s condition, we have

$$\begin{array}{c}\mathcal{T}(\widetilde{\mathsf{{\rm Y}}})\le \mathcal{T}\left(\mathrm{conv}(\{0\}\cup (\widetilde{\mathsf{{\rm Y}}}(H))\right)=\mathcal{T}(\widetilde{\mathsf{{\rm Y}}}\left(H\right))\le L^{*}\mathcal{T}\left(H\right),\end{array}$$

this implies $\mathcal{T}\left(H\right)=0$. Therefore, $\widetilde{\mathsf{{\rm Y}}}$ has a fixed point $y\in F_r$, in view of Lemma 6. Next, $u=p+\widehat{\beta }$ is a mild solution of the fractional system (1) and (2) satisfying $u\left(c\right)=u^1$, then the fractional system (1) and (2) is controllable on X. □

4. Nonlocal Conditions

Physical problems prompted the development of evolution equations with nonlocal conditions. In [54,55], the authors explored nonlocal issues for the first time in 1990, obtaining the existence and uniqueness of mild solutions for nonlocal differential equations of integer order. For more details on the systems with integer of fractional orders, one can refer [29,30,32,35,45,54,55]. Assume that nonlocal Hilfer fractional delay Volterra-Fredholm integro-differential system has the following form

$$\begin{array}{c}{D}_{0^{+}}^{\nu ,\zeta }[Ju\left(t\right)-F_1(t,u_t)]=Au\left(t\right)+Bx\left(t\right)\hfill \\ \hfill +F_2\left(t,u_t,{\int }_0^{t}e(t,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(t,\tau ,u_{\tau })d\tau \right),t\in I=(0,c],\end{array}$$

(9)

$$\begin{array}{cc}\hfill & I_{0^{+}}^{(1-\nu )(1-\zeta )}u\left(0\right)=\varphi +g(u_{t_1},u_{t_2},u_{t_3},\cdots ,u_{t_n})\in {\mathcal{R}}_l,\hfill \end{array}$$

(10)

where $0<t_1<t_2<t_3<\cdots <t_n\le d$, $g:{\mathcal{R}}_l^n\to {\mathcal{R}}_l$ and satisfies the following:

(H6)

$g:{\mathcal{R}}^n\to \mathcal{R}$ is continuous, there exists $K_i\left(g\right)>0$ such that

$$\begin{array}{c}\hfill \parallel g(u_1,u_2,\cdots ,u_n)-g(w_1,w_2,\cdots ,w_n)\parallel \le \sum _{i=1}^n{K}_i\left(g\right){\parallel u_i-w_i\parallel }_{{\mathcal{R}}_l},\end{array}$$

for all $u_i,w_i\in {\mathcal{R}}_l$ and consider $K_g=sup\{\parallel g(u_1,u_2,\cdots ,u_n)\parallel :u_i\in {\mathcal{R}}_l\}$.

Definition 10.

A function $u:(-\infty ,c]\to X$ is said to be a mild solution of (9) and (10) if $u_0=\varphi +g(u_{t_1},u_{t_2},u_{t_3},\cdots ,u_{t_n})\left(0\right))\in {\mathcal{R}}_l$ on $(-\infty ,0]$ and

$$\begin{array}{cc}\hfill u\left(t\right)=& J^{-1}{\mathcal{P}}_{\nu ,\zeta }\left(t\right)J[\varphi \left(0\right)-F_1(0,\varphi \left(0\right)+g(u_{t_1},u_{t_2},u_{t_3},\cdots ,u_{t_n})\left(0\right))]+J^{-1}{F}_1(t,u_t)\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}A{\mathcal{S}}_{\zeta }(t-s)J^{-1}{F}_1(s,u_s)ds\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)F_2\left(s,u_s,{\int }_0^{s}e(s,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(s,\tau ,u_{\tau })d\tau \right)ds\hfill \\ & +{\int }_0^t{(t-s)}^{\zeta -1}{J}^{-1}{\mathcal{S}}_{\zeta }(t-s)Bx\left(s\right)ds,t\in I,\hfill \end{array}$$

is satisfied.

Theorem 3.

Assume that the hypotheses $\left({\mathbf{H}}_{\mathbf{0}}\right)$–$\left({\mathbf{H}}_{\mathbf{6}}\right)$ are satisfied, then the fractional system (9) and (10) is controllable if

$$\begin{array}{c}\hfill L^{*}=\frac{2M{\tilde{J}}_m{K}_2(1+2{ϵ}_3^{*}+2{ϵ}_4^{*})c^{1-\eta }}{\mathsf{\Gamma }\left(\zeta \right)}\left[1+\frac{2M{\tilde{J}}_m{K}_0{ϵ}_b}{\mathsf{\Gamma }\left(\zeta \right)}\right],forsome\frac{1}{2}<\zeta <1.\end{array}$$

5. Examples

5.1. Abstract System

Assume that the Hilfer fractional differential system with control of the following form

$$\begin{array}{cc}\hfill D_{0^{+}}^{\nu ,\frac{2}{3}}[u(s,ħ)& -\frac{{\partial }^2}{\partial {ħ}^2}u(s,ħ)+{\int }_0^{\pi }\zeta (z,ħ)u(s,z)dz]=\frac{{\partial }^2}{\partial {ħ}^2}u(s,ħ)\hfill \\ & +E(s,{\int }_{-\infty }^s{\varrho }_1(\epsilon -s)u(\epsilon ,ħ)d\epsilon ,{\int }_0^{\theta }{\int }_{-\infty }^0{\xi }_2(\tau ,x,\epsilon -\tau )u(\epsilon ,ħ)d\epsilon d\tau ,\hfill \\ & {\int }_0^c{\int }_{-\infty }^0{\xi }_3(\tau ,x,\epsilon -\tau )u(\epsilon ,ħ)d\epsilon d\tau )+\mathcal{V}(s,ħ),\tau \in [0,\pi ],s\in [0,c],\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & I^{(1-\nu )\frac{1}{3}}{\left[u(s,ħ)\right]|}_{ħ=0}=u_0(ħ),ħ\in [0,\pi ],\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & u(s,0)=u(s,\pi )=0,s\ge 0,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & u(0,\mu )=s\left(\mu \right),0\le \mu \le \pi ,\hfill \end{array}$$

(14)

where $D_{0^{+}}^{\nu ,\frac{2}{3}}$ denotes the Hilfer fractional derivative of order $(\zeta =\frac{2}{3})$ and type $\nu$, $\mathcal{V}:I\times [0,1]\times [0,1]\times \mathbb{R}\to \mathbb{R}$ is continuous.

To transform the fractional system (11)–(14) to abstract form, assume $X=L^2(0,\pi )$ and $A:D\left(A\right)\subset X\to X$, $J:D\left(J\right)\subset X\to X$ be defined by $Aw=w^{″}$, and $Pw=w-A$ where $D\left(A\right)$ and $D\left(J\right)$ is given by $\{w\in U:w,w^{\prime }$ are absolutely continuous, $w\left(0\right)=w\left(\pi \right)=0\}$. Then, A and J are presented as $Aw={\sum }_{m=1}^{\infty }{n}^2⟨w,z_m⟩z_m$, $w\in D\left(A\right)$, $Jw={\sum }_{m=1}^{\infty }(1+m^2)⟨w,z_m⟩z_m$, $w\in D\left(J\right)$ where $z_m\left(x\right)=\sqrt{\frac{2}{\pi }}sin\left(mx\right)$, $m=1,2,3,\cdots$ are the orthonormal of vectors of A. Then, for $z\in U$, we have

$$P^{-1}z=\sum _{m=1}^{\infty }\frac{1}{(1+m^2)}⟨z,z_m⟩z_m,$$

$$A{J}^{-1}z=\sum _{m=1}^{\infty }\frac{m^2}{(1+m^2)}⟨z,z_m⟩z_m,$$

and

$$Q_{\mu }\left(\theta \right)z=\sum _{m=1}^{\infty }exp\left(\frac{m^2\theta }{1+m^2}\right)⟨z,z_m⟩z_m.$$

A is defined by $T\left(\theta \right)z\left(\tau \right)=z(\theta +\tau )$ for $z\in X$, $T\left(\theta \right)$ is not compact on X with $\mathcal{T}\left(T\right(\theta \left)D\right)\le \mathcal{T}\left(D\right)$, $\mathcal{T}$ is the Hausdorff measure of noncompactness.

Here A is an infinitesimal generator of a semigroup $\left\{T\right(s),s\ge 0\}$ in X and which is presented as $T\left(s\right)w\left(\epsilon \right)=w(s+\epsilon )$, for $w\in U$, $T\left(s\right)$ is not compact on X with $\mathcal{T}\left(T\right(s\left)D\right)\le \mathcal{T}\left(D\right)$. Furthermore, $s\to w(s^{\frac{2}{3}}+\epsilon )u$ is equicontinuous ([45]), where $s\ge 0$ and $ħ\in (0,\infty ).$ We assume $F_1:[0,\pi ]\times X\to X$ and $F_2:[0,\pi ]\times X\times X\times X\to X$ by

$$\begin{array}{cc}\hfill e(\theta ,& s)={\int }_{-\infty }^{\theta }{\xi }_2(\theta ,\tau ,\epsilon )s\left(\epsilon \right)d\epsilon ,\hfill \\ \hfill f(\theta ,& s)={\int }_{-\infty }^c{\xi }_3(\theta ,\tau ,\epsilon )s\left(\epsilon \right)d\epsilon ,\hfill \\ \hfill F_1\left(u\right)& \left(\epsilon \right)={\int }_0^{\pi }\zeta (z,\epsilon )u(s,\epsilon )d\epsilon ,\hfill \\ \hfill F_2(\theta ,& s,{\int }_0^{\theta }e(\epsilon ,s)d\epsilon ,{\int }_0^{c}f(\epsilon ,s)d\epsilon )\hfill \\ & =E\left(s,{\int }_{-\infty }^s{\nu }_1(\epsilon -s)u(\epsilon ,\zeta )d\epsilon ,{\int }_0^{ϵ}e(\epsilon ,s)\left(\tau \right)d\epsilon ,{\int }_0^{c}f(\epsilon ,s)\left(\tau \right)d\epsilon \right),\hfill \end{array}$$

and $D_{0^{+}}^{\nu ,\frac{2}{3}}\left(u\right)\left(s\right)\left(\mu \right)=\frac{{\partial }^{\frac{2}{3}}}{\partial {\mu }^{\frac{2}{3}}}u(s,\mu ),u\left(s\right)\left(\epsilon \right)=u(s,\epsilon ).$

Let $B:X\to X$ be given by $\left(Bx\right)\left(s\right)(ħ)=\mathcal{V}x(s,ħ),0<s<1.$ For $ħ\in (0,\pi )$, W is given by

$$\begin{array}{c}\hfill Wx(ħ)={\int }_0^1{(1-s)}^{\frac{-1}{3}}{\mathcal{S}}_{\zeta }(1-s)\mathcal{V}x(s,ħ)ds,\end{array}$$

where

$$\begin{array}{c}\hfill {\mathcal{S}}_{\frac{2}{3}}=\frac{2}{3}{\int }_0^{\infty }ħ{\xi }_{\frac{2}{3}}(ħ)x(t^{\frac{2}{3}}ħ)dħ,\end{array}$$

and for $ħ\in (0,\infty )$

$${\xi }_{\frac{2}{3}}(ħ)=\frac{3}{2}{ħ}^{-1-\frac{-5}{2}}{\overline{x}}_{\frac{2}{3}}\left({ħ}^{\frac{-3}{2}}\right),$$

$$\begin{array}{cc}\hfill {\overline{x}}_{\frac{2}{3}}(ħ)& =\frac{1}{\pi }\sum _{n=1}^{\infty }{(-1)}^{n-1}{t}^{-\frac{2}{3}n-1}\frac{\mathsf{\Gamma }(\frac{2}{3}n+1)}{n!}sin\left(\frac{2n\pi }{3}\right),\hfill \end{array}$$

where ${\xi }_{\frac{2}{3}}$ is determined on $(0,\infty )$, i.e.,

$${\xi }_{\frac{2}{3}}(ħ)\ge 0,ħ\in (0,\infty )\mathrm{and}{\int }_0^{\infty }{\xi }_{\frac{2}{3}}(ħ)dħ=1.$$

Finally $F_1$, $F_2$ and $\mathcal{V}$ satisfy the hypotheses $\left({\mathbf{H}}_{\mathbf{1}}\right)$–$\left({\mathbf{H}}_{\mathbf{5}}\right)$, thus all the requirements of the Theorem 2 are satisfied, then the fractional system (11)–(14) is controllable on I.

5.2. Filter System

An advanced filter is a framework that performs mathematical operations on an inspected, digitized sign to decrease or upgrade certain highlights of the prepared signal. Propelled by the plans examined in [13,19,29,56,57], we presented a filter design for our framework which is shown in Figure 1. Figure 1 portrays the rough pattern of block diagram which helps to improve the viability of arrangement with least measure of sources of input and which is presented as follows.

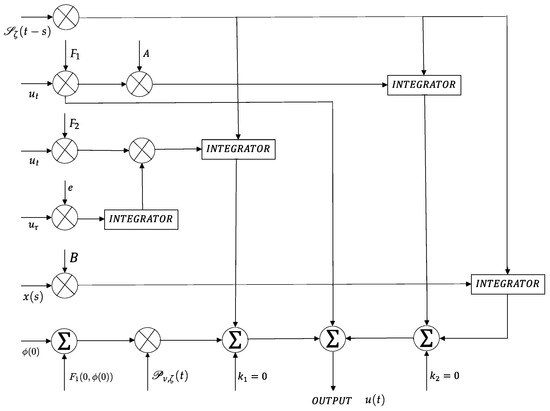
Figure 1. Filter System.

Product modulator (PM)-1 receives inputs $u_t$ and $F_1$ generates the output as $F_1(t,u_t)$. PM-2 receives A and $F_1(t,u_t)$ generates $A{F}_1(t,u_t)$. PM-4 receives $u_{\tau }$ and f generates $f(t,\tau ,u_{\tau })$. PM-4 receives $u_t$ and $F_2$ produces $F_2(t,u_t)$. PM-5 receives $u_{\tau }$ and e generates $e(t,\tau ,u_{\tau })$. PM-6 receives $F_2(t,u_t)$, $e(t,\tau ,u_{\tau })$ and $f(t,\tau ,u_{\tau })$ generates

$$F_2\left(t,u_t,{\int }_0^{t}e(t,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(t,\tau ,u_{\tau })d\tau \right).$$

PM-7 receives $x\left(t\right)$ and B generates $Bx\left(t\right)$. PM-8 receives $[\varphi \left(0\right)-F_1(0,\varphi \left(0\right))]$ and ${\mathcal{P}}_{\nu ,\zeta }\left(t\right)$ at time $t=0$, generates ${\mathcal{P}}_{\nu ,\zeta }\left(t\right)$. The integrators execute the integral of

$${\mathcal{S}}_{\zeta }\left(t\right)\left[A{\mathcal{S}}_{\zeta }\left(t\right)F_1(t,u_t)+F_2\left(t,u_t,{\int }_0^{t}e(t,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(t,\tau ,u_{\tau })d\tau \right)+Bx\left(t\right)\right],$$

over t.

Additionally, Inputs ${\mathcal{S}}_{\zeta }\left(t\right)$, $A{F}_1(t,u_t)$ are joined and multiplying with the output on the interval $(0,t)$. ${\mathcal{S}}_{\zeta }\left(t\right)$, $F_2\left(t,u_t,{\int }_0^{t}e(t,\tau ,u_{\tau })d\tau ,{\int }_0^{c}f(t,\tau ,u_{\tau })d\tau \right)$ are joined and multiplying with the output on the interval $(0,t)$. ${\mathcal{S}}_{\zeta }\left(t\right)$, $Bx\left(t\right)$ are joined and multiplying with the output on the interval $(0,t)$.

Finally, if we shift all the outputs from the integrators to summer network, then, the output of $u\left(t\right)$ is achieved, which is bounded and controllable.

6. Conclusions

The exact controllability of Sobolev-type Hilfer fractional neutral integro-differential systems via measure of noncompactness is the topic of our article. The main conclusions of our paper are based on theoretical ideas such as fractional calculus, the measure of noncompactness, and the fixed-point approach. First, we looked at the exact controllability of mild solutions for fractional evolution systems. Then we expanded on our findings to consider the system in nonlocal conditions. Finally, we presented theoretical and practical applications to aid in the efficacy of the discussion.