A Note on Approximate Controllability of Fractional Semilinear Integrodifferential Control Systems via Resolvent Operators

Abstract

This article primarily focuses on the approximate controllability of fractional semilinear integrodifferential equations using resolvent operators. Two alternative sets of necessary requirements have been studied. In the first set, we use theories from functional analysis, the compactness of an associated resolvent operator, for our discussion. The primary discussion is proved in the second set by employing Gronwall’s inequality, which prevents the need for compactness of the resolvent operator and the standard fixed point theorems. Then, we extend the discussions to the fractional Sobolev-type semilinear integrodifferential systems. Finally, some theoretical and practical examples are provided to illustrate the obtained theoretical results.

1. Introduction

Fractional calculus has played a considerable part in mathematics because some physical problems cannot be solved using differential equations of an integer order, but they can be solved using differential equations of a fractional order. Fractional systems have received plenty of attention and are widely used in engineering, physical science, chemical science, biology, and a variety of other subjects. Fractional calculus ideas have recently been successfully extended to numerous sectors, and scientists are increasingly understanding that a fractional system can well correspond to many occurrences in the realms of regular sciences and engineering. Rheology, liquid stream, scattering, microscopic structures, viscoelasticity, and optics are only a few of the important disciplines of fractional calculus currently. Although diagnostic structures are typically difficult to come by, several researchers have been impressed by the success of mathematical evaluation approaches for fractional systems in these fields. Readers can refer to [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. A Sobolev-type equation can be found in a range of physical situations, including fluid movement through fissured rocks, the propagation of small-amplitude long waves, and so forth, see [20,21,22].

In mathematical control theories and technological sectors, controllability is linked to pole assignment, quadratic optimum control, observer design, and other concepts. Exact and approximate controllability are the two primary principles of controllability that may be identified in infinite dimensional systems. Infinite-dimensional spaces contain non-closed linear subspaces. The system can be guided to any final state with exact controllability, whereas it can be steered to any smaller neighborhood of the final state with approximate controllability, we refer to [13,14,17,23,24,25,26,27,28,29,30,31,32,33]. The results of mild solutions for integrodifferential systems using resolvent operators were introduced by Grimmer [23,24,25,26,27]. In [27], the author proved the existence, uniqueness, and continuity of solutions of abstract Volterra integral equations. In [25], the authors proved the existence of analytic resolvent operators for integral equations in a Banach space by assuming that the closed operator A generates an analytic semigroup and stated the hypothesis in terms of A. The existence of a resolvent operator for such an equation is equivalent to its well-posedness obtained by the Hille-Yosida theorem; we recommend readers to [1,3,4,5,23,24,25,26,27].

The primary contributions are: the approximate controllability of fractional semilinear integrodifferential systems with control using resolvent operators. Two alternative sets of requirements have been studied. In the first set, we use theories from functional analysis, the compactness of the associated resolvent operator, for the conversation. The primary discussion is proved in the second set by employing Gronwall’s inequality, which avoids the need for the compactness of the resolvent operator and the standard fixed point theorems. In the first approach, we use the fixed point technique, and in the second approach, we relaxed the compactness of the solution operator and the application of the fixed point theorem.

Let us consider the subsequent fractional semilinear integrodifferential control systems via resolvent operators of the form

$$\begin{array}{cc}\hfill D_{\sigma }^{\alpha }\chi \left(\sigma \right)& =A\left[\chi \left(\sigma \right)+{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota )\chi \left(\iota \right)d\iota \right]+Bv\left(\sigma \right)+E(\sigma ,\chi \left(\sigma \right)),\sigma \in V=[0,c],\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \chi \left(0\right)& ={\chi }_0,{\chi }^{\prime }\left(0\right)=0,\hfill \end{array}$$

(2)

where $\alpha \in (1,2)$; $A,{\left(\mathcal{B}\left(\sigma \right)\right)}_{\sigma \ge 0}$ are closed linear operators defined on a Hilbert space X, and ${}^{c}D{{}_{0+}^{\alpha }}_{\sigma }\chi \left(\sigma \right)=D_{\sigma }^{\alpha }\chi \left(\sigma \right)$ stands for the Caputo fractional derivative of order $n-1<\alpha <n$ of $\chi$, which is given as

$$\begin{array}{c}{D}_{\sigma }^{\alpha }\chi \left(\sigma \right)={\int }_0^{\sigma }{h}_{n-\alpha }(\sigma -\iota )\frac{d^n}{d{\iota }^n}\chi \left(\iota \right)d\iota ,\end{array}$$

where n is the smallest integer greater than or equal to $\alpha$, and $h_{\beta }\left(\sigma \right):=\frac{{\sigma }^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}$$\sigma >0$, and $\beta >0$, $v(·)\in L^2(V,U)$ is a Hilbert space of admissible control functions; U is also a Hilbert space. Furthermore, the linear operator $B:U\to X$ is bounded, and $E:V\times X\to X$.

The linear system of (1)–(2) proceeds as follows:

$$\begin{array}{cc}\hfill D_{\sigma }^{\alpha }\chi \left(\sigma \right)& =A\left[\chi \left(\sigma \right)+{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota )\chi \left(\iota \right)d\iota \right]+Bv\left(\sigma \right),\sigma \in V=[0,c],\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \chi \left(0\right)& ={\chi }_0,{\chi }^{\prime }\left(0\right)=0.\hfill \end{array}$$

(4)

Next, we examine the synopsis of the project. In the second half, the theories and preliminary results for the resolvent operator, which will be used in this investigation, are provided. In Section 3 and Section 4, we provide the main discussion of our work. Then, in Section 5, an example for drawing the theory of the primary outcomes is offered.

2. Preliminaries

We provide some essential results, notations, and fundamental outcomes concerning resolvent family in this part. The resolvent set of a linear operator A is denoted by $\rho \left(A\right)$. ∃$M\ge 1$, w∋$\parallel \mathcal{T}\left(\sigma \right)\parallel \le M{e}^{w\sigma }$, $\sigma \ge 0$ (refer to [24]). Define $\mathcal{C}$ as the Banach space $C(V,X)$, equipped with ${\parallel z\parallel }_{\mathcal{C}}\equiv {sup}_{\sigma \in V}\parallel z\left(\sigma \right)\parallel$, for $z\in \mathcal{C}$.

To obtain our essential results, let us consider the following fractional integrodifferential system

$$\begin{array}{cc}\hfill D_{\sigma }^{\alpha }\chi \left(\sigma \right)=& A\chi \left(\sigma \right)+{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota )\chi \left(\iota \right)d\iota ,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \chi \left(0\right)=& z\in X,{\chi }^{\prime }\left(0\right)=0,\hfill \end{array}$$

(6)

which is connected with an $\alpha$-resolvent operator of bounded linear operators ${\left({\mathcal{R}}_{\alpha }\left(\sigma \right)\right)}_{\sigma \ge 0}$ on X.

Definition 1.

In [3] A one-parameter family of bounded linear operators ${\left({\mathcal{R}}_{\alpha }\left(\sigma \right)\right)}_{\sigma \ge 0}$ on X is said to be an α-resolvent operator of (5) and (6) provided that the subsequent characteristics are fulfilled:

(a)

${\mathcal{R}}_{\alpha }(·):[0,\infty )\to \mathcal{L}\left(X\right)$ is strongly continuous and ${\mathcal{R}}_{\alpha }\left(0\right)\chi =\chi$, ∀$\chi \in X$ and $\alpha \in (1,2)$.

(b)

For $\chi \in D\left(A\right)$, ${\mathcal{R}}_{\alpha }(·)\chi \in C([0,\infty ),\left[D\left(A\right)\right])\bigcap C^1([0,\infty ),X)$, and

$$\begin{array}{cc}\hfill & D_{\sigma }^{\alpha }{\mathcal{R}}_{\alpha }\left(\sigma \right)\chi =A{\mathcal{R}}_{\alpha }\left(\sigma \right)\chi +{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota ){\mathcal{R}}_{\alpha }\left(\iota \right)\chi d\iota ,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & D_{\sigma }^{\alpha }{\mathcal{R}}_{\alpha }\left(\sigma \right)\chi ={\mathcal{R}}_{\alpha }\left(\sigma \right)A\chi +{\int }_0^{\sigma }{\mathcal{R}}_{\alpha }(\sigma -\iota )\mathcal{B}\left(\iota \right)\chi d\iota ,\hfill \end{array}$$

(8)

for every $\sigma \ge 0$.

We now present the properties discussed in [5] to attain the mild solutions. We introduce the operator ${\left({\mathcal{R}}_{\alpha }\left(\sigma \right)\right)}_{\sigma \ge 0}$ in the following way:

$${\mathcal{R}}_{\alpha }\left(\sigma \right)=\left\{\begin{array}{ccc}{\displaystyle \frac{1}{2\pi i}{\int }_{{\mathrm{\Gamma }}_{r,\theta }}{e}^{\lambda \sigma }{F}_{\alpha }\left(\lambda \right)d\lambda ,}& \hfill \sigma >0,& \\ I,& \hfill \sigma =0.\end{array}\right.$$

(9)

We assume that the non-homogeneous system

$$\begin{array}{cc}\hfill D_{\sigma }^{\alpha }\chi \left(\sigma \right)=& A\chi \left(\sigma \right)+{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota )\chi \left(\iota \right)d\iota +f\left(\sigma \right),\sigma \in [0,c],\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \chi \left(0\right)=& {\chi }_0,{\chi }^{\prime }\left(0\right)=0,\hfill \end{array}$$

(11)

where $\alpha \in (1,2)$ and $f\in L^1([0,a],X)$. Here, ${\mathcal{R}}_{\alpha }(·)$ is the operator determined as in (9).

Definition 2.

In [3], let $\alpha \in (1,2)$; we define the family ${\left({\mathcal{T}}_{\alpha }\left(\sigma \right)\right)}_{\sigma \ge 0}$ by

$$\begin{array}{c}{\mathcal{T}}_{\alpha }\left(\sigma \right)\chi :={\int }_0^{\sigma }{h}_{\alpha -1}(\sigma -\iota ){\mathcal{R}}_{\alpha }\left(\iota \right)\chi d\iota ,\end{array}$$

for each $\sigma \ge 0$.

Definition 3.

In [3], let $f\in L^1([0,c],X)$. A function $\chi \in C\left(\right[0,a],X)$ is called a mild solution of (10) and (11) if

$$\begin{array}{c}\chi \left(\sigma \right)={\mathcal{R}}_{\alpha }\left(\sigma \right)z+{\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\iota )f\left(\iota \right)d\iota ,\sigma \in [0,c].\end{array}$$

Definition 4.

The function $\chi \in \mathcal{C}$ is called the mild solution of (1) and (2) if

$$\begin{array}{cc}\hfill \chi \left(\sigma \right)& ={\mathcal{R}}_{\alpha }\left(\sigma \right){\chi }_0+{\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\iota )E(\iota ,\chi \left(\iota \right))d\iota +{\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\iota )Bv\left(\iota \right)d\iota ,\sigma \in V,\hfill \end{array}$$

is fulfilled.

Definition 5.

The reachable set of (1) and (2) is presented as

$K_c\left(E\right)=\{\chi \left(c\right)\in X:\chi \left(\sigma \right)$ designates the mild solution of (1) and (2)}.

Suppose $E\equiv 0$, then (1) and (2) reduce to a corresponding linear system. The reachable set for this case is designated as $K_c\left(0\right)$.

Definition 6.

If $\overline{K_c\left(E\right)}=X$, then the semilinear system is approximately controllable on $[0,c]$. Here, $\overline{K_c\left(E\right)}$ denotes the closure of $K_c\left(E\right)$. Clearly, provided that $\overline{K_c\left(0\right)}=X$, then the linear system is approximately controllable.

Consider $\Psi =L^2(V,X)$. We now define $\aleph :\Psi \to \Psi$ in the following way:

$$[\aleph \chi ]\left(\sigma \right)=E(\sigma ,\chi (\sigma \left)\right);0<\sigma \le c.$$

We now present $\rho :\Psi \to \Psi$ in the following way:

$$\left[\rho \chi \right]\left(\sigma \right)={\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\zeta )\chi \left(\zeta \right)d\zeta .$$

Additionally, we present $\mathcal{L}:\Psi \to X$ in the following way:

$$\mathcal{L}\mu ={\int }_0^c{\mathcal{T}}_{\alpha }(c-\zeta )\mu \left(\zeta \right)d\zeta .$$

We take $N_0\left(\mathcal{L}\right)$ as the null space according to $\mathcal{L}$. Additionally, $N_0\left(\mathcal{L}\right)$ is a subspace of $\Psi$, which is closed, and the orthogonal space is assigned as $N_0^{\perp }\left(\mathcal{L}\right)$. Therefore, $\Psi$ is unambiguously assigned as $\Psi =N_0\left(\mathcal{L}\right)\oplus N_0^{\perp }\left(\mathcal{L}\right)$. $R\left(B\right)$, $\overline{R(B})$ denotes the range of B and closure of $R\left(B\right)$, correspondingly.

3. Integrodifferential System

3.1. Controllability Results through the Fixed Point Theorem

The topic of approximate controllability for the imagined system is the emphasis of this section. Before we begin investigating the essential results, we make the subsequent considerations:

Assumption 1.

There exists $M>0$ such that $\parallel {\mathcal{R}}_{\alpha }{\left(\varrho \right)\parallel }_{\mathcal{L}\left(H\right)}\le M$ and $\parallel {\mathcal{T}}_{\alpha }{\left(\varrho \right)\parallel }_{\mathcal{L}\left(H\right)}\le M$ for every $\varrho \in [0,c]$.

Assumption 2.

$\mathcal{L}\mu =\mathcal{L}\nu$ such that $\nu \in \overline{R\left(B\right)}$, ∀$\mu \in \Psi$.

Assumption 3.

The operator ${\mathcal{T}}_{\alpha }\left(\sigma \right)$ is compact.

Assumption 4.

The function $E(\sigma ,\chi (\sigma \left)\right)$ fulfills the Lipschitz condition. Additionally, there exists a constant $l>0$ fulfilling

$$\begin{array}{c}\hfill \parallel E(\sigma ,\chi )-E(\sigma ,\varpi )\parallel \le l\parallel \chi -\varpi \parallel ,\forall \chi ,\varpi \in X,\sigma \in [0,c].\end{array}$$

Let us consider $l_E={max}_{0\le \sigma \le c}\parallel E(\sigma ,0)\parallel$.

Clearly, by referring to Assumption (2), there exists $\nu \in \overline{R\left(B\right)}$ along $\mu -\nu =\theta \in N_0\left(\mathcal{L}\right)$, ∀$\mu \in \Psi$. Therefore, $\Psi =N_0\left(\mathcal{L}\right)\oplus \overline{R\left(B\right)}$. Accordingly, we present $P:N_0^{\perp }\mathcal{L}\to \overline{R\left(B\right)}$ is continuous, linear, and defined as $P{u}^{*}={\nu }^{*}$, and ${\nu }^{*}$ designates a unique minimum norm element in $\overline{R\left(B\right)}\cap \{u^{*}+N_0\left(\mathcal{L}\right)\}$, i.e.,

$$\begin{array}{c}\hfill \parallel P{u}^{*}\parallel =\parallel {\nu }^{*}\parallel =min\{\parallel v\parallel :v\in \{u^{*}+N_0\left(\mathcal{L}\right)\}\oplus \overline{R\left(B\right)}\}.\end{array}$$

By referring to Assumption (2), clearly, ∀$u^{*}\in N_0^{\perp }\left(\mathcal{L}\right)$, the set $\overline{R\left(B\right)}\cap \{u^{*}+N_0\left(\mathcal{L}\right)\}$ is non-void, and every $z\in \Psi$ is characterized as $z=\theta +{\nu }^{*}$. Thus, P is well defined. Additionally, $\parallel P\parallel \le \lambda$, $\lambda >0$ (refer to [34]).

Lemma 1.

In [35], let us assume that the subsequent

$${\parallel \theta \parallel }_{\Psi }\le (1+\lambda ){\parallel \chi \parallel }_{\Psi },$$

fulfills ∀$\chi \in \Psi$ and $\theta \in N_0\left(\mathcal{L}\right)$.

We now assume that $\mathrm{{\rm Y}}$ is the subspace of $\Psi$ (refer to [36]) such that

$$\begin{array}{c}\hfill \mathrm{{\rm Y}}=\{\beta \in \Psi :\beta \left(\sigma \right)=\left(\rho \theta \right)\left(\sigma \right),\theta \in N_0\left(\mathcal{L}\right)\},0\le \sigma \le c.\end{array}$$

Clearly, $\beta \left(c\right)=0$, $\forall \beta \in \mathrm{{\rm Y}}$.

We present ${\eta }_{\chi }:\mathrm{{\rm Y}}\to \mathrm{{\rm Y}}$ in the following way:

$$\begin{array}{c}\hfill {\eta }_{\chi }\left(\beta \right)=\rho \theta ;\end{array}$$

in the above, $\theta$ is presented in the following way:

$$\begin{array}{c}\hfill \aleph (\chi +\beta )=\theta +\nu ;\theta \in N_0\left(\mathcal{L}\right),\nu \in \overline{R\left(B\right)}.\end{array}$$

(12)

Theorem 1.

By referring to Assumption (2), system (3) and (4) corresponding to (1) and (2) is approximately controllable, i.e., $\overline{K_c\left(0\right)}=X$.

Proof. 

One can refer to [36] with suitable modifications. □

Lemma 2.

Under assumptions (1) and (4), ${\beta }_0\in \mathrm{{\rm Y}}$ with ${\eta }_{\chi }\left({\beta }_0\right)={\beta }_0$, if $Mlc(1+\lambda )<1$.

Proof. 

Let ${\Omega }_r=\{\chi \in \Psi :\parallel \chi \parallel \le r\}$, here $r>0$. The target is to verify ${\eta }_{\chi }$ mapping ${\Omega }_r$ into itself. By using the contradiction approach, we can verify this result. Assume $\beta \in {\Omega }_r$, then ${\eta }_{\chi }\left(\beta \right)$∉${\Omega }_r$, i.e., $\parallel {\eta }_{\chi }\left(\beta \right)\parallel >r$. By referring to Lemma 1 and Assumption (1), one can obtain

$$\begin{array}{cc}\hfill r& <\parallel {\eta }_{\chi }\left(\beta \right)\parallel =\parallel \rho \theta \parallel \le {\int }_0^{\sigma }\parallel {\mathcal{T}}_{\alpha }(\sigma -\zeta )\parallel \parallel \theta \left(\zeta \right)\parallel d\zeta \hfill \\ \hfill & \le M{\int }_0^{\sigma }\parallel \theta \left(\zeta \right)\parallel d\zeta \hfill \\ \hfill & \le M(1+\lambda ){\int }_0^{\sigma }\parallel \aleph (\chi +\beta )\left(\zeta \right)\parallel d\zeta \hfill \\ \hfill & \le M(1+\lambda ){\int }_0^{\sigma }\parallel E(\zeta ,(\chi +\beta )\left(\zeta \right))\parallel d\zeta \hfill \\ \hfill & \le M(1+\lambda ){\int }_0^{\sigma }[l\parallel (\chi +\beta )\left(\zeta \right)\parallel +l_E]d\zeta \hfill \\ \hfill & \le Ml(1+\lambda )\sqrt{\sigma }{\parallel \chi \parallel }_{\Psi }+M(lr+l_E)(1+\lambda )\sigma \hfill \\ \hfill & \le M(1+\lambda )[l\sqrt{c}\parallel \chi {\parallel }_{\Psi }+lrc+l_{E}c].\hfill \end{array}$$

Dividing the above inequality by r and taking $r⟶\infty$, one can obtain

$$Mlc(1+\lambda )\ge 1.$$

Therefore, by the contradiction approach, one can come to an end that ${\eta }_{\chi }$ maps ${\Omega }_r$ into itself.

Subsequently, we verify ${\eta }_{\chi }$ is compact. $\rho$ is compact when ${\mathcal{T}}_{\alpha }\left(\sigma \right)$ is compact (by referring to Assumption (3)); thus, ${\eta }_{\chi }$ is compact.

By referring to Schauder’s fixed point theorem, ${\beta }_0$ is the fixed point of ${\eta }_{\chi }$, i.e.,

$${\eta }_{\chi }\left({\beta }_0\right)=\rho \theta ={\beta }_0,$$

and the proof is complete. □

Theorem 2.

Suppose that the Assumptions (1)–(3) are fulfilled; provided that system (3) and (4) is approximately controllable, system (1) and (2) is also approximately controllable.

Proof. 

Assume that $\chi (·)$ is the mild solution of (3) and (4), then

$$\begin{array}{cc}\hfill \chi \left(\sigma \right)=& {\mathcal{R}}_{\alpha }\left(\sigma \right){\chi }_0+\rho Bu\left(\sigma \right),\sigma \in [0,c].\hfill \end{array}$$

(13)

Our target is to prove that $s\left(\sigma \right)=\chi \left(\sigma \right)+{\beta }_0\left(\sigma \right)$ is the mild solution of the subsequent system

$$\begin{array}{cc}\hfill D_{\sigma }^{\alpha }s\left(\sigma \right)=& A\left[s\left(\sigma \right)+{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota )\chi \left(\iota \right)d\iota \right]+(Bu-\nu )\left(\sigma \right)+E(\sigma ,s\left(\sigma \right)),\sigma \in (0,c],\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill s\left(0\right)=& {\chi }_0,s^{\prime }\left(0\right)=0.\hfill \end{array}$$

(15)

From (12), we obtain

$$\aleph (\chi +\beta )\left(\sigma \right)=\theta \left(\sigma \right)+\nu \left(\sigma \right),$$

operating $\rho$ at $\beta ={\beta }_0$, where ${\beta }_0$ is a fixed point of ${\eta }_{\chi }$ and by referring to the results on $\mathrm{{\rm Y}}$, along Lemma 2, we obtain

$$\begin{array}{cc}\hfill \rho \aleph (\chi +{\beta }_0)\left(\sigma \right)& =\rho \theta \left(\sigma \right)+\rho \nu \left(\sigma \right)\hfill \\ \hfill & ={\beta }_0\left(\sigma \right)+\rho \nu \left(\sigma \right).\hfill \end{array}$$

Now

$$\chi \left(\sigma \right)+\rho \aleph (\chi +{\beta }_0)\left(\sigma \right)=\chi \left(\sigma \right)+{\beta }_0\left(\sigma \right)+\rho \nu \left(\sigma \right).$$

Let $s\left(\sigma \right)=\chi \left(\sigma \right)+{\beta }_0\left(\sigma \right)$, then

$$\begin{array}{c}\hfill \chi \left(\sigma \right)+\rho \aleph \left(s\right)\left(\sigma \right)=s\left(\sigma \right)+\rho \nu \left(\sigma \right),\\ \hfill \Rightarrow s\left(\sigma \right)=\chi \left(\sigma \right)+\rho \aleph \left(s\right)\left(\sigma \right)-\rho \nu \left(\sigma \right).\end{array}$$

(16)

Using Equation (13), we obtain

$$\begin{array}{cc}\hfill s\left(\sigma \right)=& {\mathcal{R}}_{\alpha }\left(\sigma \right){\chi }_0+\rho (Bu-\nu )\left(\sigma \right)+\rho \aleph \left(s\right)\left(\sigma \right),\hfill \end{array}$$

which concludes the mild solution of (14) and (15) along control $(Bu-\nu )$.

Additionally, we consider ${\beta }_0\left(0\right)=0={\beta }_0\left(\tau \right)$ as

$$\begin{array}{c}\hfill s\left(0\right)=\chi \left(0\right)+{\beta }_0\left(0\right)={\chi }_0\end{array}$$

and

$$\begin{array}{c}\hfill s\left(\tau \right)=\chi \left(\tau \right)+{\beta }_0\left(\tau \right)=\chi \left(\tau \right)\in K_c\left(0\right).\end{array}$$

Additionally, because $\nu \in \overline{R\left(B\right)}$, we assume that there exists a control $v\in Y$ such that

$$\parallel Bv-\nu \parallel \le ϵ,\forall ϵ>0$$

.

Let us consider ${\chi }_w(·)$ is the mild solution of (1) and (2) with control $w=u-v$, and we can simply verify the subsequent:

$$\begin{array}{c}\hfill \parallel s\left(\tau \right)-{\chi }_w\left(\tau \right)\parallel =\parallel \chi \left(\tau \right)-{\chi }_w\left(\tau \right)\parallel \le ϵ,\end{array}$$

which gives $K_c\left(0\right)\subseteq K_c\left(E\right)$. Since $K_c\left(0\right)$ is dense in X (by referring to Assumption (2), the system (3) and (4) is approximately controllable); consequently, $K_c\left(E\right)$ is also dense in X. Therefore, system (1) and (2) is approximately controllable. □

3.2. Controllability Results without the Use of the Fixed Point Theorem

Assumption 5.

$R(\aleph )\subset \overline{R\left(B\right)}$.

Theorem 3.

Supposing Assumptions (1), (2), (4), and (5), provided that system (3) and (4) is approximately controllable, system (1) and (2) is also approximately controllable.

Proof. 

Assume $\chi (·)$ is the mild solution for (3) and (4), then

$$\begin{array}{cc}\hfill \chi \left(\sigma \right)=& {\mathcal{R}}_{\alpha }\left(\sigma \right){\chi }_0+\rho Bu\left(\sigma \right),\sigma \in [0,\tau ].\hfill \end{array}$$

By referring to Assumption (5), $\aleph \left(\chi \right)\in \overline{R\left(B\right)}$. Thus, for $ϵ>0$, there exists $w(·)\in L^2(V,U)$ with

$${\parallel \aleph \left(\chi \right)-Bw\parallel }_{\Psi }\le ϵ.$$

Let us consider $\vartheta \left(\sigma \right)$ is the mild solution with control $(u-w)$ for (1) and (2). Then,

$$\begin{array}{cc}\hfill \chi \left(\sigma \right)-\vartheta \left(\sigma \right)=& {\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\zeta )Bw\left(\zeta \right)d\zeta -{\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\zeta )[\aleph \vartheta ]\left(\zeta \right)d\zeta \hfill \\ \hfill =& {\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\zeta )[Bw-\aleph \chi ]\left(\zeta \right)d\zeta +{\int }_0^{\zeta }{\mathcal{T}}_{\alpha }(\sigma -\zeta )[\aleph \chi -\aleph \vartheta ]\left(\zeta \right)d\zeta .\hfill \end{array}$$

Applying the norm, we obtain

$$\begin{array}{cc}\hfill \parallel \chi \left(\sigma \right)-\vartheta \left(\sigma \right)\parallel \le & M{\int }_0^{\sigma }{\parallel Bw\left(\zeta \right)-[\aleph \chi ]\left(\zeta \right)\parallel }_{X}d\zeta +M{\int }_0^{\sigma }\parallel [\aleph \chi ]\left(\zeta \right)-[\aleph \vartheta ]\left(\zeta \right)\parallel d\zeta \hfill \\ \hfill \le & M\sqrt{\sigma }{\parallel Bw-\aleph \chi \parallel }_{\Psi }+Ml{\int }_0^{\sigma }\parallel \chi \left(\zeta \right)-\vartheta \left(\zeta \right)\parallel d\zeta \hfill \\ \hfill \le & Mϵ\sqrt{\sigma }+Ml{\int }_0^{\sigma }\parallel \chi \left(\zeta \right)-\vartheta \left(\zeta \right)\parallel d\zeta .\hfill \end{array}$$

By employing Gronwall’s inequality, and by assuming appropriate control w, one can create ${\parallel \chi \left(c\right)-\vartheta \left(c\right)\parallel }_X$ arbitrarily small. Therefore, the solution set of (1) and (2) is dense in (3) and (4), which is dense in X, and the proof is complete. □

4. Sobolev-Type Integrodifferential System

4.1. Controllability Results through the Fixed Point Theorem

The topic of approximate controllability for the imagined system is the emphasis of this section.

Assume that the Sobolev-type system has the subsequent form

$$\begin{array}{cc}\hfill D_{\sigma }^{\alpha }\left[K\chi \left(\sigma \right)\right]& =A\left[\chi \left(\sigma \right)+{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota )\chi \left(\iota \right)d\iota \right]+Bv\left(\sigma \right)+E(\sigma ,\chi \left(\sigma \right)),\sigma \in V=[0,c],\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \chi \left(0\right)& ={\chi }_0,{\chi }^{\prime }\left(0\right)=0.\hfill \end{array}$$

(18)

The linear system for (17) and (18) has the subsequent form

$$\begin{array}{cc}\hfill D_{\sigma }^{\alpha }\left[Kz\left(\sigma \right)\right]& =A\left[\chi \left(\sigma \right)+{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota )\chi \left(\iota \right)d\iota \right]+Bv\left(\sigma \right),\sigma \in I=(0,c],\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \chi \left(0\right)& ={\chi }_0,{\chi }^{\prime }\left(0\right)=0,\hfill \end{array}$$

(20)

By referring to [22], we introduce the subsequent characteristics on the linear operators $A:D\left(A\right)\subset X\to X$ and $K:D\left(A\right)\subset X\to X$

$\left({\mathcal{K}}_{\mathbf{1}}\right)$

A and K are closed linear operators.

$\left({\mathcal{K}}_{\mathbf{2}}\right)$

$D\left(K\right)\subset D\left(A\right)$ and K is bijective.

$\left({\mathcal{K}}_{\mathbf{3}}\right)$

$K^{-1}:X\to D\left(K\right)$ is continuous.

Additionally, because of $\left({\mathcal{K}}_{\mathbf{1}}\right)$ and $\left({\mathcal{K}}_{\mathbf{2}}\right)$, $K^{-1}$ is closed, by $\left({\mathcal{K}}_{\mathbf{3}}\right)$ and from the closed graph theorem, we have the boundedness of $A{K}^{-1}:X\to X$. We assume that $\parallel K^{-1}\parallel ={\tilde{K}}_1$ and $\parallel L\parallel ={\tilde{K}}_2$.

Definition 7.

The function $\chi \in \mathcal{C}$ is said to be the mild solution of (17) and (18) provided that

$$\begin{array}{cc}\hfill \chi \left(\sigma \right)& =K^{-1}{\mathcal{R}}_{\alpha }\left(\sigma \right)K{z}_0+{\int }_0^{\sigma }{K}^{-1}{\mathcal{T}}_{\alpha }(\sigma -\iota )E(\iota ,\chi \left(\iota \right))d\iota +{\int }_0^{\sigma }{K}^{-1}{\mathcal{T}}_{\alpha }(\sigma -\iota )Bv\left(\iota \right)d\iota ,\sigma \in I,\hfill \end{array}$$

is fulfilled.

We present $\aleph :\Psi \to \Psi$ in the following way:

$$[\aleph \chi ]\left(\sigma \right)=E(\sigma ,\chi (\sigma \left)\right);0<\sigma \le c.$$

We now present $\rho :\Psi \to \Psi$ in the following way:

$$\left[\rho \chi \right]\left(\sigma \right)={\int }_0^{\sigma }{K}^{-1}{\mathcal{T}}_{\alpha }(\sigma -\zeta )\chi \left(\zeta \right)d\zeta .$$

Additionally, we present $\mathcal{L}:\Psi \to X$ in the following way:

$$\mathcal{L}\mu ={\int }_0^c{K}^{-1}{\mathcal{T}}_{\alpha }(c-\zeta )\mu \left(\zeta \right)d\zeta .$$

Before we begin investigating the primary outcomes, we make the following assumptions:

Assumption 6.

$\mathcal{L}\mu =\mathcal{L}\nu$ such that $\nu \in \overline{R\left(B\right)}$, ∀$\mu \in \Psi$.

Lemma 3.

In [35] Let us assume that the subsequent

$${\parallel \theta \parallel }_{\Psi }\le (1+\lambda ){\parallel \chi \parallel }_{\Psi },$$

fulfills ∀$\chi \in \Psi$ and $\theta \in N_0\left(\mathcal{L}\right)$.

We now assume that $\mathrm{{\rm Y}}$ is the subspace of $\Psi$ (refer to [36]) such that

$$\begin{array}{c}\hfill \mathrm{{\rm Y}}=\{\beta \in \Psi :\beta \left(\sigma \right)=\left(\rho \theta \right)\left(\sigma \right),\theta \in N_0\left(\mathcal{L}\right)\},0\le \sigma \le c.\end{array}$$

Clearly, $\beta \left(c\right)=0$, $\forall \beta \in \mathrm{{\rm Y}}$.

We present ${\eta }_{\chi }:\mathrm{{\rm Y}}\to \mathrm{{\rm Y}}$ in the following way:

$$\begin{array}{c}\hfill {\eta }_{\chi }\left(\beta \right)=\rho \theta ;\end{array}$$

in the above, $\theta$ is presented in the following way:

$$\begin{array}{c}\hfill \aleph (\chi +\beta )=\theta +\nu ;\theta \in N_0\left(\mathcal{L}\right),\nu \in \overline{R\left(B\right)}.\end{array}$$

(21)

Theorem 4.

By referring to Assumption (6), system (19) and (20) is approximately controllable, i.e., $\overline{K_c\left(0\right)}=X$.

Proof. 

One can refer to [36] with suitable modifications. □

Lemma 4.

Under Assumptions (1) and (4), ${\beta }_0\in \mathrm{{\rm Y}}$ with ${\eta }_{\chi }\left({\beta }_0\right)={\beta }_0$ if $M{\tilde{K}}_{1}lc(1+\lambda )<1$.

Proof. 

Let ${\Omega }_r=\{\chi \in \Psi :\parallel \chi \parallel \le r\}$ where $r>0$. The target is to verify ${\eta }_{\chi }$ mapping ${\Omega }_r$ into itself. By using the contradiction approach, we can verify this result. Assume $\beta \in {\Omega }_r$, then ${\eta }_{\chi }\left(\beta \right)$∉${\Omega }_r$, i.e., $\parallel {\eta }_{\chi }\left(\beta \right)\parallel >r$. By referring to Lemma 3 and Assumption (1), one can obtain

$$\begin{array}{cc}\hfill r& <\parallel {\eta }_{\chi }\left(\beta \right)\parallel =\parallel \rho \theta \parallel \le {\int }_0^{\sigma }\parallel K^{-1}{\mathcal{T}}_{\alpha }(\sigma -\zeta )\parallel \parallel \theta \left(\zeta \right)\parallel d\zeta \hfill \\ \hfill & \le M{\tilde{K}}_1{\int }_0^{\sigma }\parallel \theta \left(\zeta \right)\parallel d\zeta \hfill \\ \hfill & \le M{\tilde{K}}_1(1+\lambda ){\int }_0^{\sigma }\parallel \aleph (\chi +\beta )\left(\zeta \right)\parallel d\zeta \hfill \\ \hfill & \le M{\tilde{K}}_1(1+\lambda ){\int }_0^{\sigma }\parallel E(\zeta ,(\chi +\beta )\left(\zeta \right))\parallel d\zeta \hfill \\ \hfill & \le M{\tilde{K}}_1(1+\lambda ){\int }_0^{\sigma }[l\parallel (\chi +\beta )\left(\zeta \right)\parallel +l_E]d\zeta \hfill \\ \hfill & \le M{\tilde{K}}_{1}l(1+\lambda )\sqrt{\sigma }{\parallel \chi \parallel }_{\Psi }+M(lr+l_E)(1+\lambda )\sigma \hfill \\ \hfill & \le M{\tilde{K}}_1(1+\lambda )[l\sqrt{c}{\parallel \chi \parallel }_{\Psi }+lrc+l_{E}c].\hfill \end{array}$$

Dividing the above inequality by r and taking $r⟶\infty$, one can obtain

$$M{\tilde{K}}_{1}lc(1+\lambda )\ge 1.$$

Subsequently, we verify ${\eta }_{\chi }$ is compact. $\rho$ is compact when ${\mathcal{T}}_{\alpha }\left(\sigma \right)$ is compact (by referring to Assumption (3)); thus, ${\eta }_{\chi }$ is compact.

By referring to Schauder’s fixed point theorem, ${\beta }_0$ is the fixed point of ${\eta }_{\chi }$, i.e.,

$${\eta }_{\chi }\left({\beta }_0\right)=\rho \theta ={\beta }_0,$$

and the proof is complete. □

Theorem 5.

Suppose that Assumptions (1), (3), and (6) are fulfilled; provided that system (19) and (20) is approximately controllable, system (17) and (18) is also approximately controllable.

Proof. 

Assume that $\chi (·)$ is the mild solution of (19) and (20), then

$$\begin{array}{cc}\hfill \chi \left(\sigma \right)=& K^{-1}{\mathcal{R}}_{\alpha }\left(\sigma \right)K{z}_0+\rho Bu\left(\sigma \right),\sigma \in [0,c].\hfill \end{array}$$

(22)

Our target is to prove that $s\left(\sigma \right)=\chi \left(\sigma \right)+{\beta }_0\left(\sigma \right)$ is the mild solution of the subsequent system

$$\begin{array}{cc}\hfill D_{\sigma }^{\alpha }Ks\left(\sigma \right)=& A\left[s\left(\sigma \right)+{\int }_0^{\sigma }\mathcal{B}(\sigma -\iota )\chi \left(\iota \right)d\iota \right]+(Bu-\nu )\left(\sigma \right)+E(\sigma ,s\left(\sigma \right)),\sigma \in (0,c],\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill s\left(0\right)=& {\chi }_0,s^{\prime }\left(0\right)=0.\hfill \end{array}$$

(24)

From (21), we obtain

$$\aleph (\chi +\beta )\left(\sigma \right)=\theta \left(\sigma \right)+\nu \left(\sigma \right),$$

operating $\rho$ at $\beta ={\beta }_0$, where ${\beta }_0$ is a fixed point of ${\eta }_{\chi }$, and by referring to the results on $\mathrm{{\rm Y}}$, along Lemma 4, we obtain

$$\begin{array}{cc}\hfill \rho \aleph (\chi +{\beta }_0)\left(\sigma \right)& =\rho \theta \left(\sigma \right)+\rho \nu \left(\sigma \right),\hfill \\ \hfill & ={\beta }_0\left(\sigma \right)+\rho \nu \left(\sigma \right).\hfill \end{array}$$

Now

$$\chi \left(\sigma \right)+\rho \aleph (\chi +{\beta }_0)\left(\sigma \right)=\chi \left(\sigma \right)+{\beta }_0\left(\sigma \right)+\rho \nu \left(\sigma \right).$$

Let $s\left(\sigma \right)=\chi \left(\sigma \right)+{\beta }_0\left(\sigma \right)$, then

$$\begin{array}{c}\hfill \chi \left(\sigma \right)+\rho \aleph \left(s\right)\left(\sigma \right)=s\left(\sigma \right)+\rho \nu \left(\sigma \right),\\ \hfill \Rightarrow s\left(\sigma \right)=\chi \left(\sigma \right)+\rho \aleph \left(s\right)\left(\sigma \right)-\rho \nu \left(\sigma \right).\end{array}$$

(25)

Using Equation (22), we obtain

$$\begin{array}{cc}\hfill s\left(\sigma \right)=& K^{-1}{\mathcal{R}}_{\alpha }\left(\sigma \right)K{z}_0+\rho (Bu-\nu )\left(\sigma \right)+\rho \aleph \left(s\right)\left(\sigma \right),\hfill \end{array}$$

which concludes the mild solution of (23) and (24) along control $(Bu-\nu )$.

Additionally, let us consider ${\beta }_0\left(0\right)=0={\beta }_0\left(\tau \right)$ as

$$\begin{array}{c}\hfill s\left(0\right)=\chi \left(0\right)+{\beta }_0\left(0\right)={\chi }_0\end{array}$$

and

$$\begin{array}{c}\hfill s\left(\tau \right)=\chi \left(\tau \right)+{\beta }_0\left(\tau \right)=\chi \left(\tau \right)\in K_c\left(0\right).\end{array}$$

Additionally, because $\nu \in \overline{R\left(B\right)}$, we assume that there exists a control $v\in Y$

$$\parallel Bv-\nu \parallel \le ϵ,\forall ϵ>0.$$

Let us consider that ${\chi }_w(·)$ is the mild solution of (17) and (18) with control $w=u-v$. One can simply verify the subsequent:

$$\begin{array}{c}\hfill \parallel s\left(\tau \right)-{\chi }_w\left(\tau \right)\parallel =\parallel \chi \left(\tau \right)-{\chi }_w\left(\tau \right)\parallel \le ϵ,\end{array}$$

which gives $K_c\left(0\right)\subseteq K_c\left(E\right)$. Since $K_c\left(0\right)$ is dense in X (by referring Assumption (2), system (3) and (4) is approximately controllable); consequently, $K_c\left(E\right)$ is also dense in X. Therefore, system (17) and (18) is approximately controllable. □

4.2. Controllability Results without the Use of the Fixed Point Theorem

Assumption 7.

$R(\aleph )\subset \overline{R\left(B\right)}$.

Theorem 6.

Supposing Assumptions (1), (4), (6), and (7), provided that system (19) and (20) is approximately controllable, system (17) and (18) is also approximately controllable.

Proof. 

Assume $\chi (·)$ is the mild solution for (19) and (20), then

$$\begin{array}{cc}\hfill \chi \left(\sigma \right)=& K^{-1}{\mathcal{R}}_{\alpha }\left(\sigma \right)K{z}_0+\rho Bu\left(\sigma \right),\sigma \in [0,\tau ].\hfill \end{array}$$

By referring to Assumption (7), $\aleph \left(\chi \right)\in \overline{R\left(B\right)}$. Thus, for $ϵ>0$, there exists $w(·)\in L^2(V,U)$ with

$${\parallel \aleph \left(\chi \right)-Bw\parallel }_{\Psi }\le ϵ.$$

Let us consider $\vartheta \left(\sigma \right)$ is the mild solution with control $(u-w)$ for (17) and (18). Then,

$$\begin{array}{cc}\hfill \chi \left(\sigma \right)-\vartheta \left(\sigma \right)=& {\int }_0^{\sigma }{K}^{-1}{\mathcal{T}}_{\alpha }(\sigma -\zeta )Bw\left(\zeta \right)d\zeta -{\int }_0^{\sigma }{K}^{-1}{\mathcal{T}}_{\alpha }(\sigma -\zeta )[\aleph \vartheta ]\left(\zeta \right)d\zeta \hfill \\ \hfill =& {\int }_0^{\sigma }{K}^{-1}{\mathcal{T}}_{\alpha }(\sigma -\zeta )[Bw-\aleph \chi ]\left(\zeta \right)d\zeta +{\int }_0^{\zeta }{K}^{-1}{\mathcal{T}}_{\alpha }(\sigma -\zeta )[\aleph \chi -\aleph \vartheta ]\left(\zeta \right)d\zeta .\hfill \end{array}$$

Applying the norm, we obtain

$$\begin{array}{cc}\hfill \parallel \chi \left(\sigma \right)-\vartheta \left(\sigma \right)\parallel \le & M{\tilde{K}}_1{\int }_0^{\sigma }{\parallel Bw\left(\zeta \right)-[\aleph \chi ]\left(\zeta \right)\parallel }_{X}d\zeta +M{\tilde{K}}_1{\int }_0^{\sigma }\parallel [\aleph \chi ]\left(\zeta \right)-[\aleph \vartheta ]\left(\zeta \right)\parallel d\zeta \hfill \\ \hfill \le & M{\tilde{K}}_1\sqrt{\sigma }{\parallel Bw-\aleph \chi \parallel }_{\Psi }+M{\tilde{K}}_{1}l{\int }_0^{\sigma }\parallel \chi \left(\zeta \right)-\vartheta \left(\zeta \right)\parallel d\zeta \hfill \\ \hfill \le & M{\tilde{K}}_1ϵ\sqrt{\sigma }+M{\tilde{K}}_{1}l{\int }_0^{\sigma }\parallel \chi \left(\zeta \right)-\vartheta \left(\zeta \right)\parallel d\zeta .\hfill \end{array}$$

By employing Gronwall’s inequality, and by assuming appropriate control w, one can create ${\parallel \chi \left(c\right)-\vartheta \left(c\right)\parallel }_X$ arbitrarily small. Therefore, the solution set of (17) and (18) is dense in (19) and (20), which is dense in X, and the proof is complete. □

5. Examples

5.1. Integrodifferential System

Let us consider the subsequent fractional integrodifferential system of the form

$$\begin{array}{cc}\hfill \frac{{\partial }^{\alpha }}{\partial {\sigma }^{\alpha }}\chi (\sigma ,\xi )& =\frac{{\partial }^2}{\partial {\xi }^2}\chi (\sigma ,\xi )+{\int }_0^{\sigma }{(\sigma -\varpi )}^{\delta }{e}^{-\gamma (\sigma -\varpi )}\frac{{\partial }^2}{\partial {\xi }^2}\chi (\varpi ,\xi )d\varpi +\mu (\sigma ,\xi )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\gamma (\sigma ,\chi (\sigma ,\xi \left)\right),(\sigma ,\xi )\in V\times [0,\pi ],\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill \chi (\sigma ,0)& =\chi (\sigma ,\pi )=0,\sigma \in [0,c],\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\chi }_{\sigma }(0,\xi )& =0,\sigma \in [0,c],\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \chi (\varpi ,\xi )& =\varphi (\varpi ,\xi ),\varpi \le 0,\xi \in [0,\pi ].\hfill \end{array}$$

(29)

In the above, $\frac{{\partial }^{\alpha }}{\partial {\sigma }^{\alpha }}=D_{\sigma }^{\alpha }$, $\alpha \in (1,2)$, and the function $\mu :V\times [0,\pi ]\to [0,\pi ]$ is continuous.

To convert the system (26)–(29) into (1) and (2), we assume $X=L^2\left([0,\pi ]\right)$ and $A:D\left(A\right)\subseteq X\to X$ is presented as $Ax=x^{″}$, with $D\left(A\right)=\{x\in X:x^{″}\in X,x\left(0\right)=x\left(\pi \right)=0\}$. A is the infinitesimal generator of an analytic semigroup on X. Therefore, A is of sectorial type and $\left({\mathbf{P}}_{\mathbf{1}}\right)$ is fulfilled. Assume $\mathcal{B}\left(\sigma \right):D\left(A\right)\subseteq X\to X$, $\sigma \ge 0$, $\mathcal{B}\left(\sigma \right)x={\sigma }^{\delta }{e}^{-\gamma \sigma }Ax$ for $x\in D\left(A\right)$. Clearly, $\left({\mathbf{P}}_{\mathbf{2}}\right)$ and $\left({\mathbf{P}}_{\mathbf{3}}\right)$ are fulfilled along with $b\left(\sigma \right)={\sigma }^{\delta }{e}^{-\gamma \sigma }$. Thus, (5) and (6) has connected $\alpha$-resolvent operators ${\left({\mathcal{R}}_{\alpha }\left(\sigma \right)\right)}_{\sigma \ge 0}$ on X.

Assume that $E(\sigma ,\psi )=\gamma (\sigma ,\chi (\sigma ,\xi \left)\right)$. Additionally, $B:U\to X$ by $Bu(\sigma ,\xi )=\mu (\sigma ,\xi )$, $0<\xi <\pi$. Let us consider that the above functions meet the hypotheses conditions above, and we conclude that (26)–(29) is approximately controllable.

5.2. Sobolev-Type Integrodifferential System

Let us consider the subsequent Sobolev-type system of the form

$$\begin{array}{cc}\hfill \frac{{\partial }^{\alpha }}{\partial {\sigma }^{\alpha }}[\chi (\sigma ,\xi )-\frac{{\partial }^2}{\partial {\xi }^2}\chi (\sigma ,\xi )]& =\frac{{\partial }^2}{\partial {\xi }^2}\chi (\sigma ,\xi )+{\int }_0^{\sigma }{(\sigma -\varpi )}^{\delta }{e}^{-\gamma (\sigma -\varpi )}\frac{{\partial }^2}{\partial {\xi }^2}\chi (\varpi ,\xi )d\varpi +\mu (\sigma ,\xi )\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +\gamma (\sigma ,\chi (\sigma ,\xi \left)\right),(\sigma ,\xi )\in V\times [0,\pi ],\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill \chi (\sigma ,0)& =\chi (\sigma ,\pi )=0,\sigma \in [0,c],\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\chi }_{\sigma }(0,\xi )& =0,\sigma \in [0,c],\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \chi (\varpi ,\xi )& =\varphi (\varpi ,\xi ),\varpi \le 0,\xi \in [0,\pi ].\hfill \end{array}$$

(33)

In the above, $\frac{{\partial }^{\alpha }}{\partial {\sigma }^{\alpha }}=D_{\sigma }^{\alpha }$, $\alpha \in (1,2)$, $\mu :V\times [0,\pi ]\to [0,\pi ]$ is a continuous function.

We convert the system (30)–(33) into (17) and (18), assume $X=L^2\left([0,\pi ]\right)$, and assume $A:D\left(A\right)\subset X\to X$, $K:D\left(K\right)\subset X\to X$ are the operators determined by $Ax=x^{″}$, and $Kx=x-x^{″}$ where $D\left(A\right)$ and $D\left(K\right)$ is presented by

$$\{x\in X:x,x^{\prime }\mathrm{are}\mathrm{absolutely}\mathrm{continuous},x\left(0\right)=x\left(\pi \right)=0\}.$$

We conclude that A is the infinitesimal generator of an analytic semigroup on X. Therefore, A is sectorial, and the properties $\left({\mathbf{P}}_{\mathbf{1}}\right)$ hold. Additionally, A and K are given by

$$Ax=\sum _{m=1}^{\infty }{m}^2\langle x,{\chi }_m\rangle {\chi }_m,x\in D\left(A\right),$$

$$Kx=\sum _{m=1}^{\infty }(1+m^2)\langle x,{\chi }_m\rangle {\chi }_m,x\in D\left(K\right).$$

Additionally, for $z\in X$, we have

$$K^{-1}z=\sum _{m=1}^{\infty }\frac{1}{(1+m^2)}\langle z,{\chi }_m\rangle {\chi }_m,$$

and

$$A{K}^{-1}z=\sum _{m=1}^{\infty }\frac{m^2}{(1+m^2)}\langle z,{\chi }_m\rangle {\chi }_m.$$

Assume that $E(\sigma ,\psi )=\gamma (\sigma ,\chi (\sigma ,\xi \left)\right)$. Additionally, $B:U\to X$ by $Bu(\sigma ,\xi )=\mu (\sigma ,\xi )$, $0<\xi <\pi$. Therefore, all the requirements are verified, and (30)–(33) is approximately controllable.

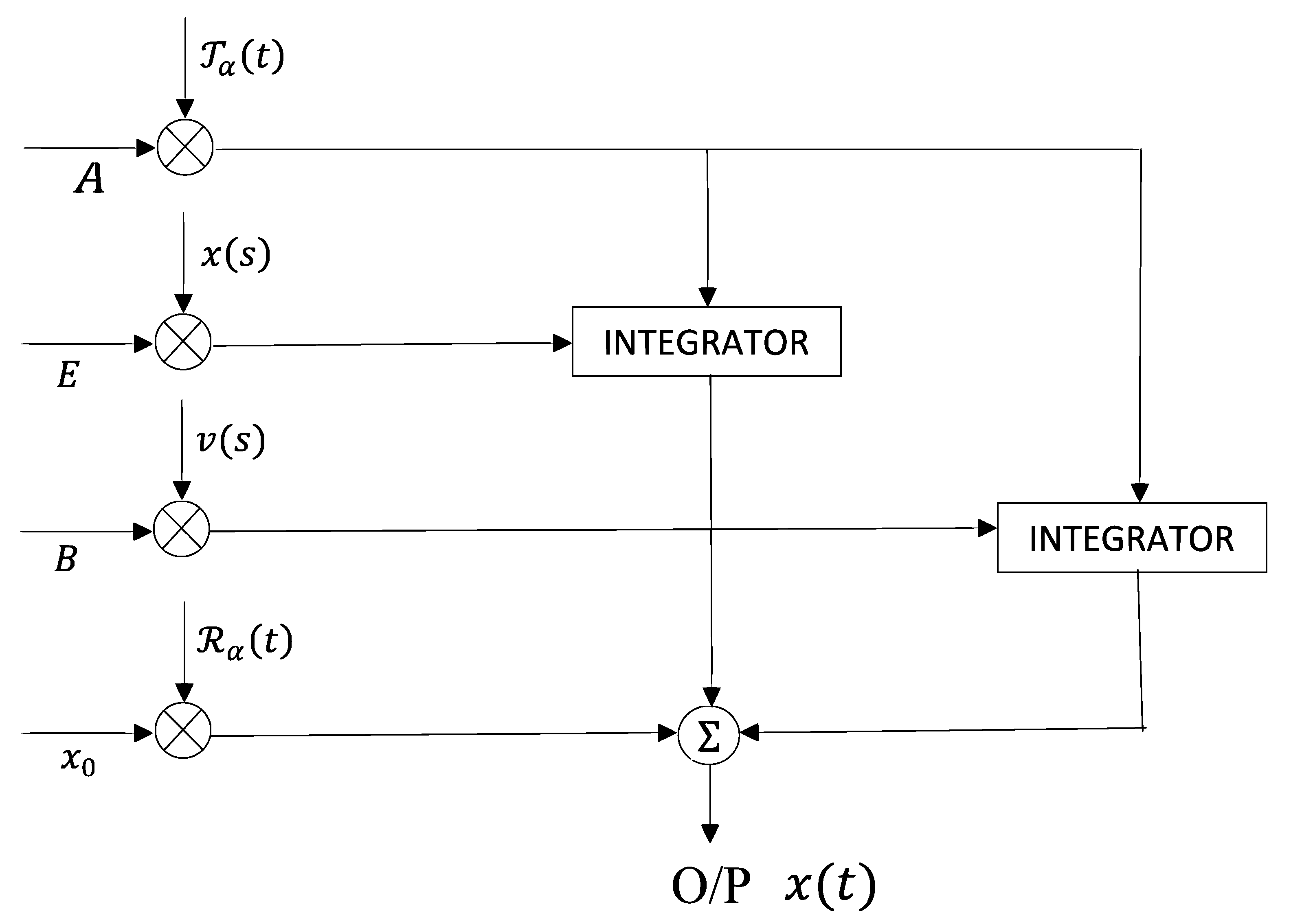
5.3. Filter System

An advanced filter is a framework that performs mathematical operations on an inspected digitized sign to decrease or upgrade certain highlights of the prepared signal. Propelled by the plans examined in [9,37], we presented a filter design for our framework, which is shown in Figure 1. Figure 1 depicts a crude block diagram pattern that aids in improving the viability of an arrangement with the fewest possible input sources.

• Product modulator (PM) 1 receives the input A, ${\mathcal{T}}_{\alpha }\left(\sigma \right)$, and presents the output as $A{\mathcal{T}}_{\alpha }\left(\sigma \right)$.
• In the same way, PM 2 receives $x\left(\iota \right)$, E, and presents $E(\iota ,x(\iota \left)\right)$.
• PM 3 receives $v\left(\iota \right)$, B and presents $Bv\left(\iota \right)$.
• PM 4 receives $x_0$ and ${\mathcal{R}}_{\alpha }\left(\sigma \right)$ at time $\sigma =0$, and presents ${\mathcal{R}}_{\alpha }\left(\sigma \right)x_0$.
• The integrators executed the integral of ${\mathcal{T}}_{\alpha }\left(\sigma \right)[E(\sigma ,x\left(\sigma \right))+Bv\left(\sigma \right)]$, over $\sigma$.
• Inputs ${\mathcal{T}}_{\alpha }\left(\sigma \right)$, E are mixed and multiplied with an integrator output over $(0,\sigma )$.
• In the same way, ${\mathcal{T}}_{\alpha }\left(\sigma \right)$, B are mixed and multiplied with an integrator output over $(0,\sigma )$.

In the end, we move all integrator outputs to the summer network. Consequently, the output $x\left(t\right)$

$$\begin{array}{cc}\hfill x\left(\sigma \right)& ={\mathcal{R}}_{\alpha }\left(\sigma \right)x_0+{\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\iota )E(\iota ,x\left(\iota \right))d\iota +{\int }_0^{\sigma }{\mathcal{T}}_{\alpha }(\sigma -\iota )Bv\left(\iota \right)d\iota ,\sigma \in V,\hfill \end{array}$$

is attained.

6. Conclusions

This discussion primarily focused on the approximate controllability of fractional integrodifferential equations using resolvent operators. Two alternative sets of necessary requirements were studied. In the first set, we used theories from functional analysis, the compactness of an associated resolvent operator, for our discussion. In the second set, Gronwall’s inequality was used to prove the primary discussion, which eliminated the need for resolvent operator compactness and traditional fixed point theorems. The concept was then extended to a Sobolev-type system.

We will concentrate on approximate controllability for fractional integrodifferential systems using resolvent operators in both deterministic and stochastic contexts in the future.