Optimization of Hyperparameters in Object Detection Models Based on Fractal Loss Function
Abstract
:1. Introduction
- (1)
- An improved genetic algorithm is proposed to solve the problem of objective optimization;
- (2)
- The improved genetic algorithm is proposed to optimize the hyperparameters of the neural network;
- (3)
- Determine a reasonable fitness function according to the relationship between the loss function and hyperparameters, and establish a mathematical model;
- (4)
- The superiority of the proposed method in the task of object detection is demonstrated by comparing with state-of-the-art object detection algorithms.
2. Related Work
2.1. Loss Function for Object Detection
2.2. Intelligent Optimization Algorithm
3. The Proposed Methods
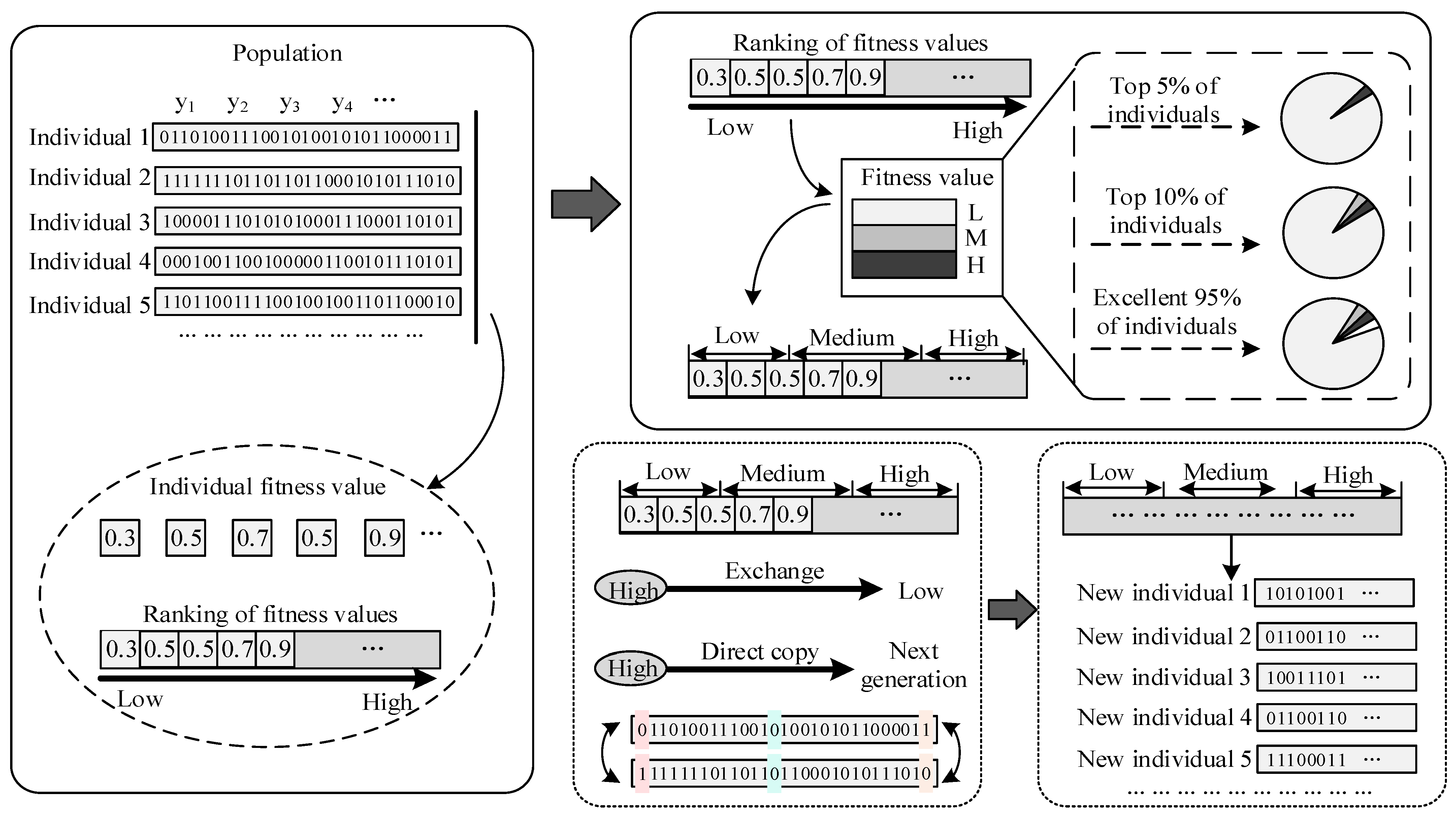
3.1. Improved Genetic Algorithm
3.2. Improved Genetic Neural Network
3.3. Fractal Dimension Calculation Method
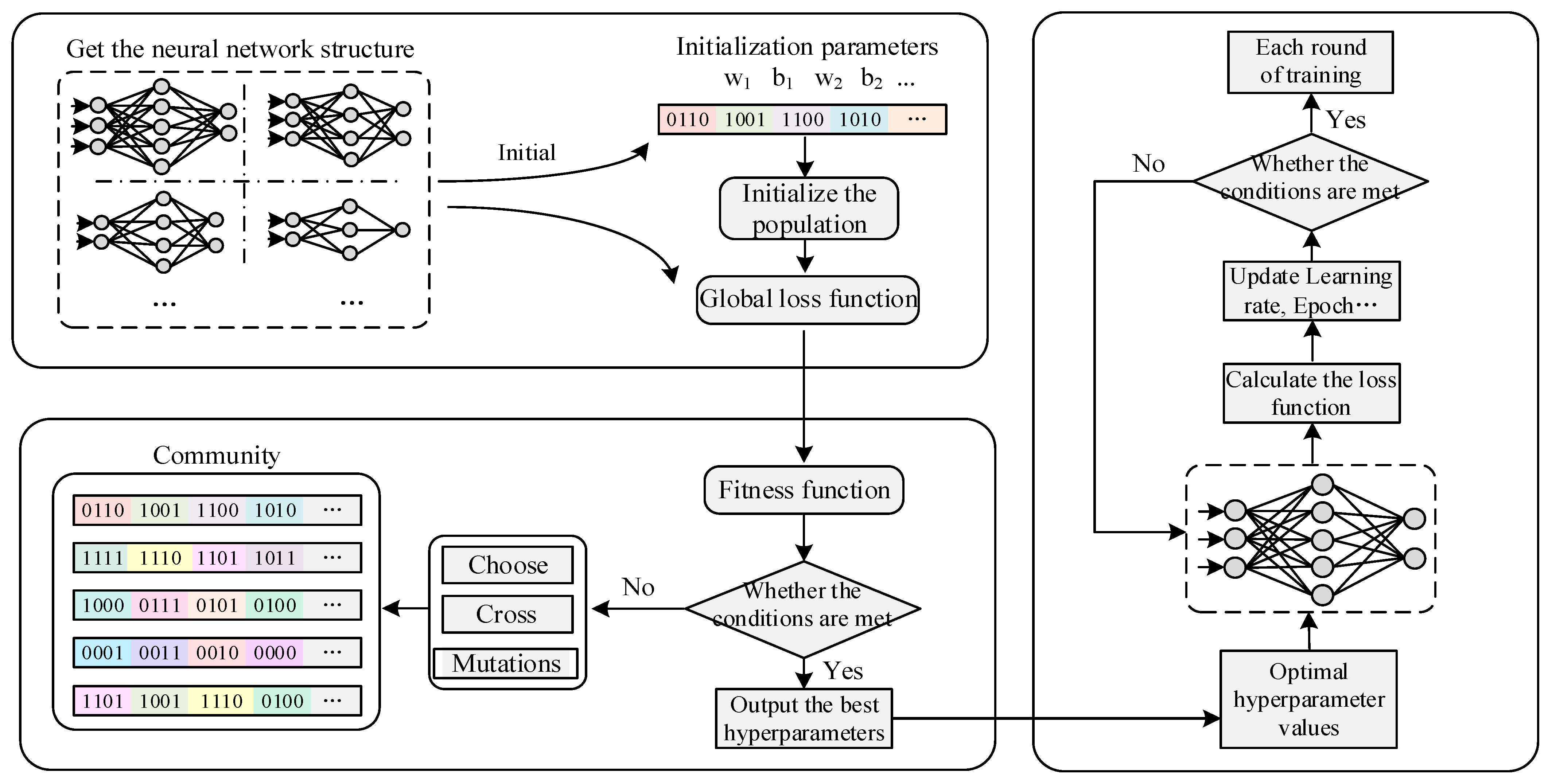
3.4. The Proposed Genetic Neural Network
- a
- The initialization of the population is provided by the following Equation (5).where Nck represents the number of convolution kernels, Sck represents the size of the convolution kernel, Nnlrepresents the number of network layers, Fac represents the activation function, Rlea represents the learning rate, Nbs represents the number of batch samples, Wdc represents the weight decay coefficient, Rdro represents the dropout ratio, and G is the regression parameter.
- b
- Encoding: encoding length when encoding in binary;where (a, b) is the value range of the independent variable, eps is the required precision, and when there are multiple independent variables, the code length is the sum of the code lengths of each independent variable.
- c
- Decoding: Convert binary numbers to decimal numbers;where L is the encoding length, X is the binary data.
- d
- Fitness function: find the minimum value;where is an appropriately large number, and f(x) is determined as the objective function by Formula (4).
- e
- Scale transformation of fitness function: here, the dynamic linear transformation method is selected to search for the optimal solution;where M represents the total number of individuals in the population, and r is a random number between [0.9, 0.999].
3.5. Visualization of the Optimization Process
4. Experiment
4.1. Experimental Environment
4.2. Verify the Performance of the Improved Genetic Algorithm
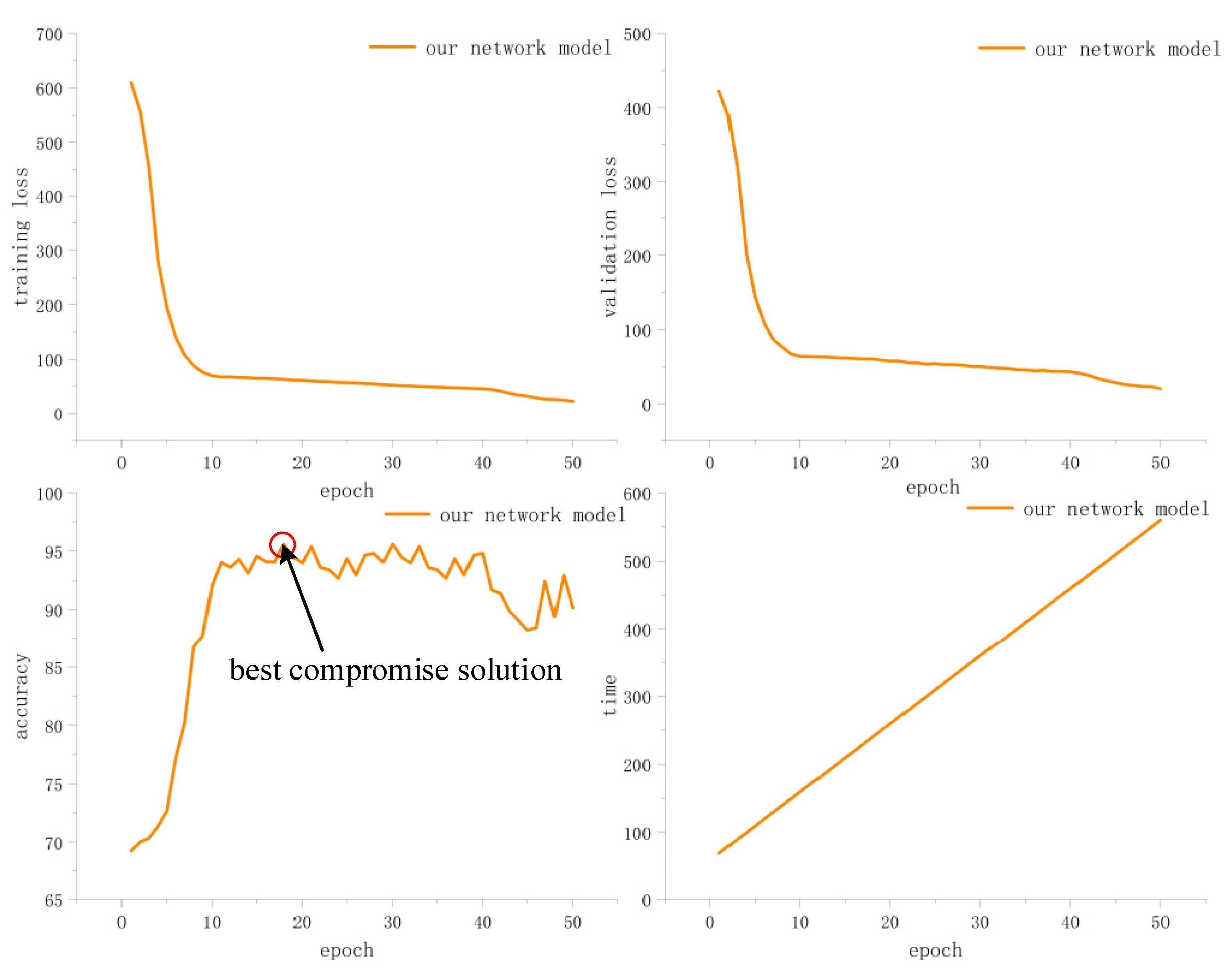
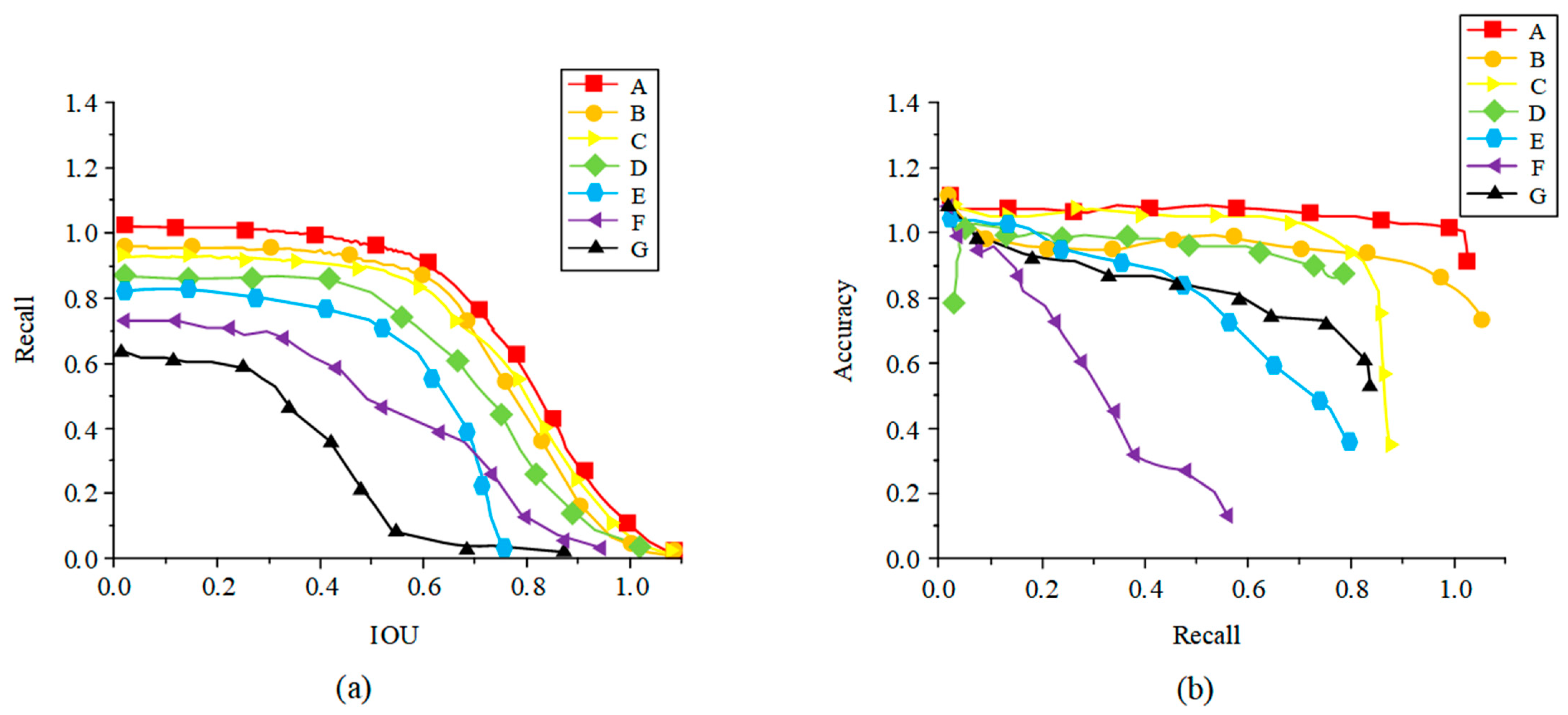
4.3. Quantitative Analysis of Experimental Results
4.4. Qualitative Analysis of Experimental Results
4.5. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mathivanan, G. Survey on Object Detection Framework: Evolution of Algorithms. In Proceedings of the 2021 5th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 2–4 December 2021; pp. 1–5. [Google Scholar]
- Liu, Y.; Sun, P.; Wergeles, N.; Shang, Y. A survey and performance evaluation of deep learning methods for small object detection. Expert Syst. Appl. 2021, 172, 114602. [Google Scholar] [CrossRef]
- Ahmed, M.; Hashmi, K.A.; Pagani, A.; Liwicki, M.; Stricker, D.; Afzal, M.Z. Survey and performance analysis of deep learning based object detection in challenging environments. Sensors 2021, 21, 5116. [Google Scholar] [CrossRef] [PubMed]
- Hua, X.; Ono, Y.; Peng, L.; Cheng, Y.; Wang, H. Target detection within nonhomogeneous clutter via total bregman divergence-based matrix information geometry detectors. IEEE Trans. Signal Process. 2021, 69, 4326–4340. [Google Scholar] [CrossRef]
- Dai, Y.; Wu, Y.; Zhou, F.; Barnard, K. Attentional local contrast networks for infrared small target detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9813–9824. [Google Scholar] [CrossRef]
- Zhan, J.; Hu, Y.; Cai, W.; Zhou, G.; Li, L. PDAM–STPNNet: A small target detection approach for wildland fire smoke through remote sensing images. Symmetry 2021, 13, 2260. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Victoria, A.H.; Maragatham, G. Automatic tuning of hyperparameters using Bayesian optimization. Evol. Syst. 2021, 12, 217–223. [Google Scholar] [CrossRef]
- Brodzicki, A.; Piekarski, M.; Jaworek-Korjakowska, J. The whale optimization algorithm approach for deep neural networks. Sensors 2021, 21, 8003. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Kang, H.; Kang, D.-Y.; Park, J. Genetic algorithm based deep learning neural network structure and hyperparameter optimization. Appl. Sci. 2021, 11, 744. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Y.; Wang, K.; Xi, B.; Li, J.; Gamba, P. Target detection with unconstrained linear mixture model and hierarchical denoising autoencoder in hyperspectral imagery. IEEE Trans. Image Process. 2022, 31, 1418–1432. [Google Scholar] [CrossRef]
- Sun, C.; Shrivastava, A.; Singh, S.; Gupta, A. Revisiting Unreasonable Effectiveness of Data in Deep Learning Era. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 843–852. [Google Scholar]
- Wang, L.; Zeng, X.; Yang, H.; Lv, X.; Guo, F.; Shi, Y.; Hanif, A. Investigation and application of fractal theory in cement-based materials: A review. Fractal Fract. 2021, 5, 247. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, Y.; Liu, S.; Shen, X.; Jia, J. Std: Sparse-to-Dense 3D Object Detector for Point Cloud. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 1951–1960. [Google Scholar]
- Karydas, C.G. Unified Scale Theorem: A Mathematical Formulation of Scale in the Frame of Earth Observation Image Classification. Fractal Fract. 2021, 5, 127. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Mishra, S.K.; Rajković, P.; Samei, M.E.; Chakraborty, S.K.; Ram, B.; Kaabar, M.K. A q-gradient descent algorithm with quasi-fejér convergence for unconstrained optimization problems. Fractal Fract. 2021, 5, 110. [Google Scholar] [CrossRef]
- Binitha, S.; Sathya, S.S. A survey of bio inspired optimization algorithms. Int. J. Soft Comput. Eng. 2012, 2, 137–151. [Google Scholar]
- Sabir, Z.; Wahab, H.A.; Javeed, S.; Baskonus, H.M. An efficient stochastic numerical computing framework for the nonlinear higher order singular models. Fractal Fract. 2021, 5, 176. [Google Scholar] [CrossRef]
- Xia, J.; Yan, Y.; Ji, L. Research on control strategy and policy optimal scheduling based on an improved genetic algorithm. Neural Comput. Appl. 2022, 34, 9485–9497. [Google Scholar] [CrossRef]
- Liang, S.; Jiao, T.; Du, W.; Qu, S. An improved ant colony optimization algorithm based on context for tourism route planning. PLoS ONE 2021, 16, e0257317. [Google Scholar] [CrossRef]
- İlhan, İ. An improved simulated annealing algorithm with crossover operator for capacitated vehicle routing problem. Swarm Evol. Comput. 2021, 64, 100911. [Google Scholar] [CrossRef]
- Kumar, S.; Jain, S.; Sharma, H. Genetic algorithms. In Advances in Swarm Intelligence for Optimizing Problems in Computer Science; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 27–52. [Google Scholar]
- Guo, P.; Cheng, W.; Wang, Y. Hybrid evolutionary algorithm with extreme machine learning fitness function evaluation for two-stage capacitated facility location problems. Expert Syst. Appl. 2017, 71, 57–68. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, G.; Deng, W.; Zhou, Y.; Luo, Q. MOMPA: Multi-objective marine predator algorithm. Comput. Methods Appl. Mech. Eng. 2021, 385, 114029. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G.; Tan, K.C. A survey on evolutionary neural architecture search. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Montgomery, J.; Bolufé-Röhler, A. Measuring the curse of dimensionality and its effects on particle swarm optimization and differential evolution. Appl. Intell. 2015, 42, 514–526. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, X.; He, Y. Remaining useful life and state of health prediction for lithium batteries based on empirical mode decomposition and a long and short memory neural network. Energy 2021, 232, 121022. [Google Scholar] [CrossRef]
- Cui, Z.; Zhao, Y.; Cao, Y.; Cai, X.; Zhang, W.; Chen, J. Malicious code detection under 5G HetNets based on a multi-objective RBM model. IEEE Netw. 2021, 35, 82–87. [Google Scholar] [CrossRef]
- Zhang, X. Construction and simulation of financial audit model based on convolutional neural network. Comput. Intell. Neurosci. 2021, 2021, 1182557. [Google Scholar] [CrossRef]
- Zahedi, L.; Mohammadi, F.G.; Amini, M.H. Hyp-abc: A novel automated hyper-parameter tuning algorithm using evolutionary optimization. arXiv 2021, arXiv:2109.05319. [Google Scholar]
- Mohakud, R.; Dash, R. Survey on hyperparameter optimization using nature-inspired algorithm of deep convolution neural network. In Intelligent and Cloud Computing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 737–744. [Google Scholar]
- Talo, M.; Baloglu, U.B.; Yıldırım, Ö.; Acharya, U.R. Application of deep transfer learning for automated brain abnormality classification using MR images. Cogn. Syst. Res. 2019, 54, 176–188. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Zhou, P.; Guo, L. Multi-class geospatial object detection and geographic image classification based on collection of part detectors. ISPRS J. Photogramm. Remote Sens. 2014, 98, 119–132. [Google Scholar] [CrossRef]
- Wang, M.C.; Uhlenbeck, G.E. On the theory of the Brownian motion II. Rev. Mod. Phys. 1945, 17, 323. [Google Scholar] [CrossRef]
- Vlašić, I.; Ðurasević, M.; Jakobović, D. Improving genetic algorithm performance by population initialisation with dispatching rules. Comput. Ind. Eng. 2019, 137, 106030. [Google Scholar] [CrossRef]
- Du, J.; Wu, F.; Xing, R.; Gong, X.; Yu, L. Segmentation and sampling method for complex polyline generalization based on a generative adversarial network. Geocarto Int. 2022, 37, 4158–4180. [Google Scholar] [CrossRef]
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Cui, C.; Corrado, G.; Thrun, S.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, J.; Li, B. ARG-Mask RCNN: An Infrared Insulator Fault-Detection Network Based on Improved Mask RCNN. Sensors 2022, 22, 4720. [Google Scholar] [CrossRef]


| No. | Function | Range | Range |
|---|---|---|---|
| 1 | 5, 5] | −39.166 | |
| 2 | 0] | −1.801 | |
| 3 | 100, 100] | −1 | |
| 4 | 5, 10] | 0 | |
| 5 | 3, 3]2, 2] | −1.0316 | |
| 6 | 1.5, 4]3, 4] | −1.913 | |
| 7 | 5, 5] | 0 | |
| 8 | 15, −5]3, 3] | 0 | |
| 9 | 10, 10] | −2.0626 | |
| 10 | 5, −5] | −1 |
| Method | Backbone | Accuracy | Precision | Recall | IOU | mAP | FPS |
|---|---|---|---|---|---|---|---|
| Cascade RCNN | ResNet-101 + FPN | 0.65 | 0.75 | 0.76 | 0.68 | 0.86 | 5 |
| GA + ResNet-101 + FPN | 0.71 | 0.76 | 0.83 | 0.68 | 0.88 | 7 | |
| Retina Net | ResNet-101 + FPN | 0.76 | 0.77 | 0.83 | 0.69 | 0.87 | 7 |
| GA + ResNet-101 + FPN | 0.84 | 0.78 | 0.83 | 0.71 | 0.91 | 10 | |
| PV-RCNN | 3D Voxel | 0.43 | 0.51 | 0.65 | 0.56 | 0.71 | 4 |
| GA + 3D Voxel | 0.54 | 0.55 | 0.65 | 0.59 | 0.69 | 8 | |
| Yolov5 | DarkNet-53 | 0.88 | 0.91 | 0.89 | 0.87 | 0.82 | 15 |
| GA + DarkNet-53 | 0.94 | 0.95 | 0.96 | 0.94 | 0.89 | 20 | |
| SSD | VGG-16 | 0.75 | 0.87 | 0.73 | 0.67 | 0.81 | 15 |
| GA + VGG-16 | 0.76 | 0.88 | 0.74 | 0.66 | 0.83 | 21 | |
| Faster RCNN | ResNet-101 + FPN | 0.79 | 0.68 | 0.73 | 0.81 | 0.87 | 9 |
| GA + ResNet-101 + FPN | 0.82 | 0.75 | 0.74 | 0.86 | 0.88 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Li, B.; Wang, J. Optimization of Hyperparameters in Object Detection Models Based on Fractal Loss Function. Fractal Fract. 2022, 6, 706. https://doi.org/10.3390/fractalfract6120706
Zhou M, Li B, Wang J. Optimization of Hyperparameters in Object Detection Models Based on Fractal Loss Function. Fractal and Fractional. 2022; 6(12):706. https://doi.org/10.3390/fractalfract6120706
Chicago/Turabian StyleZhou, Ming, Bo Li, and Jue Wang. 2022. "Optimization of Hyperparameters in Object Detection Models Based on Fractal Loss Function" Fractal and Fractional 6, no. 12: 706. https://doi.org/10.3390/fractalfract6120706
APA StyleZhou, M., Li, B., & Wang, J. (2022). Optimization of Hyperparameters in Object Detection Models Based on Fractal Loss Function. Fractal and Fractional, 6(12), 706. https://doi.org/10.3390/fractalfract6120706






