Modeling and Calibration for Some Stochastic Differential Models
Abstract
1. Introduction
2. A Predator–Prey Model
Fitting Model to Data
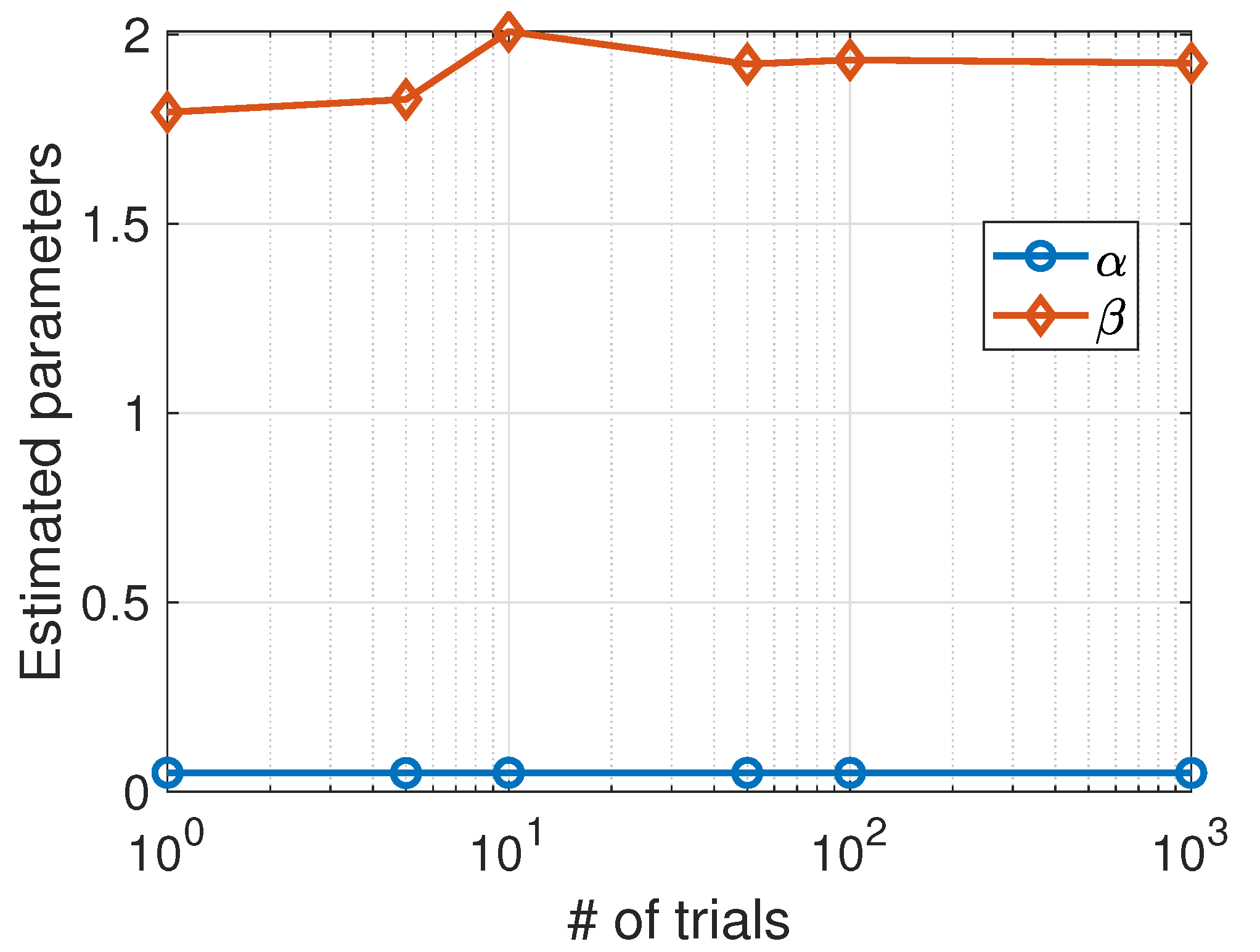
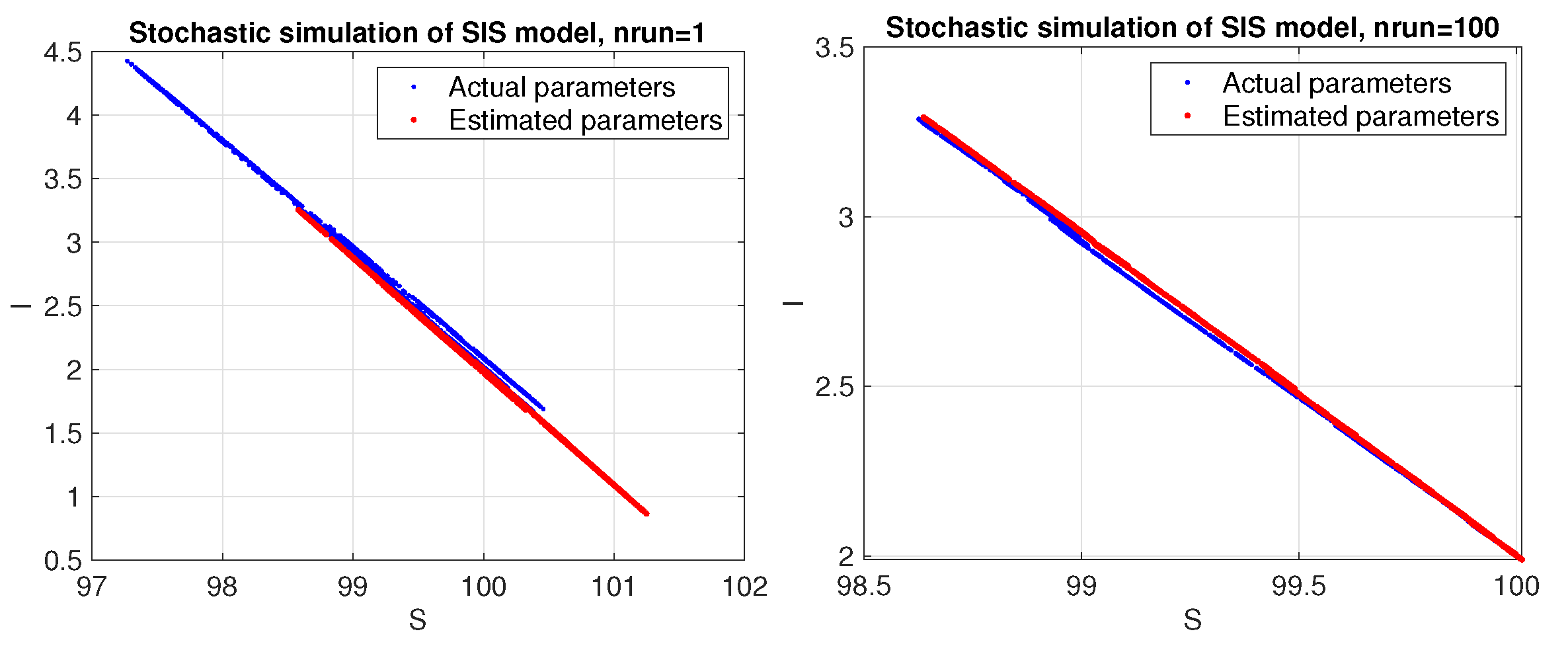
3. A Stochastic SIS Model with Deaths
Fitting Model to Data
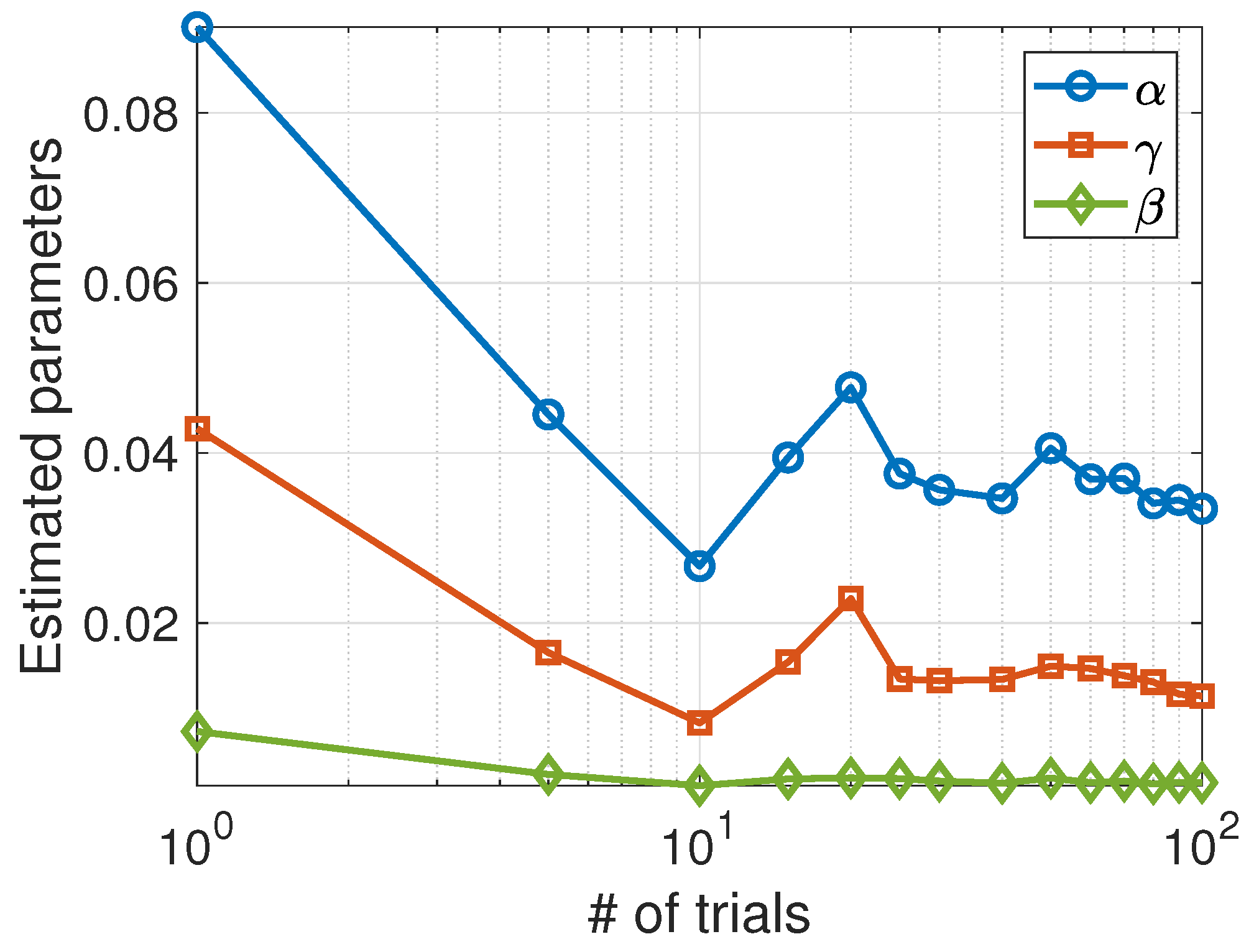
4. A Chemical-Reaction Model
Fitting Model to Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Clermont, G.; Zenker, S. The inverse problem in mathematical biology. Math. Biosci. 2015, 260, 11–15. [Google Scholar] [CrossRef] [PubMed]
- Schittkowski, K. Numerical Data Fitting in Dynamical Systems: A Practical Introduction with Applications and Software; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002; Volume 77. [Google Scholar]
- McGoff, K.; Mukherjee, S.; Pillai, N. Statistical inference for dynamical systems: A review. Stat. Surv. 2012, 9, 209–252. [Google Scholar] [CrossRef]
- Liu, Q.A.; Varshney, D.; McAuley, K.B. Parameter and uncertainty estimation in stochastic differential equation models with multi-rate data and nonstationary disturbances. Chem. Eng. Res. Des. 2022, 183, 118–133. [Google Scholar] [CrossRef]
- Nielsen, J.N.; Madsen, H.; Young, P.C. Parameter estimation in stochastic differential equations: An overview. Annu. Rev. Control. 2000, 24, 83–94. [Google Scholar] [CrossRef]
- Bishwal, J.P. Bayes and Sequential Estimation in Stochastic PDEs. In Parameter Estimation in Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2008; pp. 79–97. [Google Scholar]
- Bishwal, J.P. Maximum Likelihood Estimation in Fractional Diffusions. In Parameter Estimation in Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2008; pp. 99–122. [Google Scholar]
- Deisenroth, M.; Faisal, A.A.; Ong, C.S. Mathematics for Machine Learning. Available online: https://mml-book.github.io/book/mml-book.pdf (accessed on 2 November 2022).
- Murphy, L. Machine Learning. A Probabilistic Perspective; Massachusetts Institute of Technology: Cambridge, MA, USA, 2012. [Google Scholar]
- Higham, D. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Kloeden, P.; Platen, E. Numerical Solution of Stochastic Differential Equations; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Higham, D.; Kloeden, E. An Introduction to the Numerical Simulation of Stochastic Differential Equations; SIAM: Philadelphia, PA, USA, 2021. [Google Scholar]
- Lagarias, J.; Reeds, J.; Wright, M.; Wright, P. Convergence Properties of the Nelder–Mead Simplex Methos in Low Dimensions. SIAM J. Optimition 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Yang, W.; Cao, W.; Chung, T.; Morris, J. Applied Numerical Methods Using MATLAB; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Holmes, M. Introduction to Scientific Computing and Data Analysis; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Skvortsov, A.; Ristic, B.; Kamenev, A. Predicting population extinction from early observations of the Lotka–Volterra system. Appl. Math. Comput. 2018, 320, 371–379. [Google Scholar] [CrossRef]
- Vadillo, F. Comparing stochastic Lotka–Volterra predator–prey models. Appl. Math. Comput. 2019, 360, 181–189. [Google Scholar] [CrossRef]
- Allen, E. Modeling with Itô Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- de la Hoz, F.; Vadillo, F. A mean extinction-time estimate for a stochastic Lotka–Volterra predator–prey model. Appl. Math. Comput. 2012, 219, 170–179. [Google Scholar] [CrossRef]
- Nasell, I. Stochastic models for some epidemica infectios. Math. Biosci. 2002, 179, 1–19. [Google Scholar] [CrossRef]
- Greenhalgh, D.; Mao, Y.L.X. SDE SIS epidemicmodel with demographic stochasticity and varying populations ize. Appl. Math. Comput. 2016, 276, 218–238. [Google Scholar]
- de la Hoz, F.; Doubova, A.; Vadillo, F. Persistence-time Estimation for some Stochastic SIS Epidemic Models. Discret. Countinous Dyn. Syst. Ser. B 2015, 20, 2933–2947. [Google Scholar] [CrossRef]
- Higham, D. Modeling and Simulating Chemical Reactions. SIAM Rev. 2008, 50, 347–368. [Google Scholar] [CrossRef]
- Vadillo, F. On Stochastic Models of Chemical Reactions. Chem. Phys. 2021, 549, 111259. [Google Scholar] [CrossRef]
- Gillespie, D. Approximate accelerated stochastic simulation of chemically. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
- Gillespie, D. The Chemical Langevin and Fokker-Planck Equations for the Reversible Isomerization Reaction. J. Phys. Chem. 2002, 106, 5063–5071. [Google Scholar] [CrossRef]
- Gillespie, D.; Petzold, L. Numerical simulation for biochemicalkinetics. In System Modeling in Cellular Biology From Concepts to Nuts and Bolts; Szallasi, Z., Stelling, J., Periwal, V., Eds.; MIT Press: Cambridge, MA, USA, 2006; p. 331353. [Google Scholar]
- Schilick, T. Molecular Modeling and Simulation. An Interdisciplinary Guide, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.; Kutz, J. Data-Driven Science and Enginnering. Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Transl. from the Russian; Gordon and Breach: New York, NY, USA, 1993. [Google Scholar]
- Song, N.; Liu, Z. Parameter Estimation for Stochastic Differential Equations Driven by Mixed Fractional Brownian Motion. Abstr. Appl. Anal. 2014, 2014, 1–6. [Google Scholar] [CrossRef]



| Change | Probability |
|---|---|
| Trials | Steps | ||
|---|---|---|---|
| 1 | 59 | 0.04972620 | 1.933725 |
| 5 | 60 | 0.04924106 | 1.922077 |
| 10 | 62 | 0.05020194 | 1.929457 |
| 100 | 61 | 0.05099946 | 2.071467 |
| 1000 | 58 | 0.05018393 | 1.935545 |
| Change | Propability |
|---|---|
| # Trials | # Steps | |||
|---|---|---|---|---|
| 1 | 47 | 0.0823 | 0.0375 | 0.0057 |
| 5 | 51 | 0.0453 | 0.0188 | 0.0019 |
| 10 | 43 | 0.0425 | 0.0156 | 0.0017 |
| 50 | 47 | 0.0387 | 0.0159 | 0.0014 |
| 100 | 48 | 0.0345 | 0.0126 | 0.0013 |
| 1000 | 46 | 0.0390 | 0.0155 | 0.0013 |
| Change | Propability |
|---|---|
| # Trials | # Iteration | |||
|---|---|---|---|---|
| 1 | 41 | 0.0014 | 0.0001 | 0.1134 |
| 5 | 42 | 0.0016 | 0.0002 | 0.1074 |
| 10 | 44 | 0.0016 | 0.0004 | 0.1179 |
| 50 | 41 | 0.0016 | 0.0002 | 0.1141 |
| 100 | 42 | 0.0016 | 0.0002 | 0.1131 |
| 1000 | 37 | 0.0016 | 0.0002 | 0.1146 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moujahid, A.; Vadillo, F. Modeling and Calibration for Some Stochastic Differential Models. Fractal Fract. 2022, 6, 707. https://doi.org/10.3390/fractalfract6120707
Moujahid A, Vadillo F. Modeling and Calibration for Some Stochastic Differential Models. Fractal and Fractional. 2022; 6(12):707. https://doi.org/10.3390/fractalfract6120707
Chicago/Turabian StyleMoujahid, Abdelmalik, and Fernando Vadillo. 2022. "Modeling and Calibration for Some Stochastic Differential Models" Fractal and Fractional 6, no. 12: 707. https://doi.org/10.3390/fractalfract6120707
APA StyleMoujahid, A., & Vadillo, F. (2022). Modeling and Calibration for Some Stochastic Differential Models. Fractal and Fractional, 6(12), 707. https://doi.org/10.3390/fractalfract6120707






