Abstract
To improve the thermal performance of inserted highly-conductive material (HCM) for the cooling of a chip, the present work numerically investigates the effects of various geometric and structural parameters of a fractal T-shaped branched HCM on the maximum temperature of the chip. These parameters include the length ratios of branches at two consecutive branching levels α, the width ratio of branches at two consecutive branching levels β, the maximum branching level m, the length of the branch at the initial level L0, the thickness of the HCM H, and the total volume of the HCM V. The results indicate that the maximum temperature of the chip first drops and then rises with the increase of β, which means the existence of the optimal geometric structure of the branched HCM for the cooling of the chip. In addition, the maximum temperature of the chip decreases with the increase of m and V, decreases with the decrease of H, while first drops and then rises with the increase of α and L0. Further, the present work investigates the effects of the thermal conductivity ratio of HCM and chip γ on the optimal width ratio βm of the branched HCM with a different length ratio α, maximum branching level m, length of the branch at the initial level L0, thickness H, total volume V, and thermal conductivity of the rectangular chip Kc. It was found that βm increases with the increase of γ and V, and decreases with the increase of α, L0, and H. The present finding is beneficial to the improvement of the thermal performance of the inserted HCM via geometric optimization.
1. Introduction
Due to the increasing degree of integration of electronic products, electronic devices are suffering from more challenges involving the dramatic increase in heat flux. Searching for a wide spectrum of optimal architectures of cooling routes in heat-generating systems is of paramount interest nowadays, such as electronic components, where heat is generated within the body or induced into the outer surfaces of the piece. Thus, various optimization works have been carried out to improve the heat dissipation of electronic products to increase the lifetime of electronic devices [1,2]. Considering the dependence of the liquid cooling technique on the external driving source and consequent system complexity, the heat conduction cooling system can become an essential and straightforward alternative for the cooling of the electronic component, for which the heat generation can be released by inserting a suitable highly-conductive material (HCM) with explicit structural design into the electronic chip.
The challenge that comes with designing the highly-conductive inserts is to optimize the architecture of the paths for heat removal from a low-conductive domain (electronic component). To improve the thermal performance of the inserted HCM, Bejan [3] proposed to insert a fixed volume of tree-like HCM into the low thermal conductivity material with fixed geometric parameters to achieve the purpose of collecting heat and optimized the HCM to achieve the optimal distribution pathway. Following Bejan’s research, many scholars have conducted extensive studies and optimizations of heat conduction models and further obtained considerable model structure designs with better heat dissipation performances [4,5,6,7,8,9,10,11,12,13,14,15]. For example, Hajmohammadi et al. [12] optimized the geometric parameters of two types of fork-shaped highly-conductive pathways under a fixed volume and found that the peak temperatures of the heat generator with two types of fork-shaped pathways could be reduced by 41% and 46%. Hajmohammadi et al. [13] embedded ‘phi’ and ‘psi’-shaped highly-conductive pathways into the heat generator and found that the peak temperature of the heat generator inserted in these highly-conductive pathways was 50% below the heat generator with x-shaped pathways. Feng et al. [14] optimized the structure of the highly-conductive pathways with single and multilevel ‘+’ shapes in the square heat generator and found that the peak temperature of the square heat generator with the highly-conductive pathway with multilevel ‘+’ shape was 75.79% lower than the pathway with single ‘+’ shape. Mazloomi et al. [15] studied the conductive cooling of a rectangular chip heated from the bottom surface. They found that using side branches and increasing the thickness of the main channel could decrease the maximum temperature of the rectangular chip considerably.
Natural branches, such as leaf vein branches, tree branches, and river veins, play an essential role in transporting matter and energy. People are inspired by the branched structures of nature and apply the branch of nature to the cooling system of electronic products [16,17,18,19,20,21,22,23]. Due to the lack of reliable design standards for the design of heat conduction networks, Liu et al. [19] innovatively put forward a criterion to simulate the process of leaf vein generation and establish a generating design by combining the standard with a flexible optimization framework. Li et al. [20] presented a growth simulation method named the ‘conductivity spreading approach’ to optimize the cooling geometry inside the heat transfer system. Hajmohammadi et al. [21] investigated the optimal distribution configuration of the branched HCM with unequal branches by changing the length of the branch and found that the heat dissipation performance of the tree-like HCM with unequal branches was better than the HCM with equal branches under the fixed volume of the HCM and the number of branches. Xu et al. [22] investigated the thermal conduction law of the branched network with a circular cross-section. They obtained the result that the optimal diameter ratio of the branch makes the network achieve the highest heat transfer rate. Liu and Jing [23] numerically analyzed the influences of geometrical and structural parameters on the total thermal resistance of tree-like networks with three kinds of cross-sectional shapes (circular, rectangle, and triangle) under a fixed volume, and verified the law that the value of total thermal resistance of the tree-like heat conduction network would reach the smallest when the ratio of the cross-section area of the daughter branch and parent branch reaches the inverse of the branching number.
To further understand the thermal performance of inserted fractal tree-like HCM for the cooling of electronic chips and find the optimal structure of fractal tree-like HCM with the best cooling capability, this paper investigates the influences of various geometric and structural parameters of the T-shaped branched HCM on the maximum temperature of the chip and the influences of diverse parameters of the T-shaped branched HCM on its optimal geometric structure. The object of the work is to improve the heat dissipation performance of the HCM through geometric optimization.
2. Numerical Methods
2.1. Description of the Simulation Model
The schematic of a simulation model applied in the present work is displayed in Figure 1, which can be considered a simplified model of a heat-conduction-based cooling plate inserted with T-shaped branched HCM. The branching level of the branched HCM is 3 and the branching number at each level is 2 for the example given in Figure 1. In this simulation model, a T-shaped branched HCM with thermal conductivity of Kh is inserted into a rectangular chip with thermal conductivity of Kc. The rectangular chip can be considered a simplified model of the thermal spreader. The dimensions of the rectangular chip are Lc × Wc × Hc = 18 × 22 × 1.5 mm3. At the same time, a small heat sink with the same material as the inserted HCM is added to the outside of the chip to collect the heat from the chip through the transfer of the branched HCM. The dimensions of the heat sink are fixed at Ls × Ws × Hs = 7.5 × 0.8 × 1 mm3. The cross-section of each branch at any branching level is a rectangle with uniform dimensions. The length ratio and the width ratio of two branches at any two consecutive branching levels of the T-shaped branched HCM keep constant. The thickness of the whole branched HCM also keeps uniform. The main target of the present work is investigating the effects of various geometric and structural parameters of the T-shaped branched HCM and the thermal conductivity ratio of the HCM to the chip γ = Kh/Kc on the maximum temperature of the chip and finding the optimal geometric parameter of the T-shaped branched material with the best thermal performance for the cooling of the chip. The geometric and structural parameters of the HCM considered in the present work are as follows:
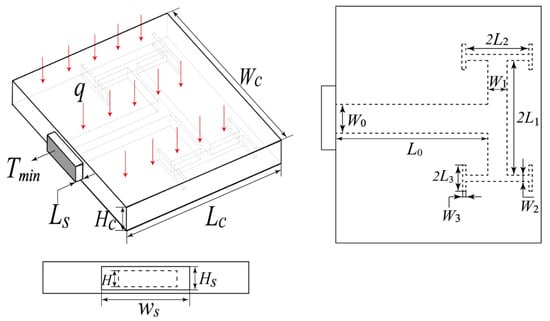
Figure 1.
Simulation model of a rectangular chip inserted with T-shaped branched HCM with m = 3.
- (1)
- α = Li+1/Li (i = 0,1,2,3,…). The α is the length ratio of branches at two consecutive branching levels.
- (2)
- β = Wi+1/Wi (i = 0,1,2,3,…). The β is the width ratio of branches at two consecutive branching levels.
- (3)
- m. The m is the maximum branching level.
- (4)
- L0. The L0 is the length of the branch at the initial level.
- (5)
- H. The H is the thickness of the HCM.
- (6)
- V. The V is the total volume of the HCM.
In this study, the geometric and structural parameters α, β, m, L0, and H of the highly-conductive material will be adjusted under several fixed volume V to study their effects on the maximum temperature of the chip. The detailed geometric and structural parameters employed in the present work are listed in Table 1, Table 2, Table 3, Table 4 and Table 5. Utilizing the parameters listed in these Tables, the width of each branch at different branching levels can be given as,

Table 1.
Geometric parameters of branched HCM with different α.

Table 2.
Geometric parameters of branched HCM with different m.

Table 3.
Geometric parameters of branched HCM with different L0.

Table 4.
Geometric parameters of branched HCM with different H.

Table 5.
Geometric parameters of branched HCM with different V.
2.2. Numerical Method
Using the above geometric model, a uniform and constant heat flux density q = 20,000 W/m2 is applied to the upper surface of the chip, and the outer surface of the heat sink is set to be the minimum temperature of Tmin = 0 °C, as shown in Figure 1. Furthermore, the other surfaces are set to be adiabatic. Since the thermal conductivity of the HCM is larger than that of the rectangular chip, the HCM will collect the heat applied on the chip and transfer it to the outer surface of the heat sink with a minimum temperature.
To simplify the numerical analysis in the study, the following assumptions are put forward for analysis:
- (1)
- The heat conduction is steady state.
- (2)
- The physical properties of the solid materials used in the study are not affected by temperature, and the heat exchange and radiation between the chip and the environment are ignored.
Based on the above assumptions, the heat transfer problem in the present work can be solved by the following governing equation,
where Ki is the thermal conductivity of the solid and Ti is the temperature of the solid. In the present work, γ = Kh/Kc under constant Kc = 10 W/(m·K) will be adjusted to study its effect on the dimensional optimization of branched material with the best thermal performance for the cooling of the chip.
Based on the governing equation and boundary conditions listed above, the Multiphysics simulation software COMSOL is used to solve the problem.
2.3. Mesh Test and Data Validation
To ensure the accuracy of the numerical study, the mesh sensitivity analysis is carried out. In this study, the model with α = 0.65, β = 0.5, L0 = 9 mm, H = 0.8 mm, V = 50 mm3, m = 3, N = 2, and γ = 100 was selected for mesh sensitivity analysis, and Table 6 presents the results of the mesh sensitivity analysis. It can be found that the result of the fourth group of grid settings is accurate enough for the numerical simulation, thus, the fourth group of grids is used for the grid setting of all the simulations with different parameter setups.

Table 6.
The mesh independence test.
In addition to the mesh sensitivity test to ensure the accuracy of the numerical calculation, the data comparison in literature [24] is also carried out to keep the correctness of the present numerical method. In the literature, a highly-conductive rectangular material is inserted in a rectangular chip to numerically study its effect on the maximum temperature of the chip. Using the model setup in the literature, the data comparison of the maximum temperature calculated by the present method with that in the literature is given in Figure 2. It can be found that the results obtained by the method used in the present work are consistent with the results in the literature. This shows that the method used in the present work is feasible.
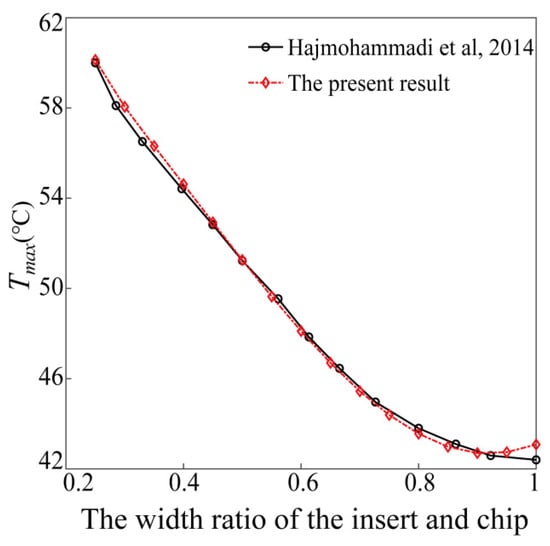
Figure 2.
Data comparison with literature [24].
3. Results and Discussion
3.1. The Thermal Performances of the Branched HCM
After testing the feasibility of the method and the accuracy of the numerical results, the effects of the length ratio of branches at two consecutive branching levels α, the width ratio of branches at two consecutive branching levels β, the maximum branching level m, the length of the branch at the initial level L0, the thickness of the HCM H and the total volume of the HCM V on the maximum temperature Tmax of the chip are illustrated and discussed in this section. As the results show in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, the maximum temperature of the chip always first drops and then rises with the increase of β. It can be inferred that the HCM has an optimal width ratio βm to minimize the maximum temperature of the chip. This result is in agreement with the previous studies on the heat conduction of tree-like networks [22,23,25,26,27].
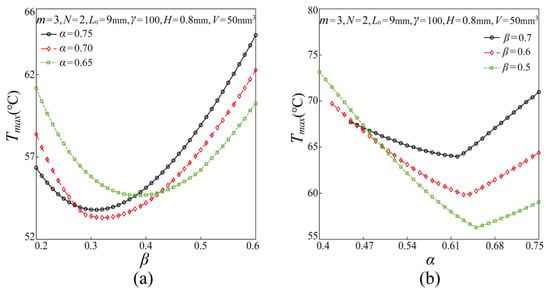
Figure 3.
(a) Effect of β on the maximum temperature of the chip with different value of α (b) Effect of α on the maximum temperature of the chip with different value of β.
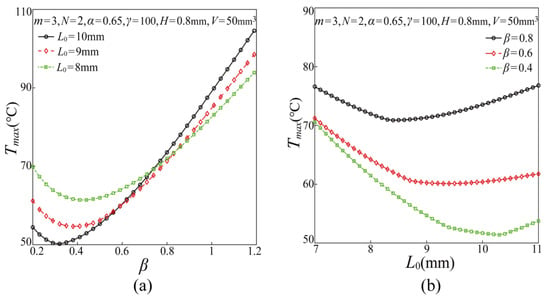
Figure 4.
(a) Effect of β on the maximum temperature of the chip with different value of L0 (b) Effect of L0 on the maximum temperature of the chip with different value of β.
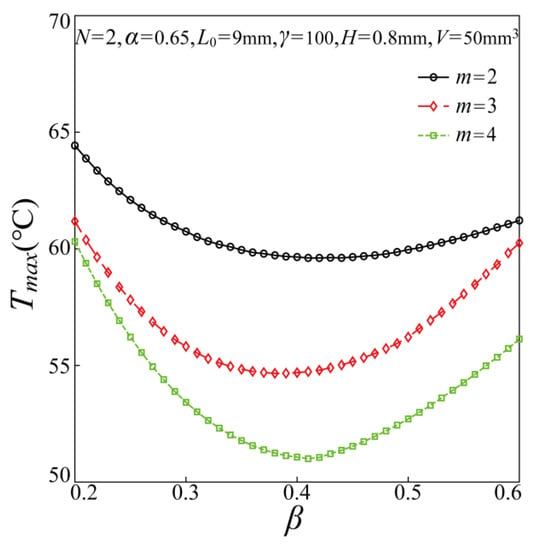
Figure 5.
Effect of β with different m on the maximum temperature of the chip.
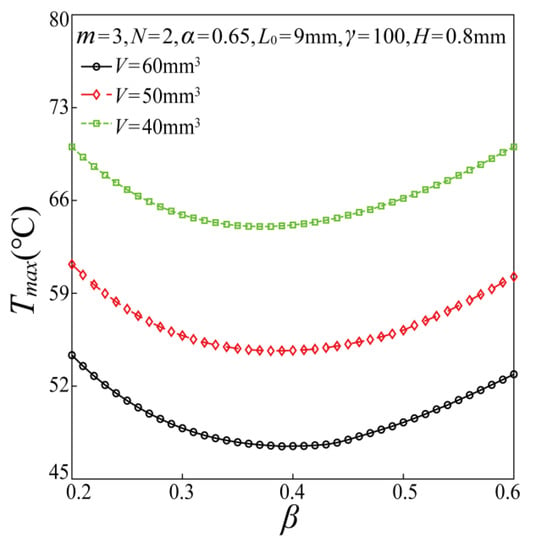
Figure 6.
Effect of β with different V on the maximum temperature of the chip.
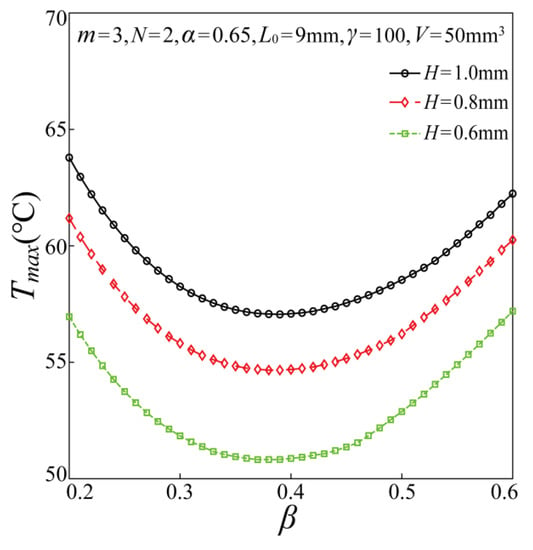
Figure 7.
Effect of β with different H on the maximum temperature of the chip.
Furthermore, from Figure 3a, it can be found that the effect of α on the maximum temperature of the chip is a nonmonotonic change, and the maximum temperature of the chip shows the transition from drop to rise with the increase of α, which indicates there might be an optimal length ratio to obtain the minimum value of the maximum temperature of the chip. To prove this, Figure 3b gives the effects of α of the T-shaped branched HCM with different β on the maximum temperature of the chip. It can be found that there is an optimal length ratio to obtain the minimum value of the maximum temperature of the chip.
In addition, it can be found from Figure 4a that the effect of L0 on the maximum temperature of the chip is also a nonmonotonic change, and the maximum temperature of the chip first decreases and then increases with L0, which means there might be an optimal length of the branch at the initial level to obtain the minimum value of the maximum temperature of the chip, which can be proved by the results shown in Figure 4b.
Regarding the effect of m on the maximum temperature of the chip, it can be found from Figure 5 that the maximum temperature declines gradually with the increase of m = 2, 3, and 4. In this paper, the maximum branching level is chosen to be 4, this is because the further increase of m may lead to the crossing of the branches, as discussed in the previous study [28], and destroy the structure of the fractal branched HCM. When m increases from 2 to 4, the minimum value of the maximum temperature of the chip reduces from 332.75 K to 324.15 K, which indicates that the branched HCM with a large branching level displays better heat dissipation performance. The main reason is that the heat exchange area between the HCM and the chip will become larger with the increase of m, thereby promoting heat dissipation performance and further reducing the maximum temperature of the chip.
In Figure 6, the effect of β on the maximum temperature of the chip was studied by adjusting the fixed volume V of the HCM under fixed parameters of α, m, L0, and H. It is found that the increase of V is beneficial to enhance the heat dissipation performance of the branched HCM. The curve of the maximum temperature gradually declines with the increase of V. The main reason is that the heat exchange area will also increase with the increase of V, which further promotes heat dissipation performance and reduces the maximum temperature of the chip. This result is consistent with previous studies [26].
In Figure 7, the effect of β on the maximum temperature of the chip was studied by adjusting H at fixed parameters of α, m, L0, and V. It can be found that the maximum temperature of the chip will gradually decline with the decrease of the thickness of the HCM, which means that reducing the thickness of the HCM can improve the heat dissipation performance of the HCM, which is also due to the increasing heat exchange area with the decrease of the thickness of the HCM.
3.2. The Optimal Width Ratio of the Branched HCM
According to the above analysis, there exists an optimal width ratio βm to make the thermal performance of the branched HCM obtain the best; thus, it might be interesting and significant to investigate the optimal width ratio. Correspondingly, Figure 8 shows the effects of the thermal conductivity ratio γ on the optimal width ratio of the branched HCM with a different length ratio α, the maximum branching level m, the length of the branch at the initial level L0, the thickness H, the total volume V and the thermal conductivity of the rectangular chip Kc. It shows that the optimal width ratio of the branched HCM always rises with the increase of γ, which means with the increased conductivity of the inserted HCM, the branched HCM with wider terminal branches is preferred. In addition, the results are apparent in Figure 8 that the optimal width ratio decreases with the increase of α, L0, and H while increasing with the increase of V. Further, it can be found that the effects of m and Kc on the optimal width ratio are nonmonotonic change, which still needs further studies. At the same time, it is found that the optimal width ratio of the branched HCM obtained in the present work is not consistent with the findings of the previous literature [22,23] regarding the optimal structure of a fractal heat-conduction network with a single material. For the fractal heat-conduction network with a single material, its optimal width ratio is always equal to the reciprocal of the branching number at each level when the cross-section shape is a rectangle with uniform height. However, when the branched HCM is inserted in the rectangular chip with lower heat conductivity, the dual-materials system increases the complexity of optimization design and leads to the discrepancy with the single-material system.
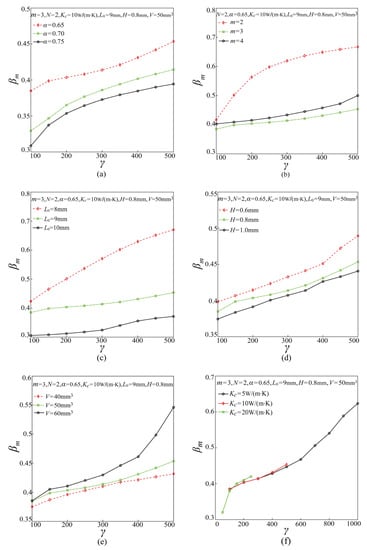
Figure 8.
Effects of γ on the optimal width ratio of the HCM with different (a) α, (b) m, (c) L0, (d) H, (e) V, and (f) Kc.
4. Conclusions
This paper proposed a rectangular chip inserted with branched HCM, and numerically investigated the influences of different geometric and structural parameters of the branched HCM, including the length ratio of branches at two consecutive branching levels α, width ratio of branches at two consecutive branching levels β, maximum branching level m, length of the branch at the initial level L0 and thickness of the HCM H on the maximum temperature of the chip under several fixed volume V. The effects of the thermal conductivity ratio γ on the optimal width ratio βm of the branched HCM with a different length ratio α, the maximum branching level m, the length of the branch at the initial level L0, the thickness H, the total volume V, and the thermal conductivity of the rectangular chip Kc are also studied.
The present work found that the maximum temperature of the chip first drops and then rises with the increase of β, which means there is an optimal geometric structure for the branched HCM to achieve the best thermal performance. In addition, the maximum temperature of the chip decreases with the increase of m and V and decreases with the decrease of H, while first drops and then rises with the increase of α and L0. For the optimal geometric structure of HCM, it obtains the result that the optimal width ratio βm of the branched HCM always increases with the increase of γ and V, while decreasing with the increase of α, L0, and H. However, the effects of m and Kc on the optimal width ratio still need further study due to the nonmonotonic variation of βm. The present finding provides a potential method to improve the cooling performance of the inserted HCM via explicit geometric optimization, which can be applied to the cooling of the microelectronic chip, LED lamp, and lithium battery. In addition, this work focus on the thermal performance of symmetric branched highly-conductive material inserted in the low-conductive material for cooling of uniform heat distribution. However, an asymmetrical branched highly-conductive material structure may be better for the cooling of the non-uniform heat and hotspot distribution, and its thermal performance and optimization design still need deep study.
Author Contributions
Conceptualization, D.J.; Software, R.Z.; Validation, D.J.; Formal analysis, R.Z. and D.J.; Investigation, R.Z.; Data curation, R.Z.; Writing—original draft, R.Z.; Writing—review & editing, D.J.; Visualization, R.Z.; Supervision, D.J.; Funding acquisition, D.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Shanghai (no. 20ZR1438100).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- He, Z.; Yan, Y.; Zhang, Z.; Lund, H.; Kaiser, M.J. Thermal management and temperature uniformity enhancement of electronic devices by micro heat sinks: A review. Energy 2021, 216, 119223. [Google Scholar] [CrossRef]
- Guo, K.; Qi, W.; Liu, B.; Liu, C.; Huang, Z.; Zhu, G. Optimization of an “area to point” heat conduction problem. Appl. Therm. Eng. 2016, 93, 61–71. [Google Scholar] [CrossRef]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Yu, L.T.; Chen, C.K. Optimization of circular fins with variable thermal parameters. J. Frankl. Inst. 1999, 336, 77–95. [Google Scholar] [CrossRef]
- Lorenzini, G.; Biserni, C.; Rocha, L.A.O. Constructal design of X-shaped conductive pathways for cooling a heat-generating body. Int. J. Heat Mass Transf. 2013, 58, 513–520. [Google Scholar] [CrossRef]
- Fagundes, T.M.; Yaghoobian, N.; Rocha, L.A.O.; Ordonez, J.C. Constructal design of branched conductivity pathways inserted in a trapezoidal body: A numerical investigation of the effect of body shape on optimal pathway structure. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2018, 19, 297–302. [Google Scholar]
- Yu, C.; Wu, S.; Huang, Y.; Yao, F.; Liu, X. Charging performance optimization of a latent heat storage unit with fractal tree-like fins. J. Energy Storage 2020, 30, 101498. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Rasouli, E.; Elmi, M.A. Geometric optimization of a highly conductive insert intruding an annular fin. Int. J. Heat Mass Transf. 2020, 146, 118910. [Google Scholar] [CrossRef]
- Lorenzini, G.; Barreto, E.X.; Beckel, C.C.; Schneider, P.S.; Rocha, L. Constructal design of I-shaped high conductive pathway for cooling a heat-generating medium considering the thermal contact resistance. Int. J. Heat Mass Transf. 2016, 93, 770–777. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Ahmadian, M.; Nourazar, S.S. Introducing highly conductive materials into a fin for heat transfer enhancement. Int. J. Mech. Sci. 2019, 150, 420–426. [Google Scholar] [CrossRef]
- Lorenzini, G.; Joneydi Shariatzadeh, O.; Hajmohammadi, M.R.; Biserni, C. Evolution in the Design of V-Shaped Highly Conductive Pathways Embedded in a Heat-Generating Piece. J. Heat Transf. 2015, 137, 61001. [Google Scholar]
- Hajmohammadi, M.R.; Abianeh, V.A.; Moezzinajafabadi, M.; Daneshi, M. Fork-shaped highly conductive pathways for maximum cooling in a heat generating piece. Appl. Therm. Eng. 2013, 61, 228–235. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Shariatzadeh, O.J.; Moulod, M.; Nourazar, S.S. Phi and Psi shaped conductive routes for improved cooling in a heat generating piece. Int. J. Therm. Sci. 2014, 77, 66–74. [Google Scholar] [CrossRef]
- Feng, H.; Chen, L.; Xie, Z.; Sun, F. Constructal design for “+” shaped high conductivity pathways over a square body. Int. J. Heat Mass Transf. 2015, 91, 162–169. [Google Scholar] [CrossRef]
- Mazloomi, A.; Sharifi, F.; Salimpour, M.R.; Moosavi, A. Optimization of highly conductive insert architecture for cooling a rectangular chip. Int. Commun. Heat Mass Transf. 2012, 39, 1265–1271. [Google Scholar] [CrossRef]
- Ji, Y.; Ding, X.; Li, H.; Xiong, M. Layout Design of Conductive Heat Channel by Emulating Natural Branch Systems. J. Bionic Eng. 2018, 15, 567–578. [Google Scholar] [CrossRef]
- Yi, P.; Liu, W.; Wang, N.; Tian, Y.; Chen, X. A novel wick structure of vapor chamber based on the fractal architecture of leaf vein. Int. J. Heat Mass Transf. 2013, 63, 120–133. [Google Scholar]
- Ding, X.; Yamazaki, K. Constructal Design of Cooling Channel in Heat Transfer System by Utilizing Optimality of Branch Systems in Nature. J. Heat Transf. 2007, 129, 245–255. [Google Scholar] [CrossRef]
- Hl, A.; Bl, A.; Lz, A.; Xin, L.B. Optimizing heat-absorption efficiency of phase change materials by mimicking leaf vein morphology. Appl. Energy 2020, 269, 114982. [Google Scholar]
- Li, B.; Hong, J.; Ge, L. Constructal design of internal cooling geometries in heat conduction system using the optimality of natural branching structures. Int. J. Therm. Sci. 2017, 115, 16–28. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Parsa, H.; Najafian, J. Proposing an optimal tree-like design of highly conductive material configuration with unequal branches for maximum cooling a heat generating piece. Int. J. Heat Mass Transf. 2019, 142, 118422. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B.; Yun, M.; Zou, M. Heat conduction in fractal tree-like branched networks. Int. J. Heat Mass Transf. 2006, 49, 3746–3751. [Google Scholar] [CrossRef]
- Liu, F.; Jing, D. Optimization of heat conduction for treelike network with arbitrary cross-sectional shape. Fractals 2022, 30, 2150257. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Moulod, M.; Shariatzadeh, O.J.; Nourazar, S.S. Essential reformulations for optimization of highly conductive inserts embedded into a rectangular chip exposed to a uniform heat flux. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 2337–2346. [Google Scholar] [CrossRef]
- Almogbel, M.; Bejan, A. Constructal optimization of nonuniformly distributed tree-shaped flow structures for conduction. Int. J. Heat Mass Transf. 2001, 44, 4185–4194. [Google Scholar] [CrossRef]
- Rocha, L.; Lorente, S.; Bejan, A. Conduction tree networks with loops for cooling a heat generating volume. Int. J. Heat Mass Transf. 2006, 49, 2626–2635. [Google Scholar] [CrossRef]
- Rocha, L.; Lorente, S.; Bejan, A. Constructal design for cooling a disc-shaped area by conduction. Int. J. Heat Mass Transf. 2002, 45, 1643–1652. [Google Scholar] [CrossRef]
- Senn, S.M.; Poulikakos, D. Laminar mixing, heat transfer and pressure drop in tree-like microchannel nets and their application for thermal management in polymer electrolyte fuel cells. J. Power Sources 2004, 130, 178–191. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).