A Comparative Study of Responses of Fractional Oscillator to Sinusoidal Excitation in the Weyl and Caputo Senses
Abstract
1. Introduction
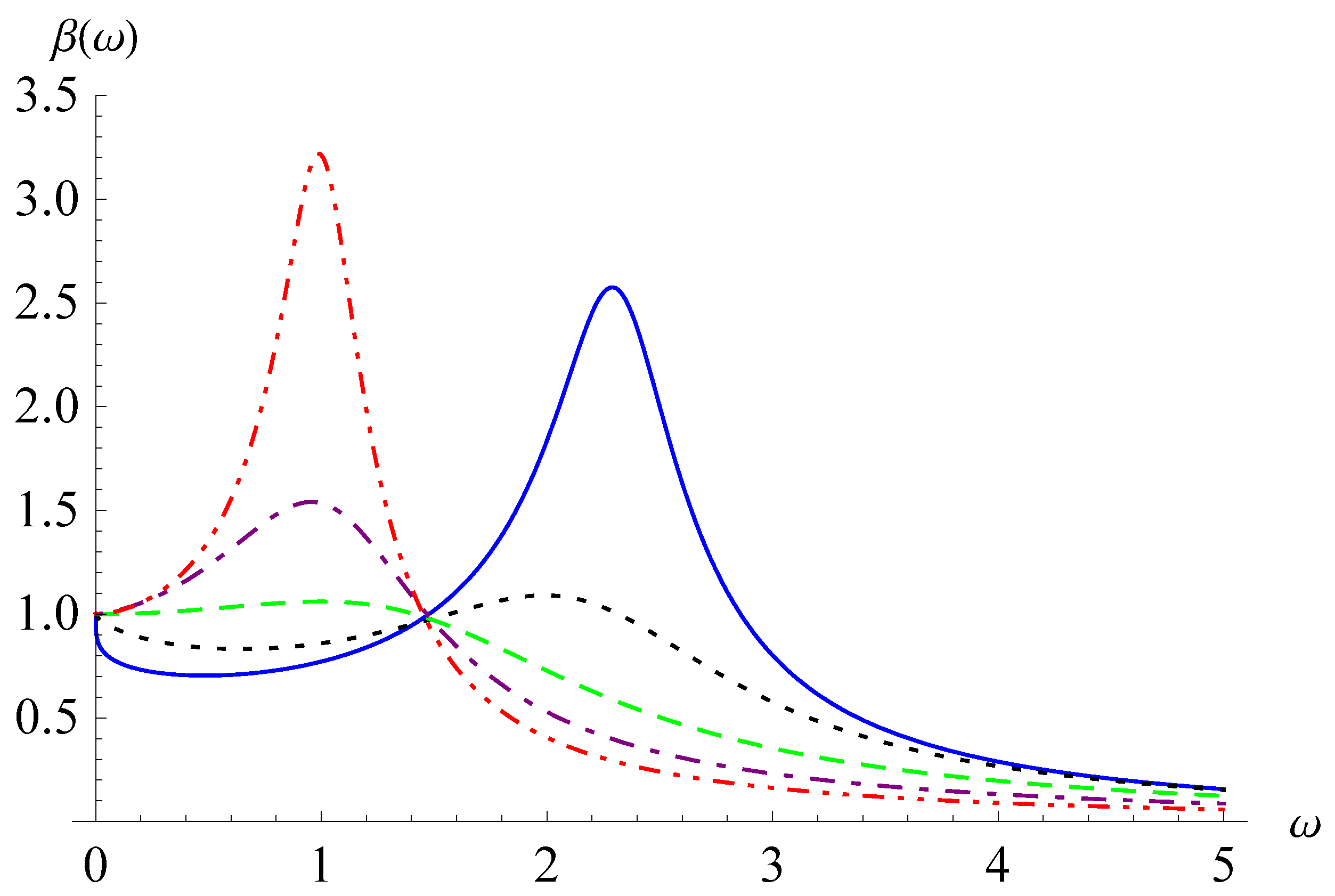
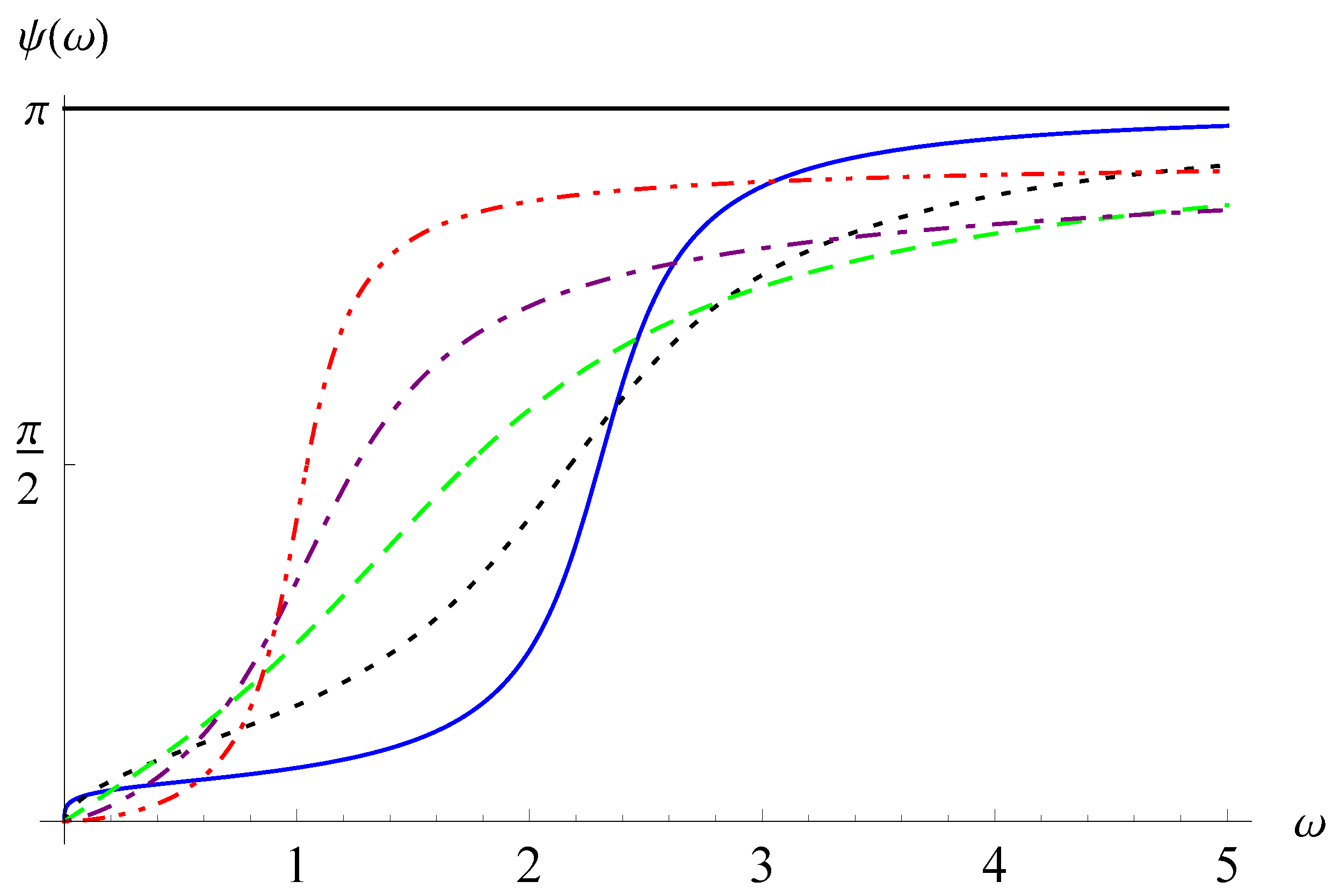
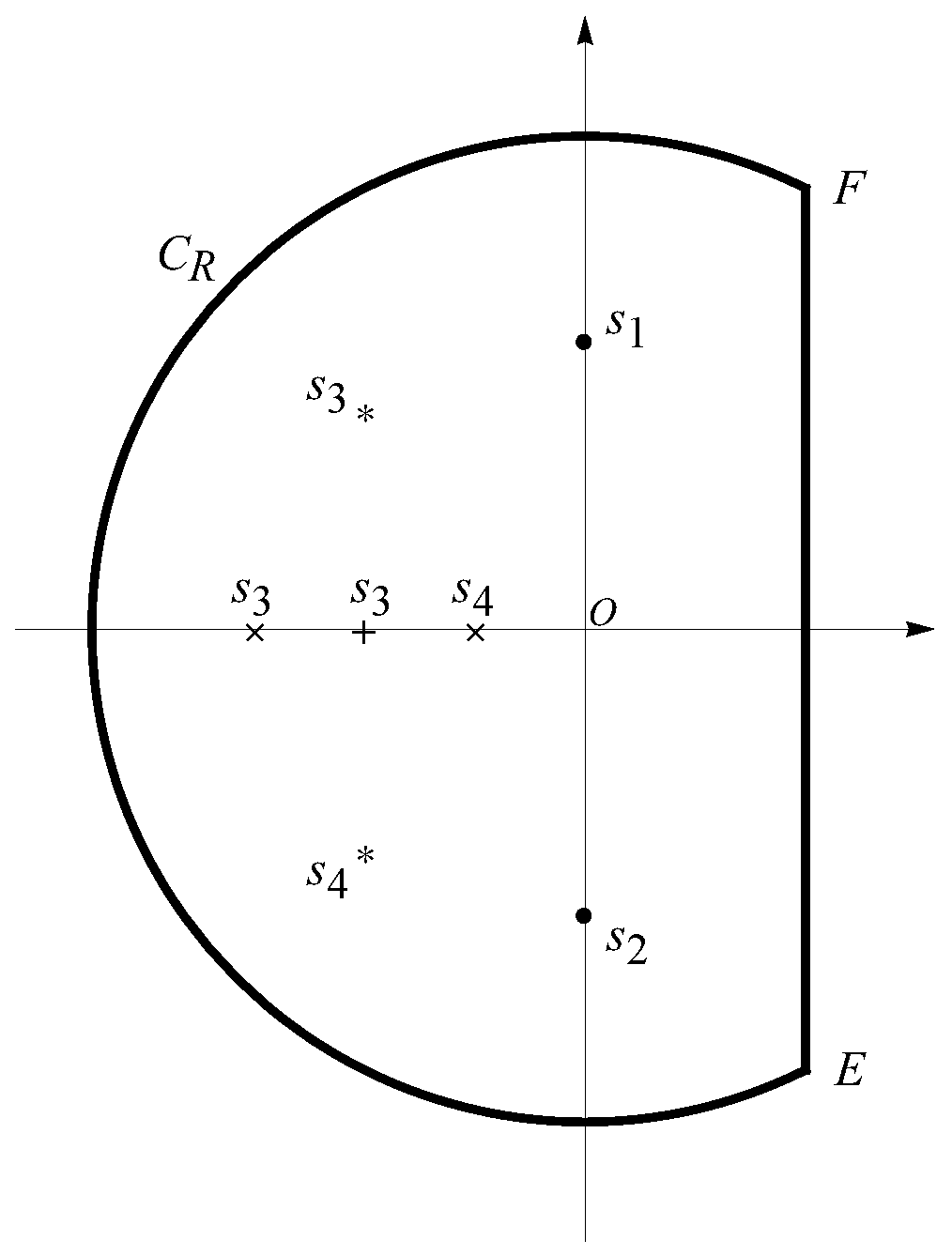
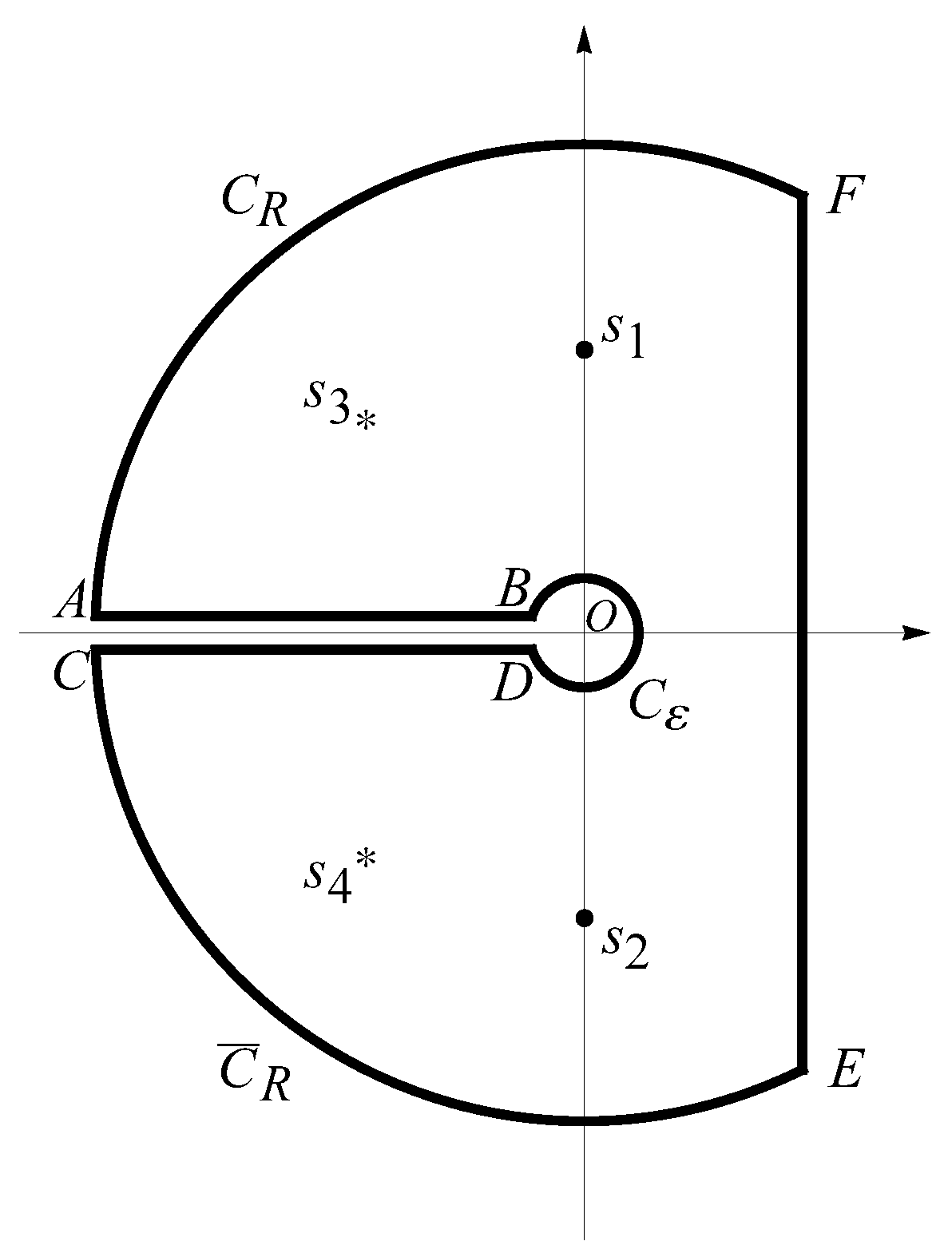
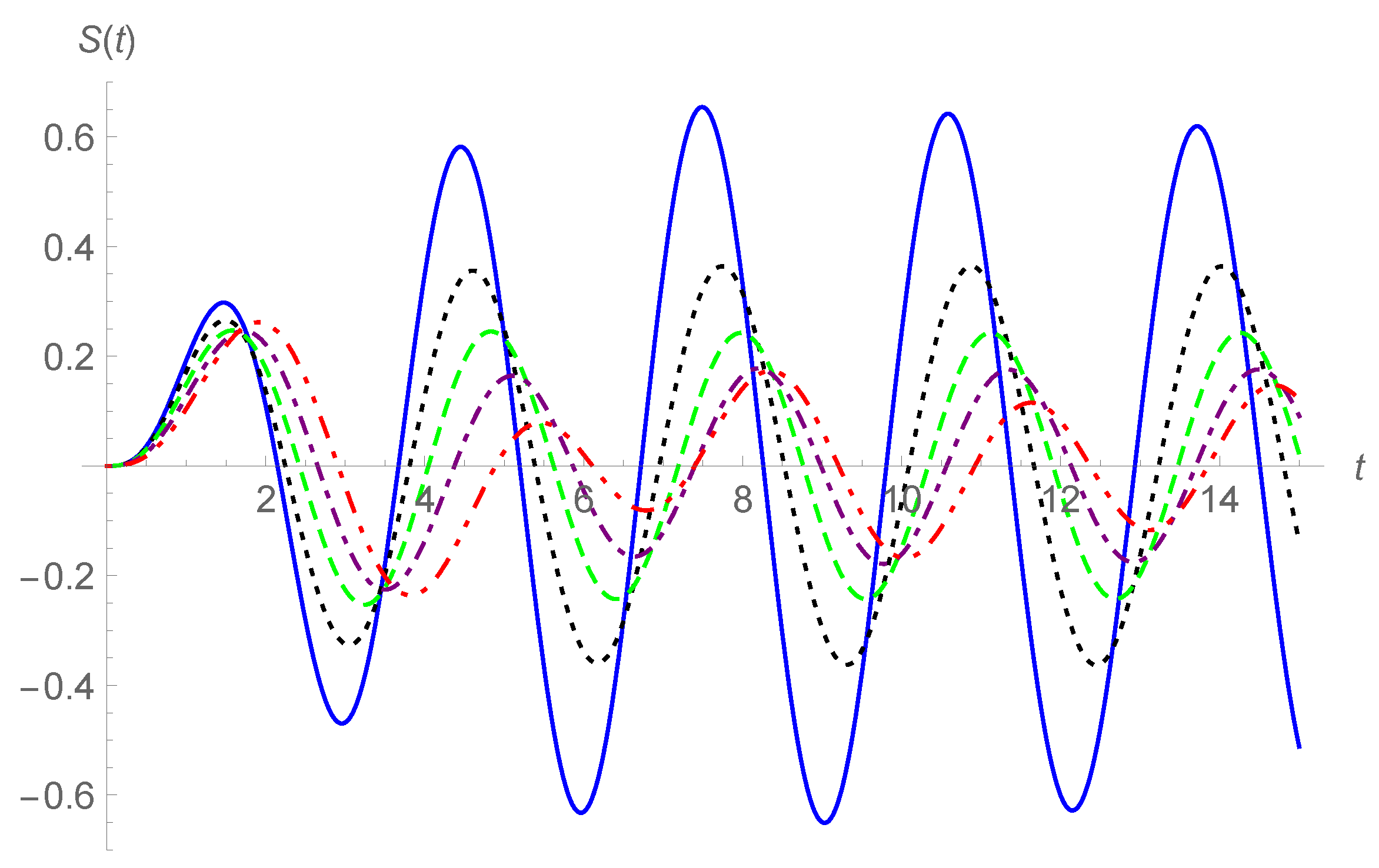
2. Oscillator Equation with the Weyl Fractional Derivative
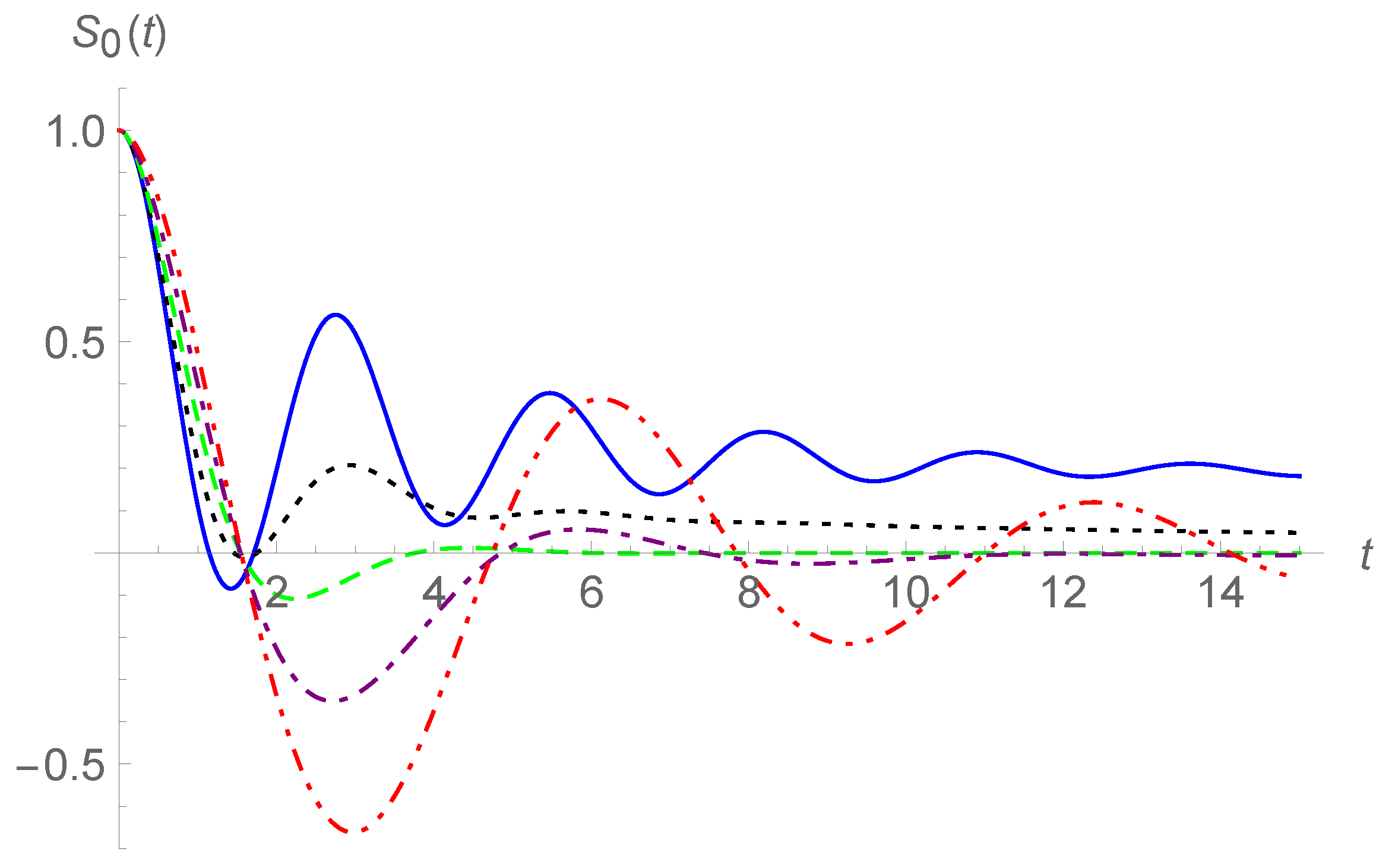
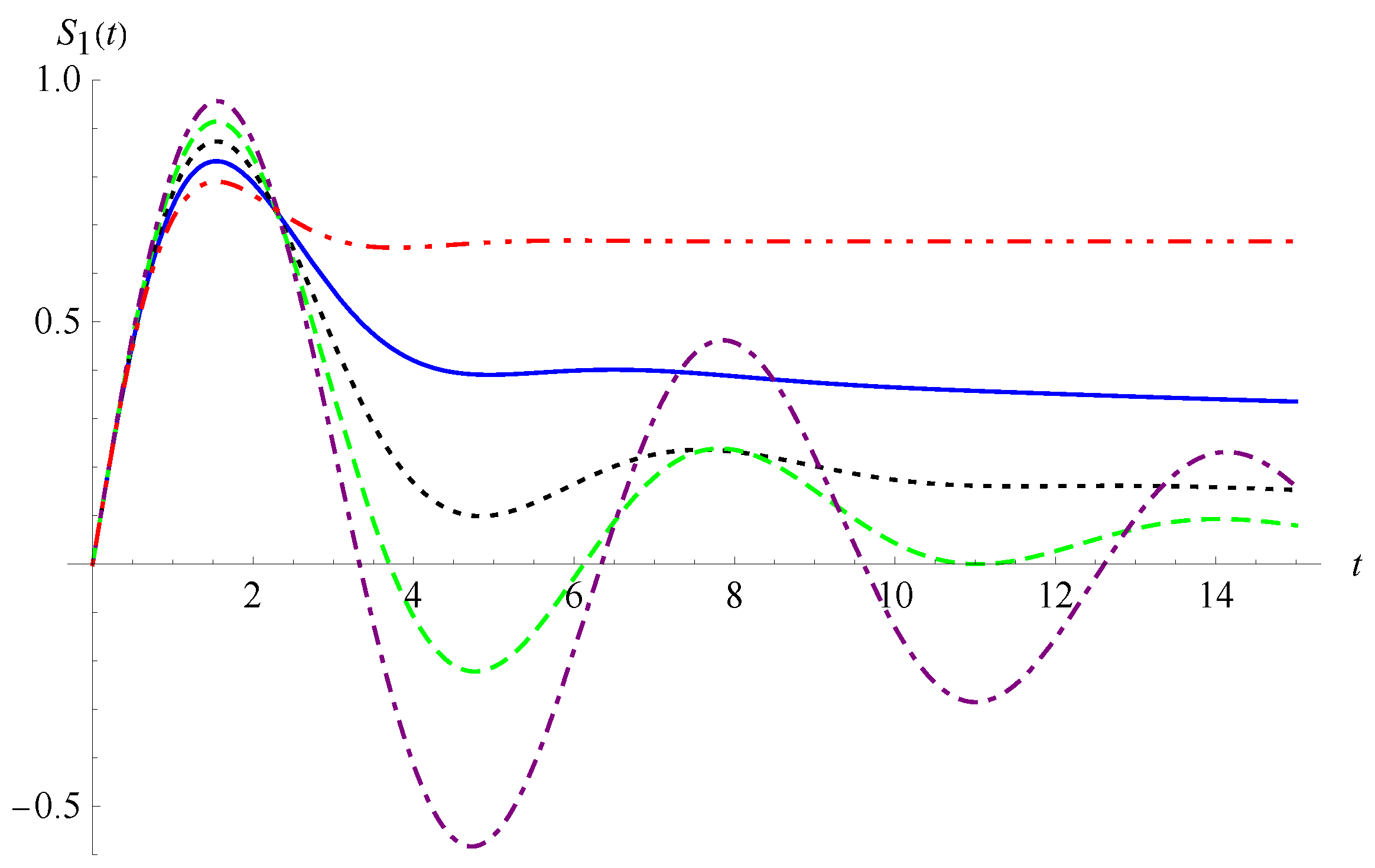
3. Oscillator Equation with the Caputo Fractional Derivative
3.1. The Integer-Order Case
3.2. The Fractional Case
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College: London, UK, 2010. [Google Scholar]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls, Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Băleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods. Series on Complexity, Nonlinearity and Chaos; World Scientific: Boston, MA, USA, 2012. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics; Wiley: New York, NY, USA, 2014. [Google Scholar]
- Li, M. Theory of Fractional Engineering Vibrations; De Gruyter: Berlin, Germany; Boston, MA, USA, 2021. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Lim, S.C.; Teo, L.P. The fractional oscillator process with two indices. J. Phys. A Math. Theor. 2009, 42, 065208. [Google Scholar] [CrossRef]
- Li, M.; Sun, X.; Xiao, X. Revisiting fractional Gaussian noise. Physica A 2019, 514, 56–62. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives–Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Palade, L.I.; Verney, V.; Attané, P. A modified fractional model to describe the entire viscoelastic behavior of polybutadienes from flow to glassy regime. Rheol. Acta 1996, 35, 265–273. [Google Scholar] [CrossRef]
- Pritz, T. Five-parameter fractional derivative model for polymeric dampling materials. J. Sound Vibr. 2003, 265, 935–952. [Google Scholar] [CrossRef]
- Duan, J.S.; Chen, Y.Q. Mechanical response and simulation for constitutive equations with distributed order derivatives. Int. J. Model. Simul. Sci. Comput. 2017, 8, 1750040. [Google Scholar] [CrossRef]
- Achar, B.N.N.; Hanneken, J.W.; Enck, T.; Clarke, T. Dynamics of the fractional oscillator. Physica A 2001, 297, 361–367. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: Novel trends and recent results. Appl. Mech. Rev. 2010, 63, 010801. [Google Scholar] [CrossRef]
- Naber, M. Linear fractionally damped oscillator. Int. J. Differ. Equat. 2010, 2010, 197020. [Google Scholar] [CrossRef]
- Wang, Z.H.; Du, M.L. Asymptotical behavior of the solution of a SDOF linear fractionally damped vibration system. Shock Vib. 2011, 18, 257–268. [Google Scholar] [CrossRef]
- Liu, L.L.; Duan, J.S. A detailed analysis for the fundamental solution of fractional vibration equation. Open Math. 2015, 13, 826–838. [Google Scholar] [CrossRef]
- Li, M. Three classes of fractional oscillators. Symmetry 2018, 10, 40. [Google Scholar] [CrossRef]
- Wang, T.; Qin, M.; Lian, H. The asymptotic approximations to linear weakly singular Volterra integral equations via Laplace transform. Numer. Algorithms 2020, 85, 683–711. [Google Scholar] [CrossRef]
- Duan, J.S.; Hu, D.C.; Li, M. Comparison of two different analytical forms of response for fractional oscillation equation. Fractal Fract. 2021, 5, 188. [Google Scholar] [CrossRef]
- Dubovski, P.B.; Slepoi, J. Analysis of solutions of some multi-term fractional Bessel equations. Fract. Calc. Appl. Anal. 2021, 24, 1380–1408. [Google Scholar] [CrossRef]
- Li, Y.; Duan, J.S. The periodic response of a fractional oscillator with a spring-pot and an inerter-pot. J. Mech. 2021, 37, 108–117. [Google Scholar] [CrossRef]
- Duan, J.S.; Hu, D.C. Vibration systems with fractional-order and distributed-order derivatives characterizing viscoinertia. Fractal Fract. 2021, 5, 67. [Google Scholar] [CrossRef]
- Shen, Y.J.; Yang, S.P.; Xing, H.J. Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative. Acta Phys. Sin. 2012, 61, 110505. [Google Scholar] [CrossRef]
- Duan, J.S.; Zhang, Y.Y. Discriminant and root trajectories of characteristic equation of fractional vibration equation and their effects on solution components. Fractal Fract. 2022, 6, 514. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.-S.; Lan, Y.-J.; Li, M. A Comparative Study of Responses of Fractional Oscillator to Sinusoidal Excitation in the Weyl and Caputo Senses. Fractal Fract. 2022, 6, 692. https://doi.org/10.3390/fractalfract6120692
Duan J-S, Lan Y-J, Li M. A Comparative Study of Responses of Fractional Oscillator to Sinusoidal Excitation in the Weyl and Caputo Senses. Fractal and Fractional. 2022; 6(12):692. https://doi.org/10.3390/fractalfract6120692
Chicago/Turabian StyleDuan, Jun-Sheng, Yu-Jie Lan, and Ming Li. 2022. "A Comparative Study of Responses of Fractional Oscillator to Sinusoidal Excitation in the Weyl and Caputo Senses" Fractal and Fractional 6, no. 12: 692. https://doi.org/10.3390/fractalfract6120692
APA StyleDuan, J.-S., Lan, Y.-J., & Li, M. (2022). A Comparative Study of Responses of Fractional Oscillator to Sinusoidal Excitation in the Weyl and Caputo Senses. Fractal and Fractional, 6(12), 692. https://doi.org/10.3390/fractalfract6120692








