The Effect of a Nonlocal Thermoelastic Model on a Thermoelastic Material under Fractional Time Derivatives
Abstract
1. Introduction
2. Materials and Methods
3. Initial and Boundary Conditions
4. Analytical Method
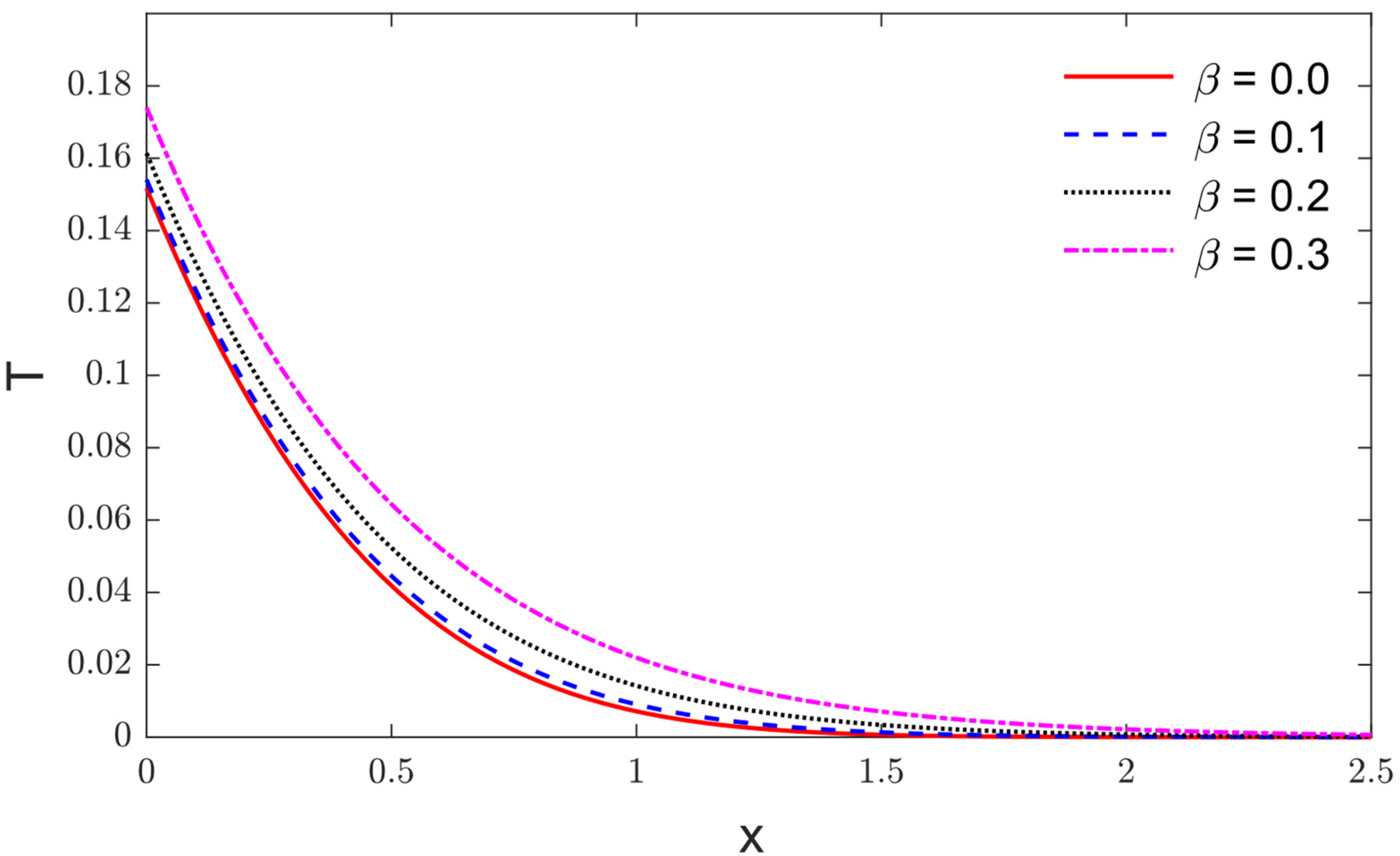
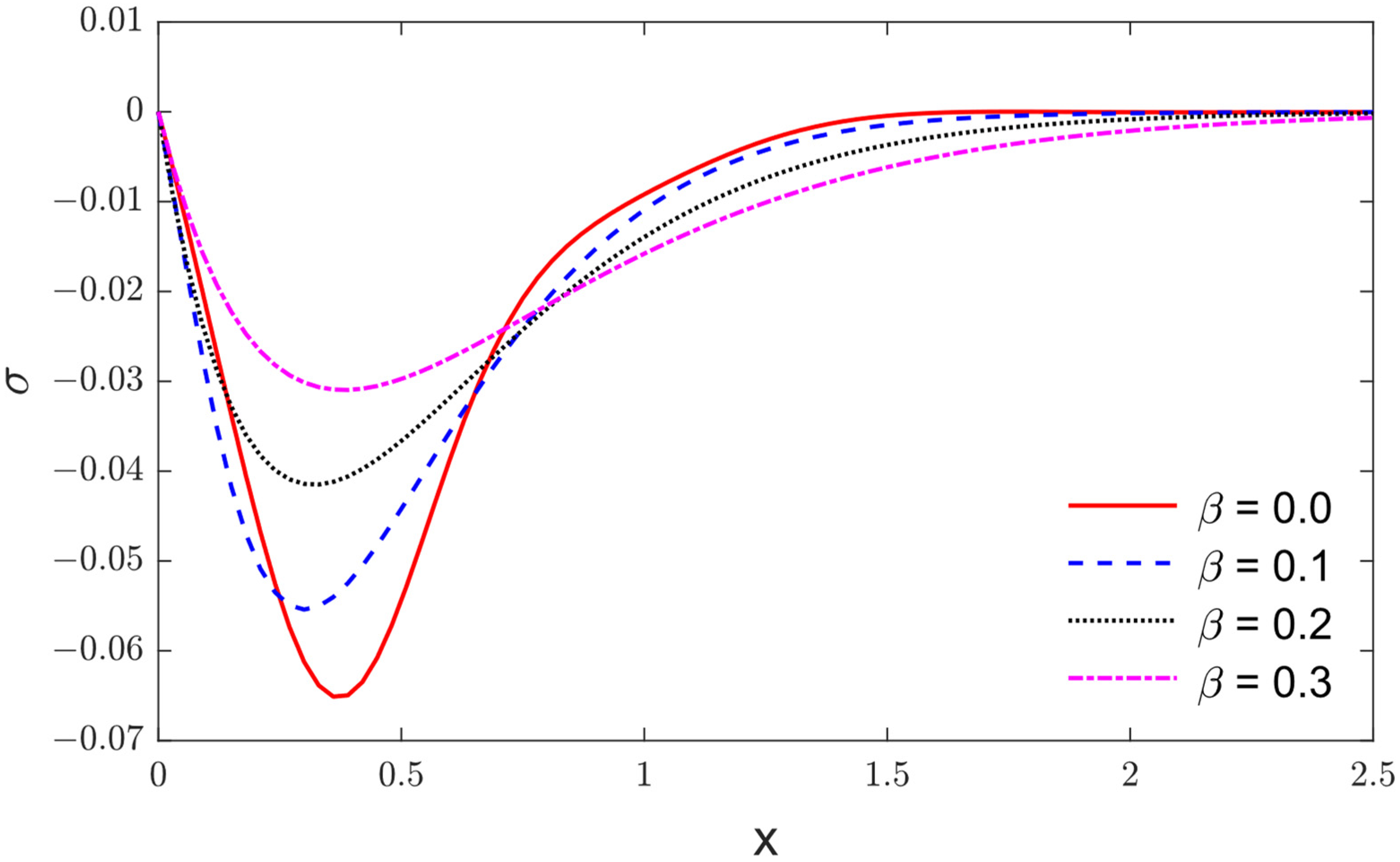
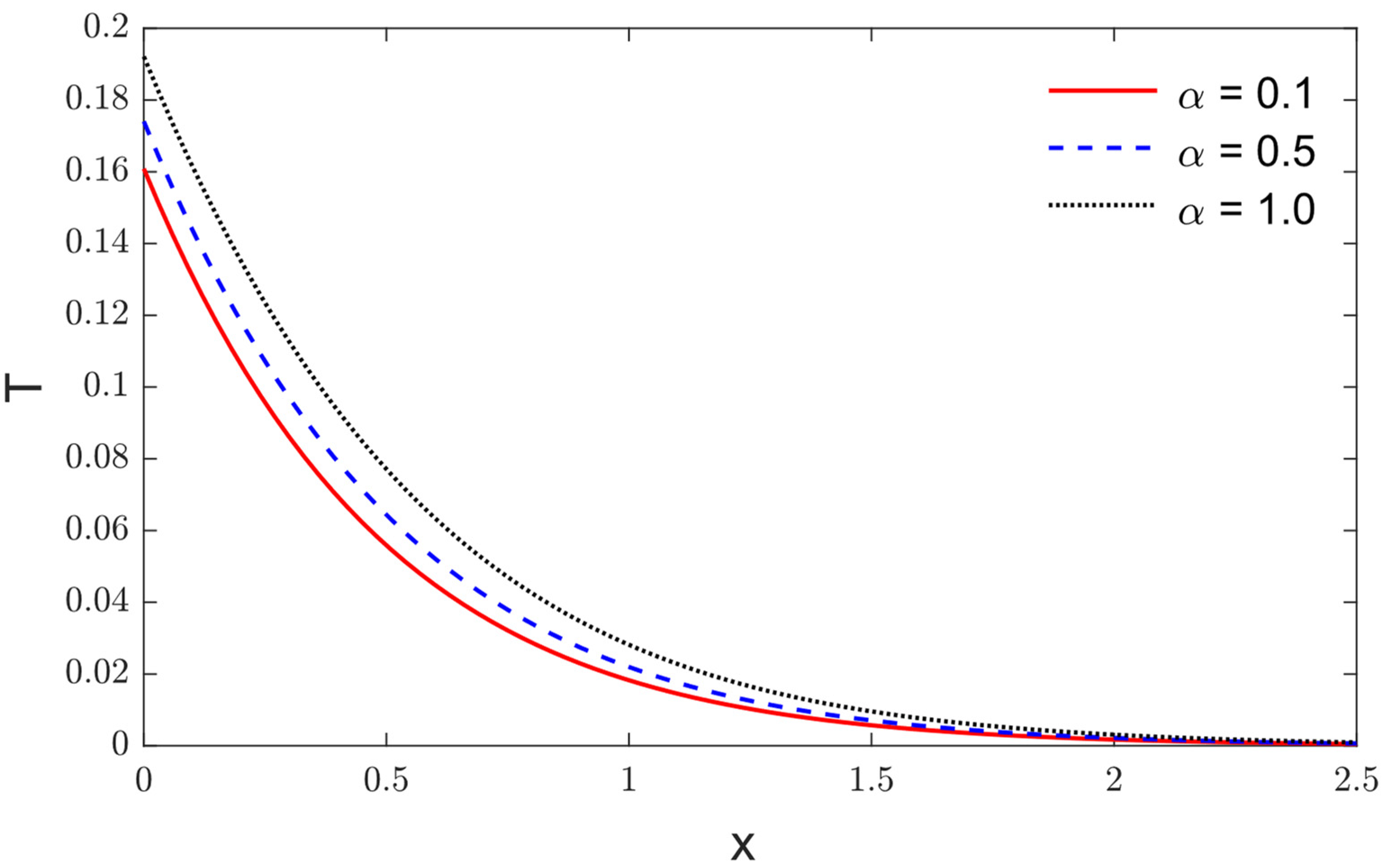
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biot, M.A. Thermoelasticity and Irreversible Thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. On undamped heat waves in an elastic solid. J. Therm. Stress. 1992, 15, 253–264. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of nonlocal thermoelasticity. Int. J. Eng. Sci. 1974, 12, 1063–1077. [Google Scholar] [CrossRef]
- Eringen, A.C. Memory-dependent nonlocal electromagnetic elastic solids and superconductivity. J. Math. Phys. 1991, 32, 787–796. [Google Scholar] [CrossRef]
- Eringen, A.C.; Wegner, J. Nonlocal continuum field theories. Appl. Mech. Rev. 2003, 56, B20–B22. [Google Scholar] [CrossRef]
- Youssef, H.M. Theory of fractional order generalized thermoelasticity. J. Heat Transf. 2010, 132, 1–7. [Google Scholar] [CrossRef]
- Youssef, H.M.; Al-Lehaibi, E.A. Variational principle of fractional order generalized thermoelasticity. Appl. Math. Lett. 2010, 23, 1183–1187. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Karamany, A.S. Fractional order theory of a perfect conducting thermoelastic medium. Can. J. Phys. 2011, 89, 311–318. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El Karamany, A.S. Theory of fractional order in electro-thermoelasticity. Eur. J. Mech. A/Solids 2011, 30, 491–500. [Google Scholar] [CrossRef]
- Ezzat, M.A. Theory of fractional order in generalized thermoelectric MHD. Appl. Math. Model. 2011, 35, 4965–4978. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The effect of fractional time derivative of bioheat model in skin tissue induced to laser irradiation. Symmetry 2020, 12, 602. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach on fractional order theory of thermoelastic diffusion problem for an infinite elastic medium with a spherical cavity. Appl. Math. Model. 2015, 39, 6196–6206. [Google Scholar] [CrossRef]
- Lotfy, K. Analytical solution of fractional order heat equation under the effects of variable thermal conductivity during photothermal excitation of spherical cavity of semiconductor medium. Waves Random Complex Media 2021, 31, 239–254. [Google Scholar] [CrossRef]
- Sarkar, N. Thermoelastic responses of a nonlocal elastic rod due to nonlocal heat conduction. ZAMM Z. Angew. Math. Mech. 2020, 100, e201900252. [Google Scholar] [CrossRef]
- Bachher, M.; Sarkar, N. Nonlocal theory of thermoelastic materials with voids and fractional derivative heat transfer. Waves Random Complex Media 2019, 29, 595–613. [Google Scholar] [CrossRef]
- Sarkar, N.; Mondal, S.; Othman, M.I.A. L–S theory for the propagation of the photo-thermal waves in a semiconducting nonlocal elastic medium. Waves Random Complex Media 2020. [Google Scholar] [CrossRef]
- Sarkar, N. Thermoelastic responses of a finite rod due to nonlocal heat conduction. Acta Mech. 2019, 231, 947–955. [Google Scholar] [CrossRef]
- Lata, P.; Singh, S. Deformation in a nonlocal magneto-thermoelastic solid with hall current due to normal force. Geomach. Eng. 2020, 22, 109–117. [Google Scholar] [CrossRef]
- Bayones, F.S.; Mondal, S.; Abo-Dahab, S.M.; Kilany, A.A. Effect of moving heat source on a magneto-thermoelastic rod in the context of Eringen’s nonlocal theory under three-phase lag with a memory dependent derivative. Mech. Based Des. Struct. Mach. 2021. [Google Scholar] [CrossRef]
- Biswas, S. The propagation of plane waves in nonlocal visco-thermoelastic porous medium based on nonlocal strain gradient theory. Waves Random Complex Media 2021. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Mohammad-Sedighi, H.; Faghidian, S.A.; Shirazi, A.H. Temperature-dependent physical characteristics of the rotating nonlocal nanobeams subject to a varying heat source and a dynamic load. Facta Univ. Ser. Mech. Eng. 2021, 19, 633–656. [Google Scholar] [CrossRef]
- Sheoran, S.S.; Chaudhary, S.; Deswal, S. Thermo-mechanical interactions in a nonlocal transversely isotropic material with rotation under Lord–Shulman model. Waves Random Complex Media 2021. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A.; Vlase, S.; Marin, M. Generalized Thermoelastic Interaction in a Half-Space under a Nonlocal Thermoelastic Model. Mathematics 2022, 10, 2168. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I.; Alshehri, H.; Marin, M. Analytical Solutions of Nonlocal Thermoelastic Interaction on Semi-Infinite Mediums Induced by Ramp-Type Heating. Symmetry 2022, 14, 864. [Google Scholar] [CrossRef]
- Marin, M.; Baleanu, D.; Vlase, S. Effect of microtemperatures for micropolar thermoelastic bodies. Struct. Eng. Mech. 2017, 61, 381–387. [Google Scholar] [CrossRef]
- Marin, M.; Abbas, I.; Kumar, R. Relaxed Saint-Venant principle for thermoelastic micropolar diffusion. Struct. Eng. Mech. 2014, 51, 651–662. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Öchsner, A.; Scutaru, M.L. Motion equation for a flexible one-dimensional element used in the dynamical analysis of a multibody system. Contin. Mech. Thermodyn. 2019, 31, 715–724. [Google Scholar] [CrossRef]
- Alzahrani, F.; Hobiny, A.; Abbas, I.; Marin, M. An eigenvalues approach for a two-dimensional porous medium based upon weak, normal and strong thermal conductivities. Symmetry 2020, 12, 848. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A.; Marin, M. Photo-thermal interactions in a semi-conductor material with cylindrical cavities and variable thermal conductivity. J. Taibah Univ. Sci. 2020, 14, 1369–1376. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int. J. Heat Mass Transf. 2018, 124, 1011–1014. [Google Scholar] [CrossRef]
- Abbas, I.A. Generalized magneto-thermoelasticity in a nonhomogeneous isotropic hollow cylinder using the finite element method. Arch. Appl. Mech. 2009, 79, 41–50. [Google Scholar] [CrossRef]
- Li, Y.; Wei, P.; Zhang, P.; Gao, X. Thermoelastic wave and thermal shock based on dipolar gradient elasticity and fractional-order generalized thermoelasticity. Waves Random Complex Media 2021. [Google Scholar] [CrossRef]
- Li, C.; Tian, X.; He, T. Analytical study of transient thermo-mechanical responses in a fractional order generalized thermoelastic diffusion spherical shell with variable thermal conductivity and diffusivity. Waves Random Complex Media 2021, 31, 1083–1106. [Google Scholar] [CrossRef]
- Kaur, I.; Singh, K. Plane wave in non-local semiconducting rotating media with Hall effect and three-phase lag fractional order heat transfer. Int. J. Mech. Mater. Eng. 2021, 16, 1–16. [Google Scholar] [CrossRef]
- Kaur, I.; Lata, P.; Singh, K. Effect of Hall current in transversely isotropic magneto-thermoelastic rotating medium with fractional-order generalized heat transfer due to ramp-type heat. Indian J. Phys. 2021, 95, 1165–1174. [Google Scholar] [CrossRef]
- Hendy, M.H.; El-Attar, S.I.; Ezzat, M.A. Two-temperature fractional Green–Naghdi of type III in magneto-thermo-viscoelasticity theory subjected to a moving heat source. Indian J. Phys. 2021, 95, 657–671. [Google Scholar] [CrossRef]
- Hammad, H.A.; Aydi, H.; De la Sen, M.; Bueno, A. Solutions of Fractional Differential Type Equations by Fixed Point Techniques for Multivalued Contractions. Complexity 2021, 2021, 5730853. [Google Scholar] [CrossRef]
- Sheoran, D.; Kumar, R.; Punia, B.S.; Kalkal, K.K. Propagation of waves at an interface between a nonlocal micropolar thermoelastic rotating half-space and a nonlocal thermoelastic rotating half-space. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Abouelregal, A.E.; Othman, M.I.A.; Hamza, A.E.; Mansour, F.E.; Kumar, R. Rotating silver nanobeam subjected to ramp-type heating and varying load via Eringen’s nonlocal thermoelastic model. Arch Appl Mech 2022, 92, 1127–1147. [Google Scholar] [CrossRef]
- Ezzat, M.A.; Alsowayan, N.S.; Al-Muhiameed, Z.I.A.; Ezzat, S.M. Fractional modelling of Pennes’ bioheat transfer equation. Heat Mass Transf. /Waerme- Und Stoffuebertragung 2014, 50, 907–914. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abouelregal, A.E. Effect of temperature dependency on constrained orthotropic unbounded body with a cylindrical cavity due to pulse heat flux. J. Therm. Sci. Technol. 2015, 10, JTST0019. [Google Scholar] [CrossRef]
- Das, N.C.; Lahiri, A.; Giri, R.R. Eigenvalue approach to generalized thermoelasticity. Indian J. Pure Appl. Math. 1997, 28, 1573–1594. [Google Scholar]
- Alzahrani, F.S.; Abbas, I.A. Fractional order gl model on thermoelastic interaction in porous media due to pulse heat flux. Geomach. Eng. 2020, 23, 217–225. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. Fractional order thermoelastic wave assessment in a two-dimension medium with voids. Geomach. Eng. 2020, 21, 85–93. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abdalla, A.E.N.N.; Alzahrani, F.S.; Spagnuolo, M. Wave propagation in a generalized thermoelastic plate using eigenvalue approach. J. Therm. Stress. 2016, 39, 1367–1377. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobiny, A.; Abbas, I. The Effect of a Nonlocal Thermoelastic Model on a Thermoelastic Material under Fractional Time Derivatives. Fractal Fract. 2022, 6, 639. https://doi.org/10.3390/fractalfract6110639
Hobiny A, Abbas I. The Effect of a Nonlocal Thermoelastic Model on a Thermoelastic Material under Fractional Time Derivatives. Fractal and Fractional. 2022; 6(11):639. https://doi.org/10.3390/fractalfract6110639
Chicago/Turabian StyleHobiny, Aatef, and Ibrahim Abbas. 2022. "The Effect of a Nonlocal Thermoelastic Model on a Thermoelastic Material under Fractional Time Derivatives" Fractal and Fractional 6, no. 11: 639. https://doi.org/10.3390/fractalfract6110639
APA StyleHobiny, A., & Abbas, I. (2022). The Effect of a Nonlocal Thermoelastic Model on a Thermoelastic Material under Fractional Time Derivatives. Fractal and Fractional, 6(11), 639. https://doi.org/10.3390/fractalfract6110639







