Partially Explore the Differences and Similarities between Riemann-Liouville Integral and Mellin Transform
Abstract
:1. Introduction
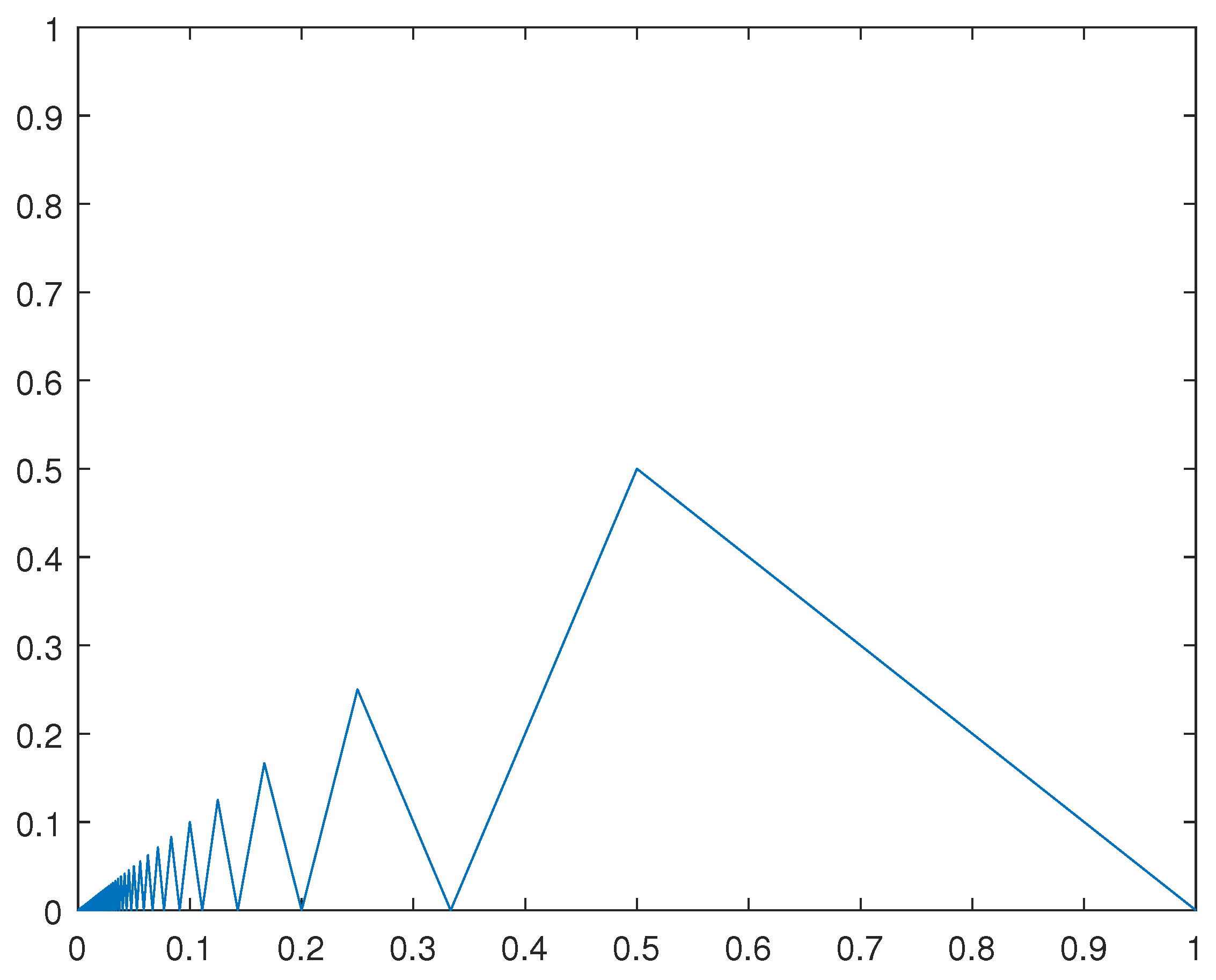
2. Constructing a Continuous and Unbounded Variational Function
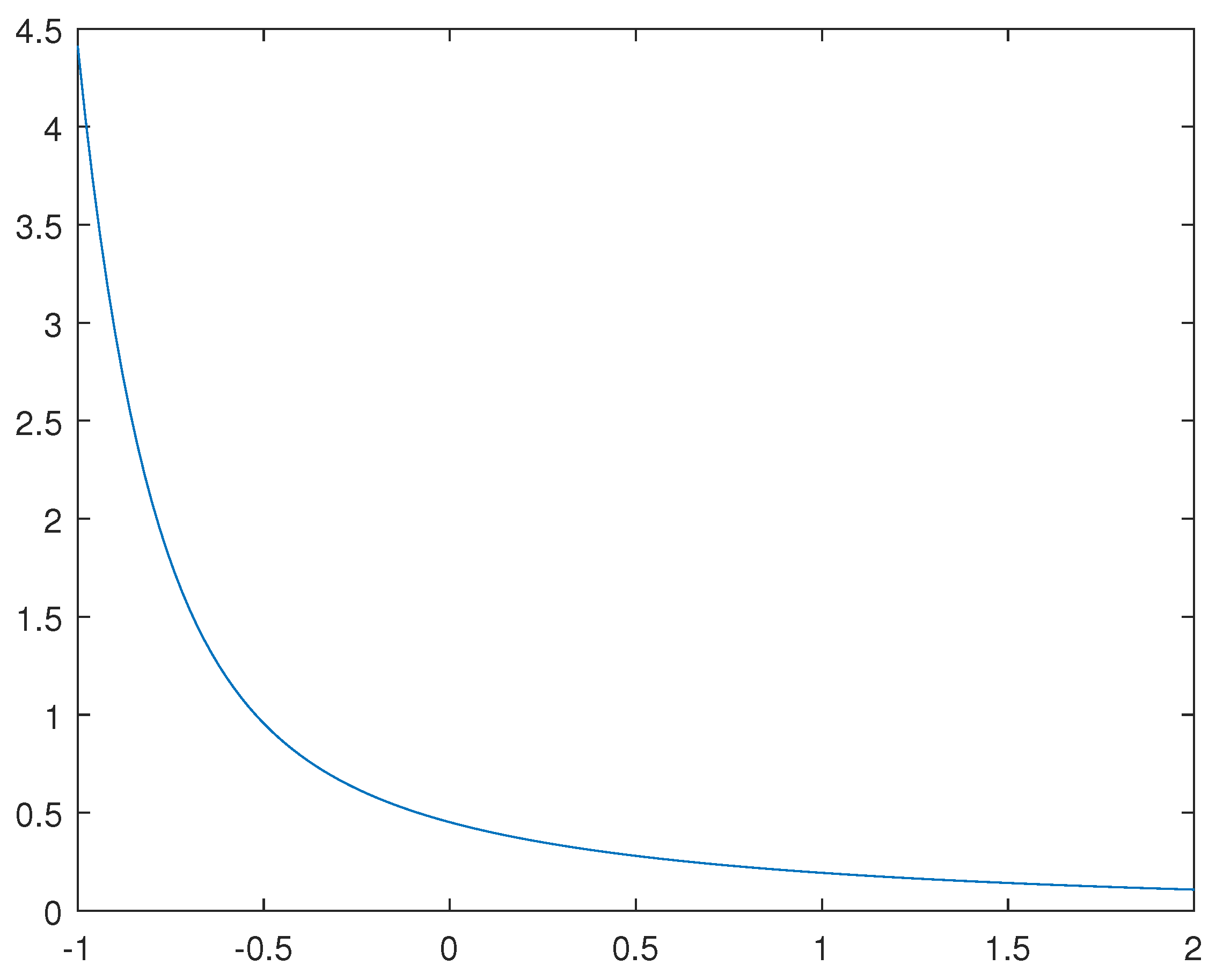
3. Riemann-Liouville Integral of
4. Mellin Transform of
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, W. Cardinality and Fractal Linear Subspace about Fractal Functions. Fractals 2022, 30, 2250146. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Baleanu, D. New relationships connecting a class of fractal objects and fractional integrals in space. Fraction. Calc. Appl. Anal. 2013, 16, 911–936. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Zhang, W.; Gubaidullin, I. Accurate relationships between fractals and fractional integrals: New approaches and evaluations. Fraction. Calc. Appl. Anal. 2017, 20, 1263–1280. [Google Scholar] [CrossRef]
- Xiao, W. Relationship of Upper Box Dimension Between Continuous Fractal Functions and Their Riemann-Liouville Fractional Integral. Fractals 2021, 29, 2150264. [Google Scholar] [CrossRef]
- Gao, H.B.; Liang, Y.S.; Xiao, W. Relationship Between Upper Box Dimension of Continuous Functions and Orders of Weyl Fractional Integral. Fractals 2021, 29, 2150223. [Google Scholar] [CrossRef]
- Noreen, A.; Saleem, I. Solution of fuzzy fractional order differential equations by fractional Mellin transform method. J. Comput. Appl. Math. 2022, 400, 113727. [Google Scholar]
- Falconer, K.J. Fractal Geometry: Mathematical Foundations and Applications, 2nd ed.; John Wiley Sons Ltd.: Hoboken, NJ, USA, 2003; Volume 161, pp. 41–42. [Google Scholar]
- Zheng, W.X.; Wang, S.W. Real Function and Functional Analysis; Higher Education Press: Beijing, China, 1980. [Google Scholar]
- Department of Mathematics, East-China Normal University. Shuxue Fenxi, Volume II, 4th ed.; Higher Education Press: Beijing, China, 2017; pp. 31–40, 192–201. [Google Scholar]
- Wang, J.; Yao, K. Dimension analysis of continuous functions with unbounded variation. Fractals 2017, 25, 1730001. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier B.V.: Amsterdam, The Netherlands, 2006; pp. 18–19, 69. [Google Scholar]
- Liang, Y.S. Box dimensions of Riemann-Liouville fractional integrals of continuous functions of bounded variation. Nonlin. Anal. 2010, 72, 4304–4306. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Xiao, W.; Liang, Y. Partially Explore the Differences and Similarities between Riemann-Liouville Integral and Mellin Transform. Fractal Fract. 2022, 6, 638. https://doi.org/10.3390/fractalfract6110638
Zhou Z, Xiao W, Liang Y. Partially Explore the Differences and Similarities between Riemann-Liouville Integral and Mellin Transform. Fractal and Fractional. 2022; 6(11):638. https://doi.org/10.3390/fractalfract6110638
Chicago/Turabian StyleZhou, Zhibiao, Wei Xiao, and Yongshun Liang. 2022. "Partially Explore the Differences and Similarities between Riemann-Liouville Integral and Mellin Transform" Fractal and Fractional 6, no. 11: 638. https://doi.org/10.3390/fractalfract6110638
APA StyleZhou, Z., Xiao, W., & Liang, Y. (2022). Partially Explore the Differences and Similarities between Riemann-Liouville Integral and Mellin Transform. Fractal and Fractional, 6(11), 638. https://doi.org/10.3390/fractalfract6110638






