A Second-Order Adaptive Grid Method for a Singularly Perturbed Volterra Integrodifferential Equation

Abstract

In this paper, an adaptive grid method for a singularly perturbed Volterra integro-differential equation is studied. Firstly, this problem is discretized by a new second-order finite difference scheme, for which a truncation error analysis is conducted. Then, based on this truncation error bound and the mesh equidistribution principle, we show that there is a mesh that provides an optimal error bound of O(N⁻²), which is robust with respect to the perturbation parameter. Finally, based on an approximation monitor function, an adaptive grid generation algorithm is constructed and some numerical results are given to support our theoretical results.

1. Introduction

In this paper, we consider an adaptive grid method for the following singularly perturbed Volterra integrodifferential equation:

$$\left\{\begin{array}{cc}\hfill & Lu\left(x\right):=\epsilon u^{\prime }\left(x\right)+a\left(x\right)u\left(x\right)+{\int }_0^{x}K(x,s)u\left(s\right)ds=f\left(x\right),x\in (0,1],\hfill \\ \hfill & u\left(0\right)=A,\hfill \end{array}\right.$$

(1)

where $0<\epsilon \ll 1$, A is a given constant, and $a\left(x\right)$, $K(x,s)$, and $f\left(x\right)$ are sufficiently smooth functions, which are independent of the parameter $\epsilon$. It is assumed that there exists a positive constant $\alpha$ such that $a\left(x\right)\ge \alpha >0$. Under these conditions, the problem (1) has a unique solution $u\left(x\right)$ (see [1,2]), which typically exhibits a boundary layer at $x=0$ as $\epsilon \to 0$. Thus, this type of problem is called singularly perturbed Volterra integrodifferential equations (SPVIDEs), which often appear in physics [3], biology [4,5], and other areas [6].

Due to the presence of this perturbation parameter, standard finite difference and finite-element methods on a uniform mesh for (1) may yield inaccurate numerical results. Therefore, some special numerical methods for SPVIDEs have been discussed in studies such as [1,7,8,9,10,11,12,13,14]. Among these methods, the authors in [7,10] developed some layer-adapted mesh methods to solve SPVIDEs. Especially, Yanman and Amiraliyev [1] proposed a new discretization scheme for problem (1), which was almost second-order uniform convergent on the Shishkin mesh.

In addition to the layer-adaptive grid method mentioned above, the adaptive grid method for singularly perturbed convection-diffusion problems has also attracted much attention over the last decade, see [15,16] and the monograph [17]. For the adaptive grid methods of SPVIDEs, Sumit et.al. [18] proposed a first-order uniform convergent adaptive grid method for a nonlinear singularly perturbed Volterra integro-differential equation. To the best of our knowledge, there are few second-order adaptive grid methods for SPVIDEs except for the Richardson extrapolation technique given in [19]. Based on the discretization scheme proposed in [1], the authors in [20] developed an adaptive grid algorithm for a singularly perturbed convection-diffusion equation. However, they did not carry out a convergence analysis. Thus, it is very desirable to construct a second-order adaptive grid method (not a hybrid discretization scheme) for singularly perturbed problems.

Motivated by [1,20], the aim of this paper is to design a new second-order adaptive grid method for a singularly perturbed Volterra integro-differential equation. By virtue of a truncation error analysis, a suitable monitor function is chosen to design an adaptive grid based on the mesh equidistribution principle. Furthermore, we prove that our presented adaptive grid method is second-order uniform-convergent with respect to the perturbation parameter. Finally, several numerical results are given to confirm our theoretical findings.

Notation. Throughout the paper, C denotes a generic positive constant that is independent of $\epsilon$ and the mesh parameter N. It may take different values in different places. For any continuous function $g\left(x\right)$, we use the notation $g_i=g\left(x_i\right)$ and ${\parallel g\parallel }_{\infty }=\underset{x\in [0,1]}{max}\left|g\left(x\right)\right|$.

2. Preliminary Results

We provide the following bounds for the derivatives of $u\left(x\right)$ (see [21,22]), which will be used in later analysis.

Lemma 1.

Assuming $K(x,s)$, $f\left(x\right)$, $a\left(x\right)$ are sufficiently smooth functions and there is a positive constant α such that $a\left(x\right)\ge \alpha >0$, then the solution $u\left(x\right)$ of problem (1) has the following bounds:

$$\begin{array}{c}\hfill |u^{\left(k\right)}\left(x\right)|\le C\left(1+\frac{1}{{\epsilon }^k}{e}^{-\frac{\alpha x}{\epsilon }}\right),x\in [0,1],k=0,1,2.\end{array}$$

(2)

To obtain our numerical discretization scheme, we consider an arbitrary nonuniform mesh ${\overline{\mathsf{\Omega }}}^N\equiv \left\{0=x_0<x_1<\cdots <x_N=1\right\}$, where N is a positive integer. For $i=1,\cdots ,N$, $h_i=x_i-x_{i-1}$ represents the local mesh step.

Similar to reference [1], we provide the construction of our numerical scheme on $\overline{\mathsf{\Omega }}$. By multiplying both sides of the first equation of (1) by ${\phi }_i\left(x\right)=e^{-\frac{a_i(x_i-x)}{\epsilon }}$ and integrating on the interval $[x_{i-1},x_i]$, then multiplying both sides by ${\chi }_i^{-1}{h}_i^{-1}$, the origin problem (1) can be written into the following integral equation:

$${\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}Lu{\phi }_i\left(x\right)dx={\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}f\left(x\right){\phi }_i\left(x\right)dx,$$

(3)

where ${\chi }_i=h_i^{-1}{\int }_{x_{i-1}}^{x_i}{\phi }_i\left(x\right)dx=\frac{1-e^{-a_i{\rho }_i}}{a_i{\rho }_i}$ and ${\rho }_i=\frac{h_i}{\epsilon }$ for $i=1\cdots ,N$.

Furthermore, for the differential part of $Lu$ defined in (1), it follows from the left side of Equation (3) that

$$\begin{array}{c}\hfill \begin{array}{cc}& {\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}\left[\epsilon u^{\prime }\left(x\right)+a\left(x\right)u\left(x\right)\right]{\phi }_i\left(x\right)dx=\epsilon {\theta }_i{D}^{-}{u}_i+a_i{u}_i\hfill \\ & +{\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}[a\left(x\right)-a\left(x_i\right)]{\phi }_i\left(x\right)u\left(x\right)ds,\hfill \end{array}\end{array}$$

(4)

where ${\theta }_i=\frac{a_i{\rho }_i{e}^{-a_i{\rho }_i}}{1-e^{-a_i{\rho }_i}}$ and $D^{-}{u}_i=\frac{u_i-u_{i-1}}{h_i}$.

Next, by using the Newton interpolating formula to $a\left(x\right)$ at points $x_{i-1}$,$x_i$ and substituting it into Equation (4), we have

$$\begin{array}{c}\hfill {\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}\left[\epsilon u^{\prime }\left(x\right)+a\left(x\right)u\left(x\right)\right]{\phi }_i\left(x\right)dx=\epsilon {\theta }_i{D}^{-}{u}_i+\left(a_i+h_i{\delta }_i{D}^{-}{a}_i\right)u_i+R_i^{\left(1\right)},\end{array}$$

(5)

where ${\delta }_i=\frac{a_i{\rho }_i}{1-e^{-a_i{\rho }_i}}-\frac{1}{a_i{\rho }_i}$, $a_i=a\left(x_i\right)$ and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill R_i^{\left(1\right)}& ={\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}\frac{a^{″}\left({\eta }_i\right)}{2}(x-x_{i-1})(x-x_i){\phi }_i\left(x\right)u\left(x\right)dx\hfill \\ & -a_{\overline{x},i}{\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}(x-x_i){\phi }_i\left(x\right)\left({\int }_x^{x_i}{u}^{\prime }\left(s\right)ds\right)dx,{\eta }_i\in [x_{i-1},x_i].\hfill \end{array}\end{array}$$

(6)

Similarly, the right hand of (3) can be written as follows:

$$\begin{array}{c}\hfill {\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}f\left(x\right){\phi }_i\left(x\right)dx={\overline{f}}_i+R_i^{\left(2\right)},\end{array}$$

(7)

where $\overline{f_i}=f_i+h_i{\delta }_i{D}^{-}{f}_i$ and

$$\begin{array}{c}\hfill R_i^{\left(2\right)}=\frac{1}{2}{\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}{f}^{″}\left({\gamma }_i\right)(x-x_{i-1})(x-x_i){\phi }_i\left(x\right)dx,{\gamma }_i\in [x_{i-1},x_i].\end{array}$$

(8)

Meanwhile, for the integral part of $Lu$, by using the trapezoidal formula with basis function ${\phi }_i\left(x\right)$ and remainder term in integral form, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\chi }_i^{-1}& h_i^{-1}{\int }_{x_{i-1}}^{x_i}{\phi }_i\left(x\right)\left({\int }_0^{x}K(x,s)u\left(s\right)ds\right)dx\hfill \\ & =\sum _{j=0}^i{\hslash }_j{\kappa }_{i,j}{u}_j+R_i^{\left(3\right)}+R_i^{\left(4\right)},\hfill \end{array}\end{array}$$

(9)

where

$$\begin{array}{ccc}& & {\kappa }_{i,j}=\kappa (x_i,x_j)=K(x_i,x_j)+h_i{\delta }_i\frac{\partial K}{\partial x}(x_i,x_j),\hfill \\ & & {\hslash }_0=\frac{h_1}{2},{\hslash }_j=\frac{h_j+h_{j+1}}{2},j=1,\cdots ,N-1,{\hslash }_N=\frac{h_N}{2},\hfill \\ & & R_i^{\left(3\right)}={\chi }_i^{-1}{h}_i^{-1}{\int }_{x_{i-1}}^{x_i}dx{\phi }_i\left(x\right){\int }_{x_{i-1}}^{x_i}\frac{d^2}{d{\xi }^2}\left({\int }_0^{\xi }K(\xi ,s)u\left(s\right)ds\right)(\xi -x)d\xi ,\hfill \\ & & R_i^{\left(4\right)}=\frac{1}{2}\sum _{j=1}^i{\int }_{x_{j-1}}^{x_j}(x_j-\xi )(x_{j-1}-\xi )\frac{d^2}{d{\xi }^2}\kappa (x_i,\xi )u\left(\xi \right)d\xi .\hfill \end{array}$$

Finally, neglecting the truncation errors given in (5), (7), and (9), we obtain the finite difference scheme of problem (1) as follows:

$$\left\{\begin{array}{c}{L}^N{u}_i^N\equiv \epsilon {\theta }_i{D}^{-}{u}_i^N+{\overline{a}}_i{u}_i^N+{\displaystyle \sum _{j=0}^i}{\hslash }_j{\kappa }_{i,j}{u}_j^N={\overline{f}}_i,1\le i\le N,\hfill \\ u_0^N=A,\hfill \end{array}\right.$$

(10)

where $u_i^N$ is an approximation solution of $u\left(x\right)$ at $x=x_i$ and ${\overline{a}}_i=a_i+(D^{-}{a}_i+K_{ii})h_i{\delta }_i$.

Next, we provide a lemma (see lemma 4.1 in [22]), which will be used in the proof of Lemma 3.

Lemma 2.

Consider the following difference problem:

$${\ell }_N{v}_i=\epsilon v_{\overline{t},i}+a_i{v}_i=F_i,i=0,1,2,\cdots ,N_0.$$

(11)

$$v_0=A.$$

(12)

Let $|F_i|\le {\mathcal{F}}_i$ and ${\mathcal{F}}_i$ be nondecreasing function. Then the solution of (11) and (12) satisfies

$$|v_i|\le |A|+{\alpha }^{-1}{\mathcal{F}}_i,i=0,1,2,\cdots ,N_0.$$

(13)

In order to derive the convergence result of the numerical solution ${\left\{u_i^N\right\}}_{i=0}^N$, we provide the following stability result.

Lemma 3.

Assume that there is a constant ${\alpha }_{*}$ such that ${\overline{a}}_i+{\hslash }_i\kappa (x_i,x_i)\ge {\alpha }_{*}>0$, $i=1,\cdots ,N.$ Then, we have

$$\underset{0\le i\le N}{max}\left|u_i^N\right|\le C\left(\underset{0\le i\le N}{max}\left|{\overline{f}}_i\right|+A\right).$$

(14)

Proof. 

For each $u_i^N$, $i=1,\cdots ,N$, we first define the following difference operator:

$${\ell }^N{u}_i^N:=\epsilon {\theta }_i{D}^{-}{u}_i^N+\left({\overline{a}}_i+{\hslash }_i{\kappa }_{i,i}\right)u_i^N.$$

(15)

Then, by using Lemma 2, we have

$$|u_i^N|\le {\alpha }_{*}^{-1}\left(|u_0^N|+|{\ell }^N{u}_i^N|\right).$$

(16)

It follows from the first equation of (10) that

$${\ell }^N{u}_i^N=L^N{u}_i^N-\sum _{j=0}^{i-1}{\hslash }_j{\kappa }_{i,j}{u}_j^N.$$

(17)

Furthermore, since $\kappa (x,s)$ is bounded, it yields

$$|{\ell }^N{u}_i^N|\le \left|{\overline{f}}_i\right|+C\sum _{j=0}^{i-1}{\hslash }_j\left|u_j^N\right|,1\le i\le N.$$

(18)

Combining with (16), we have

$$|u_i^N|\le \left(|u_0^N|+{\alpha }_{*}^{-1}{\parallel f\parallel }_{\infty }\right)+{\alpha }_{*}^{-1}\left(C\sum _{j=1}^{i-1}{\hslash }_j\left|u_j^N\right|\right).$$

(19)

Finally, applying Gronwall’s inequality to (19) yields

$$\underset{0\le i\le N}{max}\left|u_i^N\right|\le (A+{\alpha }_{*}^{-1}{\parallel f\parallel }_{\infty })exp\left({\alpha }_{*}^{-1}C\sum _{j=1}^{i-1}{\hslash }_j\right),$$

(20)

which completes the proof.    □

3. Truncation Error Analysis

Let $z_i=u_i^N-u_i$ be the error at $x_i$ in the computed solution. Then,

$$\left\{\begin{array}{c}{L}^N{z}_i=R_i,i=1,\cdots ,N,\hfill \\ z_0=0,\hfill \end{array}\right.$$

(21)

where $R_i=R_i^{\left(1\right)}+R_i^{\left(2\right)}+R_i^{\left(3\right)}+R_i^{\left(4\right)}$ is the local truncation error at nodal $x_i$.

Lemma 4.

Assuming $K(x,s)$, $f\left(x\right)$, $a\left(x\right)$ are sufficiently smooth functions and there is a positive constant α such that $a\left(x\right)\ge \alpha >0$, the truncation error $R_i$ has the following bound:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{1\le i\le N}{max}\left|R_i\right|& \le C\left[\underset{1\le i\le N}{max}{h}_i^2+\underset{1\le i\le N}{max}{h}_i{\int }_{x_{i-1}}^{x_i}\left|u^{\prime }\left(x\right)\right|dx+\underset{1\le j\le N}{max}{\left({\int }_{x_{j-1}}^{x_j}{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}dx\right)}^2\right].\hfill \end{array}\end{array}$$

Proof. 

From Lemma 3.1 of [1], we can easily obtain

$$\begin{array}{c}\hfill |R_i^{\left(1\right)}|+|R_i^{\left(2\right)}|+|R_i^{\left(3\right)}|\le C{h}_i\left(h_i+{\int }_{x_{i-1}}^{x_i}\left|u^{\prime }\left(x\right)\right|dx\right).\end{array}$$

(22)

For $R_i^{\left(4\right)}$, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill |R_i^{\left(4\right)}|& \le C\left(\sum _{j=1}^i{h}_j^3+\sum _{j=1}^i{\int }_{x_{j-1}}^{x_j}(x_j-\xi )(\xi -x_{j-1})\left|u^{\prime }\left(\xi \right)+u^{″}\left(\xi \right)\right|d\xi \right)\hfill \\ & \le C\underset{1\le j\le N}{max}{h}_j^2+\underset{1\le j\le N}{max}{\int }_{x_{j-1}}^{x_j}\left|u^{\prime }\left(\xi \right)\right|(\xi -x_{j-1})d\xi \hfill \\ & +\underset{1\le j\le N}{max}{\int }_{x_{j-1}}^{x_j}{\epsilon }^{-2}{e}^{-\frac{\alpha x}{\epsilon }}(\xi -x_{j-1})d\xi \hfill \\ & \le C\underset{1\le j\le N}{max}{h}_j^2+\underset{1\le j\le N}{max}{h}_j{\int }_{x_{j-1}}^{x_j}\left|u^{\prime }\left(x\right)\right|dx+\underset{1\le j\le N}{max}{\left({\int }_{x_{j-1}}^{x_j}{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}dx\right)}^2,\hfill \end{array}\end{array}$$

(23)

where we have used the fact that

$$\begin{array}{c}\hfill {\int }_a^b\varphi \left(s\right)(s-a)ds\le \frac{1}{2}{\left\{{\int }_a^b\varphi {\left(s\right)}^{1/2}ds\right\}}^2\end{array}$$

(24)

holds true for any positive monotonically decreasing function $\varphi \left(s\right)$ on $[a,b]$. Furthermore, combining (22) and (23), we complete the proof of this lemma.    □

4. Adaptive Grid and Convergence Analysis

Monitor functions are widely used by many researchers (see, e.g., [18,23,24,25,26,27]) to design an adaptive grid algorithm that produces layer-resolving meshes in solving singularly perturbed problems. As is stated in [26], if the monitor functions contain the exact solution of the considered problem, these approaches are called semi-discretization adaptive grid methods. For this purpose, we also study the semi-discretization adaptive grid method for problem (1). Based on the truncation error estimation given in Lemma 4, we choose the following monitor function $M(x,u(x\left)\right)$:

$$M(x,u\left(x\right))=1+|u^{\prime }\left(x\right)|+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }},$$

(25)

which is used to construct a grid ${\left\{x_i\right\}}_{i=0}^N$ satisfying

$${\int }_{x_{j-1}}^{x_j}M(x,u\left(x\right))dx=\frac{1}{N}{\int }_0^{1}M(x,u\left(x\right))dx,i=1,2,\cdots ,N.$$

(26)

Here, Equation (26) is called the mesh equidistribution principle. It is worth noting that the existence of the grid ${\left\{x_i\right\}}_{i=0}^N$ satisfying (26) can be found in [15], Theorem 3.1.

Lemma 5.

Let ${\overline{\mathsf{\Omega }}}^N={\left\{x_i\right\}}_{i=0}^N$ be a grid satisfying (26). Then, for $i=1,\cdots ,N$, we have

$$\begin{array}{ccc}& & h_i\le C{N}^{-1},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}& & {\int }_{x_{i-1}}^{x_i}\left|u^{\prime }\left(x\right)\right|dx\le C{N}^{-1},\hfill \end{array}$$

(28)

$$\begin{array}{ccc}& & {\int }_{x_{i-1}}^{x_i}{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}dx\le C{N}^{-1}.\hfill \end{array}$$

(29)

Proof. 

It follows from Lemma 1 that

$$\begin{array}{cc}\hfill & {\int }_0^1\left(1+|u^{\prime }\left(x\right)|+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}\right)dx\hfill \\ & \le C{\int }_0^1\left(1+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{\epsilon }}+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}\right)dx\hfill \\ & \le C{\int }_0^1\left(1+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{\epsilon }}\right)dx\hfill \\ & =C\left(1+\frac{1}{\alpha }\left(1-e^{-\frac{\alpha }{\epsilon }}\right)\right)\hfill \\ & \le C.\hfill \end{array}$$

(30)

Then, based on the mesh equidistribution principle (26), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill h_i& =x_i-x_{i-1}\hfill \\ & \le {\int }_{x_{i-1}}^{x_i}\left(1+|u^{\prime }\left(x\right)|+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}\right)dx\hfill \\ & =\frac{1}{N}{\int }_0^1\left(1+|u^{\prime }\left(x\right)|+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}\right)dx\hfill \\ & \le C{N}^{-1}.\hfill \end{array}\end{array}$$

(31)

Furthermore, by (25) and (26), one has

$$\begin{array}{c}\hfill \begin{array}{cc}{\int }_{x_{i-1}}^{x_i}\left|u^{\prime }\left(x\right)\right|dx\hfill & <{\int }_{x_{i-1}}^{x_i}\left(1+|u^{\prime }\left(x\right)|+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}\right)dx\hfill \\ & \le \frac{1}{N}{\int }_0^1\left(1+|u^{\prime }\left(x\right)|+{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}\right)dx\hfill \\ & \le C{N}^{-1}.\hfill \end{array}\end{array}$$

(32)

Similarly, we can prove (). The proof is completed.    □

Finally, based on the above preliminary results, we can derive the main theorem about the convergence analysis of presented scheme (10) on an adaptive grid ${\overline{\mathsf{\Omega }}}^N$.

Theorem 1.

Let $u_i$ be the exact solution of problem (1) and $u_i^N$ be the solution of (10) at the adaptive grid ${\overline{\mathsf{\Omega }}}^N={\left\{x_i\right\}}_{i=0}^N$ satisfying (26). Then, we have

$$\underset{0\le i\le N}{max}\left|u_i^N-u\left(x_i\right)\right|\le C{N}^{-2}.$$

(33)

Proof. 

Firstly, applying Lemma 2 to (21) yields

$$\underset{0\le i\le N}{max}\left|u_i^N-u\left(x_i\right)\right|\le C\underset{1\le i\le N}{max}\left|R_i\right|.$$

(34)

Then, it follows from Lemmas 4 and 5 that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{0\le i\le N}{max}\left|u_i^N-u\left(x_i\right)\right|& \le C\left[\underset{1\le i\le N}{max}{h}_i^2+\underset{1\le i\le N}{max}{h}_i{\int }_{x_{i-1}}^{x_i}\left|u^{\prime }\left(x\right)\right|dx\right.\hfill \\ & \left.+\underset{1\le i\le N}{max}{\left({\int }_{x_{i-1}}^{x_i}{\epsilon }^{-1}{e}^{-\frac{\alpha x}{2\epsilon }}dx\right)}^2\right]\hfill \\ & \le C{N}^{-2},\hfill \end{array}\end{array}$$

(35)

which completes the proof.    □

5. Numerical Results and Discussion

In Section 5.1, we shall first provide a grid generation algorithm based on the equidistribution of the monitor function (25). Numerical results and discussion are presented by two test examples in Section 5.2.

5.1. Mesh Generation Algorithm

Since the monitor function (25) includes the first-order derivative of the exact solution $u\left(x\right)$, it is difficult to obtain an adaptive grid ${\left\{x_i\right\}}_{i=0}^N$ by equidistributing the monitor function (25). In practical computation, we choose the following approximating monitor function

$${\tilde{M}}_i=1+\left|D^{-}{u}_i^N\right|+{\epsilon }^{-1}{e}^{-\frac{\alpha x_i}{2\epsilon }},i=1,\cdots ,N.$$

(36)

Therefore, the key problem of our adaptive grid method is to find ${\left\{\left(x_i,u_i^N\right)\right\}}_{i=0}^N$, with $u_i^N$ calculated from the discretization scheme ref. to Equation (10) on an adaptive grid ${\left\{x_i\right\}}_{i=0}^N$, such that

$$\begin{array}{c}\hfill h_i{\tilde{M}}_i=\frac{1}{N}\sum _{j=1}^N{h}_j{\tilde{M}}_j\mathrm{for}i=1,\cdots ,N.\end{array}$$

(37)

Finally, in order to obtain a grid ${\left\{x_i\right\}}_{i=0}^N$ and the corresponding numerical solution ${\left\{u_i^N\right\}}_{i=0}^N$ satisfying (37), we provide the following specific mesh-generation Algorithm 1, which is similar to the algorithm given in [25], Section 5.1.  

Algorithm 1: Adaptive grid algorithm

Step 1. Provide an initial uniform mesh ${\overline{\mathsf{\Omega }}}^{N,\left(0\right)}={\left\{x_i^{\left(0\right)}\right\}}_{i=0}^N$ with N mesh intervals. Choose a constant $C_0>1$ that controls the algorithm terminates. Step 2. For a given grid ${\overline{\mathsf{\Omega }}}^{N,\left(k\right)}={\left\{x_i^{\left(k\right)}\right\}}_{i=0}^N$, $k=0,1,\cdots$ and the corresponding computed solution ${\left\{u_i^{N,\left(k\right)}\right\}}_{i=0}^N$, set $h_i^{\left(k\right)}=x_i^{\left(k\right)}-x_{i-1}^{\left(k\right)}$ for each i and ${\mathsf{\Phi }}_0^{\left(k\right)}=0$ and ${\mathsf{\Phi }}_i^{\left(k\right)}={\displaystyle \sum _{j=1}^i}{h}_j^{\left(k\right)}{\tilde{M}}_j^{\left(k\right)}$ for $i=1,\cdots ,N$. Step 3. Define $C^{\left(k\right)}:=\frac{N}{{\mathsf{\Phi }}_N^{\left(k\right)}}\underset{1\le i\le N}{max}{h}_i^{\left(k\right)}{\tilde{M}}_i^{\left(k\right)}$. If $C^{\left(k\right)}\le C_0$ holds true, then go to Step 5. Otherwise go to Step 4. Step 4. For $i=0,1,\cdots ,N$, let $Y_i^{\left(k\right)}=i{\mathsf{\Phi }}_N^{\left(k\right)}/N$ and ${\varphi }^{\left(k\right)}\left(s\right)$ be a linear interpolation function through knots $\left({\mathsf{\Phi }}_i^{\left(k\right)},x_i^{\left(k\right)}\right)$. Then, generate a new mesh ${\overline{\mathsf{\Omega }}}^{N,(k+1)}={\left\{x_i^{(k+1)}\right\}}_{i=0}^N$ by $x_i^{(k+1)}={\varphi }^{\left(k\right)}\left(Y_i^{\left(k\right)}\right)$ for $i=0,1,\cdots ,N$. Let $k=k+1$ and return to Step 2. Step 5. Take ${\overline{\mathsf{\Omega }}}^{N,*}={\overline{\mathsf{\Omega }}}^{N,(k+1)}$ as the final calculation mesh and ${\left\{u_i^{N,*}\right\}}_{i=0}^N={\left\{u_i^{N,(k+1)}\right\}}_{i=0}^N$ as the corresponding numerical solution. Then, stop iteration process.

5.2. Numerical Experiments and Discussion

Example 1. The first test problem follows [1] is given by:

$$\begin{array}{cc}\hfill & \epsilon u^{\prime }+2u-{\int }_0^x(x-s)e^{1-xs}u\left(s\right)ds=e^x-x,x\in (0,1],\hfill \\ \hfill & u\left(0\right)=1.\hfill \end{array}$$

Since the exact solution of this problem is not available, the maximum errors and the convergence rates can be evaluated as follows:

$$\begin{array}{ccc}& & E_{\epsilon }^N=\underset{0\le i\le N}{max}|u_i^N-u_i^{2N}|,\hfill \end{array}$$

(38)

$$\begin{array}{ccc}& & r_{\epsilon }^N={log}_2\left(\frac{E_{\epsilon }^N}{E_{\epsilon }^{2N}}\right),\hfill \end{array}$$

(39)

where $u_i^N$ is the numerical solution calculated on an adaptive grid ${\overline{\mathsf{\Omega }}}^N={\left\{x_i\right\}}_{i=0}^N$ and $u_i^{2N}$ is the corresponding approximate solution on the mesh ${\overline{\mathsf{\Omega }}}^{2N}$, which is defined by

$$\begin{array}{c}\hfill {\overline{\mathsf{\Omega }}}^{2N}=\left\{x_{\frac{i}{2}}:i=0,1,\cdots ,2N\right\}\mathrm{with}{x}_{i+\frac{1}{2}}=\frac{x_i+x_{i+1}}{2},x_i\in {\overline{\mathsf{\Omega }}}^N,i=0,1,\cdots ,N-1.\end{array}$$

Here, we choose $C_0=1.5$, $\alpha =1$ and apply the presented adaptive grid method to solve Example 1 with different values of $\epsilon$ and N. The errors and rates of convergence for the numerical solution are displayed in Table 1. Meanwhile, in order to illustrate the computational efficiency of our presented adaptive grid algorithm, Table 1 also lists the number of iterations $Iter$. Furthermore, to compare the performance of the presented adaptive mesh with the Shishkin mesh (S-Mesh) and the method given in [20], some numerical results are given in Table 2. The numerical results of Shishkin mesh approach is come from [1].

Table 1. Numerical results of our presented adaptive grid method for Example 1.

$\mathit{\epsilon }$		$\mathit{N}=64$	$\mathit{N}=128$	$\mathit{N}=256$	$\mathit{N}=512$	$\mathit{N}=1024$	$\mathit{N}=2048$
${10}^{-1}$	$E_{\epsilon }^N$	$1.69\times {10}^4$	$4.37\times {10}^{-5}$	$1.11\times {10}^{-5}$	$2.80\times {10}^{-6}$	$7.04\times {10}^{-7}$	$1.76\times {10}^{-7}$
	$r_{\epsilon }^N$	1.95	1.98	1.99	1.99	2.00	-
	$Iter$	1	1	1	1	1	1
${10}^{-2}$	$E_{\epsilon }^N$	$1.74\times {10}^{-4}$	$5.77\times {10}^{-5}$	$1.68\times {10}^{-5}$	$4.32\times {10}^{-6}$	$1.13\times {10}^{-6}$	$2.90\times {10}^{-7}$
	$r_{\epsilon }^N$	1.60	1.78	1.96	1.93	1.97	-
	$Iter$	2	2	1	1	1	1
${10}^{-3}$	$E_{\epsilon }^N$	$1.38\times {10}^{-4}$	$3.99\times {10}^{-5}$	$1.16\times {10}^{-5}$	$3.63\times {10}^{-6}$	$1.61\times {10}^{-6}$	$3.45\times {10}^{-7}$
	$r_{\epsilon }^N$	1.79	1.78	1.69	1.64	1.75	-
	$Iter$	3	2	2	2	2	1
${10}^{-4}$	$E_{\epsilon }^N$	$1.30\times {10}^{-4}$	$3.73\times {10}^{-5}$	$1.00\times {10}^{-5}$	$2.53\times {10}^{-6}$	$6.90\times {10}^{-7}$	$1.91\times {10}^{-7}$
	$r_{\epsilon }^N$	1.80	1.89	1.99	1.87	1.85	-
	$Iter$	3	3	2	2	3	2
${10}^{-5}$	$E_{\epsilon }^N$	$1.29\times {10}^{-4}$	$3.84\times {10}^{-5}$	$9.61\times {10}^{-6}$	$2.51\times {10}^{-6}$	$6.33\times {10}^{-7}$	$1.59\times {10}^{-7}$
	$r_{\epsilon }^N$	1.75	1.99	1.94	1.99	1.99	-
	$Iter$	4	4	3	3	2	2
${10}^{-6}$	$E_{\epsilon }^N$	$1.39\times {10}^{-4}$	$3.56\times {10}^{-5}$	$9.85\times {10}^{-6}$	$2.44\times {10}^{-6}$	$6.28\times {10}^{-7}$	$1.58\times {10}^{-7}$
	$r_{\epsilon }^N$	1.97	1.85	2.01	1.96	1.99	-
	$Iter$	5	4	4	3	3	3

Table 2. Comparison of numerical results with the other methods for Example 1.

N	$\mathit{\epsilon }=2^{-12}$			$\mathit{\epsilon }=2^{-24}$
	S-Mesh [1]	Method [20]	Our Method	S-Mesh [1]	Method [20]	Our Method
64	$4.90\times {10}^{-2}$	$0.4\times {10}^{-4}$	$1.31\times {10}^{-4}$	$5.52\times {10}^{-2}$	$0.4\times {10}^{-4}$	$1.36\times {10}^{-4}$
	1.81	1.92	1.74	1.82	2.03	1.95
128	$1.37\times {10}^{-2}$	$1.05\times {10}^{-5}$	$3.94\times {10}^{-5}$	$1.56\times {10}^{-2}$	$0.97\times {10}^{-5}$	$3.53\times {10}^{-5}$
	1.84	1.87	2.01	1.86	1.97	1.95
256	$3.90\times {10}^{-3}$	$2.85\times {10}^{-6}$	$9.80\times {10}^{-6}$	$4.31\times {10}^{-3}$	$2.47\times {10}^{-6}$	$9.11\times {10}^{-6}$
	1.93	1.79	1.84	1.93	2.04	1.88
512	$1.02\times {10}^{-3}$	$0.82\times {10}^{-6}$	$2.74\times {10}^{-6}$	$1.13\times {10}^{-3}$	$0.6\times {10}^{-6}$	$2.48\times {10}^{-6}$
	1.98	1.65	1.81	1.99	1.99	2.07
1024	$2.60\times {10}^{-4}$	$2.62\times {10}^{-7}$	$7.81\times {10}^{-7}$	$2.84\times {10}^{-4}$	$1.51\times {10}^{-7}$	$5.91\times {10}^{-7}$

It can be observed from Table 1 that the numerical results obtained by the presented adaptive grid method has high accuracy and second-order convergence rate, which supports the theoretical result given in Theorem 1. Moreover, it is shown from the number of iteration $Iter$ that the above grid generation algorithm is also very efficient. From Table 2, we can see that the discretization scheme (10) computed on an adaptive mesh is more accurate and efficient than that computed on the Shishkin mesh. Since the monitor function in [20] is different from the monitor function in this paper, the results obtained by using the method in [20] may be better than our results. However, it is difficult to get the convergence analysis in [20].

In addition, in order to help readers have a deep understanding of adaptive grid method, Figure 1a, which should be read from bottom to top, directly reflects the moving process of the adaptive mesh for $\epsilon ={10}^{-4}$ and $N=64$. Meanwhile, Figure 1b provides the corresponding graph of numerical solution. Obviously, it is shown that the solution of the test problem has a boundary layer at $x=0$, which is also clearly reflected in Figure 1.

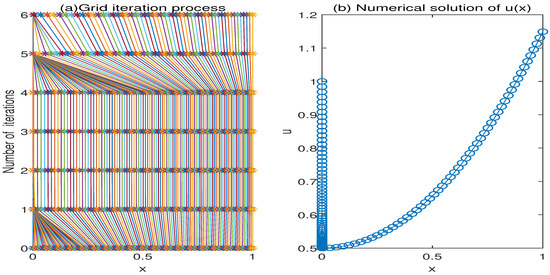
Figure 1. Evolution of the adaptive mesh and numerical solution of Example 1 with $\epsilon ={10}^{-4}$ and $N=64$. (a) Grid iteration process, (b) Numerical solution of $u\left(x\right)$.

Example 2. The second test example in [1] is

$$\begin{array}{ccc}& & \epsilon u^{\prime }+u+{\int }_0^{x}xu\left(s\right)ds=-\frac{\epsilon }{(1+x^2)}+\frac{1}{1+x}+x\epsilon \left(1-e^{-\frac{x}{\epsilon }}\right)+xln(1+x),0<x\le 1,\hfill \\ & & u\left(0\right)=2\hfill \end{array}$$

with the analytic solution $u\left(x\right)=e^{-\frac{x}{\epsilon }}+\frac{1}{1+x}.$ Then, the maximum point-wise errors are calculated by

$$\begin{array}{c}\hfill E_{\epsilon }^N=\underset{0\le i\le N}{max}\left|u_i^N-u\left(x_i\right)\right|.\end{array}$$

The rates of convergence are computed by using Equation (38). In order to solve this test Example 2 by using our presented adaptive grid method, we first choose $C_0=1.1$ and $\alpha =1$. Then, Table 3 provides the results obtained using our presented adaptive grid method for $\epsilon ={10}^{-2k},k=1,2,3,4,$ and $N=64,128,256,512,1024,2048$. In addition, the comparison of numerical results with Shishkin mesh is listed in Table 4. For smaller values of $\epsilon$, one can see that the convergence rates of the presented adaptive grid are close to 2. For larger values of N, the number of iterations $Iter$ of our adaptive grid generation given in Section 5.1 is also very small. Figure 2 provides the evolution of the above mesh-generation algorithm and the corresponding graph of numerical solution with $\epsilon ={10}^{-4}$, $N=64$. It is shown that the numerical solution of example 2 has a boundary lay at $x=0$.

Table 3. Numerical results of our presented adaptive grid method for Example 2.

$\mathit{\epsilon }$		$\mathit{N}=64$	$\mathit{N}=128$	$\mathit{N}=256$	$\mathit{N}=512$	$\mathit{N}=1024$	$\mathit{N}=2048$
${10}^{-2}$	$E_{\epsilon }^N$	$3.99\times {10}^{-4}$	$1.41\times {10}^{-4}$	$4.21\times {10}^{-5}$	$1.10\times {10}^{-5}$	$2.93\times {10}^{-6}$	$7.53\times {10}^{-7}$
	$r_{\epsilon }^N$	1.51	1.75	1.93	1.92	1.96	-
	$Iter$	2	2	2	1	1	1
${10}^{-4}$	$E_{\epsilon }^N$	$8.93\times {10}^{-5}$	$2.23\times {10}^{-5}$	$5.36\times {10}^{-6}$	$1.34\times {10}^{-6}$	$4.15\times {10}^{-7}$	$1.98\times {10}^{-7}$
	$r_{\epsilon }^N$	2.01	2.05	2.00	1.69	1.07	-
	$Iter$	3	3	3	2	2	3
${10}^{-6}$	$E_{\epsilon }^N$	$8.33\times {10}^{-5}$	$2.47\times {10}^{-5}$	$5.37\times {10}^{-6}$	$1.34\times {10}^{-6}$	$3.32\times {10}^{-7}$	$8.33\times {10}^{-8}$
	$r_{\epsilon }^N$	1.74	2.21	1.99	2.02	1.99	-
	$Iter$	5	8	4	3	3	3
${10}^{-8}$	$E_{\epsilon }^N$	$9.87\times {10}^{-5}$	$2.46\times {10}^{-5}$	$5.36\times {10}^{-6}$	$1.33\times {10}^{-6}$	$3.34\times {10}^{-7}$	$8.21\times {10}^{-8}$
	$r_{\epsilon }^N$	2.01	2.20	2.01	1.99	2.02	-
	$Iter$	7	9	5	5	4	3

Table 4. Comparison of numerical results with the other methods for Example 2.

N	$\mathit{\epsilon }=2^{-12}$			$\mathit{\epsilon }=2^{-24}$
	S-Mesh [1]	Method [20]	Our Method	S-Mesh [1]	Method [20]	Our Method
64	$1.03\times {10}^{-2}$	$0.32\times {10}^{-4}$	$1.38\times {10}^{-4}$	$1.07\times {10}^{-2}$	$4.23\times {10}^{-5}$	$8.22\times {10}^{-5}$
	1.83	2.00	2.03	1.83	2.45	1.91
128	$2.89\times {10}^{-3}$	$0.79\times {10}^{-5}$	$3.38\times {10}^{-5}$	$1.02\times {10}^{-3}$	$0.77\times {10}^{-5}$	$2.18\times {10}^{-5}$
	1.88	1.73	2.10	1.88	2.01	1.84
256	$7.84\times {10}^{-4}$	$2.39\times {10}^{-6}$	$7.85\times {10}^{-6}$	$8.21\times {10}^{-4}$	$1.93\times {10}^{-6}$	$6.09\times {10}^{-6}$
	1.95	1.07	2.16	1.96	2.01	2.20
512	$2.03\times {10}^{-4}$	$1.14\times {10}^{-6}$	$1.76\times {10}^{-6}$	$2.11\times {10}^{-4}$	$0.48\times {10}^{-6}$	$1.32\times {10}^{-6}$
	1.99	1.15	1.42	1.99	2.00	2.01
1024	$5.10\times {10}^{-5}$	$5.12\times {10}^{-7}$	$6.59\times {10}^{-7}$	$5.30\times {10}^{-5}$	$1.19\times {10}^{-7}$	$3.27\times {10}^{-7}$

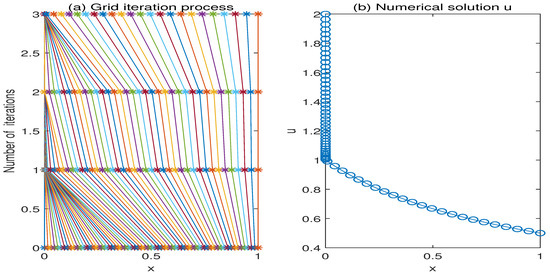
Figure 2. Grid iteration process and numerical solution with $\epsilon ={10}^{-4}$ and $N=64$ for Example 2. (a) Grid iteration process, (b) Numerical solution u.

6. Conclusions

As far as we known, most of adaptive grid methods used to solve singularly perturbed problems, which contain a first-order derivative term, are only first-order accurate. For this reason, based on the fitted finite difference scheme proposed in [1], this paper mainly discussed a second-order adaptive grid method for a singularly perturbed first-order Volterra integrodifferential equation. By using the truncation error analysis of the presented discretization scheme (10), we constructed a suitable monitor function, which is used to design an adaptive grid. It is shown from the convergence analysis that our presented adaptive method is uniformly convergent and independent of the perturbation parameter in the discrete maximum norm.